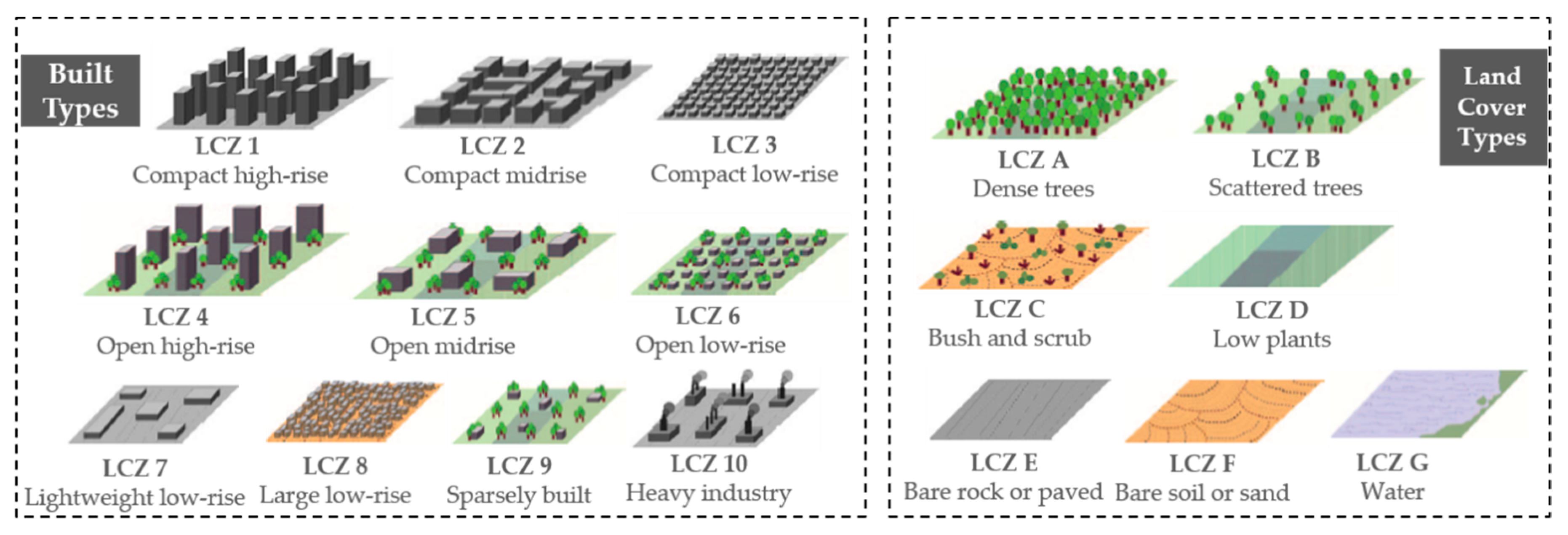
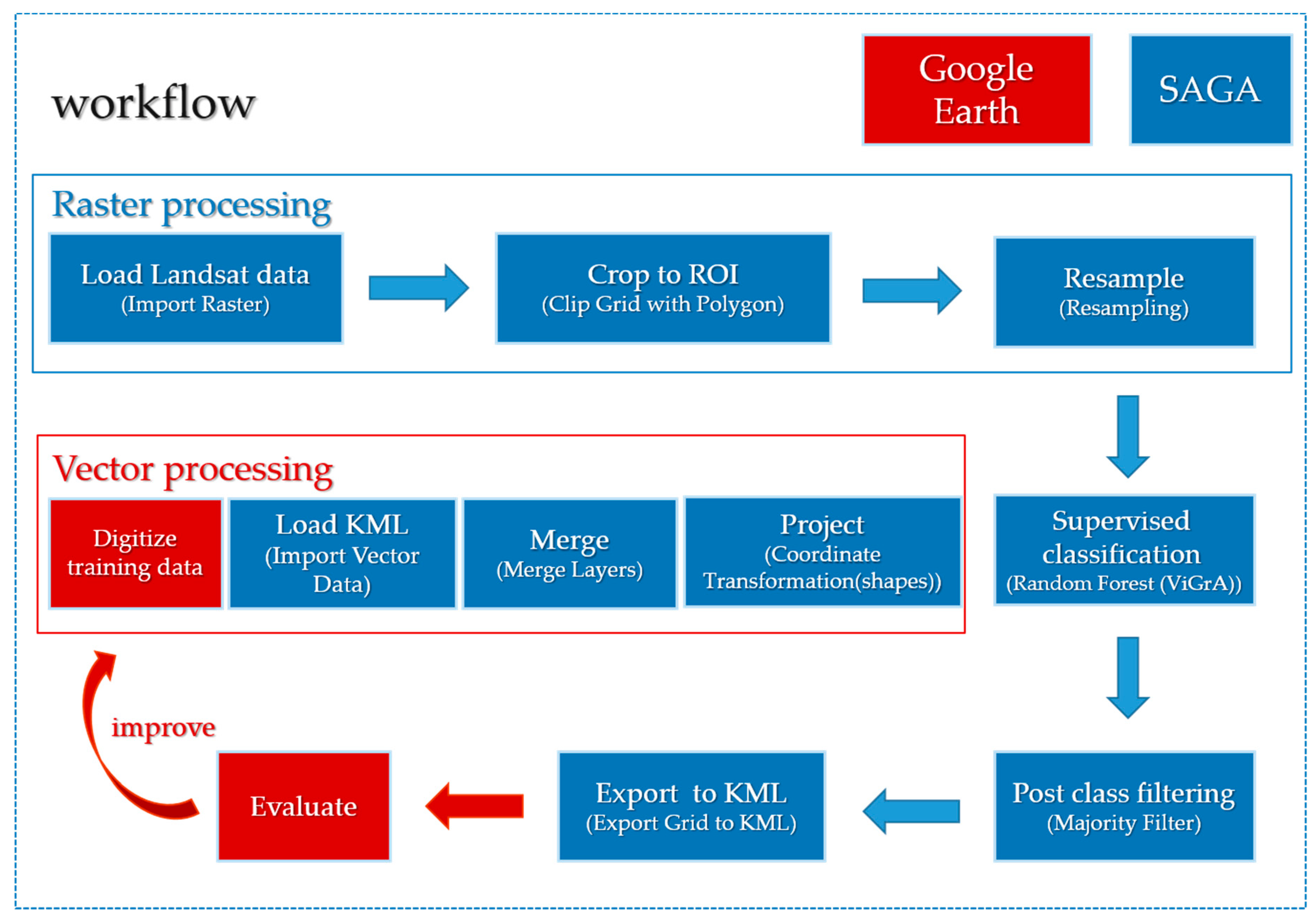
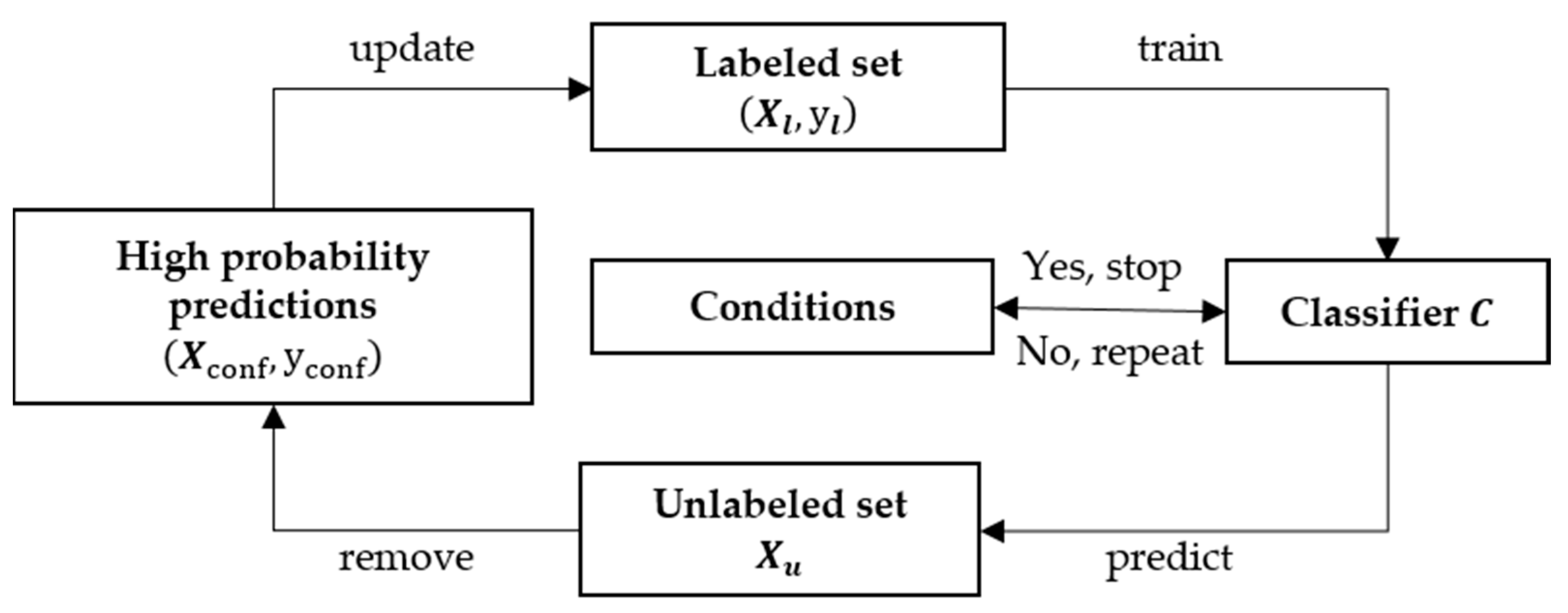
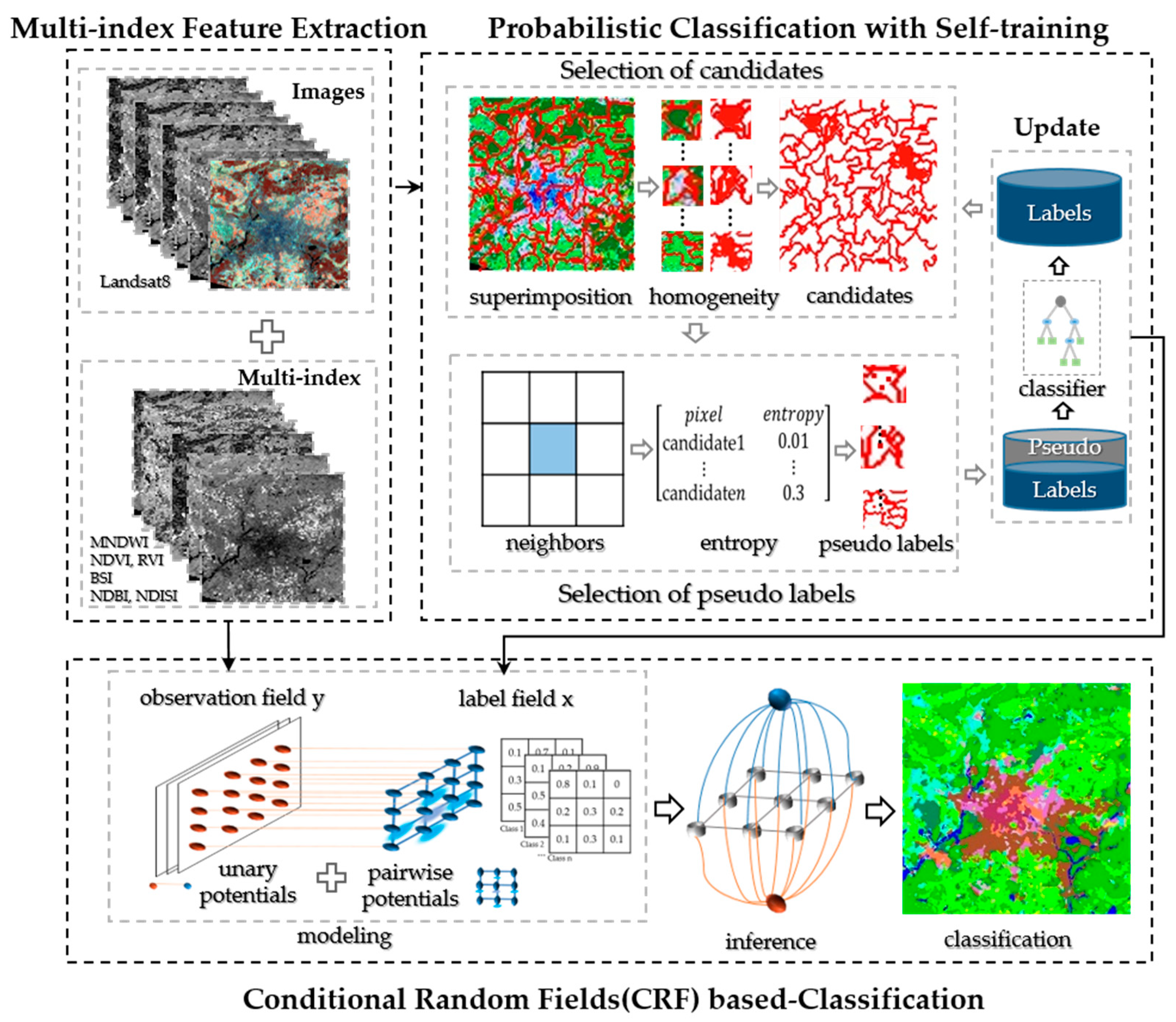
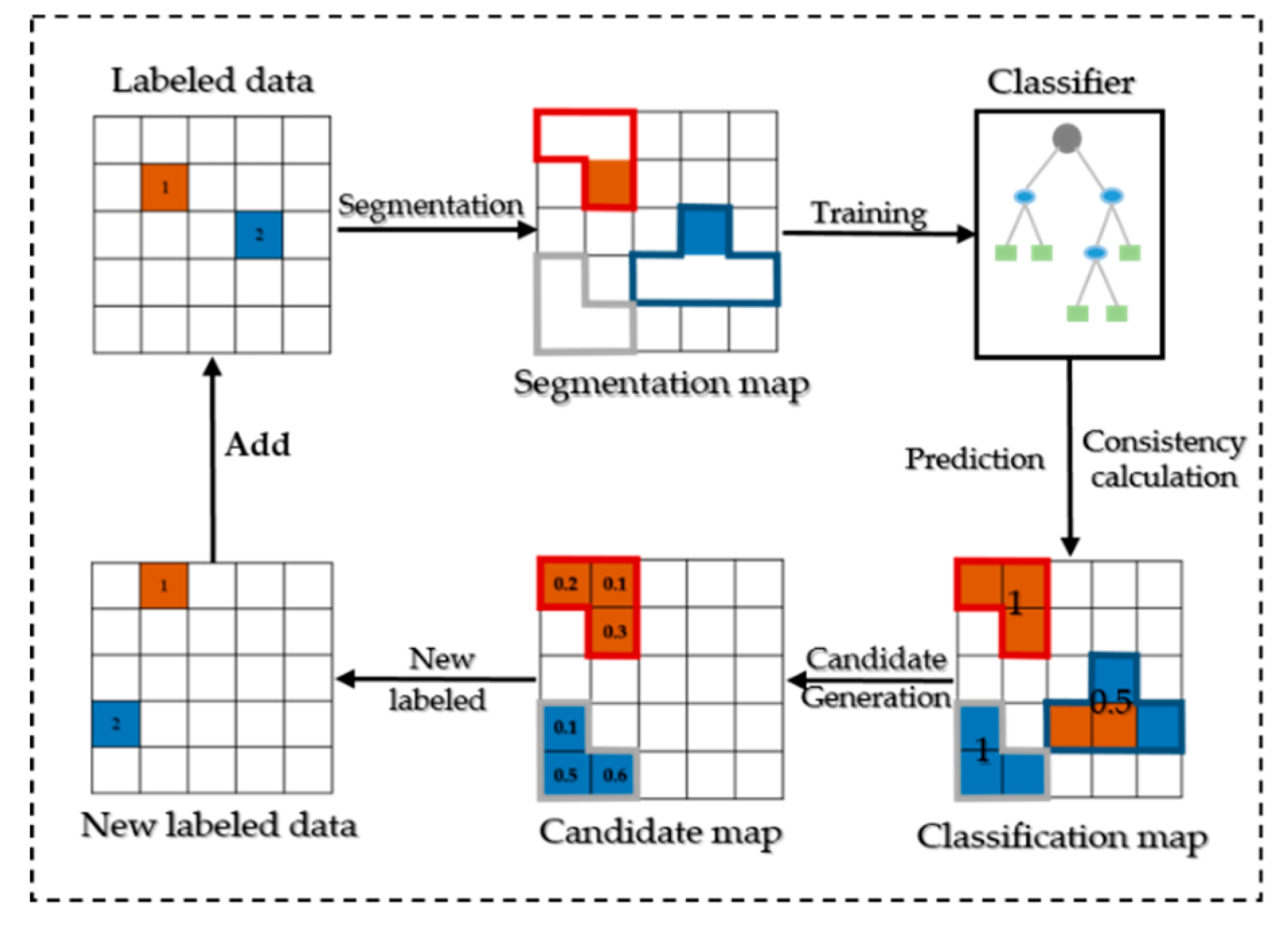
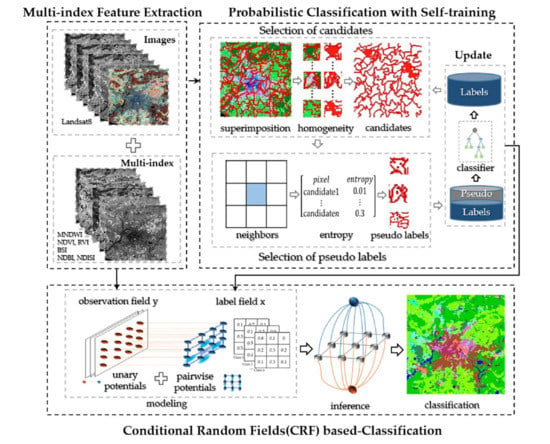
3.2.1. Berlin Experiments
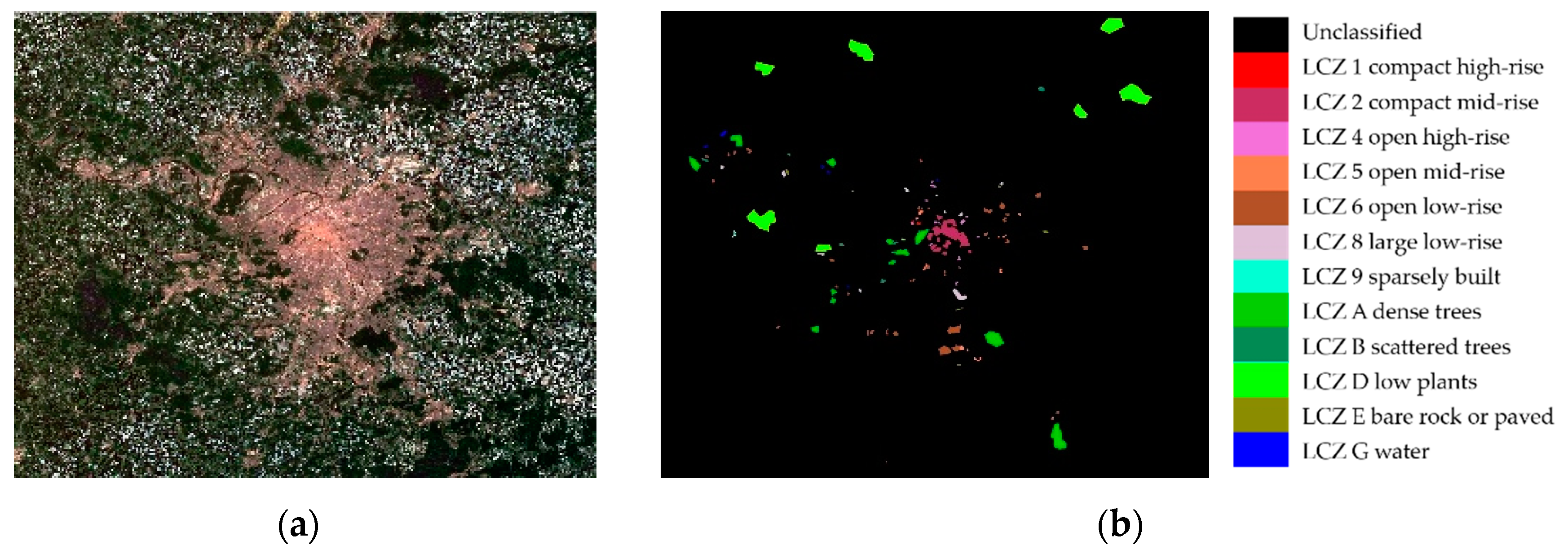
As a city with high attention to urban planning, Berlin in Germany has a balanced urban spatial structure, making itself a model for urban studies. The LCZ types in Berlin are six LCZ built types (i.e., LCZ 2 compact mid-rise, LCZ 4 open high-rise, LCZ 5 open mid-rise, LCZ 6 open low-rise, LCZ 8 large low-rise, and LCZ 9 sparsely built) and six LCZ natural types (i.e., LCZ A dense trees, LCZ B scattered trees, LCZ C bush or scrub, LCZ D low plants, LCZ F bare soil or sand, and LCZ G water). The first experiment was conducted using two down-sampled Landsat 8 images with a 100-m spatial resolution from 2017DFC, which were acquired on 25th March and 10th April 2014. The experimental images contained 666 × 643 pixels, with seven multi-spectral bands (1–7) and two thermal infrared bands (10–11). A false-color image consisting of three bands (Red, green and blue (RGB)) is shown in
Figure 6a. The spatial distribution of the corresponding labels is presented in
Figure 6b, and the number of labeled samples for each type is given in
Table 1. In addition, the training data were randomly sampled from the ground truth for each class.
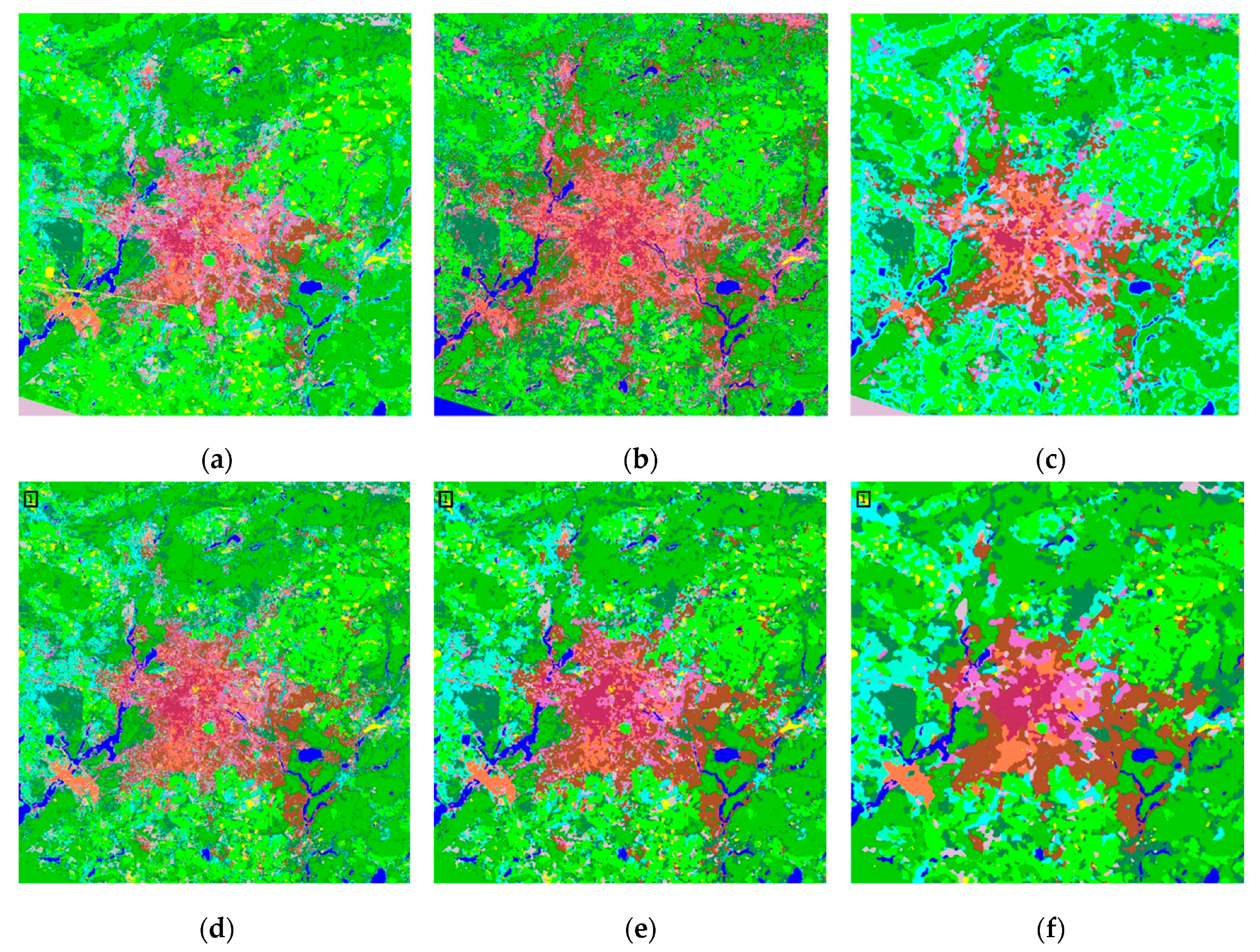
The LCZ classification maps obtained by the different frameworks (i.e., NB, SVM, CI-WUDAPT, RF, RF+MJ(WUDAPT), RF+CRF, RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)) for the Berlin images are displayed in
Figure 7a–i, respectively. As the figures show, classification without spatial-contextual information, i.e., RF, presents lots of salt-and-pepper noise. After inputting the spatial constraints from the majority-filter-based spatial smoothing, the other LCZ prediction using the RF+MJ(WUDAPT) workflow produces a smoother LCZ mapping result with a better visual effect. However, the majority filter only considers the narrow neighborhood information given by the predictions, and the small, isolated noise areas remain to be solved. The RF+CRF method generates a much better performance in mitigating the above problem. Nevertheless, misclassification arises from the insufficient training samples, as in area 1 of
Figure 7d, where the LCZ F bare soil or sand (yellow) is supposed to be LCZ D low plant (green), which also confuses the CRF modeling, causing the area 1 of
Figure 7f (i.e., RF+CRF) to be mislabeled as LCZ F bare soil or sand. Considering this, the semi-supervised self-training methods were then applied to improve the initial predictions. Supported by the enriched training samples from the pseudo-labels, the RF+ST method provides a cleaner map than RF and the comparison between the results of RF+ST+MJ and RF+MJ also reveals the same case. Moreover, area 1 of
Figure 7g,h is corrected to LCZ D low plants (green). The RF+ST+CRF(SCSF) workflow exhibits a competitive performance in solving the misclassified noise, with the help of the use of unlabeled data through the improved self-training method and the unified spatial-contextual information-based classification through CRF. Furthermore, results of NB and SVM shown in
Figure 7a,b present relatively poor performance with lots of fragile segments. For the prediction of CI-WUDAPT, the smoother boundaries among different classes are presented after the extraction of regional spatial-contextual from features, while heavy misclassified phenomena appeared with the limited training samples (10 samples per class), such as massive LCZ G water (blue) being obviously misclassified to LCZ C bush or scrub (light blue). From the aspect of visual performance, the proposed SCSF delivers the better solution in handling the fragile segments and misclassified areas, which proves the superior capability of the SCSF.
In addition,
Table 2 provides the pairwise comparison between the nine methods (i.e., NB, SVM, CI-WUDAPT, RF, RF+MJ(WUDAPT), RF+CRF, RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)) using McNemar’s test. The value of McNemar’s test indicates the difference between the two results of classifiers, while if the value is greater than
, it is considered a significant difference. Furthermore, the greater the value, the more significant the difference. Data shows that all the values are greater than
, especially for the method between SCSF and SVM, which has a considerably big value, 2970.46, showing the significant difference among two approaches. Moreover, significant differences among every two methods are provided from the statistical aspect in Berlin.
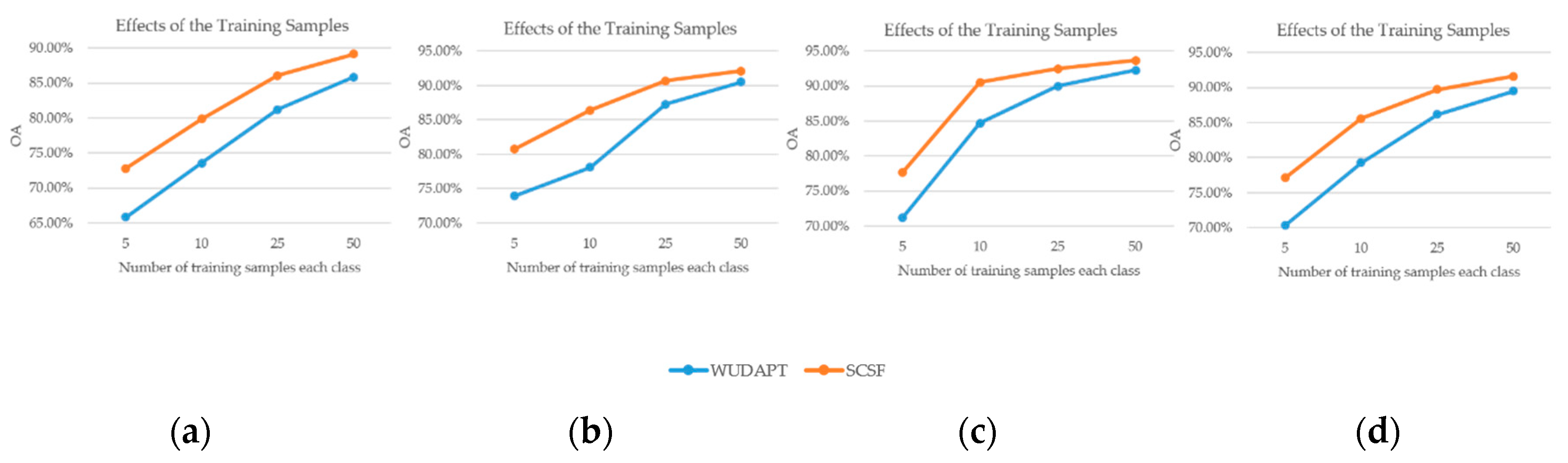
To better assess the effectiveness of the proposed SCSF method, a quantitative comparison of the different methods (i.e., NB, SVM, CI-WUDAPT, RF, RF+MJ(WUDAPT), RF+CRF, RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)) is provided in
Table 3. This shows that the classification workflows considering spatial-contextual information (i.e., CI-WUDAPT, RF+MJ(WUDAPT), RF+CRF, RF+ST+MJ, and RF+ST+CRF(SCSF)) give a great improvement of nearly 5–18% in OA over the single classification results (i.e., NB, SVM, RF, and RF+ST) and an improvement of 0.06–0.2 in Kappa, proving the significance of the spatial-contextual information for LCZ mapping. Furthermore, the CRF-based classification workflows (i.e., RF+CRF and RF+ST+CRF(SCSF)) deliver an enhancement of approximately 4% in terms of OA and 0.05 in Kappa, compared with the independent majority-filter-based approaches (i.e., RF+MJ and RF+ST+MJ), which means that simultaneously modeling the correlation between labels and samples, in addition to the spatial relationship among samples, is very helpful. In addition, the accuracies of the self-training-based semi-supervised methods (i.e., RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)) are higher than those of the supervised methods (i.e., RF, RF+MJ(WUDAPT), and RF+CRF), with improvements of nearly 2% and 0.2 in OA and Kappa, respectively, demonstrating the effectiveness of the generated pseudo-labels. The SVM classifier generates the worst accuracy with 18% lower than the SCSF in OA, which may be optimized through complex adjustment of its parameters. The CI-WUDAPT gives relatively high accuracy among the supervised methods; however, there is still a gap of 5% OA and 0.06 Kappa compared with the SCSF. The proposed RF+ST+CRF(SCSF) workflow shows the best quantitative performance among all the compared methods with only 10 labeled samples for each class, and the accuracies of 79.83% and 0.77 for OA and Kappa are also acceptable. However, the scattered LCZ types (i.e., LCZ 4 open high-rise, LCZ B scattered tree, and LCZ C bush or scrub) present inferior accuracies with semi-supervised methods, showing that the spatial-contextual information is insufficiently obtained from these LCZ types, which reduce the accuracies.
3.2.2. São Paulo Experiments
The second experimental area is São Paulo, Brazil, a city in the southern hemisphere with a more diverse urban form. The LCZ types in São Paulo cover almost all the built and natural classes except for LCZ 7 lightweight low-rise and LCZ C bush or scrub. Two cloudless Landsat-8 images from 2017DFC acquired on 8th February 2014 and 23rd September 2015 constituted the second experimental dataset. As in the first experiment, the images were down-sampled to a 100-m spatial resolution with a 1067 × 871 pixel dimension. Nine bands (i.e., bands 1–7 and 10–11) covering the infrared to visible spectrum were prepared. The RGB (i.e., bands 4, 3, 2) false-color image and the spatial distribution of the labeled data are shown in
Figure 8a,b, respectively. Information about the class numbers is provided in
Table 4.
The LCZ maps produced by the different approaches (i.e., NB, SVM, CI-WUDAPT, RF, RF+MJ(WUDAPT), RF+CRF, RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)) are shown in
Figure 9a–i. Differing from Berlin, much more salt-and-pepper noise appears in São Paulo with the RF-based classification (i.e., RF), which shows obvious changes after the majority-filter-based spatial smoothing (i.e., RF+MJ) and the CRF-based classification (i.e., RF+CRF). Although the prediction of RF+CRF presents much smoother class boundaries than the first two maps, the provided low-quality probabilistic map, which directly influences the modeling of the potential function, still brings a huge amount of misclassification. In particular, area 1 (green) of
Figure 9f is supposed to be water, while the mislabeled spatial context confuses the CRF model, and the blue water region becomes green vegetation. Area 2 of
Figure 9f is also heavily influenced by its surrounding mislabeled data, where LCZ 3 compact low-rise (rose red) is misclassified as LCZ 2 compact mid-rise (dark red). To relieve the above phenomena, the improved self-training-based classification (i.e., RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)) was further adopted. Further improvements are apparent in
Figure 9g–i with the improved self-training-based classification workflows (i.e., RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)), and the appearance of scattered noise is much relieved when compared with the supervised results (i.e., RF, RF+MJ(WUDAPT), and RF+CRF). In particular, areas 1–2 of
Figure 9i are accurately predicted to be real LCZ types, i.e., LCZ G water (blue) and LCZ 3 compact low-rise (rose red). The LCZ map generated by the proposed SCSF method provides not only an apparent visual improvement in better boundaries than the non-spatial-contextual information classification workflow (i.e., RF+ST) but also a cleaner and more accurate prediction than the result without self-training (i.e., RF+CRF). Moreover, the classifications of the NB, SVM, and CI-WUDAPT deliver quite different performances from that of SCSF. There are lots of misclassified noises that appear in
Figure 9a,b and large misclassified areas stand out in
Figure 9c, which prove that the visual performance of the SCSF is better than the previous researches.
Moreover, McNemar’s test between different methods (i.e., NB, SVM, CI-WUDAPT, RF, RF+MJ(WUDAPT), RF+CRF, RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)) is shown in
Table 5. All the values obtained among pairwise classification workflow are much greater than
, which means significant differences were found for the compared methods. The value of McNemar’s test between NB and SCSF is the biggest, indicating that the proposed workflow gives a significant statistical improvement compared with the classification of NB.
A quantitative report of the accuracies of the different methods (i.e., NB, SVM, CI-WUDAPT, RF, RF+MJ(WUDAPT), RF+CRF, RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)) is given in
Table 6. To evaluate the ability of the spatial-contextual information, the accuracies of RF and RF+ST serve as a baseline in the main part of the experiments and are compared with other workflows (i.e., RF+MJ(WUDAPT), RF+CRF, RF+ST+MJ, and RF+ST+CRF(SCSF)). The accuracies of the majority-filter-based spatial smoothing methods (i.e., RF+MJ(WUDAPT) and RF+ST+MJ) present an improvement of about 7% in OA and 0.07–0.08 in Kappa, while the CRF-based methods (i.e., RF+CRF and RF+ST+CRF(SCSF)) show a great improvement of nearly 12% in OA and 0.13–0.14 in Kappa. In addition, the generation of pseudo-labels from the self-training method provides an improvement of 3–4% in OA and 0.03–0.04 in Kappa for the supervised workflows (i.e., RF, RF+MJ(WUDAPT), and RF+CRF) and the corresponding semi-supervised approaches (i.e., RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)), which demonstrates the effectiveness of the proposed strategy. Moreover, the NB classifier presents the worst performance with just 65.27% OA and 0.6 Kappa, which may prove that this kind of method is unsuitable for a city with diverse urban form in the case of limited samples. With the direct utilization of the spatial-contextual information, CI-WUDAPT shows 5-13% improvement in OA with the traditional approaches (i.e., NB, and SVM); however, the proposed SCSF method delivers a more superior performance in terms of OA and Kappa, with 86.4% and 0.84, respectively. Nevertheless, the LCZ types (i.e., LCZ 2 compact mid-rise, LCZ 4 open high-rise, LCZ 5 open mid-rise, LCZ B scattered trees, LCZ D low plants, LCZ E bare rock or paved, and LCZ F bare soil or sand) with relatively small testing samples present poor performance, which can be explained by the testing samples in São Paulo being clustered in the center areas and unable to reflect well the comprehensive condition.
3.2.3. Paris Experiments
The city of Paris in France was selected as the last experimental study area to assess the performance of the proposed SCSF method in a high-density city. The LCZ types are seven built types (i.e., LCZ 1 compact high-rise, LCZ 2 compact mid-rise, LCZ 4 open high-rise, LCZ 5 open mid-rise, LCZ 6 open low-rise, LCZ 8 large low-rise, and LCZ 9 sparsely built) and five natural types ( i.e., LCZ A dense trees, LCZ B scattered trees, LCZ D low plants, LCZ E bare rock or paved, and LCZ G water), revealing the multiformity of the urban region in Paris. The third experimental dataset comprised two Landsat 8 images of 1160 × 988 pixels provided by 2017DFC individually acquired on 19th May 2014 and 27th September 2015. The spatial resolution was again equal to 100 m after down-sampling, and the band information was the same as before, i.e., bands 1–7 and 10–11, amounting to nine channels.
Figure 10a shows the false-color RGB image (i.e., bands 4,3,2), and an overview of the corresponding types is presented in
Figure 10b. The sample numbers of each class are listed in
Table 7.
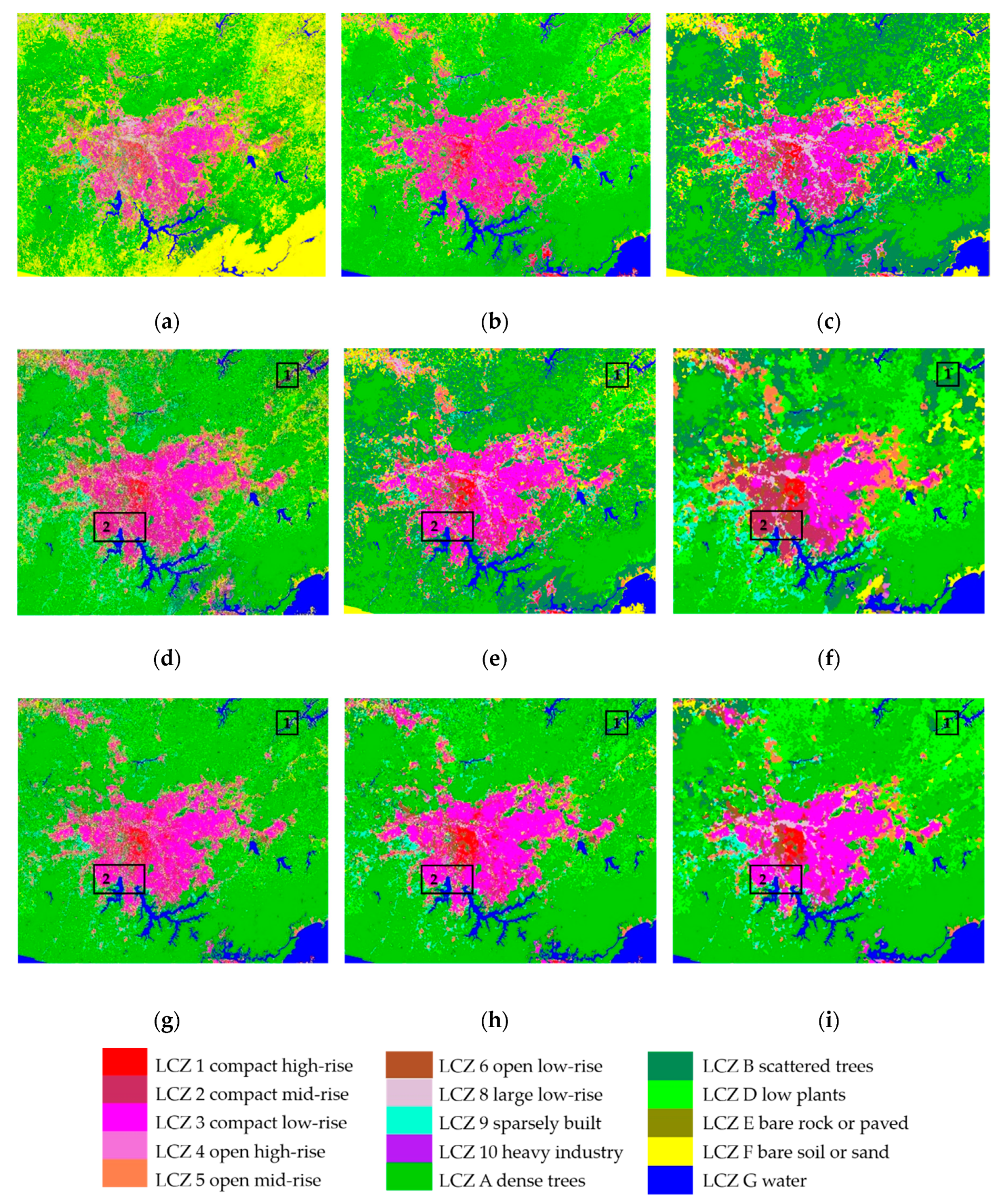
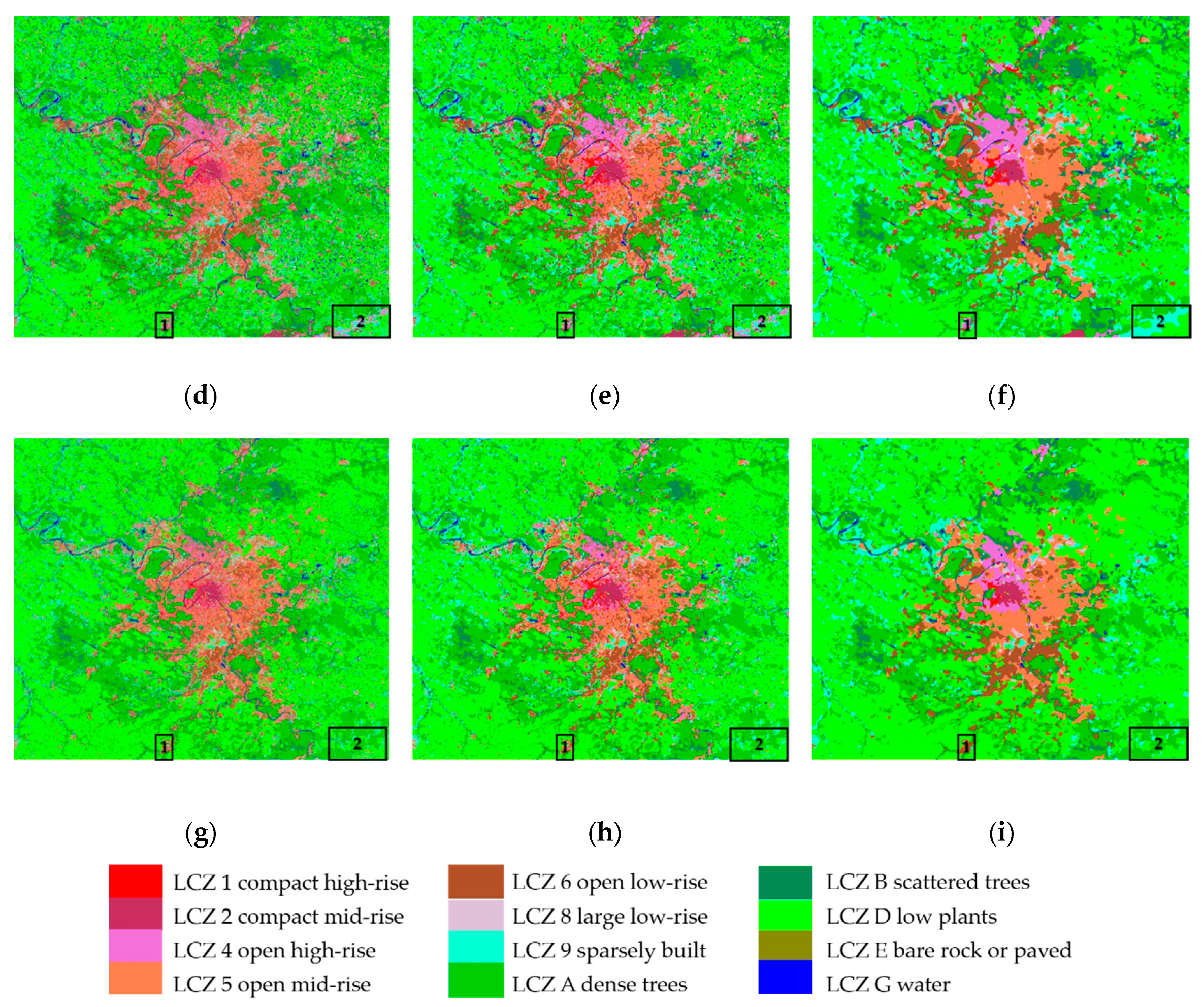
The performance of the different methods (i.e., NB, SVM, CI-WUDAPT, RF, RF+MJ(WUDAPT), RF+CRF, RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)) is shown in
Figure 10a–i. The visual appearance of the salt-and-pepper noise in Paris seems more serious than for Berlin and São Paulo, while the variation of the categories is moderate. Compared with the results in the second column (i.e., RF and RF+ST), the other classification workflows (i.e., RF+MJ(WUDAPT), RF+CRF, RF+ST+MJ, and RF+ST+CRF(SCSF)) show an improvement in alleviating the noise issue with the further information from the spatial context. However, as in the São Paulo experiments, confusion appears in the results of RF+CRF, where the LCZ 4 open high-rise (rose red) in area 1 of
Figure 11f is supposed to be LCZ 6 open low-rise (brown) and the LCZ C bush or scrub (light blue) in area 2 of
Figure 11f is supposed to be LCZ A dense trees (green), which may have been caused by the insufficient training samples. The LCZ maps in the third row are the improved approaches (i.e., RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)), and supported by the enrichment of the training data, the confused pixels decrease a lot from the beginning of the classification, compared with
Figure 11d,f, which proves the significance of the training information. In particular, the misclassified areas 1–2 of
Figure 11f are corrected to the real types, i.e., LCZ 6 open low-rise (brown) and LCZ A dense trees (green). The classifications of NB, SVM, and CI-WUDAPT in Paris are better than the above cities, which have less evident misclassified segments. However, the LCZ G water nearly disappears in
Figure 11a and fragile noises or areas still stand out in
Figure 11b,c. In addition, the developed SCSF workflow produces the best visual performance, with the elimination of the isolated pixels and the small, isolated areas.
Moreover, in order to give the statistical comparisons, McNemar’s values between the abovementioned methods (i.e., NB, SVM, CI-WUDAPT, RF, RF+MJ(WUDAPT), RF+CRF, RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)) are given in
Table 8. Similar to the other two cities, all the values of McNemar’s test in Paris are also greater than
, while the value between RF+CRF and SCSF (35.66) is relatively small compared with the RF and RF+CRF methods (1854.59) and the RF and SCSF methods (1854.51), showing that, although the semi-supervised approach gives some improvements in Paris, the spatial-contextual information-based CRF methods perform with more statistical significance.
In terms of the quantitative performance shown in
Table 9, the experimental accuracies for Paris are much better than expected and reach the highest level among all three experiments. As in the previous experiments, the accuracies present different improvements with the assistance of the spatial context and the use of unlabeled data. To be specific, the result of the proposed SCSF method shows an improvement of about 7% in OA and 0.1 in Kappa compared with RF+ST; however, this is not apparent in the comparison with RF+ST+MJ and RF+CRF. The explanation for this is that, when the initial classification is already acceptable, the performance improvement of the proposed approach may not be that significant, since SCSF is aimed at solving the unreliable probability issue. Moreover, the accuracies of SCSF prevail over those of NB, SVM, and CI-WUDAPT, presenting about 6–16% and 0.08–0.2 improvement in OA and Kappa, respectively. In particular, LCZ types with an aggregation effect, such as LCZ D low plants, are obviously improved after fusing the spatial-contextual information. In contrast, the accuracies of some LCZ types which have dispersed spatial distribution and relatively small testing samples (i.e., LCZ 9 sparsely built, LCZ B scattered trees, and LCZ E bare rock or paved) present a decreased trend. Reasons can be explained as follows: (1) the SCSF is a spatial-contextual information-based method and, when the LCZ types are scattered or sparse, the spatial-contextual information is provided insufficiently, which may degrade the accuracies of these LCZ types; (2) the small number of testing samples for these LCZ types are unable to credibly evaluate the real condition.
In brief summary, for the main experimental part, the proposed SCSF gives the best performance in all three study areas compared with other five methods (i.e., RF, RF+MJ(WUDAPT), RF+CRF, RF+ST, and RF+ST+MJ) in terms of OA and Kappa, showing that the spatial-contextual information-based self-training classification framework for LCZs is undoubtedly effective. The values from McNemar’s test between the proposed SCSF with others are considerably large, which represents the significant differences from the statistical aspect. Moreover, the methods considering the spatial-contextual information (i.e., RF+MJ (WUDAPT), RF+CRF, RF+ST+MJ, and RF+ST+CRF(SCSF)) performed better than the other approaches (i.e., RF, and RF+ST), especially the CRF-based methods (i.e., RF+CRF, and RF+ST+CRF(SCSF)), which produce the best accuracies in OA and Kappa. Moreover, the semi-supervised approaches (i.e., RF+ST, RF+ST+MJ, and RF+ST+CRF(SCSF)) in the three experiments provide different improvements compared with the supervised methods (i.e., RF, RF+MJ, and RF+MJ (WUDAPT)).
Furthermore, the performances of the different methods (i.e., NB, SVM, and CI-WUDAPT) in three study areas are also considered to compare with the proposed SCSF, and the NB and SVM present relatively poor performances with many salt-and-pepper noises and misclassified areas. Moreover, the spatial-contextual information-based approaches (i.e., CI-WUDAPT, and SCSF) generate smoother predictions and SCSF delivers the best visual performance. Compared with the traditional machine learning classifier (i.e., NB and SVM), the proposed SCSF gives improvements of 10.65%–21.23% in OA with 0.13–0.24 in Kappa and 13.19%–18.58% in OA with 0.16–0.2 in Kappa, respectively. For CI-WUDAPT, the SCSF also outperforms it with 5.34%–7.75% in OA and 0.06–0.09 in Kappa, which proves the effectiveness of SCSF with the consideration of spatial-contextual information and self-training method.