Abstract
Land cover change (LCC) is typically characterized by infrequent changes over space and time. Data-driven methods such as deep learning (DL) approaches have proven effective in many domains for predictive and classification tasks. When applied to geospatial data, sequential DL methods such as long short-term memory (LSTM) have yielded promising results in remote sensing and GIScience studies. However, the characteristics of geospatial datasets selected for use with these methods have demonstrated important implications on method performance. The number of data layers available, the rate of LCC, and inherent errors resulting from classification procedures are expected to influence model performance. Yet, it is unknown how these can affect compatibility with the LSTM method. As such, the main objective of this study is to explore the capacity of LSTM to forecast patterns that have emerged from LCC dynamics given varying temporal resolutions, persistent land cover classes, and auxiliary data layers pertaining to classification confidence. Stacked LSTM modeling approaches are applied to 17-year MODIS land cover datasets focused on the province of British Columbia, Canada. This geospatial data is reclassified to four major land cover (LC) classes during pre-processing procedures. The evaluation considers the dataset at variable temporal resolutions to demonstrate the significance of geospatial data characteristics on LSTM method performance in several scenarios. Results indicate that LSTM can be utilized for forecasting LCC patterns when there are few limitations on temporal intervals of the datasets provided. Likewise, this study demonstrates improved performance measures when there are classes that do not change. Furthermore, providing classification confidence data as ancillary input also demonstrated improved results when the number of timesteps or temporal resolution is limited. This study contributes to future applications of DL and LSTM methods for forecasting LCC.
1. Introduction
Land cover changes (LCCs) are typically slow changes occurring across Earth’s surface over long periods of time [1]. The aggregated effects of changes have global implications, contributing to local, regional, and global climate changes, loss of biodiversity, and, ultimately, disturbing the capacity of systems to sustain people [2,3]. Therefore, analyzing and representing LCC processes are important tasks in various disciplines such as geography [4], hydrology [5], and climatology [6].
LCC has been previously assessed at local, regional, and global extents [7]. LCC has also been linked to changes in precipitation, air temperature, and ecology at local and regional scales. Furthermore, LCC studies conducted at a global scale have assessed the cumulative implications of land change processes such as urban growth and deforestation [8]. Addressing LCC from a top-down perspective, data-driven modeling tactics enable the extraction and detections of patterns that have resulted from local interactions [9]. Top-down approaches are primarily focused on overall patterns that result from processes, utilizing satellite and aggregated data sources such as Census data to obtain rates of land change over time.
Previous studies have introduced and assessed methodologies for forecasting LCC. Such methods have included cellular, agent-based, data-driven, and hybrid modeling approaches [10]. In particular, data-driven methods including machine learning (ML) approaches have been increasingly considered for LCC forecasting [11]. The goal of data-driven methodologies is for models to “learn” patterns existing in datasets while reducing the manual operations required to utilize the method [12]. Applied to LC datasets, the aim is to use these automated, statistical methods to identify and analyze spatial patterns that have resulted from underlying processes of LCC over time. ML methods employed in LC simulations and assessments have previously included neural networks (NNs) [13], decision trees (DTs), and support vector machines (SVMs) [14].
While ML approaches have demonstrated promising results for forecasting and detecting LCC, challenges include the infrequence of LC changes and obtaining appropriate labeled training datasets [15]. Recent advances in a subfield of ML called deep learning (DL) have demonstrated the capacity of these increasingly complex models. Such models exhibit aptness for learning more complicated relationships existing in training datasets while simultaneously achieving substantial improvements in predictive performance measures. DL approaches such as recurrent neural networks (RNNs) are best suited for sequential or timeseries data [16]. An improved RNN architecture called long short-term memory (LSTM) has garnered increased attention for geospatial applications, with demonstrated aptitude to forecast LCC [17] and to classify LC [18] by leveraging patterns obtained from timeseries data.
LSTM approaches have been previously utilized for simulating patterns resulting from dynamic geospatial systems [19,20,21,22]. The method has been leveraged to learn LC changes in transfer learning applications [19]. It proved effective in learning changes in binary and multi-class LC datasets created for three variable-sized study areas focused on different cities in China. LSTM has also been employed to reveal natural disturbances such as fires and floods, or human disturbances such as deforestation and urban growth, using satellite image timeseries datasets from a moderate-resolution imaging spectroradiometer (MODIS) data product [20]. LSTM has also been effectively utilized in short- and long-term forecasts of sea surface temperature [21]. Using geographic datasets pertaining to weather, pollution, and influenza spread, LSTM has been successfully applied in prediction of influenza propagation in the state of Georgia in the United States as well [22].
Though prior research has made evident that LSTM is useful for geospatial applications, the implications of varying temporal resolution have not yet been applied to real-world LC datasets. The goal of this study is to evaluate the effectiveness of LSTM networks for LCC forecasting considering actual and hybrid datasets, where hybrid datasets are created by integrating an actual dataset with a hypothetical persistent class. Considering variable geospatial properties such as temporal resolution and the number of data layers obtainable to train LSTM models, the aim is to quantify the repercussions of changing temporal resolution of LC datasets on quality of forecasts produced. Real-world LC datasets feature inevitable classification errors, further impacting method performance. In addition to changing temporal resolution, this study intends to demonstrate the impacts of persistent LC classes and to determine if improved performance can be obtained using available classification confidence layers.
However, the effectiveness of these methods to forecast or classify change is impacted by the characteristics of the geospatial dataset selected. In this research study, a sensitivity analysis is used to explore LSTM response to changing geospatial data characteristics to evaluate the impact of increasing temporal resolution. It is hypothesized that method performance will be impeded by coarser temporal resolutions. Thus, the main objective of this study is to evaluate the effectiveness of data-driven approaches such as LSTM for LCC applications where the amount of change is typically small or occurring at slow rates over long periods of time. Additionally, this study demonstrates the implications of the characteristics of geospatial datasets selected for use with this method, namely temporal resolution and influence of persistent classes. Such an assessment of the method’s sensitivity to temporal resolution has not yet been conducted in the presence of classification errors that exist in real-world datasets.
It is expected that results will demonstrate that coarser temporal resolutions will have negative repercussions on method performance. Likewise, it is expected that erroneous values due to classification procedures will impact the results. To further observe the effects of potentially inaccurate values, hybrid data scenarios are also created by adapting the original LC dataset to maintain one persistent class across all data layers. The classification confidence layer associated with the original LC data product will be incorporated to a secondary modeling approach applied to scenarios involving real-world and hybrid datasets. By including this ancillary data layer, the aim is to reduce epistemic imperfection and determine if improvements can be obtained by indicating potential at each cell to contain erroneous values [23]. Thus, the three main objectives of this study are; (1) to evaluate the sensitivity of the method to varying temporal resolutions, (2) to assess the implications of persistent LC classes in hybrid scenarios, and (3) to examine potential improvements by providing classification confidence layers as model input in scenarios utilizing real-world and hybrid datasets.
2. Methods
2.1. Recurrent Neural Networks
RNNs were introduced as a variant of traditional NN modeling approaches, devised for sequential data [16]. To do this, a recurrent connection was added to traditional neurons, allowing information from previous elements in timeseries data to be propagated when weight updates occur for subsequent elements observed by the network. The recurrent connection allowed information to be propagated through the entire timeseries input, with weights being updated with respect to the entire timeseries input. However, a major problem arose when these networks were utilized to learn dependencies across long input sequences. For instance, information pertaining to critical features from early in a sequence could not be connected to data elements occurring later in the sequence. This phenomenon ensues from the vanishing (or exploding) gradient problem [24]. This implies that network weights tend toward either very small (vanishing) or very large (exploding) values, negating the ability of the network to learn important information as weight updates become infinitesimal or massive.
Long Short-Term Memory
LSTM is an improved variation of the traditional RNN architecture [16]. With internal memory cells and gating functions controlling the propagation of information through a unit, LSTMs have proven capable in mitigating the effects of the vanishing gradient problem that was detrimental to earlier RNN implementations [25]. The input gate (it), forget gate (ft), output gate (ot), and input modulation gate (gt) control the propagation of new information in, within, or out of the unit to be considered with the next element in the input sequence (Figure 1). While other LSTM variants exist, it has been determined in large-scale studies that the standard LSTM architecture performance remains most effective [26]. The following equations have been obtained from Donahue et al. [27].
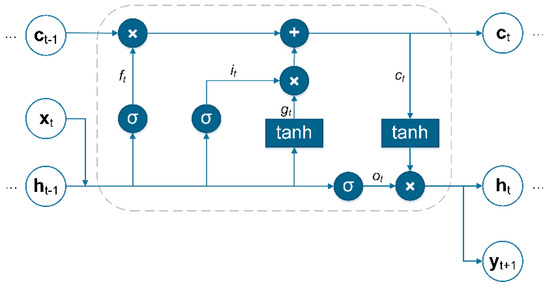
Figure 1.
An long short-term memory (LSTM) unit (Figure adapted from [28] and [29]).
When an input sequence is provided, (x0, x1, …, xt−1, xt), a hidden state, ht−1, is either initialized at the start of the sequence or propagated from a computation considering a previous input sequence element. The amount of data from the next element in the input sequence, xt, and how much of the hidden state from the previous timestep, ht−1, should be committed to the internal memory cell ct is determined by the input gate (it). How much information propagated through this gate is specified as follows:
where the sigmoid function () limits resulting values to the range of (0,1). Wxi and Whi are learnable weight matrix parameters and bi is a learnable bias parameter [30].
Next, a critical component of the LSTM unit is called a forget gate (ft) [25]. By using gating functions to “forget” information, this component allows the network to ignore non-critical information during training procedures [30,31]. The vector resulting from the forget gate is denoted as follows:
where the sigmoid function () limits resulting values to the range of (0,1). Wxf and Whf are learnable weight matrix parameters and bf is a learnable bias parameter.
The next component of the LSTM cell is called the output gate (ot). This mitigates the degree to which the value or state stored in the cell’s internal memory, ct, should be propagated to the new hidden state, ht, to be computed. The behavior of the output gate is represented as follows:
where Wxo and Who are learnable weight matrix parameters and b0 is a learnable bias parameter.
Utilizing a hyperbolic tangent function, the input modulation gate (gt) scales input values xt and ht before all or part of the resulting value is committed to the cell’s internal memory in (5). The output of the input modulation gate is computed as:
where Wxc and Whc are learnable weight matrix parameters and bc is a learnable bias parameter.
The cell’s internal memory is then updated, using the outputs of the forget gate (ft), the previous internal memory state (ct−1), input gate (it), and input modulation gate (gt):
where element-wise multiplication is symbolized by .
Finally, the new hidden state is computed as follows:
where ht becomes the next ht−1, and the next element in the input sequence is considered.
2.2. Study Area and Datasets
The “MODIS Terra+Aqua Combined Land Cover product” featuring global annual LC data was first obtained [32]. This dataset features 13 scientific data layers, including land cover, surface hydrology, and classification confidence layers. This dataset features 17 LC classes using the “MCD12Q1 International Geosphere-Biosphere Programme (IGBP)” classification system [33]. It features 500-m spatial resolution with data layers available annually from 2001 to 2017. Additional details regarding this dataset are shown in Table 1. The number of timesteps, temporal resolution, and numerous geospatial data layers available in the MODIS dataset motivated the selection of this data for this study, despite coarse spatial resolution inhibiting studies at smaller spatial scales. Thus, the data is further processed to consider the province of British Columbia, Canada. Located in the Pacific Northwest region, the province features diverse ecosystems including coastal forests, sub-boreal forests, and alpine tundra [34,35]. Dense coniferous forests are the most prevalent vegetation cover found in British Columbia [35].

Table 1.
Overview of original moderate-resolution imaging spectroradiometer (MODIS) land cover dataset characteristics.
First, using the Geospatial Data Abstraction Library (v2.2.4), the desired 17-class LC data layer and respective classification confidence layer were obtained and combined to create a multidimensional mosaic dataset for each timestep [36]. The raster mosaics were then extracted and re-projected to the NAD 1983 BC Environment Albers projected coordinate system with the provincial boundary of British Columbia obtained from the 2016 Canadian Census Boundary Files [37]. These operations were conducted using the data management tools available in Esri’s ArcGIS Pro (v2.4.0) and applied to both the LC and classification confidence layers [38]. When using the “Project Raster” tool available in ArcGIS Pro [39], the “Nearest Neighbor” resampling technique was used as “it is suitable for discrete data, such as land cover” [39]. The nearest neighbor resampling technique is utilized for the discrete and continuous datasets to maintain the related confidence layer data with the respective LC class for each cell [40]. Different resampling techniques including “bilinear interpolation” and “cubic convolution” are only relevant for continuous datasets [40].
Classes are aggregated to form four LC classes to improve model performance and to reduce computation time. For this study, the 17 available LC classes have been aggregated to forest, anthropogenic areas, non-forest areas, and water as presented in Table 2. This reclassification procedure was also conducted in Esri’s ArcGIS Pro [38]. The new aggregated class labels were named as per [42]. The aggregated “forest” class includes areas with forest cover greater than 60%, decided due to the predominant vegetation type in the province being coniferous trees [35]. Datasets were subsequently resampled to 1 km spatial resolution to reduce the computation time required. Confidence data layers have been processed to this spatial resolution as well, featuring continuous percentage values at each cell (Figure 2).

Table 2.
Original LC classes from [33] used to produce four aggregate LC classes.
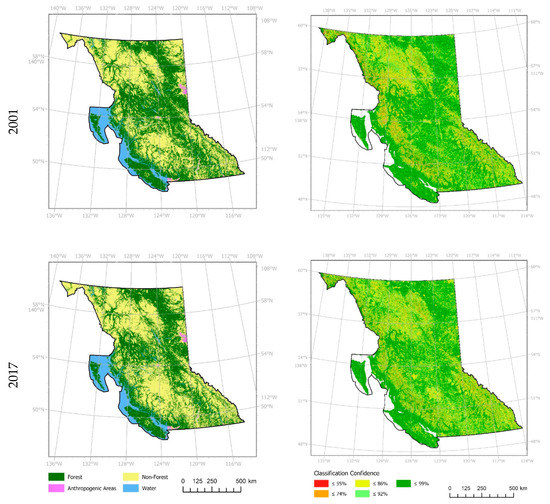
Figure 2.
Land cover maps for British Columbia generated using actual data for years 2001 and 2017 are shown on the left. Corresponding classification confidence maps for years 2001 and 2017 are shown on the right.
For the purpose of investigating the performance of the LSTM method given a persistent class, a hybrid dataset has been created. To create the hybrid dataset, the actual LC data is amalgamated with a hypothetical persistent water class used for persistent water dataset experiments. The water class has been chosen to become a persistent class given the observed fluctuation of its boundaries through all data layers that potentially are due to classification errors. For example, the number of cells denoted as water abruptly changed from 90,963 to 94,290 between 2016 to 2017 (Figure 3). To make the water class persistent through time, all water cells present in the study area from 2002 to 2017 were converted to “No Data.” Next, the cells containing water in the study area in 2001 were overlaid to the same location from 2001 through 2017. Cells that were occupied by water in 2002 to 2017 that were not water cells in 2001 remain “No Data” and are thus excluded in the model evaluation procedure. These procedures were enabled by reading data using the Geospatial Data Abstraction Library and modifying the data programmatically using the Python programming language (v3.6.5) [43].
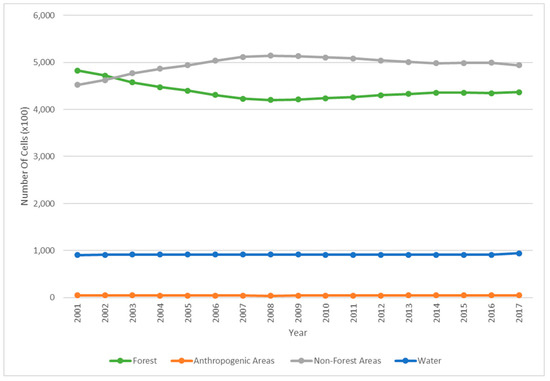
Figure 3.
Number of cells composing each land cover class per year in the study area covering British Columbia, Canada from 2001 to 2017.
2.3. Training and Testing Procedures
Following the data preparation procedures, datasets must be further processed to create training and testing datasets for use with the LSTM method. Input sequences composing the training and testing datasets are created using a moving-window approach [20]. Training sets are thus denoted as (x0, x1, x2, …, xT−3), while the target LC class is denoted by (yT−2). Input sequences in the test set are denoted as (x1, x2, x3, …, xT−2), while the target LC class is denoted by (yT−1). The training and test sets are dependent on the temporal resolution being utilized with the currently trained model. Table 3 presents the years used in training and testing procedures with respective temporal resolutions. The subsequent timestep to be forecasted, or the training targets (yT−2) and testing targets (yT−1), have been underlined (Table 3). Both training and testing datasets are one-hot encoded to represent LC classes at each timestep [19,44]. The LC classification confidence layer is processed in the same way, without the one-hot encoding procedure. Comprising the confidence layers are continuous values representing percentages ranging from 0 to 100. Zero indicates no confidence in the LC classification result for a cell, while values nearing 100 indicate high confidence in LC classification algorithm results for a given cell [33].

Table 3.
Years used to compose training and test datasets considering the four temporal resolution scenarios. The years used for training and testing target data have been underlined.
The overall number of cells per class considering the real LC dataset has been shown in Figure 3. Although there are many ways of composing the training sets, due to the scarcity of cells undergoing change [15], it is necessary to apply an improved sampling strategy to form the training sets used in each scenario. This means that strategies such as random sampling or obtaining equal counts from each class are disadvantageous for phenomena such as LCC. Samardžić-Petrović et al. [45] propose a balanced sampling strategy, demonstrating the benefits of equal counts of persistent cells and changed cells used to compose the training set. Changed cells are denoted as such if they have undergone one or many changes between x0 and yT−2. However, due to the large discrepancy between changed and persistent cell counts, persistent cells cannot be simply randomly sampled. Therefore, all changed cells are added to the training data set, while persistent cells are sampled at random across the entire study area while maintaining the original distributions of classes found in the entire set of persistent cells [45,46]. This technique impacts the number of inputs available for training for each temporal resolution. That is, if changes occurred during timesteps unavailable in the creation of the training set for the temporal resolution being considered, the cell would be marked as persistent. This sampling procedure is also applied to the scenarios considering the hybrid data, ignoring the additional cells marked as “No Data.” Due to the increased number of cells ignored in the hybrid datasets, training and testing datasets are smaller in scenarios in which this dataset is used.
Following model training procedures, testing or validation can occur with a dataset withheld from the training dataset [47]. The “one-step” ahead forecasting convention used to test or validate respective models is adopted from [20,47]. Previous methods have utilized subsets of available datasets for testing, following suit with training dataset creation procedures [45,46]. However, in this study, the balanced sampling strategy has been employed for only the training dataset creation procedure. To create the test set, all cells (except for those containing “No Data”) are considered in the evaluation of the entire forecasted map. That is, the number of cells forecasted correctly as changed or persistent are calculated for all cells available in the forecasted map in all scenarios.
2.4. Model Specifications
The LSTM-based approach for forecasting LCC includes a stacked LSTM model (Figure 4). Figure 4 depicts the model considering training input sequences x0 to x14, considering one-year temporal resolution. The “Dense” layer refers to a fully-connected neural network layer used as the output layer. By stacking LSTM layers, these models have been demonstrated to have improved capacity to capture increasingly complex relationships subsisting in input datasets [48,49]. In this study, three LSTM layers are used in a stacked modeling approach accepting categorical LC input sequence data. Each LSTM layer is composed of 128 neurons per layer. The input layer is compatible with one-hot encoded input sequences. Between each layer, various dropout regularization factors were also tested before settling on a factor of 0.5 between each layer [20,50]. The dropout factor controls the probability of neurons being discarded during the training procedure. For instance, if a factor of 0.5 is applied between each layer, the probability that the information from a neuron is “dropped” becomes 50%. This simple tactic has proven effective in preventing overfitting and improving representations learned by RNNs [51].
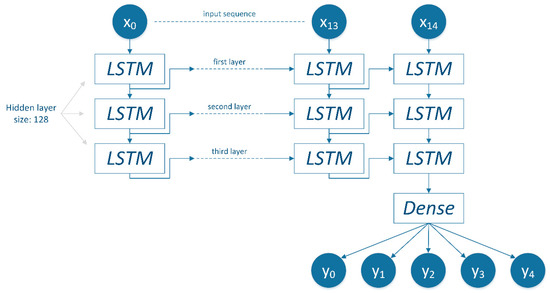
Figure 4.
Stacked LSTM model with a land cover input sequence example using one-year temporal resolution.
To incorporate the classification confidence layer, this configuration is concatenated with an additional input layer and LSTM layer. This branched configuration is required to provide mixed input types to models, a prevalent approach in applications such as image captioning [52,53]. The model branch accepts the confidence layer as input. The output of this branch is concatenated with output resulting from the stacked LSTM used to consider the LC class sequences. This configuration is demonstrated in Figure 5. The application of the dropout regularization terms remains the same in the model branch considering LC input sequences.
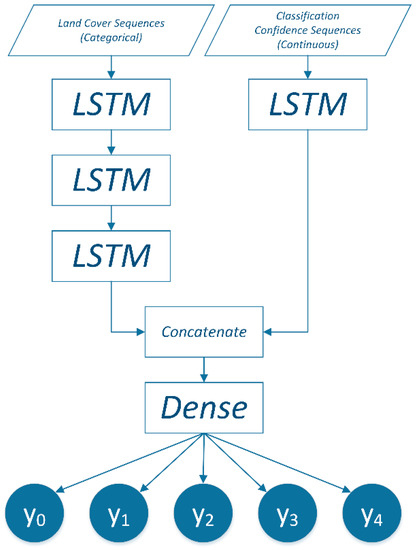
Figure 5.
Stacked LSTM model configured for land cover and classification confidence input layers.
Models were developed using Python (v3.6.5) and the Keras API (v2.2.0) [54]. The Keras API aids in simplifying DL model prototyping workflows while affording users the functionality of Google’s TensorFlow GPU implementation (v1.8.0) [54]. TensorFlow is “an open-source machine learning framework” that provides users advanced functionality to fine-tune ML and DL models [55]. The optimization method used was the adaptive moment estimation or “Adam” algorithm [56] due to its demonstrated success and robustness to model hyperparameters. The learning rates used are those determined by Kingma and Ba [56], available as default values with the Keras API [57]. Categorical cross-entropy is utilized as the objective function to accommodate the multi-class data being used with this method [28].
The Softmax activation function [12] was employed in the output layer. This ensures a vector of probabilities corresponding to each class label for each cell is output from the model. This activation function is commonly used with multi-class classification and predictive models [12,58]. In this study, there are four LC classes. The fifth class (y0 in Figure 4 and Figure 5) denotes a “No Data” option which is unrepresented in the training and test sets. The maximal number of epochs the models are enabled to train for is 1000 epochs, with early-stopping callbacks utilized to prevent overfitting [59]. Early stopping terminates model fitting when there have been no improvements to a model’s objective function within a specified number of epochs. The batch size was set to 32. Considering the actual data, models to be trained featured 332,421 internal parameters. When utilizing the additional confidence input layer, the number of internal parameters increased to 399,621 with the addition of the secondary input branch (Figure 5). Models have been trained and tested using a NVIDIA GeForce GTX 1080 Ti GPU.
2.5. Experiment Overview
Using the original datasets that have undergone pre-processing procedures described in Section 2.1, two experiments are performed, including (1) training and evaluating the stacked LSTM model considering only the LC dataset (Figure 4) and (2) training and evaluating the mixed input stacked LSTM model considering both the LC dataset and the ancillary classification confidence layer (Figure 5). In the evaluation procedure, all cells apart from those assigned “No Data” are involved.
The experiments using the hybrid datasets focus on assessing whether performance may increase or decrease when a class remains persistent through all timesteps. Considering the hybrid dataset, the two experiments conducted to assess the repercussions of the persistent water class include (1) training and evaluating the stacked LSTM model (Figure 4) and (2) training and evaluating the mixed input stacked LSTM model considering both the hybrid dataset and the classification confidence layer (Figure 5). In the evaluations considering the hybrid dataset, a greater number of cells will be marked as “No Data” due to data creation procedures described in Section 2.3, implying more cells will be omitted during the evaluation procedure.
3. Results
Constructing four models for each experiment, each model was trained with training sets featuring one-, two-, four-, and eight-year temporal resolutions, respectively. Computation time required to run each model configuration (Figure 4 and Figure 5) with all temporal resolution options and both the actual and hybrid datasets exceeded one day. Training set composition has been shown in Table 4 for experiments involving the actual datasets (Table 4a) and hybrid datasets (Table 4b). The number of training samples for each temporal resolution option in Table 4 indicate that as the temporal resolution becomes coarser, the number of cells changed becomes smaller with the lesser number of years available. Likewise, the number of persistent cells in the respective training sets becomes smaller to uphold the balanced sampling strategy posed in Section 2.3. Though the water class is persistent through all timesteps (Table 4b), the percentage of persistent water cells obtained for the respective training sets maintains the sampling strategy when considering the hybrid dataset. The years composing the test set will vary for each temporal resolution considered. The timesteps involved in training and testing each model in all experiments is demonstrated in Table 3. To examine differences in forecasted outputs, metrics and maps are produced at the provincial extent. Additionally, a smaller spatial extent focused on the Central Okanagan region is selected for verification and visual assessment (Figure 6). This data was extracted from the “Regional District Boundaries” file available for the province of British Columbia [60].

Table 4.
Composition of each training set and for each temporal resolution. The number of cells belonging to each class has been shown, along with the original percentage of cells belonging to each class in the respective datasets for (a) the actual dataset and (b) the hybrid dataset.
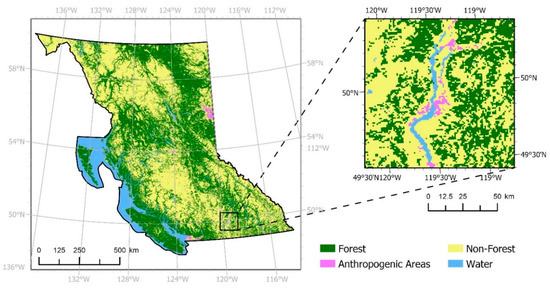
Figure 6.
Actual land cover data for the Central Okanagan Region used for verification and visual assessment comparing forecasted outputs for 2017.
To evaluate the method, cells are marked as changed if they have undergone a transition between 2001 and 2017. Likewise, the evaluation does not consider cells marked as “No Data.” This operation considers all timesteps and is then used to compare to the forecasted output generated from each of the models. Each model in every experiment is tested to forecast the LC geospatial data available for 2017 when using actual and hybrid datasets, respectively. Evaluation metrics are considered per category by “cell-by-cell comparison,” indicating which cells were forecasted as persistent or changed [61]. Instead of utilizing the traditional kappa metric, this study employs a set of metrics from [46] used to highlight trends in the method’s capacity to forecast LCC.
Analyses are conducted using the results produced with actual LC datasets depicted in Figure 7 and Table 5. Considering both the actual LC and classification confidence layers with the model structure shown in Figure 5, obtained results in 2017 for the study area are shown in Figure 8 and Table 6. Centered on the Central Okanagan region, Figure 9 showcases a comparison of forecasts obtained using the respective model specifications. The number of correctly changed cells produced in respective forecasts decreases for two non-majority classes (forest and anthropogenic areas) for both modeling scenarios as temporal resolution becomes coarser (Table 5 and Table 6). Likewise, the number of cells changed incorrectly to persistent increases as temporal resolution becomes coarser.
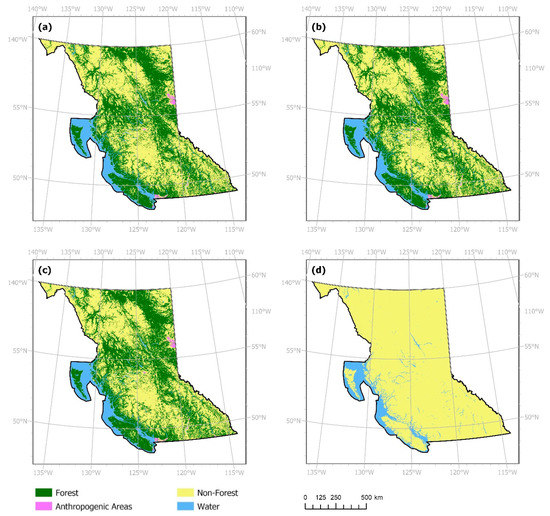
Figure 7.
Land cover classes obtained for year 2017 from models trained using the actual land cover dataset with (a) one-year, (b) two-year, (c) four-year, and (d) eight-year temporal resolution.

Table 5.
Number of cells correctly and incorrectly simulated per class using the actual land cover dataset with the four temporal resolution options.
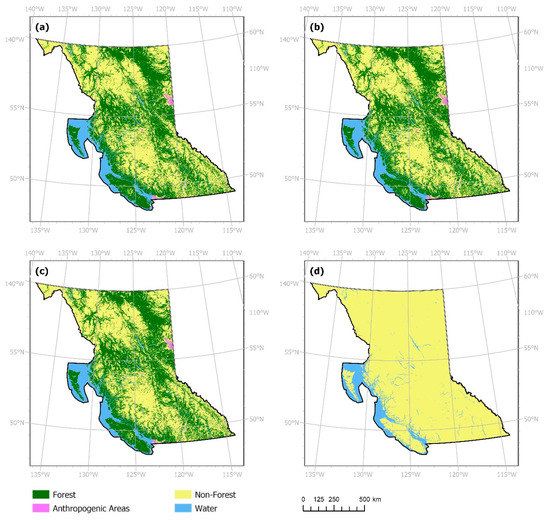
Figure 8.
Land cover classes obtained for year 2017 from models trained using the actual land cover dataset and classification confidence layer with (a) one-year, (b) two-year, (c) four-year, and (d) eight-year temporal resolution.

Table 6.
Number of cells correctly and incorrectly forecasted per class using the actual land cover dataset and classification confidence layer with the four temporal resolution options.
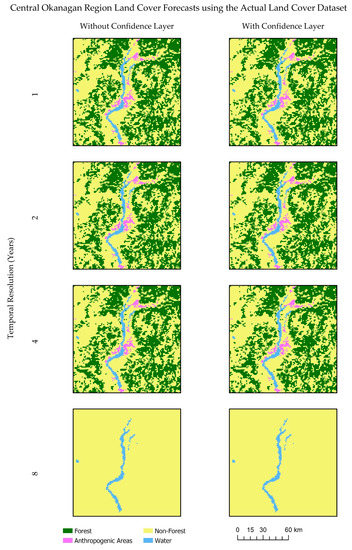
Figure 9.
Comparison of land cover forecasts centered on the Central Okanagan region, British Columbia, using the actual land cover dataset without and with classification confidence layer.
The hybrid dataset experiments feature a persistent water class developed from the actual dataset, where water cells from 2001 are made persistent through all timesteps. Results of these subsequent experiments using the hybrid LC dataset as input have been shown in Figure 10 and Table 7. Outcomes of experiments utilizing both the hybrid LC and classification confidence layers have been shown in Figure 11 and Table 8. Focusing on the Central Okanagan region, Figure 12 showcases a comparison of forecasts obtained using the respective model specifications. With the persistent water class data as input, models created as per both specifications forecasted several correctly changed cells (Table 7 and Table 8).
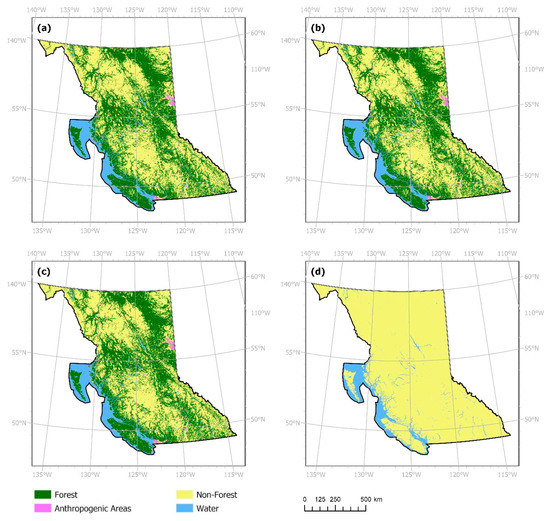
Figure 10.
Forecasted land cover classes obtained for year 2017 from models trained using the hybrid dataset with (a) one-year, (b) two-year, (c) four-year, and (d) eight-year temporal resolution.

Table 7.
Number of cells correctly and incorrectly forecasted per class using the hybrid dataset with the four temporal resolution options.
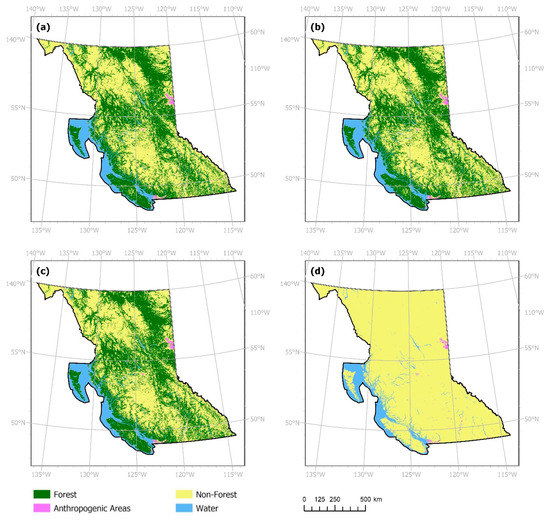
Figure 11.
Forecasted land cover classes obtained for year 2017 from models trained using the hybrid dataset and classification confidence layer with (a) one-year, (b) two-year, (c) four-year, and (d) eight-year temporal resolution.

Table 8.
Number of cells correctly and incorrectly forecasted per class using the hybrid dataset and classification confidence layer with the four temporal resolution options.
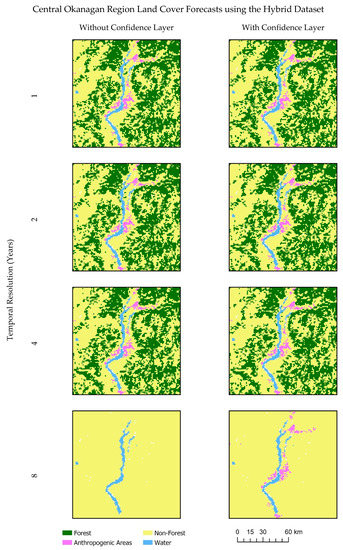
Figure 12.
Comparison of land cover forecasts centered on the Central Okanagan region, British Columbia, using the hybrid dataset without and with classification confidence layer.
4. Discussion
Across all experiments, in utilizing the coarsest temporal resolution possible (eight-year temporal resolution), results obtained were poor and erratic (Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, Table 5, Table 6, Table 7 and Table 8). This scenario involves one input feature mapped to one output feature for training and testing. By comparing models trained with four temporal resolutions, it was also observed that there is an overall bias for this method to forecast persistent cells, despite the balanced sampling regime used. This bias toward unchanged cells was also demonstrated in prior studies considering LSTM [19]. This method also demonstrates a bias toward the persistent majority class (non-forest), especially as the number of timesteps decreased and temporal resolution became coarser in all experiments.
Overall, the effects of increasing or decreasing temporal resolution were as expected. It was observed that method performance is impeded in scenarios involving coarser temporal resolutions. When forecasting land cover, the LSTM method forecasts a greater number of persistent cells than changed cells as temporal resolution becomes coarser. This is demonstrated in Table 5, where the number of persistent cells forecasted correctly increases as temporal resolution becomes coarser. The capacity of the models to forecast changed cells increases as temporal resolution becomes finer (Table 5). For instance, the models trained with the finest temporal resolution (one-year) produced the forecast with the most correctly transitioned cells for forest and anthropogenic areas. Therefore, it is observed that LSTM models are most effective when provided with increased numbers of timesteps and finer temporal resolutions in both the real-world and hybrid application.
While the classification confidence layer slightly increased the number of changed cells forecasted correctly in experiments where actual LC data is used, the greatest increase was seen in experiments using the hybrid dataset containing the persistent water class. This suggests the method’s sensitivity to classification errors, paralleling findings indicating the method’s sensitivity to random noise [20]. The mixed input configuration is thus one approach for mitigating situations where fewer classes undergo abrupt or rapid changes.
4.1. Actual Dataset Experiments
Using the actual dataset, the models trained with one-year temporal resolution yielded highest counts of correctly simulated cells across the forest, anthropogenic areas, and non-forest area classes. This is exhibited by results including only the LC data layer (Figure 7), and the LC data layer with the confidence layer as ancillary data (Figure 8). This includes both changed and persistent cells belonging to each respective class. Similarly, the model trained with the finest temporal resolution forecasted the least number of changed cells incorrectly as persistent. That is, the number of changed cells simulated as persistent increases with temporal resolution. It is also observed that the highest number of simulation errors exists in “changed cells simulated incorrectly as persistent” counts (Table 5 and Table 6).
The exemption to the aforementioned trends is the water class, exhibiting slightly increased counts of correctly simulated cells as temporal resolution becomes coarser. Overall, models performed poorly when forecasting water. Assumed to be mostly persistent, erroneous values may have factored in to poor performance for simulating this specific class. For instance, from 2016 to 2017, the number of cells occupied by water changes from 90,963 to 94,290 (Figure 3). This abrupt change occurring at the end of the available timeseries may be due to classification errors or discrepancies when annual data products were created.
It was hypothesized that adding the classification confidence layer would mitigate the effects of erroneous values and thus enhance LCC forecasts when considering all temporal resolution options. However, results obtained using the mixed input models failed to significantly improve in scenarios involving finer temporal resolutions (Table 6). This is also evident in the map produced for the Central Okanagan region (Figure 9). By including the LC classification confidence layer, the capacity for the models to forecast changes improved marginally as temporal resolution became coarser. For instance, Table 5 shows the model trained with eight-year temporal resolution data to forecast only two of the four possible classes, including the majority class (non-forest areas) and water cells. While still obtaining suboptimal results, models trained with both types of inputs forecasted some cells in forest and anthropogenic classes, albeit less than 1% in each class, respectively.
4.2. Hybrid Dataset Experiments
Following suit with results shown in Section 3, the models trained with finer temporal resolutions obtained the most favorable results (Table 7 and Table 8). Models trained with the eight-year temporal resolution option forecasted only non-forest areas and persistent water cells (Table 7). It is also observed that cells occupied by persistent water through all timesteps have been forecasted with no errors across all modeling scenarios considering both exclusively the hybrid dataset as well as the mixed inputs.
Like results obtained in Section 3, the addition of the classification confidence layer as input to the model increased model performance slightly when considering coarser temporal resolutions and fewer timesteps. It similarly had little to no effect on LCC forecasting performance in scenarios where finer temporal resolutions were considered. However, when the considering the hybrid dataset with eight-year temporal resolution, the addition of the classification confidence layer as model input contributed to success in forecasting anthropogenic areas, with 92.6% of persistent anthropogenic areas forecasted correctly (Table 8). This can be viewed in Figure 12 at the smaller spatial extent.
5. Conclusions
The stacked LSTM modeling approach for forecasting LCC aims to detect patterns occurring across the temporal dimension to forecast forest, anthropogenic areas, non-forested non-anthropogenic areas, and water. Compared to previous applications of LSTM for prediction and classification tasks utilizing geospatial data, real-world applications thus far had not considered the implications and importance of the choice of geospatial input data characteristics on method performance. For slow-changing geospatial systems such as LCC, it is demonstrated that obtaining datasets that feature many timesteps and finer temporal resolutions enable more optimal models to be obtained. It is also indicative of potential issues arising when considering the LSTM method for use with geospatial datasets that are limited in the number of data layers or timesteps.
With demonstrated bias toward training datasets, future work should consider improved sampling strategies to further address this issue. Similarly, a consequence of the sampling regime employed was a significant loss of potential training data samples. Maintaining and obtaining additional high-quality training samples available should continue to be a priority for further research involving LSTM.
Future works should also consider strategies to use this method to its fullest potential when real-world geospatial datasets have limited layers available. For instance, additional data layers should be considered to increase method performance, especially if classes undergo more rapid changes. Moreover, different LC class aggregation strategies may produce improved results. This may entail differing compositions of or replacements of one or many of the forest, anthropogenic areas, non-forest areas, and water classes. It would be beneficial to consider sensitivity analyses of increasing LC class cardinality and implications of changing spatial resolution on method performance. Such experiments will require computational resources such as a distributed computing facility to efficiently run experiments with increasing LC classes and spatial resolutions.
Since this evaluation was conducted at a provincial scale, future works should also consider the implications of spatial extent and resolution on method performance. It is also recommended that future work utilize additional evaluation metrics that consider not only location-based metrics, but also spatial pattern metrics. While the integration of the available classification confidence layer available in the “MODIS Terra+Aqua Combined Land Cover Product” [32] was considered, further sensitivity analyses should be conducted to assess the effects of perturbations in input sequences and model response. Additional auxiliary or contextual data to provide more detail pertaining to spatial features in given input sequences should also be explored. This could include deriving additional layers pertaining to local spatial autocorrelation. Though the classification confidence layer did not enhance LCC forecasting performance in situations involving fine temporal resolution data, this additional data layer may be advantageous in data-scarce scenarios where improving temporal resolution or increasing the number of timesteps is not an option. It should be assessed whether increasing the number of additional features may improve the forecasting performance of the method or increase robustness of the method to varying geospatial input data characteristics such as temporal resolution, LC class cardinality, and the number of timesteps available. As such, geospatial data characteristics such as LC class cardinality can be maintained instead of undergoing aggregation in pre-processing procedures, while maintaining or enhancing yielded performance measures.
Given the lack of research endeavors exploring the effectiveness of LSTM for LCC forecasting, it was inconclusive as to what geospatial dataset characteristics were required to optimize the use of this modeling approach. By training and testing models using geospatial datasets with varying characteristics, this work aimed to contribute to future LCC forecasting applications by providing recommendations and an assessment displaying under which circumstances the method is most effective. In this application, it was determined that increasing the number of timesteps and obtaining data with finer temporal resolution enable the most optimal models to be developed for LCC forecasting. Likewise, the number of classes exhibiting change also showed impactful to method performance. Lastly, integrating additional data layers such as classification confidence proved useful in mitigating the effects of coarser temporal resolution on the method’s capacity to simulate LCC.
Author Contributions
Conceptualization, Formal analysis, Investigation, Methodology, Writing—original draft, Writing—review & editing, A.v.D. and S.D; Funding acquisition, Supervision, S.D.; Software, A.v.D.
Funding
This research was funded by Natural Sciences and Engineering Research Council (NSERC) of Canada Discovery Grant RGPIN-2017-03939.
Acknowledgments
The authors are grateful for the full support of this study by the Natural Sciences and Engineering Research Council (NSERC) of Canada Discovery Grant awarded to the second author. We are thankful for the valuable and constructive comments from three anonymous reviewers, as well as to the SFU Open Access Fund for sponsoring the publication of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Geist, H.; McConnell, W.; Lambin, E.F.; Moran, E.; Alves, D.; Rudel, T. Causes and Trajectories of Land-Use/Cover Change. In Land-Use and Land-Cover Change; Springer: Berlin/Heidelberg, Germany, 2008; pp. 41–70. [Google Scholar]
- Lambin, E.F.; Turner, B.L.; Geist, H.J.; Agbola, S.B.; Angelsen, A.; Bruce, J.W.; Coomes, O.T.; Dirzo, R.; Unther Fischer, G.U.; Folke, C.; et al. The causes of land-use and land-cover change: Moving beyond the myths. Glob. Environ. Chang. 2001, 11, 261–269. [Google Scholar] [CrossRef]
- Findell, K.L.; Berg, A.; Gentine, P.; Krasting, J.P.; Lintner, B.R.; Malyshev, S.; Santanello, J.A.; Shevliakova, E. The impact of anthropogenic land use and land cover change on regional climate extremes. Nat. Commun. 2017, 8, 989. [Google Scholar] [CrossRef] [PubMed]
- Meyer, W.B.; Turner, B.L. Land-use/land-cover change: Challenges for geographers. GeoJournal 1996, 39, 237–240. [Google Scholar] [CrossRef]
- Yang, W.; Long, D.; Bai, P. Impacts of future land cover and climate changes on runoff in the mostly afforested river basin in North China. J. Hydrol. 2019, 570, 201–219. [Google Scholar] [CrossRef]
- Chase, T.N.; Pielke, R.A.; Kittel, T.G.F.; Nemani, R.R.; Running, S.W. Simulated impacts of historical land cover changes on global climate in northern winter. Clim. Dyn. 2000, 16, 93–105. [Google Scholar] [CrossRef]
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Seto, K.C.; Guneralp, B.; Hutyra, L.R. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools. Proc. Natl. Acad. Sci. USA 2012, 109, 16083–16088. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Lü, Y.; Comber, A.; Fu, B.; Harris, P.; Wu, L. Spatially explicit simulation of land use/land cover changes: Current coverage and future prospects. Earth-Sci. Rev. 2019, 190, 398–415. [Google Scholar] [CrossRef]
- Verburg, P.H.; Kok, K.; Pontius, R.G.; Veldkamp, A. Modeling Land-Use and Land-Cover Change. In Land-Use and Land-Cover Change; Springer: Berlin/Heidelberg, Germany, 2008; pp. 117–135. [Google Scholar]
- Patil, S.D.; Gu, Y.; Dias, F.S.A.; Stieglitz, M.; Turk, G. Predicting the spectral information of future land cover using machine learning. Int. J. Remote Sens. 2017, 38, 5592–5607. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; ISBN 0387310738. [Google Scholar]
- Maithani, S. Neural networks-based simulation of land cover scenarios in Doon valley, India. Geocarto Int. 2015, 30, 163–185. [Google Scholar] [CrossRef]
- Otukei, J.R.; Blaschke, T. Land cover change assessment using decision trees, support vector machines and maximum likelihood classification algorithms. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S27–S31. [Google Scholar] [CrossRef]
- Karpatne, A.; Jiang, Z.; Vatsavai, R.R.; Shekhar, S.; Kumar, V. Monitoring Land-Cover Changes: A Machine-Learning Perspective. IEEE Geosci. Remote Sens. Mag. 2016, 4, 8–21. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Khandelwal, A.; Nayak, G.; Gerber, J.; Carlson, K.; West, P.; Kumar, V. Incremental Dual-memory LSTM in Land Cover Prediction. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD ’17, Halifax, NS, Canada, 13–17 August 2017; ACM Press: New York, NY, USA, 2017; pp. 867–876. [Google Scholar]
- Sun, Z.; Di, L.; Fang, H. Using long short-term memory recurrent neural network in land cover classification on Landsat and Cropland data layer time series. Int. J. Remote Sens. 2019, 40, 593–614. [Google Scholar] [CrossRef]
- Lyu, H.; Lu, H.; Mou, L. Learning a Transferable Change Rule from a Recurrent Neural Network for Land Cover Change Detection. Remote Sens. 2016, 8, 506. [Google Scholar] [CrossRef]
- Kong, Y.-L.L.; Huang, Q.; Wang, C.; Chen, J.J.; Chen, J.J.; He, D. Long Short-Term Memory Neural Networks for Online Disturbance Detection in Satellite Image Time Series. Remote Sens. 2018, 10, 452. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.; Dong, J.; Zhong, G.; Sun, X. Prediction of Sea Surface Temperature Using Long Short-Term Memory. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1745–1749. [Google Scholar] [CrossRef]
- Liu, L.; Han, M.; Zhou, Y.; Wang, Y. LSTM recurrent neural networks for influenza trends prediction. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); LNBI; Springer: Cham, Switzerland, 2018; Volume 10847, pp. 259–264. ISBN 9783319949673. [Google Scholar]
- Boulila, W.; Ayadi, Z.; Farah, I.R. Sensitivity analysis approach to model epistemic and aleatory imperfection: Application to Land Cover Change prediction model. J. Comput. Sci. 2017, 23, 58–70. [Google Scholar] [CrossRef]
- Hochreiter, S. The Vanishing Gradient Problem During Learning Recurrent Neural Nets and Problem Solutions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Ball, J.E.; Anderson, D.T.; Chan, C.S. A Comprehensive Survey of Deep Learning in Remote Sensing: Theories, Tools and Challenges for the Community. J. Appl. Remote Sens. 2017, 11, 042609. [Google Scholar] [CrossRef]
- Greff, K.; Srivastava, R.K.; Koutnik, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A Search Space Odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2222–2232. [Google Scholar] [CrossRef] [PubMed]
- Donahue, J.; Hendricks, L.A.; Guadarrama, S.; Rohrbach, M.; Venugopalan, S.; Darrell, T.; Saenko, K. Long-term recurrent convolutional networks for visual recognition and description. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Bostony, MA, USA, 7–12 June 2015; pp. 2625–2634. [Google Scholar]
- Rußwurm, M.; Körner, M. Multi-temporal land cover classification with long short-term memory neural networks. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2017, 42, 551–558. [Google Scholar] [CrossRef]
- Understanding LSTM Networks. Available online: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ (accessed on 19 August 2019).
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Gers, F.A. Learning to forget: Continual prediction with LSTM. In Proceedings of the 9th International Conference on Artificial Neural Networks: ICANN ’99, Edinburgh, UK, 7–10 September 1999; IEE: London, UK, 1999; Volume 2, pp. 850–855. [Google Scholar]
- Friedl, M.; Sulla-Menashe, D. MCD12Q1 MODIS/Terra+Aqua Land Cover Type Yearly L3 Global 500m SIN Grid V006 [Data Set]. Available online: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mcd12q1_v006 (accessed on 30 January 2019).
- Sulla-Menashe, D.; Friedl, M.A. User Guide to Collection 6 MODIS Land Cover (MCD12Q1 and MCD12C1) Product; USGS: Reston, VA, USA, 2018; pp. 1–18.
- Meidinger, D.; Pojar, J. Ecosystems of British Columbia; British Columbia Ministry of Forests: Victoria, BC, Canada, 1991.
- Mathys, A.S.; Coops, N.C.; Simard, S.W.; Waring, R.H.; Aitken, S.N. Diverging distribution of seedlings and mature trees reflects recent climate change in British Columbia. Ecol. Model. 2018, 384, 145–153. [Google Scholar] [CrossRef]
- GDAL/OGR Contributors GDAL/OGR Geospatial Data Abstraction Software Library; Open Source Geospatial Found: Beaverton, OR, USA, 2019.
- Statistics Canada. Boundary Files, 2016 Census; Statistics Canada: Ottawa, ON, Canada, 2016.
- Esri. ArcGIS Pro: 2.0; Esri: Redlands, CA, USA, 2017. [Google Scholar]
- Esri Project Raster. Available online: https://pro.arcgis.com/en/pro-app/tool-reference/data-management/project-raster.htm (accessed on 19 August 2019).
- ESRI Cell Size and Resampling in Analysis. Available online: http://desktop.arcgis.com/en/desktop/latest/guide-books/extensions/spatial-analyst/performing-analysis/cell-size-and-resampling-in-analysis.htm (accessed on 27 August 2019).
- LP DAAC—Homepage. Available online: https://lpdaac.usgs.gov/ (accessed on 25 July 2019).
- Voight, C.; Hernandez-Aguilar, K.; Garcia, C.; Gutierrez, S. Predictive Modeling of Future Forest Cover Change Patterns in Southern Belize. Remote Sens. 2019, 11, 823. [Google Scholar] [CrossRef]
- van Rossum, G. Python 3.6 Language Reference; Samurai Media Limited: Surrey, Thames Ditton, UK, 2016. [Google Scholar]
- Rußwurm, M.; Körner, M. Multi-Temporal Land Cover Classification with Sequential Recurrent Encoders. ISPRS Int. J. Geo-Inf. 2018, 7, 129. [Google Scholar] [CrossRef]
- Samardžić-Petrović, M.; Dragićević, S.; Kovačević, M.; Bajat, B. Modeling Urban Land Use Changes Using Support Vector Machines. Trans. GIS 2016, 20, 718–734. [Google Scholar] [CrossRef]
- Samardžić-Petrović, M.; Kovačević, M.; Bajat, B.; Dragićević, S. Machine Learning Techniques for Modelling Short Term Land-Use Change. ISPRS Int. J. Geo-Inf. 2017, 6, 387. [Google Scholar] [CrossRef]
- Chi, J.; Kim, H. Prediction of Arctic Sea Ice Concentration Using a Fully Data Driven Deep Neural Network. Remote Sens. 2017, 9, 1305. [Google Scholar]
- Pascanu, R.; Gulcehre, C.; Cho, K.; Bengio, Y. How to Construct Deep Recurrent Neural Networks. In Proceedings of the 2nd International Conference on Learning Representations (ICLR), Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Hermans, M.; Schrauwen, B. Training and Analysing Deep Recurrent Neural Networks. Adv. Neural Inf. Process. Syst. 2013, 26, 190–198. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Pham, V.; Bluche, T.; Kermorvant, C.; Louradour, J. Dropout Improves Recurrent Neural Networks for Handwriting Recognition. In Proceedings of the International Conference on Frontiers in Handwriting Recognition (ICFHR), Crete, Greece, 1–4 September 2014; pp. 285–290. [Google Scholar]
- Karpathy, A.; Fei-Fei, L. Deep Visual-Semantic Alignments for Generating Image Descriptions. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 664–676. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Shen, C.; Wang, P.; Dick, A.; van den Hengel, A. Image Captioning and Visual Question Answering Based on Attributes and External Knowledge. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1367–1381. [Google Scholar] [CrossRef] [PubMed]
- Chollet, F. Keras: The Python Deep Learning Library. Available online: https://keras.io (accessed on 26 January 2019).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Kingma, D.P.; Lei Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Keras Optimizers—Keras Documentation. Available online: https://keras.io/optimizers/ (accessed on 9 November 2019).
- Ienco, D.; Gaetano, R.; Dupaquier, C.; Maurel, P. Land Cover Classification via Multitemporal Spatial Data by Deep Recurrent Neural Networks. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1685–1689. [Google Scholar] [CrossRef]
- Raskutti, G.; Wainwright, M.J.; Yu, B. Early stopping for non-parametric regression: An optimal data-dependent stopping rule. In Proceedings of the 2011 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 28–30 September 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1318–1325. [Google Scholar]
- Elections BC Regional District Boundaries—Road Centreline Aligned—Datasets—Data Catalogue. Available online: https://catalogue.data.gov.bc.ca/dataset/regional-district-boundaries-road-centreline-aligned (accessed on 25 July 2019).
- Ahmed, B.; Ahmed, R.; Zhu, X. Evaluation of model validation techniques in land cover dynamics. ISPRS Int. J. Geo-Inf. 2013, 2, 577–597. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).