A New Algorithm for the Retrieval of Atmospheric Profiles from GNSS Radio Occultation Data in Moist Air and Comparison to 1DVar Retrievals
Abstract
1. Introduction
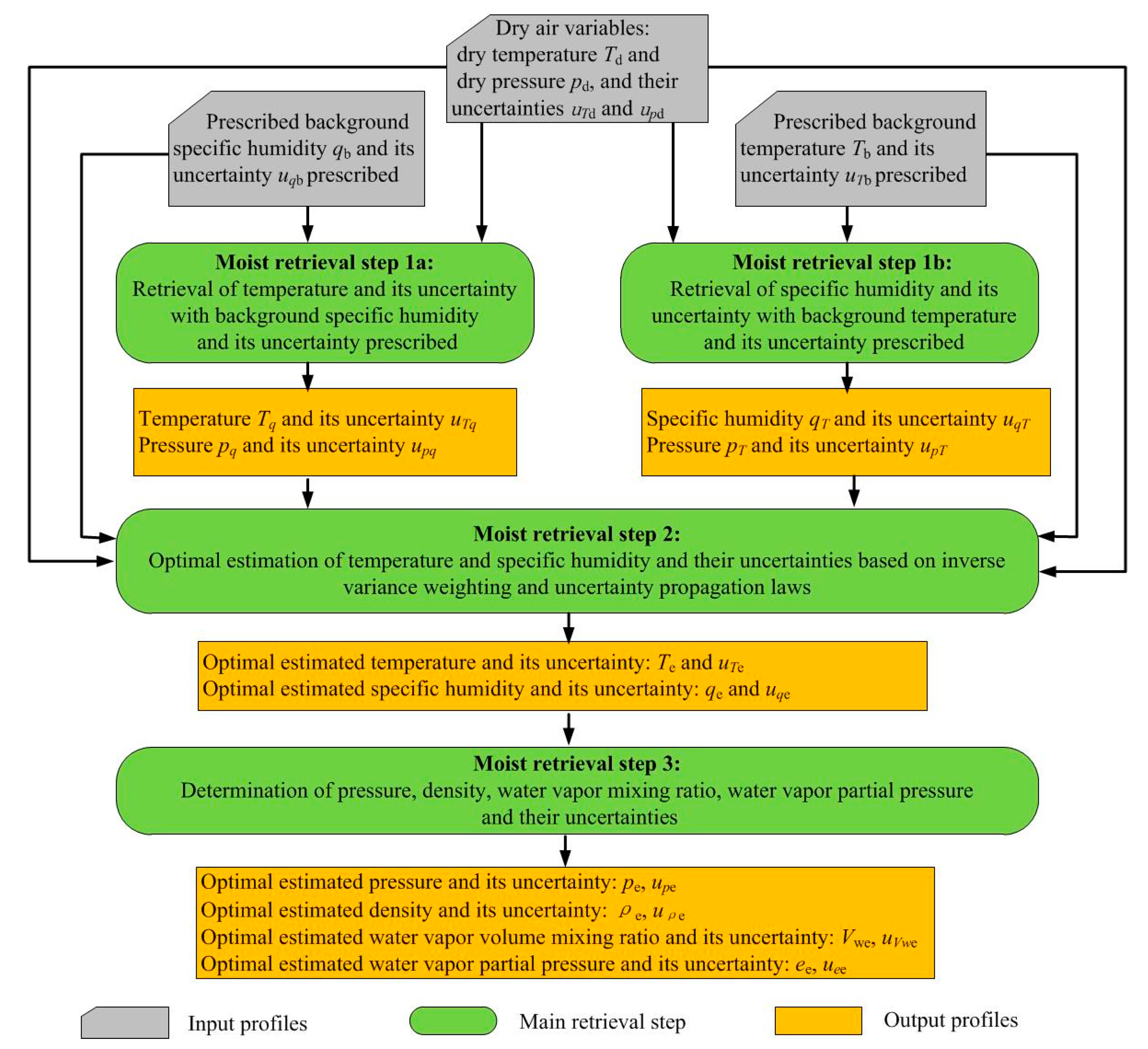
2. Methodology—The New Moist Air Retrieval Algorithm
2.1. Algorithm Basis
2.2. Algorithm Description
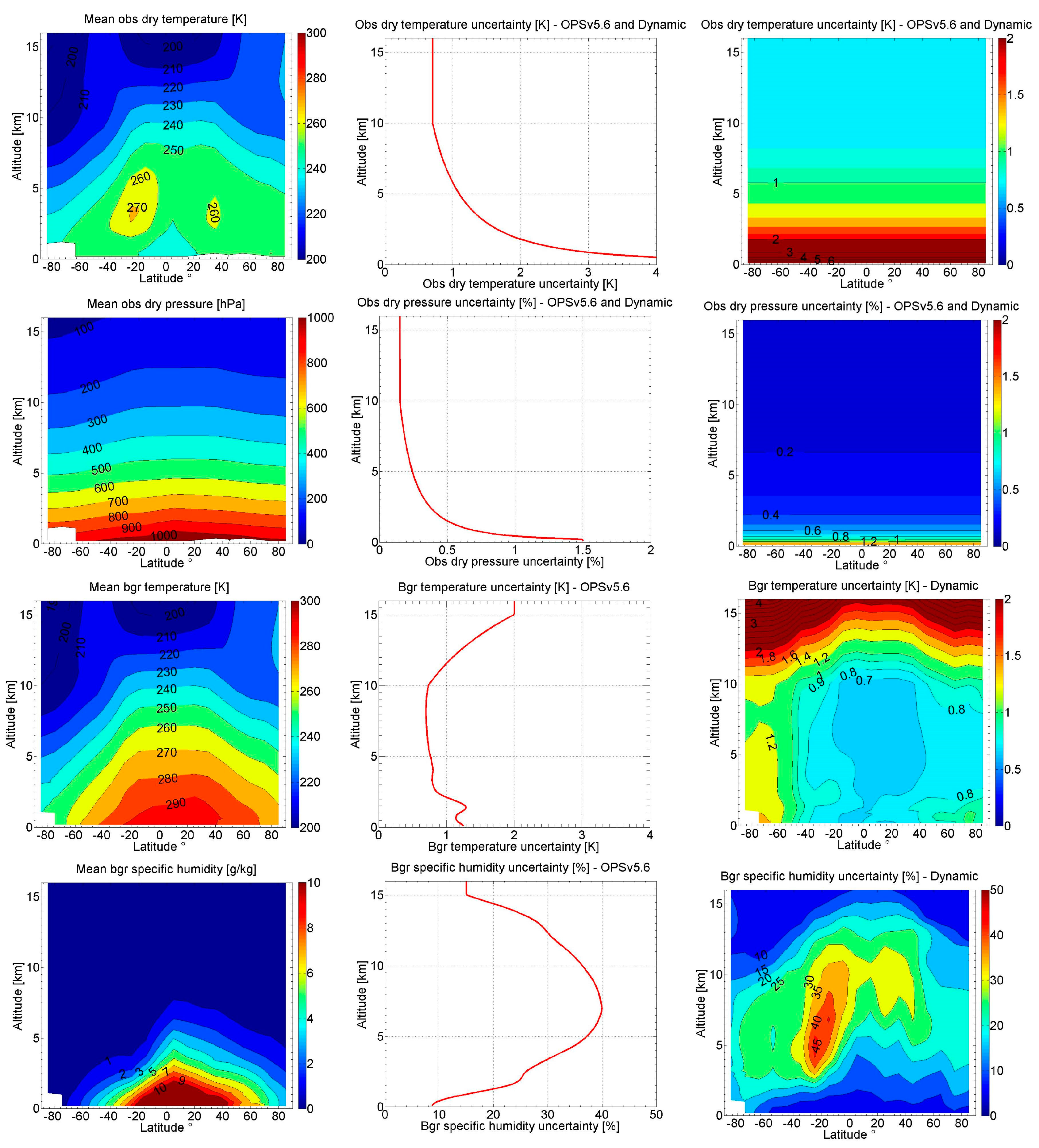
2.3. Modeling of Observation and Background Uncertainties
2.3.1. Observation Uncertainty Modeling
2.3.2. Background Uncertainty Modeling
2.4. Inspection of Intermediate Variables
3. Results—Algorithm Performance Evaluation by Comparison to 1DVar Retrievals
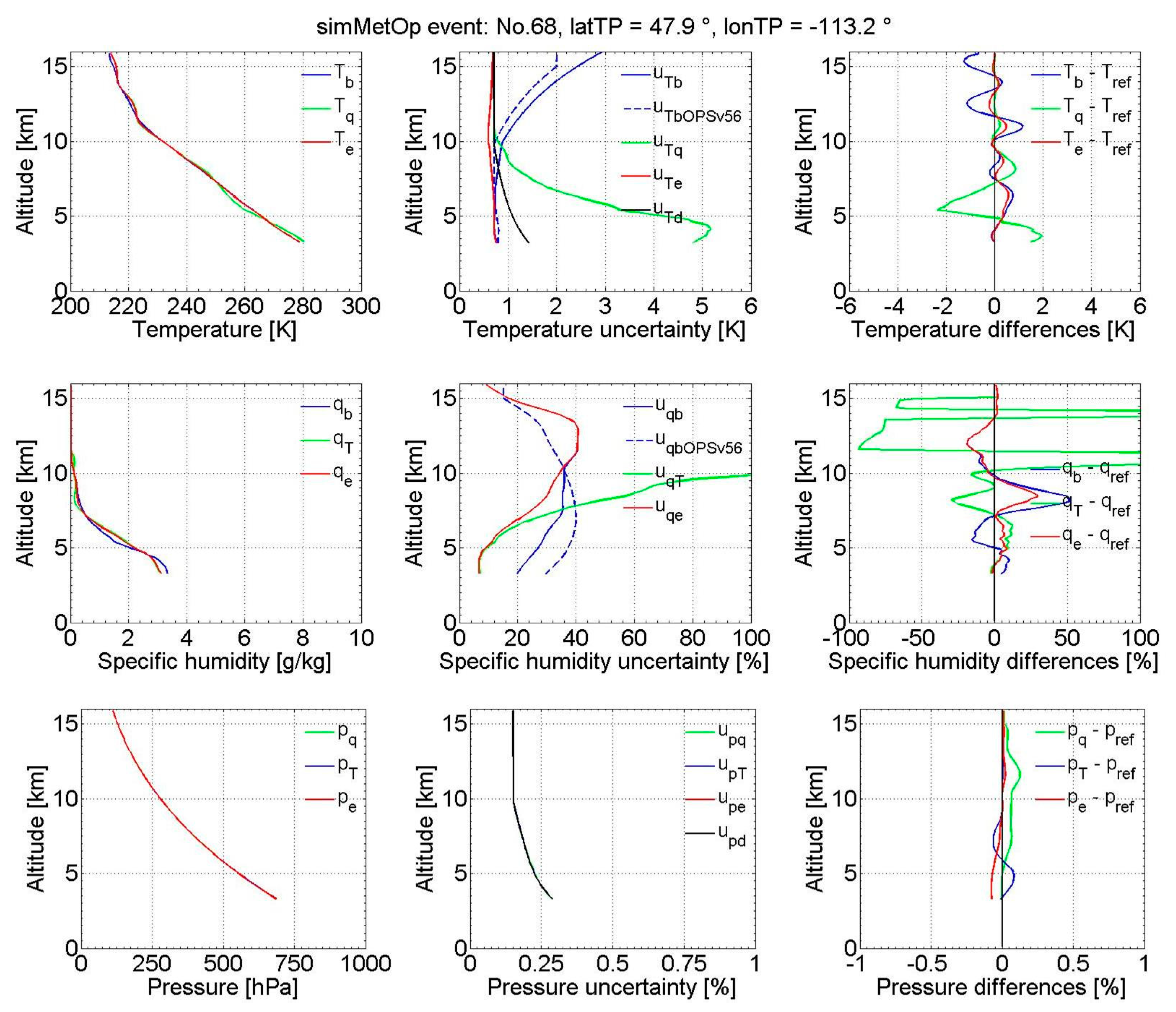
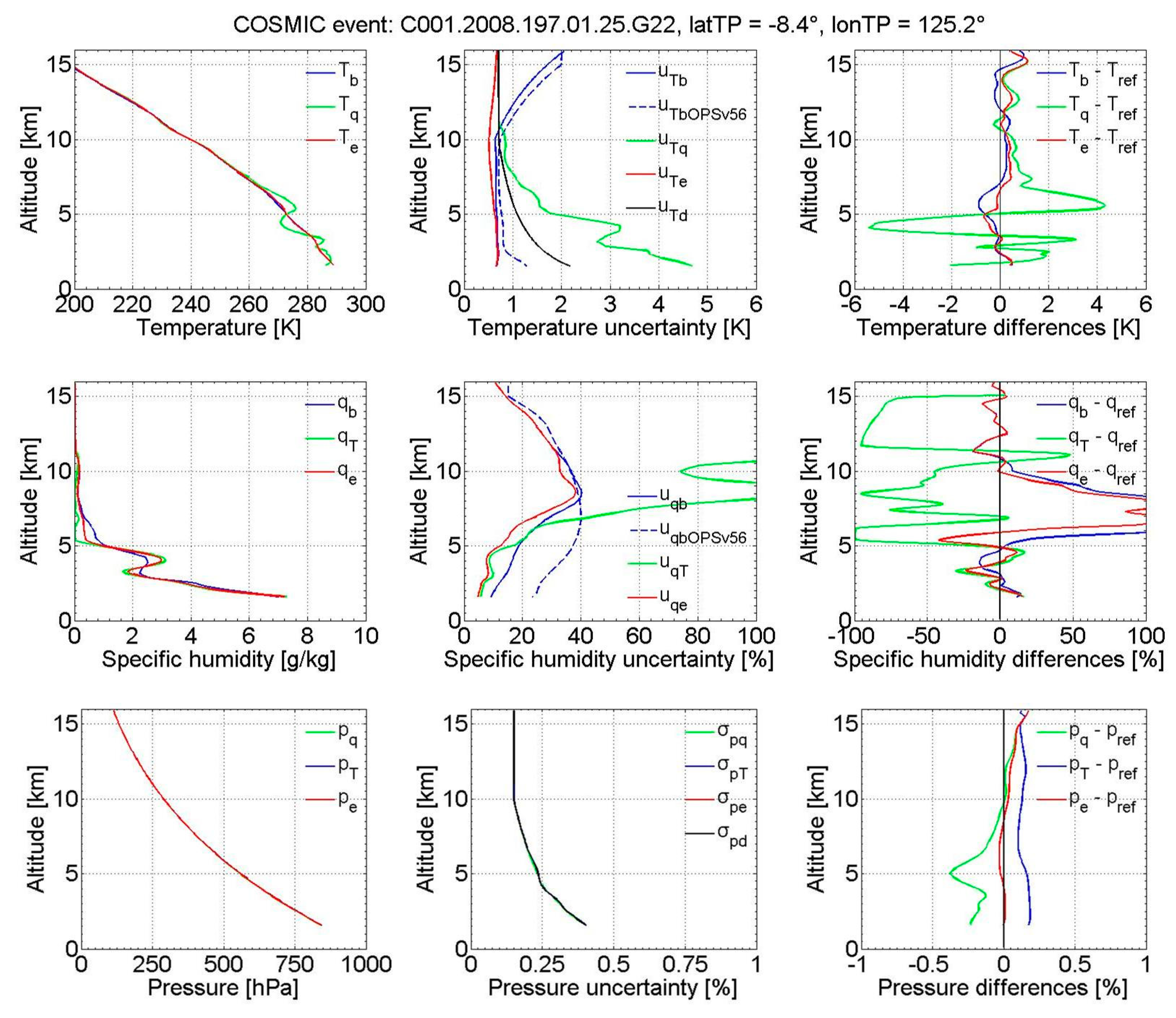
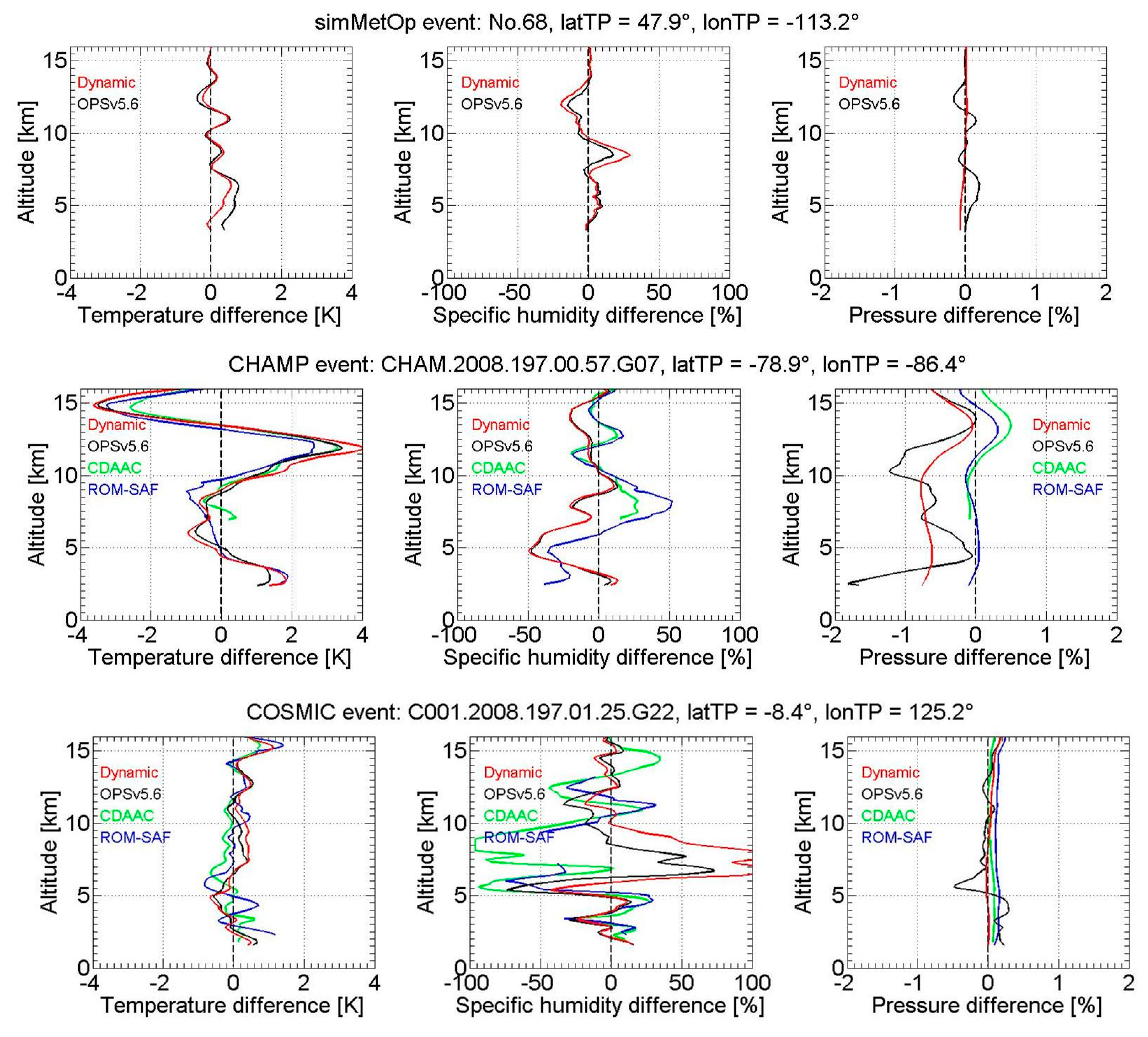
3.1. Insights from Individual Event Profiles
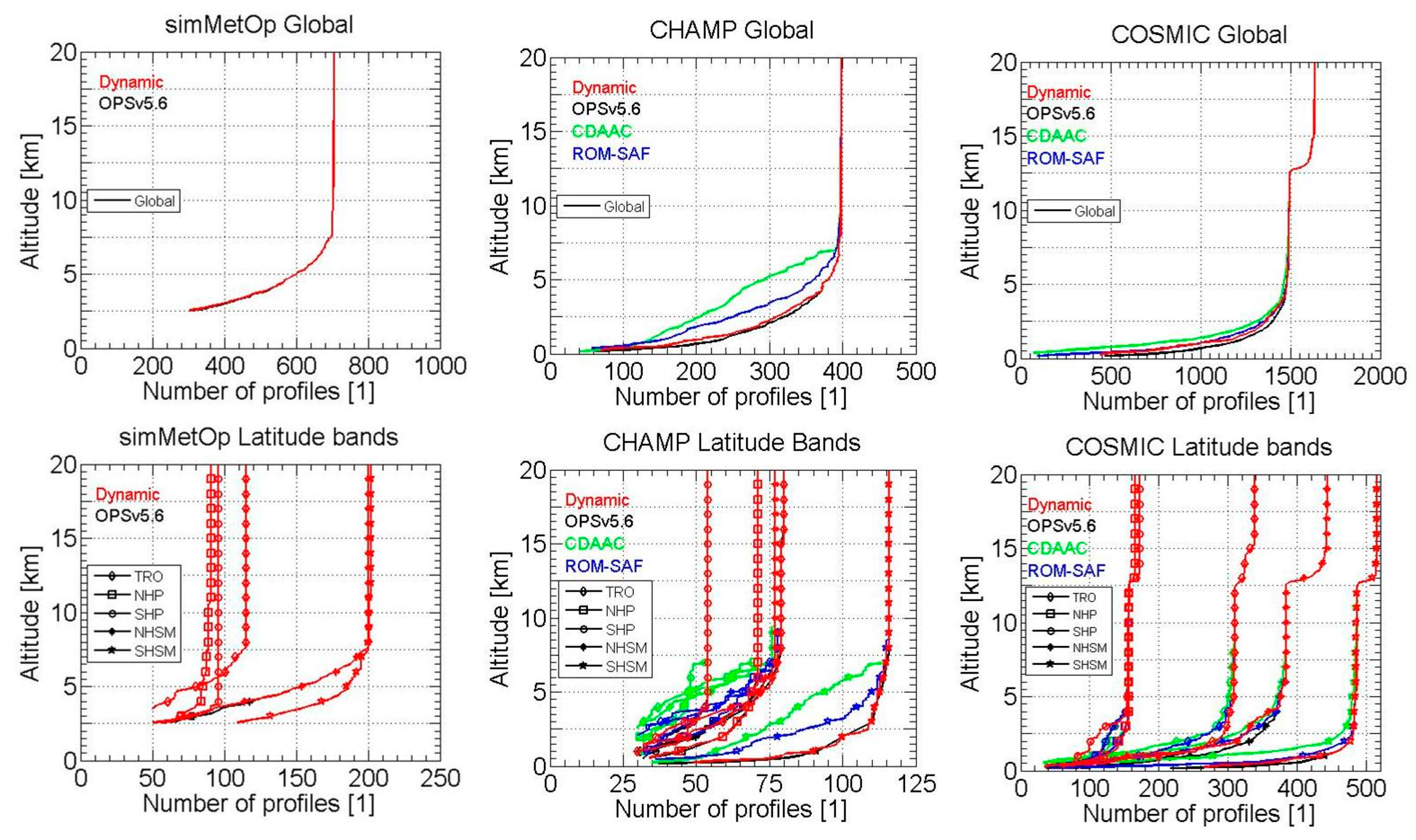
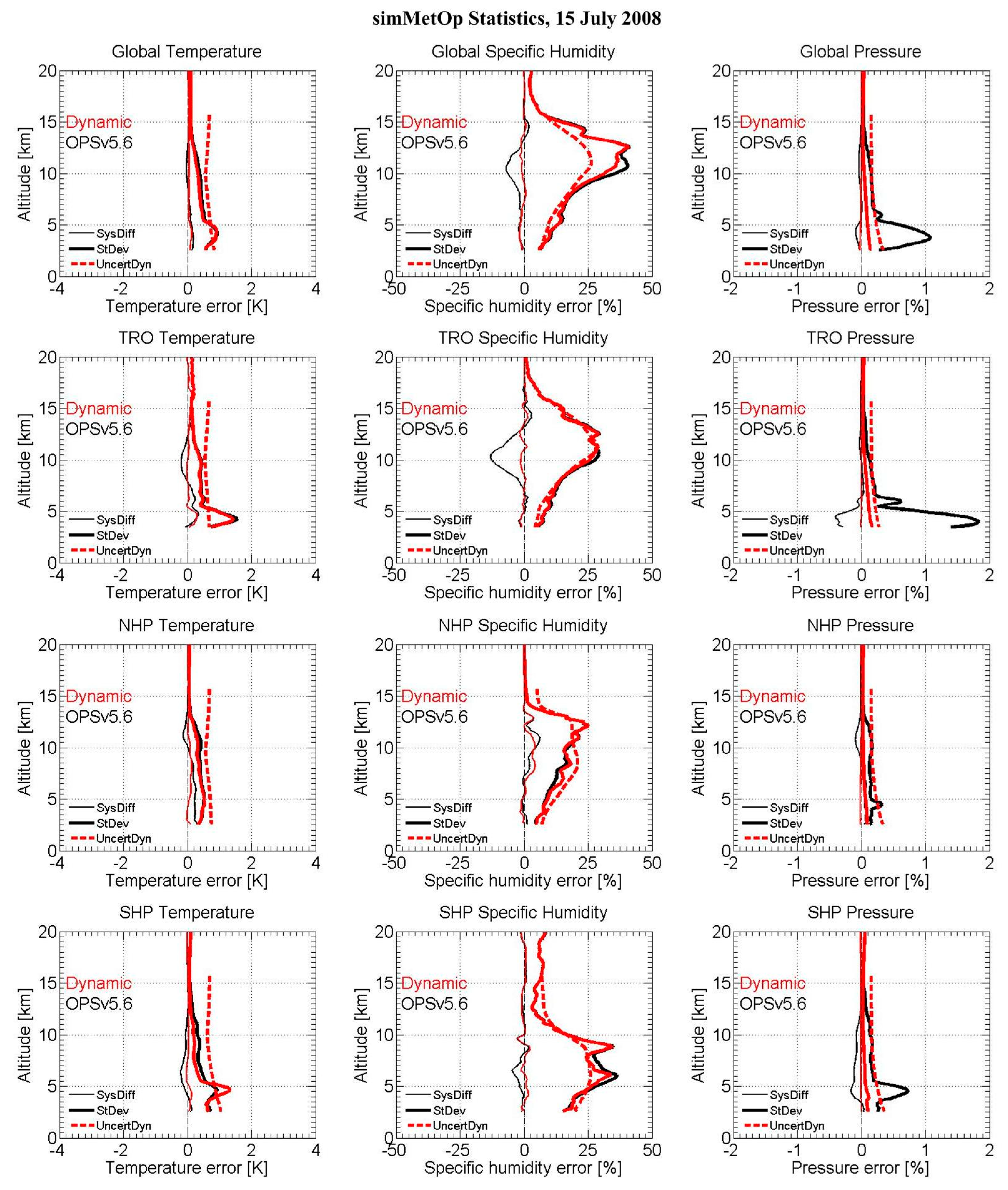
3.2. Statistical Ensemble Results
3.3. Simple Observation-to-Background Weighting Ratio Profiles and Comparative Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Detailed Numerical-Algorithm Formulations of Steps 1a and 1b
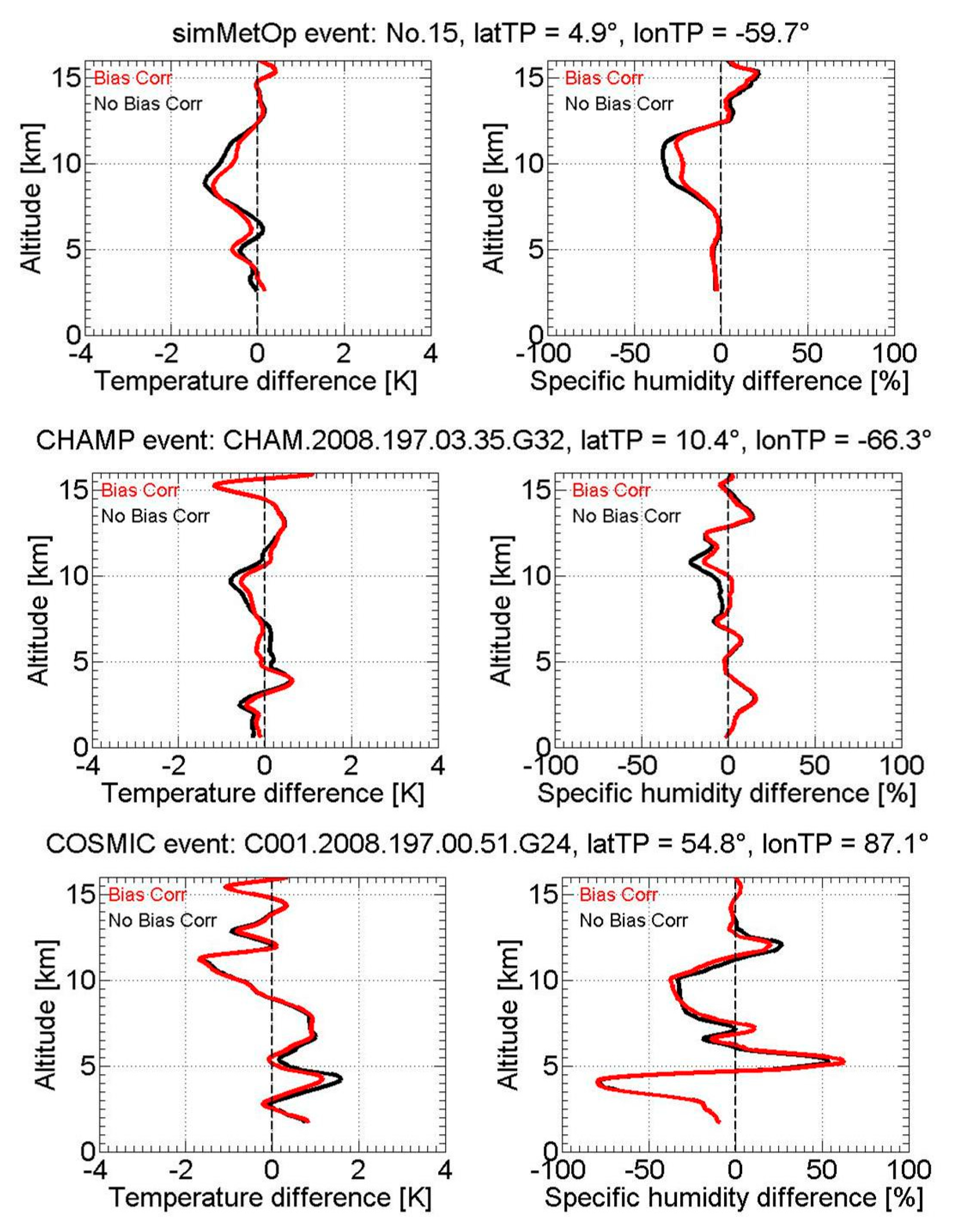
Appendix B. Bias Correction of Background Profiles and Its Effects
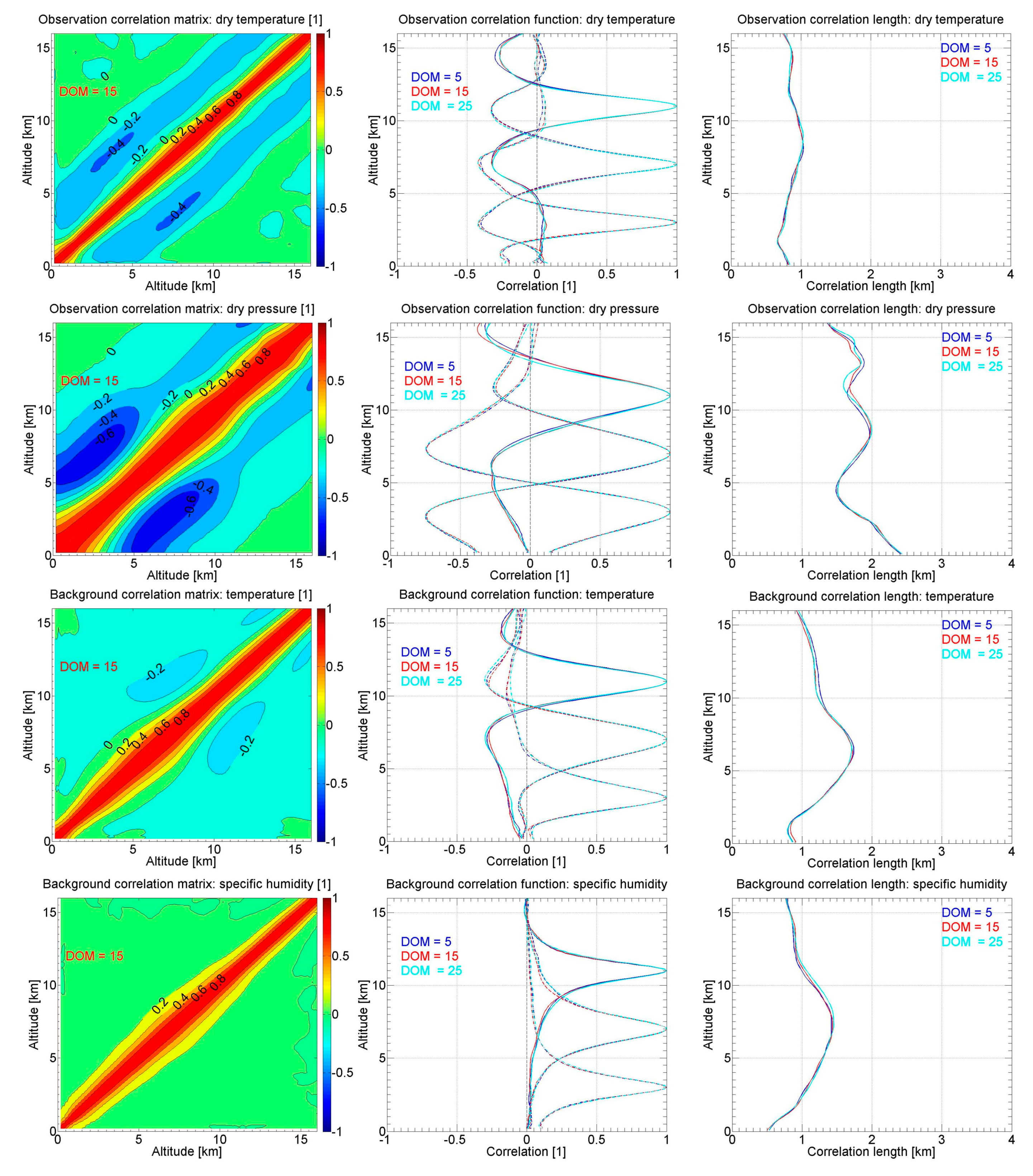
Appendix C. Vertical Correlations of Observations and Background Errors
References
- Melbourne, W.G. The application of spaceborne GPS to atmospheric limb sounding and global change monitoring. JPL Publ. 1994, 147, 1–26. [Google Scholar]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Hajj, G.A.; Kursinski, E.R.; Romans, L.J.; Bertiger, W.I.; Leroy, S.S. A technical description of atmospheric sounding by GPS occultation. J. Atmos. Sol. Terr. Phys. 2002, 64, 451–469. [Google Scholar] [CrossRef]
- Kirchengast, G. Occultations for probing atmosphere and climate: Setting the scene. In Occultations for Probing Atmosphere and Climate; Kirchengast, G., Foelsche, U., Steiner, A.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 1–8. [Google Scholar]
- Anthes, R.A. Exploring Earth’s atmosphere with radio occultation: Contributions to weather, climate and space weather. Atmos. Meas. Tech. 2011, 4, 1077–1103. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Hardy, K.R.; Romans, L.J.; Schofield, J.T. Observing tropospheric water vapor by radio occultation using the Global Positioning System. Geophys. Res. Lett. 1995, 22, 2365–2368. [Google Scholar] [CrossRef]
- Healy, S.B.; Eyre, J.R. Retrieving temperature, water vapour and surface pressure information from refractive-index profiles derived by radio occultation: A simulation study. Q. J. R. Meteorol. Soc. 2000, 126, 1661–1683. [Google Scholar] [CrossRef]
- Ware, R.; Exner, M.; Gorbunov, M.; Hardy, K.; Herman, B.; Kuo, Y.; Meehan, T.; Melbourne, W.; Rocken, C.; Schreiner, W.; et al. GPS sounding of the atmosphere from low Earth orbit: Preliminary results. B. Am. Meteorol. Soc. 1996, 77, 19–40. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Syndergaard, S.; Flittner, D.; Feng, D.; Hajj, G.; Herman, B.; Ward, D.; Yunck, T. A microwave occultation observing system optimized to characterize atmospheric water, temperature and geopotential via absorption. J. Atmos. Ocean. Technol. 2002, 19, 1897–1914. [Google Scholar] [CrossRef]
- Schweitzer, S.; Kirchengast, S.; Schwaerz, M.; Fritzer, J.; Gorbunov, M.E. Thermodynamic state retrieval from microwave occultation data and performance analysis based on end-to-end simulations. J. Geophys. Res. 2011, 116, D10301. [Google Scholar] [CrossRef]
- Liu, C.L.; Kirchengast, G.; Syndergaard, S.; Kursinski, E.R.; Du, Q.F. A review of low earth orbit occultation using microwave and infrared-laser signals for monitoring the atmosphere and climate. Adv. Space Res. 2017, 60, 2776–2811. [Google Scholar] [CrossRef]
- Tarantola, A.T.; Valette, B. Generalized nonlinear inverse problems solved using the least squares criterion. Rev. Geophys. Space Phys. 1982, 20, 219–232. [Google Scholar] [CrossRef]
- Lorenc, A.C. Analysis methods for numerical weather prediction. Q. J. R. Meteorol. Soc. 1986, 112, 1177–1194. [Google Scholar] [CrossRef]
- Rodgers, C.D. Retrieval of atmospheric temperature and composition from remote measurements of thermal radiation. Rev. Geophys. 1976, 14, 609–624. [Google Scholar] [CrossRef]
- Eyre, J.R. Assimilation of radio occultation measurements into a numerical weather prediction system. ECMWF Tech. Memo. No. 199 1994. [Google Scholar] [CrossRef]
- Zou, X.; Kuo, Y.-H.; Guo, Y.R. Assimilation of atmospheric radio refractivity using a nonhydostatic adjoint model. Mon. Weather. Rev. 1995, 123, 2229–2249. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Healy, S.B.; Romans, L.J. Initial results of combining GPS occultation with ECMWF global analyses within a 1DVar framework. Earth Planets Space 2000, 52, 885–892. [Google Scholar] [CrossRef]
- Palmer, P.I.; Barnett, J.; Eyre, J.; Healy, S.B. A non-linear optimal estimation inverse method for radio occultation measurements of temperature, humidity and surface pressure. J. Geophys. Res. 2000, 105, 17513–17526. [Google Scholar] [CrossRef]
- Von Engeln, A.; Nedoluha, G.; Kirchengast, G.; Bühler, S. One-dimensional variational (1-D Var) retrieval of temperature, water vapor, and a reference pressure from radio occultation measurements: A sensitivity analysis. J. Geophys. Res. 2003, 108, 4337. [Google Scholar] [CrossRef]
- ROM-SAF, Algorithm Theoretical Baseline Document: Level 2B and 2C 1DVar products Version 3.1. 2018. Available online: http://www.romsaf.org/product_documents.php (accessed on 20 October 2019).
- Wee, T.-K.; Kuo, Y.-H. Advanced stratospheric data processing of radio occultation with a variational combination for multifrequency GNSS signals. J. Geophys. Res. Atmos. 2014, 119, 11011–11039. [Google Scholar] [CrossRef]
- Vergados, P.; Mannucci, A.J.; Ao, C.O. Assessing the performance of GPS radio occultation measurements in retrieving tropospheric humidity in cloudiness: A comparison study with radiosondes, ERA-Interim, and AIRS data sets. J. Geophys. Res. 2014, 119, 7718–7731. [Google Scholar] [CrossRef]
- Kireev, S.; Ho, S.-P. NOAA STAR 1DVAR Retrieval Algorithm to Process Radio Occultation Data; IROWG: Elsinore, Denmark, 2019; p. 19025. [Google Scholar]
- Rieckh, T.; Anthes, R.; Randel, W.; Ho, S.-P.; Foelsche, U. Evaluating tropospheric humidity from GPS radio occultation, radiosonde, and AIRS from high-resolution time series. Atmos. Meas. Tech. 2018, 11, 3091–3109. [Google Scholar] [CrossRef]
- Rieckh, T.; Anthes, R.; Randel, W.; Ho, S.-P.; Foelsche, U. Tropospheric dry layers in the tropical western Pacific: Comparisons of GPS radio occultation with multiple data sets. Atmos. Meas. Tech. 2017, 10, 1093–1110. [Google Scholar] [CrossRef]
- ROM-SAF. The Radio Occultation Processing Package (ROPP) Overview. 2018. Available online: http://www.romsaf.org/software_docs.php (accessed on 20 October 2019).
- ROM-SAF. Algorithm Theoretical Baseline Document: Level 2A refractivity profiles Version 1.6. 2018. Available online: http://www.romsaf.org/product_documents.php (accessed on 20 October 2019).
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q.J.R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- COSMIC Data Analysis and Archive Center (CDAAC). Available online: https://cdaac-www.cosmic.ucar.edu/cdaac/cgi_bin/fileFormats.cgi?type=wetPrf (accessed on 20 October 2019).
- COSMIC Project Office. Variational Atmospheric Retrieval Scheme (VARS) for GPS Radio Occultation Data; Report; University Corporation for Atmospheric Research: Boulder, CO, USA, 2005.
- Steiner, A.K.; Kirchengast, G. Error analysis for GNSS radio occultation data based on ensembles of profiles from end-to-end simulations. J. Geophys. Res. 2005, 110, D15307. [Google Scholar] [CrossRef]
- Ho, S.-P.; Zhou, X.; Kuo, Y.-H.; Hunt, D.; Wang, J.-H. Global Evaluation of Radiosonde Water Vapor Systematic Biases using GPS Radio Occultation from COSMIC and ECMWF Analysis. Remote Sens. 2010, 2, 1320–1330. [Google Scholar] [CrossRef]
- Teng, W.-H.; Huang, C.-Y.; Ho, S.-P.; Kuo, Y.-H.; Zhou, X.-J. Characteristics of Global Precipitable Water in ENSO Events Revealed by COSMIC Measurements. J. Geophy. Res. 2013, 118, 1–15. [Google Scholar] [CrossRef]
- Zeng, Z.; Ho, S.-P.; Sokolovskiy, S. The Structure and Evolution of Madden- Julian Oscillation from FORMOSAT-3/COSMIC Radio Occultation Data. J. Geophy. Res. 2012, 117, D22108. [Google Scholar] [CrossRef]
- Kirchengast, G.; Fritzer, J.; Schwärz, M. ESA-OPSGRAS—Reference Occultation Processing System (OPS) for GRAS on MetOp and Other Past and Future RO Missions; WEGC-IGAM/UniGraz Proposal to ESA/ESTEC, Doc-Id: WEGC/ESA-OPSGRAS/Prop/v4May10; University of Graz: Graz, Austria, 2010. [Google Scholar]
- Scherllin-Pirscher, B.; Steiner, A.K.; Kirchengast, G. Deriving dynamics from GPS radio occultation: Three-dimensional wind fields for monitoring the climate. Geophys. Res. Lett. 2014, 41, 7367–7374. [Google Scholar] [CrossRef]
- Ladstädter, F.; Steiner, A.K.; Schwärz, M.; Kirchengast, G. Climate intercomparison of GPS radio occultation, RS90/92 radiosondes and GRUAN from 2002 to 2013. Atmos. Meas. Tech. 2015, 8, 1819–1834. [Google Scholar] [CrossRef]
- Scherllin-Pirscher, B.; Steiner, A.K.; Kirchengast, G.; Schwaerz, M.; Leroy, S.S. The power of vertical geolocation of atmospheric profiles from GNSS radio occultation. J. Geophys. Res. Atmos. 2017, 122, 1595–1616. [Google Scholar] [CrossRef]
- Kirchengast, G.; Schwärz, M.; Schwarz, J.; Scherllin-Pirscher, B.; Pock, C.; Innerkofler, J.; Proschek, V.; Steiner, A.K.; Danzer, J.; Ladstädter, F.; et al. The reference occultation processing system approach to interpret GNSS radio occultation as SI-traceable planetary system refractometer. In Proceedings of the OPAC-IROWG International Workshop, Seggau/Leibnitz, Austria, 8–14 September 2016; Available online: http://wegcwww.uni-graz.at/opacirowg2016/data/public/files/opacirowg2016_Gottfried_Kirchengast_presentation_261.pdf (accessed on 20 October 2019).
- Kirchengast, G.; Schwärz, M.; Angerer, B.; Schwarz, J.; Innerkofler, J.; Proschek, V.; Ramsauer, J.; Fritzer, J.; Scherllin-Pirscher, B.; Rieckh, T.; et al. Reference OPS DAD—Reference Occultation Processing System (rOPS) Detailed Algorithm Description; Tech. Rep. for ESA and FFG No. 1/2018, Doc-Id: WEGC-rOPS-2018-TR01, Issue 2.0; Wegener Center, Univ. of Graz: Graz, Austria, 2018. [Google Scholar]
- Schwarz, J.; Kirchengast, G.; Schwärz, M. Integrating uncertainty propagation in GNSS radio occultation retrieval: From bending angle to dry-air atmospheric profiles. Earth Space Sci. 2017, 4, 200–228. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Kirchengast, G. Wave-optics uncertainty propagation and regression-based bias model in GNSS radio occultation bending angle retrievals. Atmos. Meas. Tech. 2018, 11, 111–125. [Google Scholar] [CrossRef]
- Schwarz, J.; Kirchengast, G.; Schwärz, M. Integrating uncertainty propagation in GNSS radio occultation retrieval: From excess phase to atmospheric bending angle profiles. Atmos. Meas. Tech. 2018, 11, 2601–2631. [Google Scholar] [CrossRef]
- Schwarz, J. Benchmark Quality Processing of Radio Occultation Data with Integrated Uncertainty Propagation; Scientific Rep. No. 77-2018; Wegener Center Verlag: Graz, Austria, 2018; Available online: http://wegcwww.uni-graz.at/publ/wegcreports/2018/WCV-SciRep-No77-JSchwarz-July2018.pdf (accessed on 20 October 2019).
- Gruber, D. Climate-Quality Processing of Radio Occultation Data: Refractivity and Atmospheric Profiles Retrieval and Numerical Error Estimation. Master’s Thesis, University of Graz, Graz, Austria, 2014. [Google Scholar]
- Thayer, G. An improved equation for the refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Foelsche, U. Physics of Refractivity, in Tropospheric Water Vapor Imaging by Combination of Ground-Based and Spaceborne GNSS Sounding Data. Ph.D. Thesis, University of Graz, Graz, Austria, 1999. [Google Scholar]
- Healy, S.B. Refractivity Coefficients Used in the Assimilation of GPS Radio Occultation Measurements; GRAS SAF Report 09; Danish Meteorol. Inst.: Copenhagen, Denmark, 2009. [Google Scholar]
- Rüeger, J.M. Refractive Index Formulae for Electronic Distance Measurement with Radio and Millimetre Waves. In Proceedings of the JS28, Integration of Techniques and Corrections to Achieve Accurate Engineering, FIG XXII International Congress, Washington DC, USA, 13 January 2002. [Google Scholar]
- Aparicio, J.M.; Laroche, S. An evaluation of the expression of the atmospheric refractivity for GPS signals. J. Geophys. Res. 2011, 116, D11104. [Google Scholar] [CrossRef]
- Scherllin-Pirscher, B.; Kirchengast, G.; Steiner, A.K.; Kuo, Y.-H.; Foelsche, U. Quantifying uncertainty in climatological fields from GPS radio occultation: An empirical-analytical error model. Atmos. Meas. Tech. 2011, 4, 2019–2034. [Google Scholar] [CrossRef]
- Li, Y.; Kirchengast, G.; Scherllin-Pirscher, B.; Wu, S.; Schwärz, M.; Fritzer, J.; Zhang, S.; Carter, B.A.; Zhang, K. A new dynamic approach for statistical optimization of GNSS radio occultation bending angles for optimal climate monitoring utility. J. Geophys. Res. 2013, 118, 13022–13040. [Google Scholar] [CrossRef]
- Li, Y.; Kirchengast, G.; Scherllin-Pirscher, B.; Norman, R.; Yuan, Y.B.; Schwaerz, M.; Fritzer, J.; Zhang, K. Dynamic statistical optimization of GNSS radio occultation bending angles: An advanced algorithm and its performance analysis. Atmos. Meas. Tech. 2015, 8, 3447–3465. [Google Scholar] [CrossRef]
- Fritzer, J.; Kirchengast, G.; Pock, M. End-to-End Generic Occultation Performance Simulation and Processing System Version 5.6 Software User Manual (EGOPS5.6 SUM); Tech. Rep. for ESA/ESTEC No. 1/2010; Wegener Center and IGAM/Inst. of Physics, Univ. of Graz: Graz, Austria, 2010. [Google Scholar]
- Schwärz, M.; Kirchengast, G.; Scherllin-Pirscher, B.; Schwarz, J.; Ladstädter, F.; Angerer, B. Multi-Mission Validation by Satellite Radio Occultation—Extension Project (Final Report); Tech. Rep. for ESA/ESRIN No. 01/2016; Wegener Center, Univ. of Graz: Graz, Austria, 2016. [Google Scholar]
- Angerer, B.; Ladstädter, F.; Scherllin-Pirscher, B.; Schwärz, M.; Steiner, A.K.; Foelsche, U.; Kirchengast, G. Quality aspects of the Wegener Center multi-satellite GPS radio occultation record OPSv5.6. Atmos. Meas. Tech. 2017, 10, 4845–4863. [Google Scholar] [CrossRef]
- Schreiner, W.; Rocken, C.; Sokolovskiy, S.; Syndergaard, S.; Hunt, D. Estimates of the precision of GPS radio occultations from the COSMIC/FORMOSAT-3 mission. Geophys. Res. Lett. 2007, 34, L04808. [Google Scholar] [CrossRef]
| p | |||||
|---|---|---|---|---|---|
| 10.0 km | 20.0 km | 0.7 K | 3 K kmp | 0.5 | |
| 10.0 km | 17.0 km | 0.15% | 0.7 %kmp | 0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Kirchengast, G.; Scherllin-Pirscher, B.; Schwaerz, M.; Nielsen, J.K.; Ho, S.-p.; Yuan, Y.-b. A New Algorithm for the Retrieval of Atmospheric Profiles from GNSS Radio Occultation Data in Moist Air and Comparison to 1DVar Retrievals. Remote Sens. 2019, 11, 2729. https://doi.org/10.3390/rs11232729
Li Y, Kirchengast G, Scherllin-Pirscher B, Schwaerz M, Nielsen JK, Ho S-p, Yuan Y-b. A New Algorithm for the Retrieval of Atmospheric Profiles from GNSS Radio Occultation Data in Moist Air and Comparison to 1DVar Retrievals. Remote Sensing. 2019; 11(23):2729. https://doi.org/10.3390/rs11232729
Chicago/Turabian StyleLi, Ying, Gottfried Kirchengast, Barbara Scherllin-Pirscher, Marc Schwaerz, Johannes K. Nielsen, Shu-peng Ho, and Yun-bin Yuan. 2019. "A New Algorithm for the Retrieval of Atmospheric Profiles from GNSS Radio Occultation Data in Moist Air and Comparison to 1DVar Retrievals" Remote Sensing 11, no. 23: 2729. https://doi.org/10.3390/rs11232729
APA StyleLi, Y., Kirchengast, G., Scherllin-Pirscher, B., Schwaerz, M., Nielsen, J. K., Ho, S.-p., & Yuan, Y.-b. (2019). A New Algorithm for the Retrieval of Atmospheric Profiles from GNSS Radio Occultation Data in Moist Air and Comparison to 1DVar Retrievals. Remote Sensing, 11(23), 2729. https://doi.org/10.3390/rs11232729






