Assessment of the Impacts of Image Signal-to-Noise Ratios in Impervious Surface Mapping
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
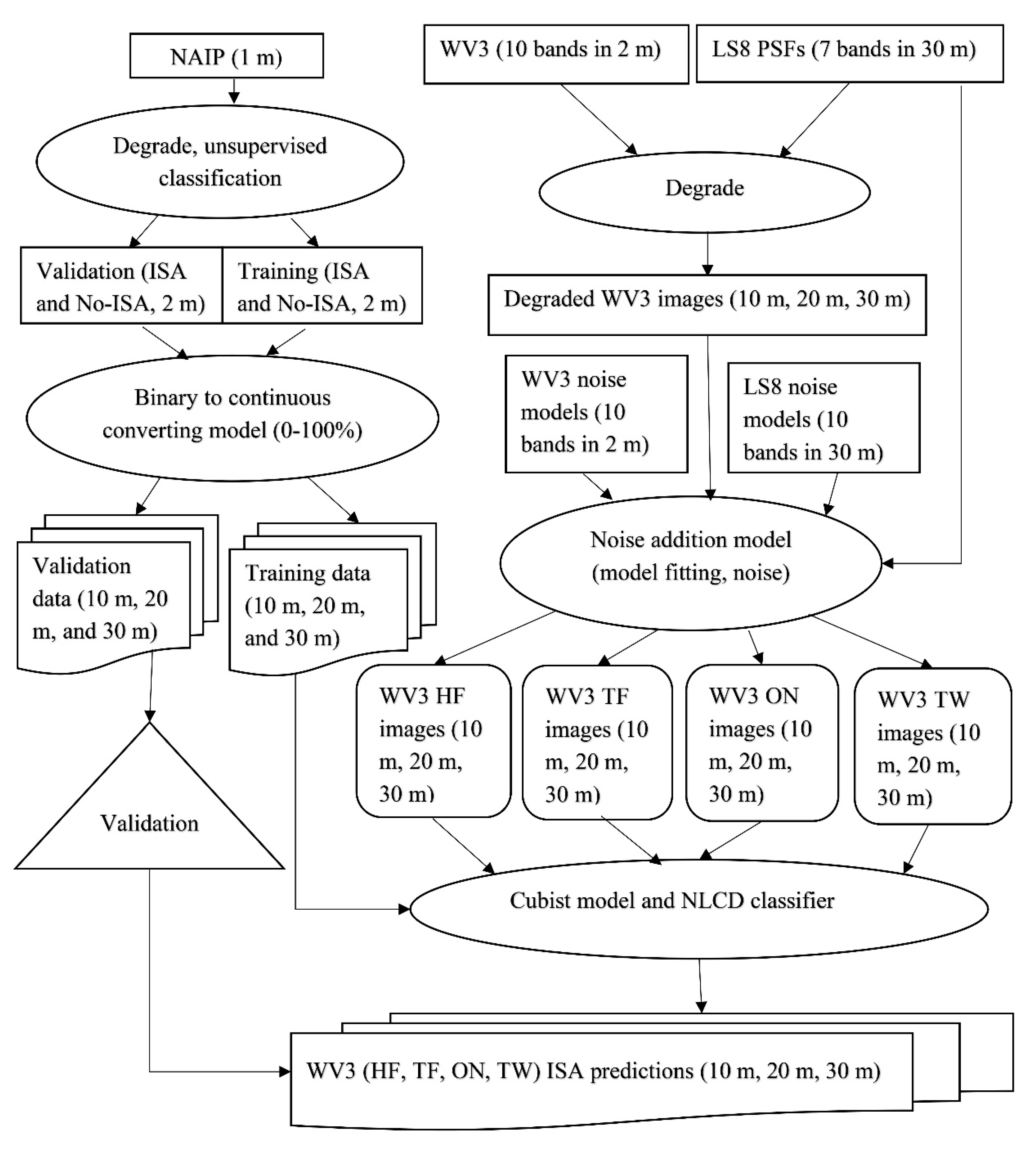
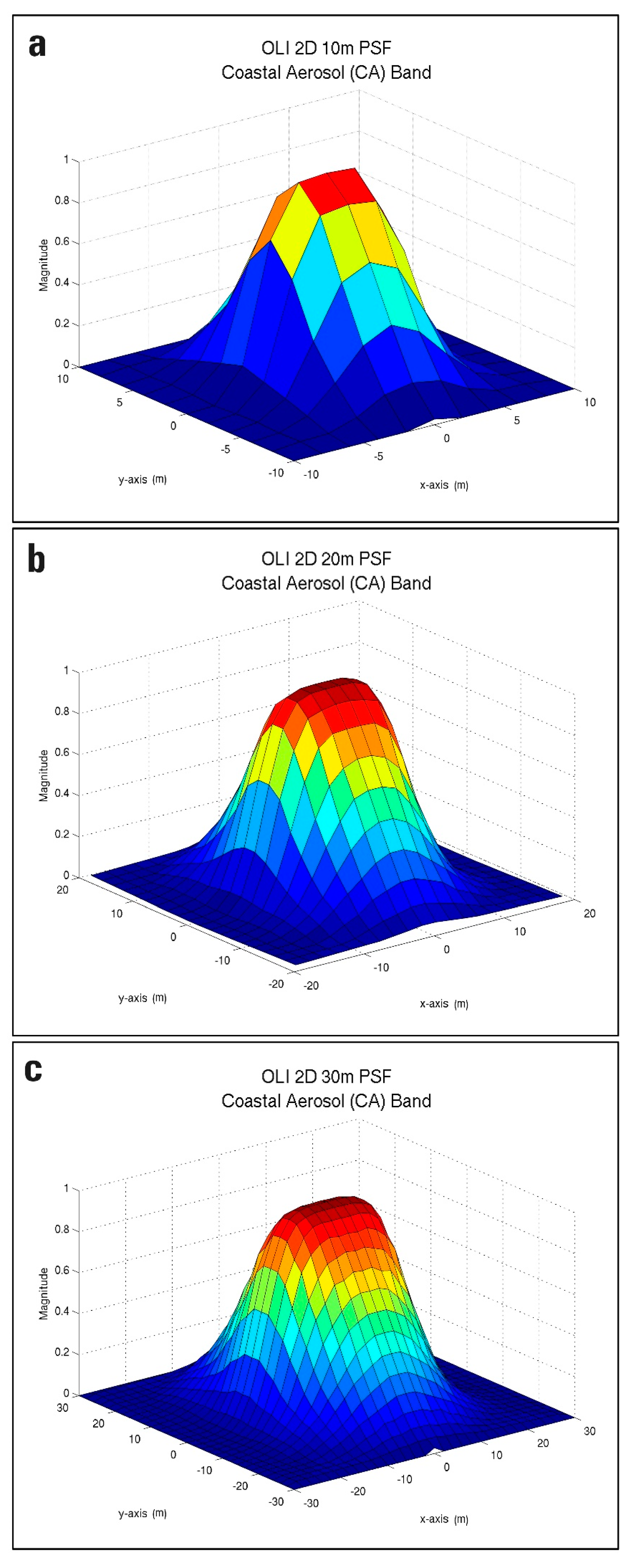
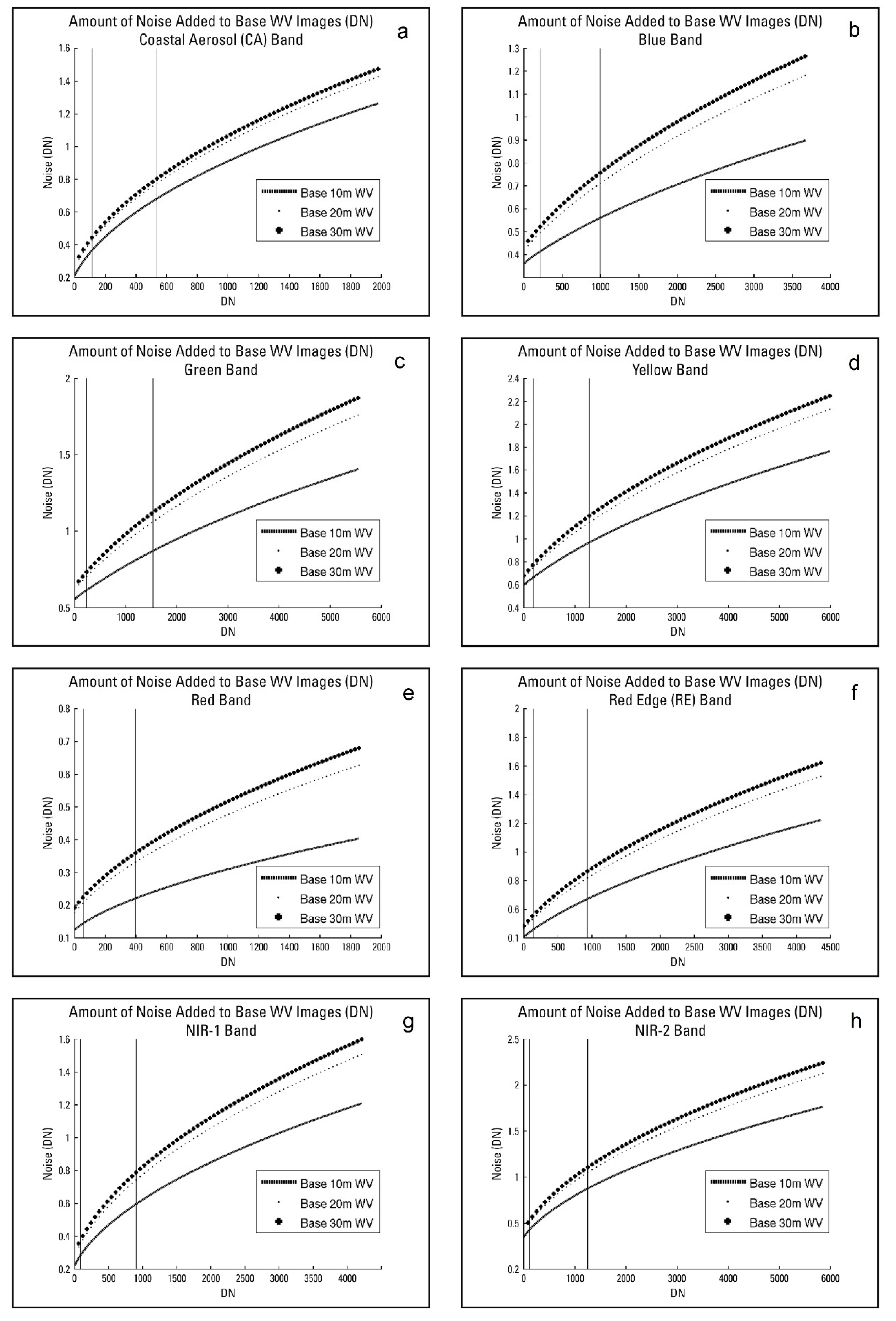
2.2. Simulation of WV3 Images with Different SNRs
3. Impervious Surface Mapping at Different Spatial Resolutions
3.1. Continuous Field Mapping with Remote Sensing Data
3.2. Accuracy Assessments for ISA Estimated by Images with Different SNRs
4. Results
4.1. Characteristics of Impervious Surfaces from Using Different SNR Data
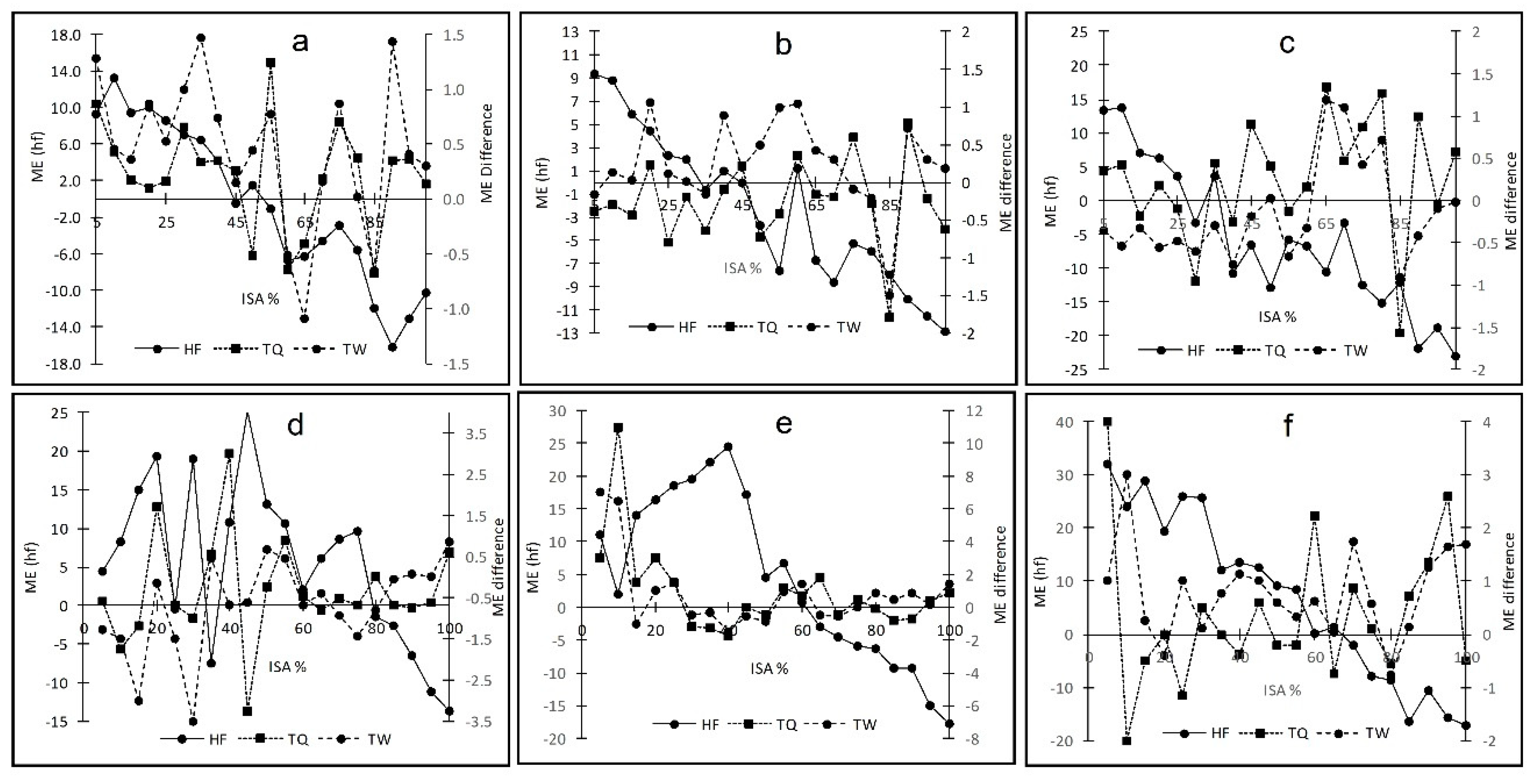
4.2. Accuracy of Impervious Surface Estimates
5. Discussion
5.1. Impact of Different SNR Data on Impervious Surface Mapping Accuracy
5.2. Implications for Future Landsat Missions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wulder, M.A.; Coops, N.C.; Roy, D.P.; White, J.C.; Hermosilla, T. Land cover 2.0. Int. J. Remote Sens. 2018, 39, 4254–4284. [Google Scholar] [CrossRef] [Green Version]
- Grekousis, G.; Mountrakis, G.; Kavouras, M. An overview of 21 global and 43 regional land-cover mapping products. Int. J. Remote Sens. 2015, 36, 5309–5335. [Google Scholar] [CrossRef]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S.; et al. Finer resolution observation and monitoring of global land cover: First mapping results with landsat tm and etm+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef]
- Topaloǧlu, R.H.; Sertel, E.; Musaoǧlu, N. Assessment of classification accuracies of sentinel-2 and landsat-8 data for land cover/use mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 1055–1059. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: Esa’s optical high-resolution mission for gmes operational services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Zhu, Z.; Liang, L.; Yu, B.; Cao, W. Mapping annual urban dynamics (1985–2015) using time series of landsat data. Remote Sens. Environ. 2018, 216, 674–683. [Google Scholar] [CrossRef]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using spot-5 hrg imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Seto, K.C.; Shepherd, J.M. Global urban land-use trends and climate impacts. Curr. Opin. Environ. Sustain. 2009, 1, 89–95. [Google Scholar] [CrossRef]
- IPCC. The physical science basis. In The Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 36. [Google Scholar]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef]
- Weng, Q.; Quattrochi, D.A.; Carlson, T.N. Remote sensing of urban environments: Special issue. Remote Sens. Environ. 2012, 117, 1–2. [Google Scholar] [CrossRef]
- Schneider, A.; Friedl, M.A.; Potere, D. Mapping global urban areas using modis 500-m data: New methods and datasets based on ‘urban ecoregions’. Remote Sens. Environ. 2010, 114, 1733–1746. [Google Scholar] [CrossRef]
- Small, C. A global analysis of urban reflectance. Int. J. Remote Sens. 2005, 26, 661–681. [Google Scholar] [CrossRef]
- Song, X.-P.; Sexton, J.O.; Huang, C.; Channan, S.; Townshend, J.R. Characterizing the magnitude, timing and duration of urban growth from time series of landsat-based estimates of impervious cover. Remote Sens. Environ. 2016, 175, 1–13. [Google Scholar] [CrossRef]
- Sexton, J.O.; Song, X.-P.; Huang, C.; Channan, S.; Baker, M.E.; Townshend, J.R. Urban growth of the Washington, D.C.–baltimore, md metropolitan region from 1984 to 2010 by annual, landsat-based estimates of impervious cover. Remote Sens. Environ. 2013, 129, 42–53. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Jebuv, M.N. A comparative assessment between object and pixel-based classification approaches for land use/land cover mapping using spot 5 imagery. Geocarto Int. 2014, 29, 351–369. [Google Scholar] [CrossRef]
- Shao, Z.; Fu, H.; Fu, P.; Yin, L. Mapping urban impervious surface by fusing optical and sar data at the decision level. Remote Sens. 2016, 8, 845. [Google Scholar] [CrossRef]
- Clark, M.L. Comparison of simulated hyperspectral hyspiri and multispectral landsat 8 and sentinel-2 imagery for multi-seasonal, regional land-cover mapping. Remote Sens. Environ. 2017, 200, 311–325. [Google Scholar] [CrossRef]
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Gong, P.; Liu, H.; Zhang, M.; Li, C.; Wang, J.; Huang, H.; Clinton, N.; Ji, L.; Li, W.; Bai, Y.; et al. Stable classification with limited sample: Transferring a 30-m resolution sample set collected in 2015 to mapping 10-m resolution global land cover in 2017. Sci. Bull. 2019, 64, 370–373. [Google Scholar] [CrossRef]
- Xian, G.; Crane, M. Assessments of urban growth in the tampa bay watershed using remote sensing data. Remote Sens. Environ. 2005, 97, 203–215. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. Use of impervious surface in urban land-use classification. Remote Sens. Environ. 2006, 102, 146–160. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Oltra-Carrió, R.; Sòria, G.; Bianchi, R.; Paganini, M. Impact of spatial resolution and satellite overpass time on evaluation of the surface urban heat island effects. Remote Sens. Environ. 2012, 117, 50–56. [Google Scholar] [CrossRef]
- Mathieu, R.; Freeman, C.; Aryal, J. Mapping private gardens in urban areas using object-oriented techniques and very high-resolution satellite imagery. Landsc. Urban Plan. 2007, 81, 179–192. [Google Scholar] [CrossRef]
- Willkomm, M.; Follmann, A.; Dannenberg, P. Rule-based, hierarchical land use and land cover classification of urban and peri-urban agriculture in data-poor regions with rapideye satellite imagery: A case study of nakuru, kenya. J. Appl. Remote Sens. 2019, 13, 016517. [Google Scholar] [CrossRef]
- Bouziani, M.; Goïta, K.; He, D.C. Automatic change detection of buildings in urban environment from very high spatial resolution images using existing geodatabase and prior knowledge. ISPRS J. Photogramm. Remote Sens. 2010, 65, 143–153. [Google Scholar] [CrossRef]
- Li, P.; Song, B.; Guo, J.; Xiao, X. A multilevel hierarchical image segmentation method for urban impervious surface mapping using very high resolution imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 103–116. [Google Scholar] [CrossRef]
- Hamedianfar, A.; Shafri, H.Z.M. Detailed intra-urban mapping through transferable obia rule sets using worldview-2 very-high-resolution satellite images. Int. J. Remote Sens. 2015, 36, 3380–3396. [Google Scholar] [CrossRef]
- Pacifici, F.; Chini, M.; Emery, W.J. A neural network approach using multi-scale textural metrics from very high-resolution panchromatic imagery for urban land-use classification. Remote Sens. Environ. 2009, 113, 1276–1292. [Google Scholar] [CrossRef]
- Weng, Q. Remote sensing of impervious surfaces in the urban areas: Requirements, methods, and trends. Remote Sens. Environ. 2012, 117, 34–49. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. Extraction of urban impervious surfaces from an ikonos image. Int. J. Remote Sens. 2009, 30, 1297–1311. [Google Scholar] [CrossRef]
- Dare, P.M. Shadow analysis in high-resolution satellite imagery of urban areas. Photogramm. Eng. Remote Sens. 2005, 71, 169–177. [Google Scholar] [CrossRef]
- Hsieh, P.-F.; Lee, L.C.; Chen, N.-Y. Effect of spatial resolution on classification errors of pure and mixed pixels in remote sensing. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2657–2663. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Esch, T.; Heldens, W.; Hirner, A.; Keil, M.; Marconcini, M.; Roth, A.; Zeidler, J.; Dech, S.; Strano, E. Breaking new ground in mapping human settlements from space—The global urban footprint. ISPRS J. Photogramm. Remote Sens. 2017, 134, 30–42. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, H.; Wang, Y. A new scheme for urban impervious surface classification from sar images. ISPRS J. Photogramm. Remote Sens. 2018, 139, 103–118. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Lin, H. Improving the impervious surfaces estimation with combined use of optical and sar remote sensing images. Remote Sens. Environ. 2014, 141, 155–167. [Google Scholar] [CrossRef]
- Jensen, J.R.; Cowen, D.C. Remote sensing of urban/suburb an infrastructure and socio-economic attributes. Photogramm. Eng. Remote Sens. 1999, 65, 611–622. [Google Scholar]
- Corner, B.; Narayanan, R.; Reichenbach, S. Noise estimation in remote sensing imagery using data masking. Int. J. Remote Sens. 2003, 4, 689–702. [Google Scholar] [CrossRef]
- Asmat, A.; Atkinson, P.M.; Foody, G.M. Geostatistically estimated image noise is a function of variance in the underlying signal. Int. J. Remote Sens. 2010, 31, 1009–1025. [Google Scholar] [CrossRef]
- De Boer, J.F.; Cense, B.; Park, B.H.; Pierce, M.C.; Tearney, G.J.; Bouna, B.E. Improved signal-to-noise ratio in spectral-domain compared with time-domain optical coherence tomography. Opt. Lett. 2003, 28, 2067–2069. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Sargent, I.M.; Foody, G.M.; Williams, J. Interpreting image-based methods for estimating the signal-to-noise ratio. Int. J. Remote Sens. 2005, 26, 5099–5115. [Google Scholar] [CrossRef]
- Liu, L.; Liu, X.; Hu, J. Effects of spectral resolution and snr on the vegetation solar-induced fluorescence retrieval using fld-based methods at canopy level. Eur. J. Remote Sens. 2017, 48, 743–762. [Google Scholar] [CrossRef]
- Jorge, D.; Barbosa, C.; De Carvalho, L.; Affonso, A.; Lobo, F.; Novo, E. Snr (signal-to-noise ratio) impact on water constituent retrieval from simulated images of optically complex amazon lakes. Remote Sens. 2017, 9, 644. [Google Scholar] [CrossRef]
- Gerace, A.D.; Schott, J.R.; Nevins, R. Increased potential to monitor water quality in the near-shore environment with landsat’s next-generation satellite. J. Appl. Remote Sens. 2013, 7, 1–18. [Google Scholar] [CrossRef]
- Huang, C.; Townshend, J.R.; Liang, S.; Kalluri, S.N.V.; DeFries, R.S. Impact of sensor’s point spread function on land cover characterization: Assessment and deconvolution. Remote Sens. Environ. 2002, 80, 203–212. [Google Scholar] [CrossRef]
- Xie, Y.; Weng, Q. Updating urban extents with nighttime light imagery by using an object-based thresholding method. Remote Sens. Environ. 2016, 187, 1–13. [Google Scholar] [CrossRef]
- Powell, R.; Roberts, D.; Dennison, P.; Hess, L. Sub-pixel mapping of urban land cover using multiple endmember spectral mixture analysis: Manaus, Brazil. Remote Sens. Environ. 2007, 106, 253–267. [Google Scholar] [CrossRef]
- Wu, C.; Murray, A.T. Estimating impervious surface distribution by spectral mixture analysis. Remote Sens. Environ. 2003, 84, 493–505. [Google Scholar] [CrossRef]
- USDA. Naip Imagery. Available online: https://www.fsa.usda.gov/programs-and-services/aerial-photography/imagery-programs/naip-imagery/index (accessed on 1 May 2018).
- Kruse, F.A.; Baugh, W.M.; Perry, S.L. Validation of digitalglobe worldview-3 earth imaging satellite shortwave infrared bands for mineral mapping. J. Appl. Remote Sens. 2015, 9, 096044. [Google Scholar] [CrossRef]
- Forster, B.C.; Best, P. Estimation of spot p-mode point spread function and derviation of a deconvolution filter. ISPRS J. Photogramm. Remote Sens. 1994, 49, 32–42. [Google Scholar] [CrossRef]
- USGS. Landsat Geometry. Available online: https://www.usgs.gov/land-resources/nli/landsat/landsat-geometry (accessed on 1 June 2018).
- DigitalGlobe. Worldview3. Available online: http://worldview3.digitalglobe.com/ (accessed on 1 April 2018).
- Morfitt, R.; Barsi, J.; Levy, R.; Markham, B.; Micijevic, E.; Ong, L.; Scaramuzza, P.; Vanderwerff, K. Landsat-8 operational land imager (oli) radiometric performance on-orbit. Remote Sens. 2015, 7, 2208–2237. [Google Scholar] [CrossRef]
- Xian, G.; Homer, C. Updating the 2001 national land cover database impervious surface products to 2006 using landsat imagery change detection methods. Remote Sens. Environ. 2010, 114, 1676–1686. [Google Scholar] [CrossRef]
- Xian, G.; Homer, C.; Rigge, M.; Shi, H.; Meyer, D. Characterization of shrubland ecosystem components as continuous fields in the northwest united states. Remote Sens. Environ. 2015, 168, 286–300. [Google Scholar] [CrossRef]
- Wylie, B.K.; Pastick, N.J.; Picotte, J.J.; Deering, C.A. Geospatial data mining for digital raster mapping. GISci. Remote Sens. 2019, 56, 406–429. [Google Scholar] [CrossRef]
- Shi, H.; Auch, R.F.; Vogelmann, J.E.; Feng, M.; Rigge, M.; Senay, G.; Verdin, J.P. Case study comparing multiple irrigated land datasets in arizona and colorado, USA. J. Am. Water Resour. Assoc. 2018, 54, 505–526. [Google Scholar] [CrossRef]
- Gu, Y.; Wylie, B.K.; Boyte, S.P.; Picotte, J.; Howard, D.M.; Smith, K.; Nelson, K.J. An optimal sample data usage strategy to minimize overfitting and underfitting effects in regression tree models based on remotely-sensed data. Remote Sens. 2016, 8, 943. [Google Scholar] [CrossRef]
- Maclachlan, A.; Roberts, G.; Biggs, E.; Boruff, B. Subpixel land-cover classification for improved urban area estimates using landsat. Int. J. Remote Sens. 2017, 38, 5763–5792. [Google Scholar] [CrossRef]
- Yang, L.; Xu, R.; Lei, T.; Li, J.; Ouyang, T. Design of near-infrared soil moisture measring instrument. Nongye Gongcheng Xuebao Trans. Chin. Soc. Agric. Eng. 2015, 31, 1–9. [Google Scholar]
- Darwish, W.; Tang, S.; Li, W.; Chen, W. A new calibration method for commercial rgb-d sensors. Sensors 2017, 17, 1204. [Google Scholar] [CrossRef]
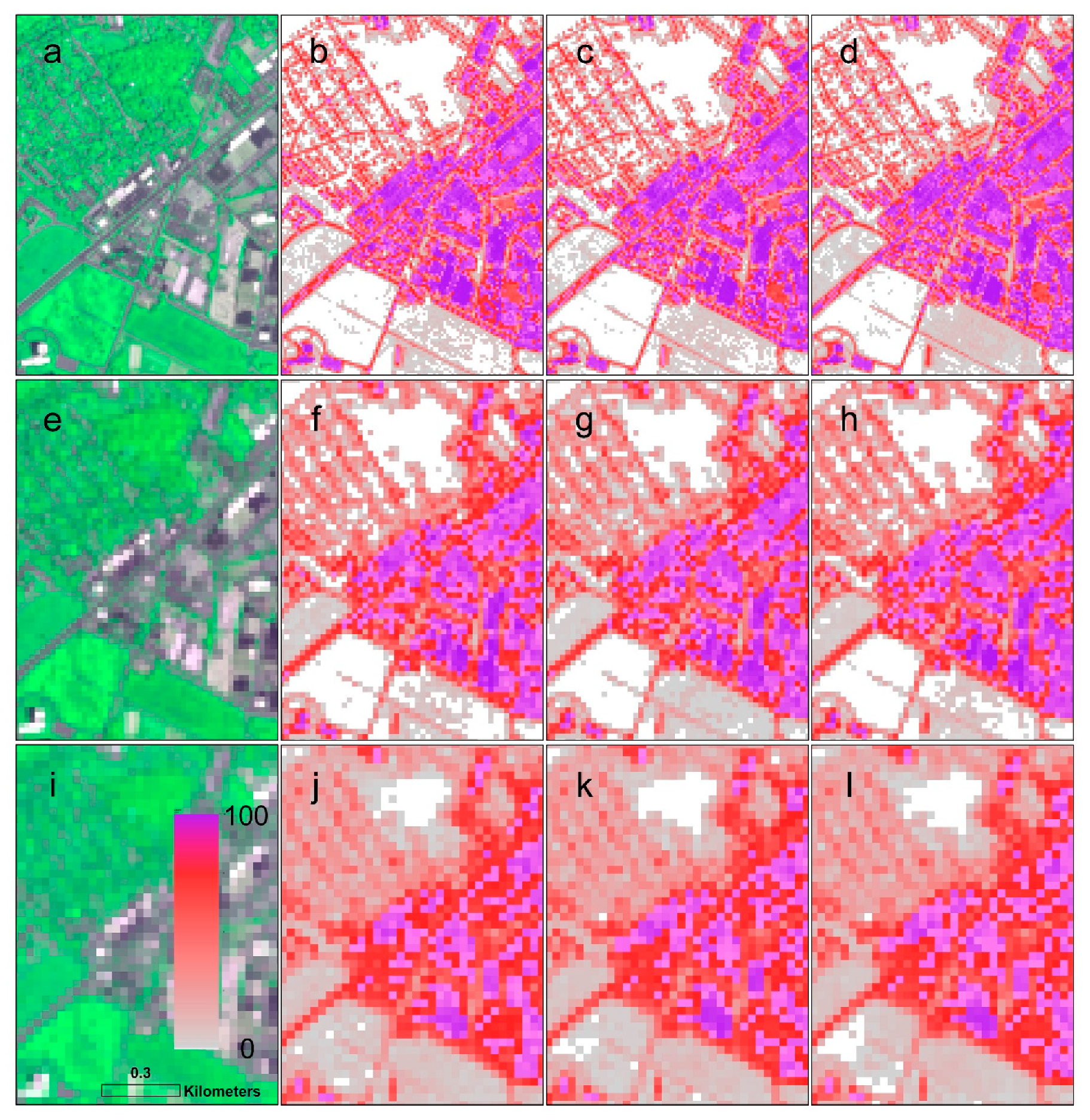
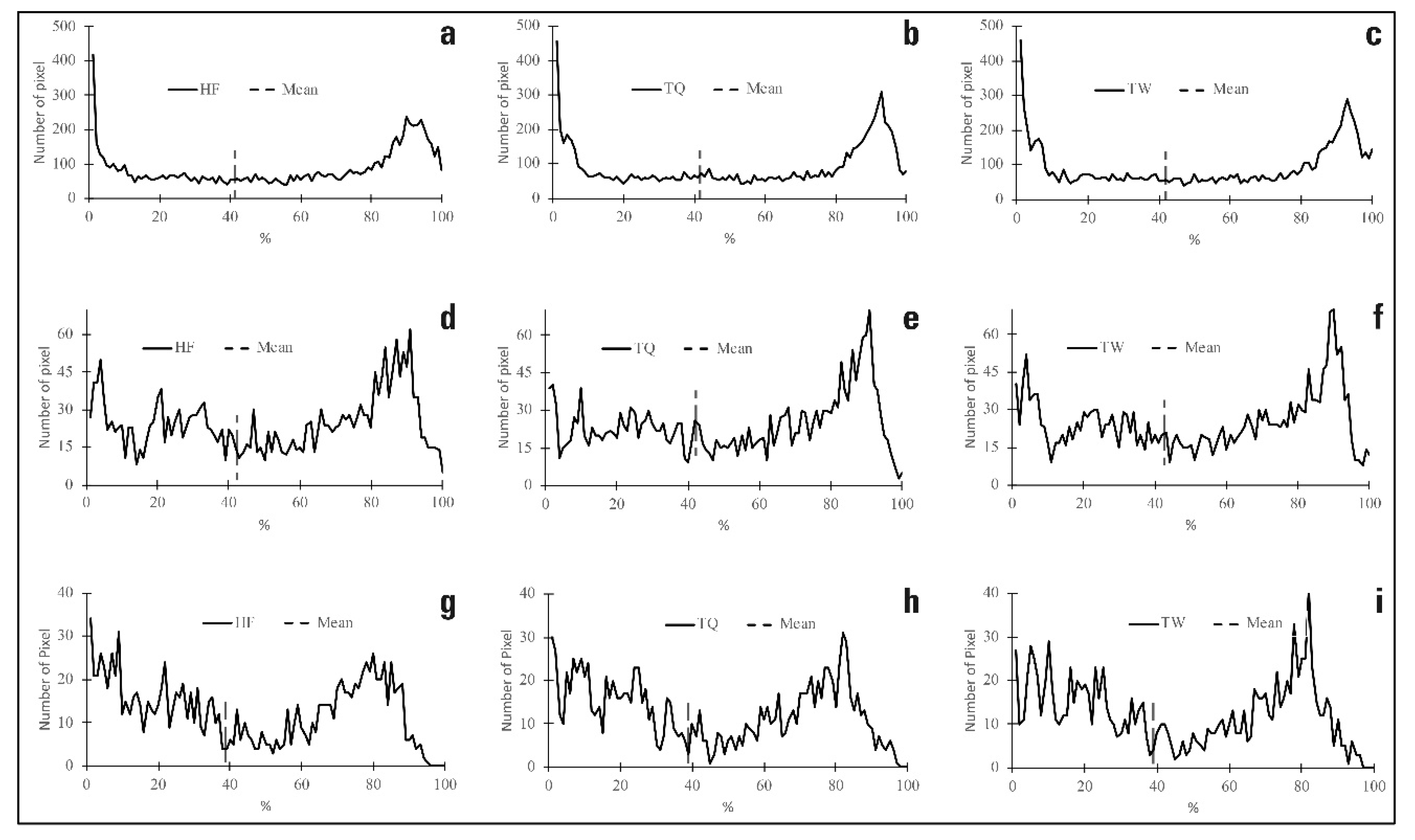

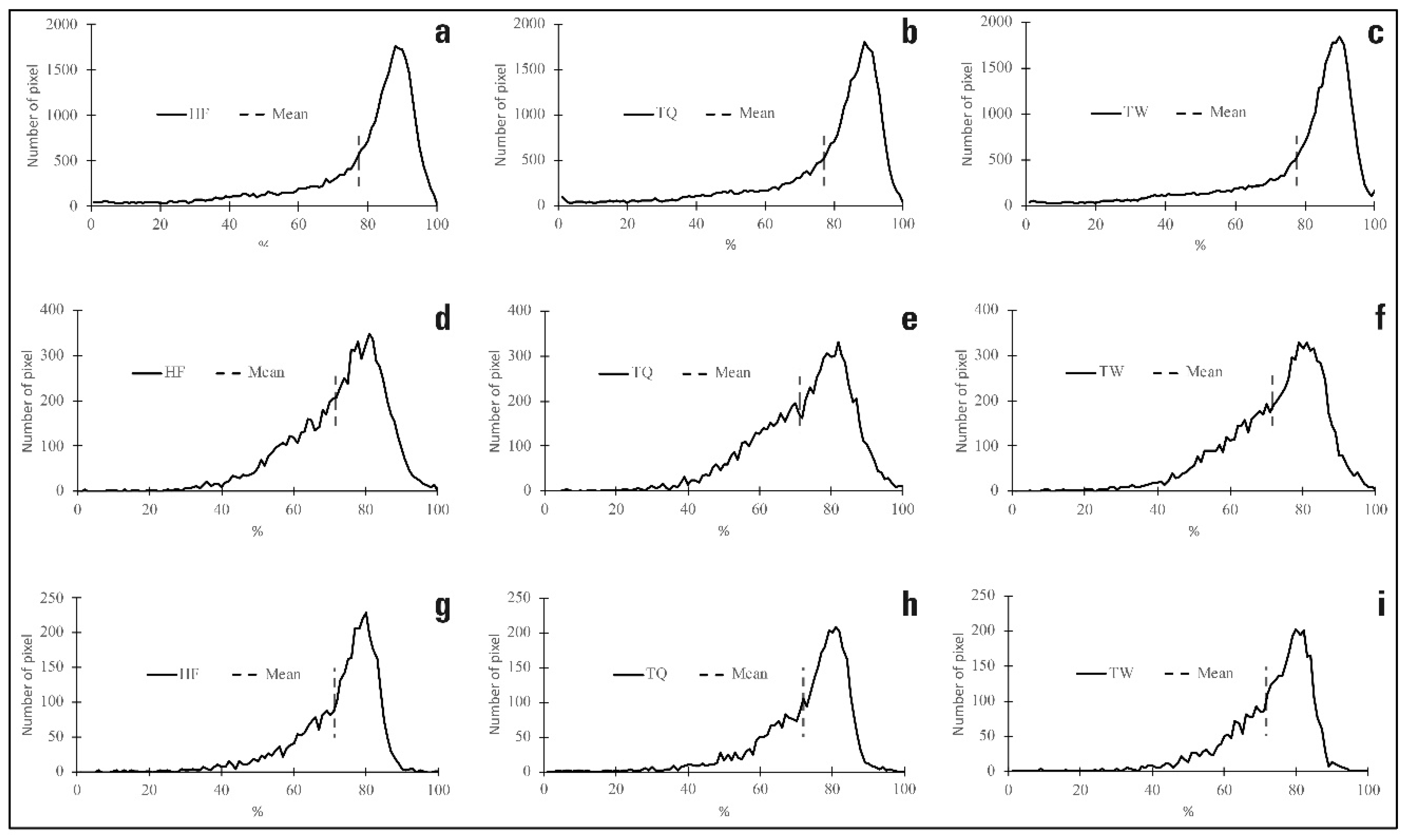
| Source (Bands) | NAIP (Blue, Green, Red, NIR-1); WV3 (Coastal, Blue, Green, Yellow, Red, Red edge, NIR-1, NIR-2 (2 m, 10 m, 20 m, 30 m)) | |
| Location | Beltsville, MD | San Francisco, CA |
| Date | 24/07/2015 (NAIP) 17/05/2017 (WV3) | 25/06/2016 (NAIP) 08/03/2017 (WV3) |
| Sensor | Area | Beltsville, MD | San Francisco, CA | ||
|---|---|---|---|---|---|
| WorldView-3 | Training | Validation | Training | Validation | |
| 10 m | 10,000 | 350 | 10,000 | 300 | |
| 20 m | 8000 | 290 | 8000 | 250 | |
| 30 m | 7000 | 290 | 7000 | 250 | |
| Resolution | SNR levels | RMSE | ME | RAE | r2 | M_m | M_v |
|---|---|---|---|---|---|---|---|
| 10 m | HF | 19.95 | −0.47 | −0.90 | 0.67 | 53 | |
| TQ | 19.83 | −0.22 | −0.42 | 0.67 | 52 | 51 | |
| TW | 19.68 | 0.01 | 0.02 | 0.68 | 51 | ||
| 20 m | HF | 17.29 | −0.34 | −0.82 | 0.70 | 36 | |
| TQ | 17.29 | −0.63 | −1.50 | 0.70 | 36 | 35 | |
| TW | 17.12 | −0.12 | −0.29 | 0.70 | 36 | ||
| 30 m | HF | 22.39 | −1.48 | −3.86 | 0.48 | 30 | |
| TQ | 22.49 | −1.25 | −3.27 | 0.48 | 30 | 31 | |
| TW | 22.43 | −1.71 | −4.47 | 0.48 | 31 |
| Resolution | SNR levels | RMSE | ME | RAE | r2 | M_m | M_v |
|---|---|---|---|---|---|---|---|
| 10 m | HF | 17.69 | 0.66 | 1.00 | 0.62 | 76 | |
| TQ | 17.02 | 0.45 | 0.68 | 0.64 | 75 | 71 | |
| TW | 16.90 | 0.37 | 0.56 | 0.65 | 74 | ||
| 20 m | HF | 16.91 | −1.02 | −1.42 | 0.49 | 68 | |
| TQ | 16.94 | −0.79 | −1.21 | 0.49 | 68 | 70 | |
| TW | 16.77 | −0.68 | −1.04 | 0.50 | 69 | ||
| 30 m | HF | 17.28 | 0.95 | 1.54 | 0.46 | 65 | |
| TQ | 17.36 | 1.38 | 2.23 | 0.46 | 65 | 64 | |
| TW | 17.36 | 1.03 | 2.71 | 0.47 | 64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xian, G.; Shi, H.; Anderson, C.; Wu, Z. Assessment of the Impacts of Image Signal-to-Noise Ratios in Impervious Surface Mapping. Remote Sens. 2019, 11, 2603. https://doi.org/10.3390/rs11222603
Xian G, Shi H, Anderson C, Wu Z. Assessment of the Impacts of Image Signal-to-Noise Ratios in Impervious Surface Mapping. Remote Sensing. 2019; 11(22):2603. https://doi.org/10.3390/rs11222603
Chicago/Turabian StyleXian, George, Hua Shi, Cody Anderson, and Zhuoting Wu. 2019. "Assessment of the Impacts of Image Signal-to-Noise Ratios in Impervious Surface Mapping" Remote Sensing 11, no. 22: 2603. https://doi.org/10.3390/rs11222603
APA StyleXian, G., Shi, H., Anderson, C., & Wu, Z. (2019). Assessment of the Impacts of Image Signal-to-Noise Ratios in Impervious Surface Mapping. Remote Sensing, 11(22), 2603. https://doi.org/10.3390/rs11222603






