1. Introduction
SAR image segmentation is a foundation for many high-level interpretation tasks. Accurate segmentation can greatly reduce the difficulty of subsequent advanced tasks (e.g., target recognition [
1,
2], target detection [
3], change detection [
4], etc.). With the development of Synthetic Aperture Radar (SAR) imaging sensors, the resolution of SAR images has increased considerably [
5,
6], which also brings the explosion of SAR data, termed big SAR imagery data. The common segmentation frameworks aim at assigning optimal labels to each pixel using some classifiers (e.g., fuzzy-based classification [
7], associative classification [
8], sparse representation [
9]). The computational burden of these algorithms in big SAR data is still a handicap.
With the appearance of superpixel generation models (e.g., Simple Linear Iterative Clustering (SLIC) [
10]), the superpixel-wise segmentation algorithms have received considerable attention [
11]. The superpixel generation models usually employ the unsupervised clustering algorithms to cluster the adjacent and similar pixels together to form a superpixel. Superpixels can greatly improve the efficiency of the segmentation algorithm in big data while preserving the images’ edge information. As the over-segmented image becomes graph-structure data, most of the previous superpixel-wise segmentation methods employ the probabilistic graphical models (e.g., Conditional Random Fields (CRF) [
11,
12]) to segment the nodes of the graphs [
13]. Probabilistic graphical models can capture the appearance and spatial consistency [
14,
15], but they usually have a heavy computational burden [
16]. Take CRF as an example: in addition to learning the coefficients utilizing Structured Support Vector Machine (SSVM) [
17] or other classifiers [
18,
19,
20], the testing stage of CRF also requires an inference algorithm to find the optimal label sequence by pursuing the Maximum A Posteriori (MAP).
In order to improve the computational efficiency of the segmentation algorithms in the test phase, we propose to use the Graph Convolution Network (GCN) to segment the nodes of graph structure data. GCN is an important variant of Graph Neural Networks (GNNs) proposed in the last two years, which generalizes Convolutional Neural Networks (CNN) to the graph domain and can directly deal with more general graphs, e.g., directed and undirected graphs. GCN can capture the dependence of graphs via message passing between the nodes of graphs and have ground-breaking performance on many tasks. Unlike CRF, GCN can directly predict the optimal label sequence of superpixels without the inference algorithm. Moreover, GCN is easier to implement using deep learning methods and has a powerful fitting capacity.
At present, there are two main types of graph convolution methods, namely spatial approaches [
21,
22,
23] and non-spectral approaches [
24,
25,
26]. Graph belongs to non-Euclidean structures, and the number of the adjacent nodes of different nodes is not the same. Non-spatial methods aim at transforming graph-structure data into the Euclidean structure by redefining the neighbour regions of nodes [
27], so that all the nodes have the same number of the adjacent nodes and the traditional CNN [
28] can process the data. These types of approaches generally have two steps: (1) select the most representative nodes to form the sequence of the nodes to be segmented, and (2) define a fixed size neighbouring field for each selected node. The nodes in the neighbouring field are regarded as the adjacent nodes of the centred node. Researchers need to design a screening rule to ensure that the numbers of nodes in the neighbouring fields for all the selected nodes are equal. Many parameters need to be manually designed according to experience or experimental results, which leads to instable performance on segmentation.
The spectral models were first proposed by Bruna et al. [
21]. Bruna et al. defined the Fourier transform on graphs and deduced the convolution operation in the Fourier domain using the convolution theorem. Because of the need for computing the Eigen decomposition of the graph Laplacian, this type of convolution operation has potentially intensive computations. Later, Defferrard et al. [
22] improved the convolution using Chebyshev expansion of the graph Laplacian to estimate the filters, avoiding computing the Eigen decomposition of the graph Laplacian. Kipf et al. [
23] further simplified the GCN using an efficient layer-wise propagation rule that was based on a first-order approximation of spectral convolutions on graphs. As the parameters of this type of GCN are limited and can be automatically learned using stochastic gradient descent, it has been successfully applied in many machine learning problems.
More recently, Petar et al. [
29] proposed the Graph Attention Network (GAT) by combining the attention mechanisms with the GCN models. The focus of attention is an important regulatory mechanism in biological vision systems, which refers to the fact that humans selectively spend more computing resources on the regions of interest in the scenes. Attention mechanisms have been widely applied in deep learning, which contribute to making deep networks focus on the most relevant parts of the input to make decisions. The specific implementation of GAT is to compute the attention coefficients between two adjacent nodes in each convolutional layer. The attention coefficients indicate how close the two nodes are in the feature space. However, in each layer of GAT, the coefficients are calculated by the use of the output of the previous layer. In the deeper layers of GAT, more noisy information from the neighbourhoods is propagated into the nodes, inevitably reducing the precision of the attention coefficients. Inaccurate coefficients in turn lead to more noise embedded into the features of the nodes through the following convolution operation.
In this work, we propose a novel superpixel-wise Attention GCN (AGCN) for SAR image segmentation. In order to reduce the computational cost while maintaining the edge information of the input image, the input is over-segmented to superpixels. Then, a trained CNN is used to extract the features of the superpixels, converting the input image into a graph. Finally, a novel attention GCN is proposed for node segmentation on the graph-structure data. The novel aspects of our proposed algorithm consist of the following aspects:
(1) This method combines CNN and GCN networks to perform image segmentation rapidly in big SAR imagery data. CNNs are extremely efficient architectures at exploiting the translational invariance of a signal, but cannot directly process graph-structure data. In our approach, CNN is used to explore the feature vectors of superpixels. Then, an attention GCN is introduced to predict the labels of nodes on graphs.
(2) We propose a novel attention GCN model to improve the segmentation results. Compared to the previous attention GCN models (e.g., GAT), our AGCN has only one attention layer, which means less learnable network parameters and less computation burden in each training iteration. The attention mechanism layer is located before the graph convolution layers. One benefit is that the learned attention coefficients can be utilized to update the graph Laplacian, so that the following graph convolution layers can pay more attention to the important nodes. Another benefit is that this structure can prevent the negative influence of noisy information from context nodes for the attention coefficients.
The rest of this paper is organized as follows. Previous graph convolution networks in the spectral domain are reviewed in
Section 2.
Section 3 presents the proposed method, including the architecture and training steps of our AGCN network. Experiments and the results are presented in
Section 4.
Section 5 presents the discussion in terms of pros and cons.
Section 6 gives the conclusion.
2. Related Work
In this section, we review the previous GCN-based approaches for node classification or segmentation, which are closely related to our method. Shuman et al. [
30] first generalized the Fourier transform to the signals defined on graphs and further defined the convolution operation for graph-structure data. The convolution operation is the multiplication of a graph-structure signal
with a filter
, expressed as:
where
represents the diagonal matrix of the eigenvalues of the normalized graph Laplacian
(
is the adjacency matrix of the graph, and
D denotes the degree matrix).
represents the eigenvectors of
.
is the result of the Fourier transform of
. Later on, Bruna et al. [
21,
31] simplified
as a matrix parameterized by
. The output of the graph convolution operation is:
One disadvantage of the this GCN model is the potentially intense computations, which require computing the Eigen decomposition of the graph Laplacian and the product of , and . The total computational complexity is , where is the number of the nodes in a graph. Moreover, there are parameters to be learned, making training difficult and time consuming.
In response to the above problems, Defferrard et al. [
22] designed a fast localized convolutional filter on graphs, where the filter
is approximated as a polynomial filter:
where
is a trainable polynomial coefficient. The spectral filter approximated by the
-order polynomials are
-localized. In other words, this convolution opera only depends on nodes that are at a maximum of
steps away from the central node (
-order neighbourhood). Consequently, the formulation of convolution on graphs can be written as:
In this case, a convolution filter contains only
parameters, and there is no need to calculate the Eigen decomposition in the convolution operation. However, the computational complexity of
is still high with
. A solution to this problem is to parametrize
as a truncated expansion in terms of Chebyshev polynomials up to the
order [
23], namely:
where
and
is the maximum eigenvalue of
.
denotes the Chebyshev coefficient vector. The definition of the Chebyshev polynomial is
, where
and
. Kipf et al. [
23] approximated
and limited the layer-wise convolution operation to
, deducing the linear formulation of a layer of GCN as follows:
where
and
. This definition is finally generalized to an input signal
as follows:
where
denotes a set of filters.
is the convolved signal matrix.
is the dimension of nodes’ feature vectors, and
is the number of filters. The complexity of the above layer-wise convolution operation reduces to
, where
denotes the number of edges.
It has been proven that attention mechanisms can effectively improve the performance of CNN-based models by guiding these algorithms to focus on the most relevant parts of the input to make decisions. Petar et al. [
29] introduced a self-attention strategy into the GCN network, namely GAT. In GAT, the importance of different neighbouring nodes for the central node in a specific task is different. In each layer of GAT, the attention coefficients between two adjacent nodes are first computed as follows:
where
is the feature vector of node
i.
is a weight matrix, linearly transforming
;
denotes transposition, and
represents the concatenation operation.
performs self-attention on the nodes.
indicates the importance of node
’s information to node
. Then, the normalized attention coefficients are employed to calculate a linear combination of the features corresponding to them, to serve as the hidden representations for each node.
where
denotes some neighbourhood of node
in the graph. The more important node
is to node
, the more the subsequent convolution operation will pay attention to node
when computing the hidden feature of node
, thus improving the accuracy of node classification.
3. Methodology
GAT needs to calculate the attention coefficient and perform the convolution operation in each layer of the network. The hidden feature of the central node is the weighted sum of its adjacent node features. This means that, after the convolution operation, the central node will include both the characteristics of the node itself and the information of the surrounding nodes. The attention coefficient in the next layer cannot accurately indicate the importance of node ’s features to that of node . The inaccuracy of attention coefficients further reduces the precision of the hidden representation of nodes in the next layer. As the number of the convolution layers increases, the noise in the node representation will grow exponentially, causing poor segmentation results.
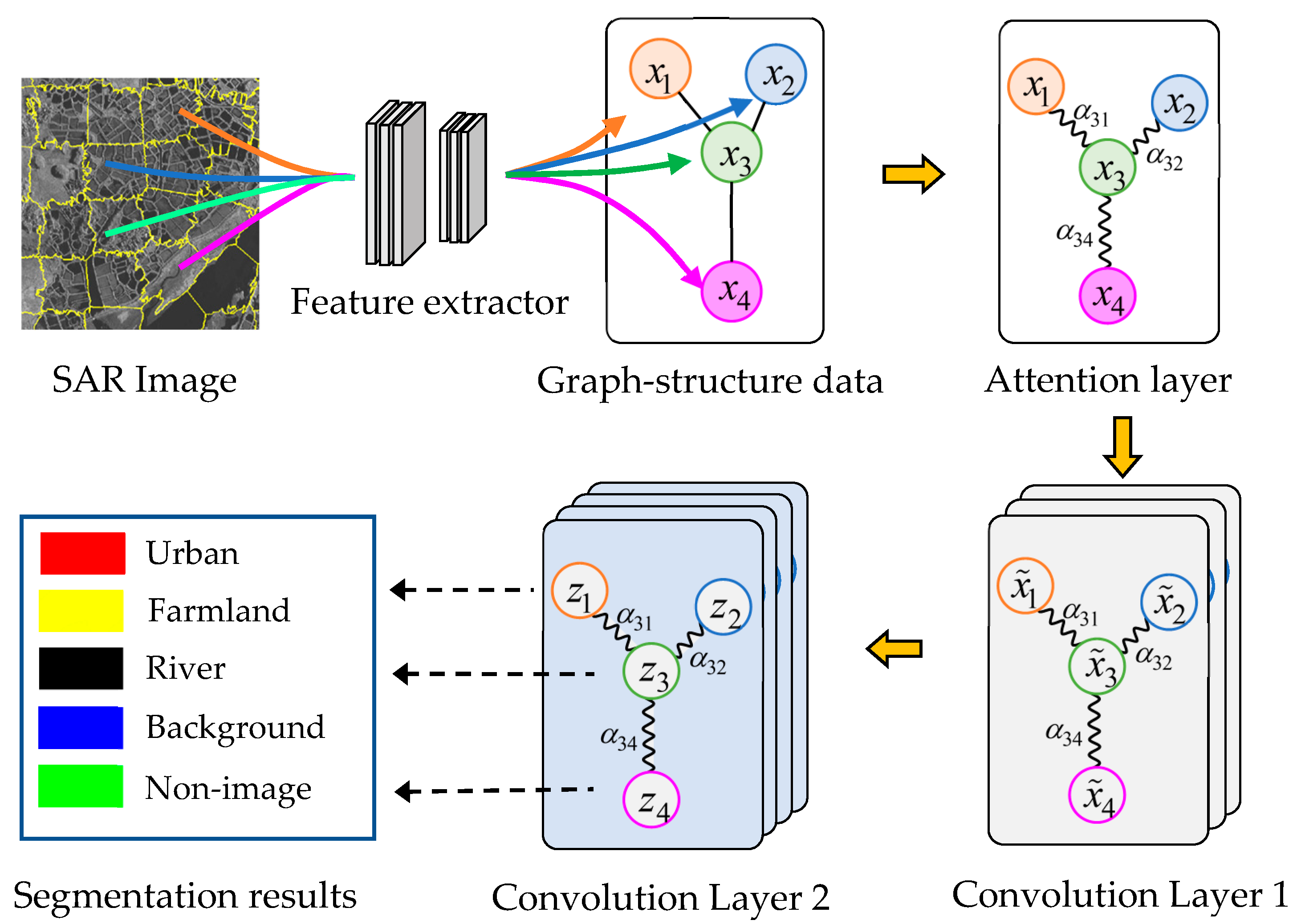
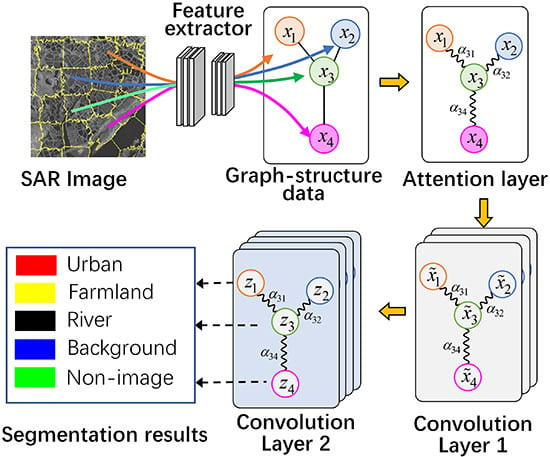
This paper presents a new Attention GCN model (AGCN) that resolves this problem. The structure of the AGCN for SAR image segmentation is shown in
Figure 1. The method firstly uses an over-segmentation algorithm SLIC to segment the input image into a set of superpixels. It models the input SAR image into a graph, where a node represents a superpixel and adjacent superpixels are connected with the edges. Then, a supervised CNN is employed to extract the feature vectors of superpixels. The AGCN shown in
Figure 1 contains an attention layer and two graph convolution layers, where
in Convolution Layer 1 represents the feature of node
after the first convolution and
indicates the predicted class of node
by the second convolutional layer. The attention layer aims to calculate the attention coefficients between adjacent nodes, i.e.,
, and revise the graph Laplacian. The subsequent graph convolutional layers explore the hidden feature of nodes and segment the nodes based on the updated graph Laplacian.
3.1. Graph Construction
In order to meet the real-time requirements in processing big SAR imagery data, we first need to over-segment the large-scale airborne SAR images into superpixels using the SLIC proposed in [
10]. Compared with the rectangular patches frequently used in deep learning, superpixels can preserve the edge information of the scene, while effectively speeding up the segmentation algorithm. We represent the superpixels obtained from a SAR image as
, where
is the number of superpixels.
An input SAR image is modelled as an undirected graph model , where each superpixel corresponds to a vertex. Each node is only connected to its neighbouring nodes. In other words, those nodes sharing common boundaries will be connected by edges. and respectively represent the set of all the vertices and edges.
In order to extract the feature of irregular superpixels using CNN, we place each superpixel into a rectangular patch. The centroid of the superpixel is located at the central of the patch. The pixels in the patch not belonging to the superpixel regions are set as zero. The CNN network consists of several convolutional layers, fully connected layers, and a SoftMax layer, which are updated with a random gradient descent method. After training, the convolutional layers and fully connected layers form the feature extraction network, and the feature vector of superpixel is expressed as .
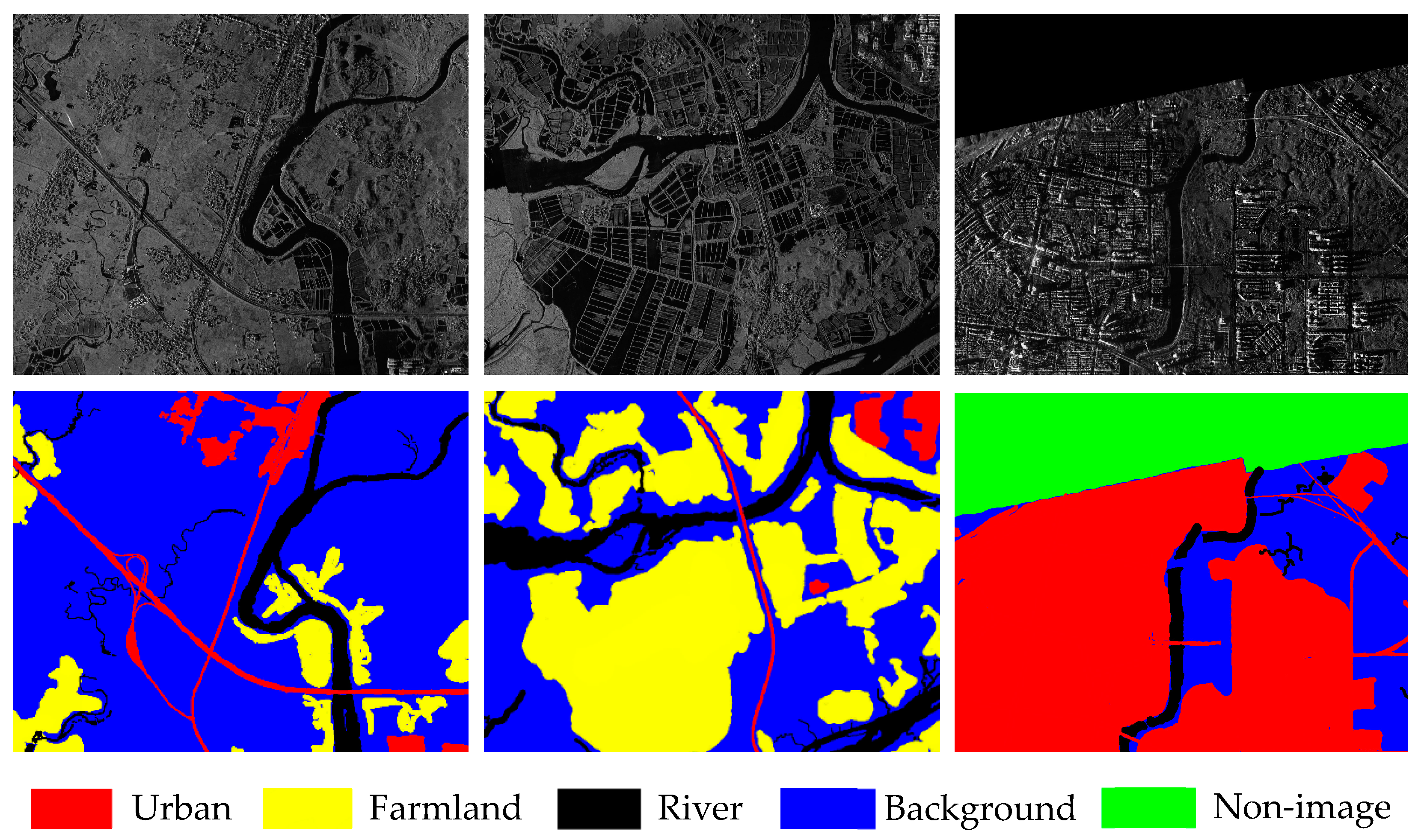
3.2. Superpixel-Based Voting
The ground truth in the training set only provides the pixel-wise labels. Although SLIC considers the various text features and boundary information in the process of over-segmentation, it is still possible to include different kinds of pixels in one superpixel. Hence, we utilize a majority voting strategy to obtain the labels of superpixels. Let
denote the ground truth of a training image.
represents the corresponding area of
in the ground truth
. There are
pixels in the superpixel, i.e.,
, and the category of the
mth pixel is represented as
. Then, the number of pixels in
belonging to each category is counted, and the most frequent class will be selected as the category of
, represented as:
where
denotes an indicator function,
,
.
is the possible class in the training dataset. The same voting scheme is applied in all the superpixels in both the training and testing dataset to acquire their labels.
3.3. Attention Mechanism Layer
The first layer of the network is the attention layer. Similar to the GAT model, we inject the graph structure into the mechanism by performing masked attention; we only compute the attention coefficients between adjacent nodes. In all the follow-up experiments, these will be exactly the first-order neighbours of node
. In our framework, the attention coefficients
is defined as:
where
is a
parameter vector, representing the weights of diverse elements of the feature vectors.
is essentially a linear combination of the combined features.
indicates the importance of node
j to node
in the task of segmentation. The more important node
is to node
, the greater the attention coefficient
eij. Note that the GAT model requires a learnable parameter matrix
to transform linearly the features of nodes into higher-level features before we calculate attention coefficients in Equation (8). The linear transformation matrix
is also the convolution kernel in Equation (9). The input features extracted by CNN already obtain sufficient expressive power, and there is no need to transform the feature again. Furthermore, the subsequent convolution operations are also linear transformations for node features, so the transformation here is repetitive and redundant. It is also difficult to ensure the simultaneously accuracy of the convolution operation and the linear transformation during the training process.
Then, we employ the SoftMax function to normalize the attention coefficients of each node:
where
are all the neighbourhoods of node
i in the graph.
represents the normalized attention coefficient.
indicates the activation function LeakyReLU. Normalization realizes
and makes coefficients easily comparable across different nodes. Let
represent the attention coefficient vector of node
. If node
, the corresponding attention coefficient
, and we define
. The coefficient vectors of all the nodes form the matrix of attention coefficients
. It can be seen that
is a symmetric matrix, i.e.,
.
In the following spectral convolution layers, we adopt the definition used in Equation (7), where the convolution of a signal
(a C-dimensional feature vector for each node) and
filters is defined as
.
is named as the generalized graph Laplacian, and it contains the structure information of the graph. In order to make the learned attention coefficients guide the following convolution operation, we utilize the attention coefficient matrix to update
:
where
is the Hadamard product, representing the product of the corresponding elements of two matrices. The above process is the attention layer of the AGCN network. The elements of the updated generalized graph Laplacian
not only represent the structural information of the graph model (which nodes are connected), but also denotes the relationship between the two adjacent nodes in the feature space. Subsequent convolution layers can pay more attention to important nodes with the following expression:
3.4. Attention Graph Convolutional Network
In this section, we will provide a multi-layer attention GCN for node segmentation on graphs. In the GAT model, each layer needs to calculate the attention coefficients before convolution. However, we find that this improvement leads to the decline in performance of GAT when segmenting many SAR images. It is because much context information from adjacent superpixels has flown into the central superpixels after the first convolution operation. In the second convolution layer, these features are then utilized to calculate the attention coefficients. The existence of background information makes it impossible for coefficients to represent accurately the relationship between two nodes in feature space. The inaccurate coefficients further cause more noise in the following convolution operation. These errors are propagated to the next convolution layer. With the layers being deeper, the errors in the coefficients and nodes’ features will expand exponentially, leading to a sharper decline in the final segmentation. Moreover, there are more speckle noise and clusters in SAR images, making the situation even worse.
Unlike GAT, AGCN shown in
Figure 1 is composed of an attention layer and two convolution layers. The attention layer aims at calculating attention coefficients. These coefficients are used to guide the subsequent convolution layers by revising the graph Laplacian. As no background information is contained in nodes’ features, the coefficients can accurately indicate the relationship between two adjacent superpixels in the feature space.
Specifically, an input SAR image is over-segmented into
superpixels, and the feature vector set is represented as
. As depicted in
Figure 1, this AGCN model contains an attention layer and two graph convolutional layers. The attention layer aims at optimizing the generalized graph Laplacian
. Then, the input graph-structure signal propagates layer by layer with the following rule:
where
is the trainable weight matrix of the
graph convolution layer;
represents an activation function.
denotes the input signal of the
layer. In the first convolutional layer,
, and the learnable parameter matrix is
.
indicates the number of the convolution kernels and is equal to the dimension of the output features of nodes.
Similarly,
represents the parameter matrix of the second convolutional layer, and
is the dimension of each node’s feature in the output. The second convolutional layer outputs
, where
. Finally, we utilize the SoftMax function to normalize
. The
element of
is expressed as
, meaning the probability that node
i belongs to the class
. The AGCN model is trained to minimize cross-entropy on the training nodes. The loss function
is defined as:
where
indicates the one-hot encoding labels of
N superpixels and
is the
element of
. Parameters
,
and
are then updated using the Adam Stochastic Gradient Descent (SGD) optimizer.
The pseudocode of the proposed method is presented in Algorithm 1, which explains the training of AGCN in detail.
| Algorithm 1: Training AGCN for Image Segmentation. |
![Remotesensing 11 02586 i001 Remotesensing 11 02586 i001]() |
6. Conclusions
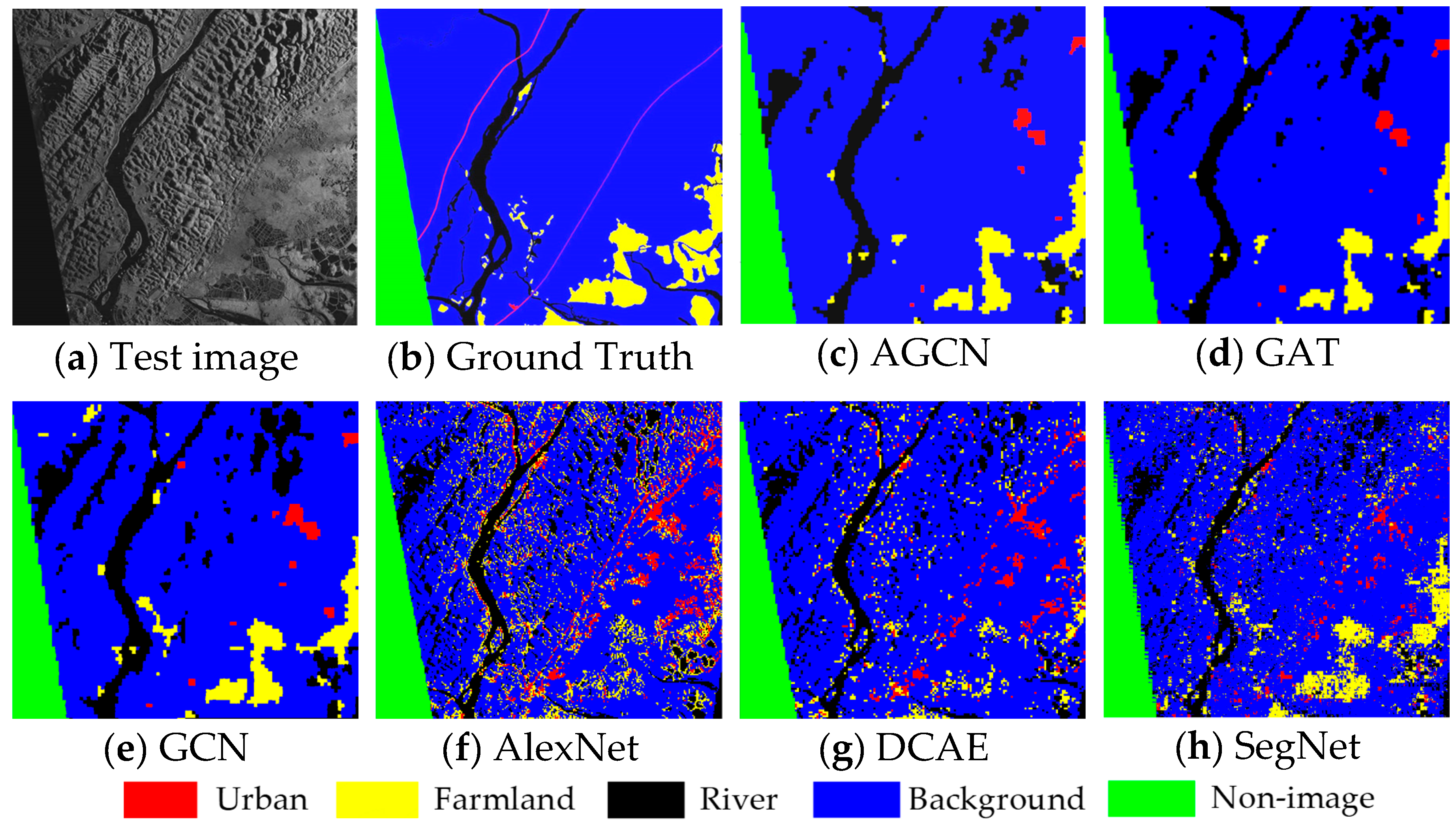
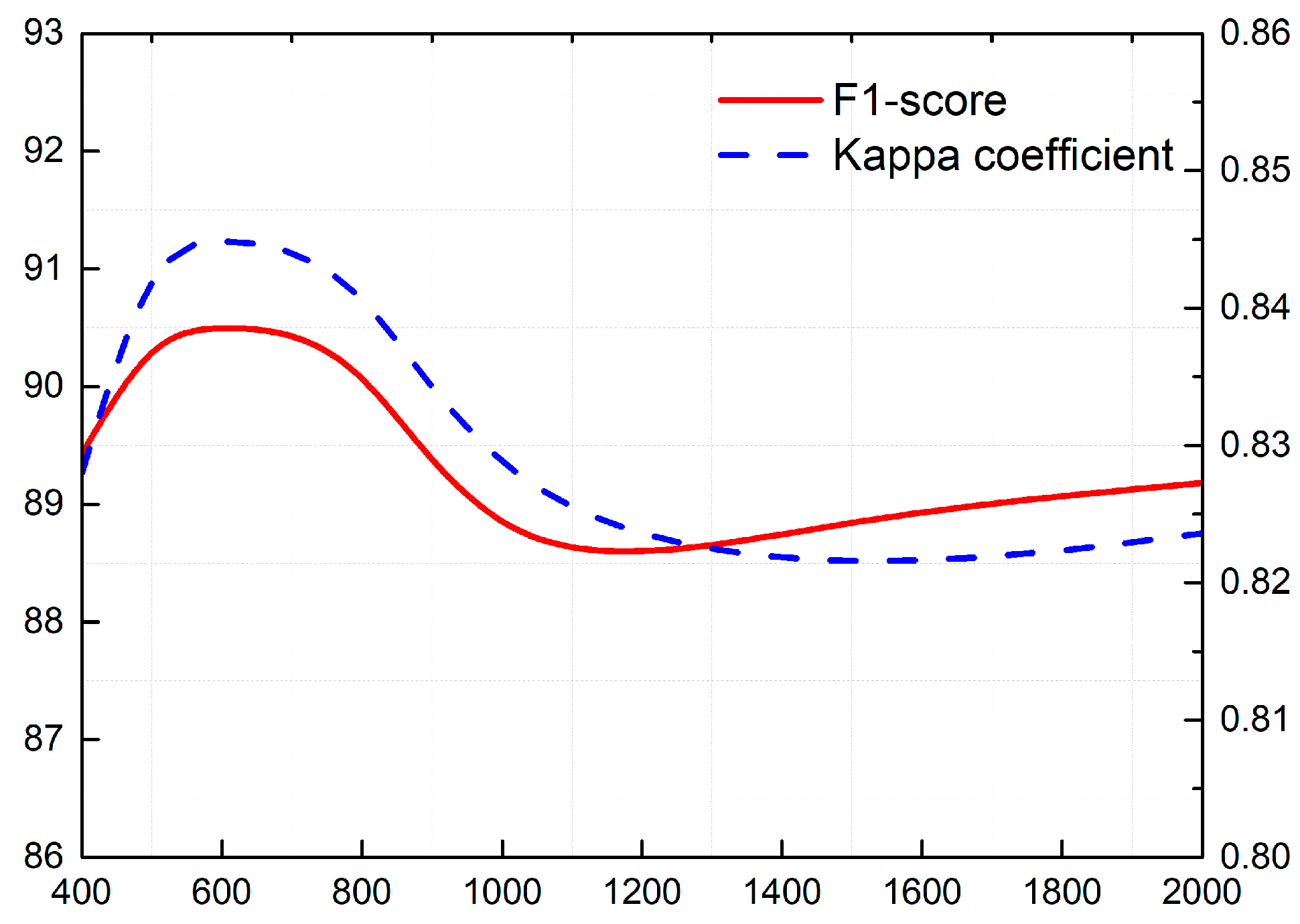
To address segmentation problems in big SAR data, we presented a novel Attention Graph Convolution Network (AGCN) in this study. In order to improve the efficiency of the segmentation algorithm, the input images were first over-segmented into superpixels, converted to graph-structured data. The previous spectral convolution methods generally ignored the various functions of the neighbouring nodes on the central nodes. In AGCN, an attention layer was introduced to calculate the attention coefficients of adjacent nodes before graph convolution operations. The greater the attention coefficients were, the greater the correlation there was between two nodes. The attention coefficients were utilized to update the generalized graph Laplacian, guiding the subsequent convolution operations to focus on the most relevant nodes to make decisions. AGCN can address the shortcomings of previous methods based on attention and spectral convolution. A number of experiments on two airborne SAR image datasets showed that: (1) The introduction of the attention layer improved the performance of the graph convolution networks. For SAR images with different scenes, AGCN could obtain higher segmentation accuracy and better preserve the neighbour consistency in the results. (2) The added attention layer did not introduce costly matrix operation. In the condition of using the same data and hardware configuration, our method required less computational time during the test stage than GAT and some common pixel-wise segmentation algorithms, e.g., SegNet.
In terms of limitations, it should be noted that different land-use categories in SAR images are in different scale spaces, while the superpixels used in AGCN only have one scale. Hence, AGCN is prone to errors when segmenting some thin areas, such as rivers and roads. In future research, we will attempt to improve the accuracy of the over-segmentation method and implement segmentation in multiple scale spaces in order to maintain high segmentation performance for all kinds of regions. Furthermore, the number of spaceborne SAR images is much larger than that of airborne images. We also plan to further reduce the computational complexity of the algorithm, so that it can better segment the large quantity of satellite images.