Landslide Detection Using Multi-Scale Image Segmentation and Different Machine Learning Models in the Higher Himalayas
Abstract
1. Introduction
2. Study Area
3. Methodology and Data
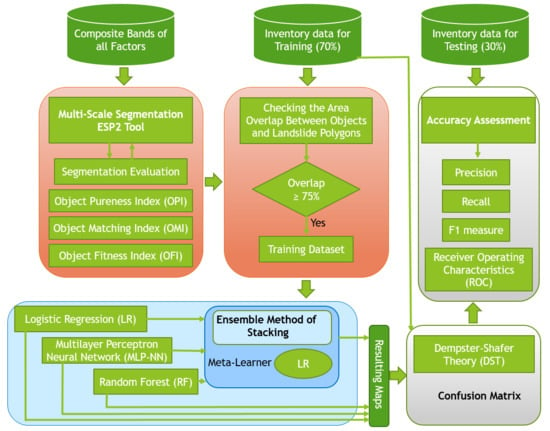
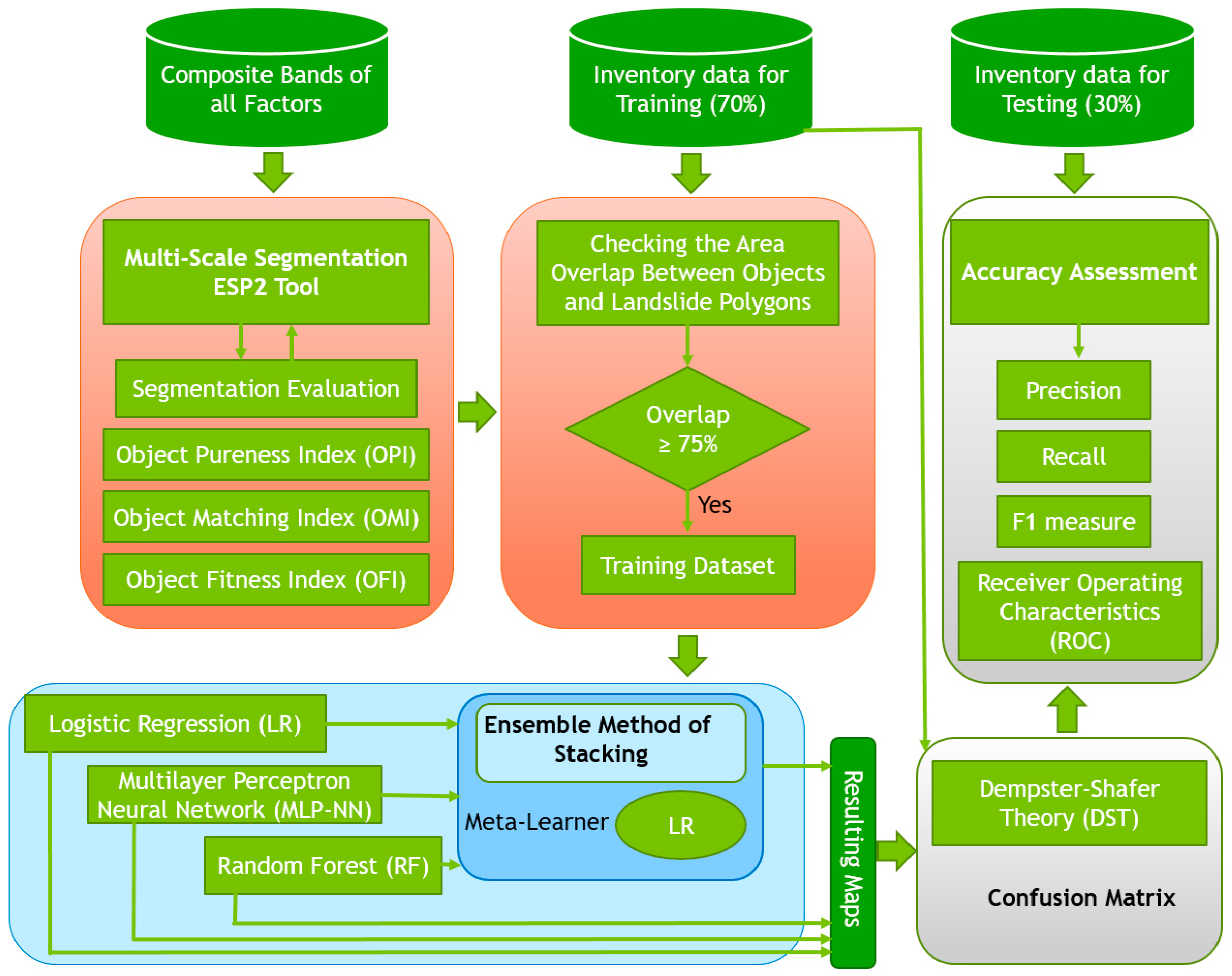
3.1. Overall Workflow
- Preparing multispectral images, the spectral index, and topographic derivatives for modeling;
- Generating multi-scale segments using the ESP2 tool and scale value intervals;
- Segmentation analysis and evaluation;
- Training ML and stacking methods on multi-scale datasets at the object level;
- Fusing multi-scale ML results using DST;
- Applying different accuracy assessment metrics.
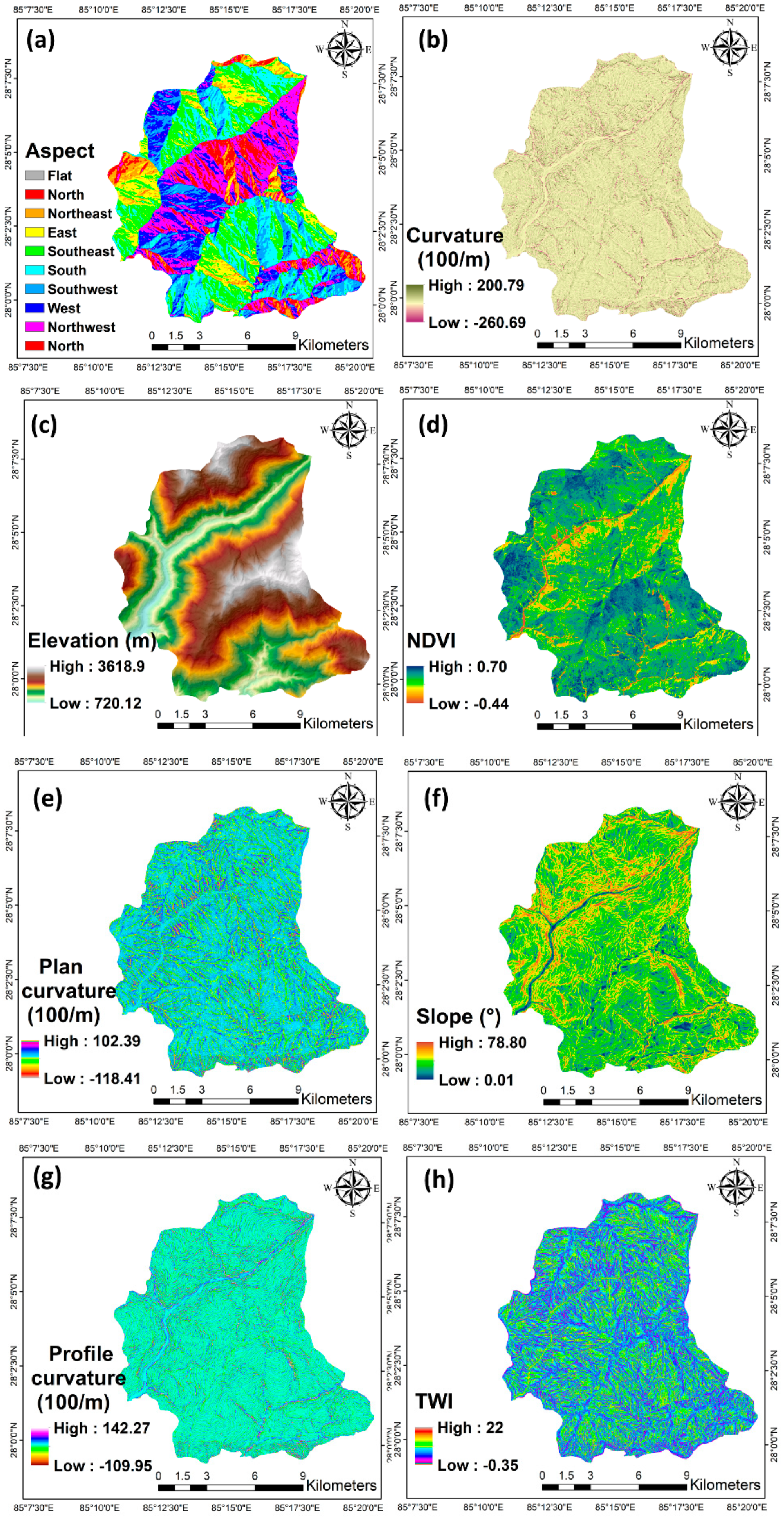
3.2. Datasets
3.3. Object-Based Image Analysis (OBIA)
3.3.1. Multi-Scale Image Segmentation
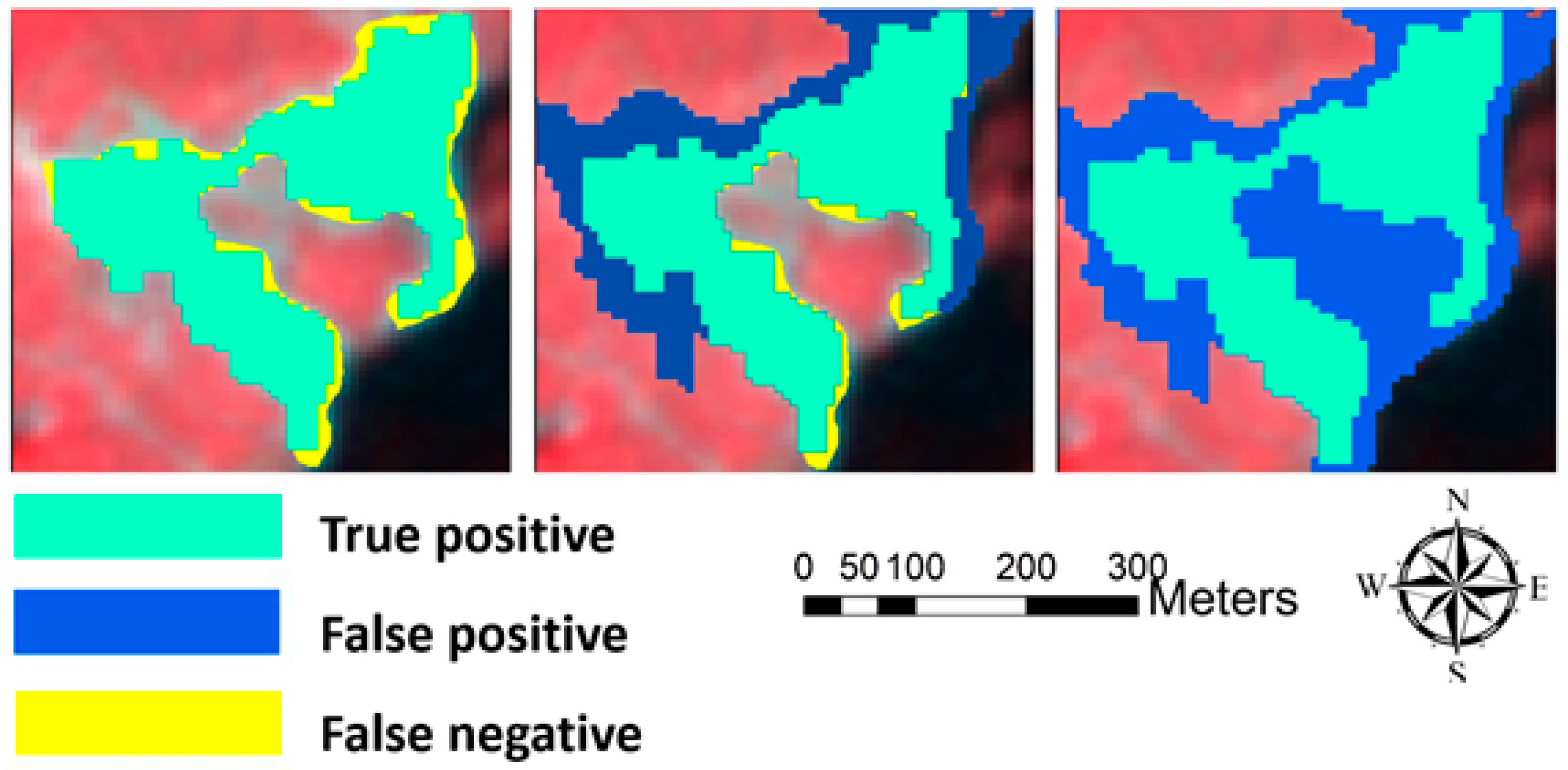
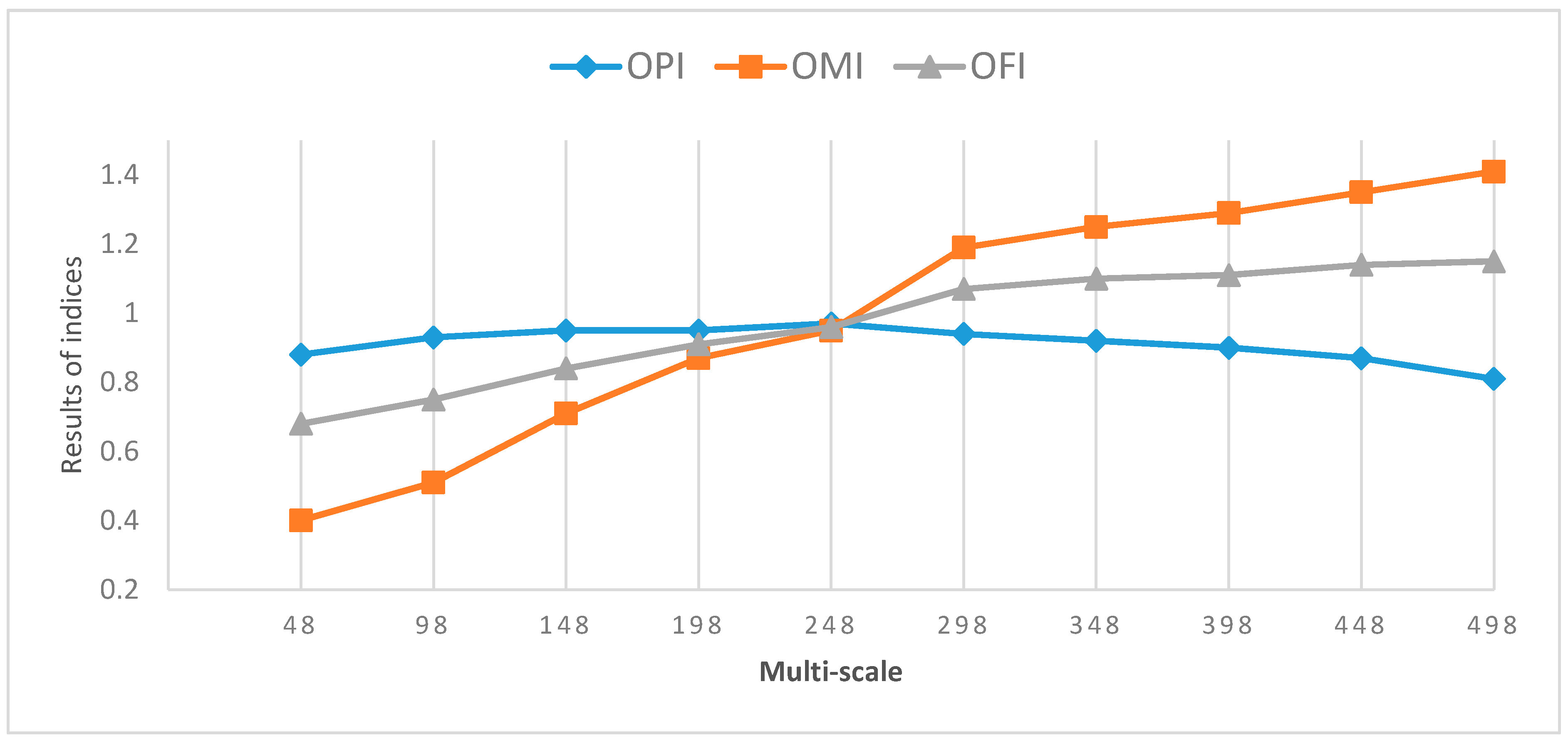
3.3.2. Segmentation Accuracy Evaluation
3.4. Machine Learning Methods
3.4.1. Multilayer Perceptron Neural Network (MLP-NN)
3.4.2. Logistic Regression (LR)
3.4.3. Random Forest (RF)
3.4.4. Stacking Machine Learning (ML) Methods
3.5. Integration of MLP-NN and OBIA for Landslide Detection
3.6. Dempster–Shafer Theory (DST)
Fusion of Multi-Scale Results via DST
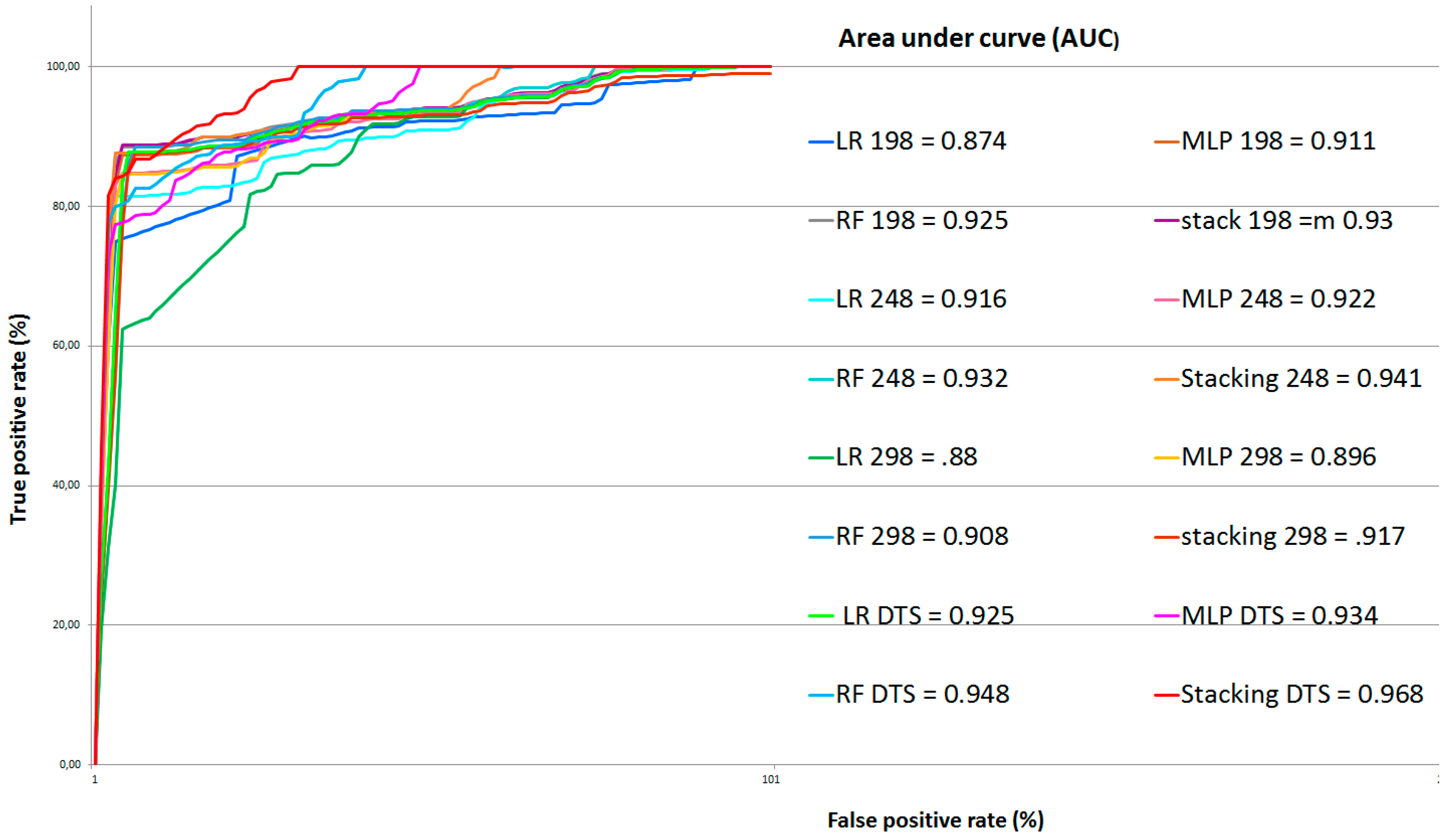
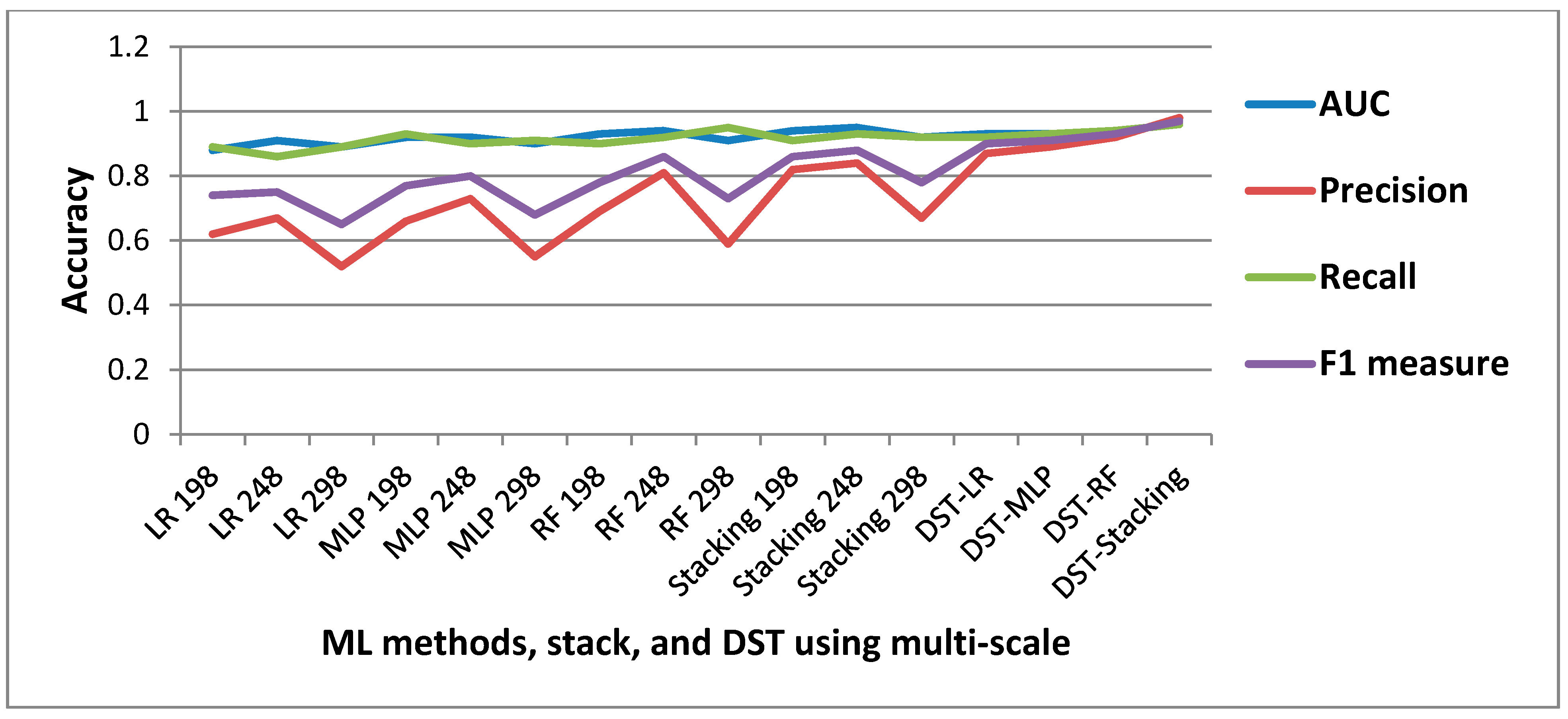
4. Accuracy Assessment and Comparison
5. Results and Discussion
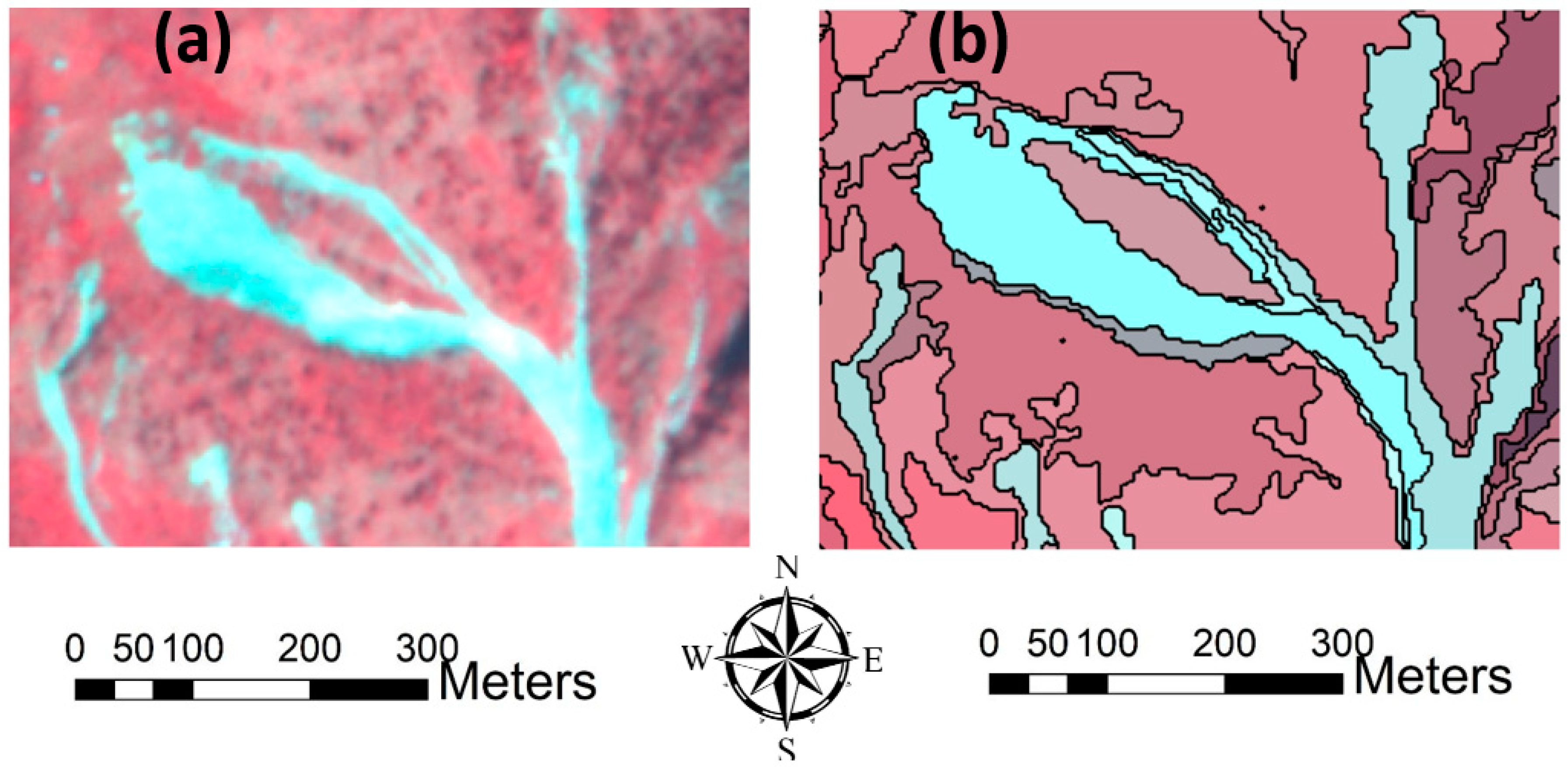
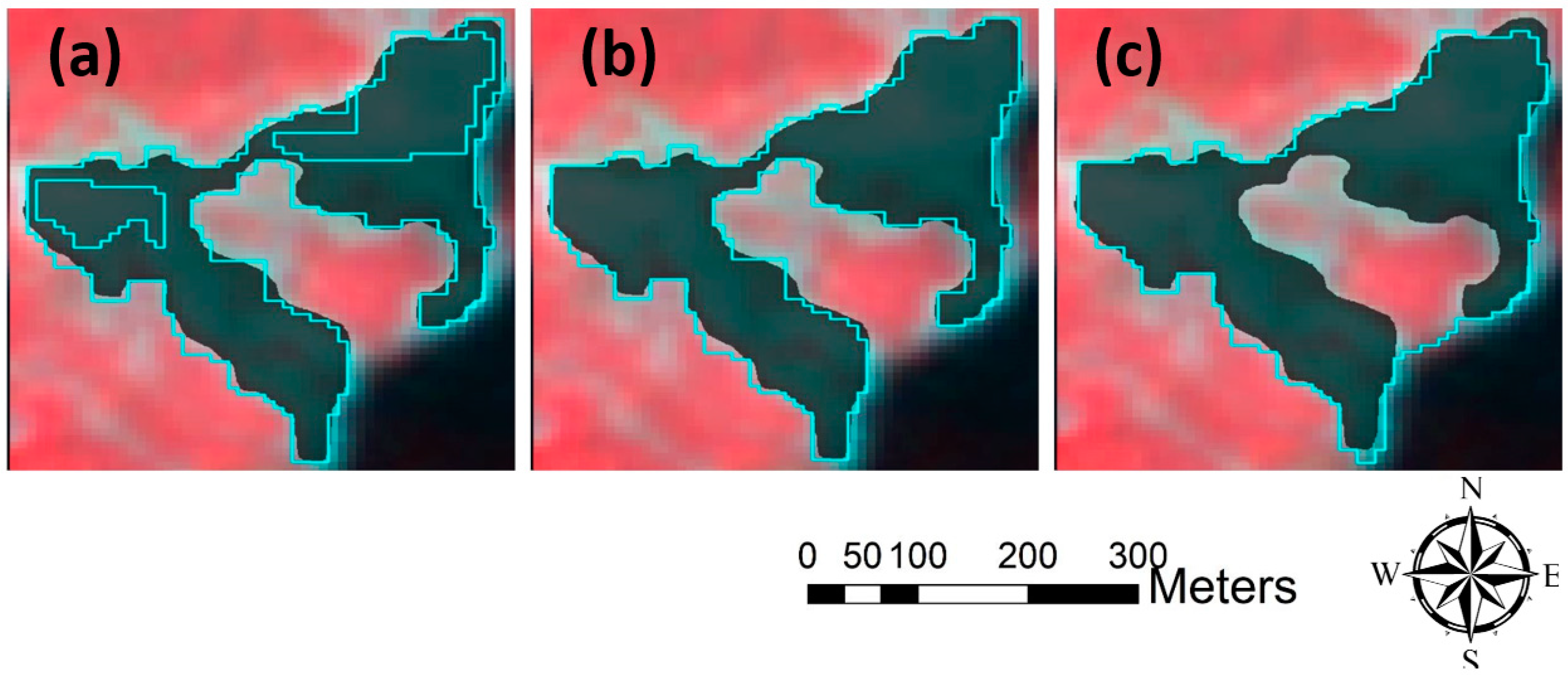
5.1. Image Segmentation
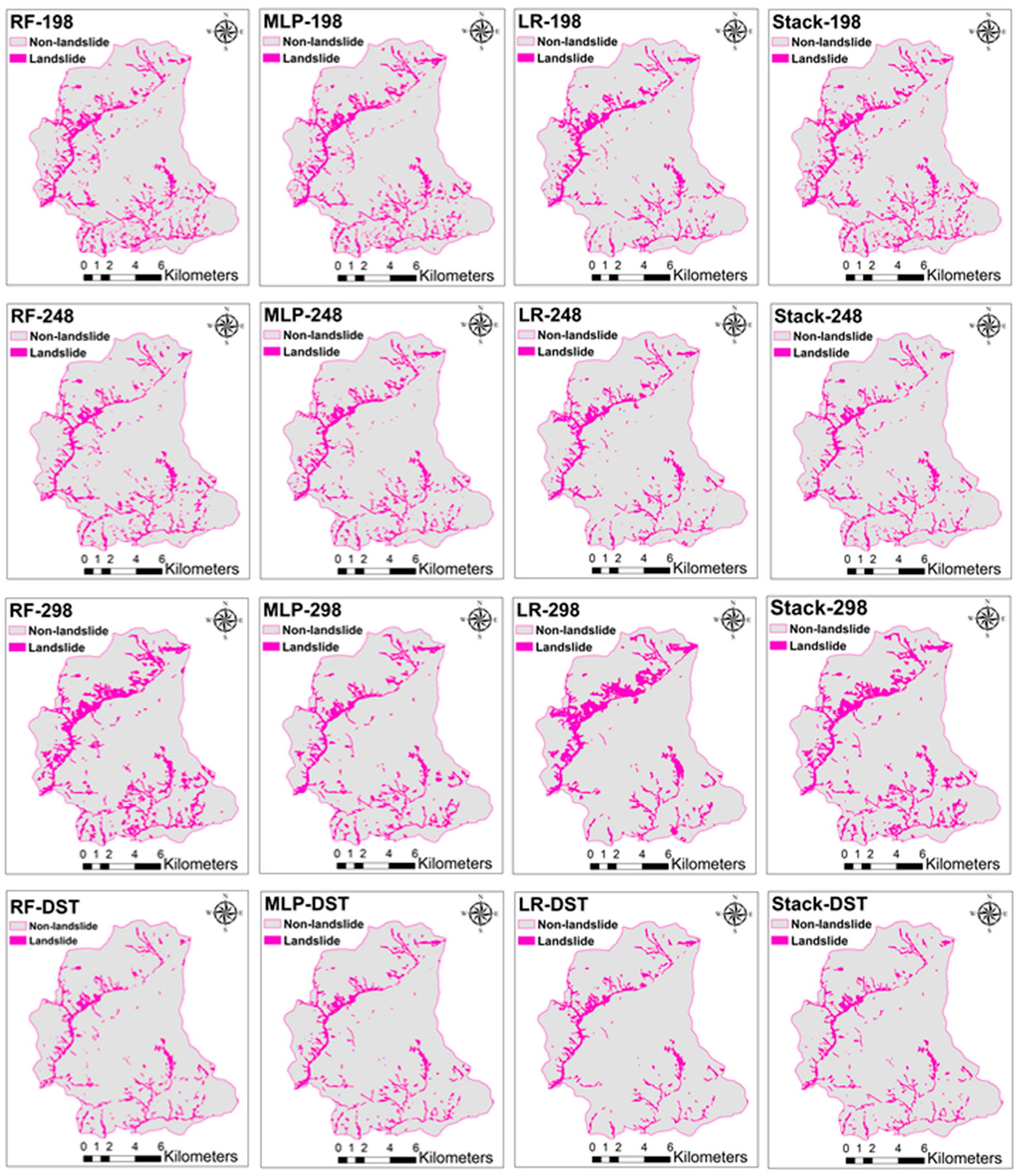
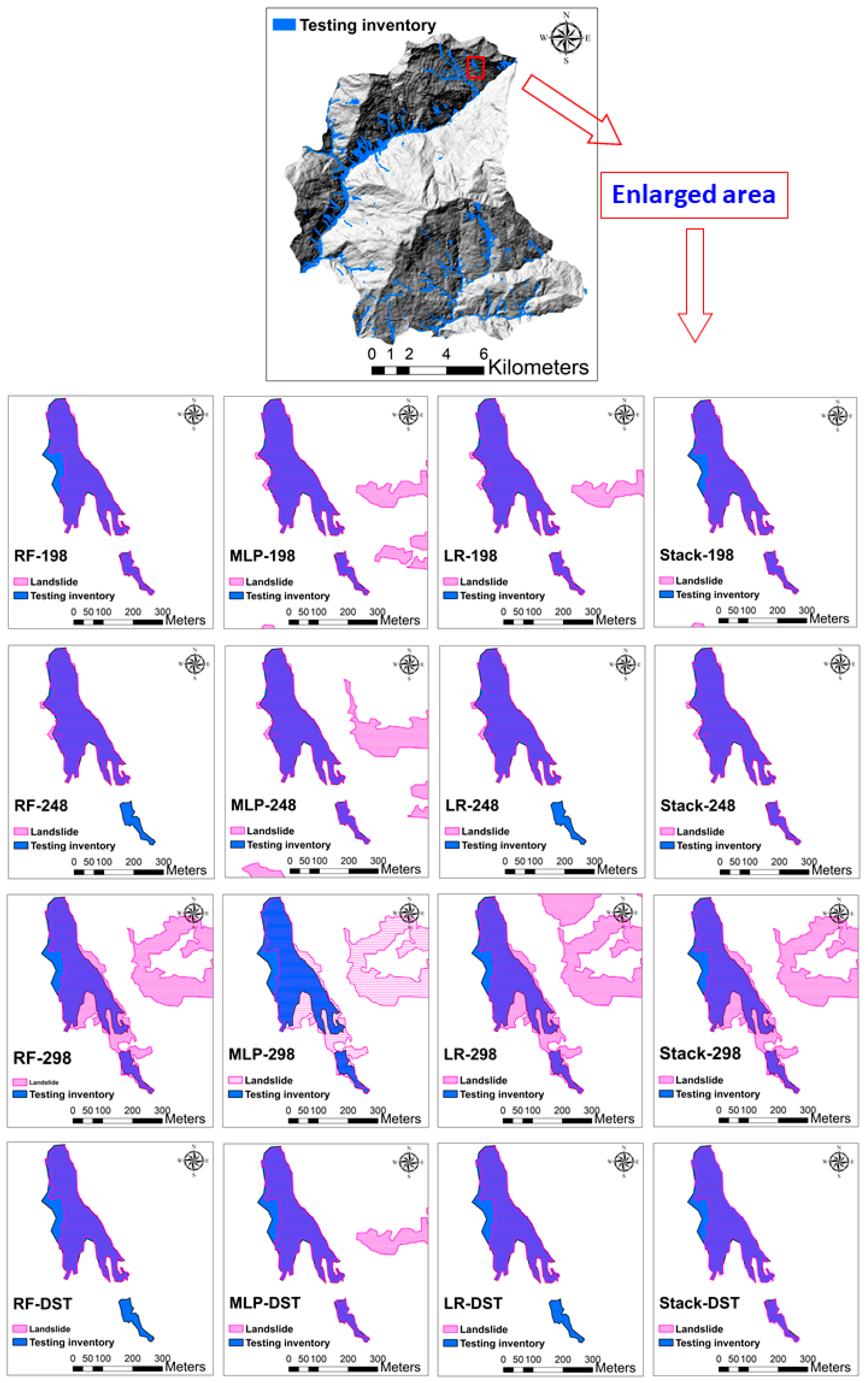
5.2. Landslide Detection using ML and Stacking Methods
5.3. Results of Fusion and Optimization using DST
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AUC | area under the curve |
| BPA | backpropagation algorithm |
| BPT | Bayesian probability theory |
| bpa | basic probability assignments |
| Bel | belief function |
| CSV | comma separate values |
| CLT | central limit theorem |
| DST | Dempster–Shafer theory |
| DEM | digital elevation model |
| DN | digital number |
| EO | Earth observation |
| ESP2 | estimation of scale parameters |
| EBF | evidential belief function |
| FP | false positive |
| FN | false negative |
| FST | fuzzy set theory |
| FLA | fusion level analysis |
| GPS | global positioning system |
| GIS | geographic information system |
| GIScience | geographic information science |
| GLCM | grey level co-occurrence matrix |
| HR | high-resolution |
| IU | image understanding |
| LR | logistic regression |
| KNN | K-nearest neighbour |
| LMT | logistic model tree |
| MSL | mean sea level |
| MLP-NN | multilayer perceptron neural network |
| ML | machine learning |
| MRS | multiresolution segmentation |
| NDVI | normalized differential vegetation index |
| OFI | object fitness index |
| OBIA | object-based image analysis |
| OMI | object matching index |
| OPI | object pureness index |
| Pl | plausibility function |
| RF | random forest |
| ROC | receiver operating characteristic |
| RS | remote sensing |
| SP | scale parameter |
| SD | standard deviation |
| SVM | support vector machines |
| TWI | topographic wetness index |
| TP | true positive |
| VHR | very high-resolution |
| WoE | weights of evidence |
References
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of Different Machine Learning Methods and Deep-Learning Convolutional Neural Networks for Landslide Detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef]
- Cruden, D.M. A simple definition of a landslide. Bull. Eng. Geol. Environ. 1991, 43, 27–29. [Google Scholar] [CrossRef]
- Pawłuszek, K.; Marczak, S.; Borkowski, A.; Tarolli, P. Multi-Aspect Analysis of Object-Oriented Landslide Detection Based on an Extended Set of LiDAR-Derived Terrain Features. ISPRS Int. J. Geo-Inf. 2019, 8, 321. [Google Scholar]
- Hong, H.; Chen, W.; Xu, C.; Youssef, A.M.; Pradhan, B.; Tien Bui, D. Rainfall-induced landslide susceptibility assessment at the Chongren area (China) using frequency ratio, certainty factor, and index of entropy. Geocarto Int. 2017, 32, 139–154. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.-T. Landslide inventory maps: New tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Pourghasemi, H.; Gayen, A.; Park, S.; Lee, C.-W.; Lee, S. Assessment of landslide-prone areas and their zonation using logistic regression, logitboost, and naïvebayes machine-learning algorithms. Sustainability 2018, 10, 3697. [Google Scholar] [CrossRef]
- Goetz, J.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T.; Tiede, D.; Moghaddam, M.H.R. Evaluating fuzzy operators of an object-based image analysis for detecting landslides and their changes. Geomorphology 2017, 293, 240–254. [Google Scholar] [CrossRef]
- Manconi, A.; Casu, F.; Ardizzone, F.; Bonano, M.; Cardinali, M.; De Luca, C.; Gueguen, E.; Marchesini, I.; Parise, M.; Vennari, C. Brief communication: Rapid mapping of landslide events: The 3 December 2013 Montescaglioso landslide, Italy. Nat. Hazards Earth Syst. Sci. 2014, 14, 1835–1841. [Google Scholar] [CrossRef]
- Meena, S.R.; Tavakkoli Piralilou, S. Comparison of Earthquake-Triggered Landslide Inventories: A Case Study of the 2015 Gorkha Earthquake, Nepal. Geosciences 2019, 9, 437. [Google Scholar] [CrossRef]
- Mezaal, M.; Pradhan, B.; Rizeei, H. Improving Landslide Detection from Airborne Laser Scanning Data Using Optimized Dempster–Shafer. Remote Sens. 2018, 10, 1029. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Baatz, M.; Schäpe, A. Multiresolution Segmentation: An Optimization Approach for High Quality Multi-SCALE image Segmentation. In Angewandte Geographische Informations Verarbeitung XII; Wichmann Verlag: Karlsruhe, Germany, 2000; pp. 12–23. [Google Scholar]
- Blaschke, T.; Piralilou, S.T. The near-decomposability paradigm re-interpreted for place-based GIS. In Proceedings of the 1st Workshop on Platial Analysis (PLATIAL’18), Heidelberg, Germany, 20–21 September 2018; pp. 20–21. [Google Scholar]
- Aryal, J.; Josselin, D. Environmental Object Recognition in a Natural Image: An Experimental Approach Using Geographic Object-Based Image Analysis (GEOBIA). Int. J. Agric. Environ. Inf. Syst. 2014, 5, 1–18. [Google Scholar] [CrossRef]
- Blaschke, T.; Hay, G.J.; Kelly, M.; Lang, S.; Hofmann, P.; Addink, E.; Feitosa, R.Q.; Van der Meer, F.; Van der Werff, H.; Van Coillie, F. Geographic object-based image analysis–towards a new paradigm. ISPRS J. Photogramm. Remote Sens. 2014, 87, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Rajbhandari, S.; Aryal, J.; Osborn, J.; Lucieer, A.; Musk, R. Leveraging Machine Learning to Extend Ontology-Driven Geographic Object-Based Image Analysis (O-GEOBIA): A Case Study in Forest-Type Mapping. Remote Sens. 2019, 11, 503. [Google Scholar] [CrossRef]
- Martha, T.R.; Kerle, N.; van Westen, C.J.; Jetten, V.; Kumar, K.V. Segment optimization and data-driven thresholding for knowledge-based landslide detection by object-based image analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4928–4943. [Google Scholar] [CrossRef]
- Albrecht, F.; Lang, S.; Hölbling, D. Spatial accuracy assessment of object boundaries for object-based image analysis. Proc. Geobia 2010, 38, C7. [Google Scholar]
- Radoux, J.; Bogaert, P. Good practices for object-based accuracy assessment. Remote Sens. 2017, 9, 646. [Google Scholar] [CrossRef]
- Costa, H.; Foody, G.M.; Boyd, D.S. Supervised methods of image segmentation accuracy assessment in land cover mapping. Remote Sens. Environ. 2018, 205, 338–351. [Google Scholar] [CrossRef]
- Drăguţ, L.; Csillik, O.; Eisank, C.; Tiede, D. Automated parameterisation for multi-scale image segmentation on multiple layers. ISPRS J. Photogramm. Remote Sens. 2014, 88, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Van Den Eeckhaut, M.; Kerle, N.; Poesen, J.; Hervás, J. Object-oriented identification of forested landslides with derivatives of single pulse LiDAR data. Geomorphology 2012, 173, 30–42. [Google Scholar] [CrossRef]
- Wessel, M.; Brandmeier, M.; Tiede, D. Evaluation of Different Machine Learning Algorithms for Scalable Classification of Tree Types and Tree Species Based on Sentinel-2 Data. Remote Sens. 2018, 10, 1419. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T. Optimizing Sample Patches Selection of CNN to Improve the mIOU on Landslide Detection. In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management: GISTAM, Heraklion, Greece, 3–5 May 2019; Volume 1, p. 8. [Google Scholar] [CrossRef]
- Heleno, S.; Matias, M.; Pina, P.; Sousa, A.J. Semiautomated object-based classification of rain-induced landslides with VHR multispectral images on Madeira Island. Nat. Hazards Earth Syst. Sci. 2016, 16, 1035–1048. [Google Scholar] [CrossRef]
- Keyport, R.N.; Oommen, T.; Martha, T.R.; Sajinkumar, K.; Gierke, J.S. A comparative analysis of pixel-and object-based detection of landslides from very high-resolution images. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 1–11. [Google Scholar] [CrossRef]
- Bui, D.T.; Ho, T.-C.; Pradhan, B.; Pham, B.-T.; Nhu, V.-H.; Revhaug, I. GIS-based modeling of rainfall-induced landslides using data mining-based functional trees classifier with AdaBoost, Bagging, and MultiBoost ensemble frameworks. Environ. Earth Sci. 2016, 75, 1101. [Google Scholar]
- Chen, W.; Shahabi, H.; Shirzadi, A.; Li, T.; Guo, C.; Hong, H.; Li, W.; Pan, D.; Hui, J.; Ma, M. A novel ensemble approach of bivariate statistical-based logistic model tree classifier for landslide susceptibility assessment. Geocarto Int. 2018, 33, 1398–1420. [Google Scholar] [CrossRef]
- Feizizadeh, B. A Novel Approach of Fuzzy Dempster–Shafer Theory for Spatial Uncertainty Analysis and Accuracy Assessment of Object-Based Image Classification. IEEE Geosci. Remote Sens. Lett. 2018, 15, 18–22. [Google Scholar] [CrossRef]
- Mora, B.; Wulder, M.A.; White, J.C. An approach using Dempster–Shafer theory to fuse spatial data and satellite image derived crown metrics for estimation of forest stand leading species. Inf. Fusion 2013, 14, 384–395. [Google Scholar] [CrossRef]
- Mohammady, M.; Pourghasemi, H.R.; Pradhan, B. Landslide susceptibility mapping at Golestan Province, Iran: A comparison between frequency ratio, Dempster–Shafer, and weights-of-evidence models. J. Asian Earth Sci. 2012, 61, 221–236. [Google Scholar] [CrossRef]
- Klein, J.; Lecomte, C.; Miché, P. Hierarchical and conditional combination of belief functions induced by visual tracking. Int. J. Approx. Reason. 2010, 51, 410–428. [Google Scholar] [CrossRef]
- Nguyen, K.; Denman, S.; Sridharan, S.; Fookes, C. Score-level multibiometric fusion based on Dempster–Shafer theory incorporating uncertainty factors. IEEE Trans. Hum.-Mach. Syst. 2014, 45, 132–140. [Google Scholar] [CrossRef]
- Rajghatta, C. Is This the ‘Big Himalayan Quake’We Feared? Time of India. Available online: https://timesofindia.indiatimes.com/world/south-asia/Is-this-the-Big-Himalayan-Quake-we-feared/articleshow/47055477.cms (accessed on 25 April 2015).
- USGS. M 7.8–36 km E of Khudi, Nepal; USGS: Reston, VA, USA, 2015. [Google Scholar]
- Gnyawali, K.R.; Adhikari, B.R. Spatial Relations of Earthquake Induced Landslides Triggered by 2015 Gorkha Earthquake Mw = 7.8. In Workshop on World Landslide Forum; Springer: Berlin/Heidelberg, Germany, 2017; pp. 85–93. [Google Scholar]
- Regmi, A.D.; Dhital, M.R.; Zhang, J.-Q.; Su, L.-J.; Chen, X.-Q. Landslide susceptibility assessment of the region affected by the 25 April 2015 Gorkha earthquake of Nepal. J. Mt. Sci. 2016, 13, 1941–1957. [Google Scholar] [CrossRef]
- Roback, K.; Clark, M.K.; West, A.J.; Zekkos, D.; Li, G.; Gallen, S.F.; Chamlagain, D.; Godt, J.W. The size, distribution, and mobility of landslides caused by the 2015 Mw7. 8 Gorkha earthquake, Nepal. Geomorphology 2018, 301, 121–138. [Google Scholar] [CrossRef]
- Planet Team. Planet Application Program Interface: In Space for Life on Earth; Planet Team: San Francisco, CA, USA, 2017. [Google Scholar]
- Sezer, E.A.; Pradhan, B.; Gokceoglu, C. Manifestation of an adaptive neuro-fuzzy model on landslide susceptibility mapping: Klang valley, Malaysia. Expert Syst. Appl. 2011, 38, 8208–8219. [Google Scholar] [CrossRef]
- Meena, S.R.; Ghorbanzadeh, O.; Hölbling, D.; Albrecht, F.; Blaschke, T. A Conceptual framework for web-based Nepalese landslide information system. Nat. Hazards Earth Syst. Sci. Discuss. 2019, 2019. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Pourghasemi, H.R.; Indra, P.; Dholakia, M. Landslide susceptibility assesssment in the Uttarakhand area (India) using GIS: A comparison study of prediction capability of naïve bayes, multilayer perceptron neural networks, and functional trees methods. Theor. Appl. Climatol. 2017, 128, 255–273. [Google Scholar] [CrossRef]
- Meena, S.R.; Ghorbanzadeh, O.; Blaschke, T. A Comparative Study of Statistics-Based Landslide Susceptibility Models: A Case Study of the Region Affected by the Gorkha Earthquake in Nepal. ISPRS Int. J. Geo-Inf. 2019, 8, 94. [Google Scholar] [CrossRef]
- Meena, S.R.; Mishra, B.K.; Blaschke, T. Landslide susceptibility mapping of the Kullu Valley, Himachal Himalayas, India: A GIS-based comparative study of FR, AHP and SMCE methods. In Proceedings of the International Workshop on Climate Change and Extreme Events in the Himalayan Region, IIT, Mandi, Himachal Pradesh, India, 18–20 April 2019. [Google Scholar]
- Meena, S.R.; Mishra, B.K.; Tavakkoli Piralilou, S. A Hybrid Spatial Multi-Criteria Evaluation Method for Mapping Landslide Susceptible Areas in Kullu Valley, Himalayas. Geosciences 2019, 9, 156. [Google Scholar] [CrossRef]
- Conforti, M.; Pascale, S.; Robustelli, G.; Sdao, F. Evaluation of prediction capability of the artificial neural networks for mapping landslide susceptibility in the Turbolo River catchment (northern Calabria, Italy). Catena 2014, 113, 236–250. [Google Scholar] [CrossRef]
- Wang, Q.; Li, W. A GIS-based comparative evaluation of analytical hierarchy process and frequency ratio models for landslide susceptibility mapping. Phys. Geogr. 2017, 38, 318–337. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Naghibi, S.A. Prioritization of landslide conditioning factors and its spatial modeling in Shangnan County, China using GIS-based data mining algorithms. Bull. Eng. Geol. Environ. 2018, 77, 611–629. [Google Scholar] [CrossRef]
- Valencia Ortiz, J.A.; Martínez-Graña, A.M. A neural network model applied to landslide susceptibility analysis (Capitanejo, Colombia). Geomat. Nat. Hazards Risk 2018, 9, 1106–1128. [Google Scholar] [CrossRef]
- Augustin, H.; Sudmanns, M.; Tiede, D.; Lang, S.; Baraldi, A. Semantic Earth Observation Data Cubes. Data 2019, 4, 102. [Google Scholar] [CrossRef]
- Blaschke, T.; Feizizadeh, B.; Hölbling, D. Object-based image analysis and digital terrain analysis for locating landslides in the Urmia Lake Basin, Iran. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4806–4817. [Google Scholar] [CrossRef]
- Aksoy, B.; Ercanoglu, M. Landslide identification and classification by object-based image analysis and fuzzy logic: An example from the Azdavay region (Kastamonu, Turkey). Comput. Geosci. 2012, 38, 87–98. [Google Scholar] [CrossRef]
- Pradhan, B.; Jebur, M.N.; Shafri, H.Z.M.; Tehrany, M.S. Data fusion technique using wavelet transform and Taguchi methods for automatic landslide detection from airborne laser scanning data and quickbird satellite imagery. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1610–1622. [Google Scholar] [CrossRef]
- Qiu, H.; Li, H.; Wu, Q.; Meng, F.; Ngan, K.N.; Shi, H. A2RMNet: Adaptively Aspect Ratio Multi-Scale Network for Object Detection in Remote Sensing Images. Remote Sens. 2019, 11, 1594. [Google Scholar] [CrossRef]
- Ye, S.; Pontius, R.G.; Rakshit, R. A review of accuracy assessment for object-based image analysis: From per-pixel to per-polygon approaches. ISPRS J. Photogramm. Remote Sens. 2018, 141, 137–147. [Google Scholar] [CrossRef]
- Karpatne, A.; Ebert-Uphoff, I.; Ravela, S.; Babaie, H.A.; Kumar, V. Machine learning for the geosciences: Challenges and opportunities. IEEE Trans. Knowl. Data Eng. 2018, 31, 1544–1554. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Goldarag, Y.J.; Mohammadzadeh, A.; Ardakani, A. Fire risk assessment using neural network and logistic regression. J. Indian Soc. Remote Sens. 2016, 44, 885–894. [Google Scholar] [CrossRef]
- Haykin, S.; Network, N. A comprehensive foundation. Neural Netw. 2004, 2, 41. [Google Scholar]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Lee, S. Application of logistic regression model and its validation for landslide susceptibility mapping using GIS and remote sensing data. Int. J. Remote Sens. 2005, 26, 1477–1491. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Colkesen, I.; Sahin, E.K.; Kavzoglu, T. Susceptibility mapping of shallow landslides using kernel-based Gaussian process, support vector machines and logistic regression. J. Afr. Earth Sci. 2016, 118, 53–64. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Stumpf, A.; Kerle, N. Object-oriented mapping of landslides using Random Forests. Remote Sens. Environ. 2011, 115, 2564–2577. [Google Scholar] [CrossRef]
- Rahmati, O.; Choubin, B.; Fathabadi, A.; Coulon, F.; Soltani, E.; Shahabi, H.; Mollaefar, E.; Tiefenbacher, J.; Cipullo, S.; Ahmad, B.B. Predicting uncertainty of machine learning models for modelling nitrate pollution of groundwater using quantile regression and UNEEC methods. Sci. Total Environ. 2019, 688, 855–866. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Lee, S.; Oh, H.-J. Ensemble-based landslide susceptibility maps in Jinbu area, Korea. In Terrigenous Mass Movements; Springer: Berlin/Heidelberg, Germany, 2012; pp. 193–220. [Google Scholar]
- Sikora, R. A modified stacking ensemble machine learning algorithm using genetic algorithms. In Handbook of Research on Organizational Transformations through Big Data Analytics; IGI Global: Hershey, PA, USA, 2015; pp. 43–53. [Google Scholar]
- Feizizadeh, B.; Blaschke, T.; Nazmfar, H. GIS-based ordered weighted averaging and Dempster–Shafer methods for landslide susceptibility mapping in the Urmia Lake Basin, Iran. Int. J. Digit. Earth 2014, 7, 688–708. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Lu, L.; Bai, Z. Land cover classification information decision making fusion based on Dempster-Shafer theory: Results and uncertainty. In Proceedings of the International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, Shanghai, China, 25–27 June 2008; pp. 240–247. [Google Scholar]
- Baraldi, P.; Zio, E. A comparison between probabilistic and dempster-shafer theory approaches to model uncertainty analysis in the performance assessment of radioactive waste repositories. Risk Anal. 2010, 30, 1139–1156. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Rottensteiner, F.; Trinder, J.; Clode, S.; Kubik, K. Using the Dempster–Shafer method for the fusion of LIDAR data and multi-spectral images for building detection. Inf. Fusion 2005, 6, 283–300. [Google Scholar] [CrossRef]
- Stein, A.; Aryal, J.; Gort, G. Use of the Bradley-Terry model to quantify association in remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 852–856. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Schneider, L.C. Land-cover change model validation by an ROC method for the Ipswich watershed, Massachusetts, USA. Agric. Ecosyst. Environ. 2001, 85, 239–248. [Google Scholar] [CrossRef]
- Mas, J.-F.; Soares Filho, B.; Pontius, R.; Farfán Gutiérrez, M.; Rodrigues, H. A suite of tools for ROC analysis of spatial models. ISPRS Int. J. Geo-Inf. 2013, 2, 869–887. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Naghibi, S.A. A comparative study of landslide susceptibility maps produced using support vector machine with different kernel functions and entropy data mining models in China. Bull. Eng. Geol. Environ. 2017, 77, 647–664. [Google Scholar] [CrossRef]
| Satellite (Sensor) | Bands Wavelength (nm) | Pixel Size | Bit Depth | Orbit Altitude | Scene Size (KM) | |||
|---|---|---|---|---|---|---|---|---|
| PlanetScope | Blue | Green | Red | NIR | 3.125 m | 16 | 475 km | 24.6 × 16.4 |
| 455–515 | 500–590 | 590–670 | 780–860 | |||||
| Scale | Shape | Compactness | Layer Weights | OPI | OMI | OFI | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RGB NIR | TWI | Aspect | Profile Curvature | Elevation | NDVI | Slope | Curvature | Plan Curvature | ||||||
| 48 | 0.7 | 0.3 | 0.88 | 0.40 | 0.68 | |||||||||
| 98 | 0.7 | 0.3 | 0.93 | 0.51 | 0.75 | |||||||||
| 148 | 0.7 | 0.3 | 0.95 | 0.71 | 0.84 | |||||||||
| 198 | 0.7 | 0.3 | 0.95 | 0.87 | 0.91 | |||||||||
| 248 | 0.7 | 0.3 | 2 | 1 | 2 | 1 | 1 | 4 | 2 | 1 | 1 | 0.97 | 0.95 | 0.96 |
| 298 | 0.7 | 0.3 | 0.94 | 1.19 | 1.07 | |||||||||
| 348 | 0.7 | 0.3 | 0.92 | 1.25 | 1.10 | |||||||||
| 398 | 0.7 | 0.3 | 0.90 | 1.29 | 1.11 | |||||||||
| 448 | 0.7 | 0.3 | 0.87 | 1.35 | 1.14 | |||||||||
| 498 | 0.7 | 0.3 | 0.81 | 1.41 | 1.15 | |||||||||
| Method | Class Name | Pixels from Landslide Inventory Data Set | Total Samples | User Accuracy | Overall Accuracy | Kappa Index | |
|---|---|---|---|---|---|---|---|
| Non-Landslides | Landslides | ||||||
| LR 198 | Non-landslides | 1755 | 370 | 2125 | 82,588 | 0.761 | 0.541 |
| Landslides | 400 | 700 | 1100 | 63,636 | |||
| MLP 198 | Non-landslides | 1774 | 351 | 2125 | 83,482 | 0.769 | 0.555 |
| Landslides | 395 | 705 | 1100 | 64,091 | |||
| RF 198 | Non-landslides | 1786 | 339 | 2125 | 84,047 | 0.774 | 0.566 |
| Landslides | 389 | 711 | 1100 | 64,636 | |||
| Stacking 198 | Non-landslides | 1779 | 346 | 2125 | 83,718 | 0.778 | 0.576 |
| Landslides | 371 | 729 | 1100 | 66,273 | |||
| LR 248 | Non-landslides | 1874 | 251 | 2125 | 88,188 | 0.833 | 0.685 |
| Landslides | 289 | 811 | 1100 | 73,727 | |||
| MLP 248 | Non-landslides | 1890 | 235 | 2125 | 88,941 | 0.841 | 0.700 |
| Landslides | 279 | 821 | 1100 | 74,636 | |||
| RF 248 | Non-landslides | 1914 | 211 | 2125 | 90,071 | 0.864 | 0.749 |
| Landslides | 227 | 873 | 1100 | 79,364 | |||
| Stacking 248 | Non-landslides | 1922 | 203 | 2125 | 90,447 | 0.872 | 0.765 |
| Landslides | 209 | 891 | 1100 | 81,000 | |||
| LR 298 | Non-landslides | 1744 | 381 | 2125 | 82,071 | 0.755 | 0.528 |
| Landslides | 410 | 690 | 1100 | 62,727 | |||
| MLP 298 | Non-landslides | 1769 | 356 | 2125 | 83,247 | 0.764 | 0.545 |
| Landslides | 405 | 695 | 1100 | 63,182 | |||
| RF 298 | Non-landslides | 1778 | 347 | 2125 | 83,671 | 0.769 | 0.554 |
| Landslides | 399 | 701 | 1100 | 63,727 | |||
| Stacking 298 | Non-landslides | 1779 | 346 | 2125 | 83,718 | 0.774 | 0.567 |
| Landslides | 382 | 718 | 1100 | 65,273 | |||
| LR DST | Non-landslides | 1894 | 231 | 2125 | 89,129 | 0.861 | 0.745 |
| Landslides | 217 | 883 | 1100 | 80,273 | |||
| MLP DST | Non-landslides | 1910 | 215 | 2125 | 89,882 | 0.870 | 0.762 |
| Landslides | 206 | 904 | 1110 | 81,441 | |||
| RF DST | Non-landslides | 1970 | 155 | 2125 | 92,706 | 0.892 | 0.801 |
| Landslides | 192 | 908 | 1100 | 82,545 | |||
| Stacking DST | Non-landslides | 1976 | 149 | 2125 | 92,988 | 0.898 | 0.814 |
| Landslides | 180 | 930 | 1110 | 83,784 | |||
| Method | Scale | TP (ha) | FP (ha) | FN (ha) | Precision | Recall | F1 Measure |
|---|---|---|---|---|---|---|---|
| LR | 198 | 572.89 | 344.72 | 68.24 | 0.62 | 0.89 | 0.74 |
| 248 | 553.39 | 272.62 | 87.74 | 0.67 | 0.86 | 0.75 | |
| 298 | 570.65 | 532.20 | 70.48 | 0.52 | 0.89 | 0.65 | |
| MLP | 198 | 598.96 | 310.09 | 42.17 | 0.66 | 0.93 | 0.77 |
| 248 | 580.04 | 220.00 | 61.09 | 0.73 | 0.90 | 0.80 | |
| 298 | 580.47 | 479.65 | 60.66 | 0.55 | 0.91 | 0.68 | |
| RF | 198 | 579.54 | 265.76 | 61.59 | 0.69 | 0.90 | 0.78 |
| 248 | 588.54 | 140.23 | 52.59 | 0.81 | 0.92 | 0.86 | |
| 298 | 608.44 | 419.65 | 32.69 | 0.59 | 0.95 | 0.73 | |
| Stacking | 198 | 580.30 | 131.23 | 60.83 | 0.82 | 0.91 | 0.86 |
| 248 | 594.25 | 109.23 | 46.88 | 0.84 | 0.93 | 0.88 | |
| 298 | 591.52 | 289.60 | 49.61 | 0.67 | 0.92 | 0.78 | |
| DST | LR | 589.74 | 84.25 | 51.39 | 0.87 | 0.92 | 0.90 |
| MLP | 594.36 | 74.44 | 46.77 | 0.89 | 0.93 | 0.91 | |
| RF | 604.15 | 55.85 | 36.98 | 0.92 | 0.94 | 0.93 | |
| Stacking | 616.06 | 11.93 | 25.07 | 0.98 | 0.96 | 0.97 |
| Scale | LR | MLP | RF | Stack |
|---|---|---|---|---|
| 198 | 0.88 | 0.92 | 0.93 | 0.94 |
| 248 | 0.91 | 0.92 | 0.94 | 0.95 |
| 298 | 0.89 | 0.9 | 0.91 | 0.92 |
| DST | 0.93 | 0.93 | 0.94 | 0.96 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tavakkoli Piralilou, S.; Shahabi, H.; Jarihani, B.; Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Aryal, J. Landslide Detection Using Multi-Scale Image Segmentation and Different Machine Learning Models in the Higher Himalayas. Remote Sens. 2019, 11, 2575. https://doi.org/10.3390/rs11212575
Tavakkoli Piralilou S, Shahabi H, Jarihani B, Ghorbanzadeh O, Blaschke T, Gholamnia K, Meena SR, Aryal J. Landslide Detection Using Multi-Scale Image Segmentation and Different Machine Learning Models in the Higher Himalayas. Remote Sensing. 2019; 11(21):2575. https://doi.org/10.3390/rs11212575
Chicago/Turabian StyleTavakkoli Piralilou, Sepideh, Hejar Shahabi, Ben Jarihani, Omid Ghorbanzadeh, Thomas Blaschke, Khalil Gholamnia, Sansar Raj Meena, and Jagannath Aryal. 2019. "Landslide Detection Using Multi-Scale Image Segmentation and Different Machine Learning Models in the Higher Himalayas" Remote Sensing 11, no. 21: 2575. https://doi.org/10.3390/rs11212575
APA StyleTavakkoli Piralilou, S., Shahabi, H., Jarihani, B., Ghorbanzadeh, O., Blaschke, T., Gholamnia, K., Meena, S. R., & Aryal, J. (2019). Landslide Detection Using Multi-Scale Image Segmentation and Different Machine Learning Models in the Higher Himalayas. Remote Sensing, 11(21), 2575. https://doi.org/10.3390/rs11212575