1. Introduction
The Terrain Observation by Progressive Scan (TOPS) [
1,
2] is a new alternative data acquisition mode for synthetic aperture radar (SAR) wide-swath imaging and interferometry [
3,
4], which can achieve the same wide swath coverage as in ScanSAR mode but drastically reducing its drawbacks. It is well known that ScanSAR images suffer an azimuth variation of signal-to-noise ratio (SNR) and azimuth ambiguities, which is a consequence of integrating different azimuth antenna pattern slices depending on the azimuth target position [
5]. In TOPS mode, the use of antennas electronically steered in the azimuth dimension allowed all targets to be illuminated with the complete azimuth antenna pattern, therefore, the scalloping effect, as well as the azimuth dependence of SNR and distributed target ambiguity ratio (DTAR) in ScanSAR images, are avoided or significantly extenuated [
1,
2,
5].
However, the use of electronically-steered antennas also introduces a new issue. In orbital SAR systems, limited by the onboard storage ability, electronically-steered antennas only use a limited number of azimuth steering angles, which leads to a staircase-like antenna beam steering law [
2]. It will cause an undesired amplitude modulation for every observed target in the raw data. Such an amplitude modulation is periodic and dependent on the azimuth target position, which will introduce paired echoes [
2,
6]. The paired echoes will distort the ideal target impulse response function (IRF) by introducing symmetrically-placed distortion peaks [
6]. These spurious peaks, however, may appear in some focused images as “ghost targets”, particularly for scenarios where strong scatterers are embedded in a large scene of low backscatters [
2], such as for a wide-swath maritime surveillance usage [
7].
The effect of staircase-like beam steering is analyzed and quantified for TOPS and similar sliding-spotlight mode case in [
2,
8,
9,
10], and it is found that the maximum of the paired-echo peaks mainly depends on the steering angle step size. Therefore, the best way to avoid such an issue is to use sufficient small steering angle steps. In the TerraSAR-X TOPSAR acquisition mode, as a compromise between the performance and cost, a reasonable angle step size of about 0.03° was used [
10], which would result in an acceptable spurious peak level lower than −30 dB relative to the main signal peak [
10]. However, it has been found in [
11,
12] that the spurious peaks from very strong scatterers, even with their peak ratios lower than −32 dB, may still be observable in a scene of low backscatter.
Spaceborne SARs, like TerraSAR-X and Sentinel-1, are traditionally expensive undertakings [
13], and many potential customers may be currently unable to afford such systems. The next generation of low-cost spaceborne SAR payloads, NovaSAR-S [
7,
14] and NovaSAR-X [
15], for instance, are very attractive to many new customers and will open the door to constellations of SAR instruments and provide the possibility of future global dynamic-processes continuous observation [
13]. The payload implementation for such a lightweight SAR instrument will be founded on low cost as the primary design driver [
14,
15], therefore, if a TOPS mode is to be designed, the number of azimuth steering angles will be more strictly limited and the effect of staircase beam steering be more severe.
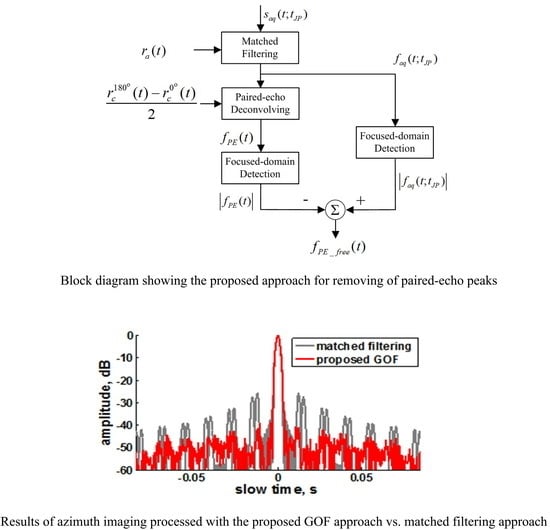
So far, however, there is no effective approach to eliminate such already existent “ghost targets” from strong scatterers caused by stair-step antenna steering in the process of SAR data imaging. It is found that by using amplitude tapering, there is a limited improvement for the reduction of the paired-echo peaks of IRF [
2,
10]. However, the use of azimuth tapering window is largely limited by the unwelcome loss of azimuth resolution. This paper aims at providing an approach implemented in SAR data processing, which can eliminate spurious peaks and restore an ideal IRF without resolution loss. Firstly, the amplitude modulated azimuth received signal is carefully modeled using the classic theory of paired echo distortion [
6]. It is found that the undesired amplitude error caused by electronic beam steering cannot be determined in advance due to each target’s random jump time of beam angle, which will prevent the precise use of optimum filtering (OF) [
16,
17] to achieve an ideal IRF. Then an extended optimum filtering (EOF), which is originally proposed in [
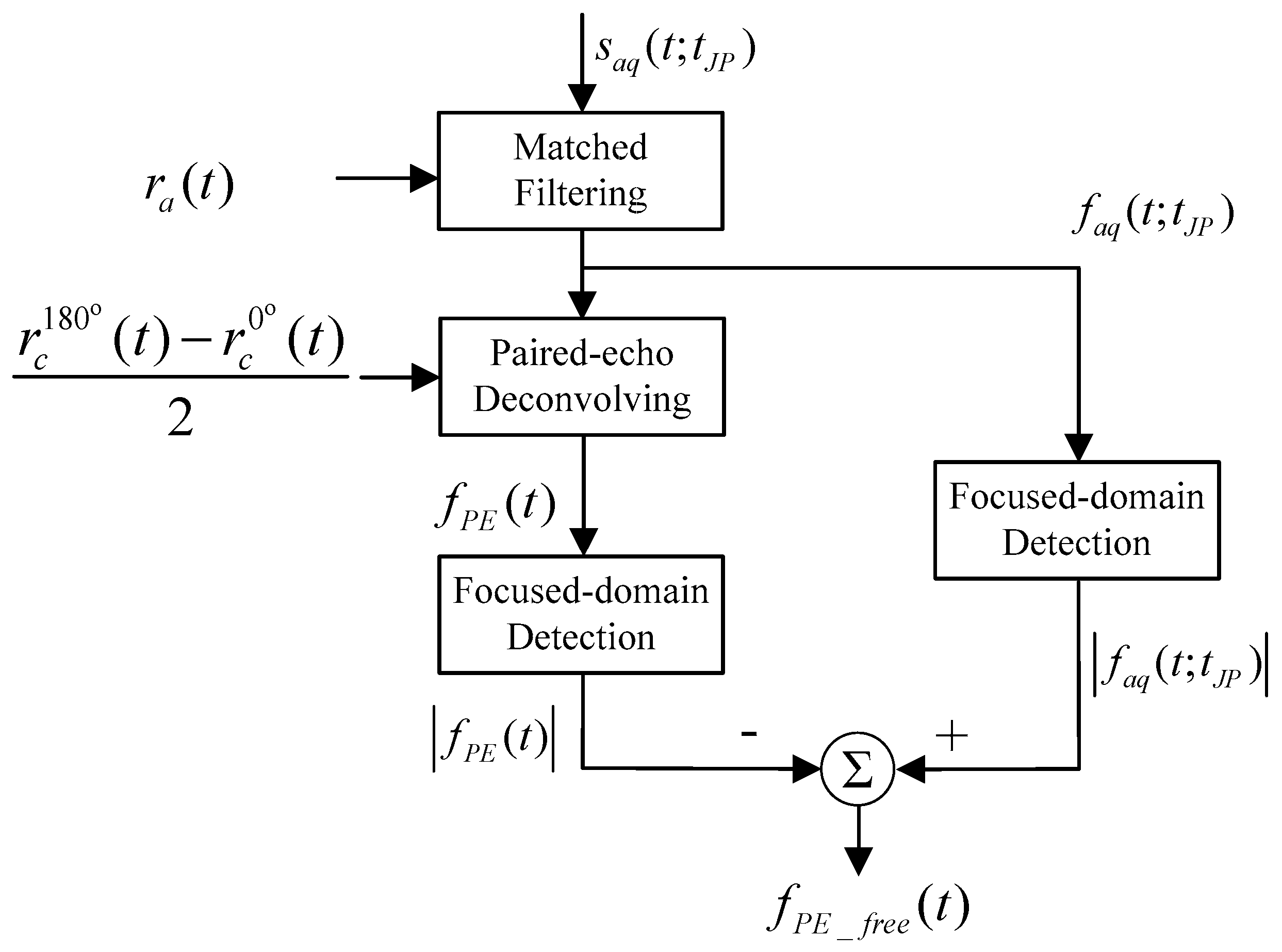
18] to remove the azimuth ambiguities in SAR images, is reintroduced here to accommodate the undetermined random modulation. However, it is found that EOF can only remove the strongest and nearest paired distortion peaks. To deal with this problem, the form of the ideal deconvolving filtering in EOF is reasonably approximated, and the limit of real receive signal basis is broken. A generalized optimum filtering (GOF) is then given. Using the proposed approach, not only the strongest and nearest paired distortion peaks, but also peripheral aliased power of the paired-echo-distorted IRF can be removed all together from the detected SAR images.
2. Paired Echoes Modeling
Assuming a sinc azimuth pattern and a continuous linear beam steering, the resulting TOPS antenna pattern as seen by a point target within its illumination time
is [
2,
8,
9,
10]:
where
represents the azimuth slow time referenced to this target’s beam center crossing,
is the beam rotation rate,
is the azimuth antenna length,
is the wavelength,
is the ground velocity, and
is the range of the closest approach. According to Equation (1), it is easy to know [
2] that the TOPS azimuth resolution is reduced with respect to the stripmap resolution by a factor that is equal to:
which is always greater than 1. However, the real electronically-steered rotation angle versus the azimuth time shows typically a staircase behavior with a constant steering step period
[
2,
10]. Therefore, the practical antenna pattern should be rewritten as:
where
is the minimum slow-time jump point of rotation angle referenced to the target’s beam center crossing point, which is a uniformly distributed random variable within the range
for each different target and dependent on the target’s azimuth position,
denotes the down-round operation. Note that the beam steering jumping happen at the same absolute slow-time points for all targets, however, a target with a randomly distributed azimuth position will have its own random absolute time of beam center crossing, therefore,
, i.e., the closest jump point of beam steering referenced to the target’s beam center crossing, is a random value less than
. Additionally, note that
is included in the round brackets so that the beam rotation angle is in accordance with the ideal continuous one at the center time of each electronically steering step. According to Equations (1)–(3), the practical antenna pattern
can be further expressed as:
where
is a periodic function with its period equaling the steering step period
:
It is well known that a periodic integrable function can be further expanded and expressed as the following Fourier series
where
. According to Equations (5) and (6), it is known that
is always less than
and far less than the whole illumination time
. On the other hand, the absolute value of the factor
is always less than 1 according to Equation (2). In a word,
is a quite short time frame, so that the following first-order Taylor expansion approximation is given:
where
represents the time derivation of
. The accuracy of the approximation in Equation (7) will be checked in the simulation section of this paper. It is now clear that the antenna pattern with the effect of staircase-like beam steering shows a typical periodic amplitude modulation, and the sine terms in Equation (7) will lead to paired echoes in the IRF [
6].
Now the antenna pattern weighted signal model will be derived. It is well known that SAR is a two-dimensional (2-D) system. However, for a typical TOPS mode, the 2-D frequency bandwidth is normally not wide, therefore the range-dimensional processing and range-azimuth decoupling are not closely related to the azimuth antenna pattern. For the sake of brevity, the azimuth one-dimensional (1-D) signal model is preferable for the following derivation [
8,
9,
19]. The azimuth 1-D signal is the echo of one target after the first and secondary range compression (SRC), as well as the range cell migration (RCM) correction.
In a continuous linear beam steering case, after an azimuth demodulation step, called baseband azimuth scaling (BAS), integrated in the TOPS mode imaging processor [
19,
20], the echo from isolated target separated in azimuth is demodulated to zero Doppler centroid and can be represented without unnecessary terms as [
8,
9]:
where
is the effective azimuth chirp rate of the received signal [
19]. In ideal conditions, the output focused signal after matched filtering is:
where
represents the ideal matched filter, and
is the Fourier transform of
, representing the ideal IRF envelope. In contrast, in the step-by-step steering case, the received signal suffering an undesired amplitude modulation becomes:
According to the approximation given by Equation (7),
can be approximated as
:
If the same matched filtering in Equation (9) is used, the paired-echo-corrupted output signal can be expressed as follows if the Fourier series in Equation (6) is used and with reasonable approximation [
6,
8,
9]:
where:
is a time parameter representing an azimuth time displacement, and the amplitude coefficient is:
and:
is a
uniformly distributed random phase determined by the target’s azimuth-time jump point
, which is further dependent on the azimuth target position. Note that Equation (11) is similar to the signal model given in [
8] and [
9], however, the random phase
is neglected in [
8,
9]. It also should be noted that the existence of the amplitude terms
will lead to a peak splitting for those paired-echo distortion peaks.
4. Simulation Results
Simulations are performed in this section. All the simulations are based on the multi-mode version of SBRAS (Space-borne Radar Advance Simulator) [
21,
22]. This multi-mode simulator supports the parameter design, raw data simulation, data focusing and performance evaluation of strip-map mode, sliding spotlight mode, TOPS mode, and so on [
21]. The implementation of this simulator for spaceborne SAR modes with azimuth beam steering could be found in [
20], [
23,
24,
25]. The designed parameters used in the simulation are listed in
Table 1, the TOPS mode raw data are simulated assuming a C-band spaceborne system with an azimuth resolution of 20 m and a beam steering rate
= 1.73°/s. The main steering stepping period
is 0.02 s, the corresponding angle stepping size of about 0.035°, which is a little larger than the stepping size of 0.03° chosen in the design of TerraSAR mode [
2,
10]. An alternative choice of
= 0.03 s (0.052° of angle stepping size) is also investigated, which is designed under the applied background of low-cost spaceborne SAR payloads.
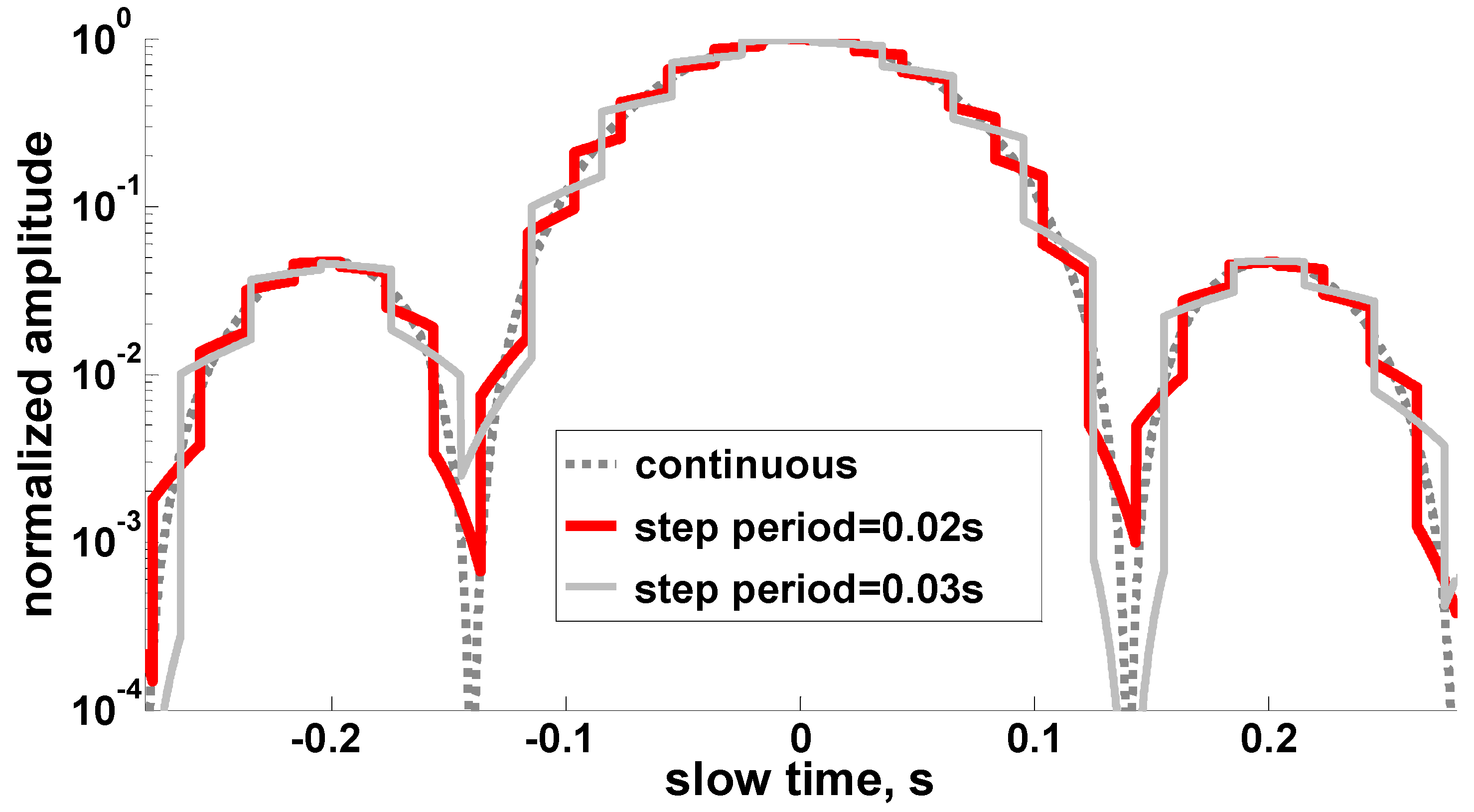
The effects of the staircase-like antenna steering to two-way antenna pattern seen by a target with the designed TOPS mode are shown in
Figure 2. The solid red line represents the case
= 0.02 s and the solid gray line represents the case
= 0.03 s. As a contrast, the ideal TOPS mode two-way antenna pattern with a continuous beam steering is also given by the grey dotted line. Here the beam steering jump point
is randomly set as
. It is found that the results in
Figure 2 are similar to the simulated TOPS antenna gain shown in Figure 3 of [
2].
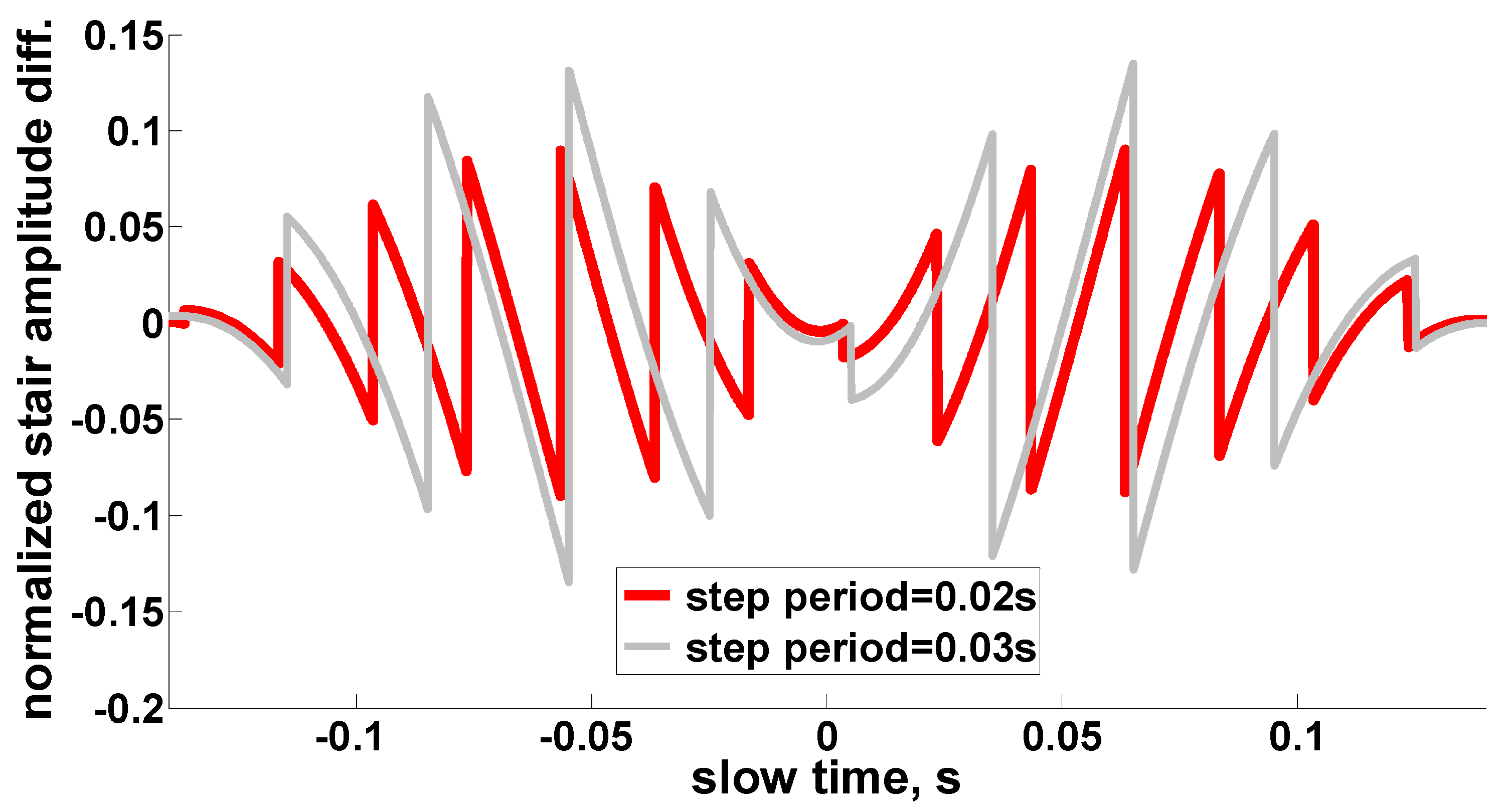
The undesired amplitude modulation caused by staircase-like steering in the raw data of a point target is represented by the difference between the ideal and the staircase antenna gain. The normalized amplitude differences of the above two antenna patterns with different stepping size are shown in
Figure 3, which is like a saw tooth signal, as analyzed in [
2]. The jump points of beam steering can be found clearly in this figure. It also can be seen that a larger stepping angle size will enlarge the undesired amplitude modulation.
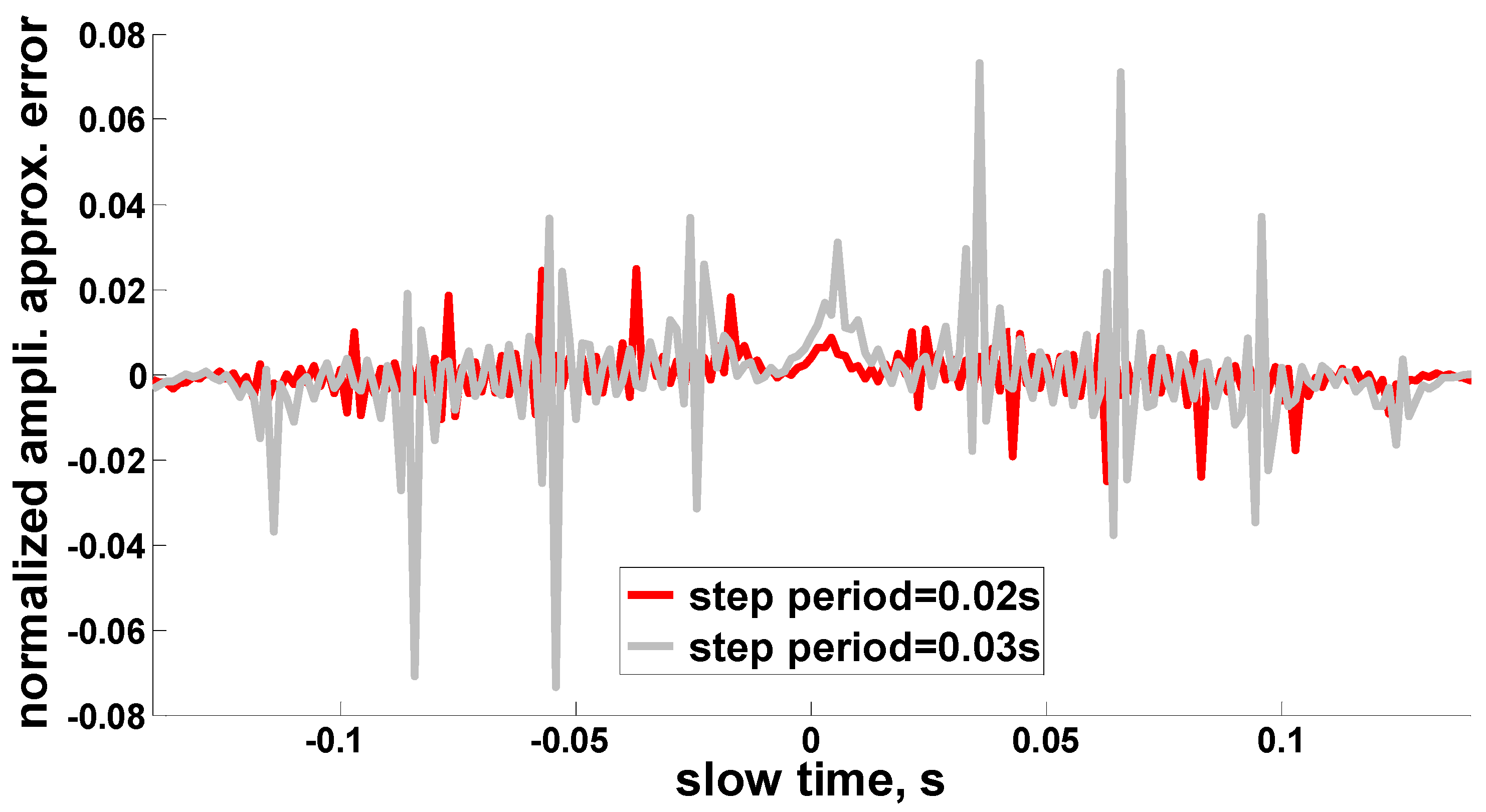
The approximation errors for the two antenna patterns using the approximate antenna pattern model given by Equation (7) are also shown in
Figure 4. The Fourier series expansion number
N is set to 6. It can be seen that the approximations perform well for both cases, i.e.,
= 0.02 s and
= 0.03 s. It is also found that the approximation errors are relatively larger around the jump points of beam steering.
In order to verify the performance of the EOF and the proposed GOF approach for targets separated in azimuth with different azimuth position,
Figure 5,
Figure 6 and
Figure 7 show the azimuth focusing processing results of three point targets at different azimuth positions in the imaged scene. The steering step period
is equal to 0.02 s for
Figure 5,
Figure 6 and
Figure 7. For GOF approach, the Fourier series expansion number is set as
N = 6 uniformly.
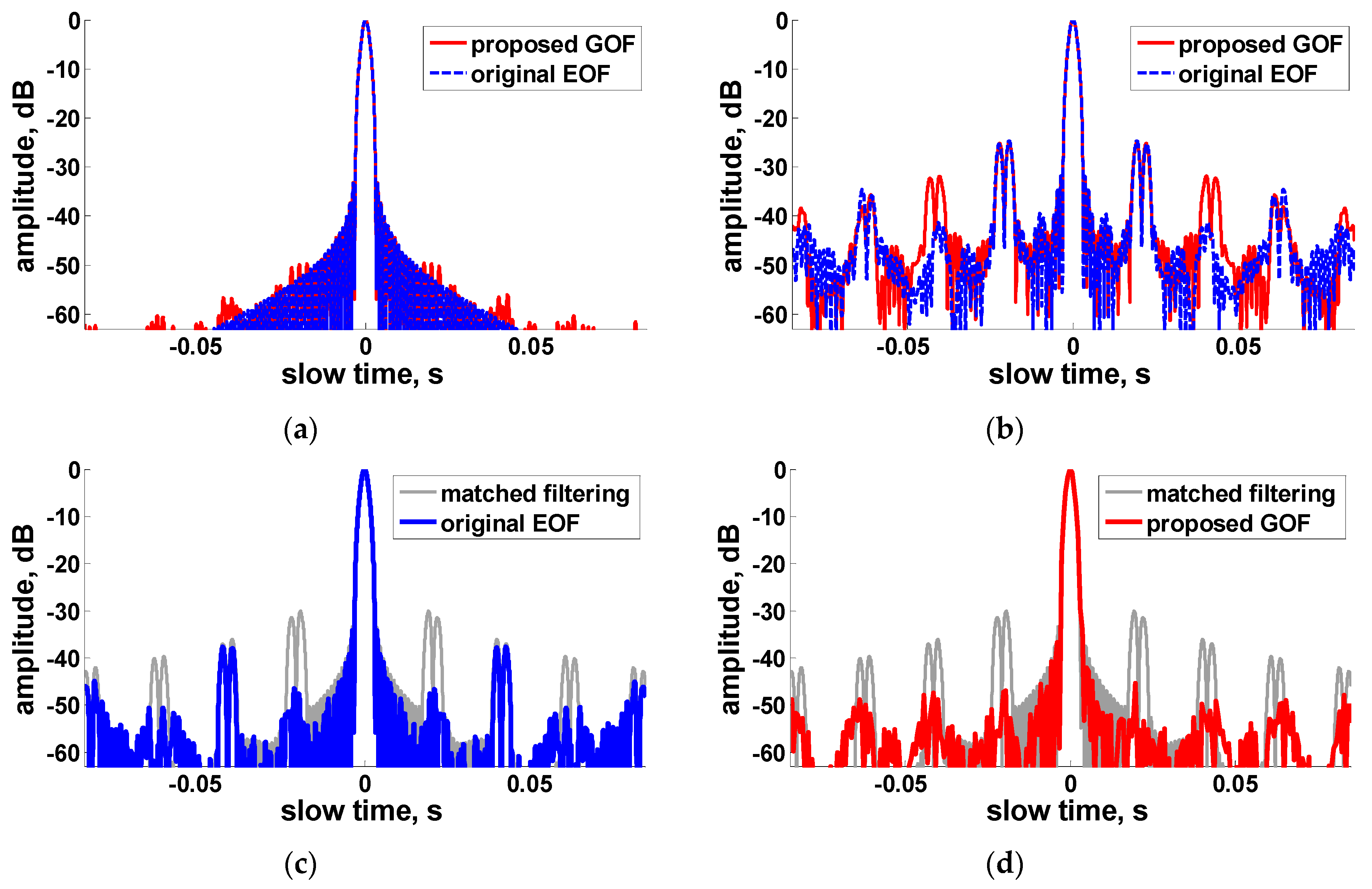
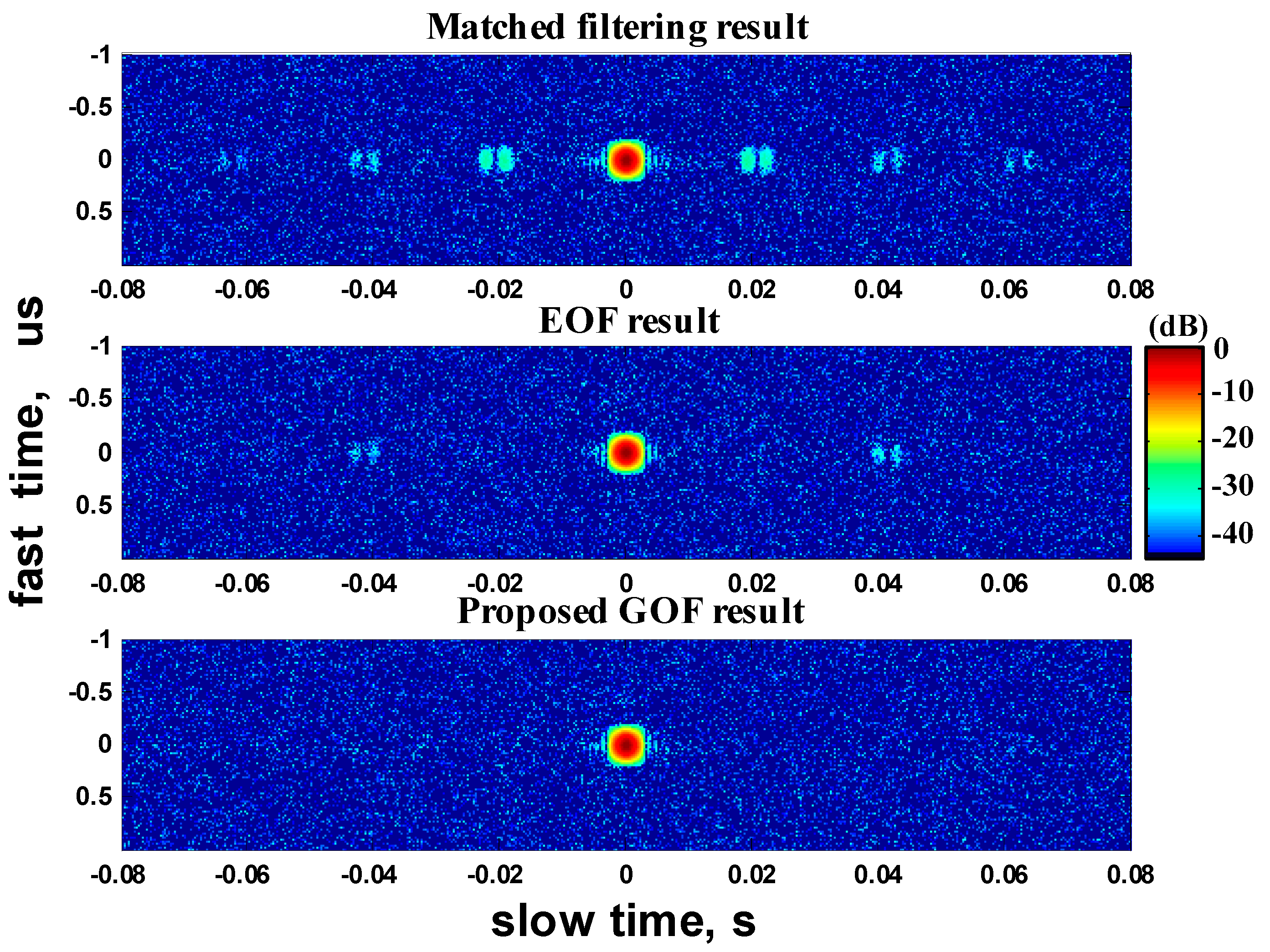
In
Figure 5, the azimuth position of the tested target is chosen purposively so that the azimuth-time jump point
= 0, corresponding to
(see Equation (15)).
Figure 5a shows the first OF-path output of EOF and GOF approaches. For the EOF approach, since the first path is predefined for
= 0, the correct
value is actually met in this path, therefore, an ideal IRF is obtained as shown in the blue lines. For the GOF approach, however, since the first-path filtering is only an approximation of OF for
= 0, only a nearly ideal IRF is obtained, as shown in the red lines.
Figure 5b shows the second OF-path output of EOF and GOF approaches, which is predefined for
=
(
) in the EOF approach. For both approaches, the “ideal” deconvolution filtering is out of operation due to the mismatched information about
, however, the output of GOF contains more useful paired-echo information, which can be used to cancel the paired echoes in the matched filtering output (see the gray lines in
Figure 5c,d). The ultimate results of both approaches are shown in (c) and (d) in contrast to the matched filtering result, respectively. It can be seen that the EOF approach can efficiently suppress the strongest paired echoes, however, due to the unsuccessful suppression for the second-strongest paired echoes, the output paired-echo peak ratio of the IRF is still about −37 dB. For the result of GOF approach, both the strongest paired distortion peaks and the peripheral power of the distorted IRF can be satisfactorily suppressed, the overall amplitude level of the paired echoes is about −49 dB.
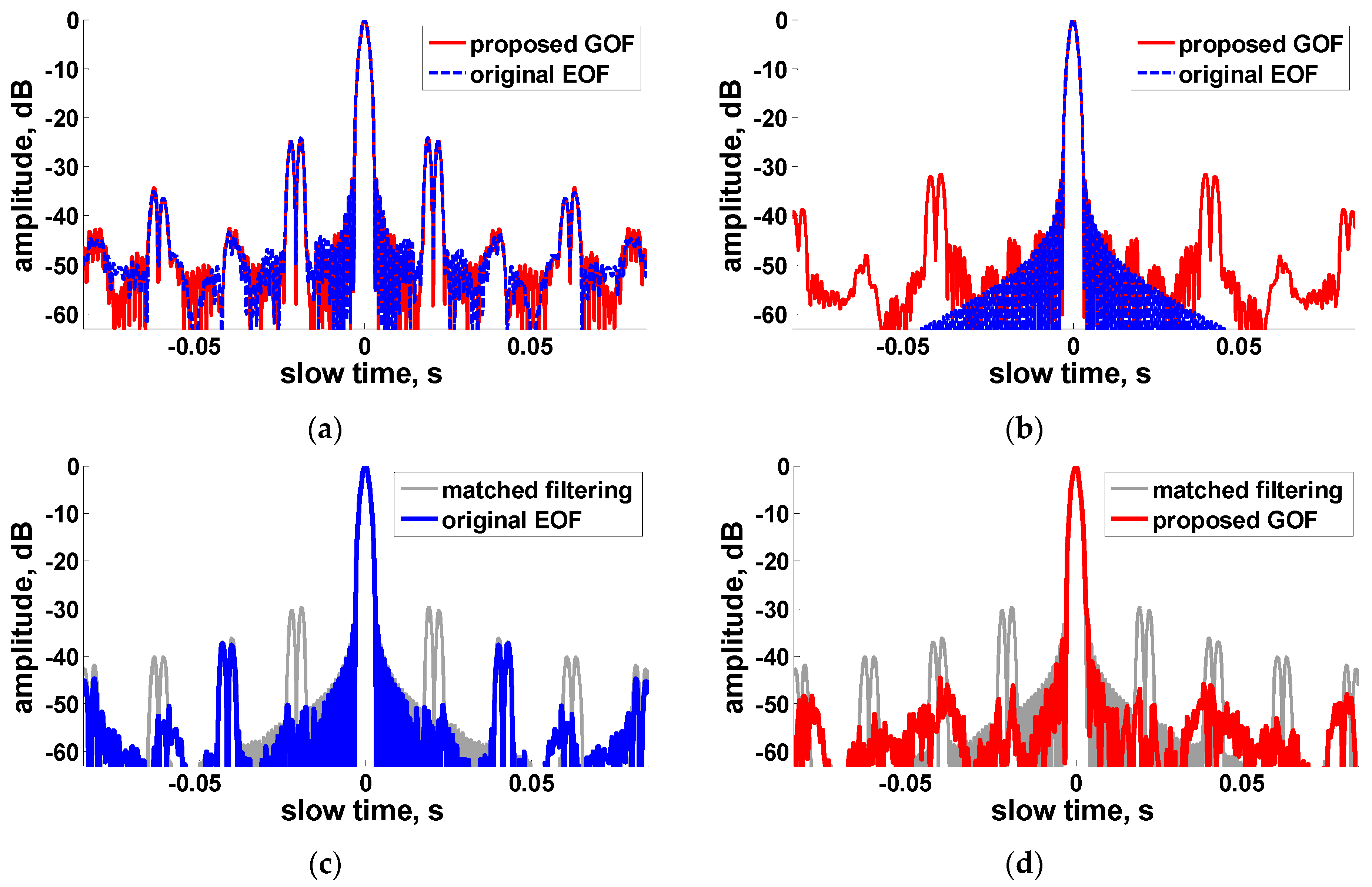
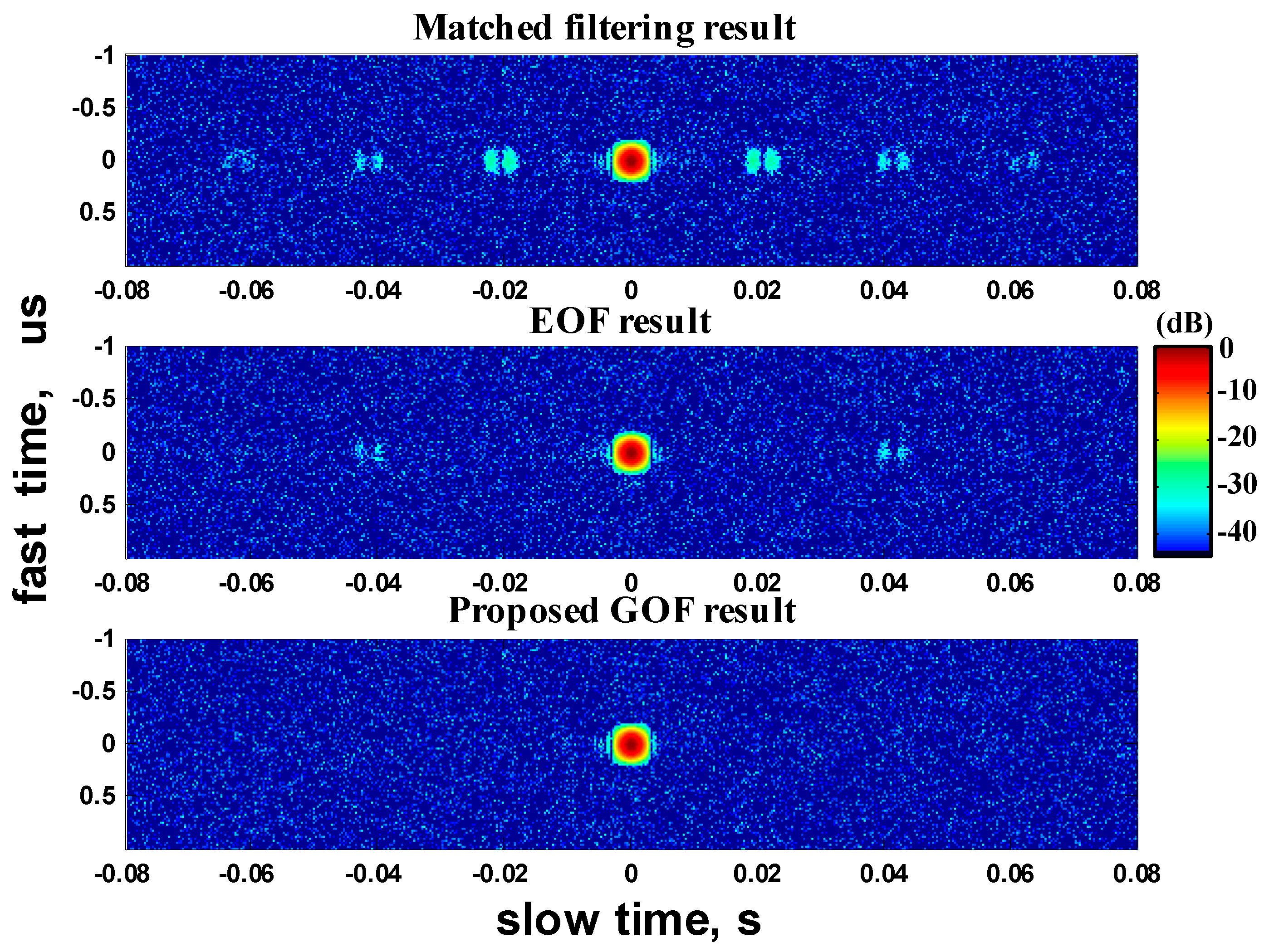
In
Figure 6, the azimuth position of the tested target is changed so that the azimuth-time jump point
, corresponding to
. Now note that in
Figure 6b, since the second path is predefined for
, this time the correct
value is met in the second path, therefore, an ideal IRF is obtained in the second OF-path as shown in the blue line. On the contrary, the second OF-path output of GOF approach shown in red line is far from an ideal IRF (in contrast to the nearly ideal IRF from the first OF-path of GOF in a matched
case, show in red lines in
Figure 5a), and this demonstrates the fact that the second OF-path of GOF is more special and is generated based on a physically nonexistent artificial “echo”. The ultimate processing results for both EOF and GOF are quite similar to the results shown in
Figure 5.
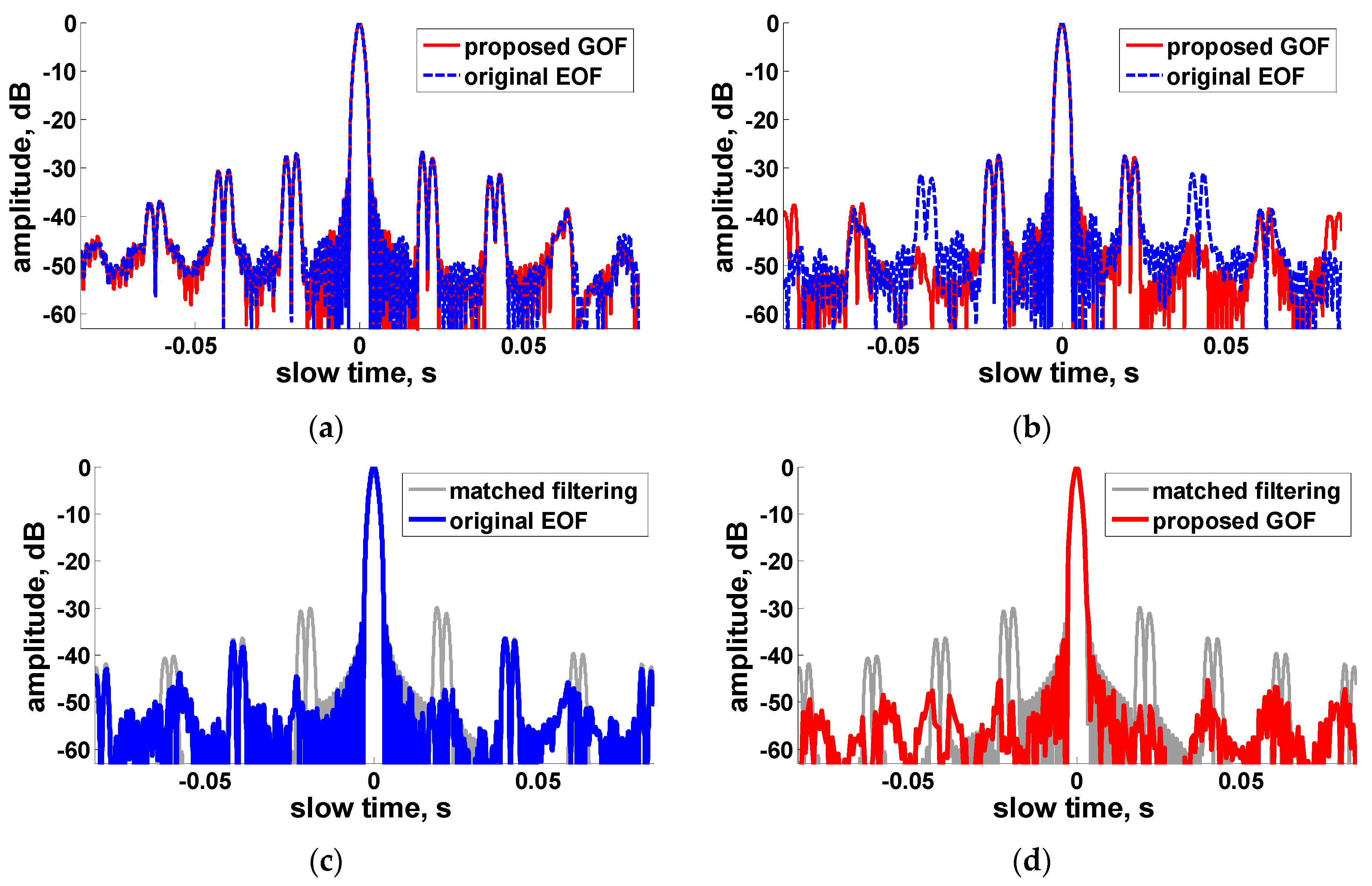
In
Figure 7, now the azimuth position of the tested target is set to make the azimuth-time jump point
equal to
. In some sense, this is the worst case for optimum matched filtering, since the real
is in the center of
, it means now the real echo is close to neither of the two OF-paths. Nevertheless, we still obtain very similar ultimate results for EOF and GOF.
Overall, from the results shown in
Figure 5,
Figure 6 and
Figure 7, it is observed that, although the second OF-path output of GOF approach is never near an ideal IRF for any one of the three targets, the combined processing with the first OF-path will obtain a satisfactory result for both suppression of the strongest paired peaks and the peripheral power of the distorted IRF. Both the performance of GOF and EOF are stable and not dependent on the target azimuth position. The original paired echo peak ratio for match filtering is −30 dB (
= 0.02 s), after the proposed GOF approach, the peak ratio is not exceed −48 dB; after the EOF approach, the peak ratio is not exceed −37 dB.
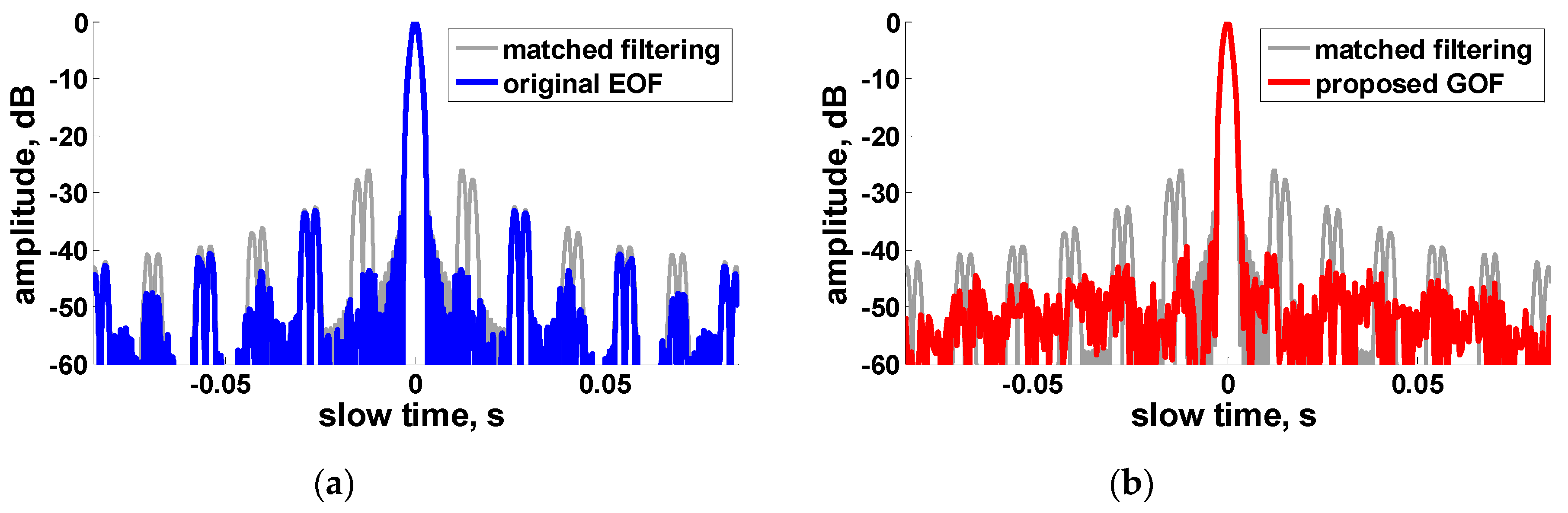
In
Figure 8, the processing results in the case that
= 0.03 s is given. It is found that with a larger angle step size, the paired echo peak ratio for conventional match filtering is about −25 dB, which is much higher than the case when
= 0.02 s. The peak ratio of the GOF result is below −40 dB, while the peak ratio of the EOF result is below −32 dB.
The azimuth 1-D simulation above is quite essential for showing the detailed processing results suited to quantitative analysis. Since SAR imaging is actually a 2-D process, the 2-D processing results are also simulated and given in
Figure 9;
Figure 10. This time nine strong point targets having different range and azimuth positions are evenly embedded in a 6 km × 6 km scene of low backscatter. They are arranged in such a way that the targets in the corner positions limit the 6 km × 6 km scene in the azimuth and range, respectively. It is found that all the nine targets have the similar processing performance.
Figure 9 and
Figure 10 show the results of two targets located at the top left corner and bottom right corner of the scene, respectively. It is found that “ghost targets” from strong point targets embedded in a scene of low backscatters in the process of conventional SAR data imaging are eliminated if the data are processed with the proposed GOF approach. However, if the data are processed with the EOF approach, there are still remnant “ghost targets”.
5. Discussion
It is found that the proposed GOF approach and the EOF approach given in [
18] share the same processing flow. The main difference between GOF and EOF is the way how to generate two OF paths. The two OF paths of EOF approach are made up of two conventional deconvolving filters generated according to the accurate signal model given by Equation (10), corresponding to two different given beam steering jump point
values, and no approximation in Equations (7) and (11) regarding paired-echo-distortion modeling is needed in the generation of the deconvolving functions. The IRFs plotted in blue in
Figure 5a and
Figure 6b have shown that perfect IRF can be achieved from one individual OF path among the two EOF paths if the correct
value is actually met. The two OF paths of GOF approach, however, cannot be regarded as conventional ideal deconvolving filters. The IRFs plotted in red in the subimages (a) and (b) of
Figure 5,
Figure 6 and
Figure 7 have shown that no perfect IRF can be achieved from any individual OF path among the two GOF paths. In this sense, GOF is a new reasonable approximation of the EOF approach originally proposed in [
18], and, in theory, EOF can obtain better single-path performance than GOF.
Nevertheless, it is found from the ultimate results that by the combination use of the two OP paths, GOF approach can achieve better suppression on the paired echo peaks than the EOF approach, esp. for the second-strongest aliased paired peaks. The GOF approach performs stably and azimuth independently in all of the simulation cases. In the case that = 0.02 s, the paired echo peak ratio can be suppressed from −30 dB to a level of about −50 dB; In the case that = 0.03 s, the peak ratio is suppressed from −25 dB to a level of −40 dB. For the EOF approach, however, the peak ratios are −37 dB and −32 dB for = 0.02 s and = 0.03 s, respectively.
In addition, a series truncation in Equations (24) and (25) is required for the GOF approach. Increasing the Fourier series expansion number can improve accuracy of the antenna pattern approximation model. Since the two-path filter functions would be pre-calculated and then can be used for the batch processing of images acquired with the same steering mode, a larger series expansion number will not increase on-line computation load. Based on these considerations, in the simulation, the series expansion number N is uniformly set as 6.