Methane Emission Estimates by the Global High-Resolution Inverse Model Using National Inventories
Abstract
1. Introduction
2. Materials and Methods
2.1. Inverse Modeling System—NTFVAR
2.1.1. The Transport Model
2.1.2. The Inverse Modeling Scheme
2.2. Prior Fluxes and Observations
2.3. Flux Estimation Uncertainties
2.4. Adjusting Prior Anthropogenic Emissions to National Reports
3. Results and Discussion
3.1. Comparison of EDGAR v4.3.2 and UNFCCC Reports
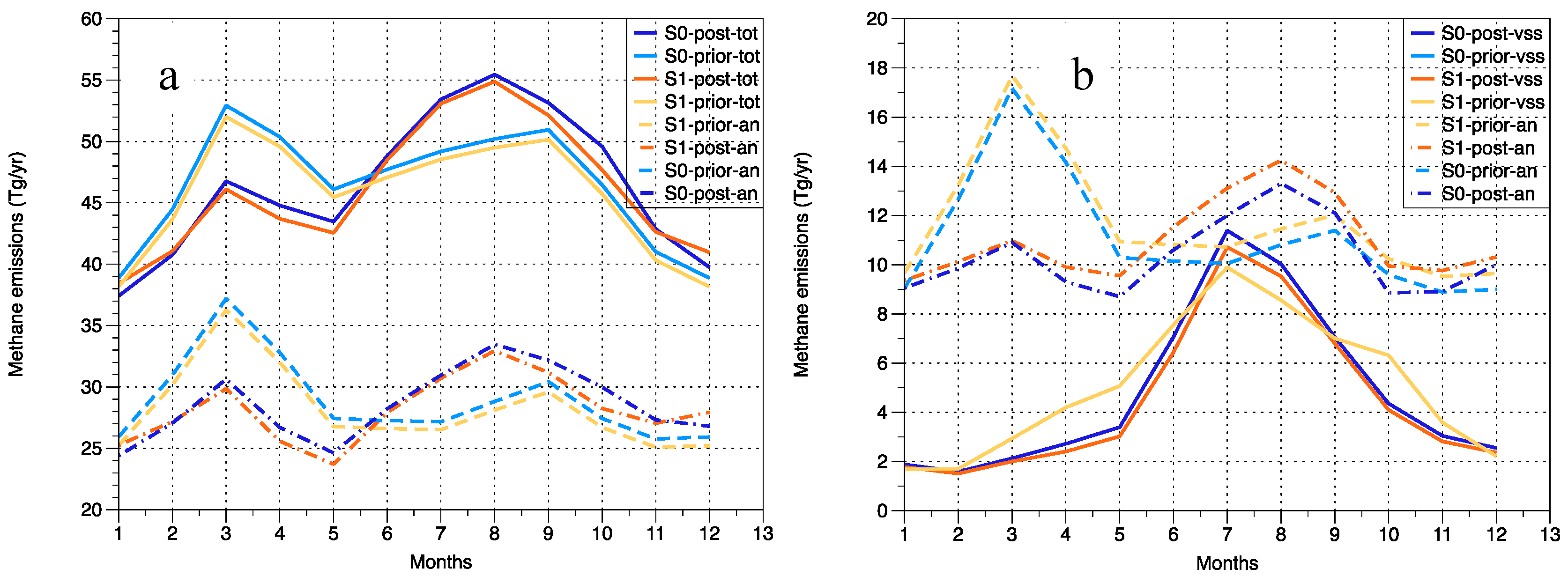
3.2. Estimation of Global Methane Emissions
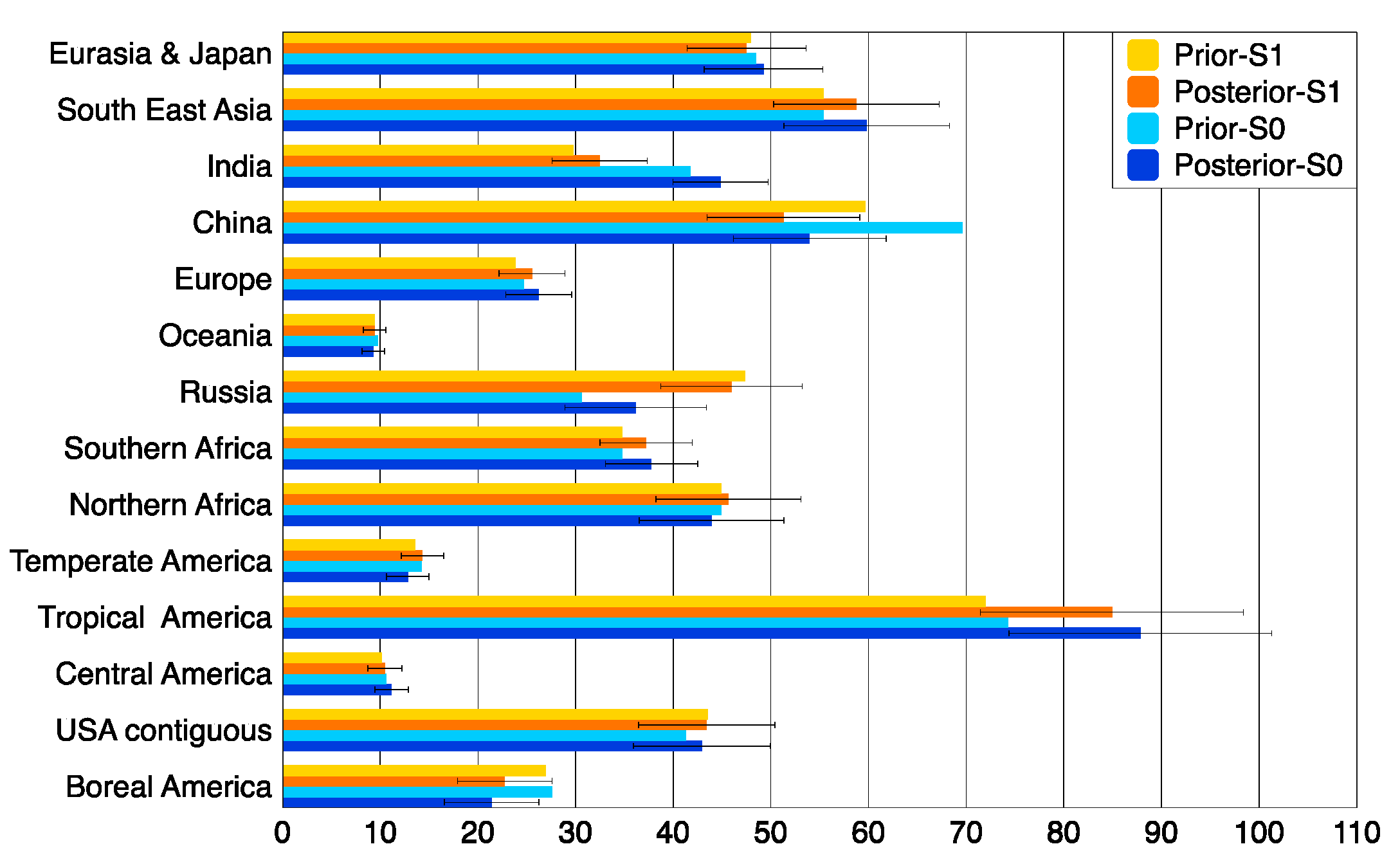
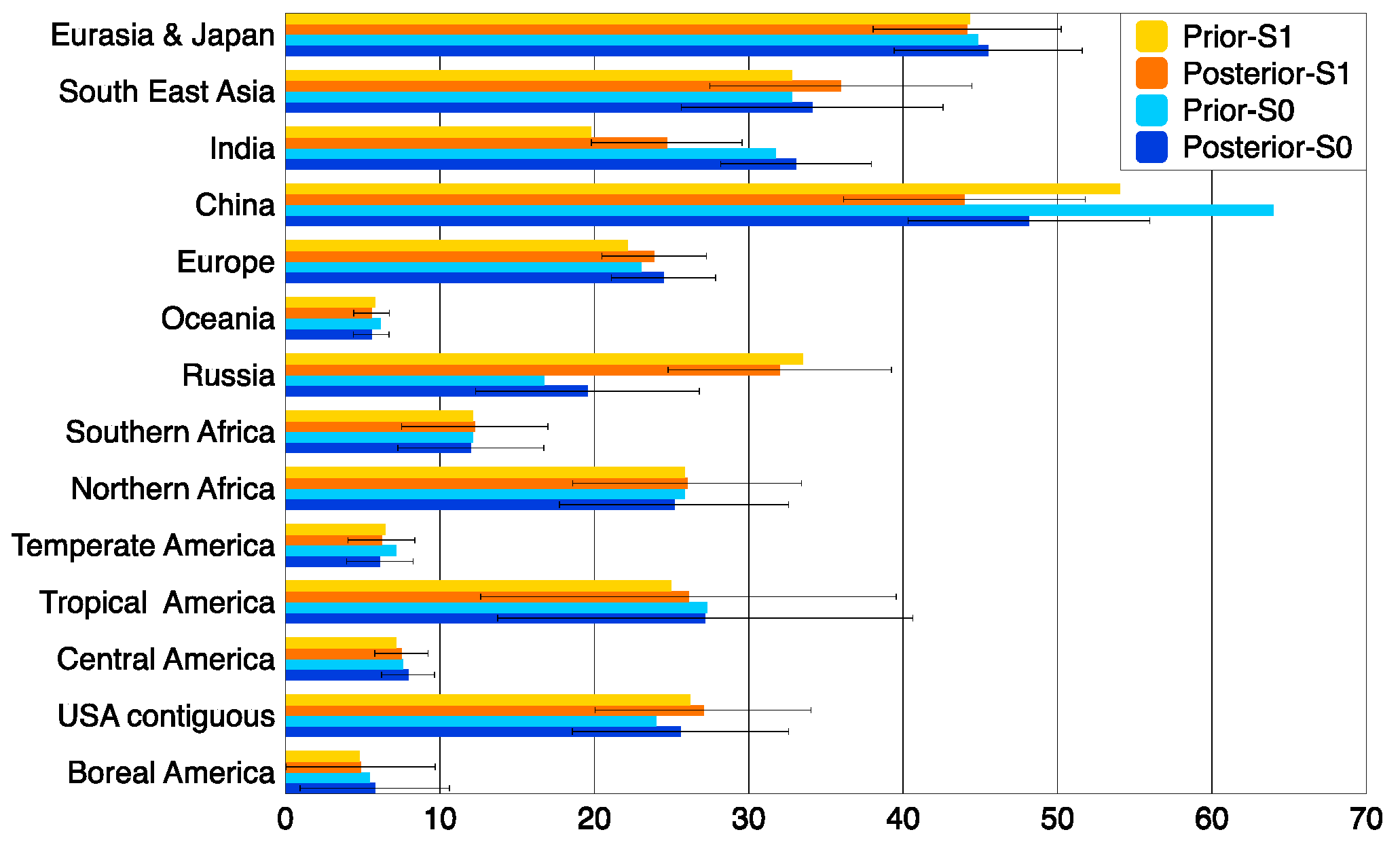
3.3. Estimation of Regional Methane Emissions
3.3.1. Total Regional Emissions
3.3.2. Regional Anthropogenic Emissions
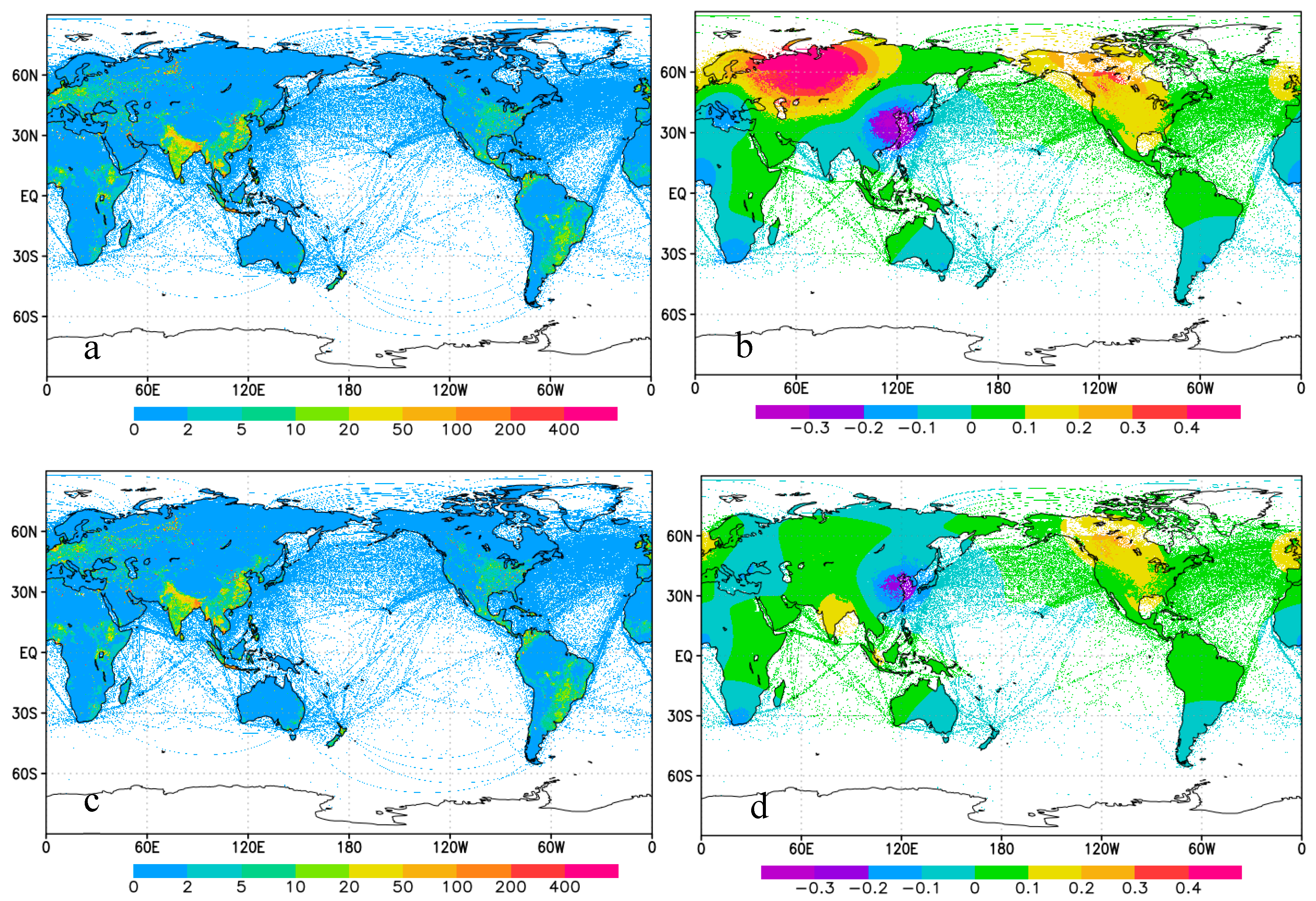
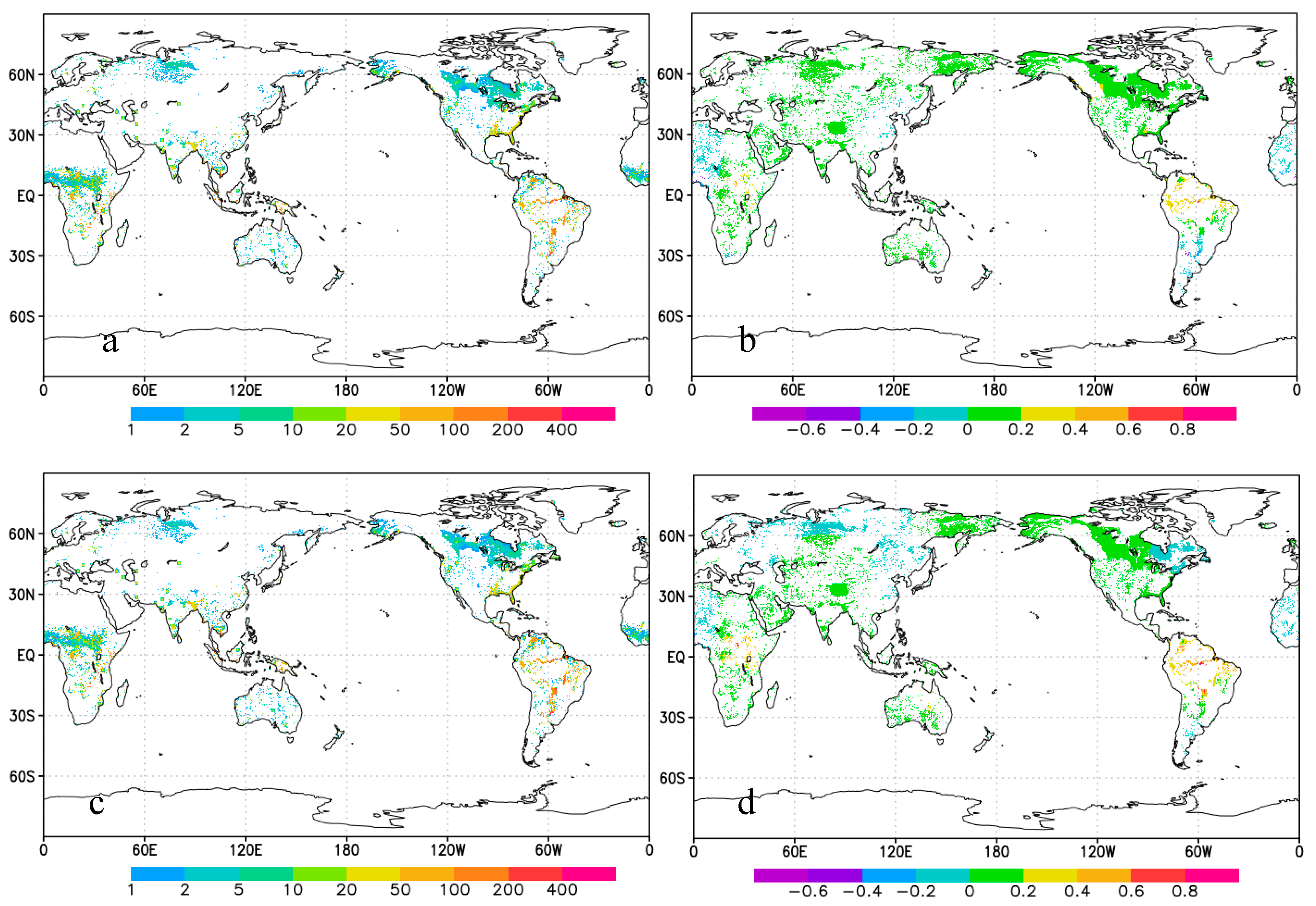
3.4. Spatial Patterns of the Flux Corrections
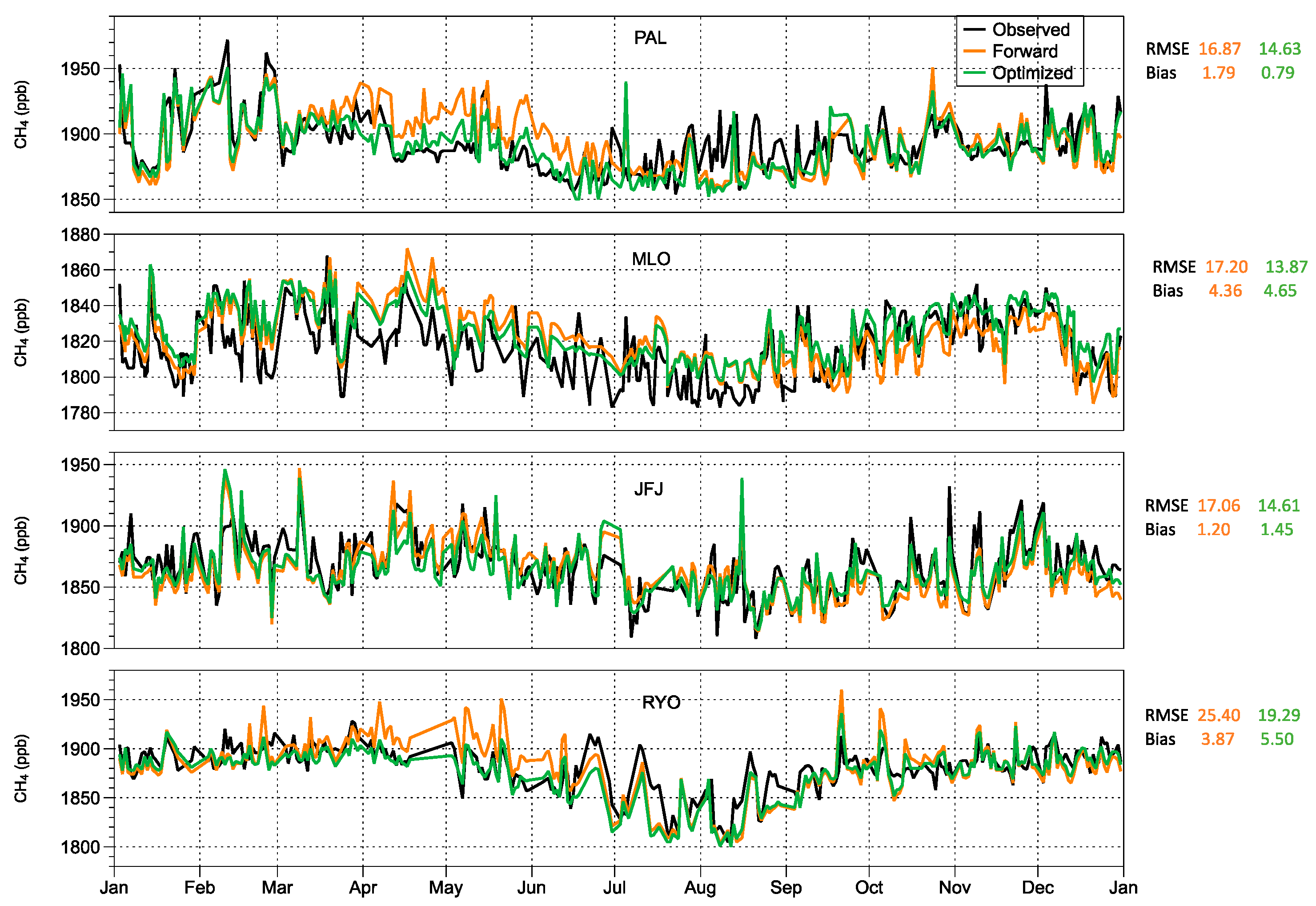
3.5. Modeled Concentrations Versus Observations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Obs.ID | Lab. | Latitude (deg. N) | Longitude (deg. E) | Altitude (m.a.s.l.) | Station Type | Sampling Type 1 | Uncertainty (ppm) |
|---|---|---|---|---|---|---|---|
| abb006 | ECCC | 49.03 | −122.3 | 93 | Station | C | 0.060 |
| abp001 | NOAA | −12.77 | −38.17 | 6 | Station | D | 0.010 |
| alt006 | ECCC | 82.45 | −62.51 | 210 | Station | C | 0.019 |
| alt001 | NOAA | 82.45 | −62.51 | 195 | Station | D | 0.019 |
| ams011 | LSCE | −37.80 | 77.54 | 70, 75 | Station | D/C | 0.010 |
| amt001 | NOAA | 45.03 | −68.68 | 157, 160 | Station | D | 0.100 |
| amy061 | KMA | 36.53 | 126.32 | 86 | Station | C | 0.063 |
| aoa019 | JMA | 24.23–34.43 | 141.04–154.02 | 200–8100 | Aircraft | D | 0.021 |
| arh015 | NIWA | −77.80 | 166.67 | 189 | Station | D | 0.010 |
| asc001 | NOAA | −7.97 | −14.40 | 90 | Station | D | 0.010 |
| ask001 | NOAA | 23.26 | 5.63 | 2715 | Station | D | 0.013 |
| ato045 | MPI-BGC | −2.15 | −59.01 | 209 | Station | C | 0.030 |
| azr001 | NOAA | 38.77 | −27.38 | 24 | Station | D | 0.021 |
| azv | NIES | 54.71 | 73.03 | 150 | Station | C | 0.050 |
| bal001 | NOAA | 55.35 | 17.22 | 28 | Station | D | 0.038 |
| bao001 | NOAA | 40.05 | −105.00 | 1884 | Station | D | 0.100 |
| beh006 | ECCC | 62.80 | −117.55 | 220 | Station | C | 0.020 |
| bgu011 | LSCE | 41.97 | 3.23 | 15 | Station | D | 0.018 |
| bhd001 | NOAA | −41.41 | 174.87 | 90 | Station | D | 0.010 |
| bis011 | LSCE | 44.38 | −1.23 | 167 | Station | C | 0.060 |
| bkt105 | EMPA | −0.20 | 100.32 | 877 | Station | C | 0.022 |
| bkt001 | NOAA | −0.20 | 100.32 | 875 | Station | D | 0.022 |
| bme001 | NOAA | 32.37 | −64.65 | 17 | Station | D | 0.020 |
| bmw001 | NOAA | 32.27 | −64.88 | 60 | Station | D | 0.015 |
| brl006 | ECCC | 50.20 | −104.71 | 630 | Station | C | 0.100 |
| brw001 | NOAA | 71.32 | −156.61 | 16, 27.5 | Station | D | 0.022 |
| brz | NIES | 56.15 | 84.33 | 230 | Station | C | 0.067 |
| bsc001 | NOAA | 44.18 | 28.66 | 5 | Station | D | 0.046 |
| bsl015 | NIWA | −29.99–33.43 | 135.07–167.55 | 30 | Ship | D | 0.032 |
| cab006 | ECCC | 69.11 | −105.14 | 47 | Station | C | 0.020 |
| cba001 | NOAA | 55.21 | −162.72 | 57 | Station | D | 0.017 |
| cbw196 | RUG | 51.97 | 4.93 | 199 | Station | C | 0.060 |
| cfa002 | CSIRO | −19.28 | 147.06 | 5 | Station | D | 0.010 |
| cgo001 | NOAA | −40.68 | 144.69 | 164 | Station | D | 0.019 |
| cgo043 | AGAGE | −40.68 | 144.68 | 94 | Station | C | 0.019 |
| cha006 | ECCC | 49.82 | −74.97 | 431 | Station | C | 0.020 |
| chi006 | ECCC | 49.68 | −74.34 | 423 | Station | C | 0.035 |
| chr001 | NOAA | 1.70 | −157.15 | 5 | Station | D | 0.020 |
| chs001 | NOAA | 68.51 | 161.53 | 64.4 | Station | D | 0.025 |
| chu006 | ECCC | 58.75 | −94.07 | 89 | Station | C | 0.030 |
| cib001 | NOAA | 41.81 | −4.93 | 850 | Station | D | 0.020 |
| cmn106 | UNIURB/ISAC | 44.18 | 10.70 | 2172 | Station | D | 0.020 |
| coi020 | NIES | 43.16 | 145.50 | 94 | Station | C | 0.027 |
| cpt036 | SAWS | −34.35 | 18.49 | 260 | Station | C | 0.010 |
| cpt001 | NOAA | −34.35 | 18.49 | 260 | Station | D | 0.010 |
| cri002 | CSIRO | 15.08 | 73.83 | 66 | Station | D | 0.036 |
| crz001 | NOAA | −46.43 | 51.85 | 202 | Station | D | 0.010 |
| cya002 | CSIRO | −66.28 | 110.52 | 55 | Station | D | 0.010 |
| dem020 | NIES | 59.79 | 70.87 | 138 | Station | C | 0.068 |
| dow006 | ECCC | 43.74 | −79.47 | 218 | Station | C | 0.100 |
| drp001 | NOAA | −65.02–58.85 | −65.73–58.65 | 10 | Ship | D | 0.010 |
| dsi001 | NOAA | 20.70 | 116.73 | 8 | Station | D | 0.020 |
| egb006 | ECCC | 44.23 | −79.78 | 276 | Station | C | 0.042 |
| eic001 | NOAA | −27.15 | −109.45 | 55, 69, 72 | Station | D | 0.010 |
| eom010 | MRI | −15.00–39.16 | −177.00–178.00 | 3788–13106 | Aircraft | D | 0.024 |
| esp006 | ECCC | 49.38 | −126.54 | 47 | Station | C | 0.015 |
| est006 | ECCC | 51.67 | −110.21 | 757 | Station | C | 0.080 |
| etl006 | ECCC | 54.35 | −104.99 | 598 | Station | C | 0.052 |
| fik011 | LSCE | 35.34 | 25.67 | 150, 152 | Station | D | 0.032 |
| fsd006 | ECCC | 49.88 | −81.57 | 250 | Station | C | 0.033 |
| gif011 | LSCE | 48.71 | 2.15 | 167 | Station | C | 0.030 |
| glh209 | UMIT | 36.07 | 14.22 | 167 | Station | C | 0.020 |
| gmi001 | NOAA | 13.39 | 144.66 | 5, 8 | Station | D | 0.023 |
| gpa002 | CSIRO | −12.25 | 131.04 | 37 | Station | D | 0.020 |
| gsn | NIER | 33.17 | 126.10 | 82, 144 | Station | C | 0.060 |
| hat020 | NIES | 24.06 | 123.81 | 47.3 | Station | C | 0.032 |
| hba001 | NOAA | −75.61 | −26.21 | 35 | Station | D | 0.010 |
| hle011 | LSCE | 32.78 | 78.96 | 4517, 4522 | Station | D | 0.020 |
| hpb001 | NOAA | 47.80 | 11.02 | 990, 941 | Station | D | 0.067 |
| hun001 | NOAA | 46.95 | 16.65 | 344 | Station | D | 0.056 |
| ice001 | NOAA | 63.40 | −20.29 | 127 | Station | D | 0.020 |
| igr020 | NIES | 63.19 | 64.42 | 72 | Station | C | 0.139 |
| inu006 | ECCC | 68.32 | −133.53 | 123 | Station | C | 0.020 |
| izo001 | NOAA | 28.31 | −16.50 | 2377.9 | Station | D | 0.020 |
| izo027 | AEMET | 28.30 | −16.48 | 2360 | Station | C | 0.020 |
| jfj005 | EMPA | 46.55 | 7.99 | 3583 | Station | C | 0.022 |
| key001 | NOAA | 25.66 | −80.16 | 6 | Station | D | 0.024 |
| kmw196 | RIVM | 53.33 | 6.28 | 0 | Station | C | 0.100 |
| krs020 | NIES | 58.25 | 82.42 | 117 | Station | C | 0.056 |
| kum001 | NOAA | 19.52 | −154.82 | 8, 41.1 | Station | D | 0.015 |
| kzd001 | NOAA | 44.45 | 75.57 | 412, 600 | Station | D | 0.038 |
| kzm001 | NOAA | 43.25 | 77.86 | 2524 | Station | D | 0.038 |
| lau015 | NIWA | −45.03 | 169.67 | 380 | Station | D/C | 0.010 |
| lef001 | NOAA | 45.95 | −90.27 | 868 | Station | D | 0.070 |
| llb006 | ECCC | 54.95 | −112.45 | 588 | Station | C | 0.092 |
| llb001 | NOAA | 54.95 | −112.45 | 546 | Station | D | 0.092 |
| lln001 | NOAA | 23.47 | 120.87 | 2867 | Station | D | 0.029 |
| lmp001 | NOAA | 35.52 | 12.62 | 50 | Station | D | 0.025 |
| lmp028 | ENEA | 35.52 | 12.62 | 45 | Station | D | 0.025 |
| lpo011 | LSCE | 48.80 | −3.58 | 20 | Station | D | 0.066 |
| lto011 | LSCE | 6.22 | −5.03 | 205 | Station | C | 0.030 |
| maa002 | CSIRO | −67.62 | 62.87 | 42 | Station | D | 0.010 |
| mex001 | NOAA | 18.98 | −97.31 | 4469 | Station | D | 0.021 |
| mhd001 | NOAA | 53.33 | −9.90 | 26 | Station | D | 0.015 |
| mhd043 | AGAGE | 53.33 | −9.90 | 8 | Station | C | 0.015 |
| mid001 | NOAA | 28.21 | −177.38 | 8, 16 | Station | D | 0.016 |
| mkn001 | NOAA | −0.06 | 37.30 | 3649 | Station | D | 0.025 |
| mlo001 | NOAA | 19.54 | −155.58 | 3402, 3437 | Station | D/C | 0.016 |
| mnm019 | JMA | 24.30 | 153.97 | 8 | Station | C | 0.016 |
| mqa002 | CSIRO | −54.48 | 158.97 | 12 | Station | D | 0.010 |
| mwo001 | NOAA | 34.22 | −118.06 | 1770.6, 1774 | Station | D | 0.100 |
| nat001 | NOAA | −5.51 | −35.26 | 20, 87 | Station | D | 0.015 |
| ngl025 | UBA-Germany | 53.17 | 13.03 | 68.4 | Station | C | 0.047 |
| nmb001 | NOAA | −23.58 | 15.03 | 461 | Station | D | 0.010 |
| nov004-070 | NIES | 55.00 | 83.00 | 400–7000 | Aircraft | D | 0.013–0.096 |
| noy | NIES | 63.43 | 75.78 | 143 | Station | C | 0.017 |
| nwr001 | NOAA | 40.05 | −105.58 | 3526 | Station | D | 0.017 |
| ope011 | LSCE | 48.55 | 5.50 | 440, 510 | Station | D/C | 0.100 |
| ota002 | CSIRO | −38.52 | 142.82 | 50 | Station | D | 0.020 |
| oxk001 | NOAA | 50.03 | 11.81 | 1172, 1185 | Station | D | 0.037 |
| pal001 | NOAA | 67.97 | 24.12 | 570 | Station | D | 0.022 |
| pal030 | FMI | 67.97 | 24.12 | 567 | Station | C | 0.022 |
| pbl011 | LSCE | 11.65 | 92.76 | 20, 21 | Station | D | 0.030 |
| pdm011 | LSCE | 42.94 | 0.14 | 2877, 2887, 2905 | Station | D | 0.034 |
| pip008 | TU | 37.81 | 141.35 | 198–3813 | Aircraft | D | 0.028 |
| poc000-s35 | NOAA | −35.00–30.00 | −179.00–178.43 | 20 | Ship | D | 0.014 |
| pon011 | LSCE | 12.01 | 79.86 | 20, 30 | Station | D | 0.030 |
| prs021 | RSE | 45.93 | 7.70 | 3490 | Station | C | 0.018 |
| psa001 | NOAA | −64.92 | −64.00 | 15 | Station | D | 0.010 |
| pta001 | NOAA | 38.95 | −123.74 | 22 | Station | D | 0.020 |
| puy011 | LSCE | 45.77 | 2.97 | 1465, 1475 | Station | D | 0.044 |
| rpb001 | NOAA | 13.16 | −59.43 | 20 | Station | D | 0.013 |
| rpb043 | AGAGE | 13.17 | −59.43 | 45 | Station | C | 0.013 |
| ryo019 | JMA | 39.03 | 141.83 | 260 | Station | C | 0.026 |
| sct001 | NOAA | 33.41 | −81.83 | 420 | Station | D | 0.100 |
| sdz001 | NOAA | 40.65 | 117.12 | 298 | Station | D | 0.098 |
| sey001 | NOAA | −4.68 | 55.53 | 7 | Station | D | 0.018 |
| sgp001 | NOAA | 36.61 | −97.49 | 374 | Station | D | 0.060 |
| shm001 | NOAA | 52.72 | 174.10 | 28 | Station | D | 0.018 |
| smo001 | NOAA | −14.25 | −170.56 | 47, 60 | Station | D | 0.010 |
| smo043 | AGAGE | −14.24 | −170.57 | 42 | Station | C | 0.010 |
| smr421 | UHELS | 61.51 | 24.17 | 306 | Station | C | 0.030 |
| snb211 | EAA | 47.05 | 12.95 | 3111 | Station | C | 0.020 |
| sod030 | FMI | 67.36 | 26.64 | 227 | Station | C | 0.030 |
| spo001 | NOAA | −89.98 | −24.80 | 2815, 2821.3 | Station | D | 0.010 |
| ssl025 | UBA-Germany | 47.92 | 7.92 | 1205 | Station | C | 0.045 |
| str001 | NOAA | 37.76 | −122.45 | 486 | Station | D | 0.100 |
| sum001 | NOAA | 72.60 | −38.42 | 3214.5 | Station | D | 0.015 |
| sur005-070 | NIES | 61.00 | 73.00 | 500–7000 | Aircraft | D | 0.015–0.070 |
| syo001 | NOAA | −69.00 | 39.58 | 16, 19 | Station | D | 0.010 |
| tap001 | NOAA | 36.73 | 126.13 | 21 | Station | D | 0.047 |
| tda008 | TU | 33.26–38.10 | 130.47–141.23 | 3962–11278 | Aircraft | D | 0.024 |
| ter055 | MGO | 69.20 | 35.10 | 42 | Station | D | 0.028 |
| thd001 | NOAA | 41.05 | −124.15 | 112 | Station | D | 0.015 |
| thd043 | AGAGE | 41.05 | −124.15 | 120 | Station | C | 0.015 |
| tik001 | MGO | 71.60 | 128.89 | 29 | Station | D | 0.030 |
| tr3011 | LSCE | 47.96 | 2.11 | 311 | Station | D | 0.100 |
| tup006 | ECCC | 42.68 | −80.33 | 266 | Station | C | 0.020 |
| ush001 | NOAA | −54.85 | −68.31 | 32 | Station | D | 0.010 |
| uta001 | NOAA | 39.90 | −113.72 | 1332 | Station | D | 0.023 |
| uto030 | FMI | 59.78 | 21.37 | 65 | Station | C | 0.030 |
| uum001 | NOAA | 44.45 | 111.10 | 1012 | Station | D | 0.036 |
| vgn | NIES | 54.50 | 62.33 | 285 | Station | C | 0.058 |
| wbi001 | NOAA | 41.73 | −91.35 | 620 | Station | D | 0.100 |
| wgc001 | NOAA | 38.27 | −121.49 | 91 | Station | D | 0.120 |
| wis001 | NOAA | 30.86 | 34.78 | 156, 482 | Station | D | 0.028 |
| wkt001 | NOAA | 31.32 | −97.33 | 708 | Station | D | 0.100 |
| wlg001 | NOAA | 36.29 | 100.90 | 3815 | Station | D | 0.023 |
| wlg033 | CMA/NOAA | 36.28 | 100.90 | 3810 | Station | D | 0.023 |
| wpc001 | NOAA | −30.45–30.10 | 136.62–170.47 | 10 | Ship | D | 0.010 |
| wpsEQ0-S35 | NIES | −36.99–54.00 | 136.64–179.90 | 10 | Ship | D | 0.010 |
| wsa006 | ECCC | 43.93 | −60.01 | 30 | Station | D/C | 0.022 |
| yak010-030 | NIES | 62.09 | 129.36 | 287, 1000–3000 | Station/Aircraft | C/D | 0.015–0.042 |
| yon019 | JMA | 24.47 | 123.02 | 30 | Station | C | 0.032 |
| zep001 | NOAA | 78.91 | 11.89 | 479 | Station | D | 0.019 |
| zot045 | MPI-BGC | 60.48 | 89.21 | 415 | Station | D/C | 0.020 |
| zsf025 | UBA-Germany | 47.42 | 10.98 | 2673.5 | Station | C | 0.020 |
References
- Etheridge, D.; Steele, L.; Francey, R.; Langenfelds, R. Atmospheric methane between 1000 AD and present: Evidence of anthropogenic emissions and climatic variability. J. Geophys. Res. Atmos. 1998, 103, 15979–15993. [Google Scholar] [CrossRef]
- Ferretti, D.; Miller, J.; White, J.; Etheridge, D.; Lassey, K.; Lowe, D.; Meure, C.; Dreier, M.; Trudinger, C.; van Ommen, T.; et al. Unexpected changes to the global methane budget over the past 2000 years. Science 2005, 309, 1714–1717. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, A.; Patra, P.; Ishijima, K.; Umezawa, T.; Ito, A.; Etheridge, D.; Sugawara, S.; Kawamura, K.; Miller, J.; Dlugokencky, E.; et al. Variations in global methane sources and sinks during 1910–2010. Atmos. Chem. Phys. 2015, 15, 2595–2612. [Google Scholar] [CrossRef]
- Saunois, M.; Jackson, R.; Bousquet, P.; Poulter, B.; Canadell, J. The growing role of methane in anthropogenic climate change. Environ. Res. Lett. 2016, 11, 120207. [Google Scholar] [CrossRef]
- Shindell, D.; Kuylenstierna, J.; Vignati, E.; van Dingenen, R.; Amann, M.; Klimont, Z.; Anenberg, S.; Muller, N.; Janssens-Maenhout, G.; Raes, F.; et al. Simultaneously Mitigating Near-Term Climate Change and Improving Human Health and Food Security. Science 2012, 335, 183–189. [Google Scholar] [CrossRef]
- Zhang, Y.; Jacob, D.; Maasakkers, J.; Sulprizio, M.; Sheng, J.; Gautam, R.; Worden, J. Monitoring global tropospheric OH concentrations using satellite observations of atmospheric methane. Atmos. Chem. Phys. 2018, 18, 15959–15973. [Google Scholar] [CrossRef]
- Prather, M.; Holmes, C.; Hsu, J. Reactive greenhouse gas scenarios: Systematic exploration of uncertainties and the role of atmospheric chemistry. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Sonnemann, G.; Grygalashvyly, M. Effective CO2 lifetime and future CO2 levels based on fit function. Ann. Geophys. 2013, 31, 1591–1596. [Google Scholar] [CrossRef]
- Feng, T.; Yang, Y.; Xie, S.; Dong, J.; Ding, L. Economic drivers of greenhouse gas emissions in China. Renew. Sustain. Energy Rev. 2017, 78, 996–1006. [Google Scholar] [CrossRef]
- Saunois, M.; Bousquet, P.; Poulter, B.; Peregon, A.; Ciais, P.; Canadell, J.; Dlugokencky, E.; Etiope, G.; Bastviken, D.; Houweling, S.; et al. The global methane budget 2000–2012. Earth Syst. Sci. Data 2016, 8, 697–751. [Google Scholar] [CrossRef]
- Lyon, D.; Zavala-Araiza, D.; Alvarez, R.; Harriss, R.; Palacios, V.; Lan, X.; Talbot, R.; Lavoie, T.; Shepson, P.; Yacovitch, T.; et al. Constructing a Spatially Resolved Methane Emission Inventory for the Barnett Shale Region. Environ. Sci. Technol. 2015, 49, 8147–8157. [Google Scholar] [CrossRef] [PubMed]
- Peischl, J.; Karion, A.; Sweeney, C.; Kort, E.; Smith, M.; Brandt, A.; Yeskoo, T.; Aikin, K.; Conley, S.; Gvakharia, A.; et al. Quantifying atmospheric methane emissions from oil and natural gas production in the Bakken shale region of North Dakota. J. Geophys. Res. Atmos. 2016, 121, 6101–6111. [Google Scholar] [CrossRef]
- Saunois, M.; Bousquet, P.; Poulter, B.; Peregon, A.; Ciais, P.; Canadell, J.; Dlugokencky, E.; Etiope, G.; Bastviken, D.; Houweling, S.; et al. Variability and quasi-decadal changes in the methane budget over the period 2000–2012. Atmos. Chem. Phys. 2017, 17, 11135–11161. [Google Scholar] [CrossRef]
- Kirschke, S.; Bousquet, P.; Ciais, P.; Saunois, M.; Canadell, J.; Dlugokencky, E.; Bergamaschi, P.; Bergmann, D.; Blake, D.; Bruhwiler, L.; et al. Three decades of global methane sources and sinks. Nat. Geosci. 2013, 6, 813–823. [Google Scholar] [CrossRef]
- Peng, S.; Piao, S.; Bousquet, P.; Ciais, P.; Li, B.; Lin, X.; Tao, S.; Wang, Z.; Zhang, Y.; Zhou, F. Inventory of anthropogenic methane emissions in mainland China from 1980 to 2010. Atmos. Chem. Phys. 2016, 16, 14545–14562. [Google Scholar] [CrossRef]
- Le Quere, C.; Andrew, R.; Friedlingstein, P.; Sitch, S.; Hauck, J.; Pongratz, J.; Pickers, P.; Korsbakken, J.; Peters, G.; Canadell, J.; et al. Global Carbon Budget 2018. Earth Syst. Sci. Data 2018, 10, 2141–2194. [Google Scholar] [CrossRef]
- Oliver, J.; Bouwman, A.; Vandermass, C.; Berdowski, J. Emission database for global atmospheric research (EDGAR). Environ. Monit. Assess. 1994, 31, 93–106. [Google Scholar] [CrossRef]
- Crippa, M.; Guizzardi, D.; Muntean, M.; Schaaf, E.; Dentener, F.; van Aardenne, J.; Monni, S.; Doering, U.; Olivier, J.; Pagliari, V.; et al. Gridded emissions of air pollutants for the period 1970–2012 within EDGAR v4.3.2. Earth Syst. Sci. Data 2018, 10, 1987–2013. [Google Scholar] [CrossRef]
- Janssens-Maenhout, G.; Crippa, M.; Guizzardi, D.; Muntean, M.; Schaaf, E.; Dentener, F.; Bergamaschi, P.; Pagliari, V.; Olivier, J.; Peters, J.; et al. EDGAR v4.3.2 Global Atlas of the three major Greenhouse Gas Emissions for the period 1970–2012. Earth Syst. Sci. Data Discuss. 2019, 2019, 959–1002. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Krol, M.; Meirink, J.; Dentener, F.; Segers, A.; van Aardenne, J.; Monni, S.; Vermeulen, A.; Schmidt, M.; Ramonet, M.; et al. Inverse modeling of European CH4 emissions 2001–2006. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Brown, M. Deduction of emissions of source gases using an objective inversion algorithm and a chemical-transport model. J. Geophys. Res. Atmos. 1993, 98, 12639–12660. [Google Scholar] [CrossRef]
- Sheng, J.; Jacob, D.; Turner, A.; Maasakkers, J.; Sulprizio, M.; Bloom, A.; Andrews, A.; Wunch, D. High-resolution inversion of methane emissions in the Southeast US using SEAC (4) RS aircraft observations of atmospheric methane: Anthropogenic and wetland sources. Atmos. Chem. Phys. 2018, 18, 6483–6491. [Google Scholar] [CrossRef]
- Turner, A.; Jacob, D.; Wecht, K.; Maasakkers, J.; Lundgren, E.; Andrews, A.; Biraud, S.; Boesch, H.; Bowman, K.; Deutscher, N.; et al. Estimating global and North American methane emissions with high spatial resolution using GOSAT satellite data. Atmos. Chem. Phys. 2015, 15, 7049–7069. [Google Scholar] [CrossRef]
- Miller, S.; Wofsy, S.; Michalak, A.; Kort, E.; Andrews, A.; Biraud, S.; Dlugokencky, E.; Eluszkiewicz, J.; Fischer, M.; Janssens-Maenhout, G.; et al. Anthropogenic emissions of methane in the United States. Proc. Natl. Acad. Sci. USA 2013, 110, 20018–20022. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.; Michalak, A.; Detmers, R.; Hasekamp, O.; Bruhwiler, L.; Schwietzke, S. China’s coal mine methane regulations have not curbed growing emissions. Nat. Commun. 2019, 10, 303. [Google Scholar] [CrossRef]
- Sheng, J.; Jacob, D.; Turner, A.; Maasakkers, J.; Benmergui, J.; Bloom, A.; Arndt, C.; Gautam, R.; Zavala-Araiza, D.; Boesch, H.; et al. 2010-2016 methane trends over Canada, the United States, and Mexico observed by the GOSAT satellite: Contributions from different source sectors. Atmos. Chem. Phys. 2018, 18, 12257–12267. [Google Scholar] [CrossRef]
- Houweling, S.; Bergamaschi, P.; Chevallier, F.; Heimann, M.; Kaminski, T.; Krol, M.; Michalak, A.; Patra, P. Global inverse modeling of CH4 sources and sinks: An overview of methods. Atmos. Chem. Phys. 2017, 17, 235–256. [Google Scholar] [CrossRef]
- Jacob, D.; Turner, A.; Maasakkers, J.; Sheng, J.; Sun, K.; Liu, X.; Chance, K.; Aben, I.; McKeever, J.; Frankenberg, C. Satellite observations of atmospheric methane and their value for quantifying methane emissions. Atmos. Chem. Phys. 2016, 16, 14371–14396. [Google Scholar] [CrossRef]
- Shirai, T.; Ishizawa, M.; Zhuravlev, R.; Ganshin, A.; Belikov, D.; Saito, M.; Oda, T.; Valsala, V.; Gomez-Pelaez, A.; Langenfelds, R.; et al. A decadal inversion of CO2 using the Global Eulerian-Lagrangian Coupled Atmospheric model (GELCA): Sensitivity to the ground-based observation network. Tellus Ser. B Chem. Phys. Meteorol. 2017, 69, 1291158. [Google Scholar] [CrossRef]
- Belikov, D.; Maksyutov, S.; Yaremchuk, A.; Ganshin, A.; Kaminski, T.; Blessing, S.; Sasakawa, M.; Gomez-Pelaez, A.; Starchenko, A. Adjoint of the global Eulerian-Lagrangian coupled atmospheric transport model (A-GELCA v1.0): Development and validation. Geosci. Model Dev. 2016, 9, 749–764. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Krol, M.; Dentener, F.; Vermeulen, A.; Meinhardt, F.; Graul, R.; Ramonet, M.; Peters, W.; Dlugokencky, E. Inverse modelling of national and European CH4 emissions using the atmospheric zoom model TM5. Atmos. Chem. Phys. 2005, 5, 2431–2460. [Google Scholar] [CrossRef]
- Manning, A.; Ryall, D.; Derwent, R.; Simmonds, P.; O’Doherty, S. Estimating European emissions of ozone-depleting and greenhouse gases using observations and a modeling back-attribution technique. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Ganesan, A.; Rigby, M.; Lunt, M.; Parker, R.; Boesch, H.; Goulding, N.; Umezawa, T.; Zahn, A.; Chatterjee, A.; Prinn, R.; et al. Atmospheric observations show accurate reporting and little growth in India’s methane emissions. Nat. Commun. 2017, 8, 836. [Google Scholar] [CrossRef] [PubMed]
- Maksyutov, S.; Oda, T.; Saito, M.; Janardanan, R.; Belikov, D.; Kaiser, J.W.; Zhuravlev, R.; Ganshin, A.; Valsala, V. Technical note: High resolution inverse modelling technique for estimating surface CO2 fluxes based on coupled NIES-TM—Flexpart transport model and its adjoint. Atmos. Chem. Phys. Discuss. 2019. in preparation. [Google Scholar]
- UNFCCC. Greenhouse Gas Inventory Data. Available online: https://di.unfccc.int/comparison_by_category (accessed on 20 November 2018).
- Ganshin, A.; Oda, T.; Saito, M.; Maksyutov, S.; Valsala, V.; Andres, R.; Fisher, R.; Lowry, D.; Lukyanov, A.; Matsueda, H.; et al. A global coupled Eulerian-Lagrangian model and 1 × 1 km CO2 surface flux dataset for high-resolution atmospheric CO2 transport simulations. Geosci. Model Dev. 2012, 5, 231–243. [Google Scholar] [CrossRef]
- Zhuravlev, R.V.; Ganshin, A.V.; Maksyutov, S.S.; Oshchepkov, S.L.; Khattatov, B.V. Estimation of global CO2 fluxes using ground-based and satellite (GOSAT) observation data with empirical orthogonal functions. Atmos. Ocean. Opt. 2013, 26, 507–516. [Google Scholar] [CrossRef]
- Ishizawa, M.; Mabuchi, K.; Shirai, T.; Inoue, M.; Morino, I.; Uchino, O.; Yoshida, Y.; Belikov, D.; Maksyutov, S. Inter-annual variability of summertime CO2 exchange in Northern Eurasia inferred from GOSAT XCO2. Environ. Res. Lett. 2016, 11, 105001. [Google Scholar] [CrossRef]
- Belikov, D.; Maksyutov, S.; Sherlock, V.; Aoki, S.; Deutscher, N.; Dohe, S.; Griffith, D.; Kyro, E.; Morino, I.; Nakazawa, T.; et al. Simulations of column-averaged CO2 and CH4 using the NIES TM with a hybrid sigma-isentropic (sigma-theta) vertical coordinate. Atmos. Chem. Phys. 2013, 13, 1713–1732. [Google Scholar] [CrossRef]
- Stohl, A.; Forster, C.; Frank, A.; Seibert, P.; Wotawa, G. Technical note: The Lagrangian particle dispersion model FLEXPART version 6.2. Atmos. Chem. Phys. 2005, 5, 2461–2474. [Google Scholar] [CrossRef]
- Hascoet, L.; Pascual, V. The Tapenade Automatic Differentiation Tool: Principles, Model, and Specification. ACM Trans. Math. Softw. 2013, 39, 20. [Google Scholar] [CrossRef]
- Giering, R.; Kaminski, T. Applying TAF to generate efficient derivative code of Fortran 77–95 programs. Proc. Appl. Math. Mech. 2003, 2, 54–57. [Google Scholar] [CrossRef]
- Van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1997, 135, 229–248. [Google Scholar] [CrossRef]
- Onogi, K.; Tslttsui, J.; Koide, H.; Sakamoto, M.; Kobayashi, S.; Hatsushika, H.; Matsumoto, T.; Yamazaki, N.; Kaalhori, H.; Takahashi, K.; et al. The JRA-25 reanalysis. J. Meteorol. Soc. Jpn. 2007, 85, 369–432. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Jpn. 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Meirink, J.; Bergamaschi, P.; Krol, M. Four-dimensional variational data assimilation for inverse modelling of atmospheric methane emissions: Method and comparison with synthesis inversion. Atmos. Chem. Phys. 2008, 8, 6341–6353. [Google Scholar] [CrossRef]
- Basu, S.; Guerlet, S.; Butz, A.; Houweling, S.; Hasekamp, O.; Aben, I.; Krummel, P.; Steele, P.; Langenfelds, R.; Torn, M.; et al. Global CO2 fluxes estimated from GOSAT retrievals of total column CO2. Atmos. Chem. Phys. 2013, 13, 8695–8717. [Google Scholar] [CrossRef]
- Weaver, A.; Courtier, P. Correlation modelling on the sphere using a generalized diffusion equation. Q. J. R. Meteorol. Soc. 2001, 127, 1815–1846. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in FORTRAN 77, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992; p. 1010. [Google Scholar]
- Gilbert, J.; Lemarechal, C. Some numerical experiments with variable-storage quasi-newton algorithms. Math. Program. 1989, 45, 407–435. [Google Scholar] [CrossRef]
- Cao, M.; Marshall, S.; Gregson, K. Global carbon exchange and methane emissions from natural wetlands: Application of a process-based model. J. Geophys. Res. Atmos. 1996, 101, 14399–14414. [Google Scholar] [CrossRef]
- Curry, C. Modeling the soil consumption of atmospheric methane at the global scale. Glob. Biogeochem. Cycles 2007, 21. [Google Scholar] [CrossRef]
- Ito, A.; Inatomi, M. Use of a process-based model for assessing the methane budgets of global terrestrial ecosystems and evaluation of uncertainty. Biogeosciences 2012, 9, 759–773. [Google Scholar] [CrossRef]
- Lehner, B.; Doll, P. Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. 2004, 296, 1–22. [Google Scholar] [CrossRef]
- Running, S.; Nemani, R.; Heinsch, F.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Kaiser, J.W.; Heil, A.; Andreae, M.O.; Benedetti, A.; Chubarova, N.; Jones, L.; Morcrette, J.-J.; Razinger, M.; Schultz, M.G.; Suttie, M.; et al. Biomass burning emissions estimated with a global fire assimilation system based on observed fire radiative power. Biogeosciences 2012, 9, 527–554. [Google Scholar] [CrossRef]
- Patra, P.; Houweling, S.; Krol, M.; Bousquet, P.; Belikov, D.; Bergmann, D.; Bian, H.; Cameron-Smith, P.; Chipperfield, M.; Corbin, K.; et al. TransCom model simulations of CH4 and related species: Linking transport, surface flux and chemical loss with CH4 variability in the troposphere and lower stratosphere. Atmos. Chem. Phys. 2011, 11, 12813–12837. [Google Scholar] [CrossRef]
- Yoshida, Y.; Kikuchi, N.; Morino, I.; Uchino, O.; Oshchepkov, S.; Bril, A.; Saeki, T.; Schutgens, N.; Toon, G.; Wunch, D.; et al. Improvement of the retrieval algorithm for GOSAT SWIR XCO2 and XCH4 and their validation using TCCON data. Atmos. Meas. Tech. 2013, 6, 1533–1547. [Google Scholar] [CrossRef]
- Chevallier, F.; Breon, F.; Rayner, P. Contribution of the Orbiting Carbon Observatory to the estimation of CO2 sources and sinks: Theoretical study in a variational data assimilation framework. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Olivier, J.G.J.; Jeroen, A.H.W. Trends in Global CO2 and Total Greenhouse Gas Emissions; PBL Publishers: Sydney, Australia, 2018; Available online: https://www.pbl.nl/en/publications/trends-in-global-co2-and-total-greenhouse-gas-emissions-2018-report (accessed on 11 January 2019).
- Hoglund-Isaksson, L. Bottom-up simulations of methane and ethane emissions from global oil and gas systems 1980 to 2012. Environ. Res. Lett. 2017, 12, 024007. [Google Scholar] [CrossRef]
- IPCC. Carbon and Other Biogeochemical Cycles. In ClimateChange 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Ribeiro, I.; Andreoli, R.; Kayano, M.; de Sousa, T.; Medeiros, A.; Guimaraes, P.; Barbosa, C.; Godoi, R.; Martin, S.; de Souza, R. Impact of the biomass burning on methane variability during dry years in the Amazon measured from an aircraft and the AIRS sensor. Sci. Total Environ. 2018, 624, 509–516. [Google Scholar] [CrossRef]
- Ishizawa, M.; Chan, D.; Worthy, D.; Chan, E.; Vogel, F.; Maksyutov, S. Analysis of atmospheric CH4 in Canadian Arctic and estimation of the regional CH4 fluxes. Atmos. Chem. Phys. 2019, 19, 4637–4658. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Karstens, U.; Manning, A.; Saunois, M.; Tsuruta, A.; Berchet, A.; Vermeulen, A.; Arnold, T.; Janssens-Maenhout, G.; Hammer, S.; et al. Inverse modelling of European CH4 emissions during 2006–2012 using different inverse models and reassessed atmospheric observations. Atmos. Chem. Phys. 2018, 18, 901–920. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, G. Methane emissions in China 2007. Renew. Sustain. Energy Rev. 2014, 30, 886–902. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Houweling, S.; Segers, A.; Krol, M.; Frankenberg, C.; Scheepmaker, R.; Dlugokencky, E.; Wofsy, S.; Kort, E.; Sweeney, C.; et al. Atmospheric CH4 in the first decade of the 21st century: Inverse modeling analysis using SCIAMACHY satellite retrievals and NOAA surface measurements. J. Geophys. Res. Atmos. 2013, 118, 7350–7369. [Google Scholar] [CrossRef]
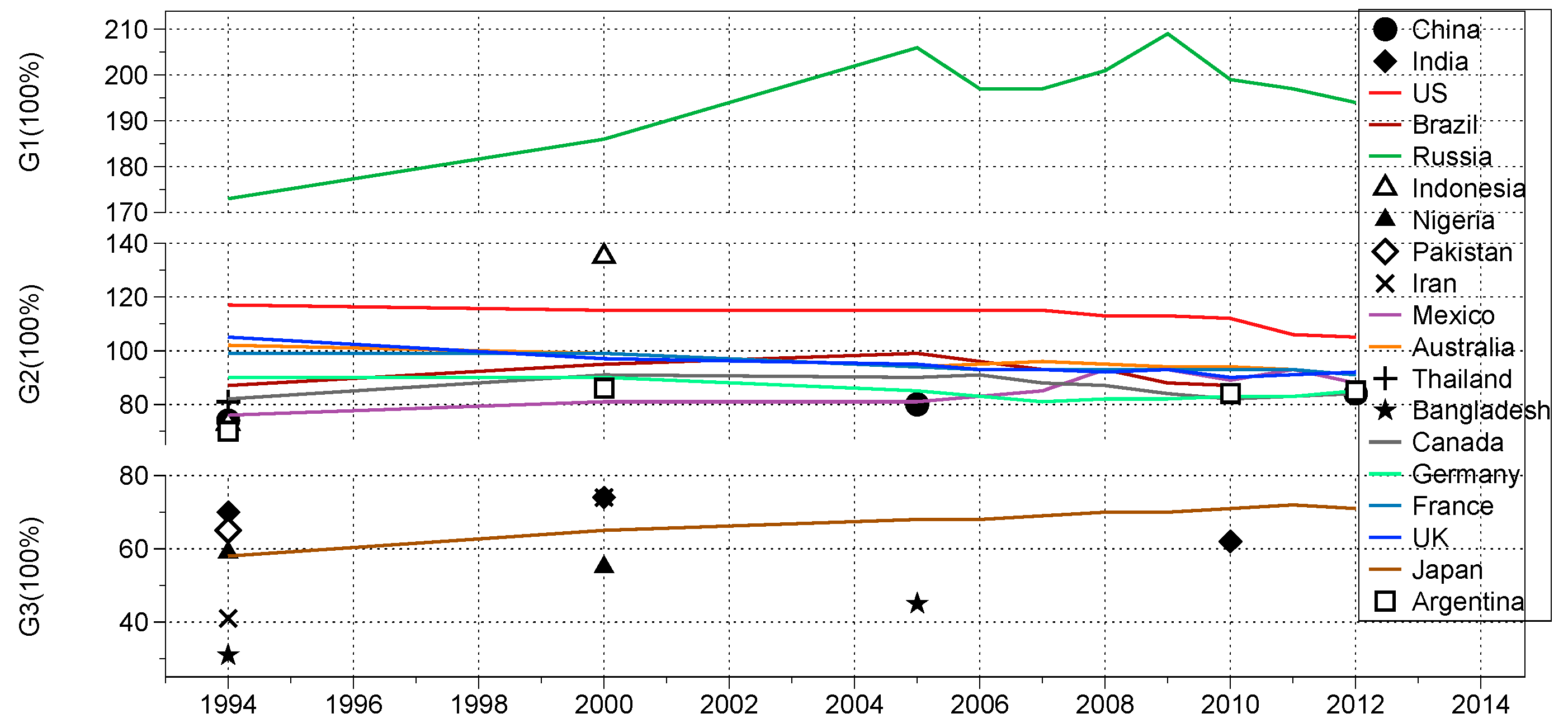
| Country Name | China | India | United States | Brazil | Russian Federation | Indonesia | Nigeria | Pakistan | Iran | Mexico |
|---|---|---|---|---|---|---|---|---|---|---|
| EDGAR (Gg) | 66,297 | 32,582 | 25,770 | 19,212 | 17,441 | 12,027 | 7252 | 7213 | 6528 | 5201 |
| UNFCCC (Gg) | 55,914 | 19,776 (2010) | 27,099 | 16,808 | 33,894 | 11,257 (2000) | 4207 (2000) | 2890 (1994) | 3606 (2000) | 4558 |
| Country Name | Australia | Thailand | Bangladesh | Canada | Argentina | Germany | France | United Kingdom | Japan | |
| EDGAR (Gg) | 4987 | 4893 | 4808 | 4679 | 4562 | 2768 | 2651 | 2624 | 1850 | |
| UNFCCC (Gg) | 4550 | 3171 (1994) | 1191 (1994) | 3939 | 3900 | 2340 | 2420 | 2424 | 1317 |
| Case | Number of Observations | Bias (ppb) | RMSE (ppb) |
|---|---|---|---|
| S0-prior ground | 89,059 | −6.49 | 45.19 |
| S0-posterior ground | 76,772 | −4.61 | 26.62 |
| S1-prior ground | 89,059 | −5.17 | 44.80 |
| S1-posterior ground | 76,481 | −4.24 | 26.40 |
| S0-prior GOSAT | 329,483 | −12.30 | 24.39 |
| S0-posterior GOSAT | 272,101 | −5.29 | 12.26 |
| S1-prior GOSAT | 329,483 | −14.56 | 24.14 |
| S1-posterior GOSAT | 254,657 | 5.59 | 8.93 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Maksyutov, S.; Tsuruta, A.; Janardanan, R.; Ito, A.; Sasakawa, M.; Machida, T.; Morino, I.; Yoshida, Y.; Kaiser, J.W.; et al. Methane Emission Estimates by the Global High-Resolution Inverse Model Using National Inventories. Remote Sens. 2019, 11, 2489. https://doi.org/10.3390/rs11212489
Wang F, Maksyutov S, Tsuruta A, Janardanan R, Ito A, Sasakawa M, Machida T, Morino I, Yoshida Y, Kaiser JW, et al. Methane Emission Estimates by the Global High-Resolution Inverse Model Using National Inventories. Remote Sensing. 2019; 11(21):2489. https://doi.org/10.3390/rs11212489
Chicago/Turabian StyleWang, Fenjuan, Shamil Maksyutov, Aki Tsuruta, Rajesh Janardanan, Akihiko Ito, Motoki Sasakawa, Toshinobu Machida, Isamu Morino, Yukio Yoshida, Johannes W. Kaiser, and et al. 2019. "Methane Emission Estimates by the Global High-Resolution Inverse Model Using National Inventories" Remote Sensing 11, no. 21: 2489. https://doi.org/10.3390/rs11212489
APA StyleWang, F., Maksyutov, S., Tsuruta, A., Janardanan, R., Ito, A., Sasakawa, M., Machida, T., Morino, I., Yoshida, Y., Kaiser, J. W., Janssens-Maenhout, G., Dlugokencky, E. J., Mammarella, I., Lavric, J. V., & Matsunaga, T. (2019). Methane Emission Estimates by the Global High-Resolution Inverse Model Using National Inventories. Remote Sensing, 11(21), 2489. https://doi.org/10.3390/rs11212489






