Improved Estimates of Geocenter Variability from Time-Variable Gravity and Ocean Model Outputs
Abstract
1. Introduction
2. Data
2.1. Time-Variable Gravity
2.2. Atmospheric Reanalyses and Ocean Models
3. Methods
3.1. Eustatic Sea Level from Land Surface Fluxes
3.2. Iterated Solutions
3.3. Spherical Harmonics of Atmospheric and Oceanic Variability
3.4. Time Series Analysis
4. Results
4.1. Simulated Geocenter Estimates
4.2. Recovered Geocenter Estimates
4.3. Uncertainty Estimates
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dong, D.; Dickey, J.O.; Chao, Y.; Cheng, M.K. Geocenter variations caused by atmosphere, ocean and surface ground water. Geophys. Res. Lett. 1997, 24, 1867–1870. [Google Scholar] [CrossRef]
- Swenson, S.C.; Chambers, D.P.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. Solid Earth 2008, 113, B08410. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010); Technical Report 36, International Earth Rotation and Reference Systems Service (IERS); Verlag des Bundesamts für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Ries, J. Reconciling Estimates of Annual Geocenter Motion from Space Geodesy. In Proceedings of the 20th International Workshop on Laser Ranging, Potsdam, Germany, 10–14 October 2016. [Google Scholar]
- Stolz, A. Changes in the Position of the Geocentre due to Seasonal Variations in Air Mass and Ground Water. Geophys. J. Int. 1976, 44, 19–26. [Google Scholar] [CrossRef][Green Version]
- Chen, J.L.; Wilson, C.R.; Eanes, R.J.; Nerem, R.S. Geophysical interpretation of observed geocenter variations. J. Geophys. Res. Solid Earth 1999, 104, 2683–2690. [Google Scholar] [CrossRef]
- Wu, X.; Ray, J.; van Dam, T.M. Geocenter motion and its geodetic and geophysical implications. J. Geodyn. 2012, 58, 44–61. [Google Scholar] [CrossRef]
- Bettadpur, S. UTCSR Level-2 Processing Standards Document; Technical Report GRACE 327-742; Center for Space Research, University of Texas: Austin, TX, USA, 2018. [Google Scholar]
- Dahle, C.; Flechtner, F.; Murböck, M.; Michalak, G.; Neumayer, H.; Abrykosov, O.; Reinhold, A.; König, R. GFZ Processing Standards Document for Level-2 Product Release 06; Technical Report GRACE 327-743; GFZ German Research Centre for Geosciences: Potsdam, Germany, 2018. [Google Scholar]
- Yuan, D.N. JPL Level-2 Processing Standards Document for Level-2 Product Release 06; Technical Report GRACE 327-744; Jet Propulsion Laboratory: Pasadena, CA, USA, 2018. [Google Scholar]
- Chambers, D.P.; Wahr, J.; Nerem, R.S. Preliminary observations of global ocean mass variations with GRACE. Geophys. Res. Lett. 2004, 31, L13310. [Google Scholar] [CrossRef]
- Velicogna, I. Increasing rates of ice mass loss from the Greenland and Antarctic ice sheets revealed by GRACE. Geophys. Res. Lett. 2009, 36, L19503. [Google Scholar] [CrossRef]
- Chen, J.L.; Rodell, M.; Wilson, C.R.; Famiglietti, J.S. Low degree spherical harmonic influences on Gravity Recovery and Climate Experiment (GRACE) water storage estimates. Geophys. Res. Lett. 2005, 32, L14405. [Google Scholar] [CrossRef]
- Cheng, M.K. Geocenter Variations from Analysis of SLR Data; Reference Frames for Applications in Geosciences; Springer: Berlin/Heidelberg, Germany, 2013; pp. 19–25. [Google Scholar] [CrossRef]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef]
- Rietbroek, R.; Fritsche, M.; Brunnabend, S.E.; Daras, I.; Kusche, J.; Schröter, J.; Flechtner, F.M.; Dietrich, R. Global surface mass from a new combination of GRACE, modelled OBP and reprocessed GPS data. J. Geodyn. 2012, 59–60, 64–71. [Google Scholar] [CrossRef]
- Wu, X.; Heflin, M.B.; Schotman, H.; Vermeersen, B.L.A.; Dong, D.; Gross, R.S.; Ivins, E.R.; Moore, A.W.; Owen, S.E. Simultaneous estimation of global present-day water transport and glacial isostatic adjustment. Nat. Geosci. 2010, 3, 642–646. [Google Scholar] [CrossRef]
- Collilieux, X.; Altamimi, Z.; Ray, J.; van Dam, T.M.; Wu, X. Effect of the satellite laser ranging network distribution on geocenter motion estimation. J. Geophys. Res. Solid Earth 2009, 114, B04402. [Google Scholar] [CrossRef]
- Zannat, U.J.; Tregoning, P. Estimating network effect in geocenter motion: Theory. J. Geophys. Res. Solid Earth 2017, 122, 8360–8375. [Google Scholar] [CrossRef]
- Tapley, B.D. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Loomis, B.D.; Rachlin, K.E.; Luthcke, S.B. Improved Earth Oblateness Rate Reveals Increased Ice Sheet Losses and Mass-Driven Sea Level Rise. Geophys. Res. Lett. 2019, 46, 6910–6917. [Google Scholar] [CrossRef]
- Flechtner, F.; Dobslaw, H.; Fagiolini, E. AOD1B Product Description Document for Product Release 05; Technical Report GRACE 327-750; GFZ German Research Centre for Geosciences: Potsdam, Germany, 2015. [Google Scholar]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Poropat, L.; Thomas, M.; Dahle, C.; Esselborn, S.; König, R.; Flechtner, F. A new high-resolution model of non-tidal atmosphere and ocean mass variability for de-aliasing of satellite gravity observations: AOD1B RL06. Geophys. J. Int. 2017, 211, 263–269. [Google Scholar] [CrossRef]
- Geruo, A.; Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Caron, L.; Ivins, E.R.; Larour, E.; Adhikari, S.; Nilsson, J.; Blewitt, G. GIA Model Statistics for GRACE Hydrology, Cryosphere, and Ocean Science. Geophys. Res. Lett. 2018, 45, 2203–2212. [Google Scholar] [CrossRef]
- Wahr, J.; DaZhong, H.; Trupin, A.S. Predictions of vertical uplift caused by changing polar ice volumes on a viscoelastic Earth. Geophys. Res. Lett. 1995, 22, 977–980. [Google Scholar] [CrossRef]
- Trupin, A.S.; Meier, M.F.; Wahr, J. Effect of melting glaciers on the Earth’s rotation and gravitational field: 1965–1984. Geophys. J. Int. 1992, 108, 1–15. [Google Scholar] [CrossRef]
- Jekeli, C. Alternative Methods to Smooth the Earth’s Gravity Field; Technical Report 327; Ohio State University, Department of Geodetic Science and Surveying, 1958 Neil Avenue: Columbus, OH, USA, 1981. [Google Scholar]
- Swenson, S.C.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- Cheng, M. Geocenter Variations from Analysis of TOPEX/Poseidon SLR Data; Technical Report 25; International Earth Rotation and Reference Systems Service (IERS): Frankfurt am Main, Germany, 1998. [Google Scholar]
- Berrisford, P.; Dee, D.P.; Poli, P.; Brugge, R.; Fielding, K.; Fuentes, M.; Kållberg, P.W.; Kobayashi, S.; Uppala, S.; Simmons, A. The ERA-Interim Archive Version 2.0; ERA Report Series; ECMWF: Reading, UK, 2011; p. 23. [Google Scholar]
- Bosilovich, M.G.; Lucchesi, R.; Suarez, M. MERRA-2: File Specification. GMAO Office Note 2016, 9, 1–73. [Google Scholar]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP–DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General Specifications and Basic Characteristics. J. Meteorol. Soc. Jpn. Ser. II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Fukumori, I. A Partitioned Kalman Filter and Smoother. Mon. Weather Rev. 2002, 130, 1370–1383. [Google Scholar] [CrossRef]
- Kim, S.B.; Lee, T.; Fukumori, I. Mechanisms Controlling the Interannual Variation of Mixed Layer Temperature Averaged over the Niño-3 Region. J. Clim. 2007, 20, 3822–3843. [Google Scholar] [CrossRef]
- Fukumori, I.; Wang, O.; Fenty, I.; Forget, G.; Heimbach, P.; Ponte, R.M. ECCO Version 4 Release 3; Technical report; JPL/Caltech and NASA Physical Oceanography: Pasadena, CA, USA, 2017. [Google Scholar]
- Forget, G.; Campin, J.M.; Heimbach, P.; Hill, C.N.; Ponte, R.M.; Wunsch, C. ECCO version 4: An integrated framework for non-linear inverse modeling and global ocean state estimation. Geosci. Model Dev. 2015, 8, 3071–3104. [Google Scholar] [CrossRef]
- Forget, G.; Ponte, R.M. The partition of regional sea level variability. Prog. Oceanogr. 2015, 137, 173–195. [Google Scholar] [CrossRef]
- Losch, M.; Menemenlis, D.; Campin, J.M.; Heimbach, P.; Hill, C. On the formulation of sea-ice models. Part 1: Effects of different solver implementations and parameterizations. Ocean Model. 2010, 33, 129–144. [Google Scholar] [CrossRef]
- Greatbatch, R.J. A note on the representation of steric sea level in models that conserve volume rather than mass. J. Geophys. Res. Oceans 1994, 99, 12767–12771. [Google Scholar] [CrossRef]
- Farrell, W.E.; Clark, J.A. On Postglacial Sea Level. Geophys. J. R. Astron. Soc. 1976, 46, 647–667. [Google Scholar] [CrossRef]
- Clark, J.A.; Lingle, C.S. Future sea-level changes due to West Antarctic ice sheet fluctuations. Nature 1977, 269, 206–209. [Google Scholar] [CrossRef]
- Mitrovica, J.X.; Milne, G.A. On post-glacial sea level: I. General theory. Geophys. J. Int. 2003, 154, 253–267. [Google Scholar] [CrossRef]
- Tamisiea, M.E.; Mitrovica, J.X. The Moving Boundaries of Sea Level Change: Understanding the Origins of Geographic Variability. Oceanography 2011, 24, 24–39. [Google Scholar] [CrossRef]
- Kendall, R.A.; Mitrovica, J.X.; Milne, G.A. On post-glacial sea level – II. Numerical formulation and comparative results on spherically symmetric models. Geophys. J. Int. 2005, 161, 679–706. [Google Scholar] [CrossRef]
- Tamisiea, M.E.; Hill, E.M.; Ponte, R.M.; Davis, J.L.; Velicogna, I.; Vinogradova, N.T. Impact of self-attraction and loading on the annual cycle in sea level. J. Geophys. Res. Oceans 2010, 115, C07004. [Google Scholar] [CrossRef]
- Boy, J.P.; Chao, B.F. Precise evaluation of atmospheric loading effects on Earth’s time-variable gravity field. J. Geophys. Res. Solid Earth 2005, 110, B08412. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Estimated effects of the vertical structure of atmospheric mass on the time-variable geoid. J. Geophys. Res. Solid Earth 2002, 107, 2194. [Google Scholar] [CrossRef]
- Velicogna, I.; Sutterley, T.C.; van den Broeke, M.R. Regional acceleration in ice mass loss from Greenland and Antarctica using GRACE time-variable gravity data. Geophys. Res. Lett. 2014, 41, 8130–8137. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Seo, K.W. S2 tide aliasing in GRACE time-variable gravity solutions. J. Geod. 2009, 83, 679–687. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Noël, B.; van de Berg, W.J.; Lhermitte, S.; Wouters, B.; Schaffer, N.; van den Broeke, M.R. Six decades of glacial mass loss in the Canadian Arctic Archipelago. J. Geophys. Res. Earth Surf. 2018, 123, 1430–1449. [Google Scholar] [CrossRef]
- Noël, B.; van de Berg, W.J.; van Wessem, J.M.; van Meijgaard, E.; van As, D.; Lenaerts, J.T.M.; Lhermitte, S.; Kuipers Munneke, P.; Smeets, C.J.P.P.; van Ulft, L.H.; et al. Modelling the climate and surface mass balance of polar ice sheets using RACMO2 – Part 1: Greenland (1958–2016). Cryosphere 2018, 12, 811–831. [Google Scholar] [CrossRef]
- Rignot, E.J.; Velicogna, I.; van den Broeke, M.R.; Monaghan, A.J.; Lenaerts, J.T.M. Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise. Geophys. Res. Lett. 2011, 38, L05503. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Ettema, J.; van den Broeke, M.R.; van Meijgaard, E.; van de Berg, W.J.; Bamber, J.L.; Box, J.E.; Bales, R.C. Higher surface mass balance of the Greenland ice sheet revealed by high-resolution climate modeling. Geophys. Res. Lett. 2009, 36, L12501. [Google Scholar] [CrossRef]
- Lenaerts, J.T.M.; van den Broeke, M.R.; van de Berg, W.J.; van Meijgaard, E.; Kuipers Munneke, P. A new, high-resolution surface mass balance map of Antarctica (1979–2010) based on regional atmospheric climate modeling. Geophys. Res. Lett. 2012, 39, L04501. [Google Scholar] [CrossRef]
- Van den Broeke, M.R.; Bamber, J.L.; Ettema, J.; Rignot, E.J.; Schrama, E.; van de Berg, W.J.; van Meijgaard, E.; Velicogna, I.; Wouters, B. Partitioning Recent Greenland Mass Loss. Science 2009, 326, 984–986. [Google Scholar] [CrossRef]
- Rignot, E.J.; Bamber, J.L.; van den Broeke, M.R.; Davis, C.H.; Li, Y.; van de Berg, W.J.; van Meijgaard, E. Recent Antarctic ice mass loss from radar interferometry and regional climate modelling. Nat. Geosci. 2008, 1, 106–110. [Google Scholar] [CrossRef]
- Hall, F.G.; Brown de Colstoun, E.; Collatz, G.J.; Landis, D.; Dirmeyer, P.; Betts, A.; Huffman, G.J.; Bounoua, L.; Meeson, B. ISLSCP Initiative II global data sets: Surface boundary conditions and atmospheric forcings for land-atmosphere studies. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Mouginot, J.; Scheuchl, B.; Rignot, E. MEaSUREs Antarctic Boundaries for IPY 2007–2009 from Satellite Radar; Version 2; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2017. [Google Scholar] [CrossRef]
- Henriksen, N.; Higgins, A.; Kalsbeek, F.; Pulvertaft, T.C.R. Greenland from Archaean to Quaternary, Descriptive text to the 1995 Geological Map of Greenland 1:2,500,000. Geol. Surv. Den. Greenl. Bull. 2009, 18, 1–126. [Google Scholar]
- Wahr, J.; Swenson, S.C.; Velicogna, I. Accuracy of GRACE mass estimates. Geophys. Res. Lett. 2006, 33, L06401. [Google Scholar] [CrossRef]
- Bandikova, T.; McCullough, C.; Kruizinga, G.L.; Save, H.; Christophe, B. GRACE accelerometer data transplant. Adv. Space Res. 2019, 64, 623–644. [Google Scholar] [CrossRef]
- Hsu, C.W.; Velicogna, I. Detection of Sea Level Fingerprints derived from GRACE gravity data. Geophys. Res. Lett. 2017, 2017GL074070. [Google Scholar] [CrossRef]
- Velicogna, I.; Wahr, J. Time-variable gravity observations of ice sheet mass balance: Precision and limitations of the GRACE satellite data. Geophys. Res. Lett. 2013, 40, 3055–3063. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]



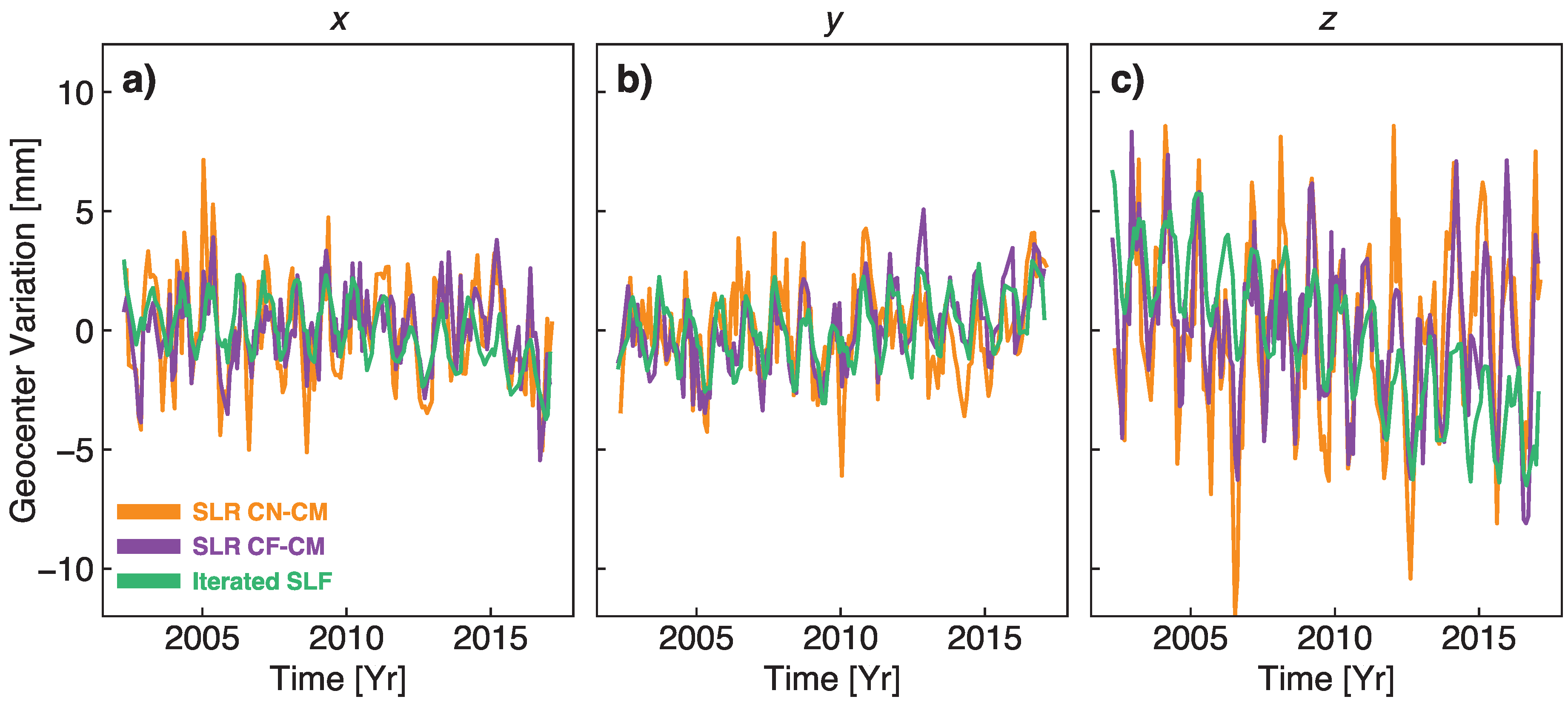
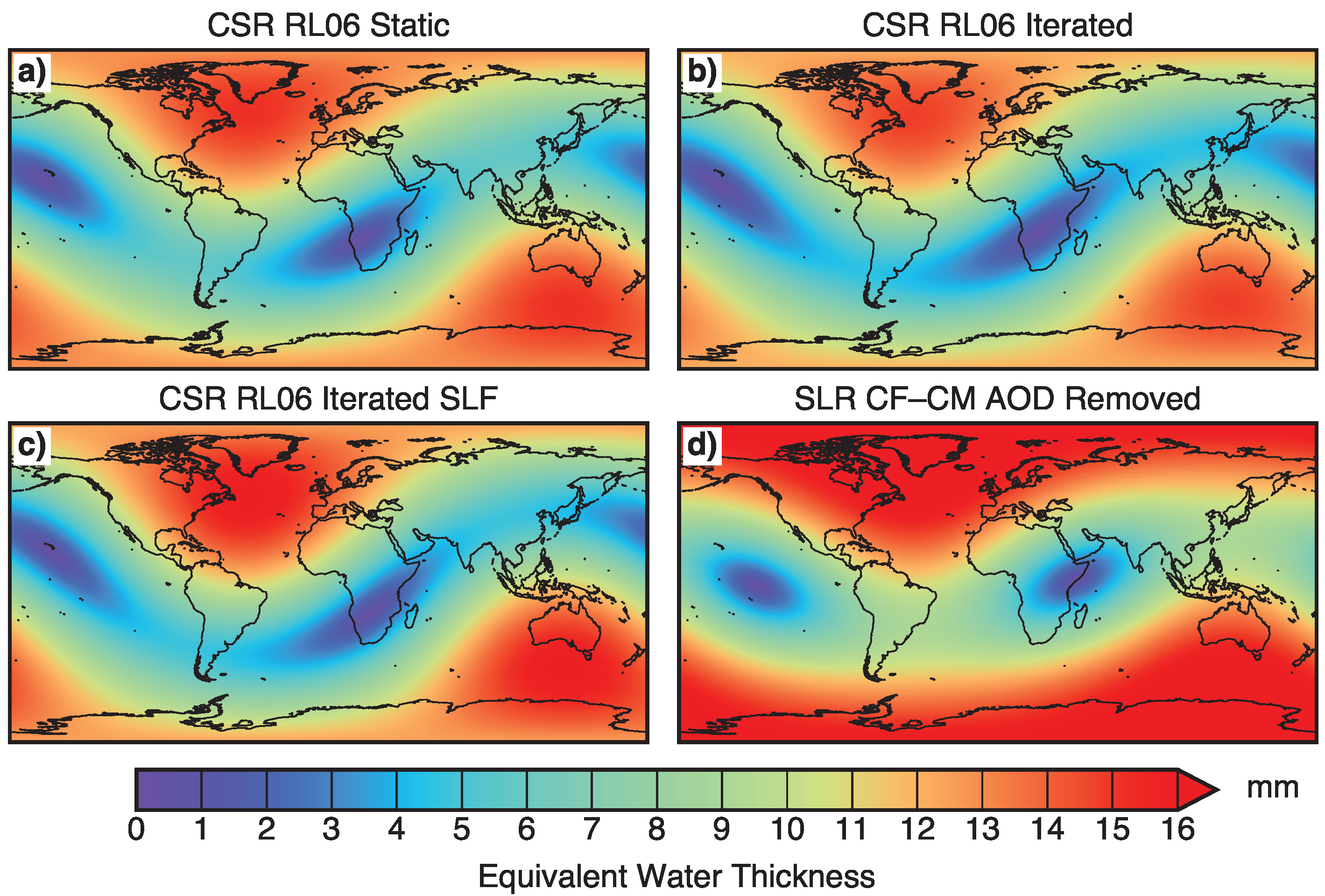
| x | y | z | ||||
|---|---|---|---|---|---|---|
| Annual Amplitude [mm] | ||||||
| CSR | 1.34 ± 0.11 | 1.54 ± 0.12 | 2.25 ± 0.16 | |||
| GFZ | 1.38 ± 0.14 | 1.56 ± 0.13 | 2.30 ± 0.16 | |||
| JPL | 1.31 ± 0.11 | 1.52 ± 0.12 | 2.20 ± 0.17 | |||
| SLR CN-CM | 1.93 ± 0.38 | 1.17 ± 0.38 | 4.25 ± 0.57 | |||
| SLR CF-CM | 1.29 ± 0.29 | 1.48 ± 0.23 | 2.97 ± 0.46 | |||
| Annual Phase [day] | ||||||
| CSR | 356.5 ± 5.0 | 151.9 ± 4.6 | 9.6 ± 4.2 | |||
| GFZ | 352.7 ± 5.7 | 150.7 ± 4.9 | 4.5 ± 4.1 | |||
| JPL | 355.0 ± 4.8 | 151.4 ± 4.7 | 7.9 ± 4.4 | |||
| SLR CN-CM | 5.5 ± 11.7 | 194.7 ± 18.9 | 52.4 ± 7.7 | |||
| SLR CF-CM | 347.9 ± 13.3 | 169.6 ± 9.0 | 46.3 ± 9.1 | |||
| Trend [mm/yr] | ||||||
| CSR | −0.15 ± 0.02 | 0.10 ± 0.02 | −0.62 ± 0.03 | |||
| GFZ | −0.19 ± 0.03 | 0.21 ± 0.03 | −0.66 ± 0.03 | |||
| JPL | −0.15 ± 0.02 | 0.11 ± 0.03 | −0.63 ± 0.03 | |||
| x | y | z | ||||
|---|---|---|---|---|---|---|
| Annual Amplitude [mm] | ||||||
| ECCO-JPL kf080i | 1.46 ± 0.20 | 1.28 ± 0.17 | 1.80 ± 0.31 | |||
| ECCO V4r3 | 1.63 ± 0.18 | 1.21 ± 0.16 | 2.31 ± 0.27 | |||
| MPIOM | 1.34 ± 0.11 | 1.55 ± 0.13 | 2.24 ± 0.16 | |||
| Annual Phase [day] | ||||||
| ECCO-JPL kf080i | 307.3 ± 7.9 | 165.5 ± 7.9 | 327.8 ± 9.9 | |||
| ECCO V4r3 | 323.0 ± 6.5 | 150.8 ± 7.7 | 326.2 ± 6.9 | |||
| MPIOM | 358.3 ± 5.0 | 150.3 ± 4.8 | 9.6 ± 4.3 | |||
| Trend [mm/yr] | ||||||
| ECCO-JPL kf080i | −0.32 ± 0.04 | 0.16 ± 0.03 | −0.48 ± 0.06 | |||
| ECCO V4r3 | −0.10 ± 0.04 | 0.12 ± 0.04 | −0.44 ± 0.06 | |||
| MPIOM | −0.12 ± 0.02 | 0.08 ± 0.03 | −0.62 ± 0.03 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sutterley, T.C.; Velicogna, I. Improved Estimates of Geocenter Variability from Time-Variable Gravity and Ocean Model Outputs. Remote Sens. 2019, 11, 2108. https://doi.org/10.3390/rs11182108
Sutterley TC, Velicogna I. Improved Estimates of Geocenter Variability from Time-Variable Gravity and Ocean Model Outputs. Remote Sensing. 2019; 11(18):2108. https://doi.org/10.3390/rs11182108
Chicago/Turabian StyleSutterley, Tyler C., and Isabella Velicogna. 2019. "Improved Estimates of Geocenter Variability from Time-Variable Gravity and Ocean Model Outputs" Remote Sensing 11, no. 18: 2108. https://doi.org/10.3390/rs11182108
APA StyleSutterley, T. C., & Velicogna, I. (2019). Improved Estimates of Geocenter Variability from Time-Variable Gravity and Ocean Model Outputs. Remote Sensing, 11(18), 2108. https://doi.org/10.3390/rs11182108






