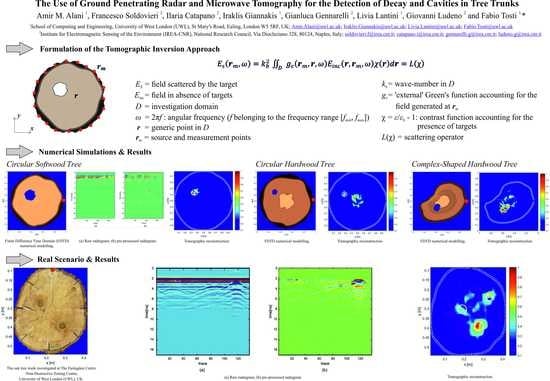
The Use of Ground Penetrating Radar and Microwave Tomography for the Detection of Decay and Cavities in Tree Trunks
Abstract
1. Introduction
2. Theoretical Background
2.1. GPR Principles
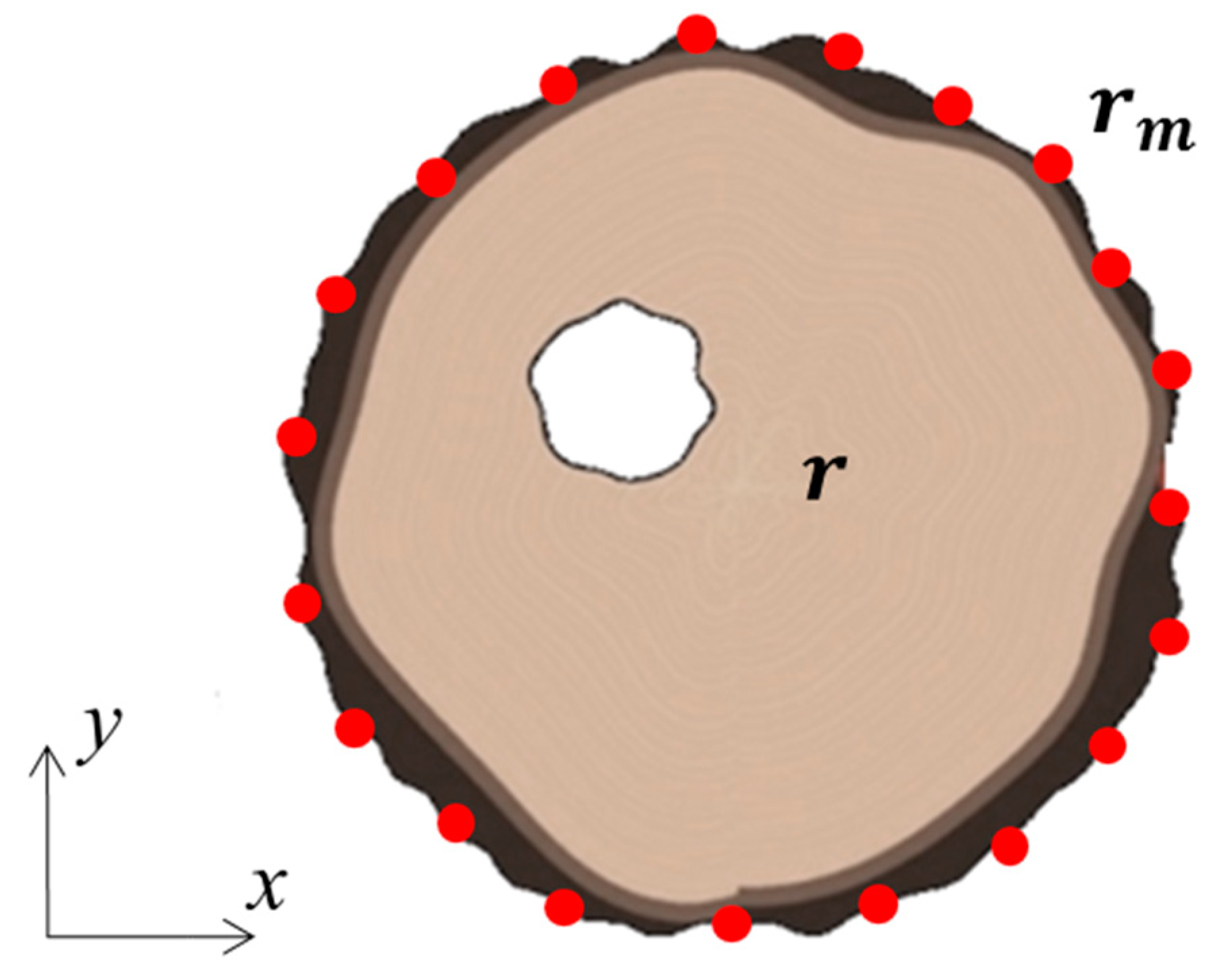
2.2. Formulation of the Tomographic Inversion Approach
2.3. Data Pre-Processing
3. Methodology
3.1. Numerical Simulations
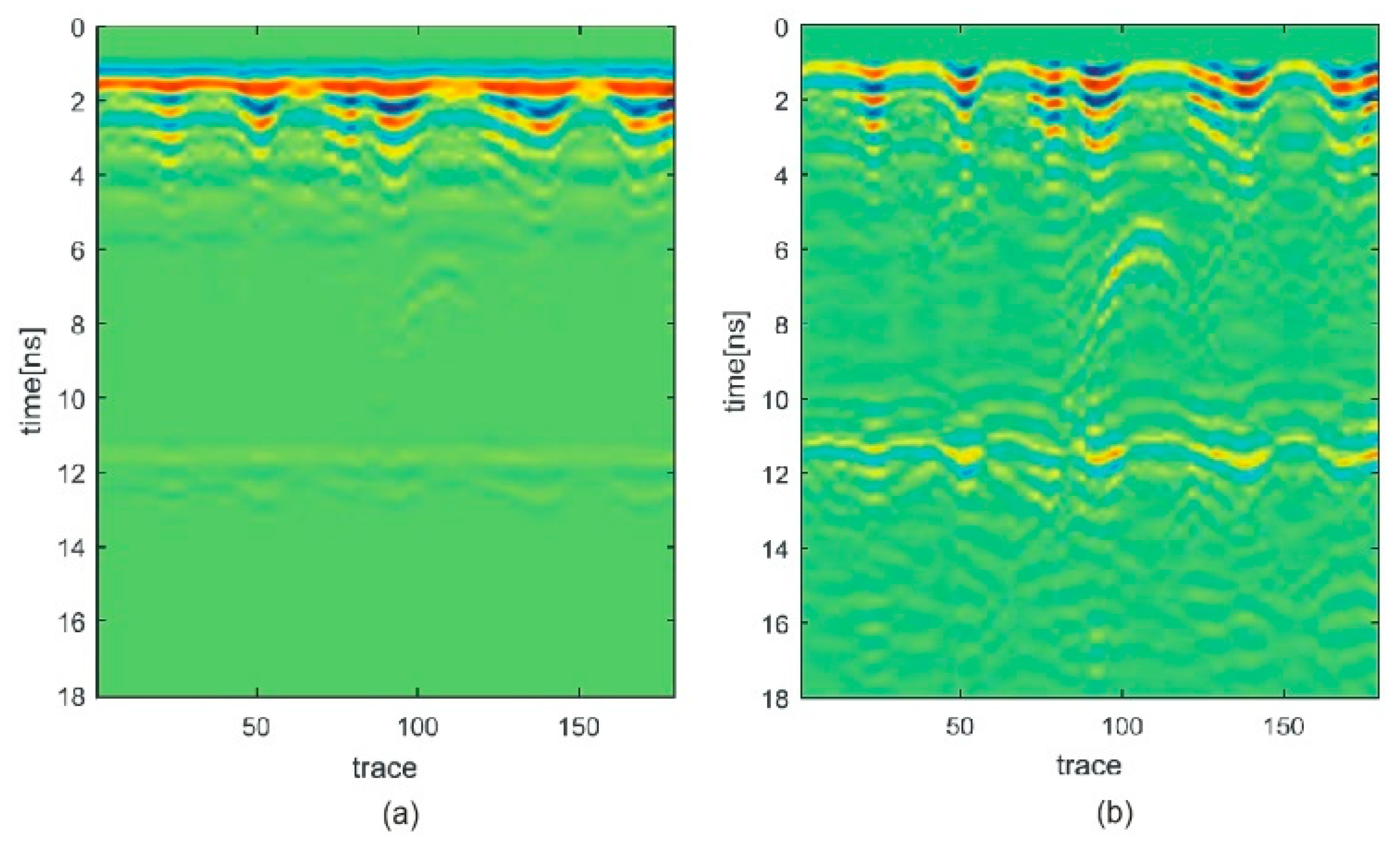
3.2. Real Data Acquisitions
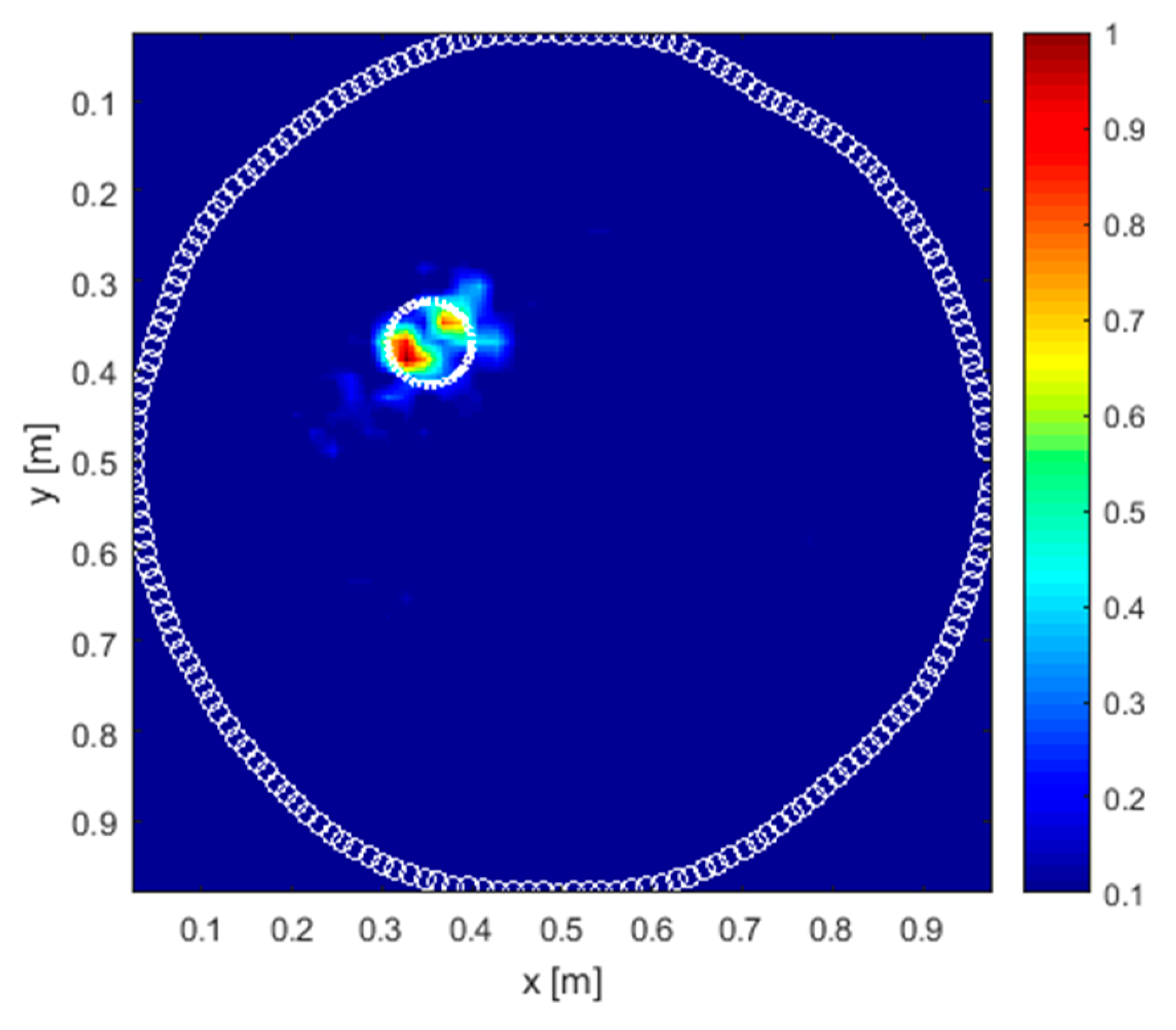
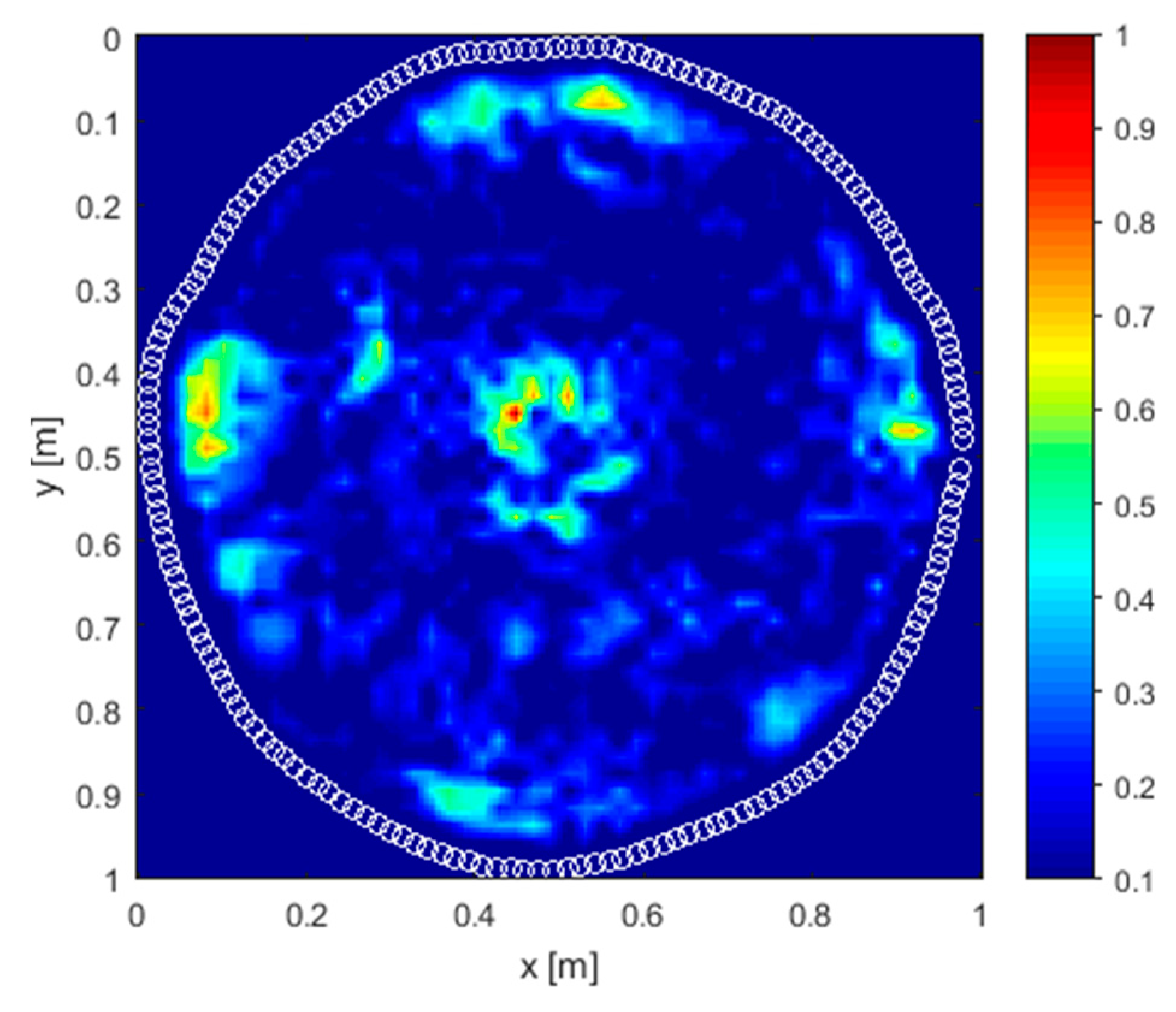
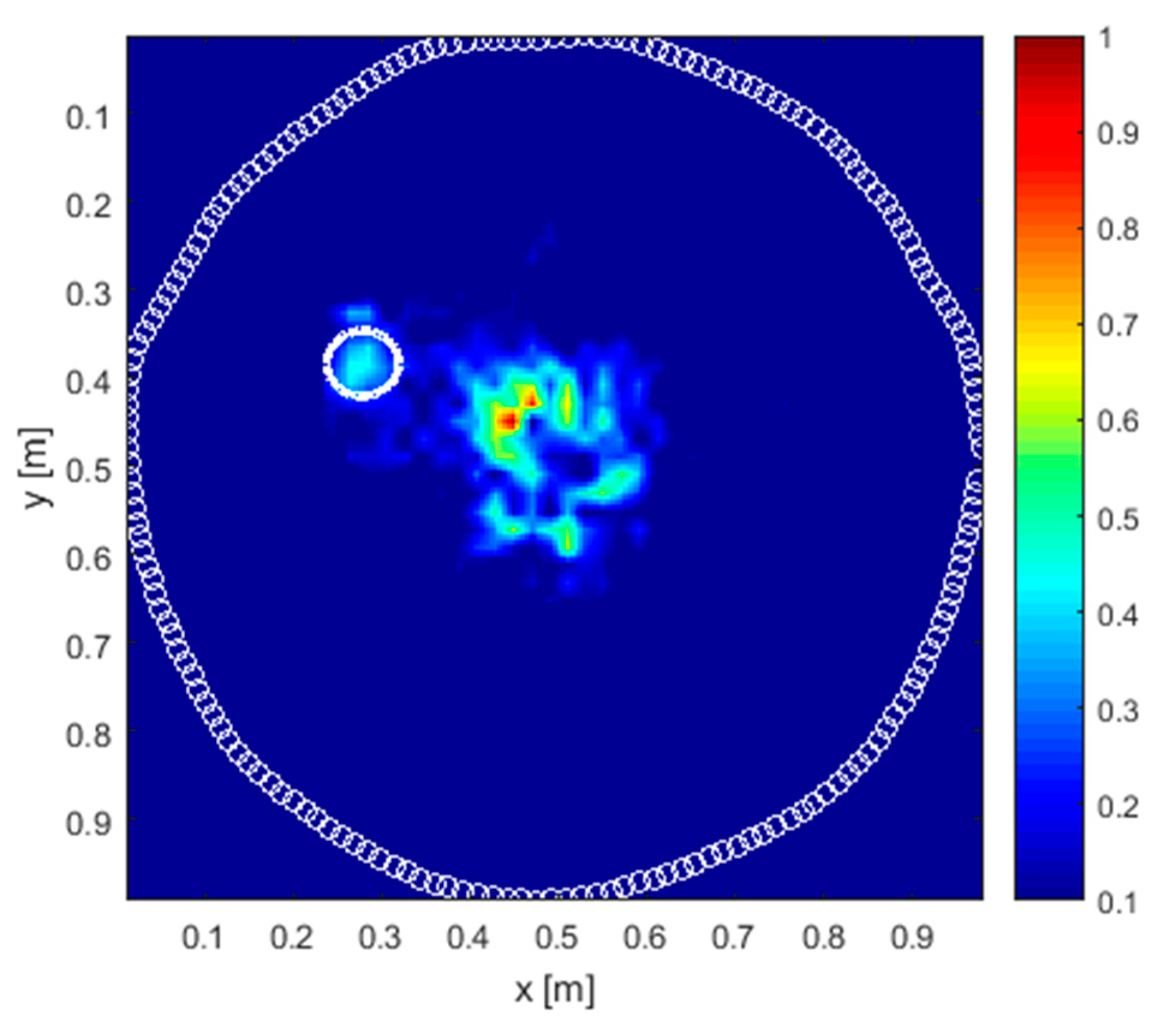
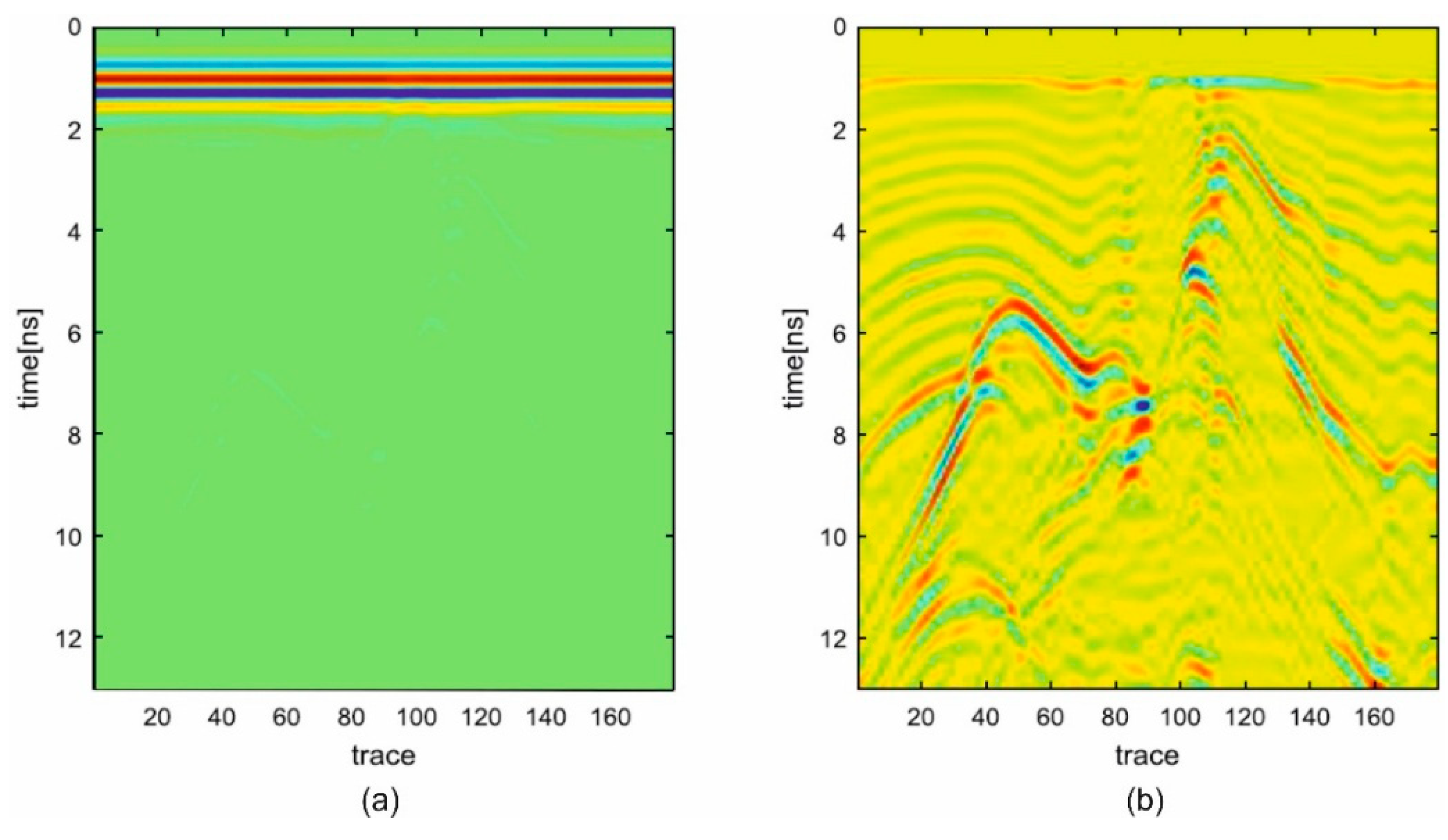
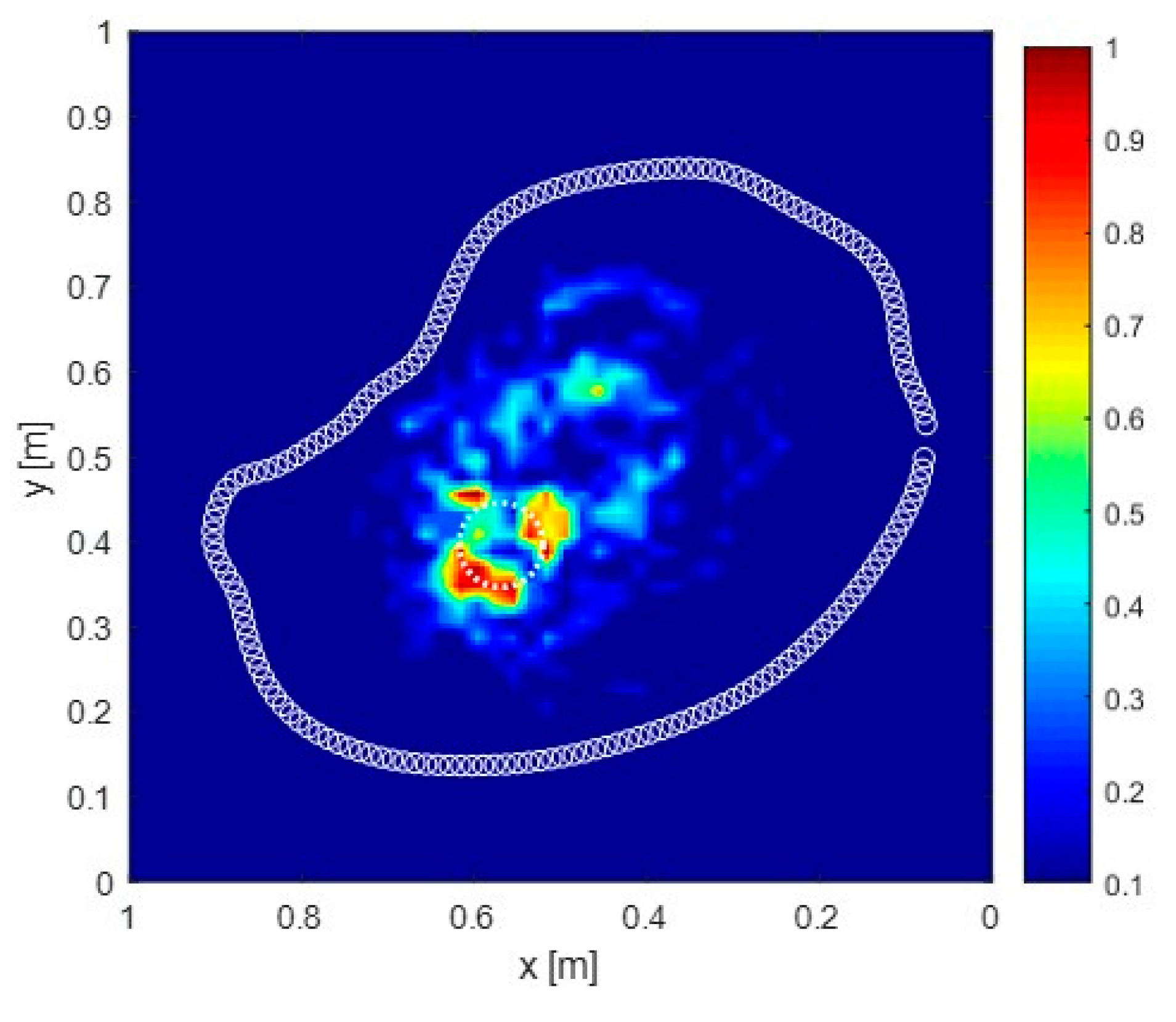
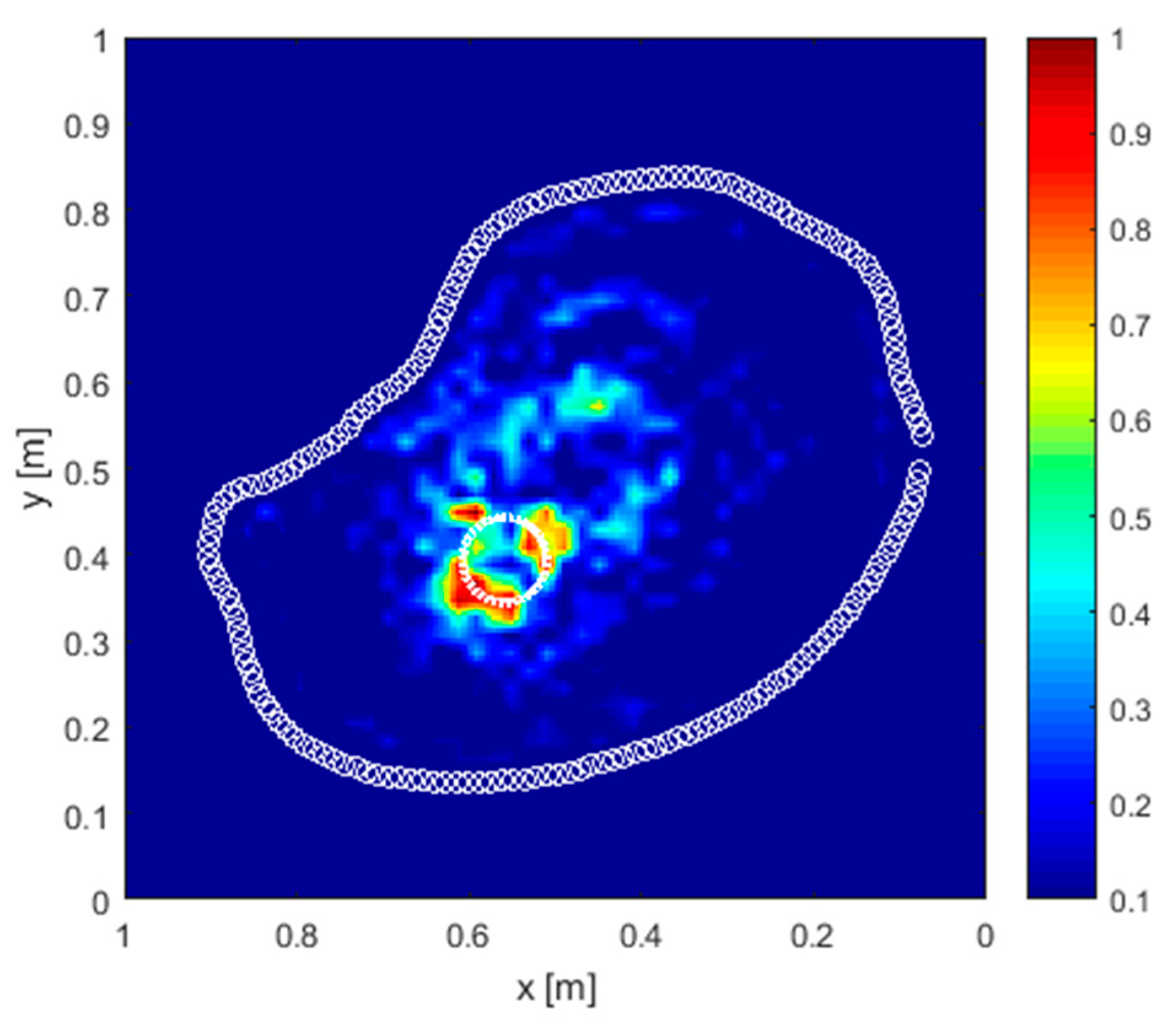
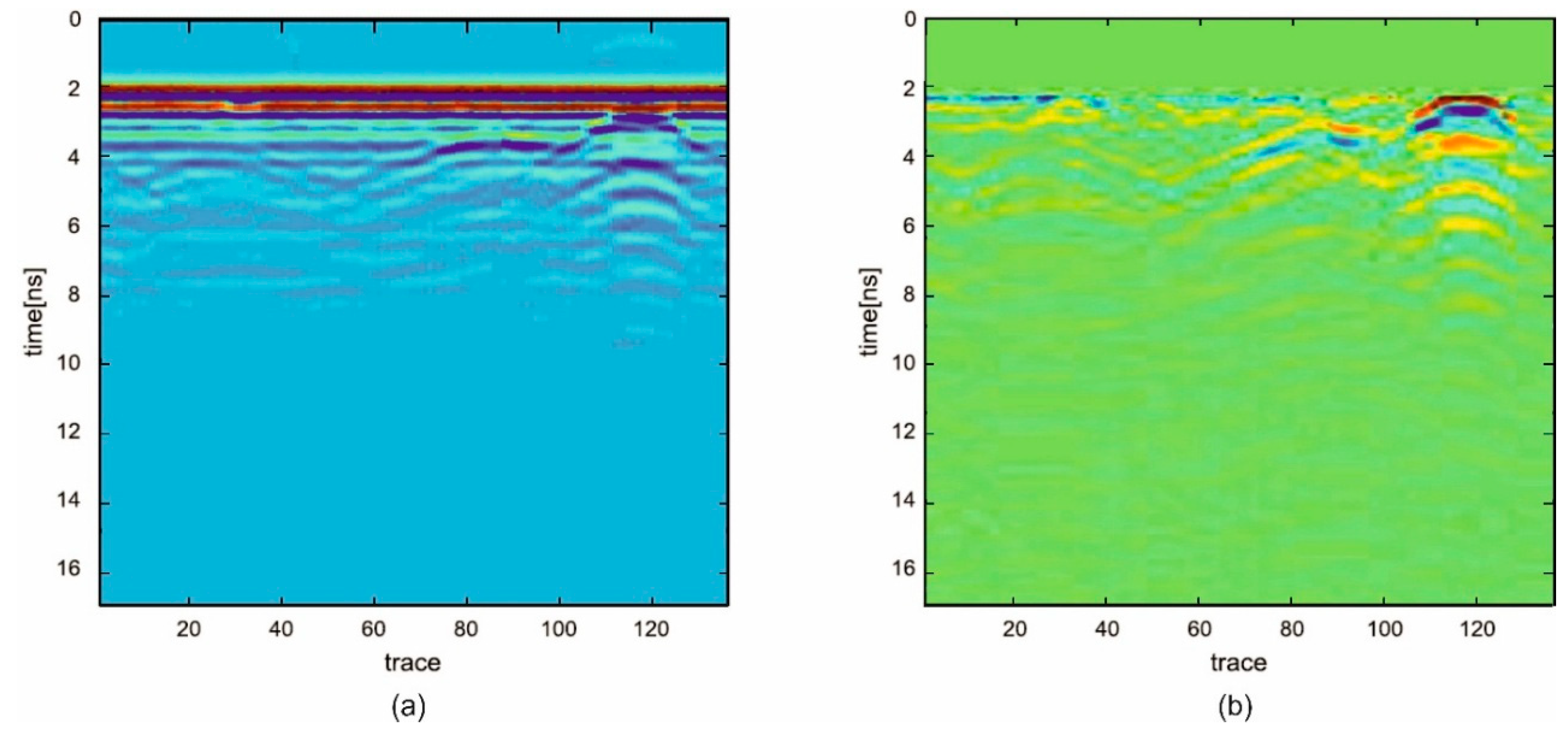
4. Results and Discussion
4.1. Numerical Simulations
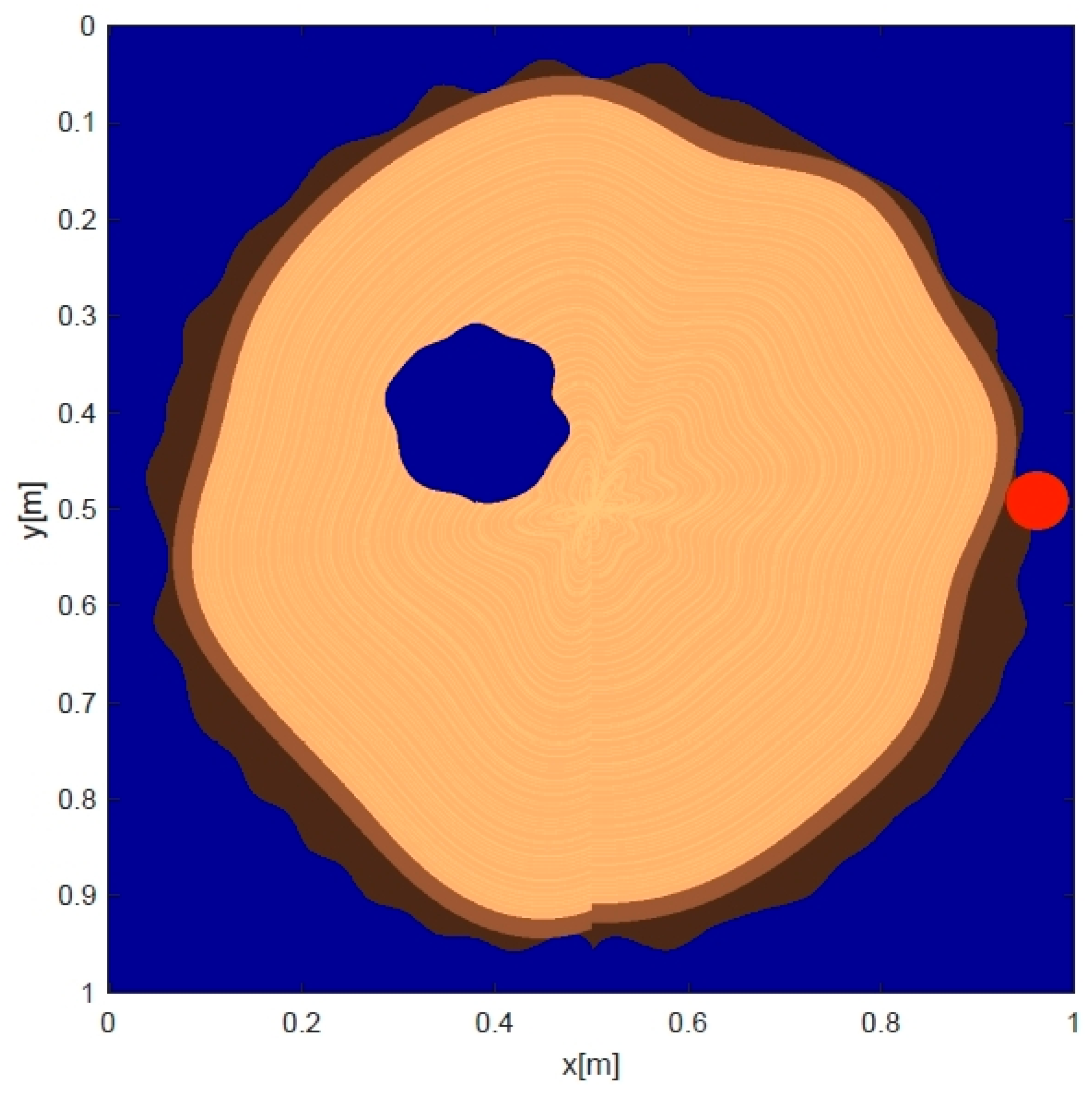
4.1.1. Circular Softwood Tree
4.1.2. Circular Hardwood Tree
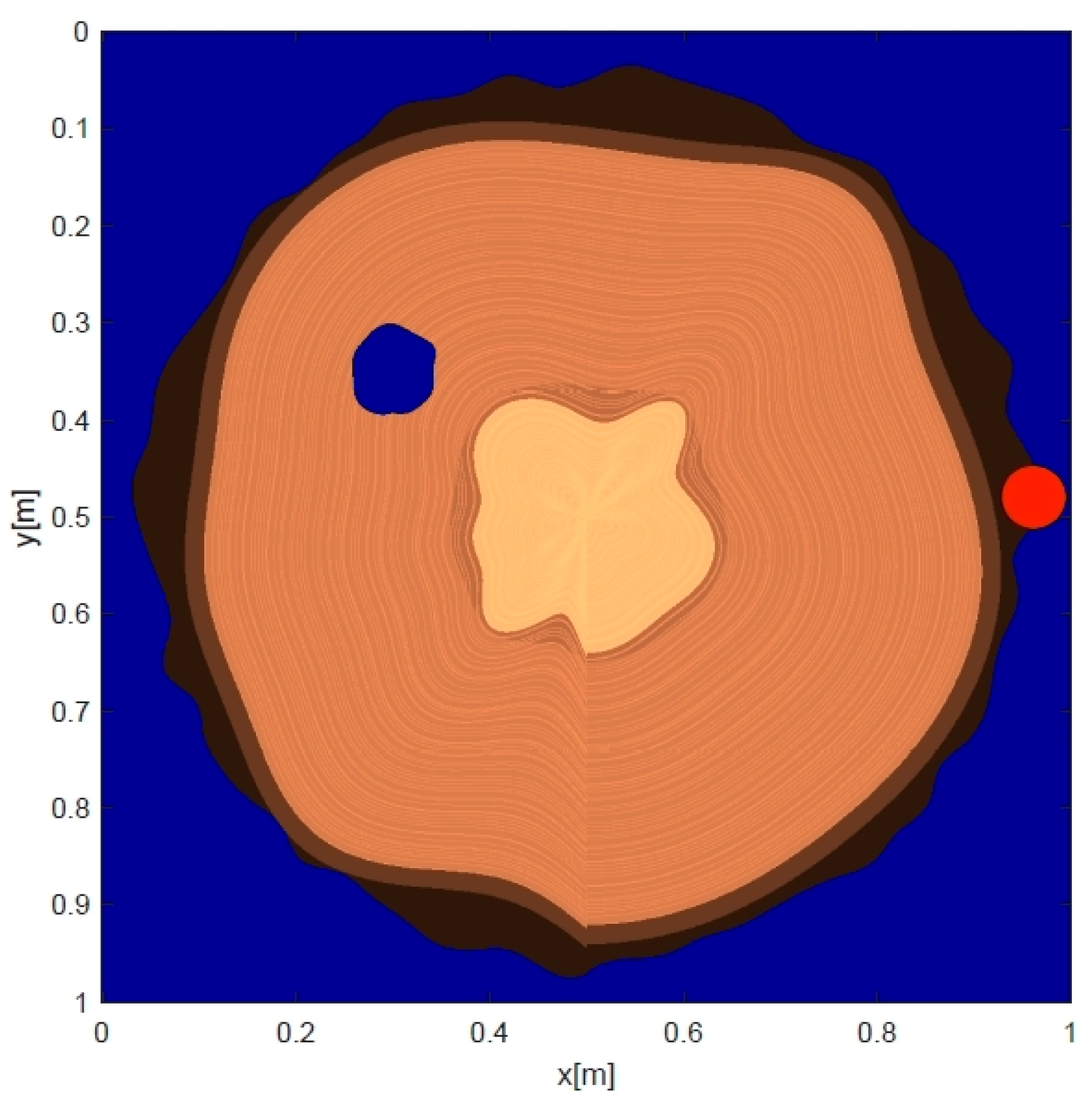
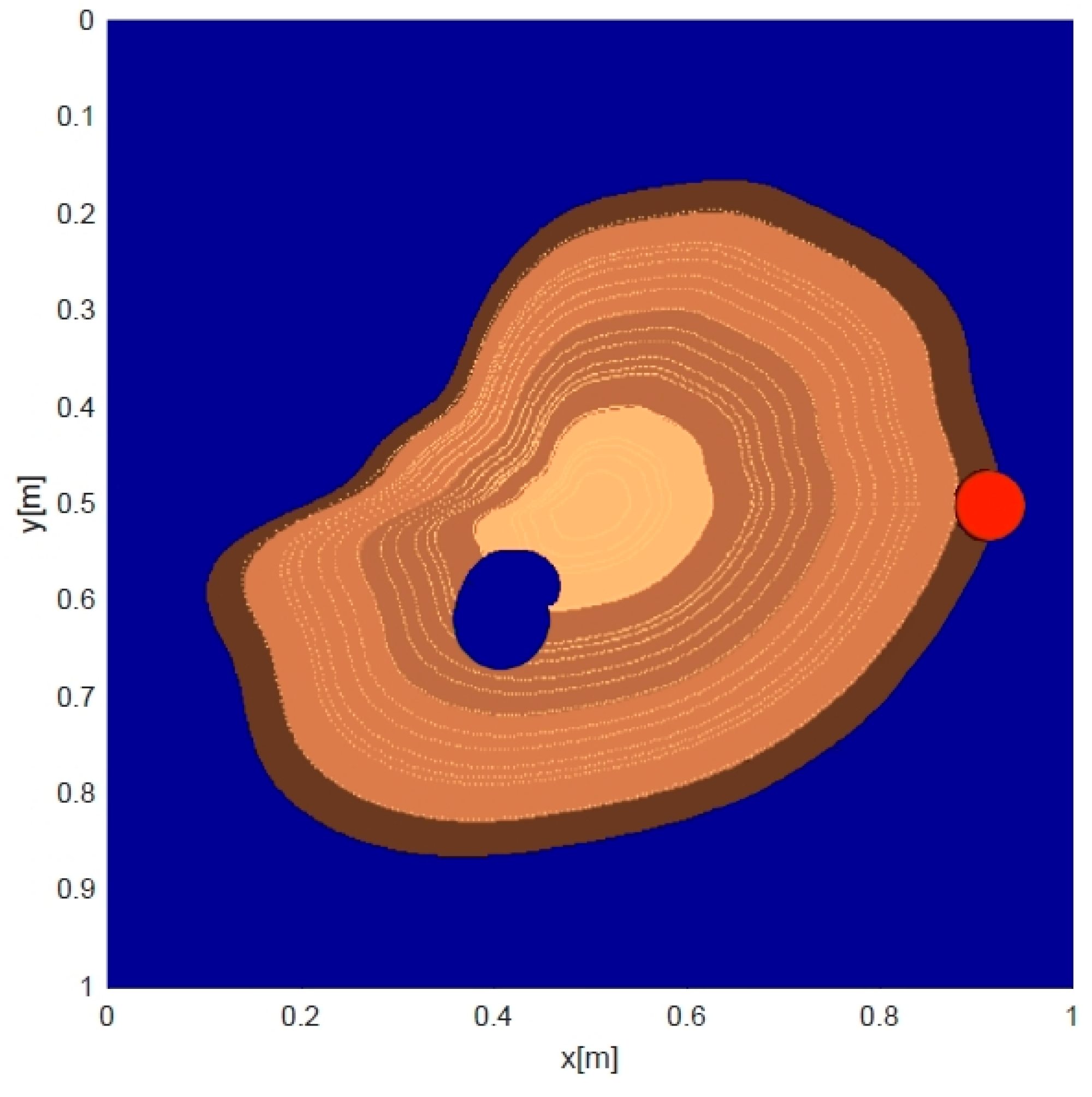
4.1.3. Complex-Shaped Hardwood Tree
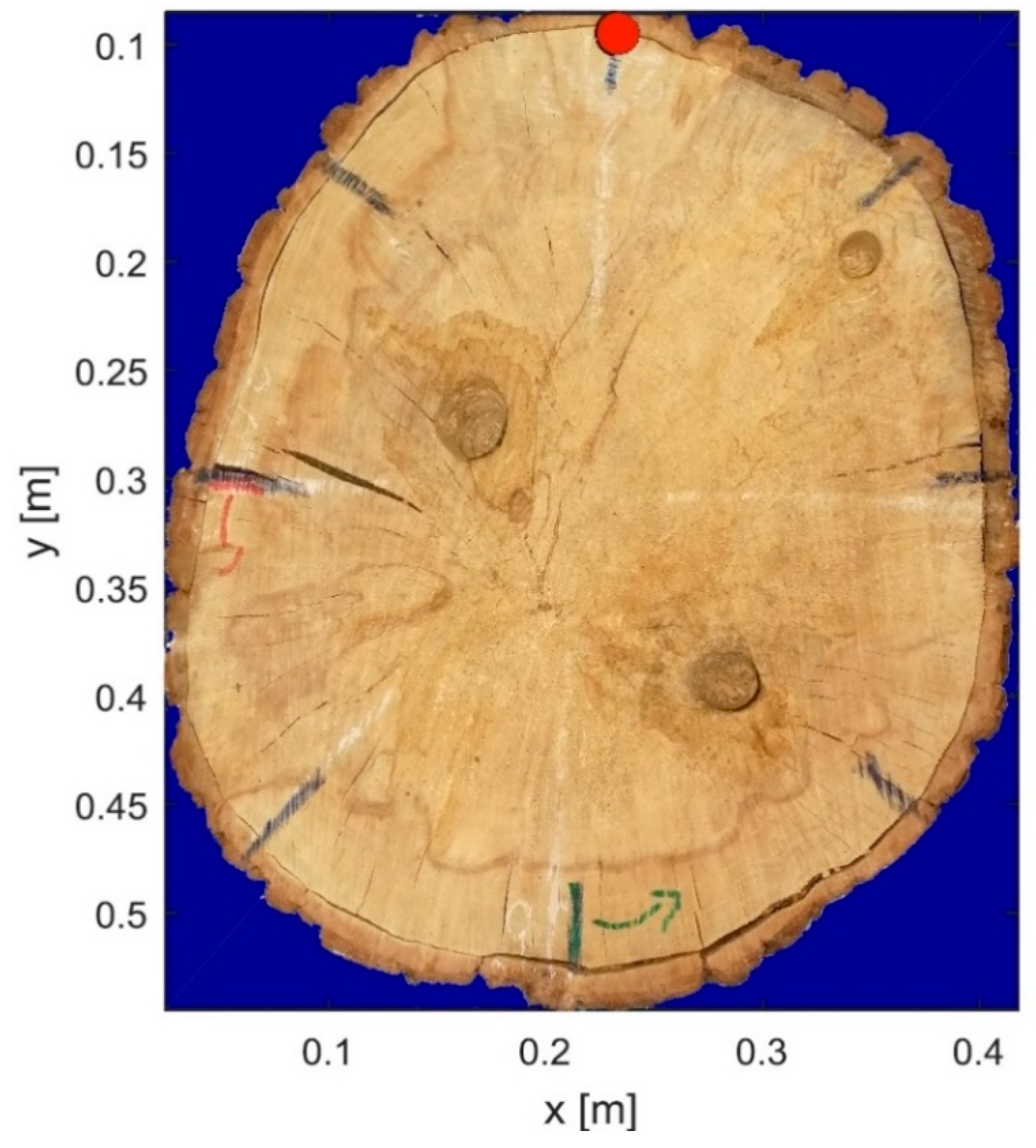
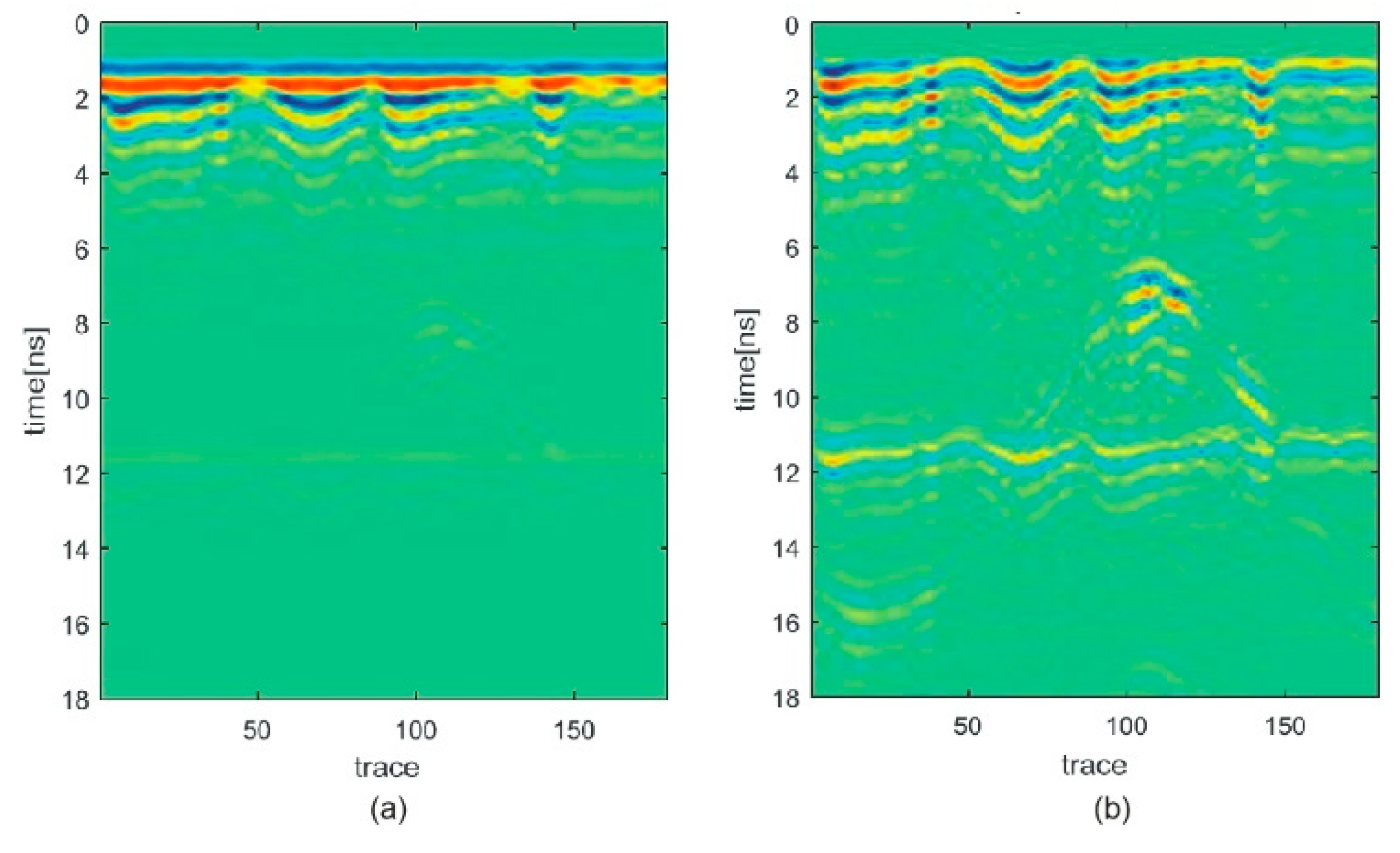
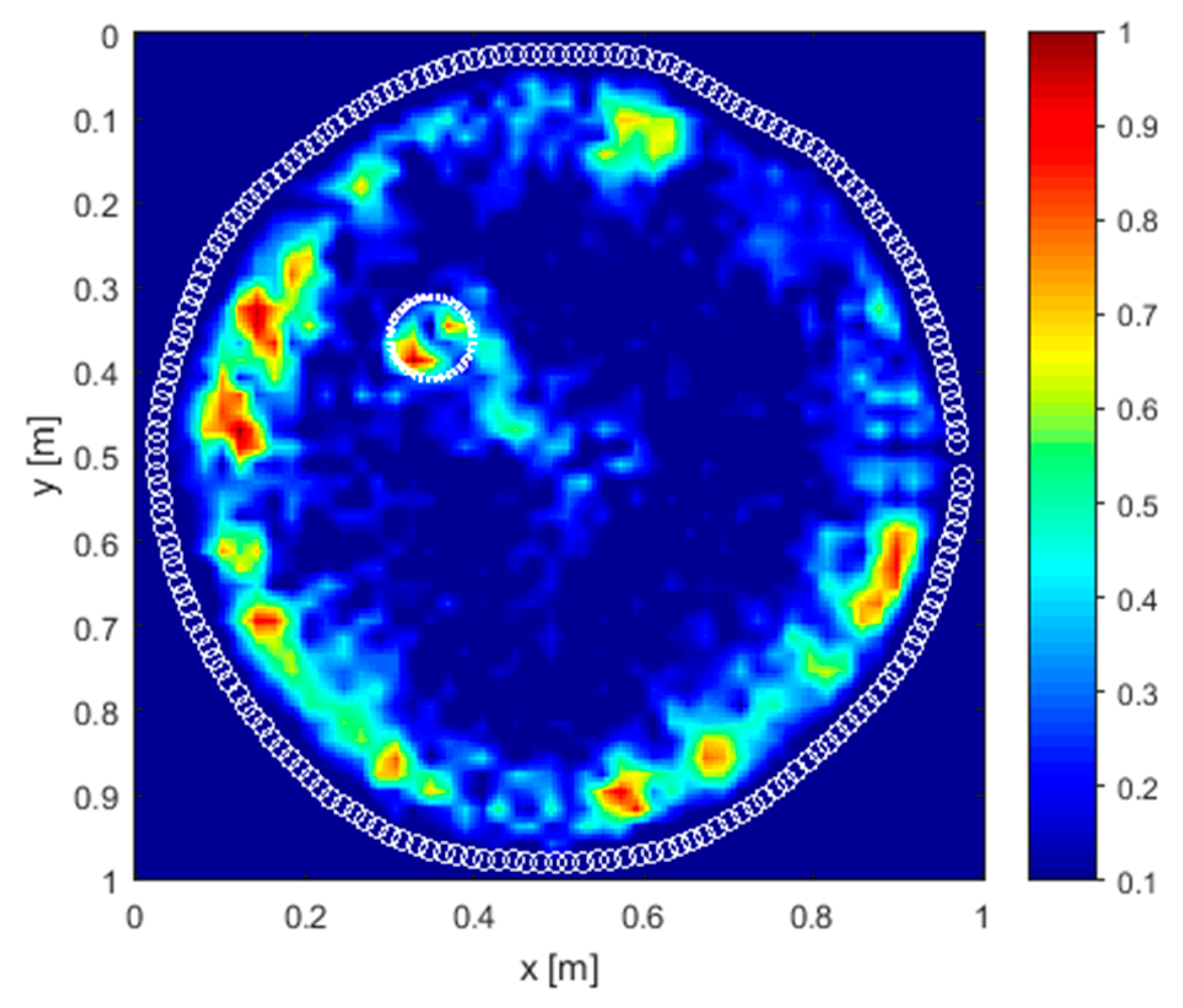
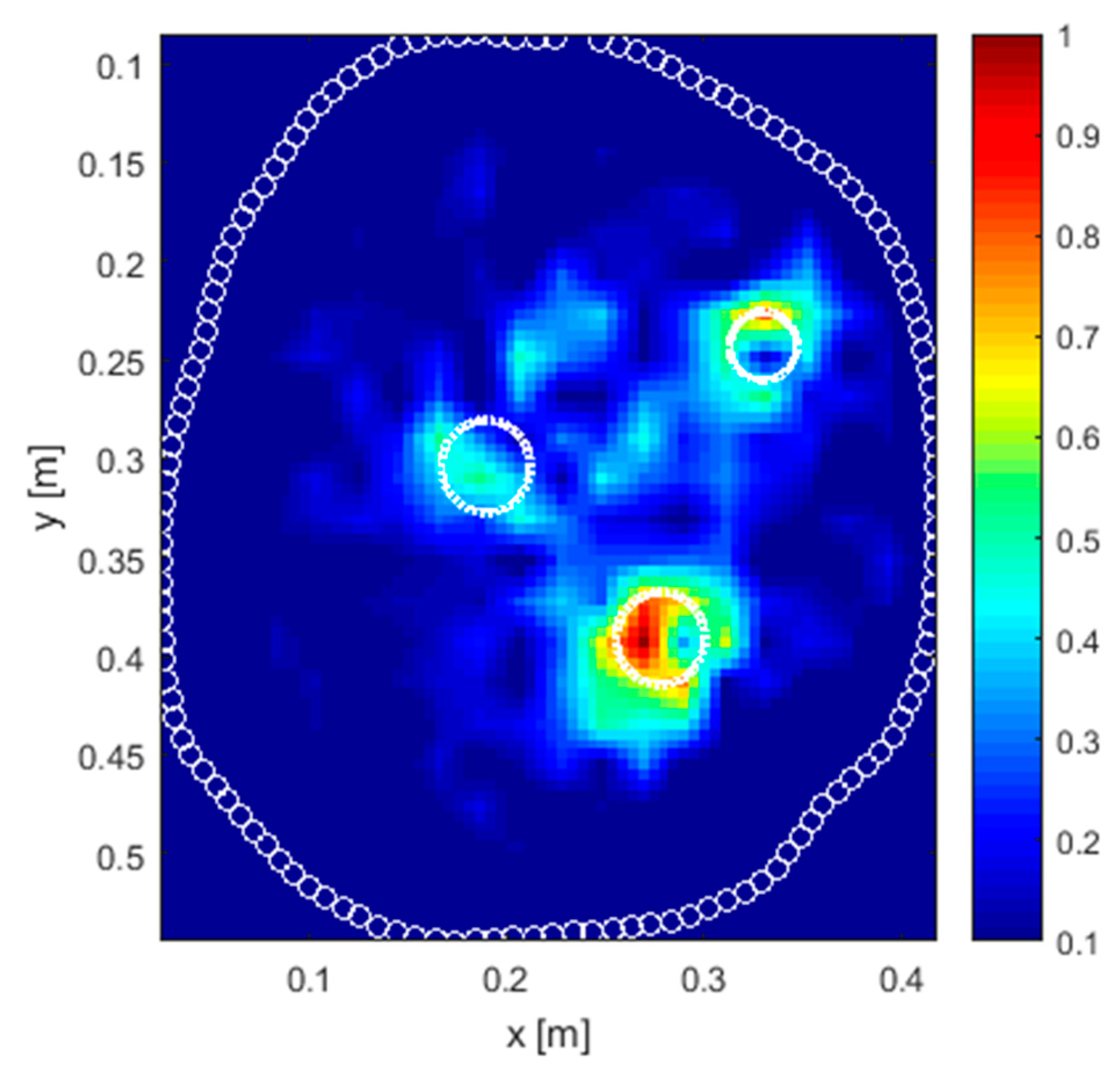
4.2. Real Scenario
5. Conclusion and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pan, Y.; Birdsey, A.B.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, A.K.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Hansen, E.M.; Goheen, E.M. Phellinus weirii and other native root pathogens as determinants of forest structure and process in western North America. Ann. Rev. Phytopathol. 2000, 38, 515–539. [Google Scholar] [CrossRef] [PubMed]
- Richardson, D.M.; Pyšek, P.; Rejmánek, M.; Barbour, M.G.; Panetta, F.D.; West, C.J. Naturalization and invasion of alien plants: Concepts and definitions. In Diversity and Distributions; Wiley Online Library: Berlin, Germany, 2001; pp. 93–107. [Google Scholar]
- Santini, A.; Ghelardini, L.; De Pace, C.; Desprez-Loustau, M.L.; Capretti, P.; Chandelier, A.; Cech, T.; Chira, D.; Diamandis, S.; Gaitniekis, T.; et al. Biogeographical patterns and determinants of invasion by forest pathogens in Europe. New Phytol. 2012, 197, 238–250. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Rejmanek, M.; Wen, J. Geographical, socioeconomic, and ecological determinants of exotic plant naturalization in the United States: Insights and updates from improved data. NeoBiota 2012, 12, 41–55. [Google Scholar] [CrossRef]
- Liebhold, A.M.; Brockerhoff, E.G.; Garrett, L.J.; Parke, J.L.; Britton, K.O. Live plant imports: The major pathway for forest insect and pathogen invasions of the US. Front. Ecol. Env. 2012, 10, 135–143. [Google Scholar] [CrossRef]
- Broome, A.; Ray, D.; Mitchell, R.; Harmer, R. Responding to ash dieback (Hymenoscyphus fraxineus) in the UK: Woodland composition and replacement tree species. Forestry 2019, 92, 108–119. [Google Scholar] [CrossRef]
- Jung, T. Beech decline in Central Europe driven by the interaction between Phytophthora infections and climatic extremes. In Forest Pathology; Wiley Online Library: Berlin, Germany, 2009; pp. 73–94. [Google Scholar]
- Anderson, P.K.; Cunningham, A.A.; Patel, N.G.; Morales, F.J.; Epstein, P.R.; Daszak, P. Emerging infectious diseases of plants: Pathogen pollution, climate change and agrotechnology drivers. Trends Ecol. Evol. 2004, 19, 535–544. [Google Scholar] [CrossRef]
- Daszak, P. Emerging Infectious Diseases of Wildlife—Threats to Biodiversity and Human Health. Science 2000, 287, 443–449. [Google Scholar] [CrossRef]
- Fisher, M.C.; Henk, D.A.; Briggs, C.J.; Brownstein, J.S.; Madoff, L.C.; McCraw, S.L.; Gurr, S.J. Emerging fungal threats to animal, plant and ecosystem health. Nature 2012, 484, 186–194. [Google Scholar] [CrossRef] [PubMed]
- Potter, C.; Harwood, T.; Knight, J.; Tomlinson, I. Learning from history, predicting the future: The UK Dutch elm disease outbreak in relation to contemporary tree disease threats. Philos. Trans. R. Soc. B Boil. Sci. 2011, 366, 1966–1974. [Google Scholar] [CrossRef]
- McMullan, M.; Rafiqi, M.; Kaithakottil, G.; Clavijo, B.J.; Bilham, L.; Orton, E.; Percival-Alwyn, L.; Ward, B.J.; Edwards, A.; Saunders, D.G.O.; et al. The ash dieback invasion of Europe was founded by two genetically divergent individuals. Nat. Ecol. Evol. 2018, 2, 1000–1008. [Google Scholar] [CrossRef] [PubMed]
- Brown, N.; Inward, D.J.G.; Jeger, M.; Denman, S. A review of Agrilus biguttatus in UK forests and its relationship with acute oak decline. For. Int. J. For. Res. 2015, 88, 53–63. [Google Scholar] [CrossRef]
- Gibbs, J.N. Intercontinental Epidemiology of Dutch Elm Disease. Ann. Rev. Phytopathol. 1978, 16, 287–307. [Google Scholar] [CrossRef]
- Papic, S.; Longauer, R.; Milenković, I.; Rozsypálek, J. Genetic predispositions of common ash to the ash dieback caused by ash dieback fungus. Genetika 2018, 50, 221–229. [Google Scholar] [CrossRef]
- Worrell, R. An Assessment of the Potential Impacts of Ash Dieback in Scotland. Available online: https://bit.ly/2ZkYhNc (accessed on 30 August 2019).
- Brown, N. Epidemiology of Acute Oak Decline in Great Britain. Available online: https://spiral.imperial.ac.uk/handle/10044/1/30827 (accessed on 30 August 2019).
- Brasier, C.M. Dual origin of recent Dutch elm disease outbreaks in Europe. Nature 1979, 281, 78–80. [Google Scholar] [CrossRef]
- Brasier, C.M.; Gibbs, J.N. Origin of the Dutch Elm Disease Epidemic in Britain. Nature 1973, 242, 607–609. [Google Scholar] [CrossRef]
- Denman, S.; Brown, N.; Kirk, S.; Jeger, M.; Webber, J. A description of the symptoms of Acute Oak Decline in Britain and a comparative review on causes of similar disorders on oak in Europe. Forestry 2014, 87, 535–551. [Google Scholar] [CrossRef]
- Ouis, D. Non destructive techniques for detecting decay in standing trees. Arboric. J. 2003, 27, 159–177. [Google Scholar] [CrossRef]
- Winistorfer, P.M.; Xu, W.; Wimmer, R. Application of A Drill Resistance Technique for Density Profile Measurement in Wood Composite Panels. Available online: https://bit.ly/2zymrVm (accessed on 30 August 2019).
- Schwarze, F.W.M.R.; Ferner, D. Ganoderma on trees—Differentiation of species and studies of invasiveness. Arboric. J. 2003, 27, 59–77. [Google Scholar] [CrossRef]
- Shortle, W.C.; Dudzik, K.R. Wood Decay in Living and Dead Trees: A Pictorial Overview. Available online: https://www.fs.usda.gov/treesearch/pubs/40899 (accessed on 30 August 2019).
- Costello, L.; Quarles, S. Detection of wood decay in blue gum and elm: An evaluation of the Resistograph and the portable drill. J. Arboric. 1999, 25, 311–317. [Google Scholar]
- Al Hagrey, S.A. Electrical resistivity imaging of tree trunks. Near Surf. Geophys. 2006, 4, 179–187. [Google Scholar] [CrossRef]
- Deflorio, G.; Fink, S.; Schwarze, F.W. Detection of incipient decay in tree stems with sonic tomography after wounding and fungal inoculation. Wood Sci. Technol. 2008, 42, 117–132. [Google Scholar] [CrossRef]
- Catena, A. Thermography shows damaged tissue and cavities present in trees. Nondestruct. Charact. Mater. 2003, 11, 515–522. [Google Scholar]
- Wei, Q.; Leblon, B.; Rocque, L.A. On the use of X-ray computed tomography for determining wood properties: A review. Can. J. Forest Res. 2011, 41, 2120–2140. [Google Scholar] [CrossRef]
- Boero, F.; Fedeli, A.; Lanini, M.; Maffongelli, M.; Monleone, R.; Pastorino, M.; Randazzo, A.; Salvadè, A.; Sansalone, A. Microwave Tomography for the Inspection of Wood Materials: Imaging System and Experimental Results. IEEE Trans. Microw. Theory Tech. 2018, 66, 3497–3510. [Google Scholar] [CrossRef]
- Goodman, D. Ground-penetrating radar simulation in engineering and archaeology. Geophysics 1994, 59, 224–232. [Google Scholar] [CrossRef]
- Catapano, I.; Gennarelli, G.; Ludeno, G.; Soldovieri, F. Applying Ground-Penetrating Radar and Microwave Tomography Data Processing in Cultural Heritage: State of the art and future trends. IEEE Signal. Process. Mag. 2019, 36, 53–61. [Google Scholar] [CrossRef]
- Giannakis, I.; Giannopoulos, A.; Yarovoy, A. Model-Based Evaluation of Signal-to-Clutter Ratio for Landmine Detection Using Ground-Penetrating Radar. IEEE Trans. Geosci. Remote. Sens. 2016, 54, 1–10. [Google Scholar] [CrossRef]
- González-Huici, M.A.; Catapano, I.; Soldovieri, F. A Comparative Study of GPR Reconstruction Approaches for Landmine Dete. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4869–4878. [Google Scholar] [CrossRef]
- Alani, A.M.; Tosti, F. GPR applications in structural detailing of a major tunnel using different frequency antenna systems. Constr. Build. Mater. 2018, 158, 1111–1122. [Google Scholar] [CrossRef]
- Lo Monte, L.; Erricolo, D.; Soldovieri, F.; Wicks, M.C. Radio frequency tomography for tunnel detection. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1128–1137. [Google Scholar] [CrossRef]
- Alani, A.M.; Aboutalebi, M.; Kilic, G. Applications of ground penetrating radar (GPR) in bridge deck monitoring and assessment. J. Appl. Geophys. 2013, 97, 45–54. [Google Scholar] [CrossRef]
- Benedetto, A.; Pajewski, L. Civil Engineering Applications of Ground Penetrating Radar. Available online: https://bit.ly/2Zn6lwZ (accessed on 30 August 2019).
- Tosti, F.; Ciampoli, L.B.; D’Amico, F.; Alani, A.M.; Benedetto, A. An experimental-based model for the assessment of the mechanical properties of road pavements using ground-penetrating radar. Constr. Build. Mater. 2018, 165, 966–974. [Google Scholar] [CrossRef]
- Catapano, I.; Ludeno, G.; Soldovieri, F.; Tosti, F.; Padeletti, G. Structural Assessment via Ground Penetrating Radar at the Consoli Palace of Gubbio (Italy). Remote Sens. 2018, 10, 45. [Google Scholar] [CrossRef]
- Tosti, F.; Pajewski, L. Applications of Radar Systems in Planetary Sciences: An Overview; Benedetto, A., Pajewski, L., Eds.; Civil Engineering Applications of Ground Penetrating Radar; Springer Transactions in Civil and Environmental Engineering; Springer: Cham, Switzerland, 2015; pp. 361–371. [Google Scholar]
- Orosei, R.; Lauro, S.E.; Pettinelli, E.; Cicchetti, A.; Coradini, M.; Cosciotti, B.; Di Paolo, F.; Flamini, E.; Mattei, E.; Pajola, M.; et al. Radar evidence of subglacial liquid water on Mars. Science 2018, 361, 490–493. [Google Scholar] [CrossRef] [PubMed]
- Carrer, L.; Bruzzone, L. Solving for ambiguities in radar geophysical exploration of planetary bodies by mimicking bats echolocation. Nat. Commun. 2017, 8, 2248. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.L.; Annan, A.P. Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy. Geophys. Prospect. 1989, 37, 531–551. [Google Scholar] [CrossRef]
- Tosti, F.; Slob, E. Determination, by Using GPR, of the Volumetric Water Content in Structures, Substructures, Foundations and Soil. In Civil Engineering Applications of Ground Penetrating Radar. Springer Transactions in Civil and Environmental Engineering; Benedetto, A., Pajewski, L., Eds.; Springer: Cham, Switzerland, 2015; pp. 163–194. [Google Scholar]
- Brunzell, H. Detection of shallowly buried objects using impulse radar. IEEE Trans. Geosci. Remote. Sens. 1999, 37, 875–886. [Google Scholar] [CrossRef]
- Ambrosanio, M.; Bevacqua, M.T.; Isernia, T.; Pascazio, V. The Tomographic Approach to Ground-Penetrating Radar for Underground Exploration and Monitoring: A more user-friendly and unconventional method for subsurface investigation. IEEE Signal. Process. Mag. 2019, 36, 62–73. [Google Scholar] [CrossRef]
- Fedeli, A.; Jezova, J.; Lambot, S.; Pastorino, M.; Randazzo, A. Nonlinear Inversion of Multifrequency GPR Data in Tomographic Configurations. In Geophysical Research Abstracts. Available online: https://bit.ly/2zwN1hx (accessed on 30 August 2019).
- Nicolotti, G.; Socco, L.V.; Martinis, R.; Godio, A.; Sambuelli, L. Application and comparison of three tomographic techniques for detection of decay in trees. J. Arboric. 2003, 29, 66–78. [Google Scholar]
- Lorenzo, H.; Perez-Gracia, V.; Novo, A.; Armesto, J. Forestry applications of ground-penetrating radar. For. Syst. 2010, 19, 5–17. [Google Scholar] [CrossRef]
- Ježová, J.; Mertens, L.; Lambot, S. Ground-penetrating radar for observing tree trunks and other cylindrical objects. Constr. Build. Mater. 2016, 123, 214–225. [Google Scholar] [CrossRef]
- Jezova, J.; Harou, J.; Lambot, S. Reflection waveforms occurring in bistatic radar testing of columns and tree trunks. Constr. Build. Mater. 2018, 174, 388–400. [Google Scholar] [CrossRef]
- Al Hagrey, S.A. Geophysical imaging of root-zone, trunk, and moisture heterogeneity. J. Exp. Bot. 2007, 58, 839–854. [Google Scholar] [CrossRef]
- Alani, A.; Ciampoli, L.B.; Lantini, L.; Tosti, F.; Benedetto, A. Mapping the Root System Of Matured Trees Using Ground Penetrating Radar. Available online: https://bit.ly/2lB3cXa (accessed on 3 September 2019).
- Tosti, F.; Bianchini Ciampoli, L.; Brancadoro, M.G.; Alani, A.M. GPR applications in mapping the subsurface root system of street trees with road safety-critical implications. Adv. Transp. Stud. 2018, 44, 107–118. [Google Scholar]
- Lantini, L.; Holleworth, R.; Egyir, D.; Giannakis, I.; Tosti, F.; Alani, A. Use of Ground Penetrating Radar for Assessing Interconnections between Root Systems of Different Matured Tree Species. Available online: https://repository.uwl.ac.uk/id/eprint/5491/ (accessed on 30 August 2019).
- Giannakis, I.; Tosti, F.; Lantini, L.; Alani, A.M. Health Monitoring of Tree Trunks Using Ground Penetrating Radar. IEEE Trans. Geosci. Remote. Sens. 2019, 1–10. [Google Scholar] [CrossRef]
- Alani, A.; Bianchini Ciampoli, L.; Tosti, F.; Brancadoro, M.G.; Pirrone, D.; Benedetto, A. Health Monitoring of a Matured Tree Using Ground Penetrating Radar–Investigation of the Tree Root System and Soil Interaction. Available online: https://repository.uwl.ac.uk/id/eprint/3913/ (accessed on 30 August 2019).
- Pastorino, M. Microwave Imaging; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Miao, Z.; Kosmas, P. Multiple-frequency DBIM-TwIST algorithm for microwave breast imaging. IEEE Trans. Antennas Propag. 2017, 65, 1. [Google Scholar] [CrossRef]
- Gilmore, C.; Abubakar, A.; Hu, W.; Habashy, T.M.; Berg, P.M.V.D. Microwave Biomedical Data Inversion Using the Finite-Difference Contrast Source Inversion Method. IEEE Trans. Antennas Propag. 2009, 57, 1528–1538. [Google Scholar] [CrossRef]
- Leucci, G.; Masini, N.; Persico, R.; Soldovieri, F. GPR and sonic tomography for structural restoration: The case of the cathedral of Tricarico. J. Geophys. Eng. 2011, 8, S76–S92. [Google Scholar] [CrossRef]
- Daniels, D.J. Ground Penetrating Radar. Available online: https://bit.ly/2LfZr2F (accessed on 30 August 2019).
- Catapano, I.; Gennarelli, G.; Ludeno, G.; Soldovieri, F.; Persico, R. Ground-Penetrating Radar: Operation Principle and Data Processing. Available online: https://bit.ly/2lVMmmi (accessed on 3 September 2019).
- Benedetto, A.; Tosti, F.; Ciampoli, L.B.; D’Amico, F. An overview of ground-penetrating radar signal processing techniques for road inspections. Signal. Process. 2017, 132, 201–209. [Google Scholar] [CrossRef]
- Soldovieri, F.; Solimene, R. Ground Penetrating Radar Subsurface Imaging of Buried. Available online: Objectshttps://bit.ly/2lvPNA0 (accessed on 30 August 2019).
- Persico, R. Introduction to Ground Penetrating Radar: Inverse Scattering and Data Processing. Available online: https://bit.ly/2UlBjQy (accessed on 30 August 2019).
- Solimene, R.; Catapano, I.; Gennarelli, G.; Cuccaro, A.; Dell’Aversano, A.; Soldovieri, F. SAR Imaging Algorithms and Some Unconventional Applications: A unified mathematical overview. IEEE Signal. Process. Mag. 2014, 31, 90–98. [Google Scholar] [CrossRef]
- Bertero, M.; Boccacci, P. Introduction to Inverse Problems in Imaging. Available online: https://bit.ly/2lTr2Og (accessed on 30 August 2019).
- Persico, R.; Bernini, R.; Soldovieri, F. The role of the measurement configuration in inverse scattering from buried objects under the Born approximation. IEEE Trans. Antennas Propag. 2005, 53, 1875–1887. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef]
- Giannakis, I.; Giannopoulos, A.; Warren, C.; Warren, C. Realistic FDTD GPR antenna models optimized using a novel linear/nonlinear Full-Waveform Inversion. IEEE Trans. Geosci. Remote. Sens. 2018, 57, 1768–1778. [Google Scholar] [CrossRef]
| Tree Section Component | Water Content [%] | [W−1m−1] | |||
|---|---|---|---|---|---|
| Cambium layer | 70 | 9 | 43 | 1 | 9.23 |
| Outer sapwood | 30 | 6.1 | 12.36 | 0.033 | 9.23 |
| Inner sapwood | 25 | 5.9 | 9.66 | 0.02 | 9.23 |
| Rings | 10 | 5.4 | 3.1 | 0.0083 | 9.23 |
| Heartwood | 5 | 5.22 | 1.43 | 0.005 | 9.23 |
| Bark | 0 | 5 | 0 | 0 | 9.23 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alani, A.M.; Soldovieri, F.; Catapano, I.; Giannakis, I.; Gennarelli, G.; Lantini, L.; Ludeno, G.; Tosti, F. The Use of Ground Penetrating Radar and Microwave Tomography for the Detection of Decay and Cavities in Tree Trunks. Remote Sens. 2019, 11, 2073. https://doi.org/10.3390/rs11182073
Alani AM, Soldovieri F, Catapano I, Giannakis I, Gennarelli G, Lantini L, Ludeno G, Tosti F. The Use of Ground Penetrating Radar and Microwave Tomography for the Detection of Decay and Cavities in Tree Trunks. Remote Sensing. 2019; 11(18):2073. https://doi.org/10.3390/rs11182073
Chicago/Turabian StyleAlani, Amir M., Francesco Soldovieri, Ilaria Catapano, Iraklis Giannakis, Gianluca Gennarelli, Livia Lantini, Giovanni Ludeno, and Fabio Tosti. 2019. "The Use of Ground Penetrating Radar and Microwave Tomography for the Detection of Decay and Cavities in Tree Trunks" Remote Sensing 11, no. 18: 2073. https://doi.org/10.3390/rs11182073
APA StyleAlani, A. M., Soldovieri, F., Catapano, I., Giannakis, I., Gennarelli, G., Lantini, L., Ludeno, G., & Tosti, F. (2019). The Use of Ground Penetrating Radar and Microwave Tomography for the Detection of Decay and Cavities in Tree Trunks. Remote Sensing, 11(18), 2073. https://doi.org/10.3390/rs11182073