1. Introduction
Earth’s atmosphere affects electromagnetic global navigation satellite system (GNSS) signals by delaying their propagation. While the ionosphere influence can be reduced using dual-frequency measurements, the delay caused by the troposphere has to be estimated during the precise positioning process. Tropospheric delay is usually expressed in the zenith direction (zenith tropospheric delay, ZTD) and it describes the total impact of neutral atmosphere on the GNSS signals. Therefore, ZTD contains delays caused by the hydrostatic (zenith hydrostatic delay, ZHD) and the wet (zenith wet delay, ZWD) part of the troposphere. Both ZHD and ZWD depend on the meteorological parameters and, consequently, changes in these parameters over time. ZHD is correlated with changes of air pressure and temperature, while ZWD depends on the amount of water vapor in the atmosphere.
The sensitivity of the ZWD parameter to the water vapor content variation has triggered the development of the so-called GNSS meteorology. It is based on the possibility of converting the ZWD to precipitable water vapor (PWV) [
1], which describes the total content of water vapor in the air column above a GNSS antenna. Short-term monitoring of the water vapor variations is an important element in monitoring and studying of rapid changes of weather conditions [
2,
3,
4]. On the other hand, estimation of the PWV long-term parameters can be used as part of investigation of the climate change [
5,
6,
7]. Vertical PWV variations can be obtained via GNSS tomography [
8]. Although this approach enables to estimate accurate humidity distribution through troposphere, it requires delivering of temperature profiles, using dense network of GNSS receivers and complex calculations. PWV can be also calculated based on the ZTD derived from GNSS processing and various external meteorological parameters. Temperature and air pressure profiles are used to estimate ZHD, which is necessary to obtain ZWD. In turn, profiles of temperature and water vapor pressure are required to calculate water vapor weighted mean temperature (
), which takes part in the conversion from ZWD to PWV. In situ measurements of the profiles can be done using radiosonde or microwave radiometers. Unfortunately, the vast majority of GNSS stations are not collocated with such instruments. Thus, it is not possible to obtain the required meteorological data. Therefore, it is necessary to apply some simplifications. ZHD can be accurately modeled using total air pressure at the GNSS antenna location [
9], while
can be obtained based on the linear relationship with the surface temperature (
):
. This relationship (henceforth named
) was firstly proposed by Bevis et al. [
1]. In their model, the
(slope) and
(intercept) coefficients were calculated on the basis of 8712 radiosonde profiles made on 13 U.S. stations over a two-year period. They determined the values of the coefficients at 0.72 and 70.2 for
and
, respectively, with the root mean square error (RMSE) at the level of 4.74 K. Braun and Van Hove [
10] used, based on a personal communication from Michael Bevis, revised version of these coefficients. Based on the profiles derived from nearly globally distributed radio-soundings stations, updated coefficients values were estimated:
and
.
A linear regression analysis of the radiosonde profiles was also conducted by Mendes and Langley [
11] who based on the data from stations located between 62°S to 83°N proposed that the following coefficients can be used:
and
. Ross and Rosefeld [
12] found that geographical localization may affect the reliability of the
model and have proposed to use the nonlinear function (
) for stations located at higher latitudes. Consequently, regional models have started to be developed. Here, Emardson et al. [
13] can be mentioned, who have proposed to use a model which included information about time of the year for the Scandinavia region, or Solbrig et al. [
14], who have used simple
but estimated specifically for the territory of Germany. Despite the fact that they only included data from Germany, they obtained results (
,
) similar to those presented by Mendes and Langley on a global scale. The optimization of the
for the specific area was also undertaken by, e.g., Liu et al. for Taiwan [
15], Baltink et al. for the Netherlands [
16], Bokoye et al. for Canada [
17], Suresh et al. for India [
18], Sappucci for Brazil [
19], Mekik and Deniz for Turkey [
20], Liu et al. for China [
21], or Zhang et al. for Tahiti [
22]. These works show the importance of developing accurate spatio-temporal models of
. Simultaneously, new global coefficients were also modeled. Based on the data from the numeric model, Schueler et al. [
23] proposed three approaches: Harmonics, which took into account the day of year and seasonal variations of
, a linear
, and a combined periodic/linear assumption. Yao et al. [
24] have proposed a station location (latitude, longitude, and elevation) and season-dependent coefficients for the
linear relation. Lan et al. [
25] proposed a gridded model with 2°
2.5° window size to deliver the site-accurate
and
coefficients, while Yao et al. [
26] developed a globally applicable global weighted mean temperature (GWMT) model which considered annual cycle, as well as semi-annual and diurnal variation of
sourced from the Global Geodetic Observing System (GGOS).
All so far developed models have some advantages and limitations. Local models are best suited to the prevailing weather conditions occurring over a given region, while global models can be used on larger scale. On the other hand, in the case of global models, the coverage of radio-sounding (RS) stations is not uniform. This evokes the need to accept a compromise between model accuracy and global availability or the need to source data from weather models, not in situ observations. The numerical weather models, in turn, contain the average values of meteorological parameters, which can cause deterioration of the results. Until now, there is a lack of a regional model that could be used across the European continent with high accuracy. In this paper, we focus on a regional model of the
relationship, developed exclusively on the basis of in situ measurements. In total, we used observations from 109 RS stations evenly distributed throughout Europe to deliver and validate reliable coefficients of the
. More details about the employed data are given in
Section 2 together with a description of the methodology. The accuracy of the selected models is assessed in
Section 3. The process of estimation of new coefficients is presented in
Section 4, while the results are described and discussed in
Section 5.
2. Data and Methodology
ZTD, together with the station coordinates, is a direct product of GNSS processing. It contains hydrostatic (ZHD) and wet components (ZWD):
ZWD is strictly correlated to the amount of water vapor in the atmosphere and can be converted to PWV by:
where
is a dimensionless quantity dependent on
:
where
is the specific gas constant of water vapor (461.5 J/kg K), and:
where
denotes air refractivity parameters. Here, we applied the “best average” values estimated by Ruger [
27], equal to 77.689 ± 0.0094 K/hPa, 71.295 ± 1.3 K/hPa, and 3.75463 × 10
5 ± 0.0076 K
2/hPa, respectively.
and
are the molar masses of wet and dry air expressed in g/mol.
We have stated that
can be obtained by vertical integration of the temperature in the atmosphere and requires measurements from a sounding station or a microwave radiometer, or data from an accurate and validated numerical weather model. The other way is to use the linear relationship with the
. To estimate
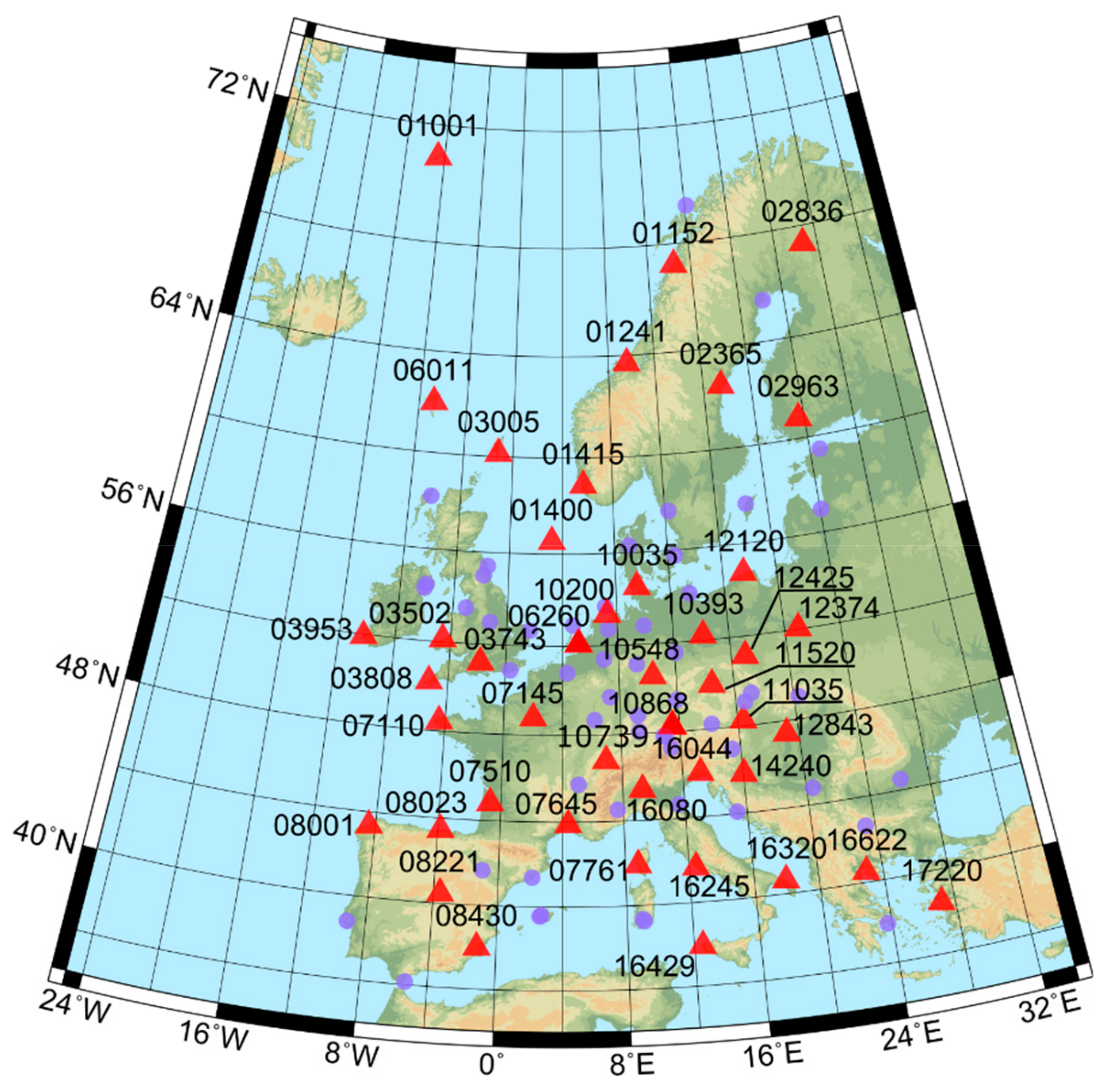
coefficients, it is necessary to know both values at the station location. In this study, observations from 109 RS stations located in Europe were used (
Figure 1). Values of
were derived directly from the measurements while
were calculated by vertical integration of the temperature (
) and water vapor pressure (
) profiles:
where
is a station altitude and
denotes the maximum height of the atmospheric profile. We used only profiles made up to at least 8 km.
Thus obtained time series of
and
were divided into two groups. The first of them contained stations which have been working since 1994 to 2018, collected at least 80% of observations, and were free from visible shifts and significant gaps (henceforth named estimation group). This group consists of 49 stations and constitutes a basis for estimation new coefficients of
(
Figure 1, the red triangles) using linear regression. To ensure independent verification of our results, we selected the second group containing 60 RS stations (
Figure 1, the light violet circles). These stations (henceforth named external group) have at least 2 years of observations and together with the estimation group were used as an external indicator of the accuracy of all coefficients shown in this paper. All observations were obtained from Earth System Research Laboratory (ESRL) database and were checked before analysis. Incomplete or too low (below 8 km) profiles as well as abnormal recorded values were removed from further processing.
In
Section 5, we provide the impact of the new estimated coefficients on the PWV. Therefore, we had to extract ZWD from Equation (1). To this end, we used the Saastamoinen hydrostatic model [
9] and surface meteorological parameters derived from the ERA5 model [
28] and interpolated at the locations of the stations [
29]. As we focus on PWV differences, this approach was acceptable.
3. Accuracy of the Existing Coefficients
Here, we present the assessment of the accuracy of the
coefficients that can be adopted in Europe. We took into consideration only these models which were estimated based on the in situ observations. In the described analysis, all 109 RS stations presented in
Figure 1 were used. For each of them the
values were estimated using Equation (5). They were compared to the
values calculated from the relationship with
and various coefficients. Obtained differences have allowed for an assessment which coefficients provide better accuracy and if this accuracy is evenly distributed over the entire area.
We decided to consider coefficients developed by Bevis et al. [
1] (henceforth named Bevis coefficients), since they are still one of the most commonly used. Moreover, their revised versions [
10] (BevisRev coefficients) as well as values presented by Mendes and Langley [
11] (Mendes coefficients) and Solbrig [
14] (Solbrig coefficients) were taken into account.
Figure 2 presents the RMSE values for each of the analyzed station and set of coefficients. Using Bevis coefficients, we achieved mean RMSE value at the level of 3.1 ± 0.4 K. As it is seen in
Figure 2a, the distribution of RMSE for the individual stations is not homogeneous. The greatest consistency can be found in the north-east area, where for most of the stations the RMSE value is below 3.0 K. This may result from the fact that these stations are located in the temperate oceanic climate zone for which the Atlantic Ocean has a smoothing effect. Similar results can be found when BevisRev coefficients were used (
Figure 2b). In this case the mean RMSE was at the level 3.3 ± 0.4 K. These slightly poorer results are probably caused by the spatial distribution of stations used for coefficients estimation (regional in Bevis and global in BevisRev). Application of Mendes coefficients (
Figure 2c) did not bring significant difference in results—the mean RMSE value was 3.1 ± 0.5 K. Interesting results were obtained for
values estimated based on Solbrig coefficients (
Figure 2d). Although the coefficients were estimated only for Germany, they can be used for stations located in almost all of Europe, especially the northern part. The obtained accuracy did not diverge significantly from others. The mean RMSE for this solution was 3.2 ± 0.6 K. In this case, the RMSE is affected by poor results obtained for stations located in the Mediterranean area. It is also worth to notice here, as opposed to the expectations, that the stations located in Germany are not characterized by higher accuracy. Summary of the provided results is given in
Table 1.
Although part of the stations is in a very good agreement with the values obtained by the way of direct measurement, the limitations of these models are also clear. This motivated us to reanalyze RS data from Europe and to verify whether it is possible to estimate coefficients with higher accuracy.
4. Estimation of the New Coefficients
In the first approach, the coefficients were estimated using the same method as in case of the above described studies. The and data from all stations belonging to the estimation group were analyzed in one common process, in which a linear regression was conducted to the whole dataset consisting of 967,277 records. As a result, the coefficients (named ETm) of the were estimated at 0.7440 ± 0.0004 and 62.84 ± 0.10, for and , respectively, with RMSE equal 3.0 K.
The second approach was preceded by an investigation of the relationship between time-varying
and
. The possible dependency between
coefficients and the time of day were investigated, e.g., by Mekik and Deniz [
19]. In their study, they proved that the differences in RMSE values obtained based on coefficients estimated during day and night are not significant, amounting to about 0.2 K, for RS stations located on the Turkish territory. To verify whether such dependency occur at European stations or not, we estimated
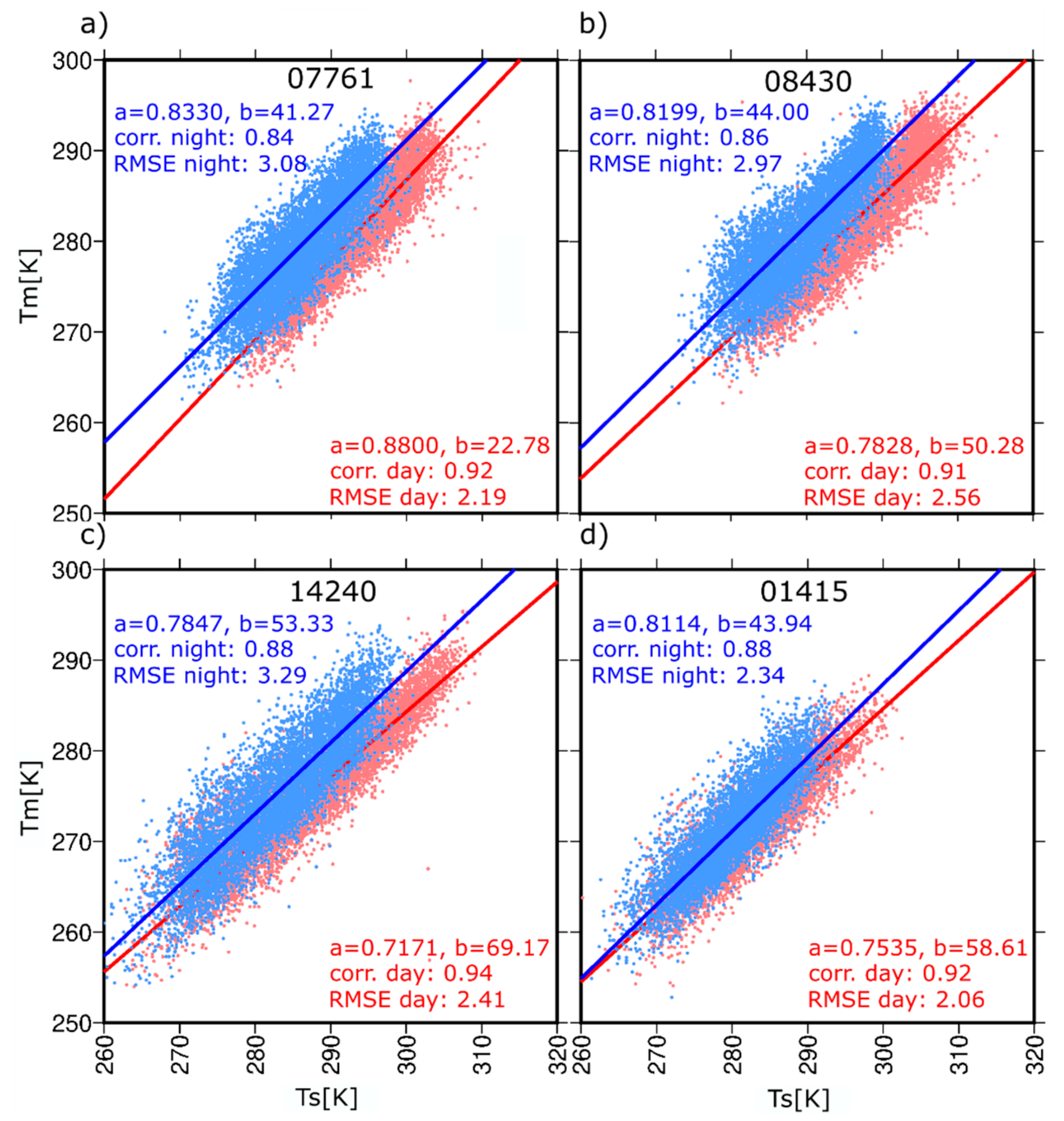
coefficients for two separated synoptic hours: At 00:00 and 12:00 UTC. We found clear differences between the
(
Figure 3a–c) estimated during the night (higher RMSE values) and the day (lower RMSE values). In the case of some stations, the RMSE between night and day drops from 3.08 K to 2.19 K, 2.97 K to 2.56 K, and from 3.29 K to 2.41 K for 07761, 08430, and 14240 station, respectively. Only for a few RS stations, the obtained differences were less significant, e.g., 01415 for which RMSE dropped from 2.34 K to 2.06 K (
Figure 3d).
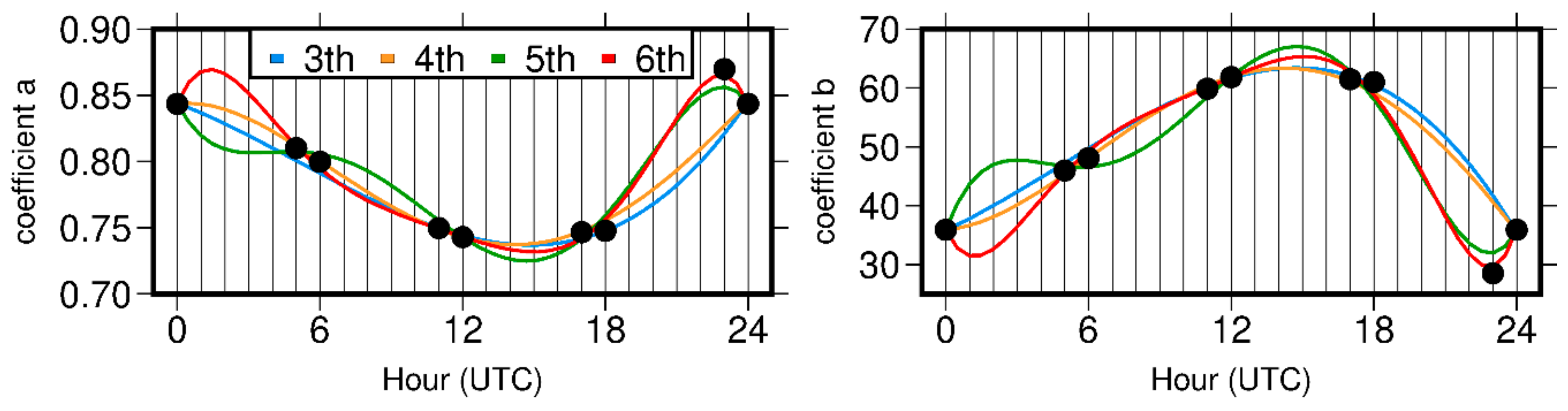
The fact that the linear regression coefficients show dependencies on the time of day prompted us to include this fact into the estimation of the new model. In this approach, observations from the 00:00 and 12:00 UTC collected from all stations belonging to the estimation group were analyzed separately. We obtained the following coefficients for daytime: = 0.7430 ± 0.004 and = 61.84 ± 0.13, and for nighttime: = 0.8436 ± 0.0006 and = 35.88 ± 0.17. These coefficients, named ETm2, were estimated with RMSE of 2.46 K and 2.91 K, respectively, for the day and the night. It is seen that the obtained RMSE are lower than in case of ETm coefficients, which proves that ETm2 ensures a better fit for the linear model.
Many RS stations had observations performed also at additional hours, mostly at 06:00 and 18:00 UTC. This fact allowed for an estimation of linear regression coefficients (ETm4) also for these terms. As a result, we have obtained four coefficients of
which are presented in
Table 2 together with RMSE. It can be seen that the uncertainties of estimated coefficients at 06:00 and 18:00 have higher values. This is due to the fact of using fewer stations for calculation than on the other terms. Nonetheless, the differences between the coefficients are significantly higher than their uncertainties. Determination the coefficients for several terms in a day can increase the
accuracy by making the simple
formula time dependent. This will cause the coefficients to be interpolated at a specific time of a day.
6. Conclusions
This paper presents a comparative analysis of the existing linear coefficients together with the development of a new form. In total, 109 RS stations over Europe were used to access and validate the accuracy of the estimation. Firstly, the Bevis, BevisRev, Mendes, and Solbrig coefficients were examined by comparing time series to the in situ measurements derived from RS stations. This indicated that Bevis and Mendes have similar accuracy and spatial distribution of the obtained results. The mean RMSE were 3.1 ± 0.4 K and 3.1 ± 0.5 K, respectively. In both cases, the highest consistency between the estimated and the observed data was found in north-western Europe, while the worst results were seen for the south-east. Similar results for north-western stations were found for the Solbrig coefficients. In other cases, significantly worse results were achieved. The estimation using BevisRev coefficients, which is Bevis global revision, was characterized by a mean RMSE at the level of 3.3 ± 0.4 K. Although this model represents a similar distribution of the results, in general, it did not achieve RMSE values as low as in the case of previous models (especially in the north-east area). In addition, stations located at the highest latitudes were represented by much lower accuracy. This is probably a consequence of using low latitude stations and stations from the southern hemisphere for coefficient estimation.
The coefficients we propose were estimated based on 49 RS stations over that were continuously operating for at least 20 years. In total, almost 970,000 records were used to estimate the coefficients following three different approaches: (i) All observations were used simultaneously to estimate one set of coefficients (ETm), (ii) two set of coefficients were estimated based on a separate calculation of observations only from 0 and 12 hours (ETm2), and (iii) the coefficients were estimated at four (00:00, 06:00, 12:00, 18:00) synoptic hours (ETm4). The determination the coefficients several times a day allowed us to perform an interpolation between terms to increase the determination accuracy. We showed that an application of even a simple linear interpolation brings tangible benefits especially for the measurements not performed at four primary synoptic hours. This might be exemplified by differences in RMSE between ETm and ETm4 models. For 101 out of 109 RS stations, we noted a reduction in RMSE value. Its mean value was 0.3 K and the highest reached up to 0.8 K (16546, Piras, Italy).
As a complement to the above approaches, we decided to apply a five-degree polynomial fitting instead of a linear interpolation to estimate and coefficients for a specific epoch during daytime (ETmPoly). Although this model is based on the exact same set of data as ETm4, we noticed some differences between the obtained results. Despite the fact that the mean RMSE of for these two models is the same (2.8 K), the STD was reduced from 0.4 K to 0.3 K. The highest differences between ETm4 and ETmPoly were found for stations which have observations out of primary synoptic hours. Here, the 11240 (Graz, Austria) station, for which RMSE was reduced by 0.4 K, can be mentioned.
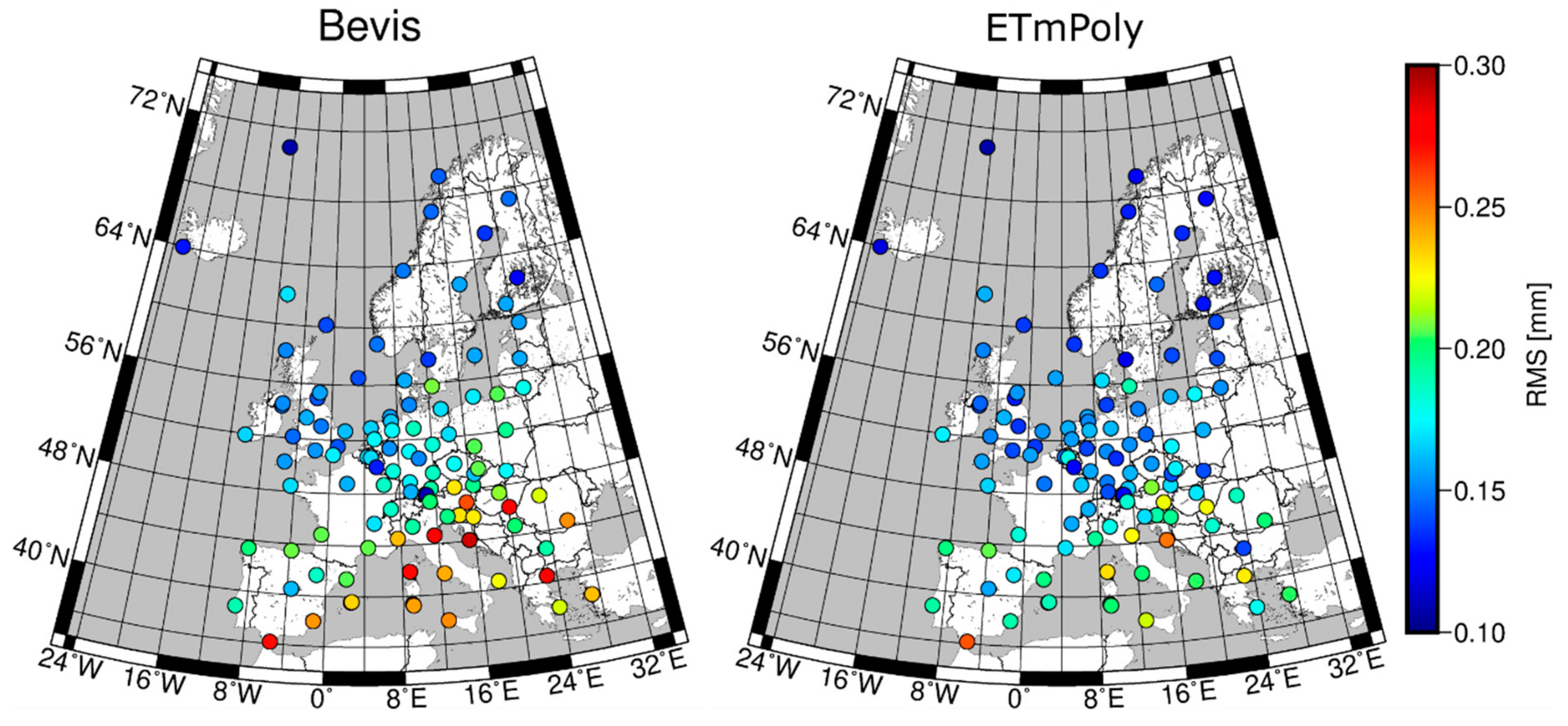
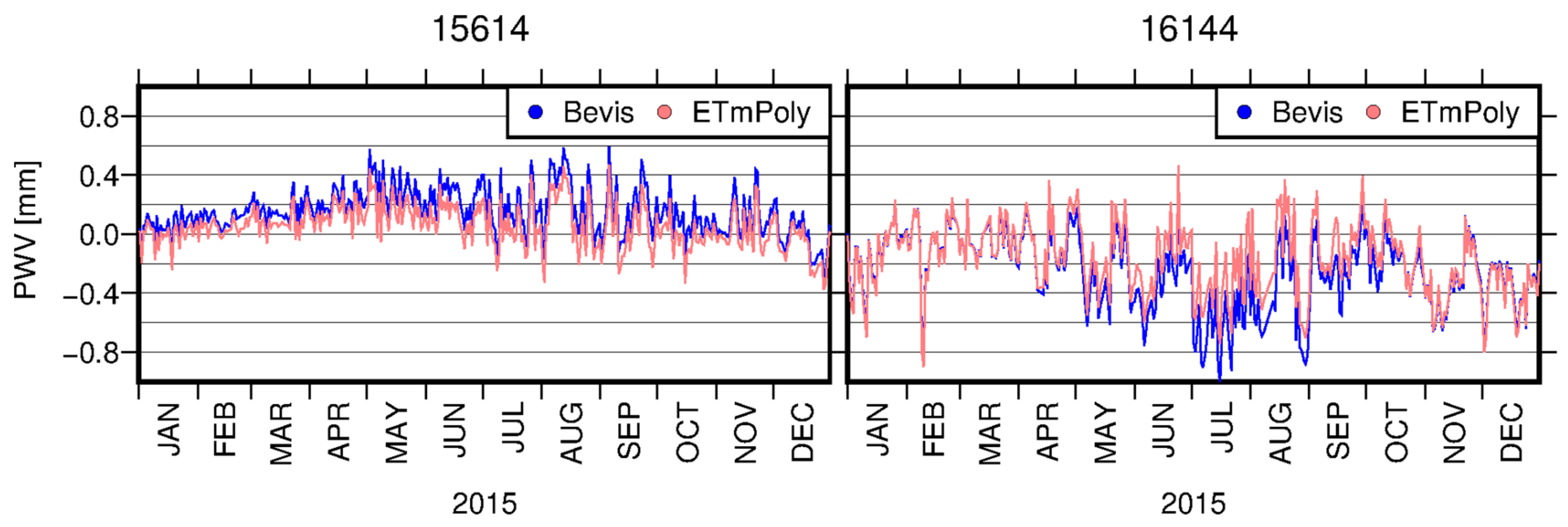
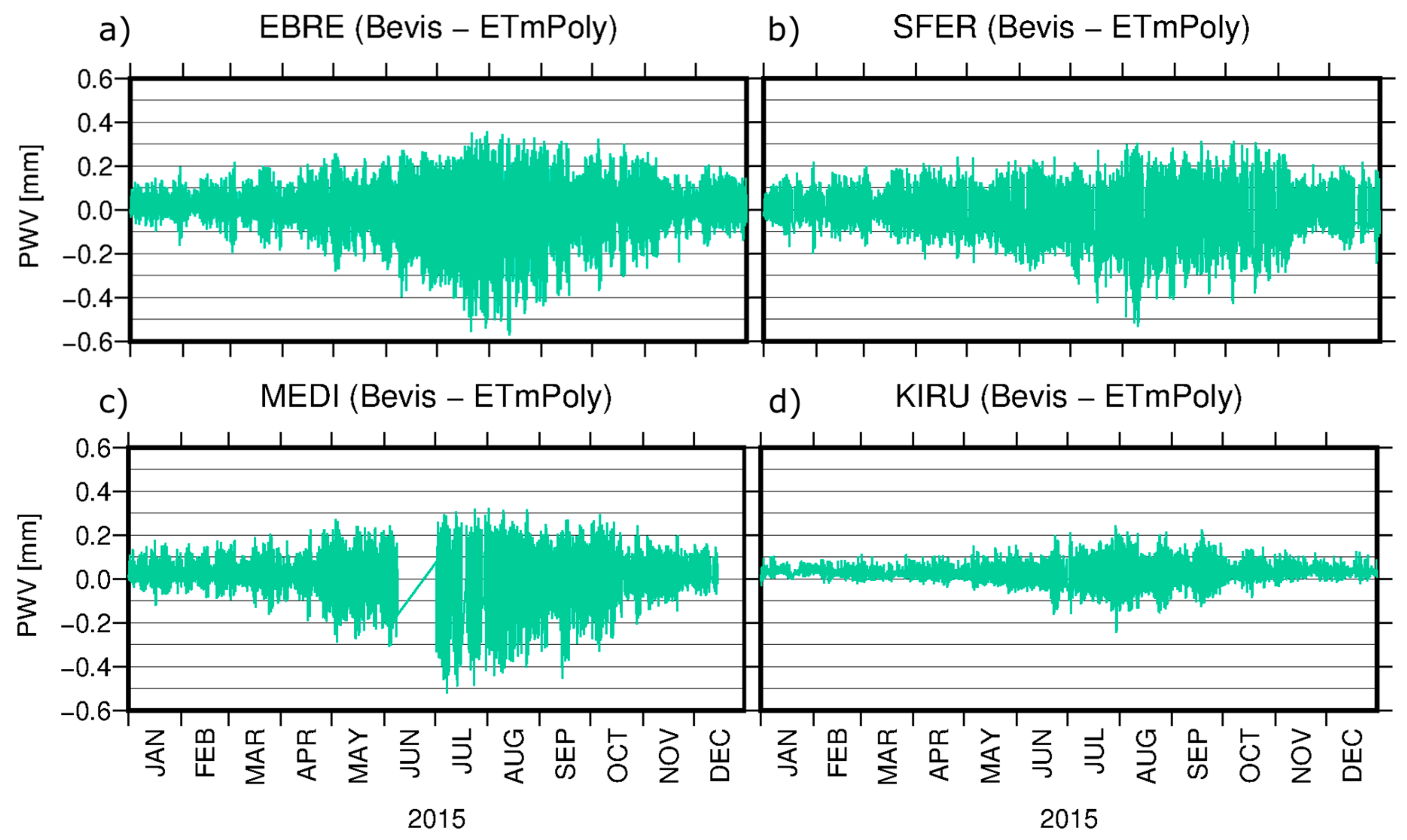
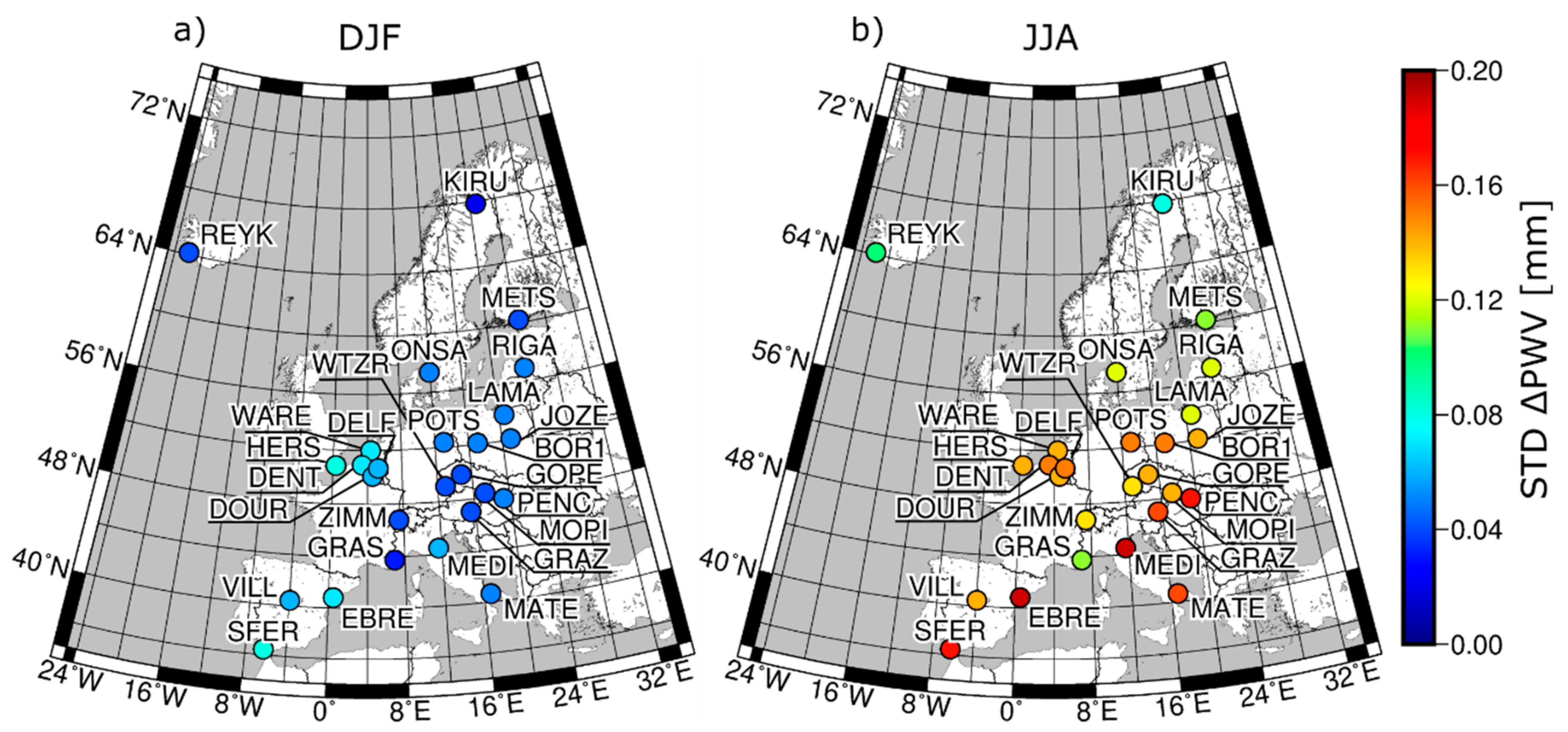
Each of the introduced models containing values of time-varying and coefficients represents higher accuracy than the Bevis model. For ETm2, ETm4, and ETmPoly we achieved accuracy at the level of 2.8 ± 0.4 K, 2.8 ± 0.4 K, and 2.8 ± 0.3 K, respectively, while in the case of Bevis model it was 3.1 ± 0.4. In addition to the RMSE, differences between the analyzed approaches can be found during estimation of the PWV value, especially based on GNSS data. We showed that although mean values of differences between, e.g., Bevis and ETmPoly coefficients may not be significant, applying these two models to the data with high temporal resolution results in discrepancies in PWV values up to 0.8 mm.
The most reliable results were obtained using ETmPoly coefficients. This is due to the fact that in addition to time-varying and coefficients, this model does not assume a linear character of the changes between main synoptic terms. Taking into account the daily variability of coefficients during the day by fitting the polynomial bring benefits and is especially important in GNSS meteorology, where time resolution of the observations is much higher than in case of RS.