Design and Analysis of a UWB MIMO Radar System with Miniaturized Vivaldi Antenna for Through-Wall Imaging
Abstract
1. Introduction
2. UWB MIMO Radar System
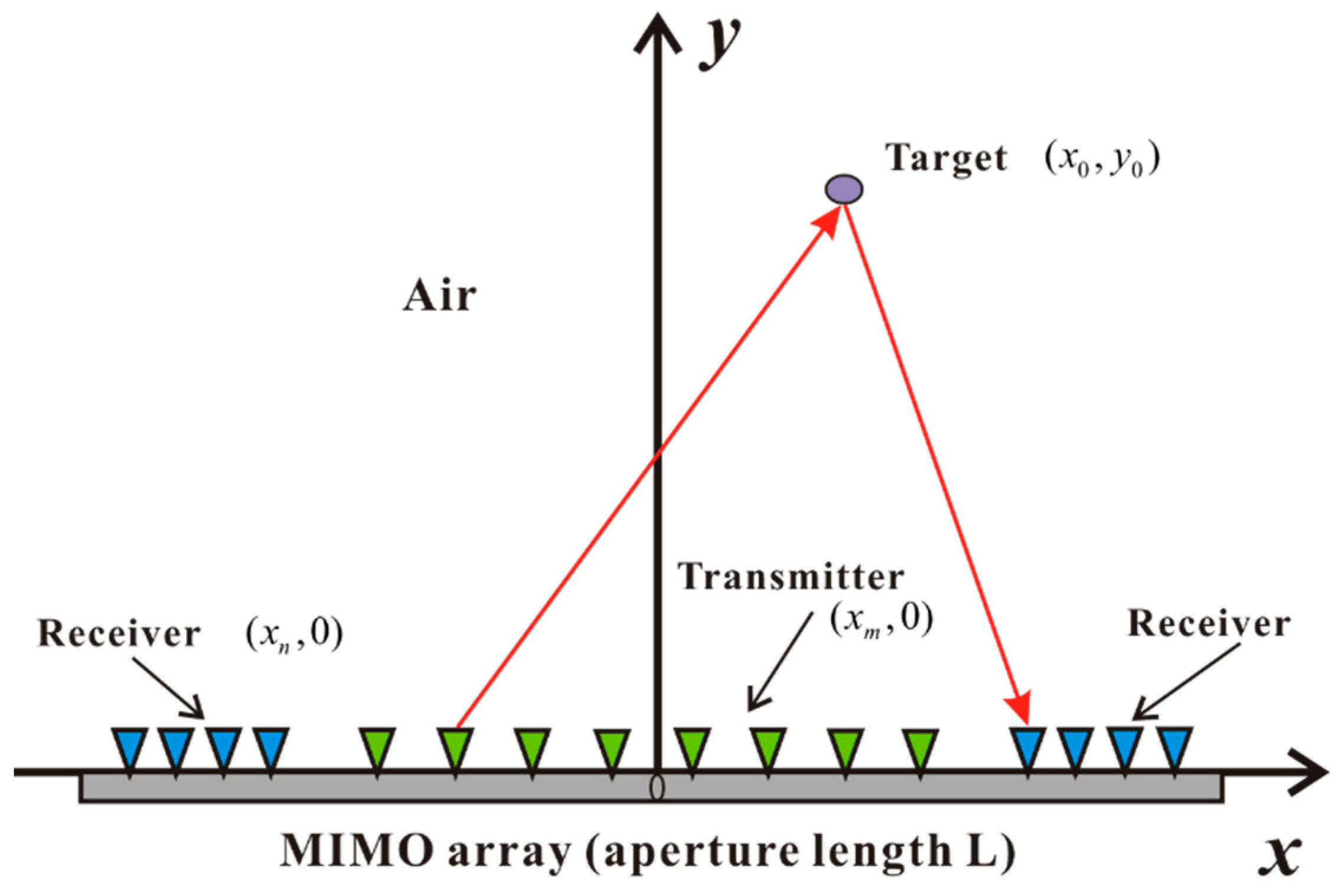
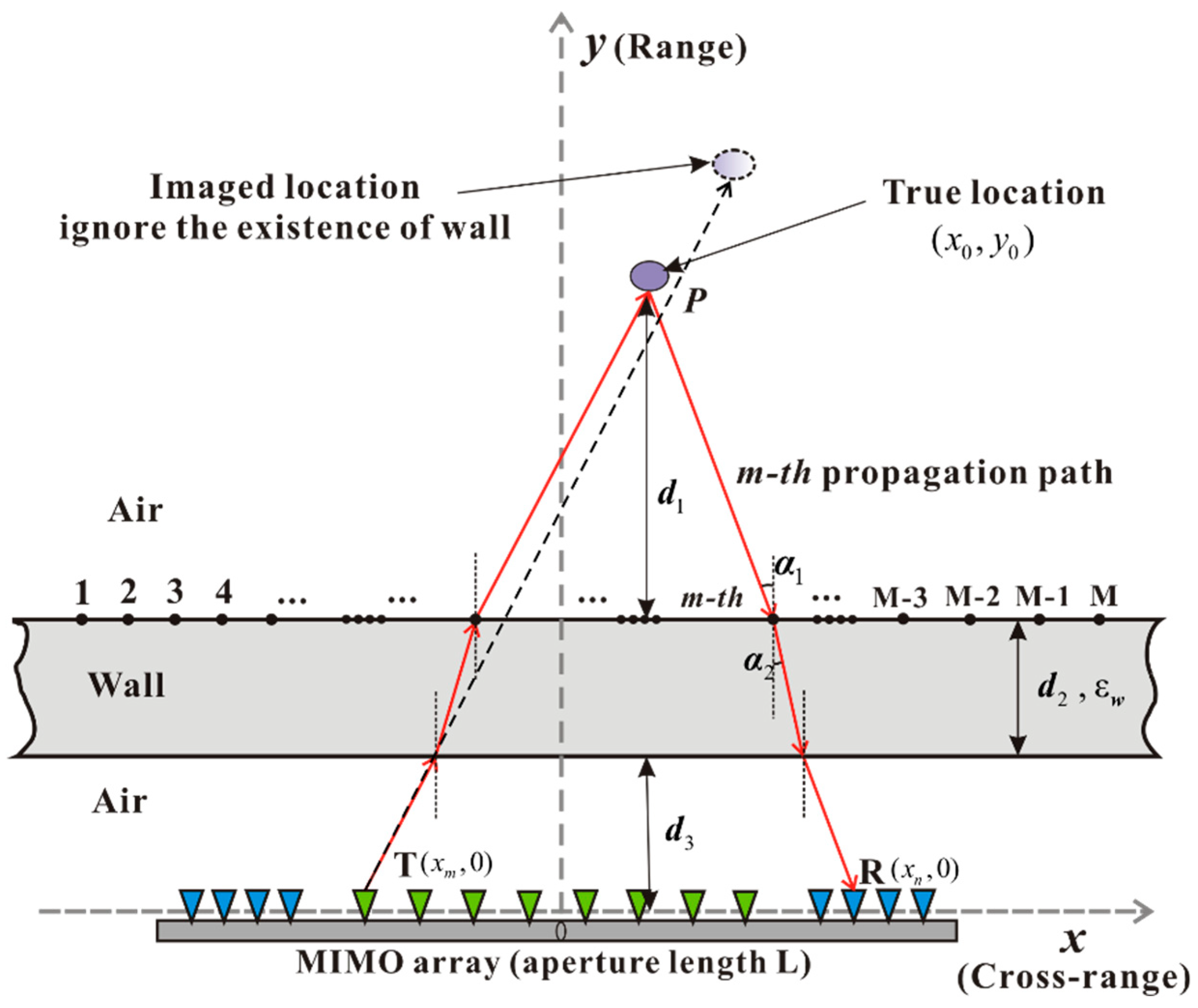
2.1. SFCW Signal Model and Conventional BP Algorithm
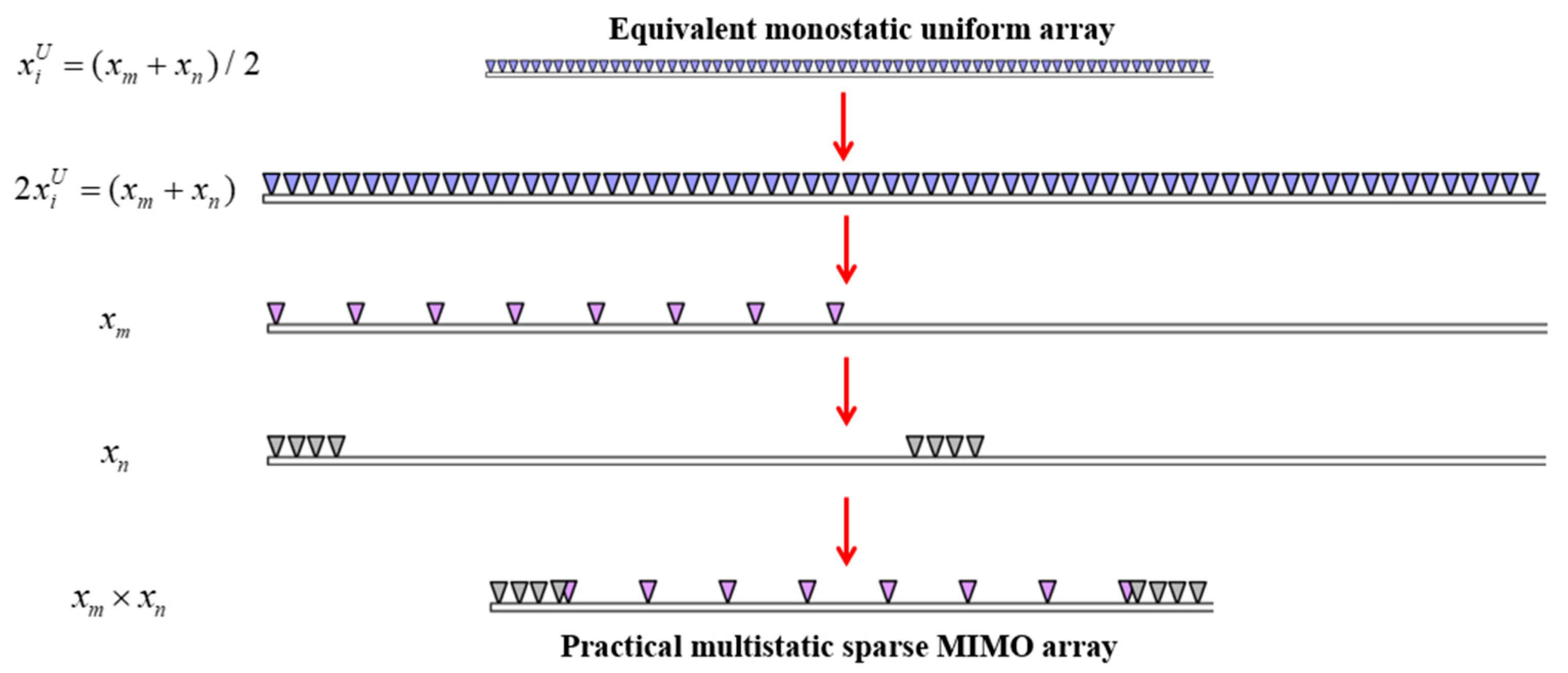
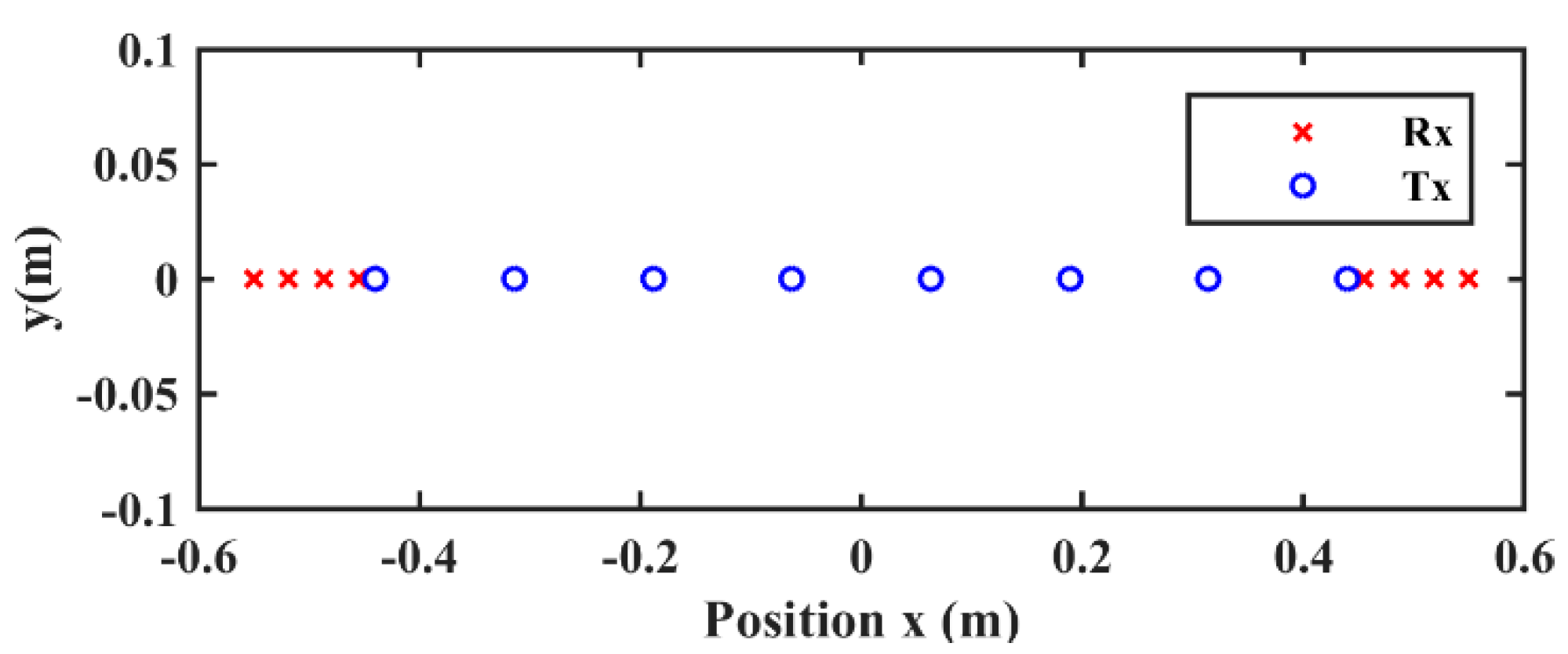
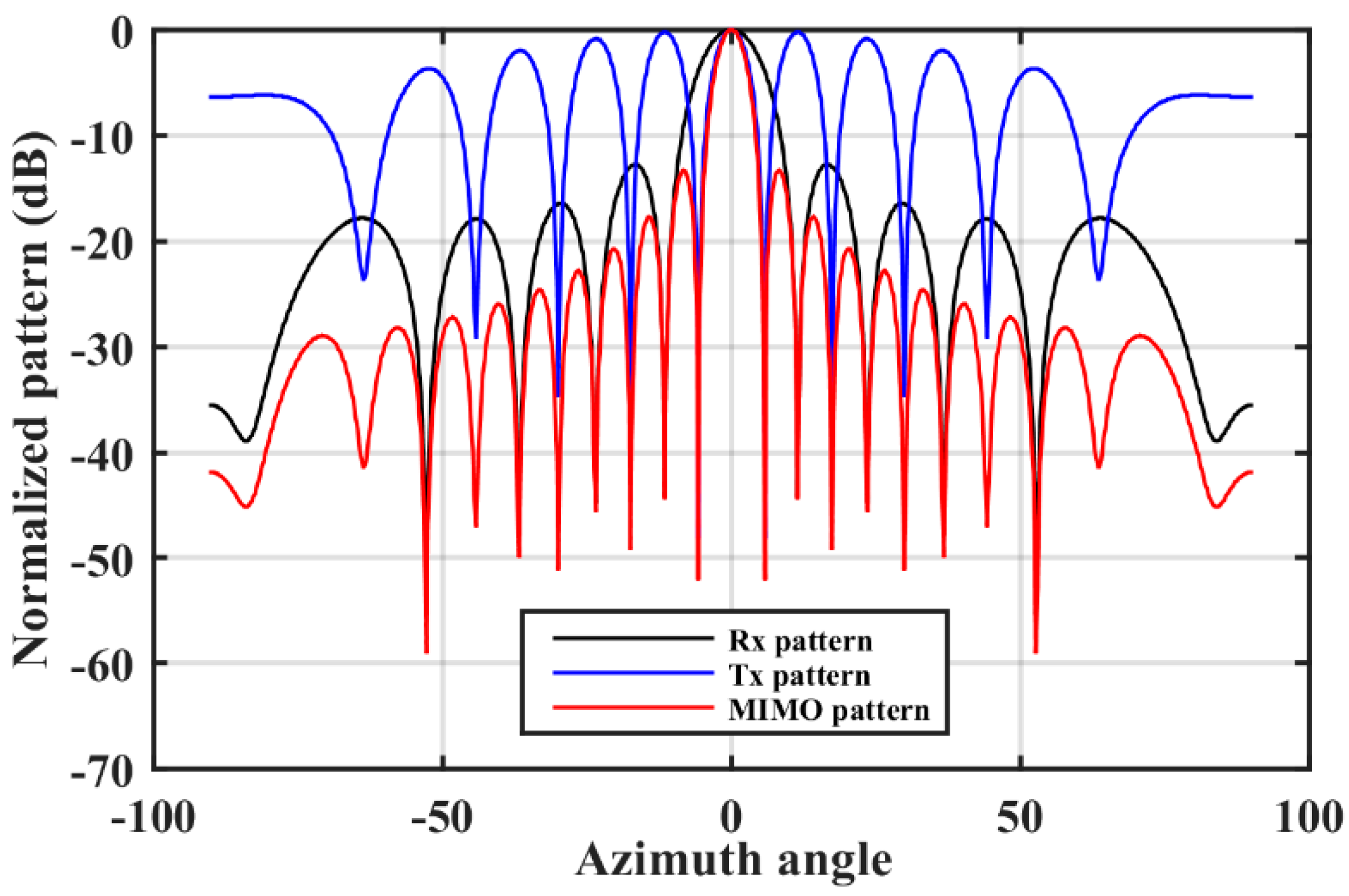
2.2. MIMO Array Topology Design
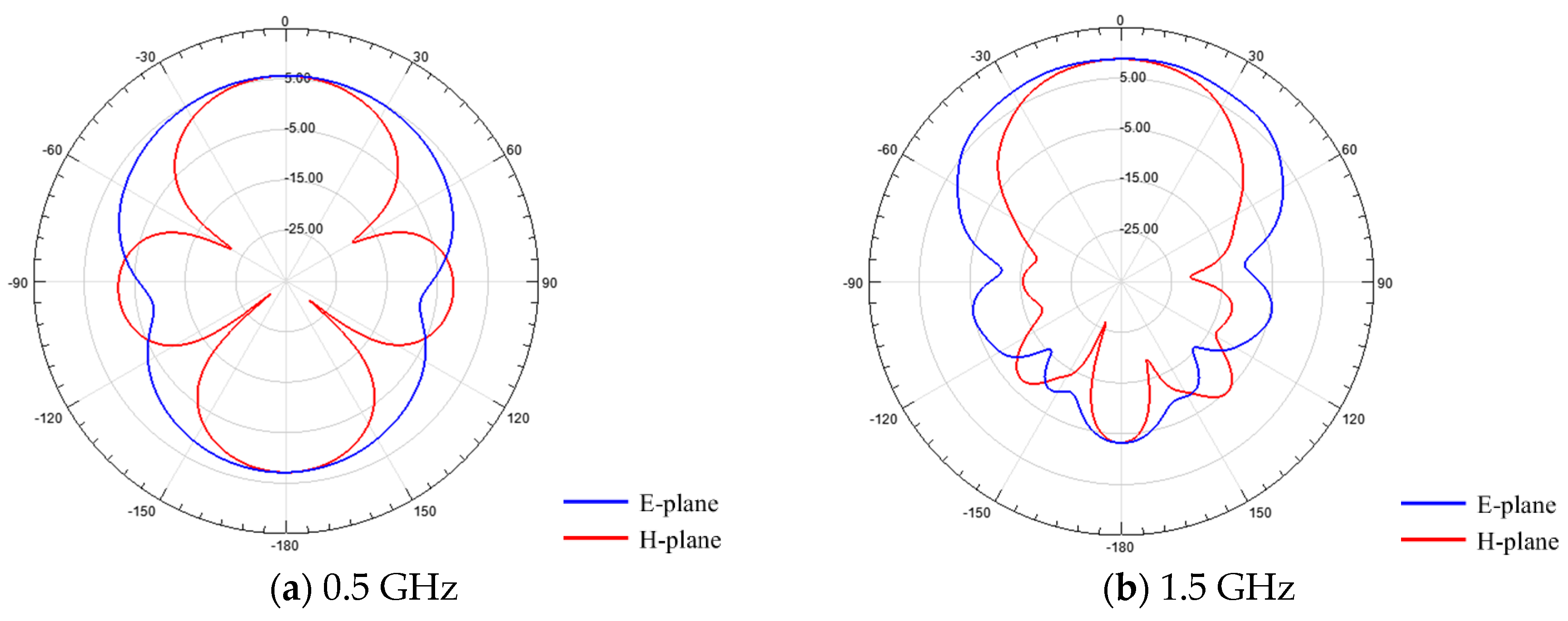
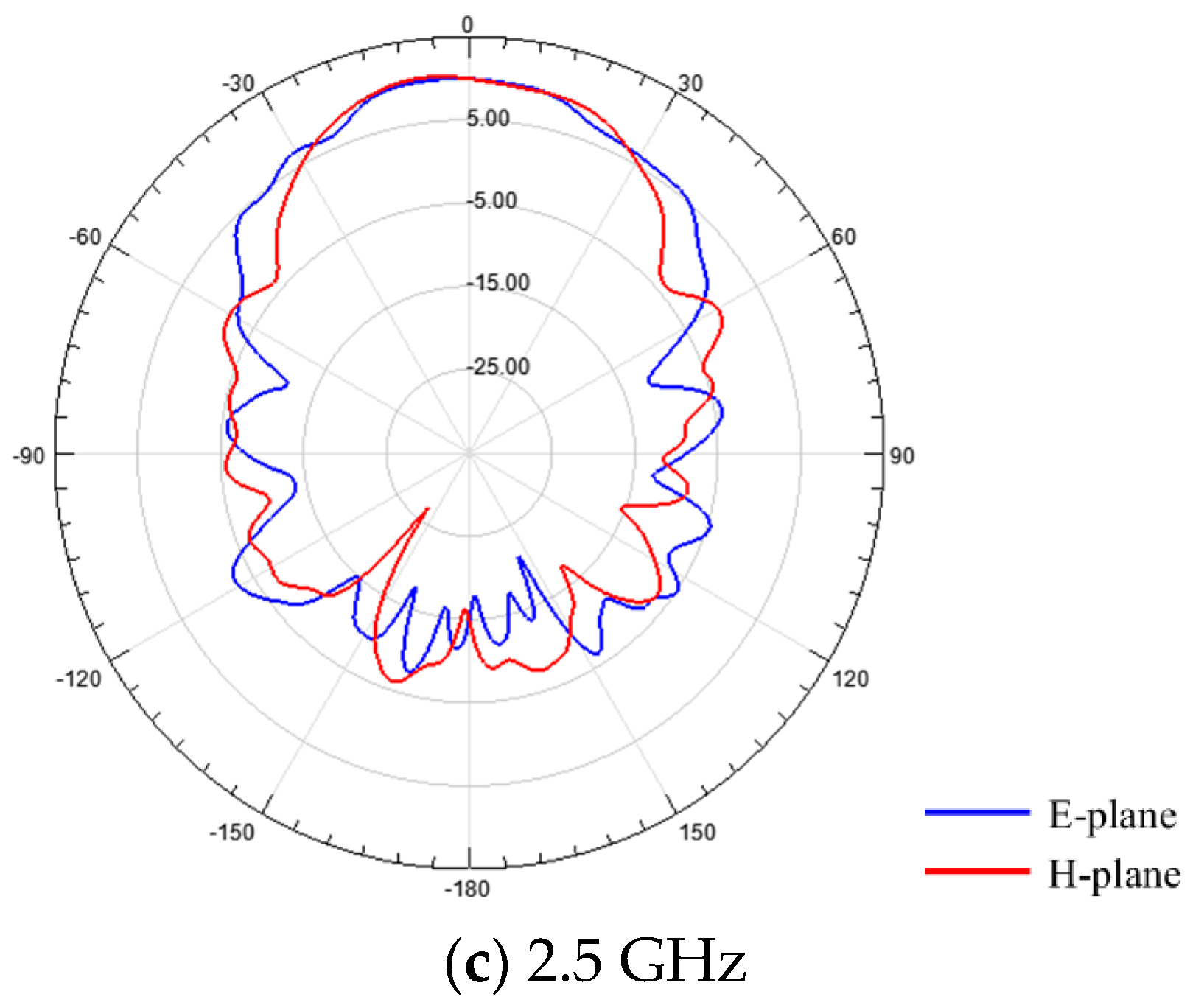
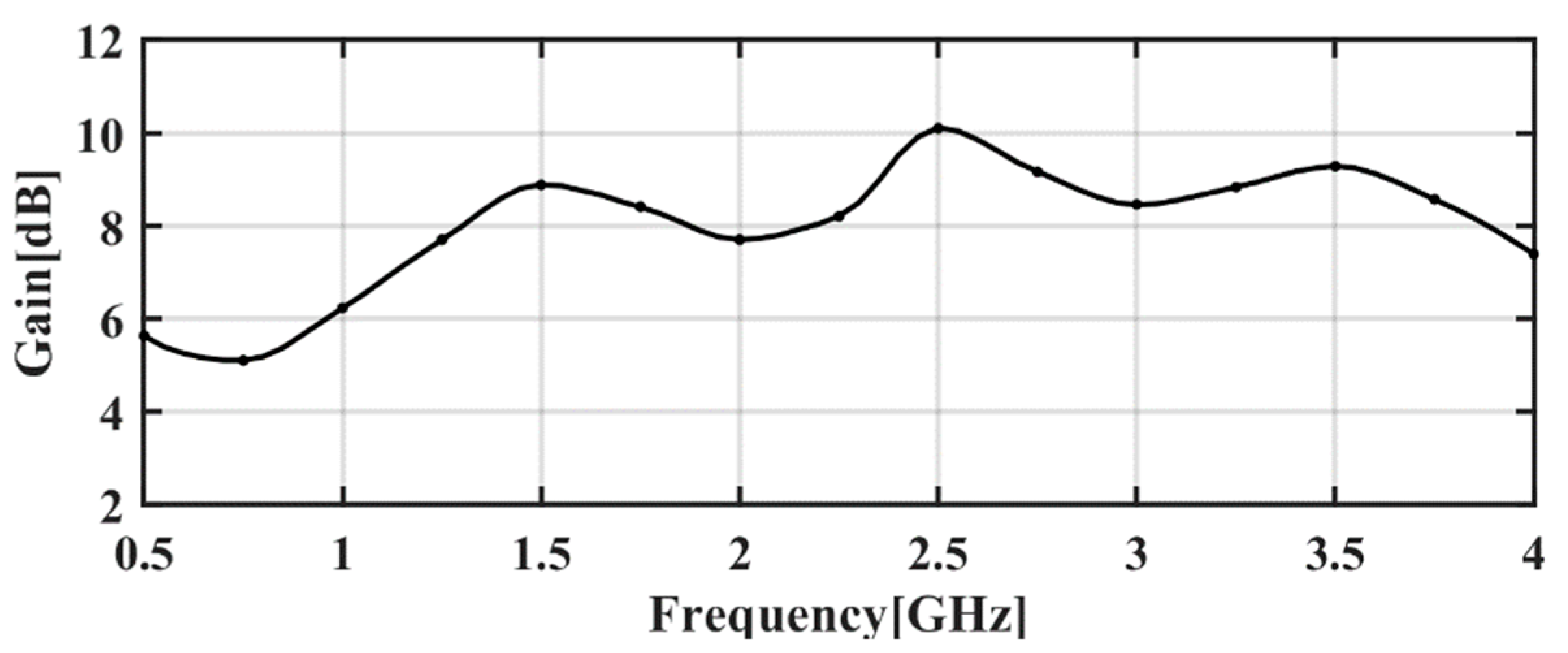
2.3. Low-Frequency UWB Miniaturized Vivaldi Antenna
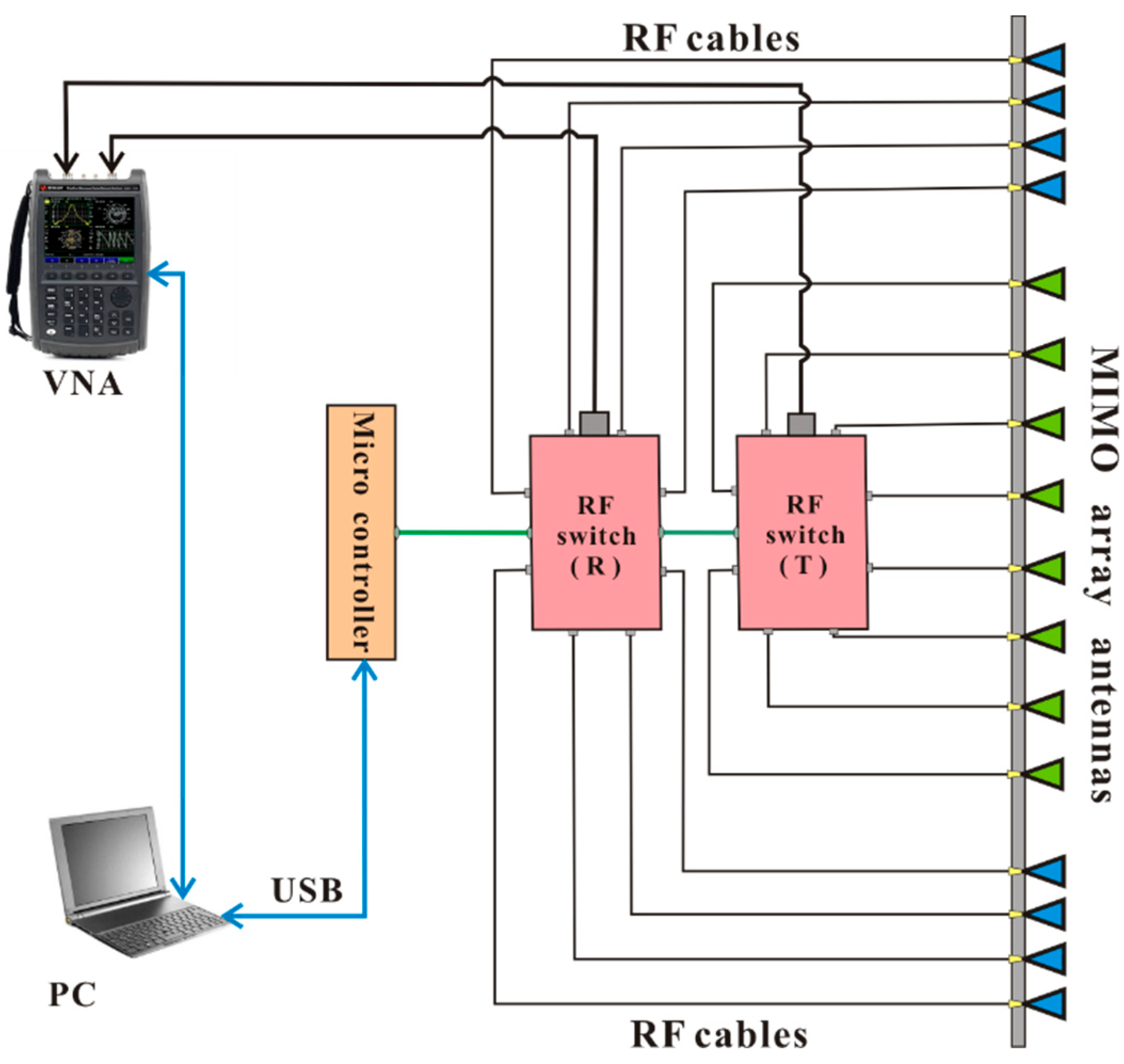
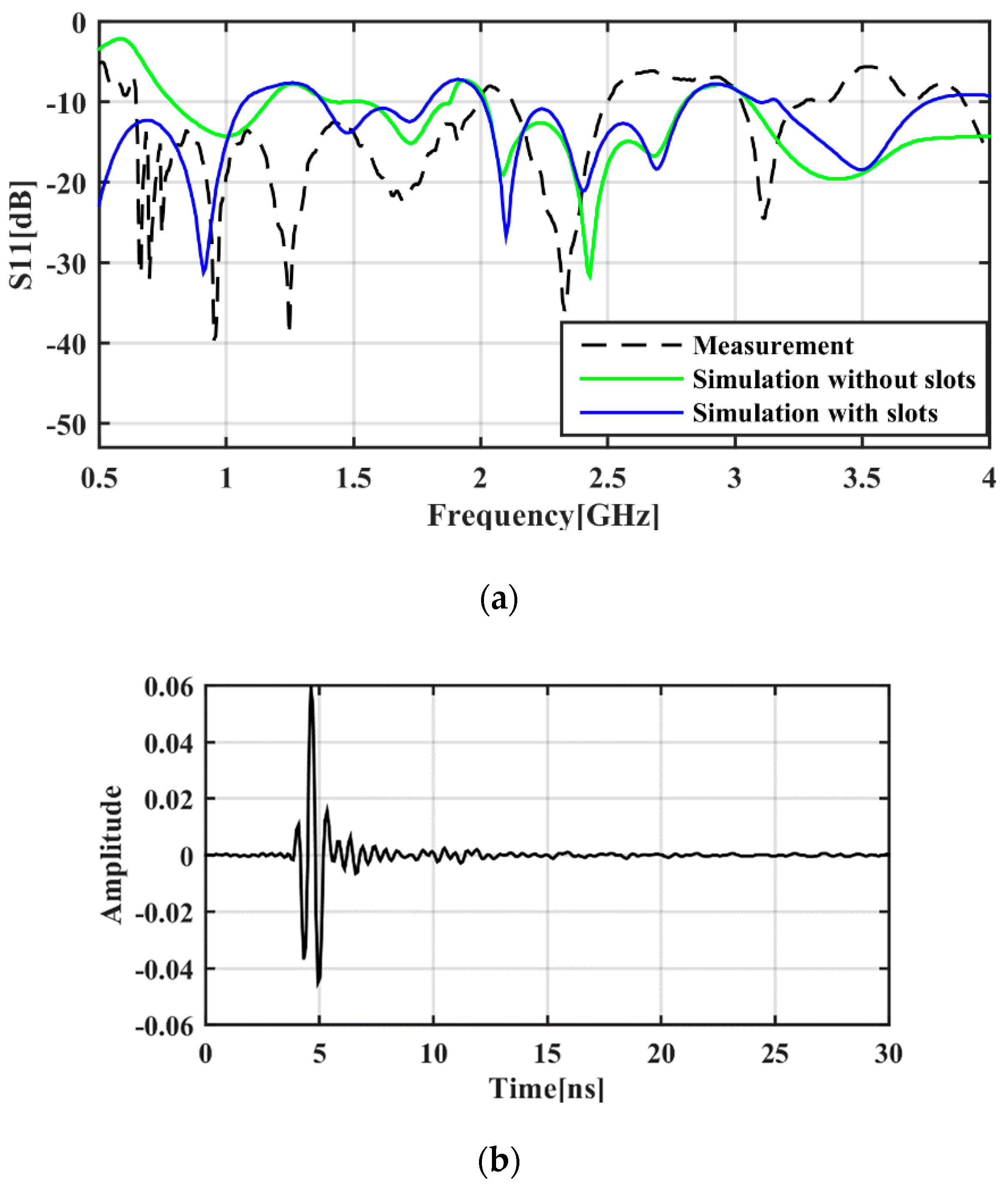
2.4. Radar Prototyping Result
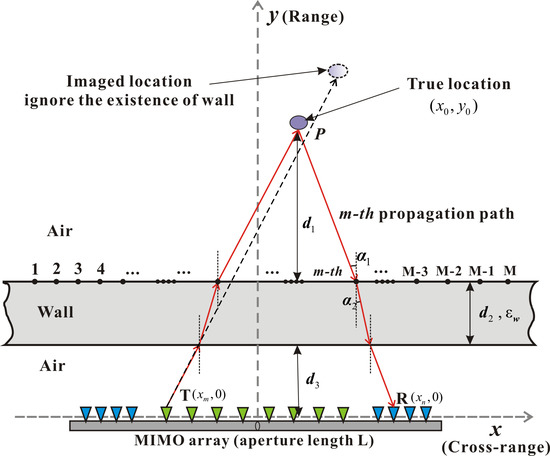
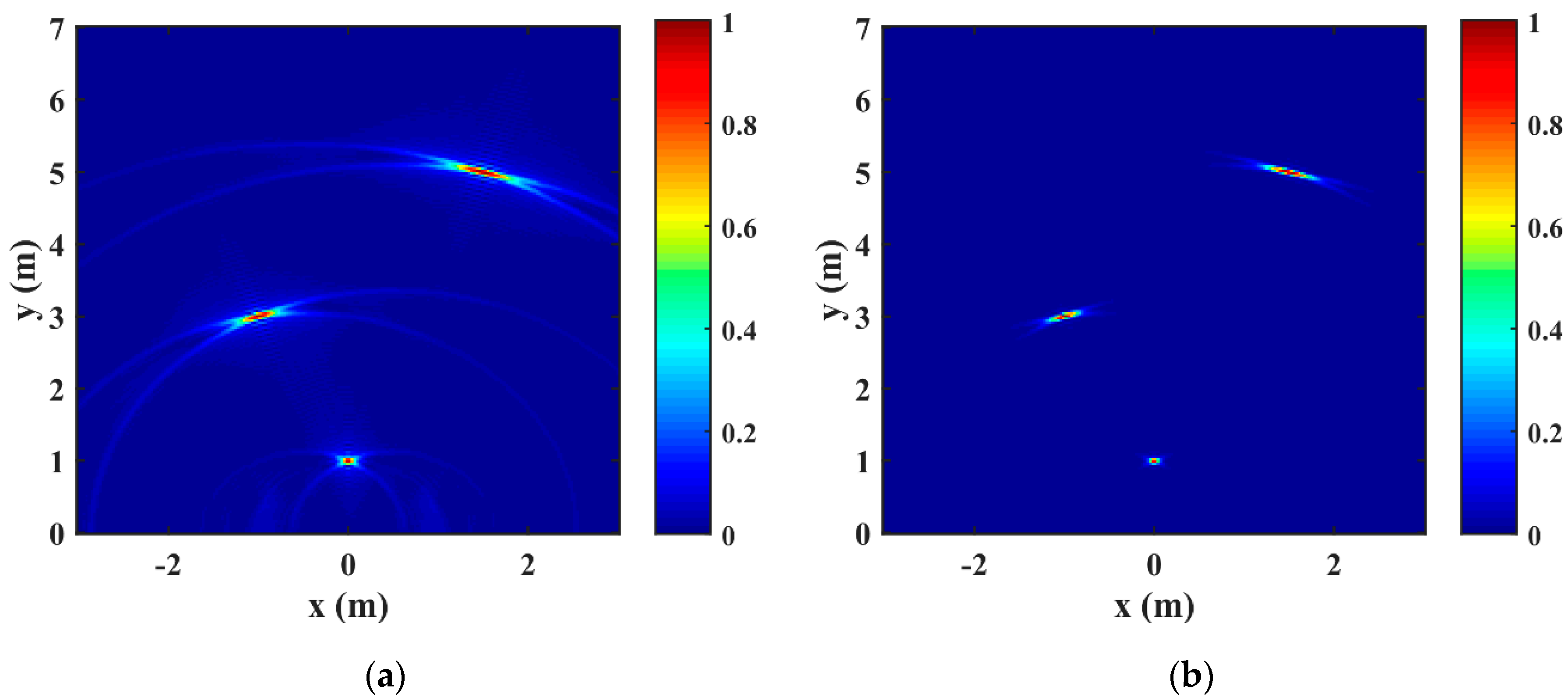
3. Through-Wall Imaging Method with the Improved BP-Based Algorithm
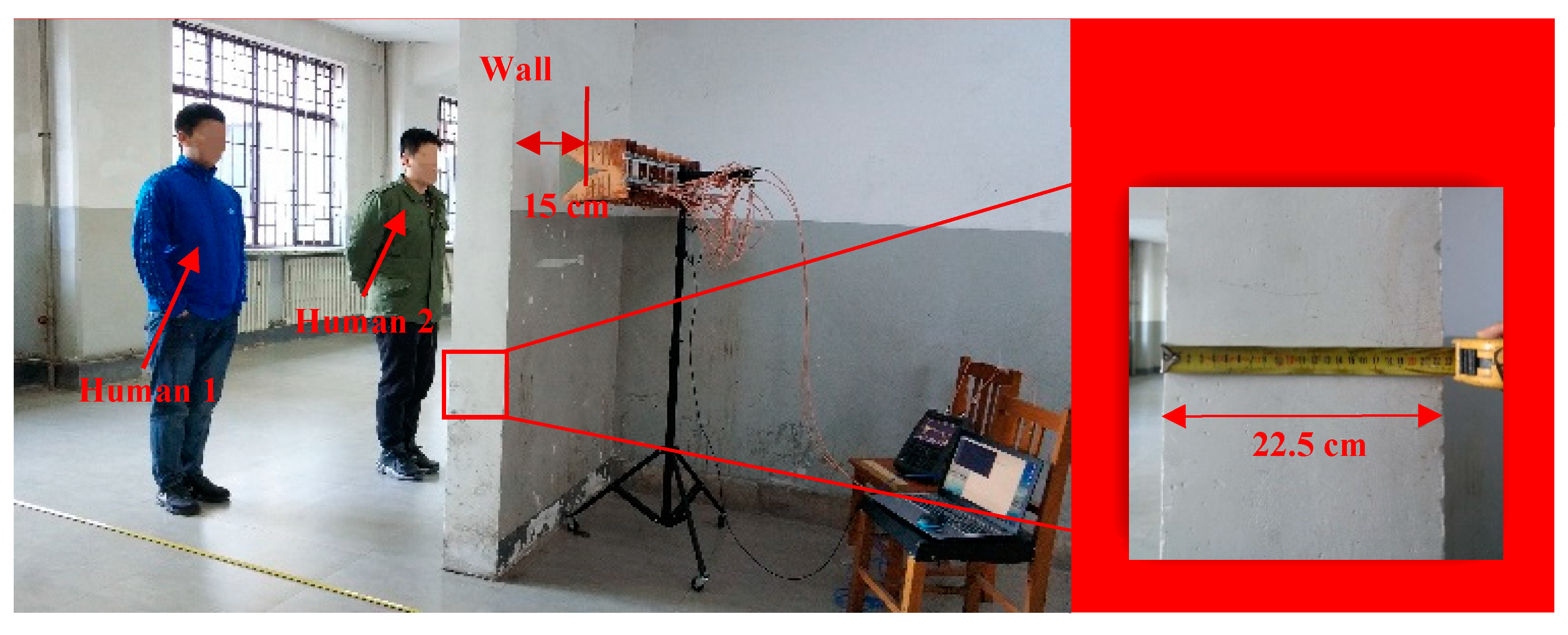
4. Experiment Results
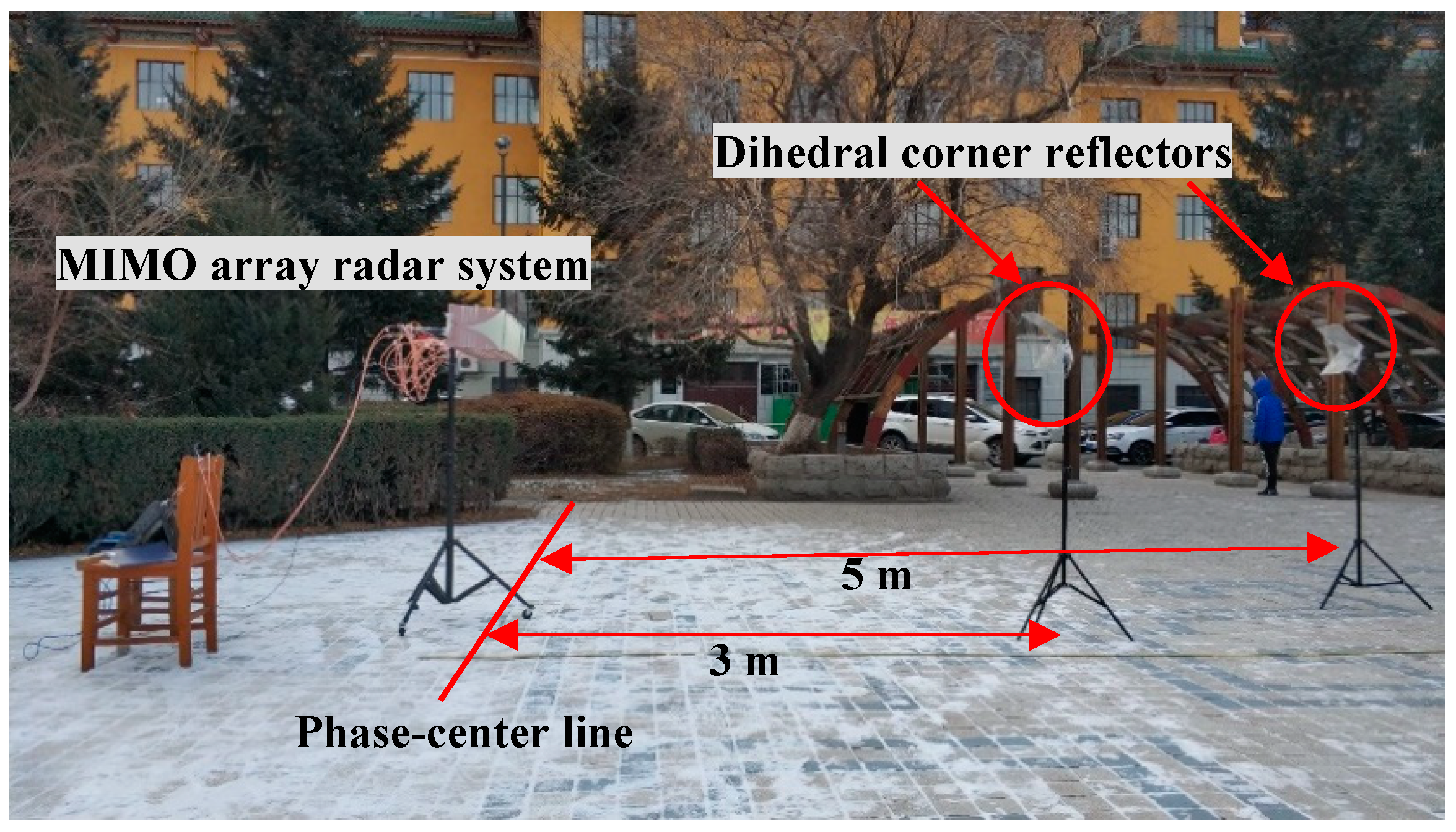
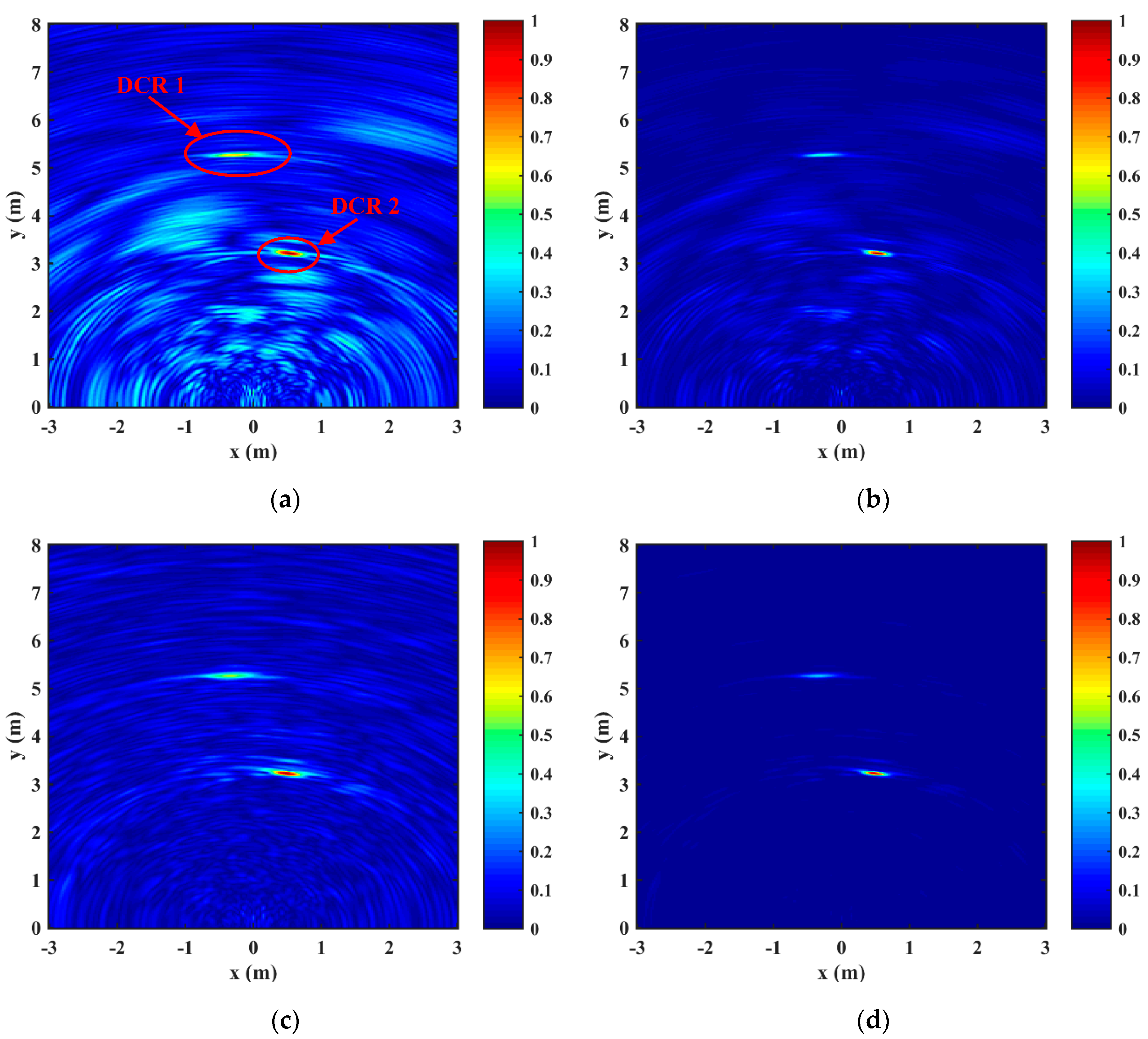
4.1. Preliminary Experimental Tests
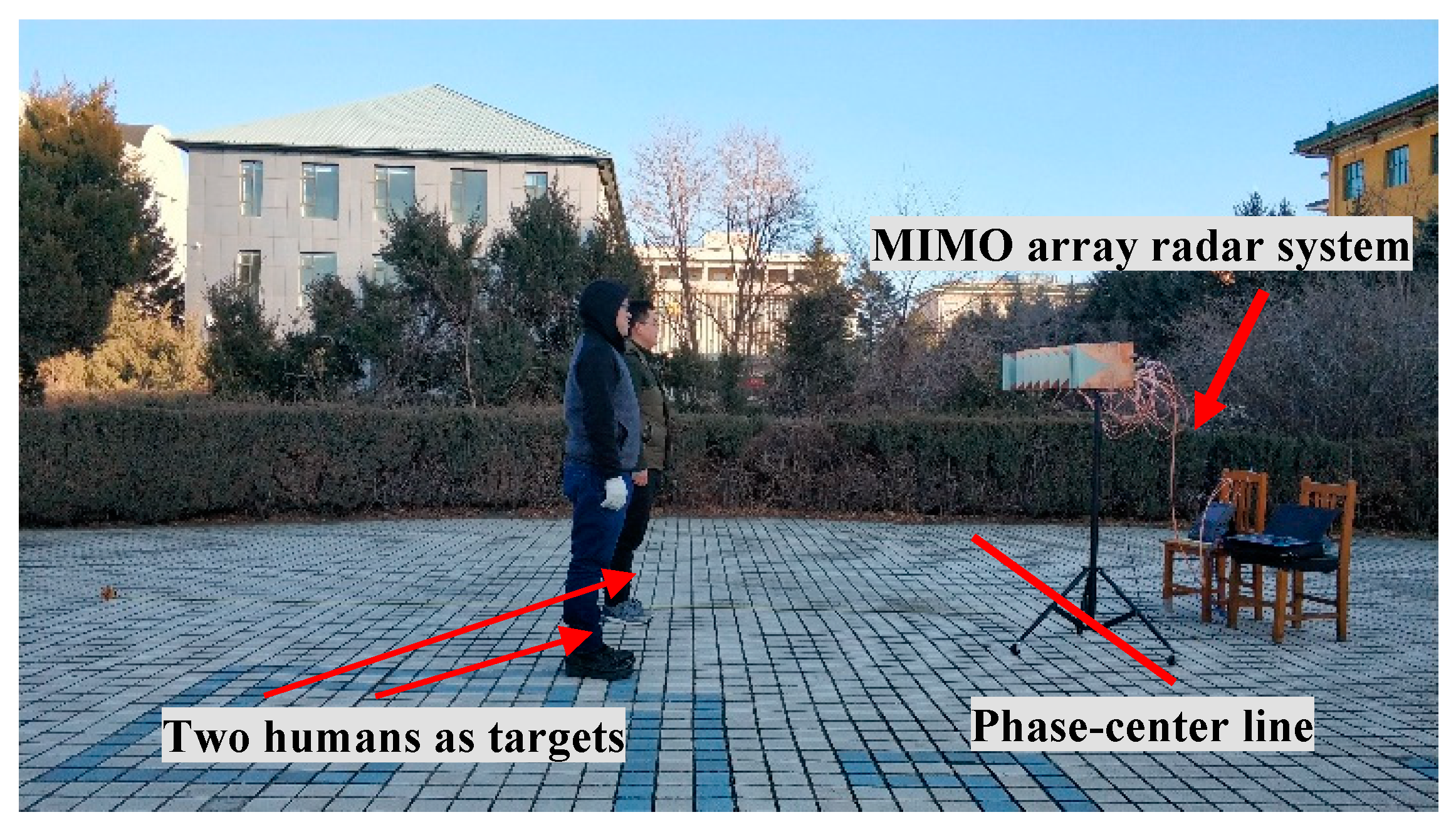
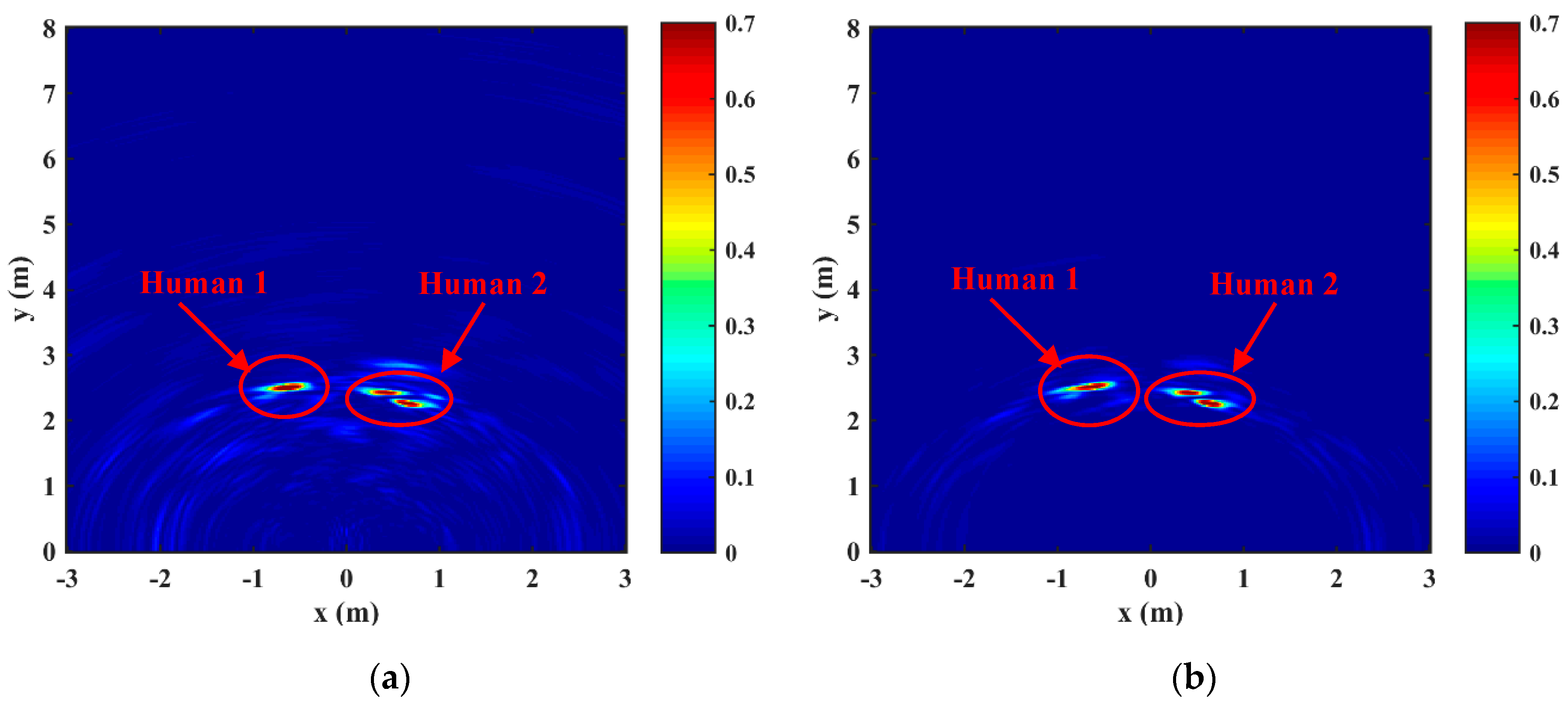
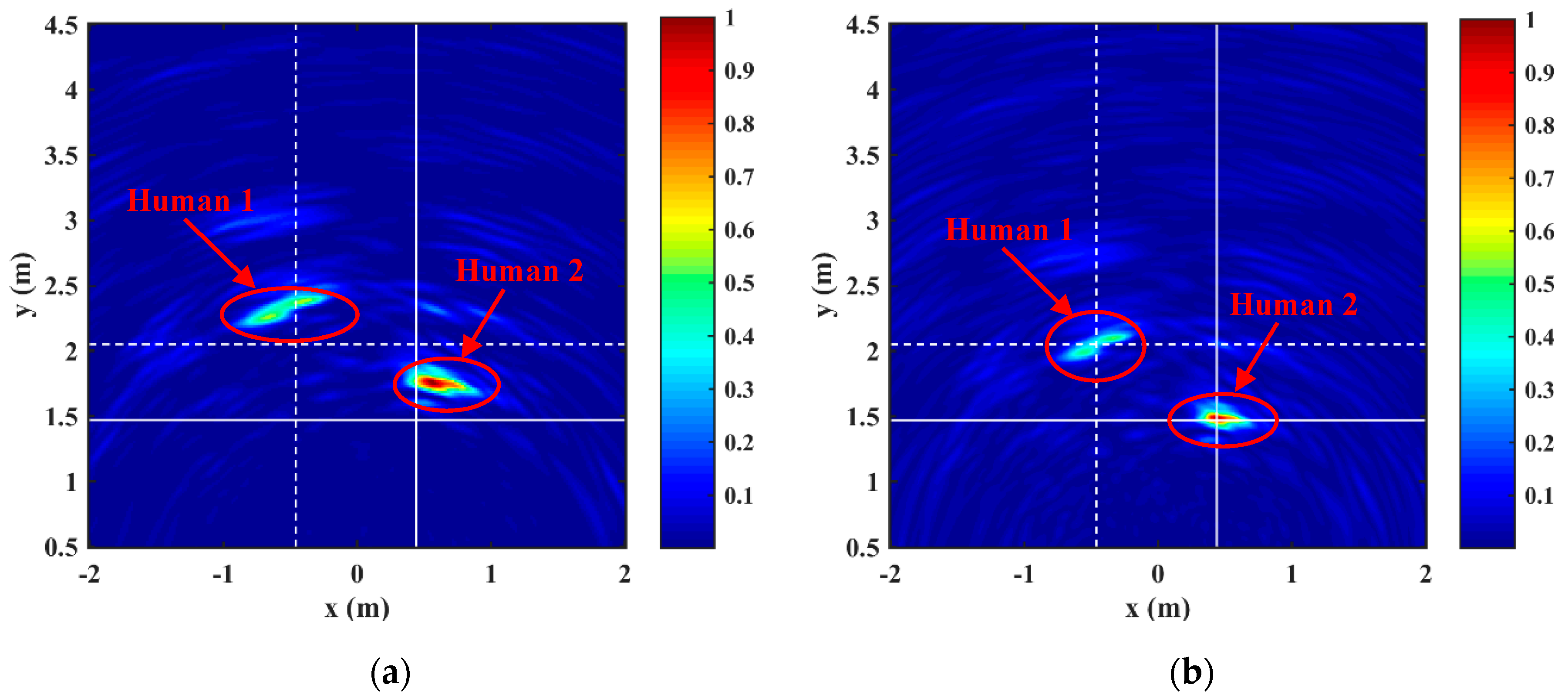
4.2. Through-Wall Experiment Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Amin, M.G. Through-the-Wall Radar Imaging; CRC Press: London, UK, 2011. [Google Scholar]
- Baranoski, E.J. Through-wall imaging: Historical perspective and future directions. J. Frankl. Inst. 2008, 345, 556–569. [Google Scholar] [CrossRef]
- Lan, F.; Kong, L.; Yang, X.; Jia, Y.; Ke, X. Life-sign detection of through-wall-radar based on fourth-order cumulant. In Proceedings of the 2013 IEEE Radar Conference, Ottawa, ON, Canada, 29 April–3 May 2013. [Google Scholar]
- Amin, M.G. Radar, signal, and image processing techniques for through the wall imaging. In Proceedings of the Digital Wireless Communications VII and Space Communication Technologies, Orlando, FL, USA, 2 June 2005. [Google Scholar]
- Nikolic, M.M.; Nehorai, A.; Djordjevic, A.R. Estimating moving targets behind reinforced walls using radar. IEEE Trans. Antennas Propag. 2009, 57, 3530–3538. [Google Scholar] [CrossRef]
- Yılmaz, B.; Özdemir, C. Design and prototype of radar sensor with Vivaldi linear array for through-wall radar imaging: An experimental study. J. Appl. Remote Sens. 2016, 10, 046012. [Google Scholar] [CrossRef]
- Ralston, T.S.; Charvat, G.L.; Peabody, J.E. Real-time through-wall imaging using an ultrawideband multiple-input multiple-output (MIMO) phased array radar system. In Proceedings of the 2010 IEEE international symposium on phased array systems and technology, Waltham, MA, USA, 12–15 October 2010. [Google Scholar]
- Guo, S.; Cui, G.; Kong, L.; Song, Y.; Yang, X. Multipath Analysis and Exploitation for MIMO Through-the-Wall Imaging Radar. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 3721–3731. [Google Scholar] [CrossRef]
- Wang, M.; Cui, G.; Yi, W.; Kong, L.; Yang, X.; Yuan, L. Time-division MIMO through-the-wall radar imaging behind multiple walls. In Proceedings of the 2015 IEEE Radar Conference, Arlington, VA, USA, 10–15 May 2015. [Google Scholar]
- Dehmollaian, M.; Thiel, M.; Sarabandi, K. Through-the-wall imaging using differential SAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1289–1296. [Google Scholar] [CrossRef]
- Laviada, J.; Arboleya, A.; López-Gayarre, F.; Las-Heras, F. Broadband synthetic aperture scanning system for three-dimensional through-the-wall inspection. IEEE Geosci. Remote Sens. Lett. 2015, 13, 97–101. [Google Scholar] [CrossRef]
- Yang, J.; Thompson, J.; Huang, X.; Jin, T.; Zhou, Z. Random-frequency SAR imaging based on compressed sensing. IEEE Trans. Geosci. Remote Sens. 2013, 51, 983–994. [Google Scholar] [CrossRef]
- Jin, T.; Chen, B.; Zhou, Z. Image-domain estimation of wall parameters for autofocusing of through-the-wall SAR imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1836–1843. [Google Scholar] [CrossRef]
- Bliss, D.W.; Forsythe, K.W. Multiple-input multiple-output (MIMO) radar and imaging: Degrees of freedom and resolution. In Proceedings of the Thrity-Seventh Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 9–12 November 2003. [Google Scholar]
- Fishler, E.; Haimovich, A.; Blum, R.; Chizhik, D.; Cimini, L.; Valenzuela, R. MIMO radar: An idea whose time has come. In Proceedings of the 2004 IEEE radar conference, Philadelphia, PA, USA, 29 April 2004. [Google Scholar]
- Narayanan, R.M.; Gebhardt, E.T.; Broderick, S.P. Through-Wall Single and Multiple Target Imaging Using MIMO Radar. Electronics 2017, 6, 70. [Google Scholar] [CrossRef]
- Pieraccini, M.; Miccinesi, L. An Interferometric MIMO Radar for Bridge Monitoring. IEEE Geosci. Remote Sens. Lett. 2019, 1–5. [Google Scholar] [CrossRef]
- Zhuge, X.; Yarovoy, A.G. Sparse multiple-input multiple-output arrays for high-resolution near-field ultra-wideband imaging. IET Microw. Antennas Propag. 2011, 5, 1552–1562. [Google Scholar] [CrossRef]
- Zhuge, X. Short-Range Ultra-Wideband Imaging with Multiple-Input Multiple-Output Arrays. Ph.D. Thesis, Delft University Technology (TUDelft), Delft, The Netherlands, 2010. [Google Scholar]
- Feng, W.; Zou, L.; Sato, M. 2D imaging by sparse array radar system. IEICE Tech. Rep. 2016, 116, 65–70. [Google Scholar]
- Schwartz, J.L.; Steinberg, B.D. Ultrasparse, ultrawideband arrays. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 376–393. [Google Scholar] [CrossRef] [PubMed]
- Maaref, N.; Millot, P. Array-based UWB FMCW through-the-wall radar. In Proceedings of the 2012 IEEE International Symposium on Antennas and Propagation, Chicago, IL, USA, 8–14 July 2012. [Google Scholar]
- Fioranelli, F.; Salous, S.; Ndip, I.; Raimundo, X. Through-the-wall detection with gated FMCW signals using optimized patch-like and Vivaldi antennas. IEEE Trans. Antennas Propag. 2015, 63, 1106–1117. [Google Scholar] [CrossRef]
- Gibson, P.J. The vivaldi aerial. In Proceedings of the 1979 9th European Microwave Conference, Brighton, UK, 17–20 September 1979. [Google Scholar]
- Fei, P.; Jiao, Y.C.; Hu, W.; Zhang, F.S. A miniaturized antipodal Vivaldi antenna with improved radiation characteristics. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 127–130. [Google Scholar]
- Rizk, J.B.; Rebeiz, G.M. Millimeter-wave Fermi tapered slot antennas on micromachined silicon substrates. IEEE Trans. Antennas Propag. 2002, 50, 379–383. [Google Scholar] [CrossRef]
- Feng, W.; Yi, L.; Sato, M. Near range radar imaging based on block sparsity and cross-correlation fusion algorithm. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2018, 11, 2079–2089. [Google Scholar] [CrossRef]
- Zhou, L.; Huang, C.; Su, Y. A fast back-projection algorithm based on cross correlation for GPR imaging. IEEE Geosci. Remote Sens. Lett. 2012, 9, 228–232. [Google Scholar] [CrossRef]
- Gumbmann, F.; Tran, P.; Schmidt, L.P. Sparse linear array design for a short range imaging radar. In Proceedings of the 2009 European Radar Conference, Rome, Italy, 30 September–2 October 2009. [Google Scholar]
- Ge, T.; Zhao, L.; Cai, Y.; Zhou, J. A grating lobes suppression technique for near-field sparse linear MIMO array imaging. In Proceedings of the 2016 CIE International Conference on Radar, Guangzhou, China, 10–13 October 2016. [Google Scholar]
- Jin, L.; Ouyang, S.; Zhou, L. Array design and imaging method for ultra-wideband multiple-input multiple-output through-the-wall radar. J. Electron. Inf. Technol. 2012, 34, 1574–1580. (In Chinese) [Google Scholar] [CrossRef]
- Fishler, E.; Haimovich, A.; Blum, R.; Cimini, L.; Chizhik, D.; Valenzuela, R. Spatial diversity in radars-models and detection performance. IEEE Trans. Signal Process. 2006, 54, 823–838. [Google Scholar] [CrossRef]
- Bellettini, A.; Pinto, M.A. Theoretical accuracy of synthetic aperture sonar micronavigation using a displaced phase-center antenna. IEEE J. Ocean. Eng. 2002, 27, 780–789. [Google Scholar] [CrossRef]
- Teni, G.; Zhang, N.; Qiu, J.; Zhang, P. Research on a novel miniaturized antipodal Vivaldi antenna with improved radiation. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 417–420. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, S.; Shi, Z.; Chen, Y. A miniaturized wideband dual-polarized linear array with balanced antipodal Vivaldi antenna. In Proceedings of the 2016 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Chengdu, China, 20–22 July 2016. [Google Scholar]
- Yang, Y.; Wang, Y.; Fathy, A.E. Design of compact Vivaldi antenna arrays for UWB see through wall applications. Prog. Electromagn. Res. 2008, 82, 401–418. [Google Scholar] [CrossRef]
- Wang, K.; Zeng, Z.; Sun, J. Through-Wall Detection of the Moving Paths and Vital Signs of Human Beings. IEEE Geosci. Remote Sens. Lett. 2018, 16, 717–721. [Google Scholar] [CrossRef]
- Song, Y.; Hu, J.; Chu, N.; Jin, T.; Zhang, J.; Zhou, Z. Building Layout Reconstruction in Concealed Human Target Sensing via UWB MIMO Through-Wall Imaging Radar. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1199–1203. [Google Scholar]
- Qi, F.; Liang, F.; Lv, H.; Li, C.; Chen, F.; Wang, J. Detection and Classification of Finer-Grained Human Activities Based on Stepped-Frequency Continuous-Wave Through-Wall Radar. Sensors 2016, 16, 885. [Google Scholar] [CrossRef] [PubMed]
- Gennarelli, G.; Ludeno, G.; Soldovieri, F. Real-Time Through-Wall Situation Awareness Using a Microwave Doppler Radar Sensor. Remote Sens. 2016, 8, 621. [Google Scholar] [CrossRef]
- Ma, Y.; Hong, H.; Zhu, X. Interaction Multipath in Through-the-Wall Radar Imaging Based on Compressive Sensing. Sensors 2018, 18, 549. [Google Scholar]



| Parameters | Value |
|---|---|
| Start frequency | 0.4 GHz |
| Stop frequency | 2.6 GHz |
| Number of frequencies | 256 |
| Number of transmitters/receivers | 8/8 |
| Range resolution | 0.068 m |
| Azimuth resolution | 5.8 rad |
| Maximum range | 17.4 m |
| Length of aperture | 1.1 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Zeng, Z.; Wang, K.; Feng, W.; Zhang, J.; Lu, Q.; Kang, X. Design and Analysis of a UWB MIMO Radar System with Miniaturized Vivaldi Antenna for Through-Wall Imaging. Remote Sens. 2019, 11, 1867. https://doi.org/10.3390/rs11161867
Hu Z, Zeng Z, Wang K, Feng W, Zhang J, Lu Q, Kang X. Design and Analysis of a UWB MIMO Radar System with Miniaturized Vivaldi Antenna for Through-Wall Imaging. Remote Sensing. 2019; 11(16):1867. https://doi.org/10.3390/rs11161867
Chicago/Turabian StyleHu, Zhipeng, Zhaofa Zeng, Kun Wang, Weike Feng, Jianmin Zhang, Qi Lu, and Xiaoqian Kang. 2019. "Design and Analysis of a UWB MIMO Radar System with Miniaturized Vivaldi Antenna for Through-Wall Imaging" Remote Sensing 11, no. 16: 1867. https://doi.org/10.3390/rs11161867
APA StyleHu, Z., Zeng, Z., Wang, K., Feng, W., Zhang, J., Lu, Q., & Kang, X. (2019). Design and Analysis of a UWB MIMO Radar System with Miniaturized Vivaldi Antenna for Through-Wall Imaging. Remote Sensing, 11(16), 1867. https://doi.org/10.3390/rs11161867