Stepwise Disaggregation of SMAP Soil Moisture at 100 m Resolution Using Landsat-7/8 Data and a Varying Intermediate Resolution
Abstract
1. Introduction
2. Materials and Methods
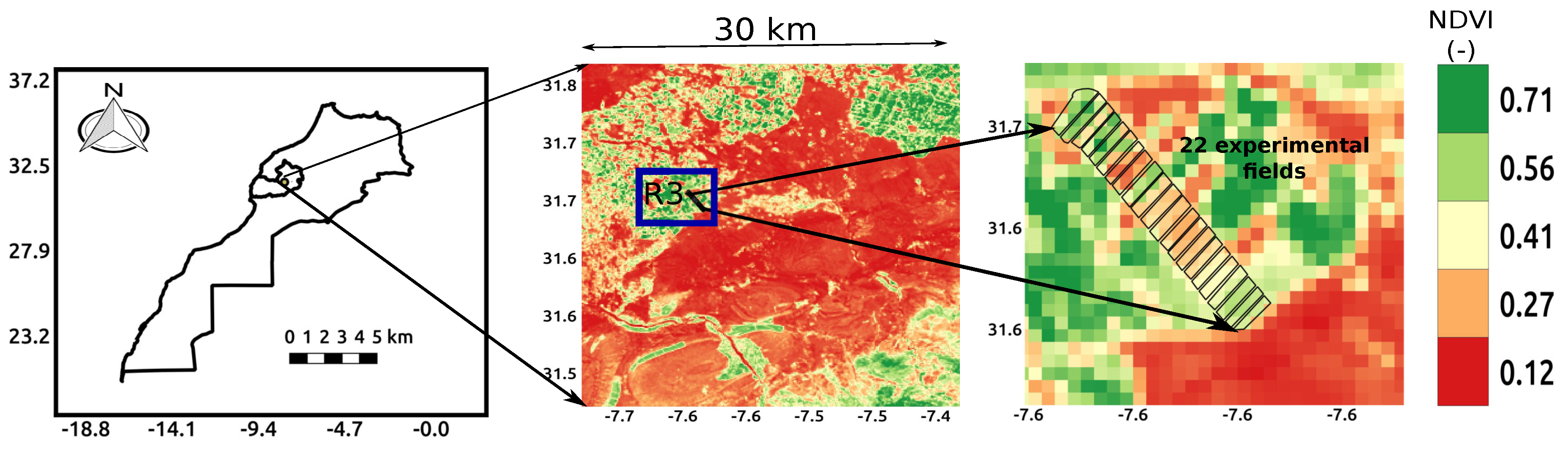
2.1. Study Area
2.2. In-Situ Data
2.3. Remote Sensing Data
2.3.1. SMAP
2.3.2. MODIS
2.3.3. Landsat
2.3.4. SRTM
2.4. DISPATCH
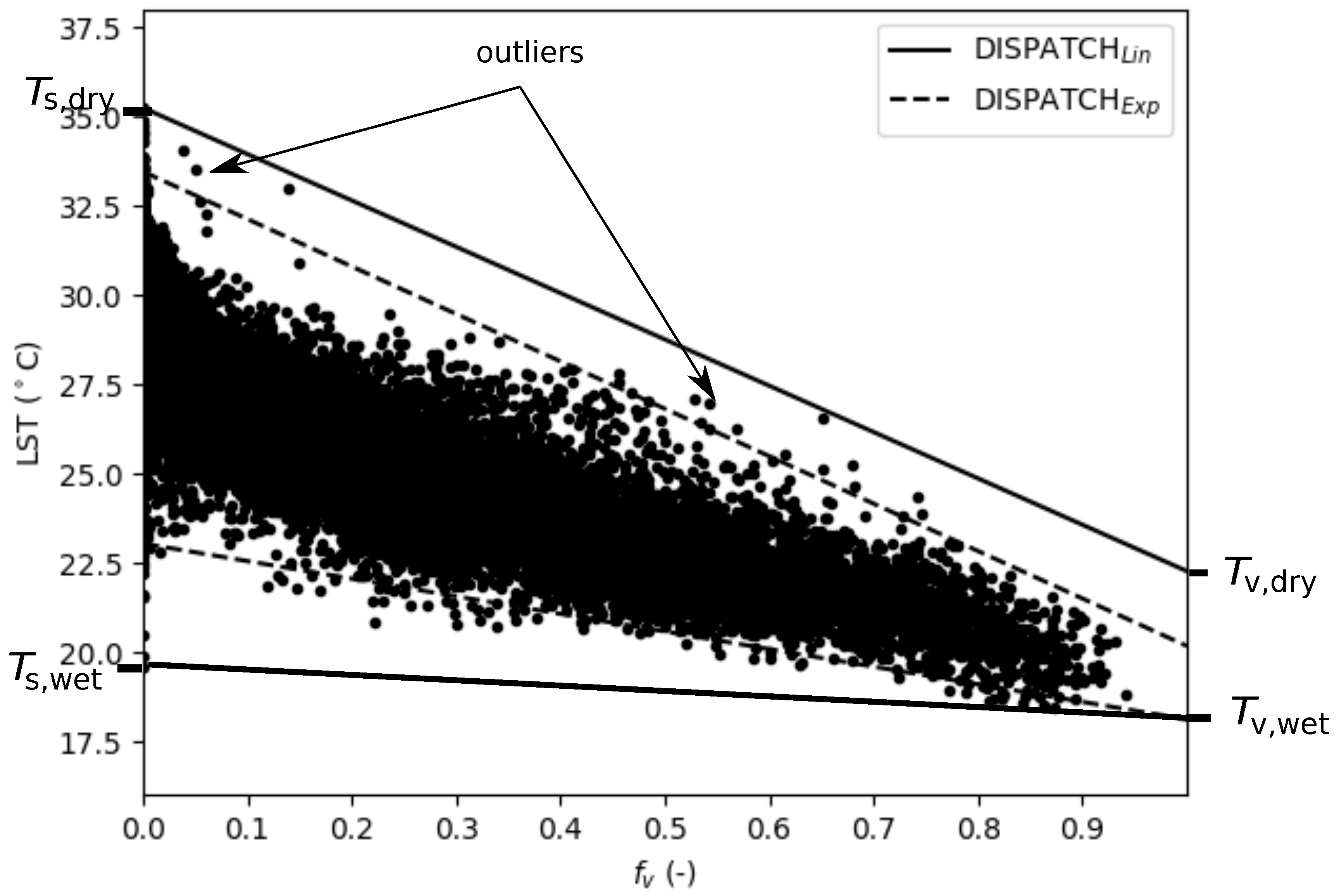
2.4.1. General Equations
2.4.2. DISPATCH at 1 km Resolution
2.4.3. DISPATCH at 100 m Resolution
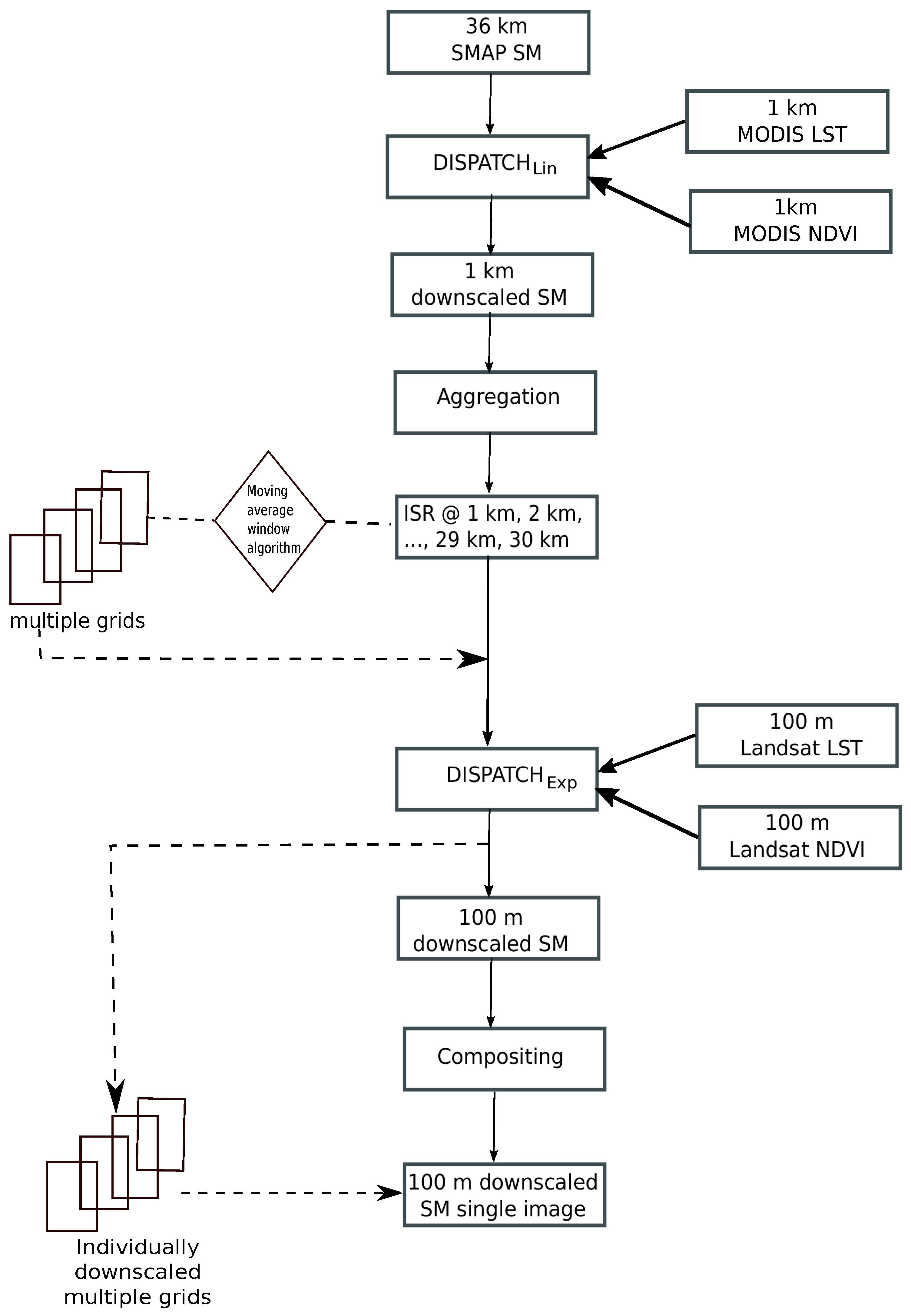
2.5. Sequential Downscaling
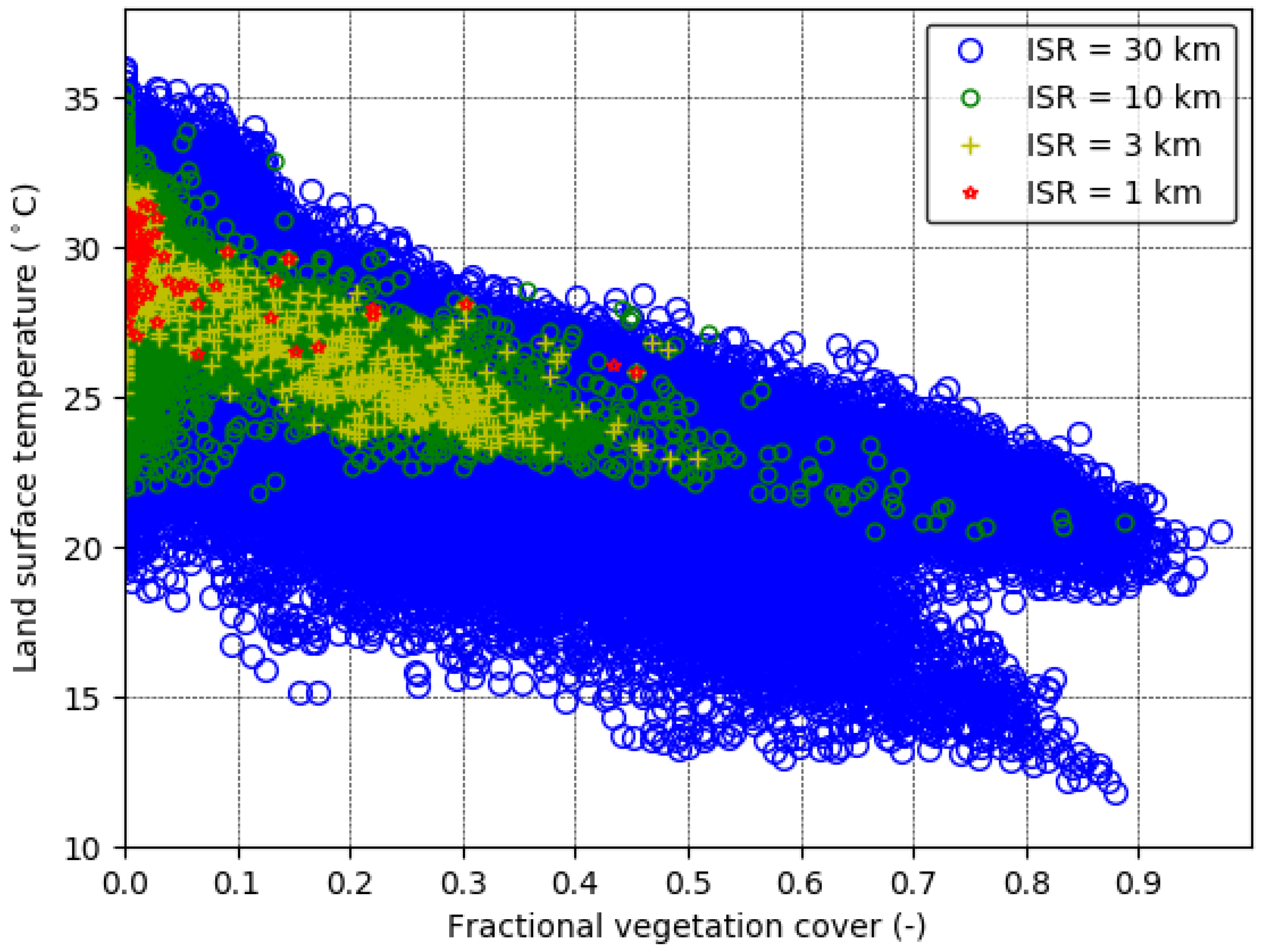
2.6. Inclusion of Multiple ISR Grids
3. Results
3.1. Calibration
3.2. Evaluation of 100 m Disaggregated SM
3.3. Reducing Boxy Artifact
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bisquert, M.; Sánchez, J.; López-Urrea, R.; Caselles, V. Estimating high resolution evapotranspiration from disaggregated thermal images. Remote Sens. Environ. 2016, 187, 423–433. [Google Scholar] [CrossRef]
- Maurer, E.P.; Wood, A.; Adam, J.; Lettenmaier, D.P.; Nijssen, B. A long-term hydrologically based dataset of land surface fluxes and states for the conterminous United States. J. Clim. 2002, 15, 3237–3251. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements ofthe global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Wagner, W. Operational Readiness of Microwave Remote Sensing of Soil Moisture: An Update. In Proceedings of the EGU General Assembly 2010, Vienna, Austria, 2–7 May 2010; Volume 12, p. 2636. [Google Scholar]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Martinuzzi, J.; Font, J.; Berger, M. Soil moisture retrieval from space: The Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Schmugge, T. Applications of passive microwave observations of surface soil moisture. J. Hydrol. 1998, 212, 188–197. [Google Scholar] [CrossRef]
- Schmugge, T.; Jackson, T. Mapping surface soil moisture with microwave radiometers. Meteorol. Atmos. Phys. 1994, 54, 213–223. [Google Scholar] [CrossRef]
- Bindlish, R.; Crow, W.T.; Jackson, T.J. Role of passive microwave remote sensing in improving flood forecasts. IEEE Geosci. Remote Sens. Lett. 2009, 6, 112–116. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Al Bitar, A.; Cabot, F.; Gruhier, C.; Juglea, S.E.; et al. The SMOS soil moisture retrieval algorithm. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1384–1403. [Google Scholar] [CrossRef]
- Malbéteau, Y.; Merlin, O.; Molero, B.; Rüdiger, C.; Bacon, S. DisPATCh as a tool to evaluate coarse-scale remotely sensed soil moisture using localized in situ measurements: Application to SMOS and AMSR-E data in Southeastern Australia. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 221–234. [Google Scholar] [CrossRef]
- Walker, J.P.; Houser, P.R. Requirements of a global near-surface soil moisture satellite mission: Accuracy, repeat time, and spatial resolution. Adv. Water Resour. 2004, 27, 785–801. [Google Scholar] [CrossRef]
- Hawley, M.E.; Jackson, T.J.; McCuen, R.H. Surface soil moisture variation on small agricultural watersheds. J. Hydrol. 1983, 62, 179–200. [Google Scholar] [CrossRef]
- Fang, B.; Lakshmi, V.; Bindlish, R.; Jackson, T.J. Downscaling of SMAP soil moisture using land surface temperature and vegetation data. Vadose Zone J. 2018, 17, 1. [Google Scholar] [CrossRef]
- Chen, N.; He, Y.; Zhang, X. NIR-Red Spectra-Based Disaggregation of SMAP Soil Moisture to 250 m Resolution Based on OzNet in Southeastern Australia. Remote Sens. 2017, 9, 51. [Google Scholar] [CrossRef]
- Tomer, S.K.; Al Bitar, A.; Sekhar, M.; Zribi, M.; Bandyopadhyay, S.; Kerr, Y. MAPSM: A spatio-temporal algorithm for merging soil moisture from active and passive microwave remote sensing. Remote Sens. 2016, 8, 990. [Google Scholar] [CrossRef]
- Piles, M.; Camps, A.; Vall-Llossera, M.; Corbella, I.; Panciera, R.; Rudiger, C.; Kerr, Y.H.; Walker, J. Downscaling SMOS-derived soil moisture using MODIS visible/infrared data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3156–3166. [Google Scholar] [CrossRef]
- Merlin, O.; Chehbouni, A.; Walker, J.P.; Panciera, R.; Kerr, Y.H. A simple method to disaggregate passive microwave-based soil moisture. IEEE Trans. Geosci. Remote Sens. 2008, 46, 786–796. [Google Scholar] [CrossRef]
- Panciera, R.; Walker, J.P.; Kalma, J.D.; Kim, E.J.; Hacker, J.M.; Merlin, O.; Berger, M.; Skou, N. The NAFE’05/CoSMOS data set: Toward SMOS soil moisture retrieval, downscaling, and assimilation. IEEE Trans. Geosci. Remote Sens. 2008, 46, 736–745. [Google Scholar] [CrossRef]
- Kim, G.; Barros, A.P. Downscaling of remotely sensed soil moisture with a modified fractal interpolation method using contraction mapping and ancillary data. Remote Sens. Environ. 2002, 83, 400–413. [Google Scholar] [CrossRef]
- Sabaghy, S.; Walker, J.P.; Renzullo, L.J.; Jackson, T.J. Spatially enhanced passive microwave derived soil moisture: Capabilities and opportunities. Remote Sens. Environ. 2018, 209, 551–580. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E. A review of spatial downscaling of satellite remotely sensed soil moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Taconet, O.; Bernard, R.; Vidal-Madjar, D. Evapotranspiration over an agricultural region using a surface flux/temperature model based on NOAA-AVHRR data. J. Clim. Appl. Meteorol. 1986, 25, 284–307. [Google Scholar] [CrossRef]
- Merlin, O.; Rudiger, C.; Al Bitar, A.; Richaume, P.; Walker, J.P.; Kerr, Y.H. Disaggregation of SMOS soil moisture in Southeastern Australia. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1556–1571. [Google Scholar] [CrossRef]
- Merlin, O.; Escorihuela, M.J.; Mayoral, M.A.; Hagolle, O.; Al Bitar, A.; Kerr, Y. Self-calibrated evaporation-based disaggregation of SMOS soil moisture: An evaluation study at 3 km and 100 m resolution in Catalunya, Spain. Remote Sens. Environ. 2013, 130, 25–38. [Google Scholar] [CrossRef]
- Merlin, O.; Stefan, V.G.; Amazirh, A.; Chanzy, A.; Ceschia, E.; Er-Raki, S.; Gentine, P.; Tallec, T.; Ezzahar, J.; Bircher, S.; et al. Modeling soil evaporation efficiency in a range of soil and atmospheric conditions using a meta-analysis approach. Water Resour. Res. 2016, 52, 3663–3684. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Molero, B.; Merlin, O.; Malbéteau, Y.; Al Bitar, A.; Cabot, F.; Stefan, V.; Kerr, Y.; Bacon, S.; Cosh, M.; Bindlish, R.; et al. SMOS disaggregated soil moisture product at 1km resolution: Processor overview and first validation results. Remote Sens. Environ. 2016, 180, 361–376. [Google Scholar] [CrossRef]
- Dumedah, G.; Walker, J.P.; Merlin, O. Root-zone soil moisture estimation from assimilation of downscaled Soil Moisture and Ocean Salinity data. Adv. Water Resour. 2015, 84, 14–22. [Google Scholar] [CrossRef]
- Escorihuela, M.J.; Quintana-Seguí, P. Comparison of remote sensing and simulated soil moisture datasets in Mediterranean landscapes. Remote Sens. Environ. 2016, 180, 99–114. [Google Scholar] [CrossRef]
- Malbeteau, Y.; Merlin, O.; Balsamo, G.; Er-Raki, S.; Khabba, S.; Walker, J.; Jarlan, L. Toward a Surface Soil Moisture Product at High Spatiotemporal Resolution: Temporally Interpolated, Spatially Disaggregated SMOS Data. J. Hydrometeorol. 2018, 19, 183–200. [Google Scholar] [CrossRef]
- Bandara, R.; Walker, J.P.; Rüdiger, C.; Merlin, O. Towards soil property retrieval from space: An application with disaggregated satellite observations. J. Hydrol. 2015, 522, 582–593. [Google Scholar] [CrossRef]
- Escorihuela, M.J.; Merlin, O.; Stefan, V.; Moyano, G.; Eweys, O.A.; Zribi, M.; Kamara, S.; Benahi, A.S.; Ebbe, M.A.B.; Chihrane, J.; et al. SMOS based high resolution soil moisture estimates for Desert locust preventive management. Remote Sens. Appl. Soc. Environ. 2018, 11, 140–150. [Google Scholar]
- Hssaine, B.A.; Merlin, O.; Ezzahar, J.; Ojha, N.; Er-raki, S.; Khabba, S. An evapotranspiration model self-calibrated from remotely sensed surface soil moisture, land surface temperature and vegetation cover fraction: Application to disaggregated SMOS and MODIS data. Hydrol. Earth Syst. Sci. 2019. under review. [Google Scholar] [CrossRef]
- Lievens, H.; Tomer, S.K.; Al Bitar, A.; De Lannoy, G.J.; Drusch, M.; Dumedah, G.; Franssen, H.J.H.; Kerr, Y.; Martens, B.; Pan, M.; et al. SMOS soil moisture assimilation for improved hydrologic simulation in the Murray Darling Basin, Australia. Remote Sens. Environ. 2015, 168, 146–162. [Google Scholar] [CrossRef]
- Leroux, L.; Baron, C.; Castets, M.; Escorihuela, M.J.; Diouf, A.; Bégué, A.; Lo Seen, D. Estimating maize grain yield in scarce field-data environment: An approach combining remote sensing and crop modeling in Burkina Faso. In Proceedings of the ABSTRACT AFRICAGIS 2017, Addis Ababa, Ethiopia, 20–24 November 2017. [Google Scholar]
- Colliander, A.; Fisher, J.B.; Halverson, G.; Merlin, O.; Misra, S.; Bindlish, R.; Jackson, T.J.; Yueh, S. Spatial downscaling of SMAP soil moisture using MODIS land surface temperature and NDVI during SMAPVEX15. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2107–2111. [Google Scholar] [CrossRef]
- French, A.N.; Hunsaker, D.J.; Thorp, K.R. Remote sensing of evapotranspiration over cotton using the TSEB and METRIC energy balance models. Remote Sens. Environ. 2015, 158, 281–294. [Google Scholar] [CrossRef]
- Loheide, S.P., II; Gorelick, S.M. A local-scale, high-resolution evapotranspiration mapping algorithm (ETMA) with hydroecological applications at riparian meadow restoration sites. Remote Sens. Environ. 2005, 98, 182–200. [Google Scholar] [CrossRef]
- Merlin, O.; Al Bitar, A.; Walker, J.P.; Kerr, Y. A sequential model for disaggregating near-surface soil moisture observations using multi-resolution thermal sensors. Remote Sens. Environ. 2009, 113, 2275–2284. [Google Scholar] [CrossRef]
- Fang, B.; Lakshmi, V. Soil moisture at watershed scale: Remote sensing techniques. J. Hydrol. 2014, 516, 258–272. [Google Scholar] [CrossRef]
- Jarlan, L.; Khabba, S.; Er-Raki, S.; Le Page, M.; Hanich, L.; Fakir, Y.; Merlin, O.; Mangiarotti, S.; Gascoin, S.; Ezzahar, J.; et al. Remote sensing of water resources in semi-arid mediterranean areas: The joint international laboratory TREMA. Int. J. Remote Sens. 2015, 36, 4879–4917. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Guemouria, N.; Duchemin, B.; Ezzahar, J.; Hadria, R. Combining FAO-56 model and ground-based remote sensing to estimate water consumptions of wheat crops in a semi-arid region. Agric. Water Manag. 2007, 87, 41–54. [Google Scholar] [CrossRef]
- Duchemin, B.; Hagolle, O.; Mougenot, B.; Benhadj, I.; Hadria, R.; Simonneaux, V.; Ezzahar, J.; Hoedjes, J.; Khabba, S.; Kharrou, M.; et al. Agrometerological study of semi-arid areas: An experiment for analysing the potential of time series of FORMOSAT-2 images (Tensift-Marrakech plain). Int. J. Remote Sens. 2008, 29, 5291–5299. [Google Scholar] [CrossRef]
- Duchemin, B.; Hadria, R.; Erraki, S.; Boulet, G.; Maisongrande, P.; Chehbouni, A.; Escadafal, R.; Ezzahar, J.; Hoedjes, J.; Kharrou, M.; et al. Monitoring wheat phenology and irrigation in Central Morocco: On the use of relationships between evapotranspiration, crops coefficients, leaf area index and remotely-sensed vegetation indices. Agric. Water Manag. 2006, 79, 1–27. [Google Scholar] [CrossRef]
- Miller, J.; Gaskin, G. ThetaProbe ML2x. In Principles of Operation and Applications; MLURI Technical Note; The Macaulay Land Use Research Institute: Aberdeen, UK, 1999. [Google Scholar]
- Amazirh, A.; Merlin, O.; Er-Raki, S.; Gao, Q.; Rivalland, V.; Malbeteau, Y.; Khabba, S.; Escorihuela, M.J. Retrieving surface soil moisture at high spatio-temporal resolution from a synergy between Sentinel-1 radar and Landsat thermal data: A study case over bare soil. Remote Sens. Environ. 2018, 211, 321–337. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Kim, S.; Jagdhuber, T.; Dunbar, S.; Yueh, S.; Colliander, A. High-resolution enhanced product based on SMAP active-passive approach using Sentinel 1 data and its applications. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS) 2017, Fort Worth, TX, USA, 23–28 July 2017; pp. 2493–2494. [Google Scholar]
- Colliander, A.; Jackson, T.J.; Bindlish, R.; Chan, S.; Das, N.; Kim, S.; Cosh, M.; Dunbar, R.; Dang, L.; Pashaian, L.; et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sens. Environ. 2017, 191, 215–231. [Google Scholar] [CrossRef]
- Chen, D.; Huang, J.; Jackson, T.J. Vegetation water content estimation for corn and soybeans using spectral indices derived from MODIS near-and short-wave infrared bands. Remote Sens. Environ. 2005, 98, 225–236. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A.; Skoković, D.; Mattar, C.; Cristóbal, J. Land surface temperature retrieval methods from Landsat-8 thermal infrared sensor data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1840–1843. [Google Scholar] [CrossRef]
- Mattar, C.; Durán-Alarcón, C.; Jiménez-Muñoz, J.C.; Santamaría-Artigas, A.; Olivera-Guerra, L.; Sobrino, J.A. Global atmospheric profiles from reanalysis information (GAPRI): A new database for earth surface temperature retrieval. Int. J. Remote Sens. 2015, 36, 5045–5060. [Google Scholar] [CrossRef]
- Moran, M.; Clarke, T.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.L.; Tang, B. An application of the Ts–VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ. 2010, 114, 540–551. [Google Scholar] [CrossRef]
- Komatsu, T.S. Toward a robust phenomenological expression of evaporation efficiency for unsaturated soil surfaces. J. Appl. Meteorol. 2003, 42, 1330–1334. [Google Scholar] [CrossRef]
- Chanzy, A.; Bruckler, L. Significance of soil surface moisture with respect to daily bare soil evaporation. Water Resour. Res. 1993, 29, 1113–1125. [Google Scholar] [CrossRef]
- Wang, J. Scale Effects on the Remote Estimation of Evapotransportation. Ph.D. Thesis, Texas State University, San Marcos, TX, USA, 2012. [Google Scholar]
- Hoehn, D.C.; Niemann, J.D.; Green, T.R.; Jones, A.S.; Grazaitis, P.J. Downscaling soil moisture over regions that include multiple coarse-resolution grid cells. Remote Sens. Environ. 2017, 199, 187–200. [Google Scholar] [CrossRef]
- Merlin, O.; Chehbouni, A.G.; Kerr, Y.H.; Njoku, E.G.; Entekhabi, D. A combined modeling and multispectral/ multiresolution remote sensing approach for disaggregation of surface soil moisture: Application to SMOS configuration. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2036–2050. [Google Scholar] [CrossRef]
- Agam, N.; Kustas, W.P.; Anderson, M.C.; Li, F.; Colaizzi, P.D. Utility of thermal sharpening over Texas high plains irrigated agricultural fields. J. Geophys. Res. Atmos. 2007, 112, D19. [Google Scholar] [CrossRef]
- Merlin, O.; Malbéteau, Y.; Notfi, Y.; Bacon, S.; Khabba, S.; Jarlan, L. Performance metrics for soil moisture downscaling methods: Application to DISPATCH data in central Morocco. Remote Sens. 2015, 7, 3783–3807. [Google Scholar] [CrossRef]
- Wilson, A.M.; Jetz, W. Remotely sensed high-resolution global cloud dynamics for predicting ecosystem and biodiversity distributions. PLoS Biol. 2016, 14, e1002415. [Google Scholar] [CrossRef]


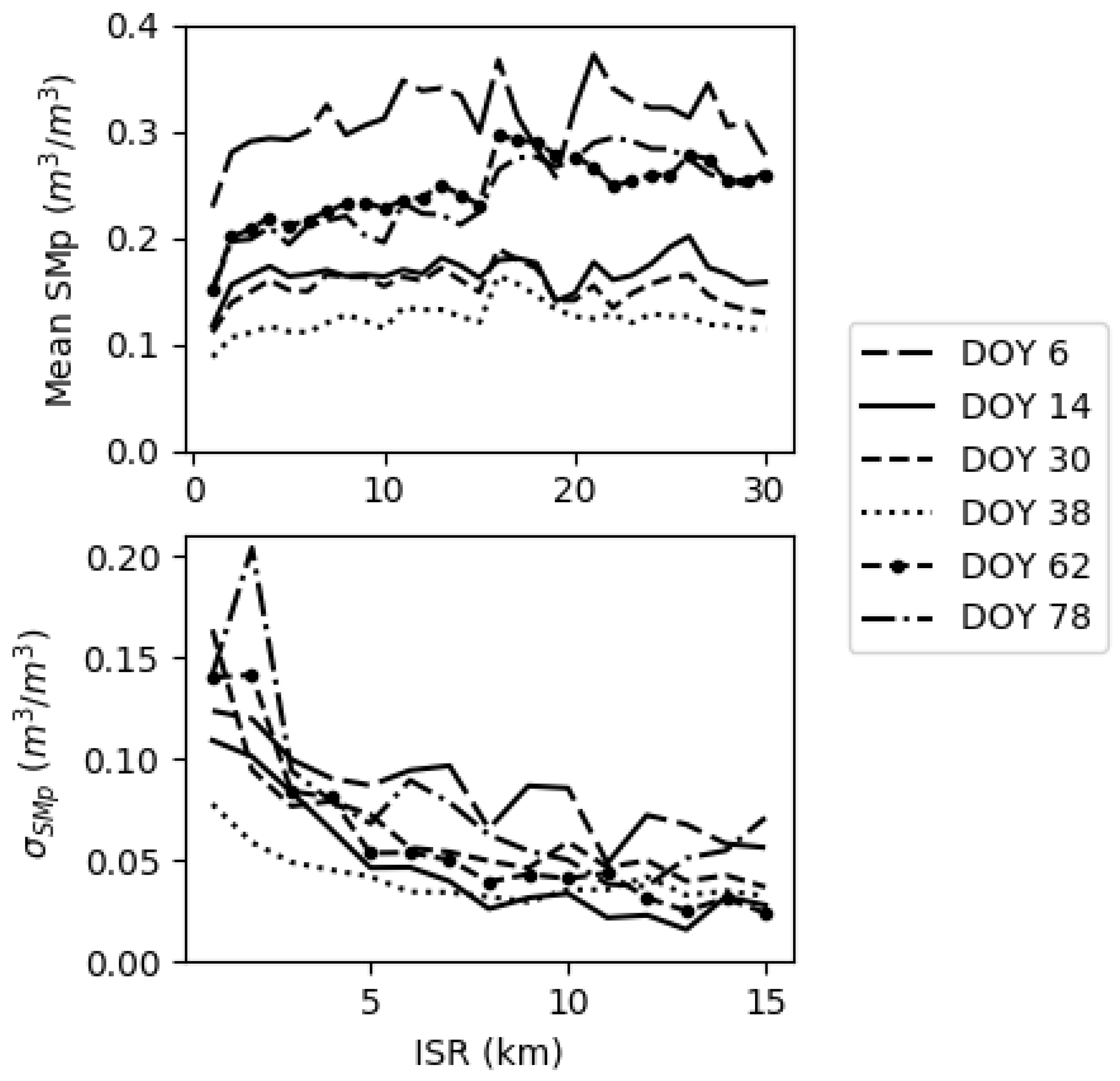
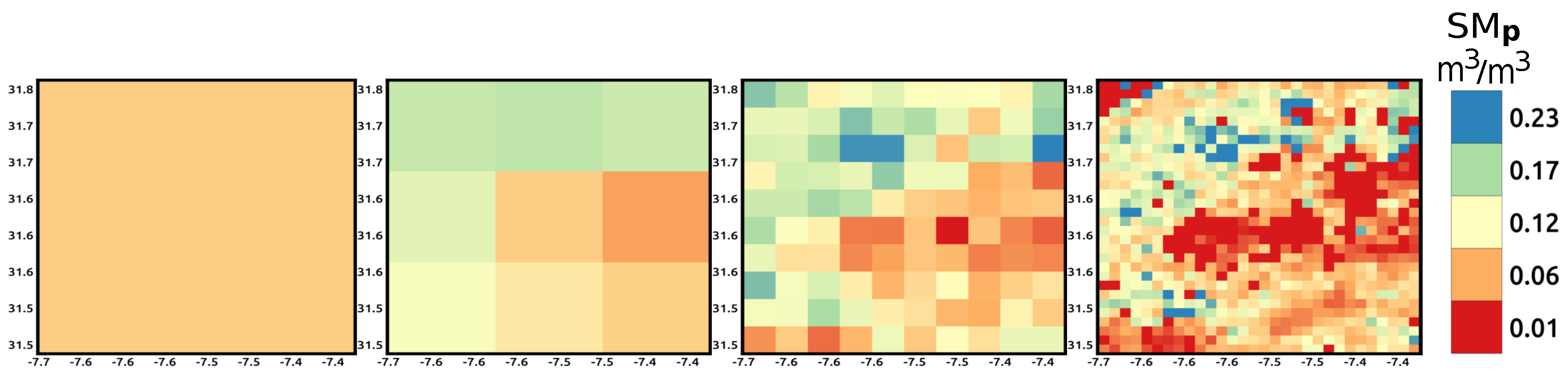
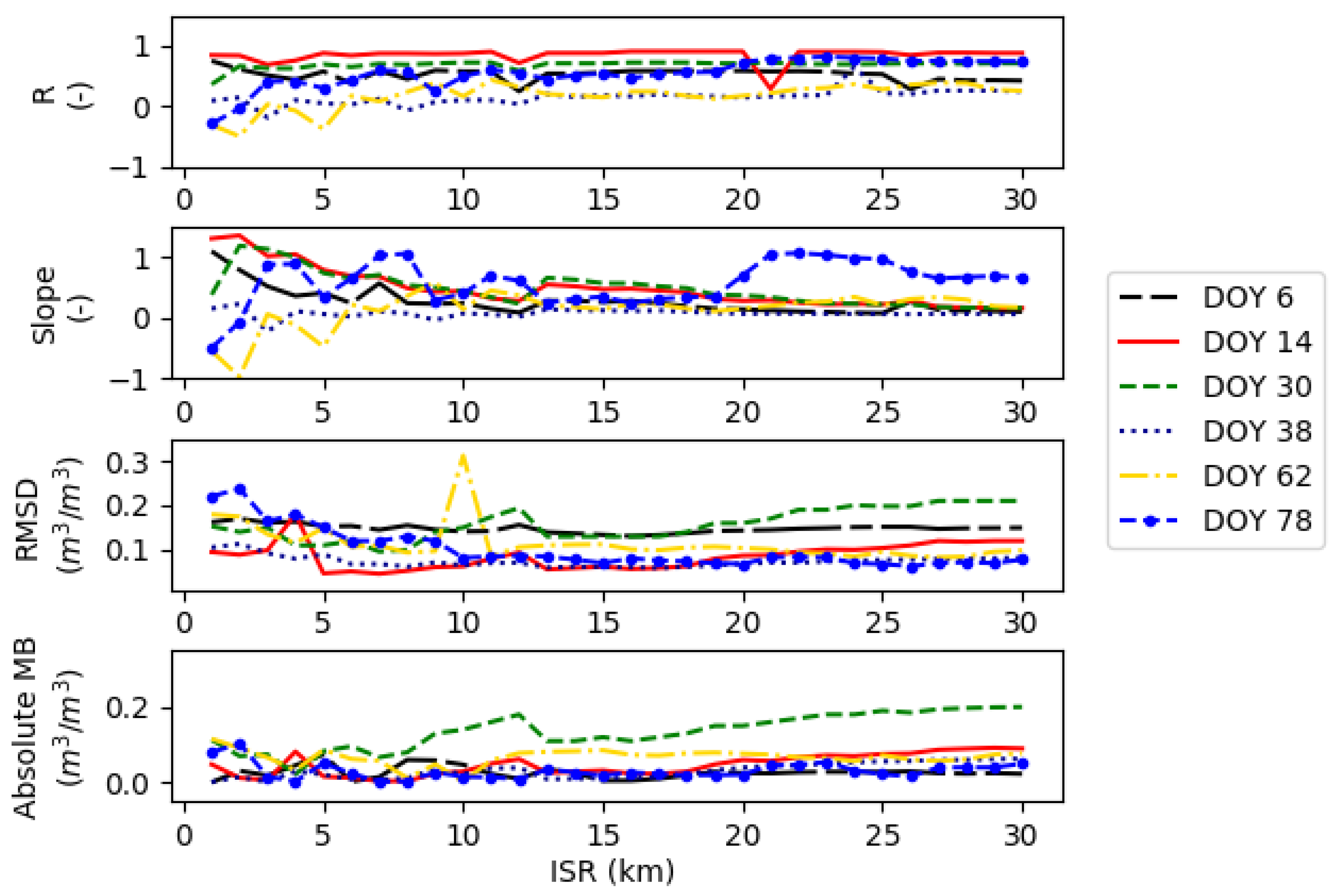
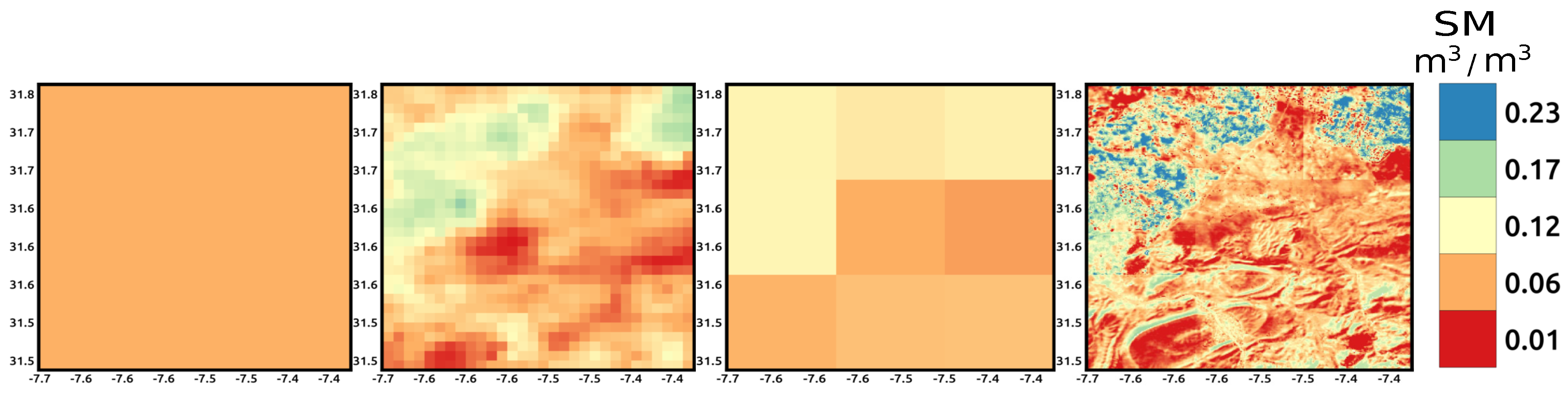
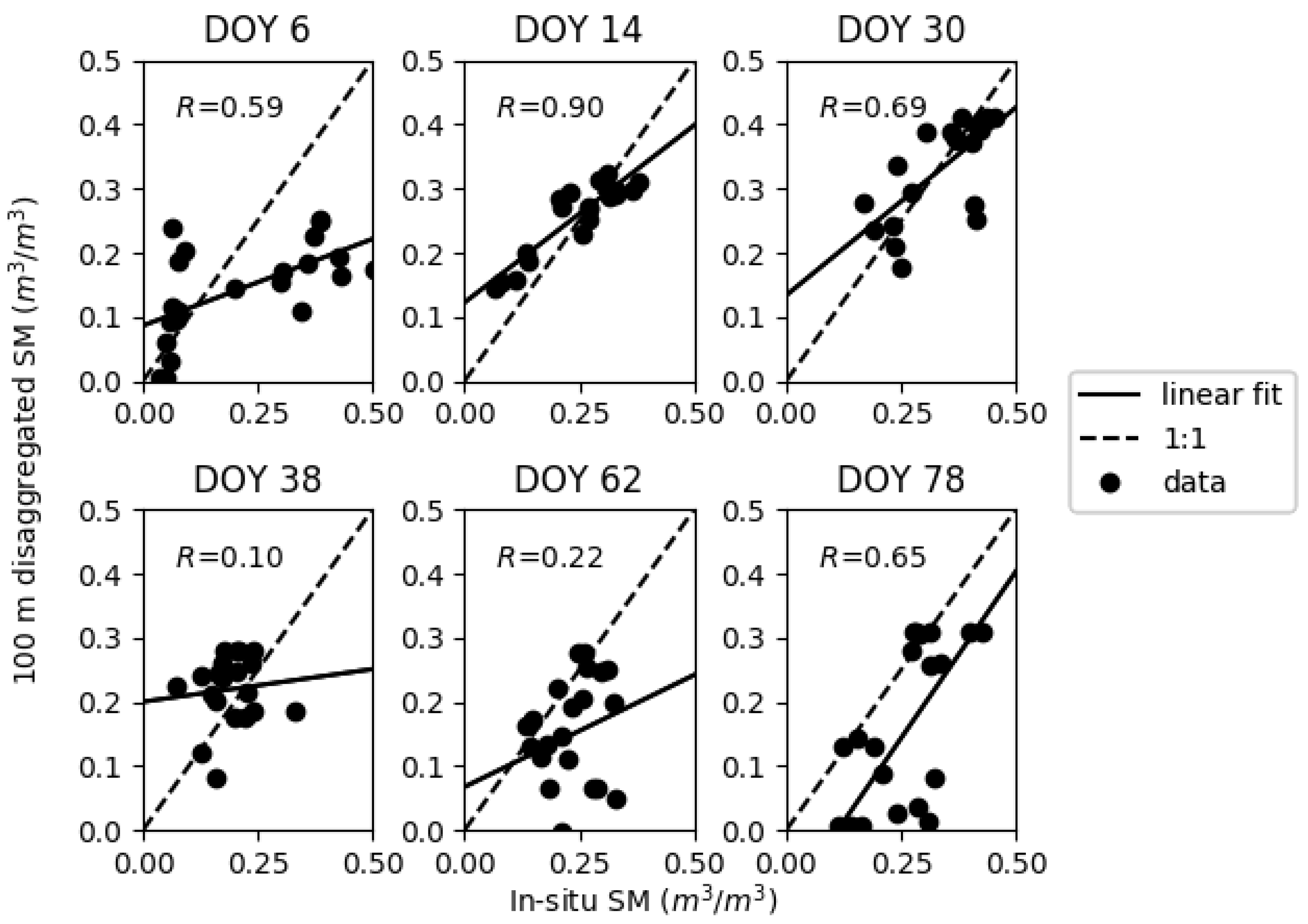
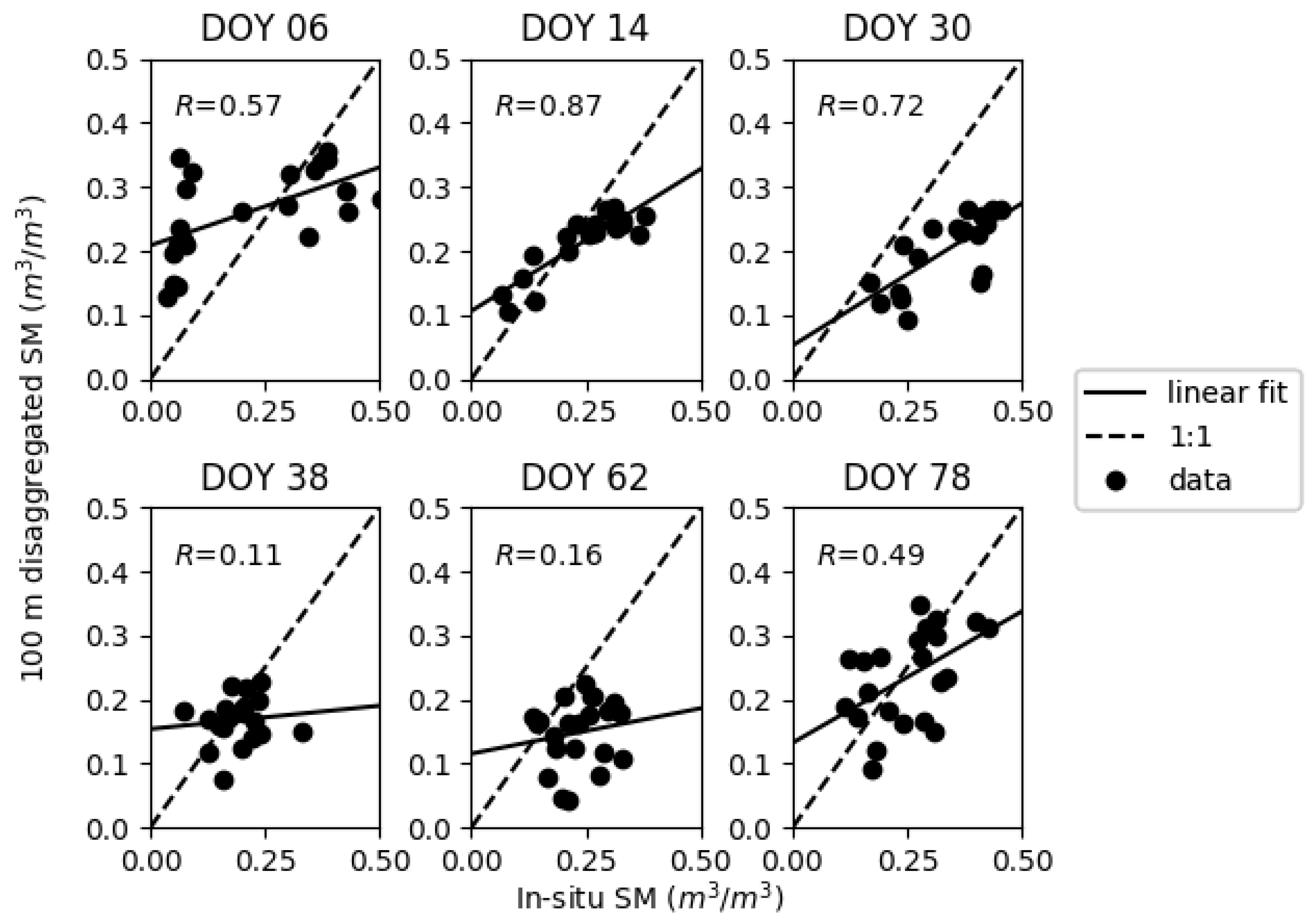
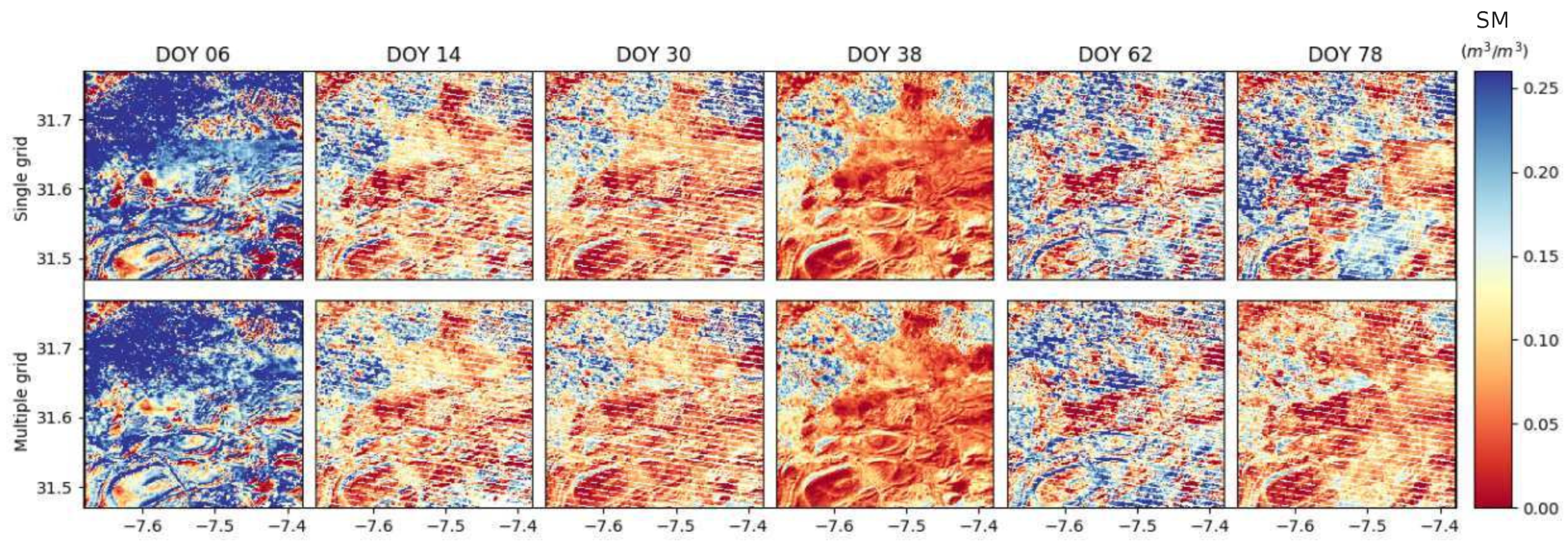
| Day of Year (DOY) | Synthetic | SMAP Single Grid | SMAP Multiple Grid | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R (-) | Slope (-) | Absolute MB (m/m) | RMSD (m/m) | R (-) | Slope (-) | Absolute MB (m/m) | RMSD (m/m) | R (-) | Slope (-) | Absolute MB (m/m) | RMSD (m/m) | |
| 6 | 0.59 | 0.27 | 0.069 | 0.15 | 0.57 | 0.24 | 0.05 | 0.14 | 0.54 | 0.23 | 0.01 | 0.14 |
| 14 | 0.90 | 0.55 | 0.014 | 0.049 | 0.87 | 0.44 | 0.03 | 0.06 | 0.90 | 0.47 | 0.03 | 0.06 |
| 30 | 0.69 | 0.59 | 0.006 | 0.066 | 0.72 | 0.44 | 0.14 | 0.15 | 0.70 | 0.52 | 0.12 | 0.14 |
| 38 | 0.10 | 0.10 | 0.03 | 0.08 | 0.11 | 0.07 | 0.02 | 0.07 | 0.12 | 0.08 | 0.03 | 0.07 |
| 62 | 0.22 | 0.35 | 0.08 | 0.13 | 0.16 | 0.14 | 0.002 | 0.31 | 0.20 | 0.21 | 0.07 | 0.10 |
| 78 | 0.65 | 1.04 | 0.11 | 0.15 | 0.49 | 0.40 | 0.02 | 0.08 | 0.54 | 0.31 | 0.12 | 0.14 |
| All | 0.53 | 0.48 | 0.052 | 0.104 | 0.55 | 0.34 | 0.05 | 0.09 | 0.57 | 0.35 | 0.08 | 0.10 |
| Day of Year (DOY) | Single Grid (m/m) | Multiple Grid (m/m) |
|---|---|---|
| 6 | 0.135 | 0.115 |
| 14 | 0.075 | 0.069 |
| 30 | 0.075 | 0.068 |
| 38 | 0.058 | 0.055 |
| 62 | 0.096 | 0.092 |
| 78 | 0.094 | 0.052 |
| All | 0.089 | 0.075 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ojha, N.; Merlin, O.; Molero, B.; Suere, C.; Olivera-Guerra, L.; Ait Hssaine, B.; Amazirh, A.; Al Bitar, A.; Escorihuela, M.J.; Er-Raki, S. Stepwise Disaggregation of SMAP Soil Moisture at 100 m Resolution Using Landsat-7/8 Data and a Varying Intermediate Resolution. Remote Sens. 2019, 11, 1863. https://doi.org/10.3390/rs11161863
Ojha N, Merlin O, Molero B, Suere C, Olivera-Guerra L, Ait Hssaine B, Amazirh A, Al Bitar A, Escorihuela MJ, Er-Raki S. Stepwise Disaggregation of SMAP Soil Moisture at 100 m Resolution Using Landsat-7/8 Data and a Varying Intermediate Resolution. Remote Sensing. 2019; 11(16):1863. https://doi.org/10.3390/rs11161863
Chicago/Turabian StyleOjha, Nitu, Olivier Merlin, Beatriz Molero, Christophe Suere, Luis Olivera-Guerra, Bouchra Ait Hssaine, Abdelhakim Amazirh, Ahmad Al Bitar, Maria Jose Escorihuela, and Salah Er-Raki. 2019. "Stepwise Disaggregation of SMAP Soil Moisture at 100 m Resolution Using Landsat-7/8 Data and a Varying Intermediate Resolution" Remote Sensing 11, no. 16: 1863. https://doi.org/10.3390/rs11161863
APA StyleOjha, N., Merlin, O., Molero, B., Suere, C., Olivera-Guerra, L., Ait Hssaine, B., Amazirh, A., Al Bitar, A., Escorihuela, M. J., & Er-Raki, S. (2019). Stepwise Disaggregation of SMAP Soil Moisture at 100 m Resolution Using Landsat-7/8 Data and a Varying Intermediate Resolution. Remote Sensing, 11(16), 1863. https://doi.org/10.3390/rs11161863







