A Modeling and Measurement Approach for the Uncertainty of Features Extracted from Remote Sensing Images
Abstract
1. Introduction
2. Characteristic Analysis of Feature Uncertainty
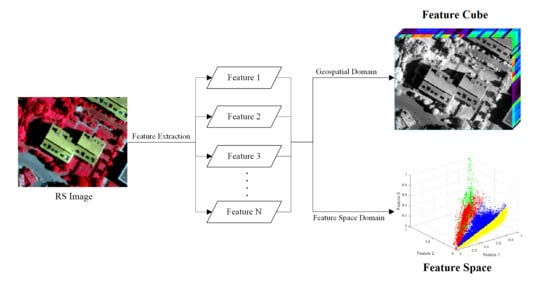
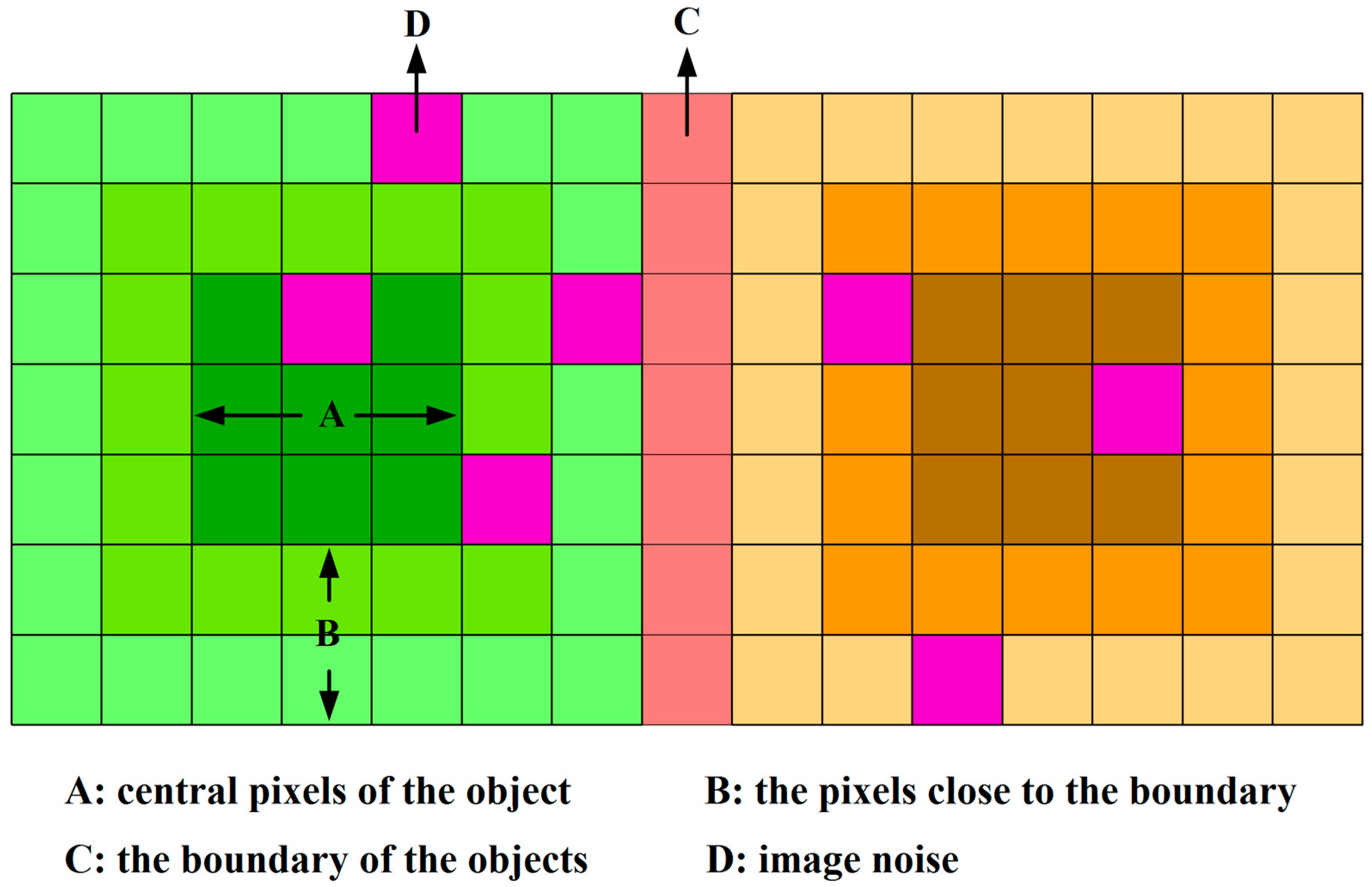
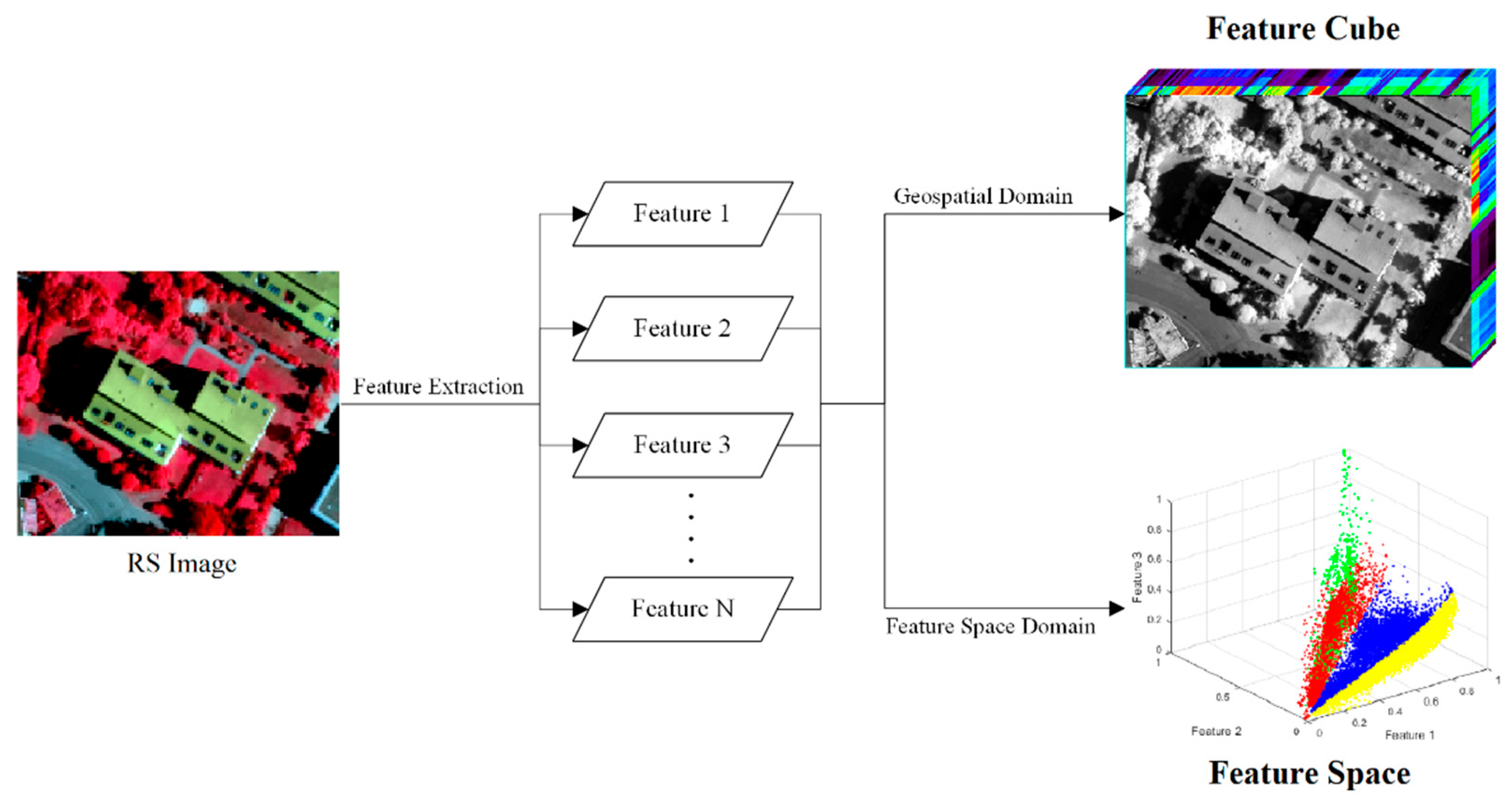
2.1. From the Perspective of the Geospatial Domain
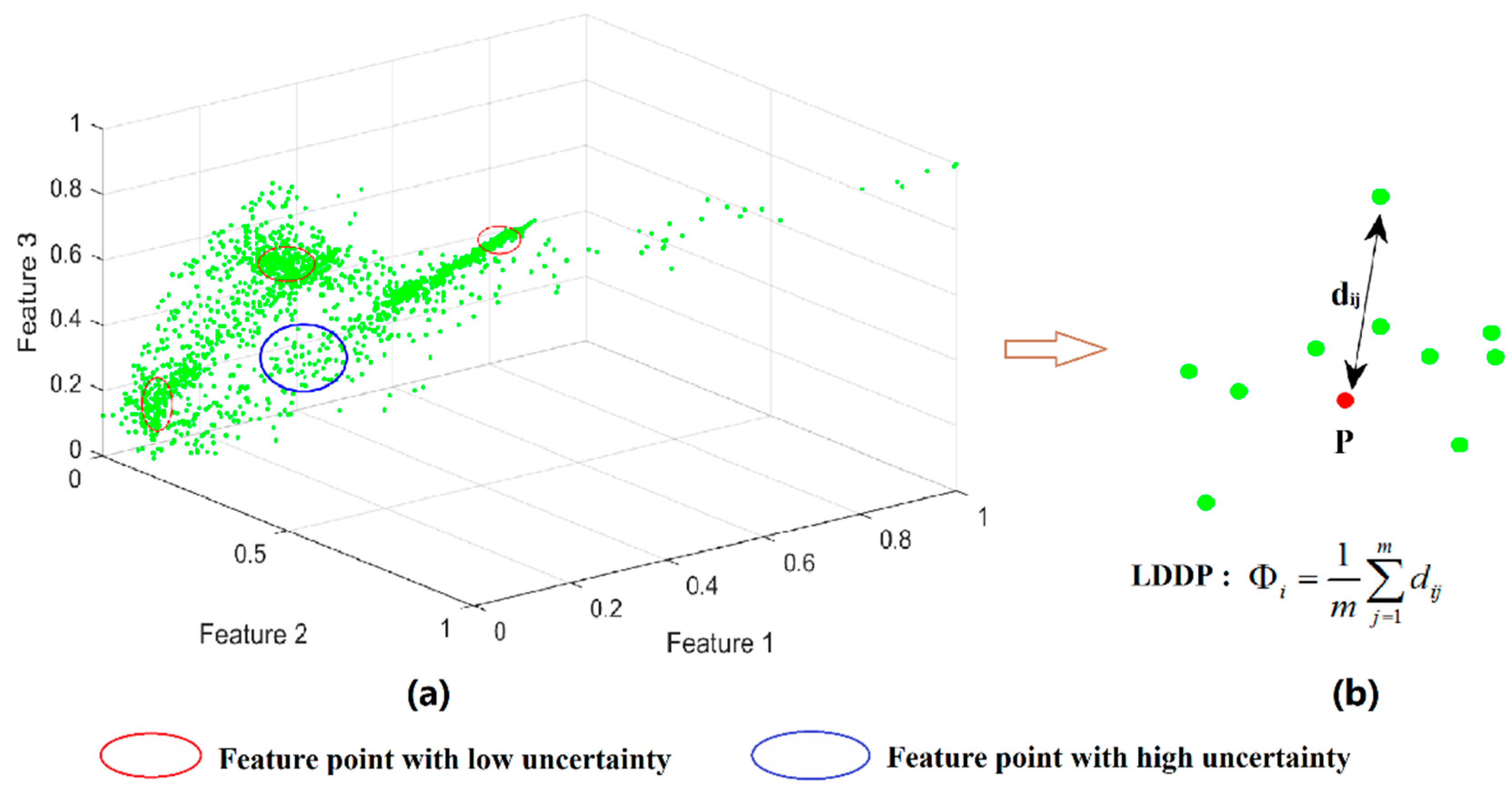
2.2. From the Perspective of the Feature Space Domain
3. Approach for Modeling and Measurement of Feature Uncertainty
3.1. Geospatial Domain
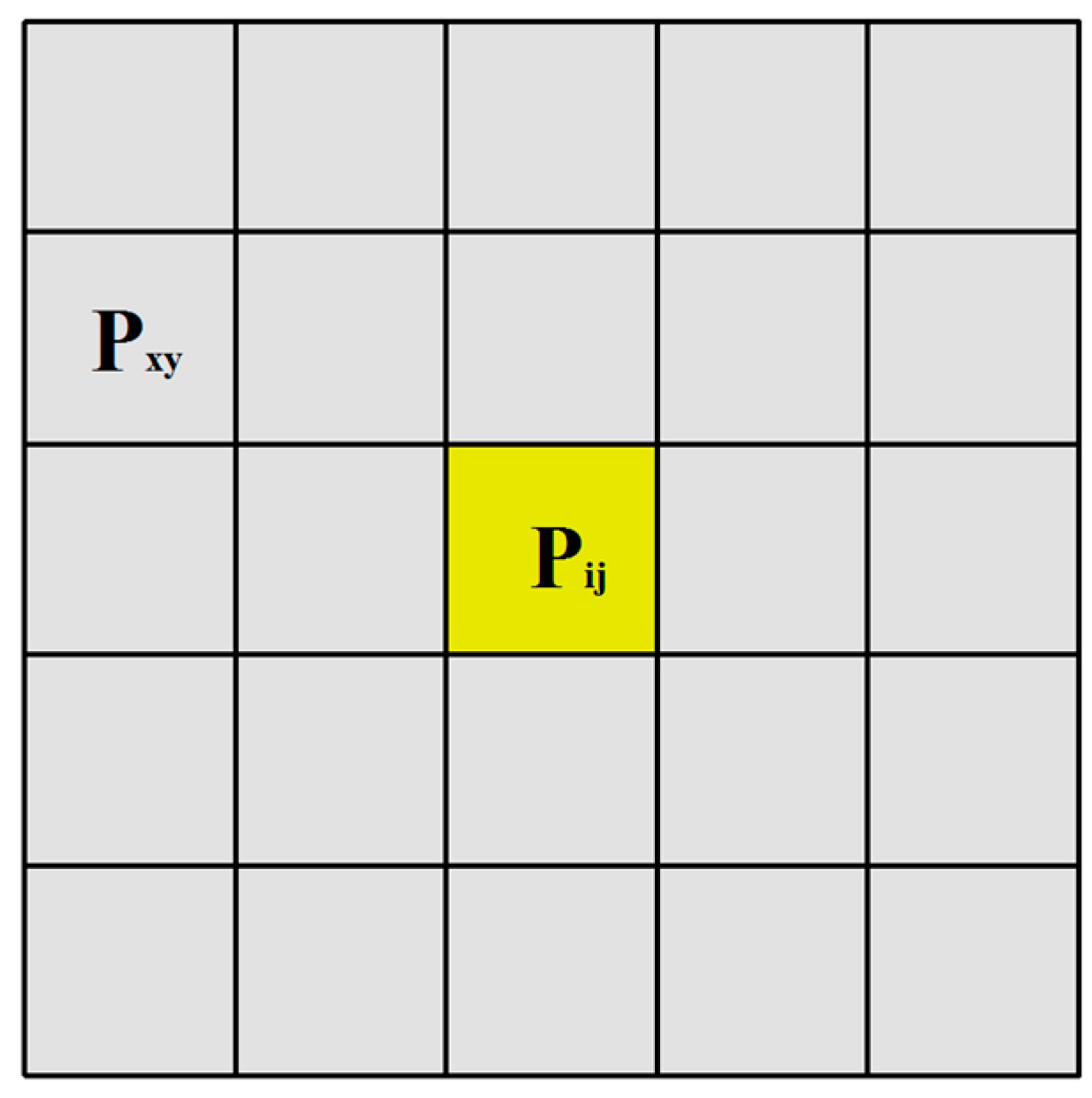
3.1.1. Uncertainty of the Single-Dimension Feature in the Geospatial Domain
3.1.2. Weights of Different Features
3.1.3. Integrating Uncertainties of Different Features to Measure the Comprehensive Feature Uncertainty in the Geospatial Domain
3.2. Feature Space Domain
3.3. Feature Uncertainty Index Integrated Geospatial and Feature Space Domains
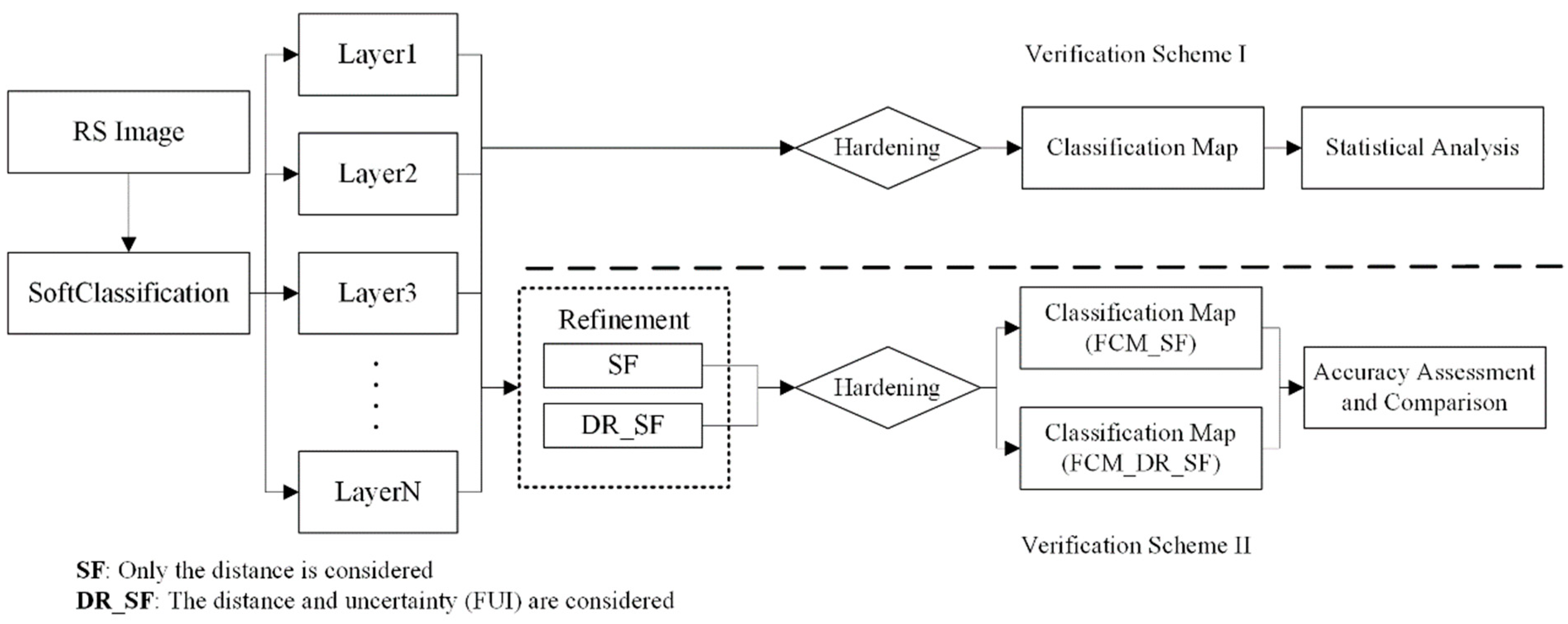
4. Validation Schemes
4.1. Scheme I: Statistical Analysis
4.2. Scheme II: Analysis of the Effect on Image Classification
5. Experimental Results and Discussion
5.1. Experimental Data and Settings
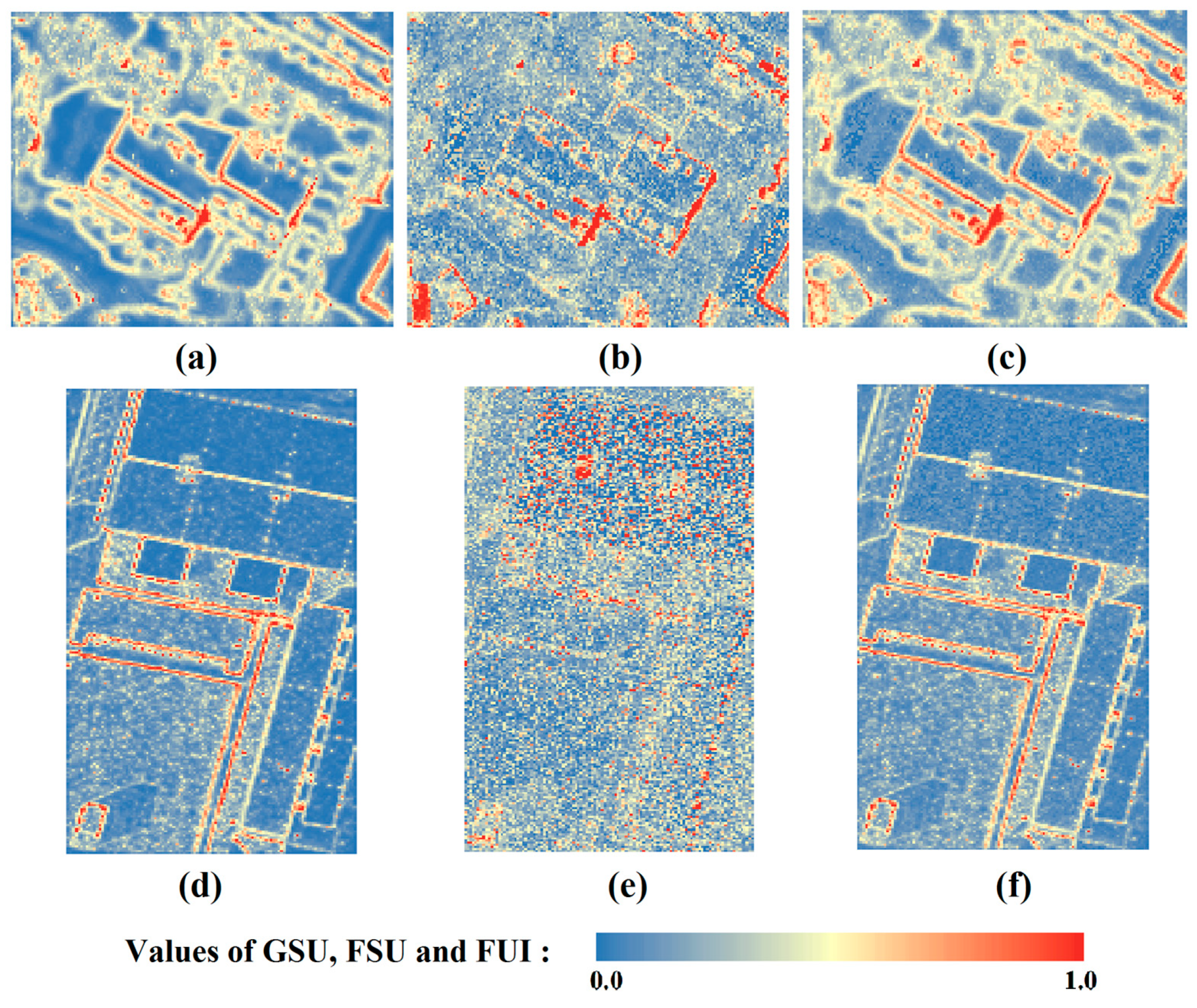
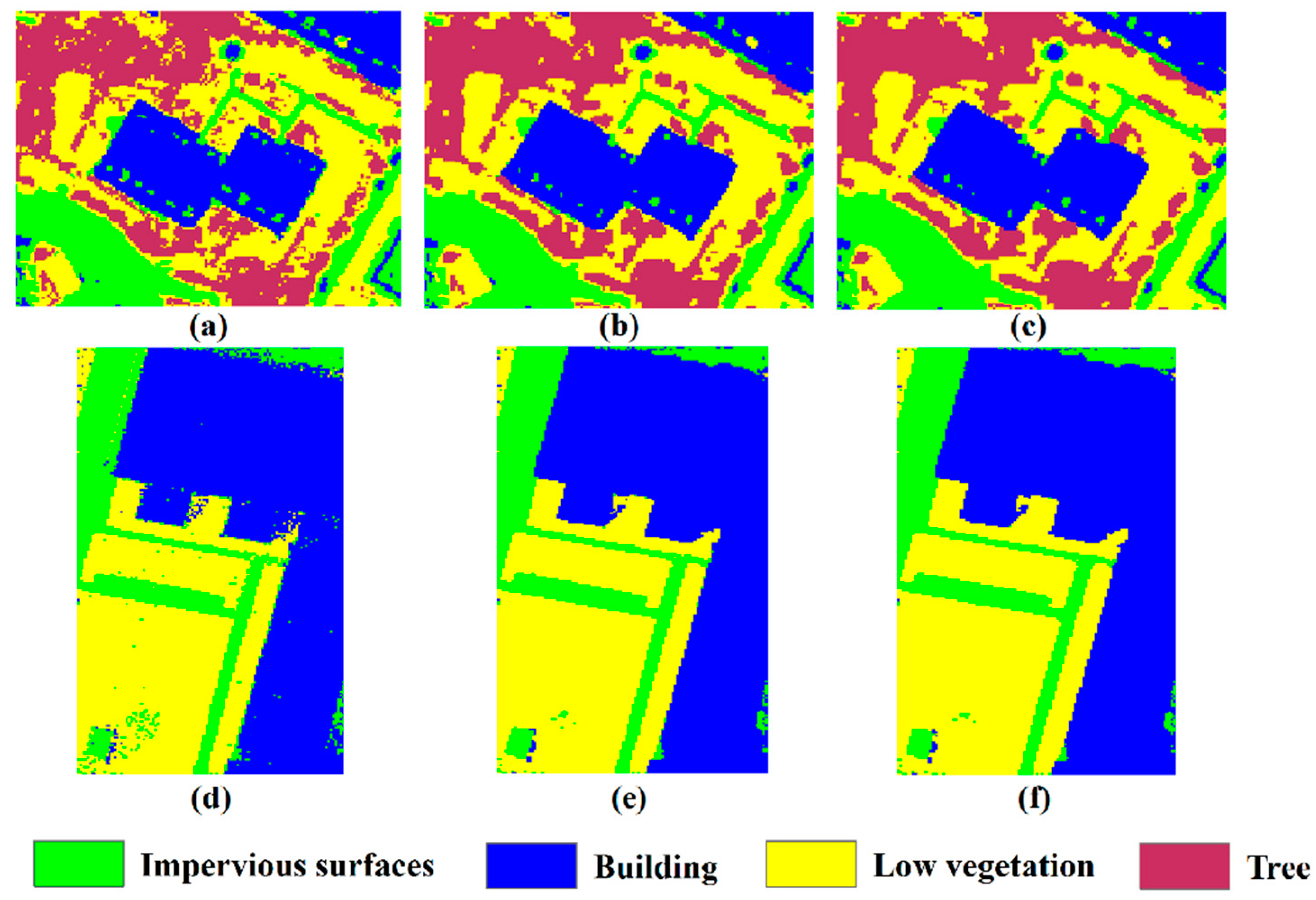
5.2. Results and Analysis
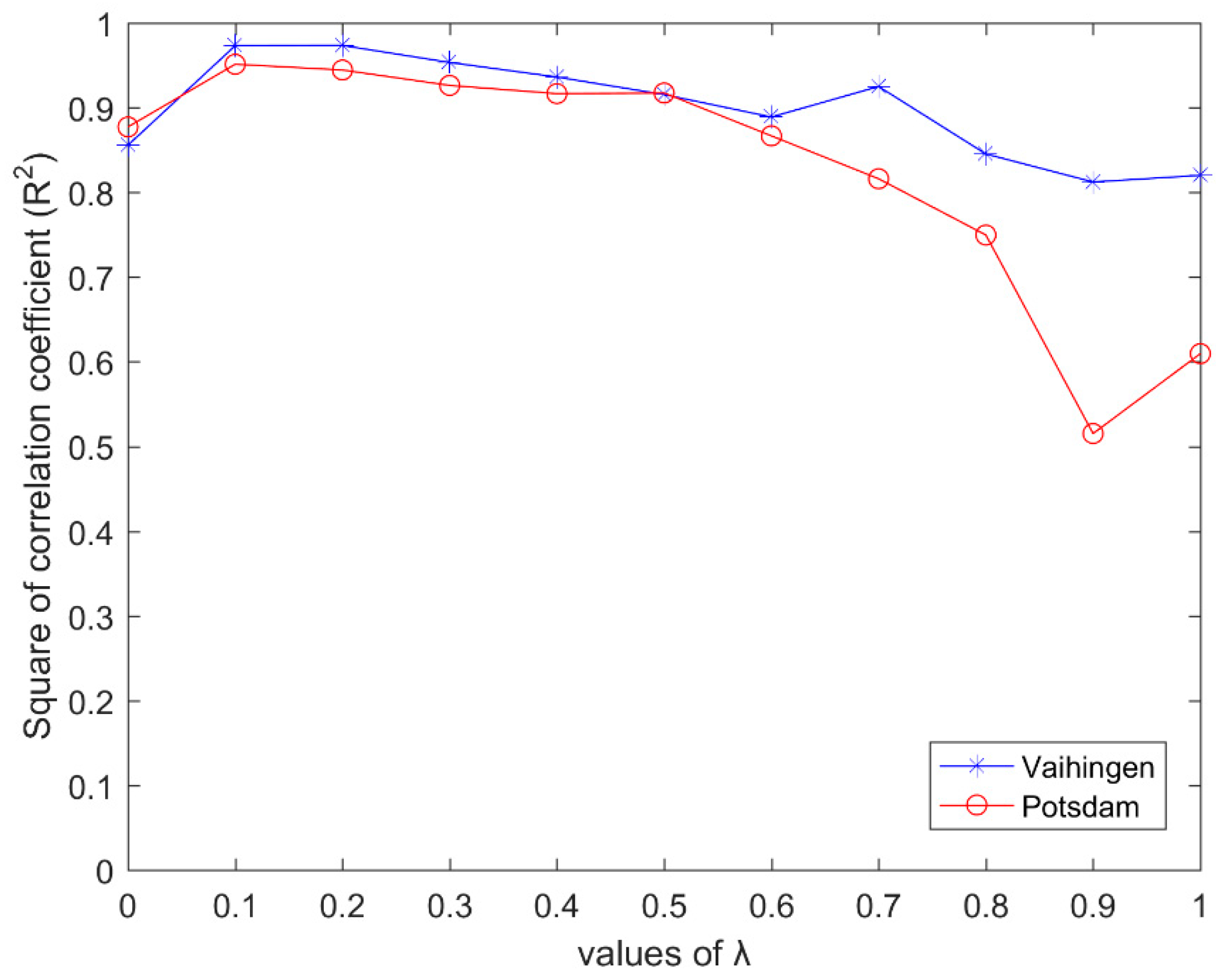
5.3. Discussion of Parameter Sensitivity
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Murthy, C.S.; Raju, P.V.; Badrinath, K.V.S. Classification of wheat crop with multi-temporal images: Performance of maximum likelihood and artificial neural networks. Int. J. Remote Sens. 2003, 24, 4871–4890. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Xia, J.; Du, P.; He, X.; Chanussot, J. Hyperspectral Remote Sensing Image Classification Based on Rotation Forest. IEEE Geosci. Remote Sens. 2014, 11, 239–243. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Zhang, P.; Lv, Z.; Shi, W. Object-Based Spatial Feature for Classification of Very High Resolution Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1572–1576. [Google Scholar] [CrossRef]
- Bialas, J.; Oommen, T.; Havens, T.C. Optimal segmentation of high spatial resolution images for the classification of buildings using random forests. Int. J. Appl. Earth Obs. Geoinf. 2019, 82, 101895. [Google Scholar] [CrossRef]
- Gonçalves, J.; Pôças, I.; Marcos, B.; Mücher, C.A.; Honrado, J.P. SegOptim—A new R package for optimizing object-based image analyses of high-spatial resolution remotely-sensed data. Int. J. Appl. Earth Obs. Geoinf. 2019, 76, 218–230. [Google Scholar] [CrossRef]
- Hossain, M.D.; Chen, D. Segmentation for Object-Based Image Analysis (OBIA): A review of algorithms and challenges from remote sensing perspective. ISPRS J. Photogramm. Remote Sens. 2019, 150, 115–134. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep Learning for Remote Sensing Data: A Technical Tutorial on the State of the Art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Romero, A.; Gatta, C.; Camps-Valls, G. Unsupervised Deep Feature Extraction for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1349–1362. [Google Scholar] [CrossRef]
- Shi, W.Z. Principles of Modelling Uncertainties in Spatial Data and Spatial Analyses; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Hand, D.J. Measurements and their Uncertainties: A Practical Guide to Modern Error Analysis by Ifan G. Hughes, Thomas P. A. Hase. Int. Stat. Rev. 2011, 79, 280. [Google Scholar] [CrossRef]
- Stastny, J.; Skorpil, V.; Fejfar, J. Visualization of uncertainty in LANDSAT classification process. In Proceedings of the 2015 38th International Conference on Telecommunications and Signal Processing (TSP), Prague, Czech Republic, 9–11 July 2015; pp. 789–792. [Google Scholar]
- Choi, M.; Lee, H.; Lee, S. Weighted SVM with classification uncertainty for small training samples. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 25–28 September 2016; pp. 4438–4442. [Google Scholar]
- Wilson, R.; Granlund, G.H. The Uncertainty Principle in Image Processing. IEEE Trans. Pattern Anal. Mach. Intell. 1984, PAMI-6, 758–767. [Google Scholar] [CrossRef]
- Carmel, Y. Controlling data uncertainty via aggregation in remotely sensed data. IEEE Geosci. Remote Sens. Lett. 2004, 1, 39–41. [Google Scholar] [CrossRef]
- Li, W.; Zhang, C. A Markov Chain Geostatistical Framework for Land-Cover Classification With Uncertainty Assessment Based on Expert-Interpreted Pixels From Remotely Sensed Imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2983–2992. [Google Scholar] [CrossRef]
- Gillmann, C.; Wischgoll, T.; Hagen, H. Uncertainty-Awareness in Open Source Visualization Solutions. In Proceedings of the IEEE Visualization Conference (VIS)—VIP Workshop, Baltimore, MD, USA, 23–28 October 2016. [Google Scholar]
- Gillmann, C.; Arbelaez, P.; Hernandez, T.J.; Hagen, H.; Wischgoll, T. An Uncertainty-Aware Visual System for Image Pre-Processing. J. Imaging 2018, 4, 109. [Google Scholar] [CrossRef]
- Giacco, F.; Thiel, C.; Pugliese, L.; Scarpetta, S.; Marinaro, M. Uncertainty Analysis for the Classification of Multispectral Satellite Images Using SVMs and SOMs. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3769–3779. [Google Scholar] [CrossRef]
- Feizizadeh, B. A Novel Approach of Fuzzy Dempster–Shafer Theory for Spatial Uncertainty Analysis and Accuracy Assessment of Object-Based Image Classification. IEEE Geosci. Remote Sens. 2018, 15, 18–22. [Google Scholar] [CrossRef]
- Gillmann, C.; Post, T.; Wischgoll, T.; Hagen, H.; Maciejewski, R. Hierarchical Image Semantics using Probabilistic Path Propagations for Biomedical Research. IEEE Comput. Graph. Appl. 2019. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, X.; Hao, M.; Shao, P.; Cai, L.; Lyu, X. Validation of Land Cover Products Using Reliability Evaluation Methods. Remote Sens. 2015, 7, 7846–7864. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Jia, X.; Kuo, B.; Crawford, M.M. Feature Mining for Hyperspectral Image Classification. Proc. IEEE 2013, 101, 676–697. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Zhang, P.; Yu, A.; Fu, Q.; Wei, X. Supervised Deep Feature Extraction for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1909–1921. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, P. An Uncertainty Descriptor for Quantitative Measurement of the Uncertainty of Remote Sensing Images. Remote Sens. 2019, 11, 1560. [Google Scholar] [CrossRef]
- Cao, S.; Yu, Q.; Zhang, J. Automatic division for pure/mixed pixels based on probabilities entropy and spatial heterogeneity. In Proceedings of the 2012 First International Conference on Agro-Geoinformatics (Agro-Geoinformatics), Shanghai, China, 2–4 August 2012; pp. 1–4. [Google Scholar]
- Lv, Z.; Zhang, P.; Atli Benediktsson, J. Automatic Object-Oriented, Spectral-Spatial Feature Extraction Driven by Tobler’s First Law of Geography for Very High Resolution Aerial Imagery Classification. Remote Sens. 2017, 9, 285. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Li, J.; Lu, B.-L. An adaptive image Euclidean distance. Pattern Recognit. 2009, 42, 349–357. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Spectral–Spatial Hyperspectral Image Classification With Edge-Preserving Filtering. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2666–2677. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 27. [Google Scholar] [CrossRef]
- Wu, T.-F.; Lin, C.-J.; Weng, R.C. Probability Estimates for Multi-class Classification by Pairwise Coupling. J. Mach. Learn. Res. 2004, 5, 975–1005. [Google Scholar]
- Pukelsheim, F. The Three Sigma Rule. Am. Stat. 1994, 48, 88–91. [Google Scholar] [CrossRef]
- Stigler, S.M. Francis Galton’s Account of the Invention of Correlation. Stat. Sci. 1989, 4, 73–79. [Google Scholar] [CrossRef]
- Huang, X.; Lu, Q.; Zhang, L.; Plaza, A. New Postprocessing Methods for Remote Sensing Image Classification: A Systematic Study. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7140–7159. [Google Scholar] [CrossRef]
- Cui, G.; Lv, Z.; Li, G.; Atli Benediktsson, J.; Lu, Y. Refining Land Cover Classification Maps Based on Dual-Adaptive Majority Voting Strategy for Very High Resolution Remote Sensing Images. Remote Sens. 2018, 10, 1238. [Google Scholar] [CrossRef]
- Lv, Z.; Shi, W.; Benediktsson, A.J.; Ning, X. Novel Object-Based Filter for Improving Land-Cover Classification of Aerial Imagery with Very High Spatial Resolution. Remote Sens. 2016, 8, 1023. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Sohn, G.; Jung, J.; Gerke, M.; Baillard, C.; Benitez, S.; Breitkopf, U. The ISPRS benchmark on urban object classification and 3D building reconstruction. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I-3, 293–298. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, T.; Shi, C.; Benediktsson, J.A.; Du, H. Novel Land Cover Change Detection Method Based on k-Means Clustering and Adaptive Majority Voting Using Bitemporal Remote Sensing Images. IEEE Access 2019, 7, 34425–34437. [Google Scholar] [CrossRef]

| Data Set | K | m | λ |
|---|---|---|---|
| Vaihingen | 5 | 15 | 0.2 |
| Potsdam | 3 | 15 | 0.1 |
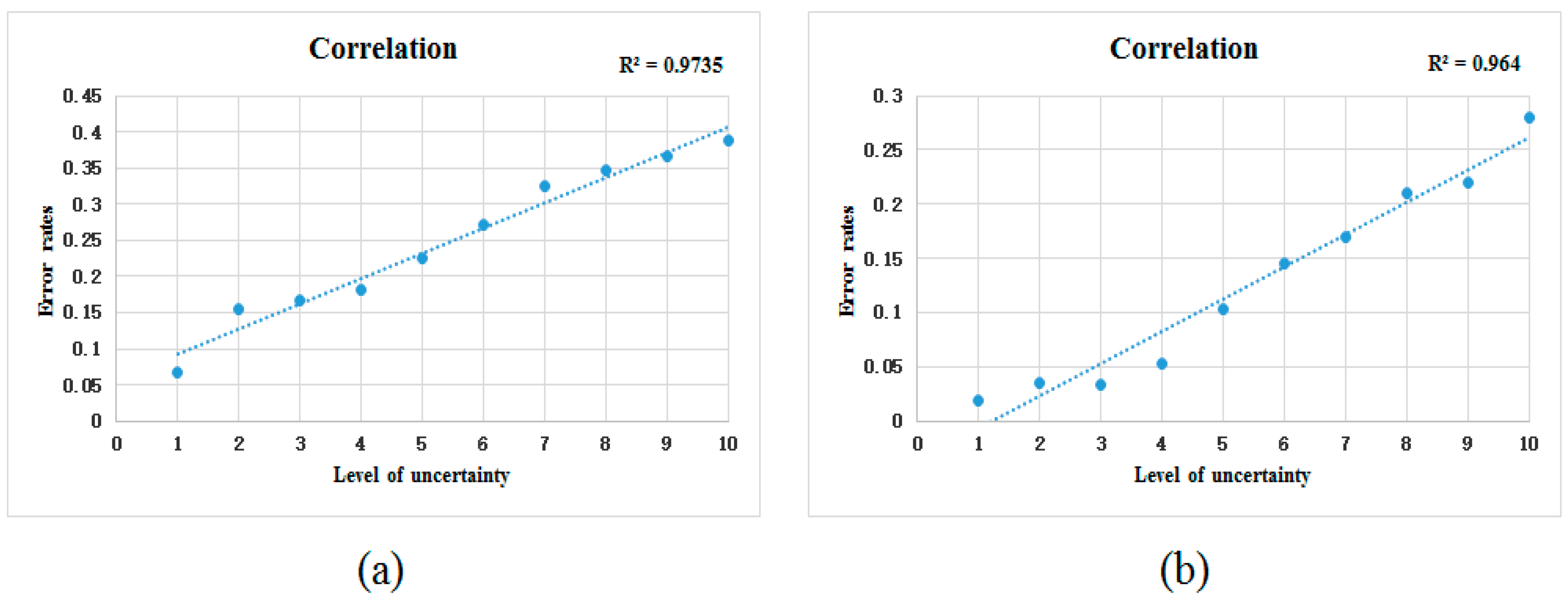
| Datasets. | Equations of the Fitted Curves | Correlation Coefficient R | R2 |
|---|---|---|---|
| Vaihingen | y = 0.0348x + 0.0578 | 0.9867 | 0.9735 |
| Potsdam | y = 0.0297x − 0.0365 | 0.9818 | 0.9640 |
| Classification maps | OA | KC | ||
|---|---|---|---|---|
| Vaihingen | Potsdam | Vaihingen | Potsdam | |
| OCM | 79.0422% | 93.0883% | 0.7144 | 0.8883 |
| FCM_SF | 80.5993% | 93.7199% | 0.7352 | 0.9014 |
| FCM_ DR_SF | 80.8998% | 93.9886% | 0.7392 | 0.9024 |
| K | 3 | 5 | 7 | 9 | 11 | |
|---|---|---|---|---|---|---|
| R2 | Vaihingen | 0.8473 | 0.9735 | 0.9418 | 0.9353 | 0.9466 |
| Potsdam | 0.964 | 0.9513 | 0.9201 | 0.9295 | 0.9235 | |
| m | 5 | 10 | 15 | 20 | 25 | |
|---|---|---|---|---|---|---|
| R2 | Vaihingen | 0.9773 | 0.9909 | 0.9735 | 0.9773 | 0.9665 |
| Potsdam | 0.9396 | 0.9498 | 0.9513 | 0.9493 | 0.943 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Zhang, P.; Xiao, Y. A Modeling and Measurement Approach for the Uncertainty of Features Extracted from Remote Sensing Images. Remote Sens. 2019, 11, 1841. https://doi.org/10.3390/rs11161841
Zhang Q, Zhang P, Xiao Y. A Modeling and Measurement Approach for the Uncertainty of Features Extracted from Remote Sensing Images. Remote Sensing. 2019; 11(16):1841. https://doi.org/10.3390/rs11161841
Chicago/Turabian StyleZhang, Qi, Penglin Zhang, and Yao Xiao. 2019. "A Modeling and Measurement Approach for the Uncertainty of Features Extracted from Remote Sensing Images" Remote Sensing 11, no. 16: 1841. https://doi.org/10.3390/rs11161841
APA StyleZhang, Q., Zhang, P., & Xiao, Y. (2019). A Modeling and Measurement Approach for the Uncertainty of Features Extracted from Remote Sensing Images. Remote Sensing, 11(16), 1841. https://doi.org/10.3390/rs11161841