Identifying Salt Marsh Shorelines from Remotely Sensed Elevation Data and Imagery
Abstract
1. Introduction
2. Materials and Methods
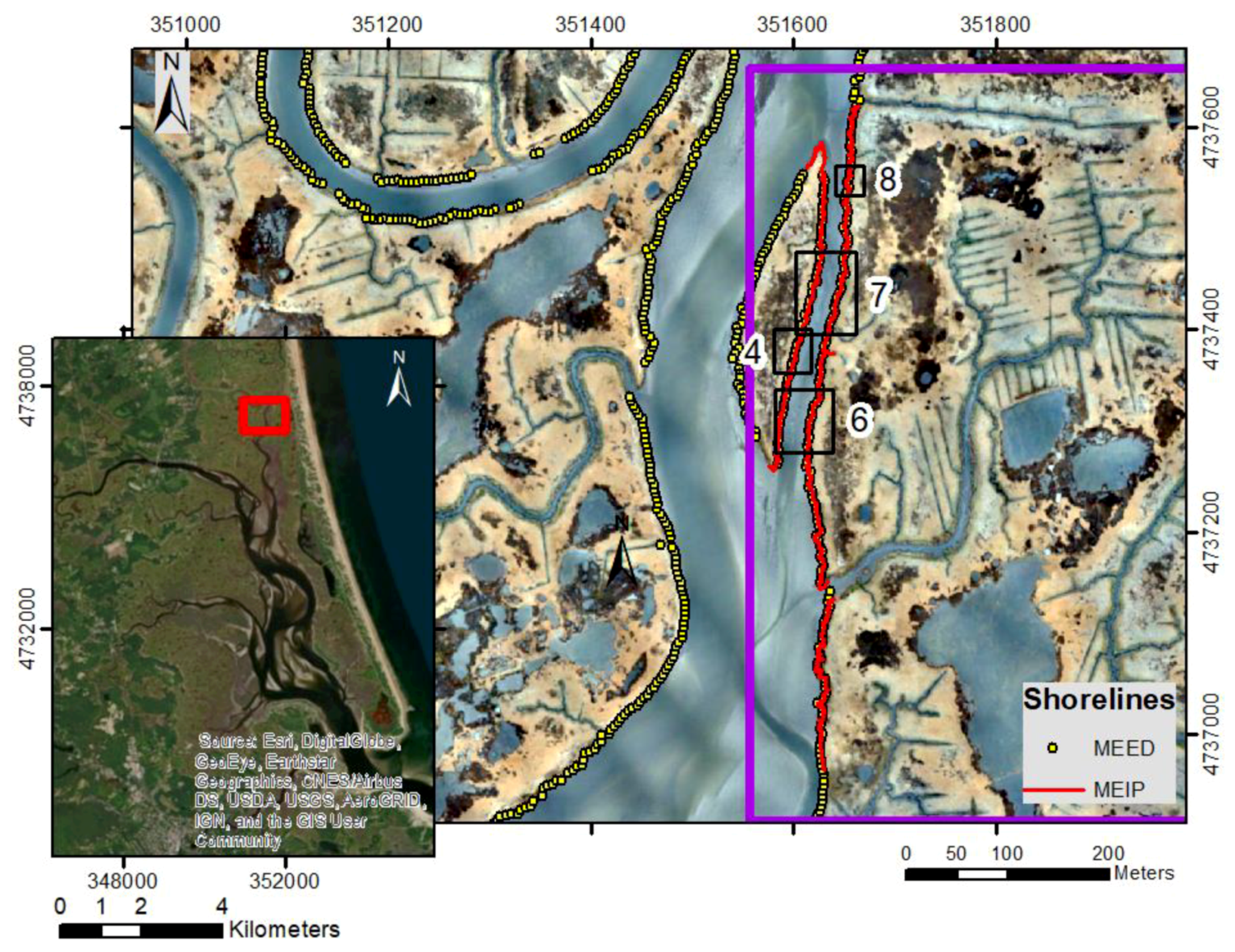
2.1. Study Area
2.2. Data
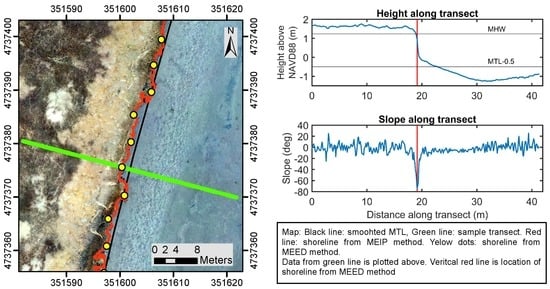
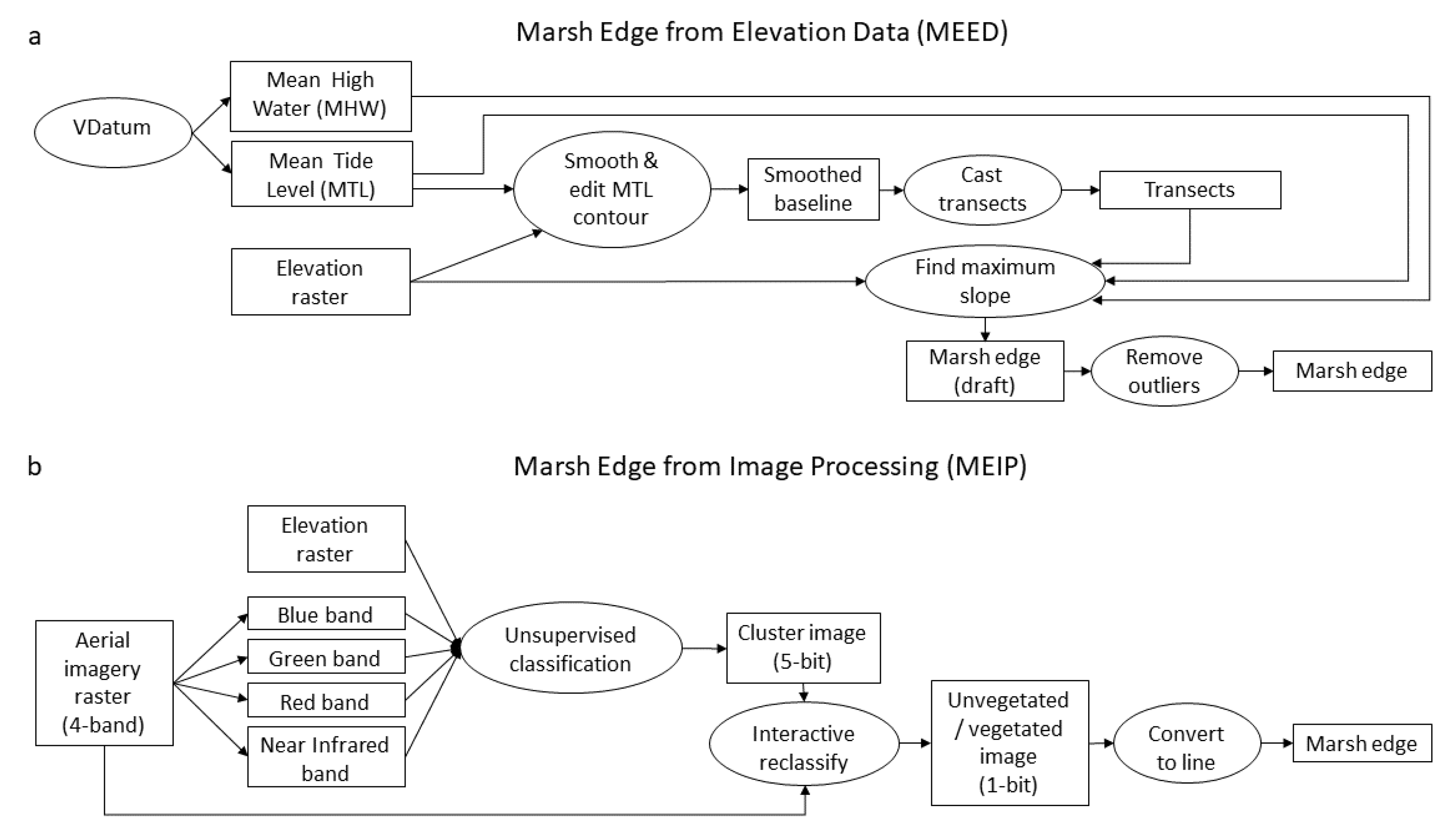
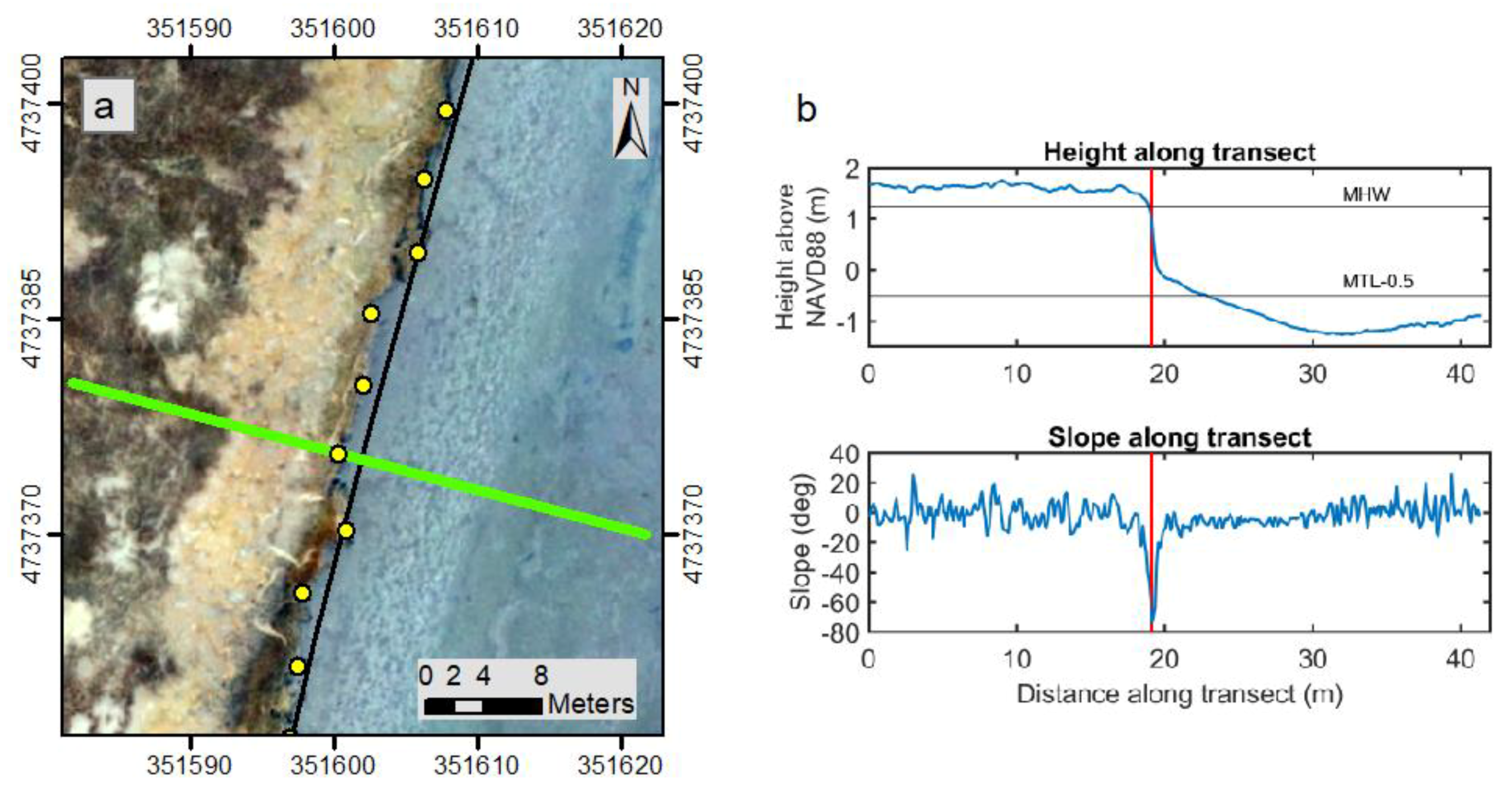
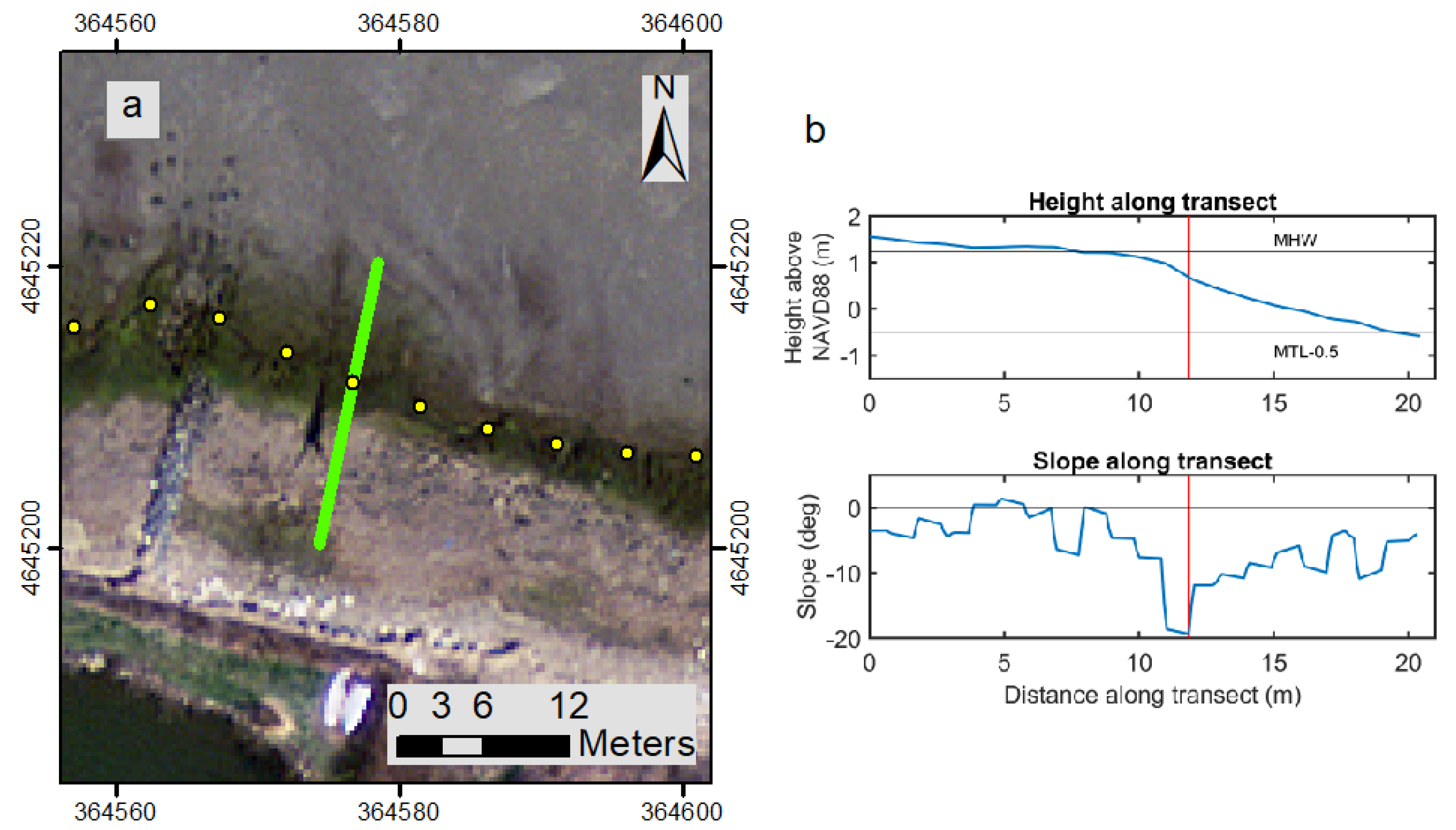
2.3. MEED Methodology
2.4. MEIP Methodology
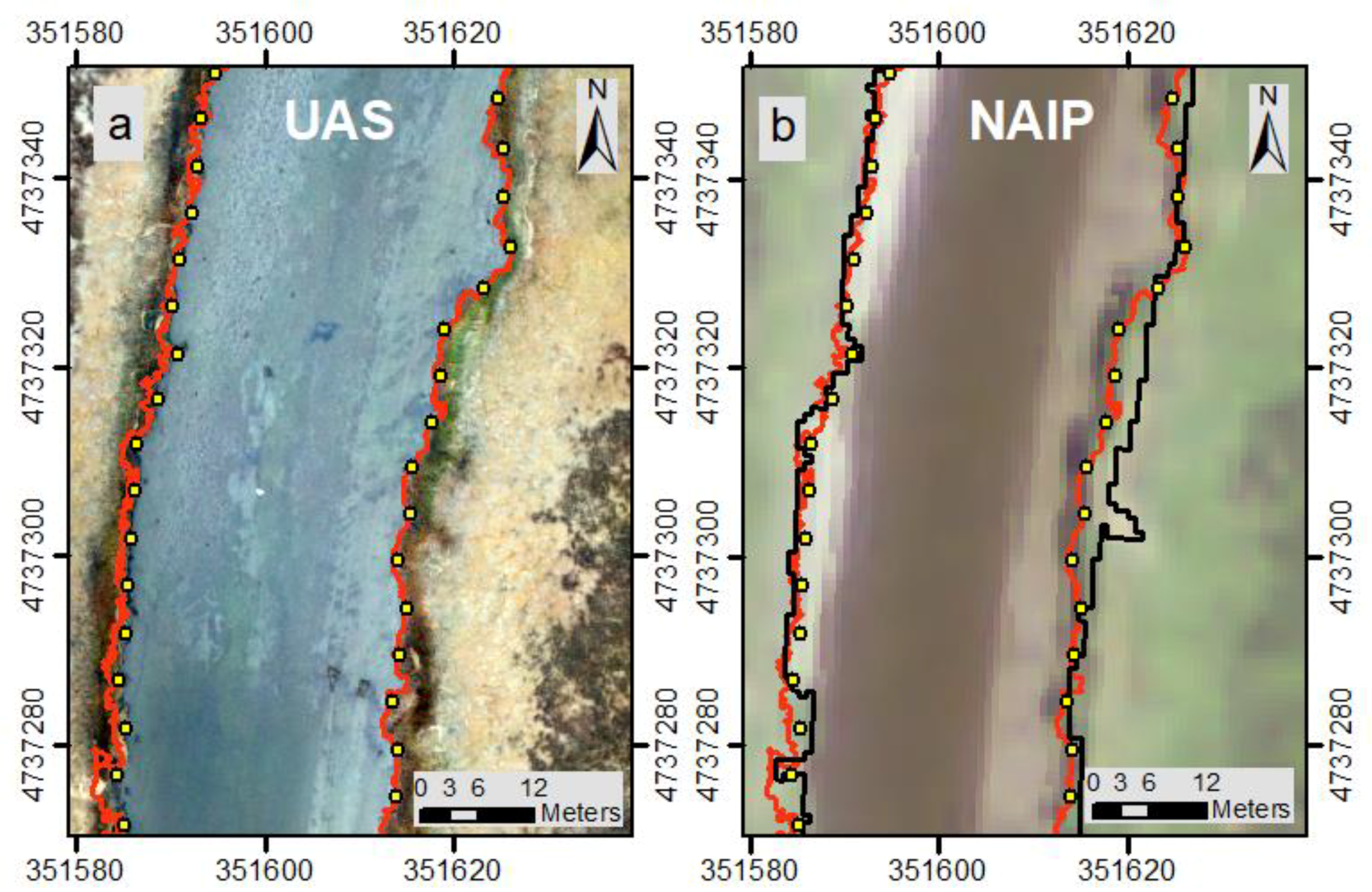
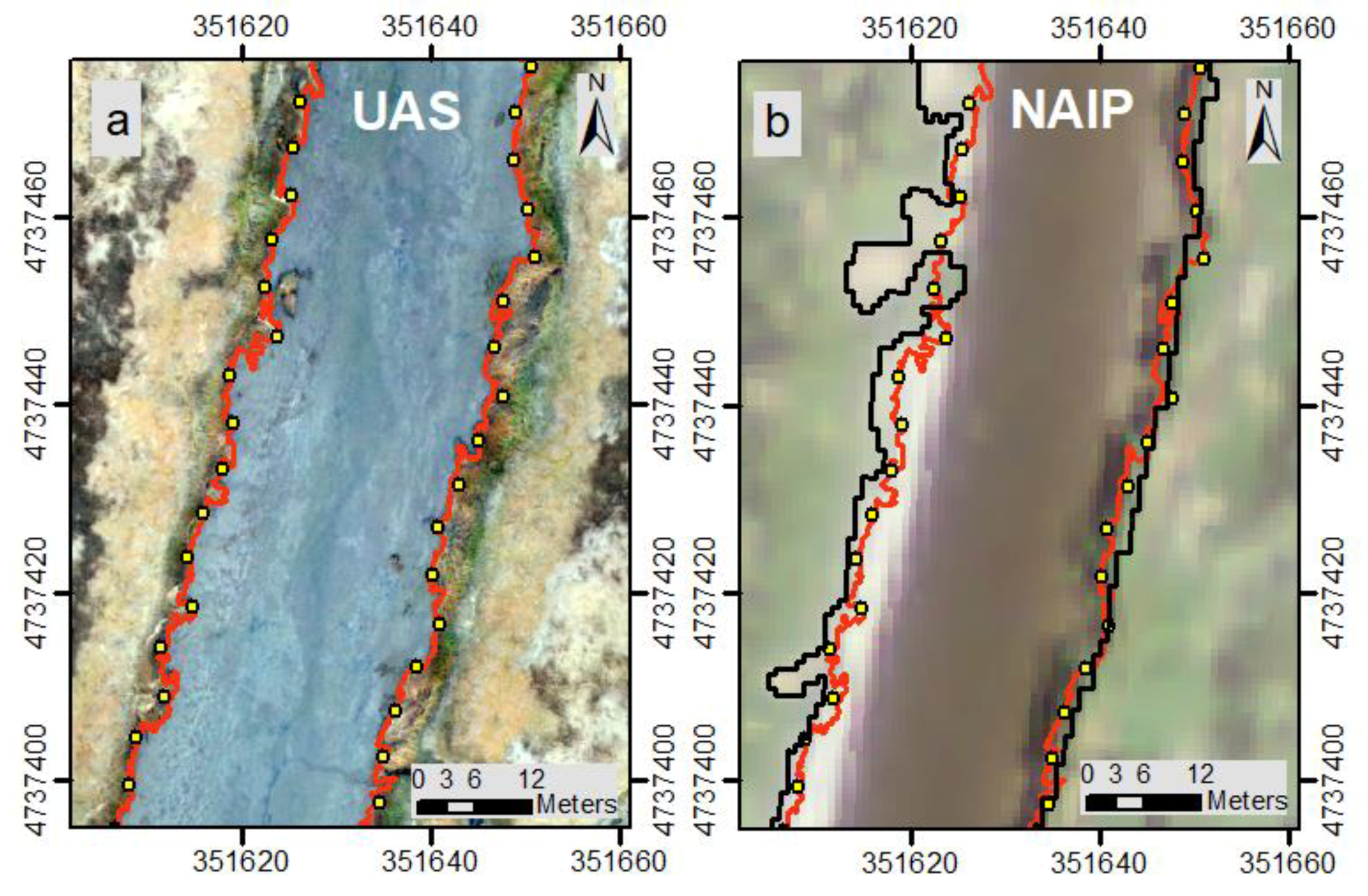
2.5. Heads-Up Digitized Shoreline
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations. UNEP Annual Report; United Nations Environmental Program: Nairobi, Kenya, 2006. [Google Scholar]
- Shepard, C.C.; Crain, C.M.; Beck, M.W. The Protective Role of Coastal Marshes: A Systematic Review and Meta-analysis. PLoS ONE 2011, 6, e27374. [Google Scholar] [CrossRef] [PubMed]
- Chmura, G.L.; Anisfeld, S.C.; Cahoon, D.R.; Lynch, J.C. Global carbon sequestration in tidal, saline wetland soils. Glob. Biogeochem. Cycles 2003, 17. [Google Scholar] [CrossRef]
- Sousa, A.I.; Lillebø, A.I.; Pardal, M.A.; Caçador, I. Productivity and nutrient cycling in salt marshes: Contribution to ecosystem health. Estuar. Coast. Shelf Sci. 2010, 87, 640–646. [Google Scholar] [CrossRef]
- Möller, I.; Kudella, M.; Rupprecht, F.; Spencer, T.; Paul, M.; Van Wesenbeeck, B.K.; Wolters, G.; Jensen, K.; Bouma, T.J.; Miranda-Lange, M.; et al. Wave attenuation over coastal salt marshes under storm surge conditions. Nat. Geosci. 2014, 7, 727–731. [Google Scholar] [CrossRef]
- Gedan, K.B.; Silliman, B.R.; Bertness, M.D. Centuries of Human-Driven Change in Salt Marsh Ecosystems. Annu. Rev. Mar. Sci. 2009, 1, 117–141. [Google Scholar] [CrossRef] [PubMed]
- Kirwan, M.L.; Megonigal, J.P. Tidal wetland stability in the face of human impacts and sea-level rise. Nature 2013, 504, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Deegan, L.A.; Johnson, D.S.; Warren, R.S.; Peterson, B.J.; Fleeger, J.W.; Fagherazzi, S.; Wollheim, W.M. Coastal eutrophication as a driver of salt marsh loss. Nature 2012, 490, 388–392. [Google Scholar] [CrossRef]
- Holdredge, C.; Bertness, M.D.; Altieri, A.H. Role of crab herbivory in die-off of New England salt marshes. Conserv. Biol. 2009, 23, 672–679. [Google Scholar] [CrossRef]
- Craft, C.; Clough, J.; Ehman, J.; Joye, S.; Park, R.; Pennings, S.; Guo, H.; Machmuller, M. Forecasting the effects of accelerated sea-level rise on tidal marsh ecosystem services. Front. Ecol. Environ. 2008, 7, 73–78. [Google Scholar] [CrossRef]
- Weston, N.B. Declining Sediments and Rising Seas: An Unfortunate Convergence for Tidal Wetlands. Estuaries Coasts 2014, 37, 1–23. [Google Scholar] [CrossRef]
- Ganju, N.K.; Defne, Z.; Kirwan, M.L.; Fagherazzi, S.; D’Alpaos, A.; Carniello, L. Spatially integrative metrics reveal hidden vulnerability of microtidal salt marshes. Nat. Commun. 2017, 8, 14156. [Google Scholar] [CrossRef] [PubMed]
- Wigand, C.; Roman, C.T.; Davey, E.; Stolt, M.; Johnson, R.; Hanson, A.; Watson, E.B.; Moran, S.B.; Cahoon, D.R.; Lynch, J.C. Below the disappearing marshes of an urban estuary: Historic nitrogen trends and soil structure. Ecol. Appl. 2014, 24, 633–649. [Google Scholar] [CrossRef] [PubMed]
- Long, J.D.; Porturas, L.D. Herbivore impacts on marsh production depend upon a compensatory continuum mediated by salinity stress. PLoS ONE 2014. [Google Scholar] [CrossRef] [PubMed]
- Defne, Z.; Ganju, N.K. Unvegetated to Vegetated Marsh Ratio in Plum Island Estuary and Parker River Salt Marsh Complex, Massachusetts. Available online: https://www.sciencebase.gov/catalog/item/5b622a13e4b006a11f6f84c5 (accessed on 24 June 2019).
- Cowart, L.; Walsh, J.P.; Corbett, D.R. Analyzing estuarine shoreline change: A case study of Cedar Island, North Carolina. J. Coast. Res. 2010, 26, 817–830. [Google Scholar] [CrossRef]
- McLoughlin, S.M.; Wiberg, P.L.; Safak, I.; McGlathery, K.J. Rates and Forcing of Marsh Edge Erosion in a Shallow Coastal Bay. Estuaries Coasts 2015, 38, 620–638. [Google Scholar] [CrossRef]
- Currin, C.; Davis, J.; Cowart, L.; Malhotra, A.; Fonseca, M. Shoreline Change in the New River Estuary, North Carolina: Rates and Consequences. J. Coast. Res. 2015, 31, 1069–1077. [Google Scholar] [CrossRef]
- Graham, D.; Sault, M.; Bailey, C.J. National Ocean Service Shoreline—Past, Present, and Future. J. Coast. Res. 2003, 19, 14–32. [Google Scholar]
- White, S. Utilization of LIDAR and NOAA’s vertical datum transformation tool (VDatum) for shoreline delineation. In Proceedings of the OCEANS 2007, Vancouver, BC, Canada, 29 September–4 October 2007; pp. 1–6. [Google Scholar]
- Schmid, K.A.; Hadley, B.C.; Wijekoon, N. Vertical accuracy and use of topographic LIDAR data in coastal marshes. J. Coast. Res. 2011, 27, 116–132. [Google Scholar] [CrossRef]
- Campbell, A.; Wang, Y. High Spatial Resolution Remote Sensing for Salt Marsh Mapping and Change Analysis at Fire Island National Seashore. Remote Sens. 2019, 11, 1107. [Google Scholar] [CrossRef]
- Kuleli, T.; Guneroglu, A.; Karsli, F.; Dihkan, M. Automatic detection of shoreline change on coastal Ramsar wetlands of Turkey. Ocean Eng. 2011, 38, 1141–1149. [Google Scholar] [CrossRef]
- White, S.M.; Madsen, E.A. Tracking tidal inundation in a coastal salt marsh with Helikite airphotos: Influence of hydrology on ecological zonation at Crab Haul Creek, South Carolina. Remote Sens. Environ. 2016, 184, 605–614. [Google Scholar] [CrossRef]
- Anders, F.J.; Byrnes, M.R. Accuracy of shoreline change rates as determined from maps and aerial photographs. Shore Beach 1991, 59, 17–26. [Google Scholar]
- Crowell, M.; Leatherman, S.P.; Buckley, M.K. Historical Shoreline Change: Error Analysis and Mapping Accuracy. J. Coast. Res. 1991, 7, 839–852. [Google Scholar]
- Robertson, W.; Whitman, D.; Zhang, K.; Leatherman, S.P. Mapping Shoreline Position Using Airborne Laser Altimetry. J. Coast. Res. 2004, 20, 884–892. [Google Scholar] [CrossRef]
- Moore, L.J.; Ruggiero, P.; List, J.H. Comparing Mean High Water and High Water Line Shorelines: Should Proxy-Datum Offsets be Incorporated into Shoreline Change Analysis? J. Coast. Res. 2006, 22, 894–905. [Google Scholar] [CrossRef]
- Ruggiero, P.; List, J.H. Improving Accuracy and Statistical Reliability of Shoreline Position and Change Rate Estimates. J. Coast. Res. 2009, 25, 1069–1081. [Google Scholar] [CrossRef]
- Stockdon, H.; Sallenger, A.; List, J.; Holman, R. Estimation of Shoreline Position and Change Using Airborne Topographic Lidar Data. J. Coast. Res. 2002, 18, 502–513. [Google Scholar]
- Weber, K.M.; List, J.H.; Morgan, K.L. An Operational Mean High Water Datum for Determination of Shoreline Position from Topographic Lidar Data; Open File Report 2005–1027; U.S. Geological Survey: Reston, VA, USA, 2005.
- White, S.A.; Parrish, C.E.; Calder, B.R.; Pe’eri, S.; Rzhanov, Y. Lidar-derived national shoreline: Empirical and stochastic uncertainty analyses. J. Coast. Res. 2011, 27, 62–74. [Google Scholar] [CrossRef]
- Farris, A.S.; Weber, K.M.; Doran, K.S.; List, J.H. Comparing Methods Used by the U.S. Geological Survey Coastal and Marine Geology Program for Deriving Shoreline Position from Lidar Data; Open-File Report 2018–1121; U.S. Geological Survey: Reston, VA, USA, 2018. [CrossRef]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Digital Shoreline Analysis System (DSAS) Version 5.0 User Guide; Open-File Report 2018–1179; U.S. Geological Survey: Reston, VA, USA, 2018. [CrossRef]
- Gibbs, A.E.; Richmond, B.M. National Assessment of Shoreline Change—Historical Shoreline Change Along the North Coast of Alaska, US–Canadian Border to Icy Cape; Open-File Report 2015–1048; U.S. Geological Survey: Reston, VA, USA, 2015. [CrossRef]
- Himmelstoss, E.A.; Kratzmann, M.G.; Hapke, C.; Thieler, E.R.; List, J. The National Assessment of Shoreline Change: A GIS Compilation of Vector Shorelines and Associated Shoreline Change Data for the New England and Mid-Atlantic Coasts; Open-File Report 2010–1118; U.S. Geological Survey: Reston, VA, USA, 2010.
- Kratzmann, M.G.; Himmelstoss, E.A.; Ruggiero, P.; Thieler, E.R.; Reid, D. The National Assessment of Shoreline Shange—A GIS Compilation of Vector Shorelines and Associated Shoreline Change Data for the Pacific Northwest Coast; Open-File Report 2012–1007; U.S. Geological Survey: Reston, VA, USA, 2010. [CrossRef]
- McKee, K.L.; Patrick, W.H. The Relationship of Smooth Cordgrass (Spartina alterniflora) to Tidal Datums: A Review. Estuaries 1988, 11, 143–151. [Google Scholar] [CrossRef]
- Balke, T.; Stock, M.; Jensen, K.; Bouma, T.J.; Kleyer, M. A global analysis of the seaward salt marsh extent: The importance of tidal range. Water Resour. Res. 2016, 52, 3775–3786. [Google Scholar] [CrossRef]
- Friedrichs, C.T.; Perry, J.E. Tidal Salt Marsh Morphodynamics: A Synthesis. J. Coast. Res. 2001, 17, 7–37. [Google Scholar]
- Mariotti, G.; Fagherazzi, S. A numerical model for the coupled long-term evolution of salt marshes and tidal flats. J. Geophys. Res.-Earth Surf. 2010, 115, 15. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Kirwan, M.L.; Mudd, S.M.; Guntenspergen, G.R.; Temmerman, S.; D’Alpaos, A.; Koppel, J.; Rybczyk, J.M.; Reyes, E.; Craft, C.; et al. Numerical models of salt marsh evolution: Ecological, geomorphic, and climatic factors. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Van De Koppel, J.; Van Der Wal, D.; Bakker, J.P.; Herman, P.M.J. Self-Organization and Vegetation Collapse in Salt Marsh Ecosystems. Am. Nat. 2005, 165, E1–E12. [Google Scholar] [CrossRef]
- Hardisky, M.A.; Gross, M.F.; Klemas, V. Remote Sensing of Coastal Wetlands. BioScience 1986, 36, 453–460. [Google Scholar] [CrossRef]
- Klemas, V. Remote sensing of emergent and submerged wetlands: An overview. Int. J. Remote Sens. 2013, 34, 6286–6320. [Google Scholar] [CrossRef]
- Brown, W.W. Wetland mapping in New Jersey and New York. Photogramm. Eng. Remote Sens. 1978, 44, 303–314. [Google Scholar]
- Cowardin, L.M.; Carter, V.; Golet, F.C.; LaRoe, E.T. Classification of Wetlands and Deepwater Habitats of the United States; U.S. Department of the Interior, US Fish and Wildlife Service: Washington, DC, USA, 1979.
- Dahl, T.E. Status and Trends of Wetlands in the Conterminous United States 2004 to 2009; Fisheries and Habitat Conservation; US Department of the Interior, US Fish and Wildlife Service: Washington, DC, USA, 2011.
- Guo, M.; Li, J.; Sheng, C.; Xu, J.; Wu, L. A Review of Wetland Remote Sensing. Sensors 2017, 17, 777. [Google Scholar] [CrossRef]
- Yang, J.; Artigas, F.J. Mapping salt marsh vegetation by integrating hyperspectral and LiDAR remote sensing. In Remote Sensing of Coastal Environments; CRC Press: Boca Raton, FL, USA, 2009; pp. 173–187. [Google Scholar]
- Ballanti, L.; Byrd, B.K.; Woo, I.; Ellings, C. Remote Sensing for Wetland Mapping and Historical Change Detection at the Nisqually River Delta. Sustainability 2017, 9, 1919. [Google Scholar] [CrossRef]
- Pande-Chhetri, R.; Abd-Elrahman, A.; Liu, T.; Morton, J.; Wilhelm, V.L. Object-based classification of wetland vegetation using very high-resolution unmanned air system imagery. Eur. J. Remote Sens. 2017, 50, 564–576. [Google Scholar] [CrossRef]
- Isaach, J.P.; Costa, C.S.B.; Rodriguez-Gallego, L.; Conde, D.; Escapa, M.; Gagliardini, D.A.; Iribarne, O. Distribution of salt marsh plant communities associated with environmental factors along a latitudinal gradient on SW Atlantic coast. J. Biogeogr. 2006, 33, 888–900. [Google Scholar] [CrossRef]
- Kumar, L.; Sinha, P. Mapping salt-marsh land-cover vegetation using high-spatial and hyperspectral satellite data to assist wetland inventory. GIScience Remote Sens. 2014, 51, 483–497. [Google Scholar] [CrossRef]
- Lane, R.C.; Liu, H.; Autrey, C.B.; Anenkhonov, A.O.; Chepinoga, V.V.; Wu, Q. Improved Wetland Classification Using Eight-Band High Resolution Satellite Imagery and a Hybrid Approach. Remote Sens. 2014, 6, 12187–12216. [Google Scholar] [CrossRef]
- Martin, R.; Brabyn, L.; Beard, C. Effects of class granularity and cofactors on the performance of unsupervised classification of wetlands using multi-spectral aerial photography. J. Spat. Sci. 2014, 59, 269–282. [Google Scholar] [CrossRef]
- Hopkinson, C.S.; Morris, J.T.; Fagherazzi, S.; Wollheim, W.M.; Raymond, P.A. Lateral Marsh Edge Erosion as a Source of Sediments for Vertical Marsh Accretion. J. Geophys. Res. Biogeosci. 2018, 123, 2444–2465. [Google Scholar] [CrossRef]
- Mariotti, G.; Fagherazzi, S. Critical width of tidal flats triggers marsh collapse in the absence of sea-level rise. Proc. Natl. Acad. Sci. USA 2013, 110, 5353–5356. [Google Scholar] [CrossRef]
- OCM Partners. U.S. Geological Survey CMGP LiDAR: Post Sandy (MA, NH, RI), 20170509 ed.; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2017. Available online: https://inport.nmfs.noaa.gov/inport/item/49846 (accessed on 23 March 2017).
- U.S. Geological Survey. High Resolution Orthoimagery. 2013. Available online: http://earthexplorer.usgs.gov (accessed on 13 April 2017).
- Ganju, N.K.; Brosnahan, S.M.; Sturdivant, E.J.; Pendleton, E.A.; Ackerman, S.D. Aerial Imagery from Unmanned Aerial Systems (UAS) Flights—Plum Island Estuary and Parker River NWR (PIEPR); U.S. Geological Survey Data Release: Reston, VA, USA, 2019. [CrossRef]
- Casella, E.; Rovere, A.; Pedroncini, A.; Stark, C.P.; Casella, M.; Ferrari, M.; Firpo, M. Drones as tools for monitoring beach topography changes in the Ligurian Sea (NW Mediterranean). Geo-Mar. Lett. 2016, 36, 151–163. [Google Scholar] [CrossRef]
- Lucieer, A.; Jong, S.M.D.; Turner, D. Mapping landslide displacements using Structure from Motion (SfM) and image correlation of multi-temporal UAV photography. Prog. Phys. Geogr. Earth Environ. 2013, 38, 97–116. [Google Scholar] [CrossRef]
- Warrick, J.A.; Ritchie, A.C.; Adelman, G.; Adelman, K.; Limber, P.W. New Techniques to Measure Cliff Change from Historical Oblique Aerial Photographs and Structure-from-Motion Photogrammetry. J. Coast. Res. 2016, 33, 39–55. [Google Scholar] [CrossRef]
- Sturdivant, J.E.; Lentz, E.E.; Thieler, E.R.; Farris, S.A.; Weber, M.K.; Remsen, P.D.; Miner, S.; Henderson, E.R. UAS-SfM for Coastal Research: Geomorphic Feature Extraction and Land Cover Classification from High-Resolution Elevation and Optical Imagery. Remote Sens. 2017, 9, 1020. [Google Scholar] [CrossRef]
- Hladik, C.; Alber, M. Accuracy assessment and correction of a LIDAR-derived salt marsh digital elevation model. Remote Sens. Environ. 2012, 121, 224–235. [Google Scholar] [CrossRef]
- Rogers, J.N.; Parrish, C.E.; Ward, L.G.; Burdick, D.M. Assessment of elevation uncertainty in salt marsh environments using discrete-return and full-waveform lidar. J. Coast. Res. 2016, 33, 107–122. [Google Scholar] [CrossRef]
- Bodansky, E.; Gribov, A.; Pilouk, M. Smoothing and Compression of Lines Obtained by Raster-to-Vector Conversion. In Graphics Recognition Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2002; pp. 256–265. [Google Scholar]
- Ball, G.H.; Hall, D.J. ISODATA, A Novel Method of Data Analysis and Pattern Classification; SRI International: Menlo Park, CA, USA, 1965. [Google Scholar]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice hall: Englewood Cliffs, NJ, USA, 1988; Volume 6. [Google Scholar]
- Farris, A.S. Marsh Shorelines of the Massachusetts Coast from 2013–2014 Topographic Lidar Data; U.S. Geological Survey data release: Reston, VA, USA, 2018. [CrossRef]
- Millette, T.L.; Argow, B.A.; Marcano, E.; Hayward, C.; Hopkinson, C.S.; Valentine, V. Salt Marsh Geomorphological Analyses via Integration of Multitemporal Multispectral Remote Sensing with LIDAR and GIS. J. Coast. Res. 2010, 26, 809–816. [Google Scholar] [CrossRef]
- Goodwin, G.C.H.; Mudd, S.M.; Clubb, F.J. Unsupervised detection of salt marsh platforms: A topographic method. Earth Surf. Dyn. 2018, 6, 239–255. [Google Scholar] [CrossRef]
- Fagherazzi, S.; Carniello, L.; Alpaos, L.; Defina, A. Critical bifurcation of shallow microtidal landforms in tidal flats and salt marshes. Proc. Natl. Acad. Sci. USA 2006, 103, 8337–8341. [Google Scholar] [CrossRef] [PubMed]
- Defina, A.; Carniello, L.; Fagherazzi, S.; D’Alpaos, L. Self-organization of shallow basins in tidal flats and salt marshes. J. Geophys. Res. Earth Surf. 2007, 112. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farris, A.S.; Defne, Z.; Ganju, N.K. Identifying Salt Marsh Shorelines from Remotely Sensed Elevation Data and Imagery. Remote Sens. 2019, 11, 1795. https://doi.org/10.3390/rs11151795
Farris AS, Defne Z, Ganju NK. Identifying Salt Marsh Shorelines from Remotely Sensed Elevation Data and Imagery. Remote Sensing. 2019; 11(15):1795. https://doi.org/10.3390/rs11151795
Chicago/Turabian StyleFarris, Amy S., Zafer Defne, and Neil K. Ganju. 2019. "Identifying Salt Marsh Shorelines from Remotely Sensed Elevation Data and Imagery" Remote Sensing 11, no. 15: 1795. https://doi.org/10.3390/rs11151795
APA StyleFarris, A. S., Defne, Z., & Ganju, N. K. (2019). Identifying Salt Marsh Shorelines from Remotely Sensed Elevation Data and Imagery. Remote Sensing, 11(15), 1795. https://doi.org/10.3390/rs11151795