Forecasting GRACE Data over the African Watersheds Using Artificial Neural Networks
Abstract
1. Introduction
2. Materials and Methods
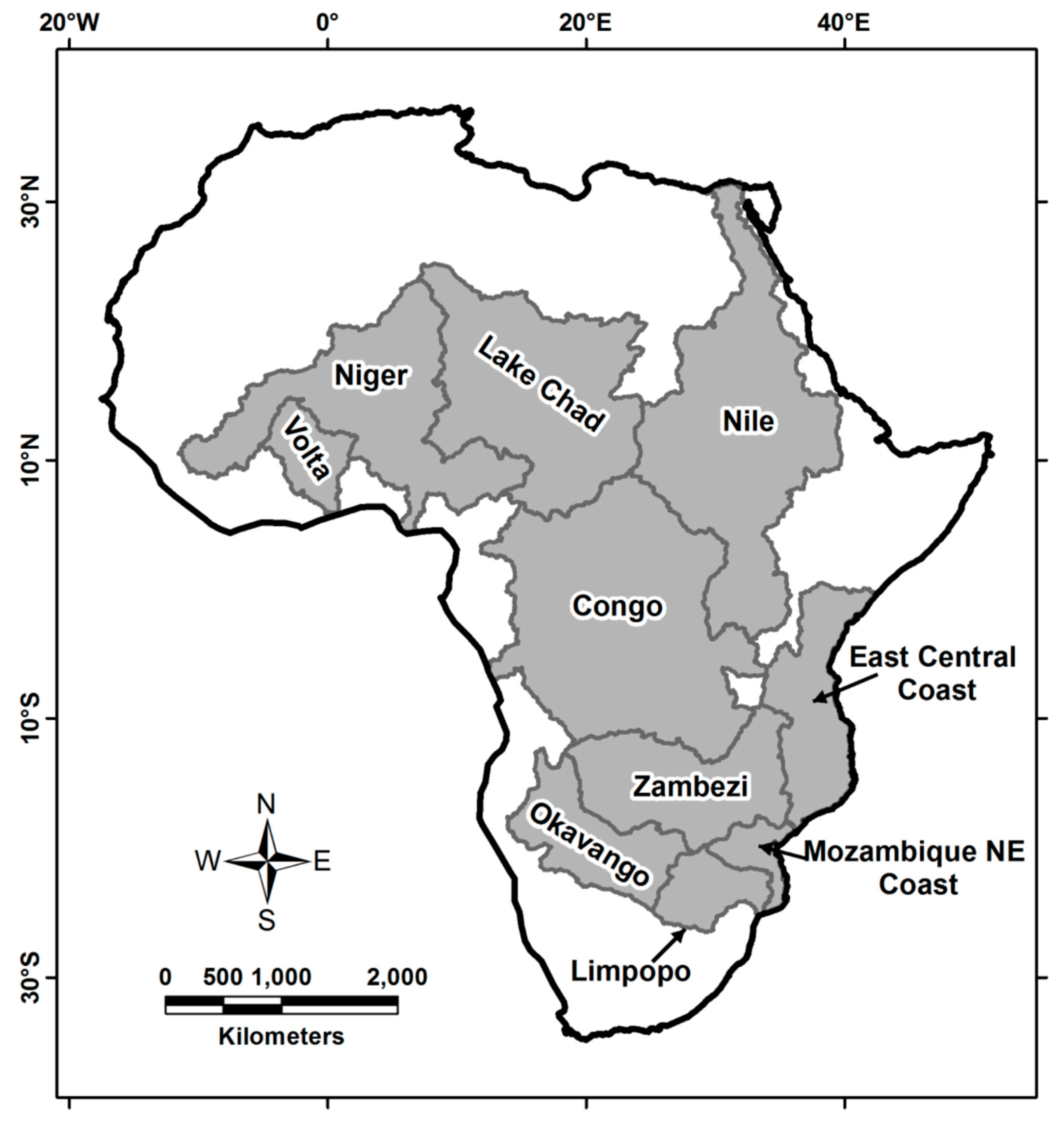
2.1. Data
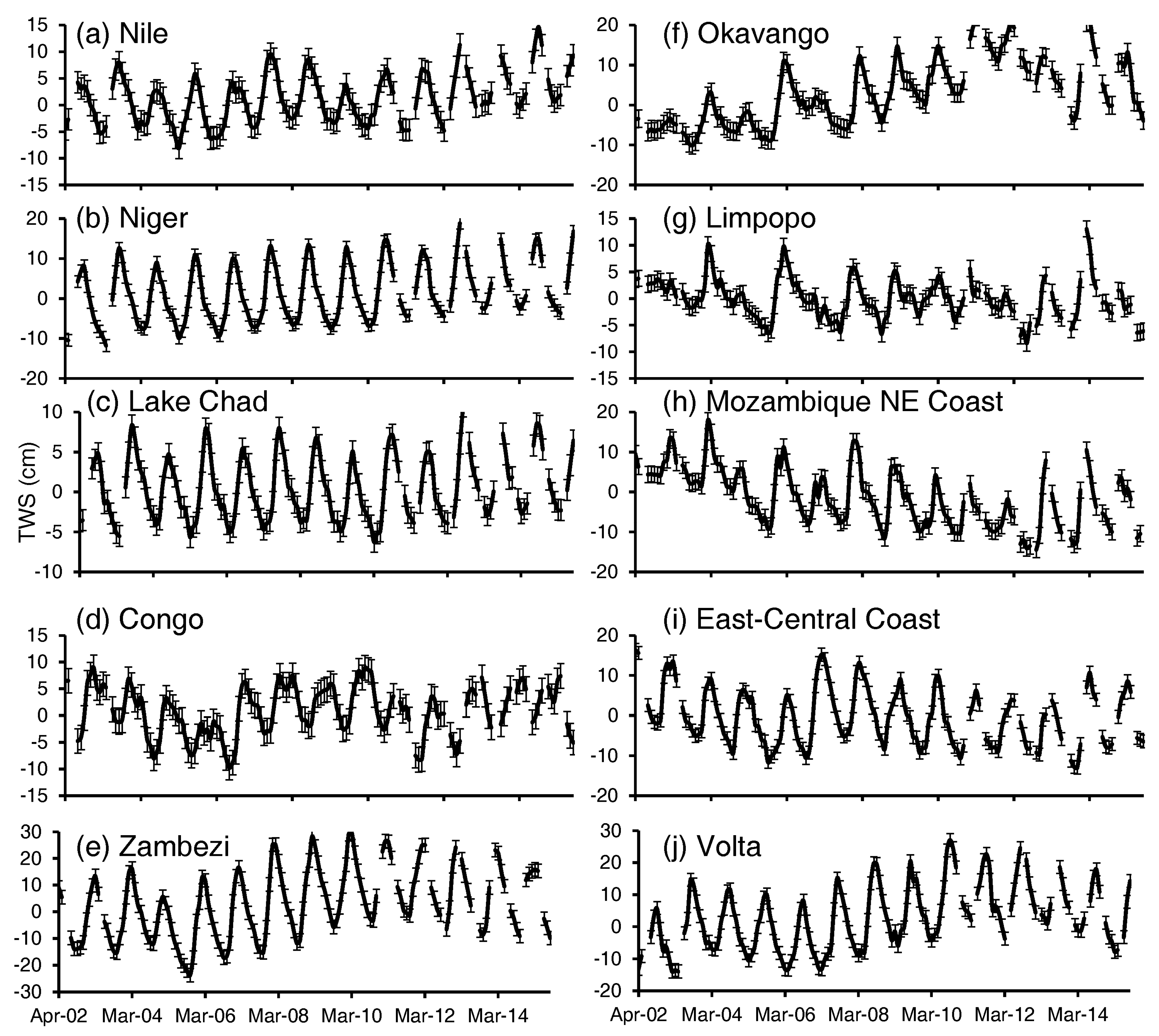
2.1.1. Gravity Recovery and Climate Experiment (GRACE)-derived Terrestrial Water Storage (TWS) (TWSGRACE)
2.1.2. Rainfall (P)
2.1.3. Evapotranspiration (ET)
2.1.4. Temperature (T)
2.1.5. Normalized Difference Vegetation Index (NDVI)
2.2. Approach
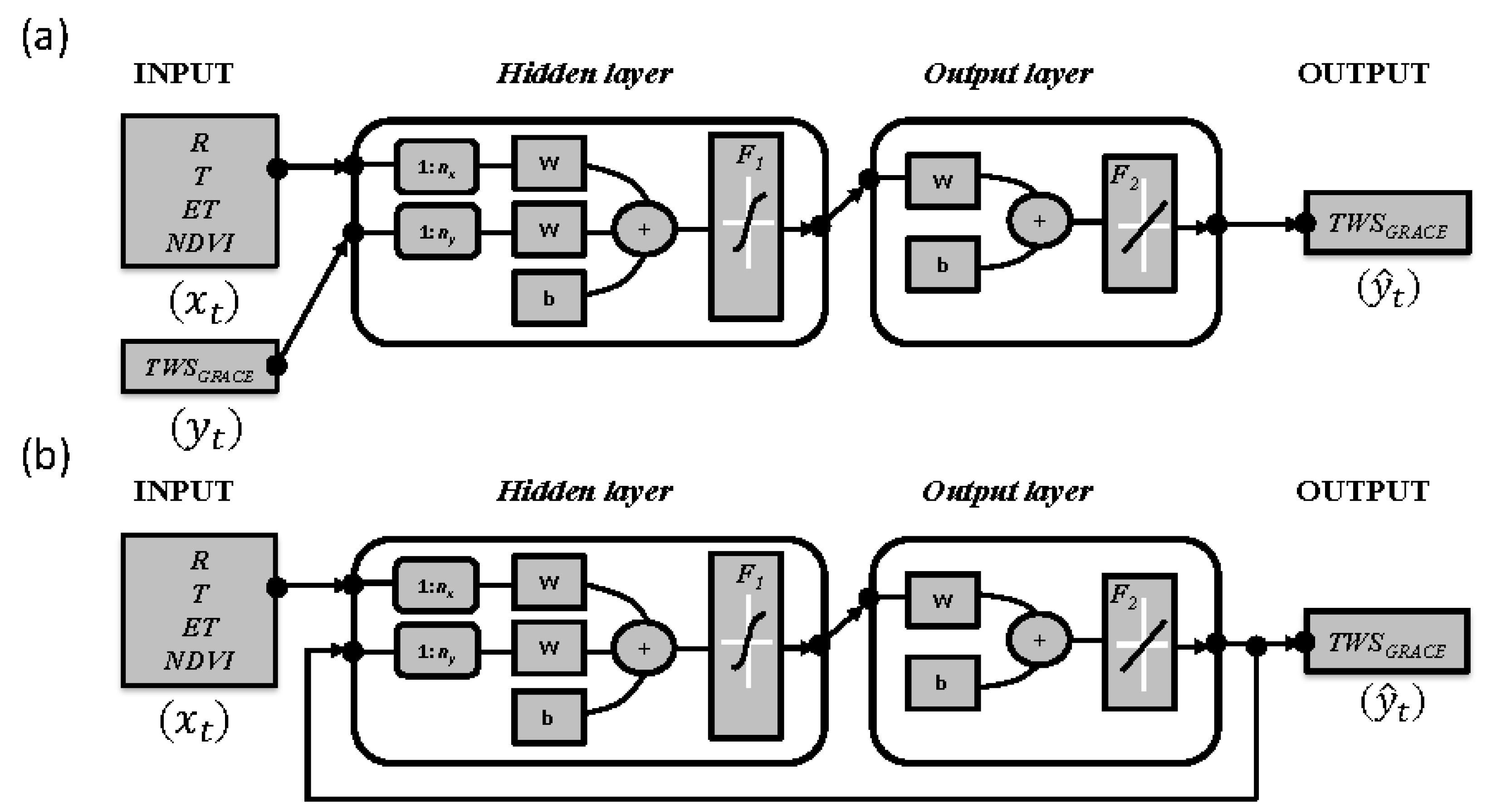
2.2.1. Nonlinear Autoregressive with Exogenous Input (NARX) Model
2.2.2. Nonlinear Autoregressive with Exogenous Input (NARX) Model Structure
2.2.3. Performance Measures
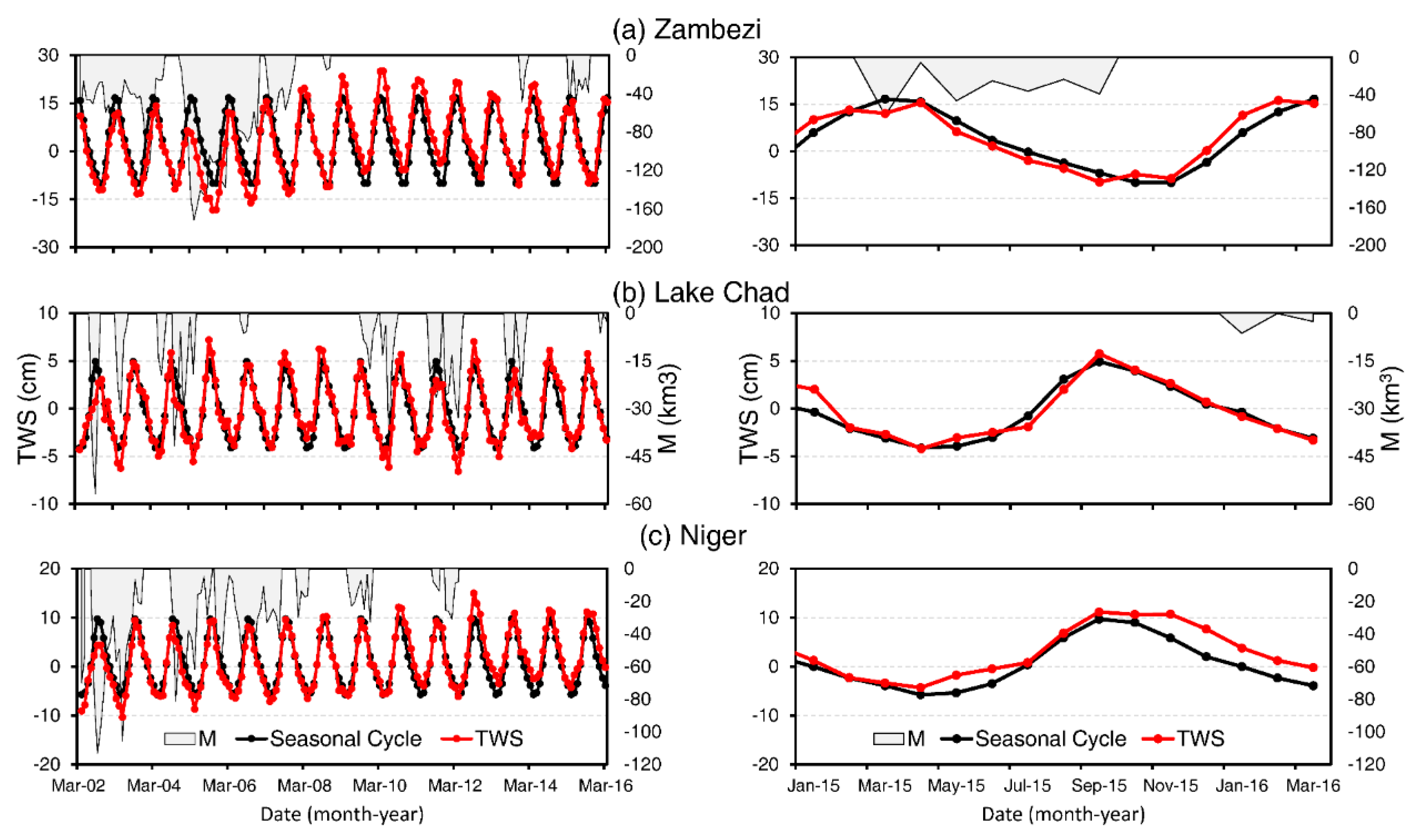
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Ahmed, M.; Sultan, M.; Yan, E.; Wahr, J. Assessing and Improving Land Surface Model Outputs over Africa using GRACE, Field, and Remote Sensing Data. Surv. Geophys. 2016, 37, 529–556. [Google Scholar] [CrossRef]
- Mohamed, A.; Sultan, M.; Ahmed, M.; Yan, E.; Ahmed, E. Aquifer recharge, depletion, and connectivity: Inferences from GRACE, land surface models, geochemical, and geophysical data. GSA Bull. 2016, 129, 1–13. [Google Scholar] [CrossRef]
- Famiglietti, J.S. The global groundwater crisis. Nat. Clim. Chang. 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef] [PubMed]
- Tapley, B.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Famiglietti, J.; Landerer, F.; Chambers, D.; Reager, J.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef]
- Ahmed, M.; Sultan, M.; Wahr, J.; Yan, E. The use of GRACE data to monitor natural and anthropogenic induced variations in water availability across Africa. Earth-Sci. Rev. 2014, 136, 289–300. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B. High resolution CSR GRACE RL05 mascons. J. Geophys. Res. 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Voss, K.A.; Famiglietti, J.S.; Lo, M.; De Linage, C.; Rodell, M.; Swenson, S.C. Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region. Water Resour. Res. 2013, 49, 904–914. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Zhong, M.; Lemoine, J.-M.; Biancale, R.; Hsu, H.-T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Joodaki, G.; Wahr, J.; Swenson, S. Estimating the human contribution to groundwater depletion in theMiddle East, fromGRACE data, land surfacemodels, and well observations. Water Resour. Res. 2014, 50, 1–14. [Google Scholar] [CrossRef]
- Castle, S.; Thomas, B.; Reager, J.; Rodell, M.; Swenson, S.; Famiglietti, J. Groundwater depleation during drought threatens future water security of the Colorado River Basin. Geophys. Res. Lett. 2014, 10, 5904–5911. [Google Scholar] [CrossRef] [PubMed]
- Fallatah, O.A.; Ahmed, M.; Save, H.; Akanda, A.S. Quantifying Temporal Variations in Water Resources of a Vulnerable Middle Eastern Transboundary Aquifer System. Hydrol. Process. 2017, 31, 4081–4091. [Google Scholar] [CrossRef]
- Fallatah, O.A.; Ahmed, M.; Cardace, D.; Boving, T.; Akanda, A.S. Assessment of Modern Recharge to Arid Region Aquifers Using an Integrated Geophysical, Geochemical, and Remote Sensing Approach. J. Hydrol. 2018. [Google Scholar] [CrossRef]
- Ahmed, M.; Abdelmohsen, K. Quantifying Modern Recharge and Depletion Rates of the Nubian Aquifer in Egypt. Surv. Geophys. 2018, 39, 729–751. [Google Scholar] [CrossRef]
- Houborg, R.; Rodell, M.; Li, B.; Reichle, R.; Zaitchik, B.F. Drought indicators based on model-assimilated Gravity Recovery and Climate Experiment (GRACE) terrestrial water storage observations. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Eicker, A.; Schumacher, M.; Kusche, J.; Döll, P.; Schmied, H.M. Calibration/Data Assimilation Approach for Integrating GRACE Data into the WaterGAP Global Hydrology Model (WGHM) Using an Ensemble Kalman Filter: First Results. Surv. Geophys. 2014, 35, 1285–1309. [Google Scholar] [CrossRef]
- Zaitchik, B.F.; Rodell, M.; Reichle, R.H. Assimilation of GRACE Terrestrial Water Storage Data into a Land Surface Model: Results for the Mississippi River Basin. J. Hydrometeorol. 2008, 9, 535–548. [Google Scholar] [CrossRef]
- Gruber, C.; Gouweleeuw, B. Short-latency monitoring of continental, ocean- and atmospheric mass variations using GRACE intersatellite accelerations. Geophys. J. Int. 2019, 217, 714–728. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Rodell, M. Water in the balance. Science 2013, 340, 1300–1301. [Google Scholar] [CrossRef] [PubMed]
- Reager, J.T.; Famiglietti, J.S. Characteristic mega-basin water storage behavior using GRACE. Water Resour. Res. 2013, 49, 3314–3329. [Google Scholar] [CrossRef] [PubMed]
- Döll, P.; Müller Schmied, H.; Schuh, C.; Portmann, F.T.; Eicker, A. Global-scale assessment of groundwater depletion and related groundwater abstractions: Combining hydrological modeling with information from well observations and GRACE satellites. Water Resour. Res. 2014, 50, 5698–5720. [Google Scholar] [CrossRef]
- Güntner, A.; Stuck, J.; Werth, S.; Döll, P.; Verzano, K.; Merz, B. A global analysis of temporal and spatial variations in continental water storage. Water Resour. Res. 2007, 43, 1–19. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L.; Seneviratne, S.I. Assessing Global Water Storage Variability from GRACE: Trends, Seasonal Cycle, Subseasonal Anomalies and Extremes. Surv. Geophys. 2016, 37, 357–395. [Google Scholar] [CrossRef]
- Döll, P.; Fritsche, M.; Eicker, A.; Müller Schmied, H. Seasonal Water Storage Variations as Impacted by Water Abstractions: Comparing the Output of a Global Hydrological Model with GRACE and GPS Observations. Surv. Geophys. 2014, 35, 1311–1331. [Google Scholar] [CrossRef]
- Forootan, E.; Safari, A.; Mostafaie, A.; Schumacher, M.; Delavar, M.; Awange, J.L. Large-Scale Total Water Storage and Water Flux Changes over the Arid and Semiarid Parts of the Middle East from GRACE and Reanalysis Products. Surv. Geophys. 2016, 1–25. [Google Scholar] [CrossRef]
- Harvey, C.L.; Dixon, H.; Hannaford, J. Developing best practice for infilling daily river flow data. Br. Hydrol. Soc. 2010, 816–823. [Google Scholar] [CrossRef][Green Version]
- Soro, G.; Noufé, D.; Goula Bi, T.; Shorohou, B. Trend Analysis for Extreme Rainfall at Sub-Daily and Daily Timescales in Côte d’Ivoire. Climate 2016, 4, 37. [Google Scholar] [CrossRef]
- Machiwal, D.; Kumar, S.; Dayal, D. Characterizing rainfall of hot arid region by using time-series modeling and sustainability approaches: A case study from Gujarat, India. Theor. Appl. Climatol. 2016, 124, 593–607. [Google Scholar] [CrossRef]
- Adeloye, A.J.; Montaseri, M. Preliminary streamflow data analyses prior to water resources planning study. Hydrol. Sci. J. 2002, 47, 679–692. [Google Scholar] [CrossRef]
- Adamowski, K.; Bougadis, J. Detection of trends in annual extreme rainfall. Hydrol. Process. 2003, 17, 3547–3560. [Google Scholar] [CrossRef]
- Markonis, Y.; Koutsoyiannis, D. Climatic Variability over Time Scales Spanning Nine Orders of Magnitude: Connecting Milankovitch Cycles with Hurst–Kolmogorov Dynamics. Surv. Geophys. 2013, 34, 181–207. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, T. Terrestrial Water Storage Anomalies Associated with Drought in Southwestern USA from GPS Observations. Surv. Geophys. 2016, 37, 1139–1156. [Google Scholar] [CrossRef]
- Yozgatligil, C.; Aslan, S.; Iyigun, C.; Batmaz, I. Comparison of missing value imputation methods in time series: The case of Turkish meteorological data. Theor. Appl. Climatol. 2013, 112, 143–167. [Google Scholar] [CrossRef]
- Campozano, L.; Sánchez, E.; Aviles, A.; Samaniego, E. Evaluation of infilling methods for time series of daily precipitation and temperature: The case of the Ecuadorian Andes. Maskana 2014, 5, 99–115. [Google Scholar] [CrossRef]
- Beauchamp, J.J.; Downing, D.J.; Railsback, S.F. Comparison of regression and time-series methods for synthesizing missing streamflow records. J. Am. Water Resour. Assoc. 1989, 25, 961–975. [Google Scholar] [CrossRef]
- Gould, P.G.; Koehler, A.B.; Ord, J.K.; Snyder, R.D.; Hyndman, R.J.; Vahid-Araghi, F. Forecasting time series with multiple seasonal patterns. Eur. J. Oper. Res. 2008, 191, 207–222. [Google Scholar] [CrossRef]
- Mwale, F.D.; Adeloye, A.J.; Rustum, R. Infilling of missing rainfall and streamflow data in the Shire River basin, Malawi—A self organizing map approach. Phys. Chem. Earth Parts A/B/C 2012, 50, 34–43. [Google Scholar] [CrossRef]
- Infilling missing daily precipitation data at multiple sites using a multivariate truncated normal distribution model. Available online: http://adsabs.harvard.edu/abs/2009AGUFM.H31D0813N (accessed on 27 July 2019).
- Tum, M.; Günther, K.P.; Böttcher, M.; Baret, F.; Bittner, M.; Brockmann, C.; Weiss, M. Global gap-free MERIS LAI time series (2002–2012). Remote Sens. 2016, 8, 69. [Google Scholar] [CrossRef]
- Hasan, E. The challenges and opportunities of hydrologic remote sensing in data-poor regions: Case study of Nile River Basin. In Proceedings of the AGU Fall Meeting 2015, San Francisco, CA, USA, 14–18 December 2015. [Google Scholar]
- Long, D.; Scanlon, B.R.; Longuevergne, L.; Sun, A.Y.; Fernando, D.N.; Save, H. GRACE satellite monitoring of large depletion in water storage in response to the 2011 drought in Texas. Geophys. Res. Lett. 2013, 40, 3395–3401. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Oleson, K.W.; Niu, G.Y.; Yang, Z.L.; Lawrence, D.M.; Thornton, P.E.; Lawrence, P.J.; Stöckli, R.; Dickinson, R.E.; Bonan, G.B.; Levis, S.; et al. Improvements to the community land model and their impact on the hydrological cycle. J. Geophys. Res. Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Döll, P.; Kaspar, F.; Lehner, B. A global hydrological model for deriving water availability indicators: Model tuning and validation. J. Hydrol. 2003, 270, 105–134. [Google Scholar] [CrossRef]
- Fan, Y.; van den Dool, H. Climate Prediction Center global monthly soil moisture data set at 0.5° resolution for 1948 to present. J. Geophys. Res. Atmos. 2004, 109, 1–8. [Google Scholar] [CrossRef]
- Forootan, E.; Kusche, J.; Loth, I.; Schuh, W.-D.; Eicker, A.; Awange, J.; Longuevergne, L.; Diekkrüger, B.; Schmidt, M.; Shum, C.K. Multivariate Prediction of Total Water Storage Changes over West Africa from Multi-Satellite Data. Surv. Geophys. 2014, 35, 913–940. [Google Scholar] [CrossRef]
- De Linage, C.; Famiglietti, J.S.; Randerson, J.T. Statistical prediction of terrestrial water storage changes in the Amazon Basin using tropical Pacific and North Atlantic sea surface temperature anomalies. Hydrol. Earth Syst. Sci. 2014, 18, 2089–2102. [Google Scholar] [CrossRef]
- Rietbroek, R.; Fritsche, M.; Dahle, C.; Brunnabend, S.-E.; Behnisch, M.; Kusche, J.; Flechtner, F.; Schröter, J.; Dietrich, R. Can GPS-Derived Surface Loading Bridge a GRACE Mission Gap? Surv. Geophys. 2014, 35, 1267–1283. [Google Scholar] [CrossRef]
- Wahr, J.; Burgess, E.; Swenson, S. Using GRACE and climate model simulations to predict mass loss of Alaskan glaciers through 2100. J. Glaciol. 2016, 62, 623–639. [Google Scholar] [CrossRef]
- Becker, M.; Meyssignac, B.; Xavier, L.; Cazenave, A.; Alkama, R.; Decharme, B. Past terrestrial water storage (1980–2008) in the Amazon Basin reconstructed from GRACE and in situ river gauging data. Hydrol. Earth Syst. Sci. 2011, 15, 533–546. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L.; Seneviratne, S.I. A global reconstruction of climate-driven subdecadal water storage variability. Geophys. Res. Lett. 2017, 44, 2300–2309. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Remote Sensing of Environment Drought and fl ood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Ferreira, V.; Andam-Akorful, S.; Dannouf, R.; Adu-Afari, E. A Multi-Sourced Data Retrodiction of Remotely Sensed Terrestrial Water Storage Changes for West Africa. Water 2019, 11, 401. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Gurney, K. An Introduction to Neural Networks; UCL Press Limited: London, UK, 1997; ISBN 0203451511. [Google Scholar]
- Govindaraju, R.S.; Rao, A.R.; Adiseshappa, R. Artificial Neural Networks in Hydrology; Kluwer Academic Publishers: Doderek, The Netherlands, 2000; ISBN 9780792362265. [Google Scholar]
- Agatonovic-Kustrin, S.; Agatonovic-Kustrin, S. Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef]
- Chang, F.-J.; Chang, Y.-T. Adaptive neuro-fuzzy inference system for prediction of water level in reservoir. Adv. Water Resour. 2006, 29, 1–10. [Google Scholar] [CrossRef]
- House-Peters, L.A.; Chang, H. Urban water demand modeling: Review of concepts, methods, and organizing principles. Water Resour. Res. 2011, 47, W05401. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Model. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Moradkhani, H.; Hsu, K.; Gupta, H.V.; Sorooshian, S. Improved streamflow forecasting using self-organizing radial basis function artificial neural networks. J. Hydrol. 2004, 295, 246–262. [Google Scholar] [CrossRef]
- Coulibaly, P.; Anctil, Ë.; Rasmussen, P.; Bobe, B. A recurrent neural networks approach using indices of low- frequency climatic variability to forecast regional annual runoff. Hydrol. Process. 2000, 2777, 2755–2777. [Google Scholar] [CrossRef]
- Coulibaly, P.; Anctil, F.; Aravena, R.; Bobée, B. Artificial neural network modeling of water table depth fluctuations. Water Resour. Res. 2001, 37, 885–896. [Google Scholar] [CrossRef]
- Coppola, E.A.; Szidarovszky, F.; Davis, D.; Spayd, S.; Poulton, M.M.; Roman, E. Multiobjective analysis of a public wellfield using artificial neural networks. Ground Water 2007, 45, 53–61. [Google Scholar] [CrossRef] [PubMed]
- Coppola, E.A.; McLane, C.F.; Poulton, M.M.; Szidarovszky, F.; Magelky, R.D. Predicting conductance due to upconing using neural networks. Ground Water 2005, 43, 827–836. [Google Scholar] [CrossRef] [PubMed]
- Coppola, E.A.; Rana, A.J.; Poulton, M.M.; Szidarovszky, F.; Uhl, V.W. A neural network model for predicting aquifer water level elevations. Ground Water 2005, 43, 231–241. [Google Scholar] [CrossRef] [PubMed]
- Chu, H.-J.; Chang, L.-C. Optimal control algorithm and neural network for dynamic groundwater management. Hydrol. Process. 2009, 23, 2765–2773. [Google Scholar] [CrossRef]
- Feng, S.; Kang, S.; Huo, Z.; Chen, S.; Mao, X. Neural networks to simulate regional ground water levels affected by human activities. Ground Water 2008, 46, 80–90. [Google Scholar] [CrossRef]
- Sun, A.Y. Predicting groundwater level changes using GRACE data. Water Resour. Res. 2013, 49, 5900–5912. [Google Scholar] [CrossRef]
- Ahmed, M.; Sultan, M.; Wahr, J.; Yan, E.; Milewski, A.; Sauck, W.; Becker, R.; Welton, B. Integration of GRACE (Gravity Recovery and Climate Experiment) data with traditional data sets for a better understanding of the timedependent water partitioning in African watersheds. Geology 2011, 39, 479–482. [Google Scholar] [CrossRef]
- Menezes, J.M.P., Jr.; Barreto, G.A. Multistep-Ahead Prediction of Rainfall Precipitation Using the NARX Network. ESTSP Proceedings 2008, 1, 87–96. [Google Scholar]
- Anh, H.P.H.; Ahn, K.K. Hybrid control of a pneumatic artificial muscle (PAM) robot arm using an inverse NARX fuzzy model. Eng. Appl. Artif. Intell. 2011, 24, 697–716. [Google Scholar] [CrossRef]
- Boussaada, Z.; Curea, O.; Remaci, A.; Camblong, H.; Mrabet Bellaaj, N. A Nonlinear Autoregressive Exogenous (NARX) Neural Network Model for the Prediction of the Daily Direct Solar Radiation. Energies 2018, 11, 620. [Google Scholar] [CrossRef]
- Ruiz, L.; Cuéllar, M.; Calvo-Flores, M.; Jiménez, M. An Application of Non-Linear Autoregressive Neural Networks to Predict Energy Consumption in Public Buildings. Energies 2016, 9, 684. [Google Scholar] [CrossRef]
- Menezes, J.; Barreto, G. A New Look at Nonlinear Time Series Prediction with NARX Recurrent Neural Network. In Proceedings of the 2006 Ninth Brazilian Symposium on Neural Networks (SBRN’06), Ribeirao Preto, Brazil, 23–27 October 2006; pp. 160–165. [Google Scholar]
- Cadenas, E.; Rivera, W.; Campos-Amezcua, R.; Heard, C. Wind Speed Prediction Using a Univariate ARIMA Model and a Multivariate NARX Model. Energies 2016, 9, 109. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. 2011, 116, B01409. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. 2008, 113, B08410. [Google Scholar] [CrossRef]
- Peltier, W.; Argus, D.F.; Drummond, R. Comment on “An Assessment of the ICE-6G_C (VM5a) Glacial Isostatic Adjustment Model” by Purcell et al. J. Geophys. Res. Solid Earth 2018, 123, 2019–2028. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, 1–11. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Adeyewa, Z.D.; Nakamura, K.; DeboAdeyewa, Z. KenjiNakamura Validation of TRMM Radar Rainfall Data over Major Climatic Regions in Africa. J. Appl. Meteorol. 2003, 42, 331–347. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Grover-Kopec, E.; Lemma, M.; Connor, S.J.; Ropelewski, C.F. Validation of satellite rainfall products over East Africa’s complex topography. Int. J. Remote Sens. 2007, 28, 1503–1526. [Google Scholar] [CrossRef]
- Beighley, R.E.; Ray, R.L.; He, Y.; Lee, H.; Schaller, L.; Andreadis, K.M.; Durand, M.; Alsdorf, D.E.; Shum, C.K. Comparing satellite derived precipitation datasets using the Hillslope River Routing (HRR) model in the Congo River Basin. Hydrol. Process. 2011, 25, 3216–3229. [Google Scholar] [CrossRef]
- Sylla, M.B.; Giorgi, F.; Coppola, E.; Mariotti, L. Uncertainties in daily rainfall over Africa: Assessment of gridded observation products and evaluation of a regional climate model simulation. Int. J. Climatol. 2013, 33, 1805–1817. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. Biogeosci. 2011, 116, 1–16. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land-atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Wanner, H.; Beer, J.; Bütikofer, J.; Crowley, T.J.; Cubasch, U.; Flückiger, J.; Goosse, H.; Grosjean, M.; Joos, F.; Kaplan, J.O.; et al. Mid- to Late Holocene climate change: An overview. Quat. Sci. Rev. 2008, 27, 1791–1828. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Bondeau, A. Towards global empirical upscaling of FLUXNET eddy covariance observations: Validation of a model tree ensemble approach using a biosphere model. Biogeosci. Discuss. 2009, 6, 5271–5304. [Google Scholar] [CrossRef]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef]
- Bonan, G.B.; Lawrence, P.J.; Oleson, K.W.; Levis, S.; Jung, M.; Reichstein, M.; Lawrence, D.M.; Swenson, S.C. Improving canopy processes in the Community Land Model version 4 (CLM4) using global flux fields empirically inferred from FLUXNET data. J. Geophys. Res. 2011, 116, 1–22. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Chaney, N.W.; Wood, E.F. Multi-site evaluation of terrestrial evaporation models using FLUXNET data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- Swenson, S.C.; Lawrence, D.M. A GRACE-based assessment of interannual groundwater dynamics in the Community Land Model. Water Resour. Res. 2015, 51, 8817–8833. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Simmons, A.J.; Jones, P.D.; da Costa Bechtold, V.; Beljaars, A.C.M.; Kållberg, P.W.; Saarinen, S.; Uppala, S.M.; Viterbo, P.; Wedi, N. Comparison of trends and low-frequency variability in CRU, ERA-40, and NCEP/NCAR analyses of surface air temperature. J. Geophys. Res. 2004, 109, D24115. [Google Scholar] [CrossRef]
- Dee, D.P.; Fasullo, J.; Shea, D.; Walsh, J. The Climate Data Guide: Atmospheric Reanalysis: Overview and Comparison Tables. Available online: https://climatedataguide.ucar.edu/climate-data/atmospheric-reanalysis-overview-comparison-tables (accessed on 1 May 2019).
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Fensholt, R.; Proud, S.R. Evaluation of Earth Observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sens. Environ. 2012, 119, 131–147. [Google Scholar] [CrossRef]
- Jiang, C.; Song, F. Sunspot Forecasting by Using Chaotic Time-series Analysis and NARX Network. J. Comput. 2011, 6, 1424–1429. [Google Scholar] [CrossRef]
- Menezes, J.M.P.; Barreto, G.A. Long-term time series prediction with the NARX network: An empirical evaluation. Neurocomputing 2008, 71, 3335–3343. [Google Scholar] [CrossRef]
- Ćirović, V.; Aleksendrić, D.; Mladenović, D. Braking torque control using recurrent neural networks. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2012, 226, 754–766. [Google Scholar] [CrossRef]
- Cocianu, C.-L.; Grigoryan, H. An Artificial Neural Network for Data Forecasting Purposes. Inform. Econ. 2015, 20, 34–45. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; ISBN 9781118675021. [Google Scholar]
- Mark, B.; Martin, H.; Howard, D. Neural Network ToolboxTM User’s Guide (R2018a); The MathWorks, Inc.: Natick, MA, USA, 2018. [Google Scholar]
- Kayri, M. Predictive Abilities of Bayesian Regularization and Levenberg–Marquardt Algorithms in Artificial Neural Networks: A Comparative Empirical Study on Social Data. Math. Comput. Appl. 2016, 21, 20. [Google Scholar] [CrossRef]
- Berry, M.J.A.; Linoff, G. Data Mining Techniques: For Marketing, Sales, and Customer Support; Wiley: Hoboken, NJ, USA, 1997; ISBN 9780471179801. [Google Scholar]
- Minns, A.W.; Hall, M.J. Artificial neural networks as rainfall-runoff models. Hydrol. Sci. J. 1996, 41, 399–417. [Google Scholar] [CrossRef]
- MacKay, D. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L.; Arnold, J.G.; Van Liew, C.W.; Moriasi, D.N. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Servat, E.; Dezetter, A. Selection of calibration objective fonctions in the context of rainfall-ronoff modelling in a Sudanese savannah area. Hydrol. Sci. J. 1991, 36, 307–330. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Lorenz, C.; Tourian, M.J.; Devaraju, B.; Sneeuw, N.; Kunstmann, H. Basin-scale runoff prediction: An Ensemble Kalman Filter framework based on global hydrometeorological data sets. Water Resour. Res. 2015, 51, 8450–8475. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Siderius, C.; Gannon, K.E.; Ndiyoi, M.; Opere, A.; Batisani, N.; Olago, D.; Pardoe, J.; Conway, D. Hydrological Response and Complex Impact Pathways of the 2015/2016 El Niño in Eastern and Southern Africa. Earths Future 2018, 6, 2–22. [Google Scholar] [CrossRef]
- Pisoni, E.; Farina, M.; Carnevale, C.; Piroddi, L. Forecasting peak air pollution levels using NARX models. Eng. Appl. Artif. Intell. 2009, 22, 593–602. [Google Scholar] [CrossRef]
- Kondrashov, D.; Feliks, Y.; Ghil, M. Oscillatory modes of extended Nile River records (A.D. 622–1922). Geophys. Res. Lett. 2005, 32, L10702. [Google Scholar] [CrossRef]
- Lucero, O.A.; Rodríquez, N.C. Relationship between interdecadal fluctuations in annual rainfall amount and annual rainfall trend in a southern mid-latitudes region of Argentina. Atmos. Res. 1999, 52, 177–193. [Google Scholar] [CrossRef]
- Krepper, C.M.; Sequeira, M.E. Low Frequency Variability of Rainfall in Southeastern South America. Theor. Appl. Climatol. 1998, 61, 19–28. [Google Scholar] [CrossRef]
- Mehta, V.M.; Delworth, T.; Mehta, V.M.; Delworth, T. Decadal Variability of the Tropical Atlantic Ocean Surface Temperature in Shipboard Measurements and in a Global Ocean-Atmosphere Model. J. Clim. 1995, 8, 172–190. [Google Scholar] [CrossRef][Green Version]
- Lucero, O.A.; Rodriguez, N.C. Spatial organization of decadal and bidecadal rainfall fluctuations in southern North America and southern South America. Atmos. Res. 2001, 57, 219–246. [Google Scholar] [CrossRef]
- Jury, M.R. The coherent variability of African river flows: Composite climate structure and the Atlantic circulation. Water SA 2003, 29, 1–10. [Google Scholar] [CrossRef][Green Version]
- Todd, M.; Washington, R. Climate variability in central equatorial Africa: Evidence of extra-tropical influence. Geophys. Res. Lett. 2003. [Google Scholar] [CrossRef]
- Labat, D.; Ronchail, J.; Callede, J.; Guyot, J.L.; De Oliveira, E.; Guimarães, W. Wavelet analysis of Amazon hydrological regime variability. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Vishwakarma, B.D.; Devaraju, B.; Sneeuw, N. What is the spatial resolution of GRACE satellite products for hydrology? Remote Sens. 2018, 10, 852. [Google Scholar] [CrossRef]
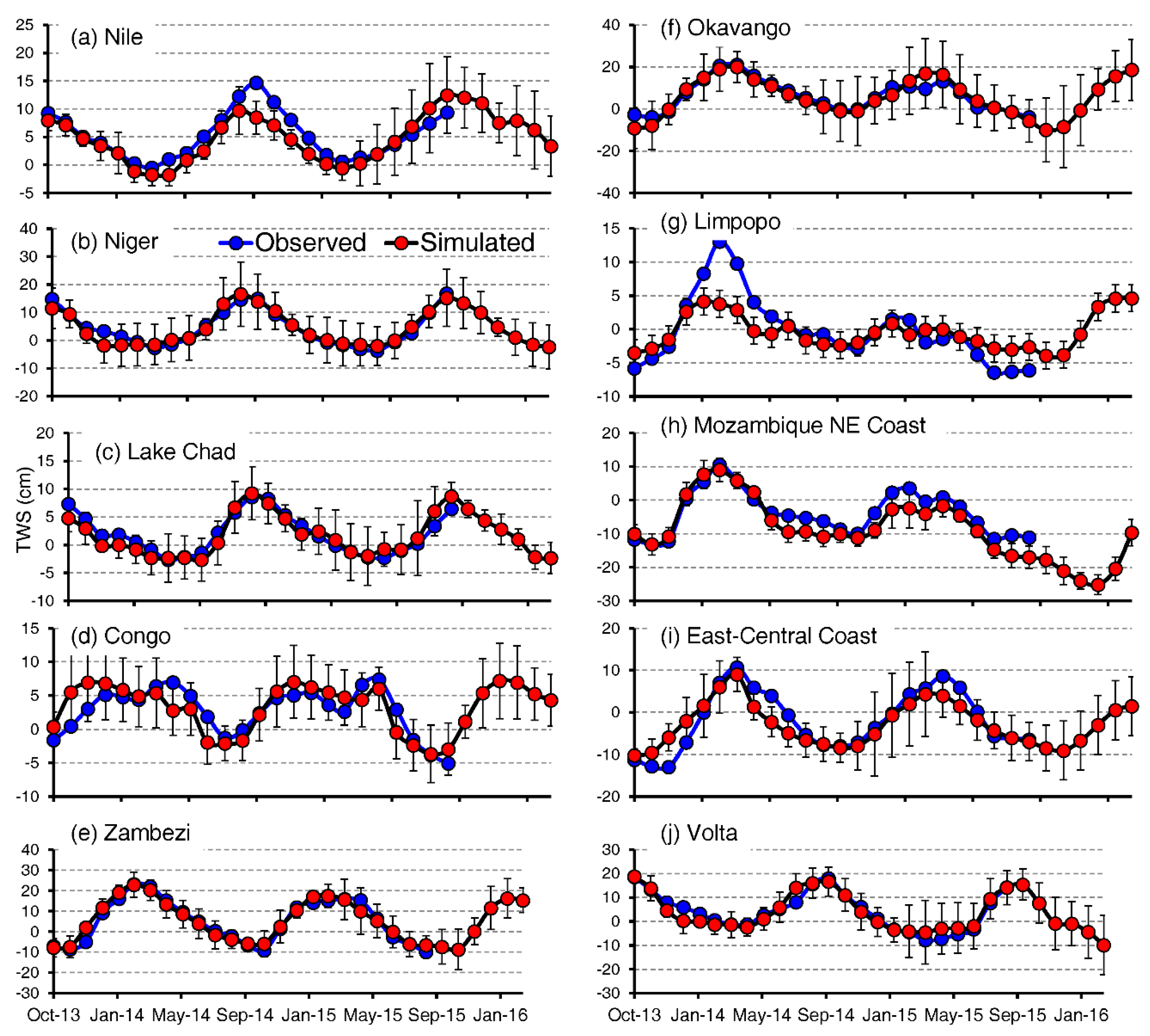
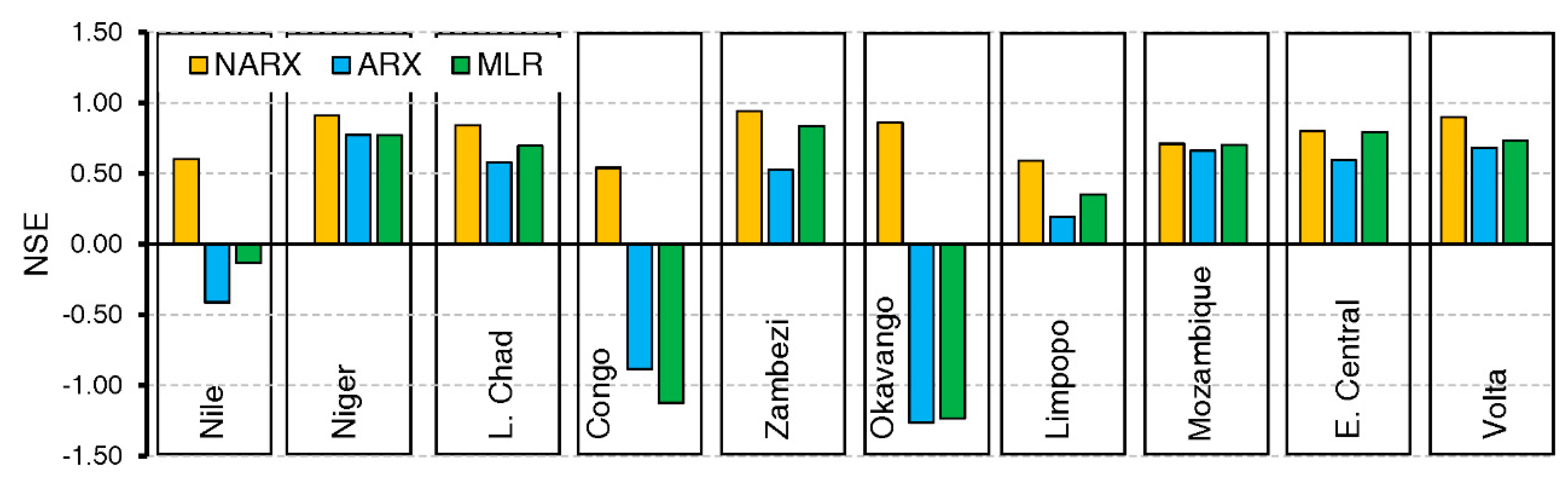
| Watershed | Architecture § | RMSE | R* | r | NSE | NSE* | Performance Category |
|---|---|---|---|---|---|---|---|
| Niger | 4-8-1-13 | 1.91 | 0.30 | 0.95 | 0.91 | 0.62 | Very Good |
| Volta | 4-8-1-13 | 2.74 | 0.31 | 0.95 | 0.90 | 0.81 | Very Good |
| Zambezi | 4-8-1-7 | 2.56 | 0.24 | 0.97 | 0.94 | 0.81 | Very Good |
| Okavango | 4-8-1-13 | 2.72 | 0.37 | 0.95 | 0.86 | 0.72 | Very Good |
| Lake Chad | 4-8-1-13 | 1.40 | 0.39 | 0.93 | 0.84 | 0.55 | Very Good |
| East Central Coast | 4-8-1-13 | 3.09 | 0.44 | 0.91 | 0.80 | 0.45 | Very Good |
| Mozambique NE Coast | 4-8-1-7 | 3.47 | 0.52 | 0.93 | 0.71 | 0.31 | Good |
| Congo | 4-5-1-24 | 2.28 | 0.66 | 0.79 | 0.54 | 0.26 | Satisfactory |
| Limpopo | 4-4-1-10 | 3.16 | 0.63 | 0.91 | 0.59 | 0.20 | Satisfactory |
| Nile | 4-7-1-24 | 2.34 | 0.60 | 0.88 | 0.60 | 0.22 | Satisfactory |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, M.; Sultan, M.; Elbayoumi, T.; Tissot, P. Forecasting GRACE Data over the African Watersheds Using Artificial Neural Networks. Remote Sens. 2019, 11, 1769. https://doi.org/10.3390/rs11151769
Ahmed M, Sultan M, Elbayoumi T, Tissot P. Forecasting GRACE Data over the African Watersheds Using Artificial Neural Networks. Remote Sensing. 2019; 11(15):1769. https://doi.org/10.3390/rs11151769
Chicago/Turabian StyleAhmed, Mohamed, Mohamed Sultan, Tamer Elbayoumi, and Philippe Tissot. 2019. "Forecasting GRACE Data over the African Watersheds Using Artificial Neural Networks" Remote Sensing 11, no. 15: 1769. https://doi.org/10.3390/rs11151769
APA StyleAhmed, M., Sultan, M., Elbayoumi, T., & Tissot, P. (2019). Forecasting GRACE Data over the African Watersheds Using Artificial Neural Networks. Remote Sensing, 11(15), 1769. https://doi.org/10.3390/rs11151769







