Oil-Slick Category Discrimination (Seeps vs. Spills): A Linear Discriminant Analysis Using RADARSAT-2 Backscatter Coefficients (σ°, β°, and γ°) in Campeche Bay (Gulf of Mexico)
Abstract
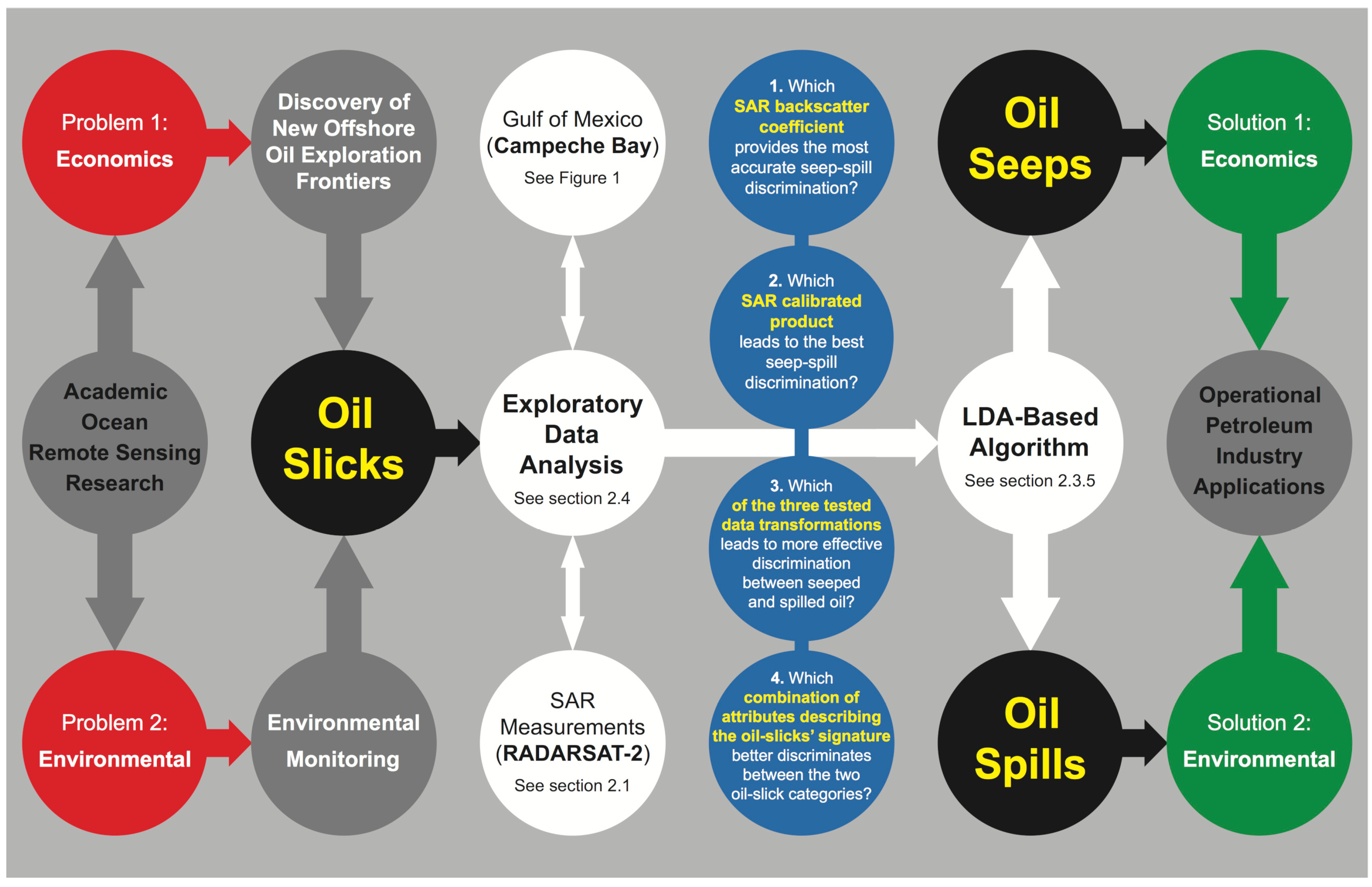
:1. Introduction
- Which SAR backscatter coefficient (i.e., sigma–naught (σ°), beta–naught (β°), and gamma–naught (γ°)) provides the most accurate seep–spill discrimination?
- Which SAR calibrated product (i.e., measures of the received radar beam given in amplitude or decibel, with or without a despeckle filter) leads to the best seep–spill discrimination?
- Which of the three tested data transformations (i.e., none, cube root, and log10) leads to more effective discrimination between seeped and spilled oil?
- Which combination of attributes describing the oil-slicks’ signature (e.g., size information and SAR basic qualitative-quantitative statistics) better discriminates between the two oil-slick categories?
2. Materials and Methods
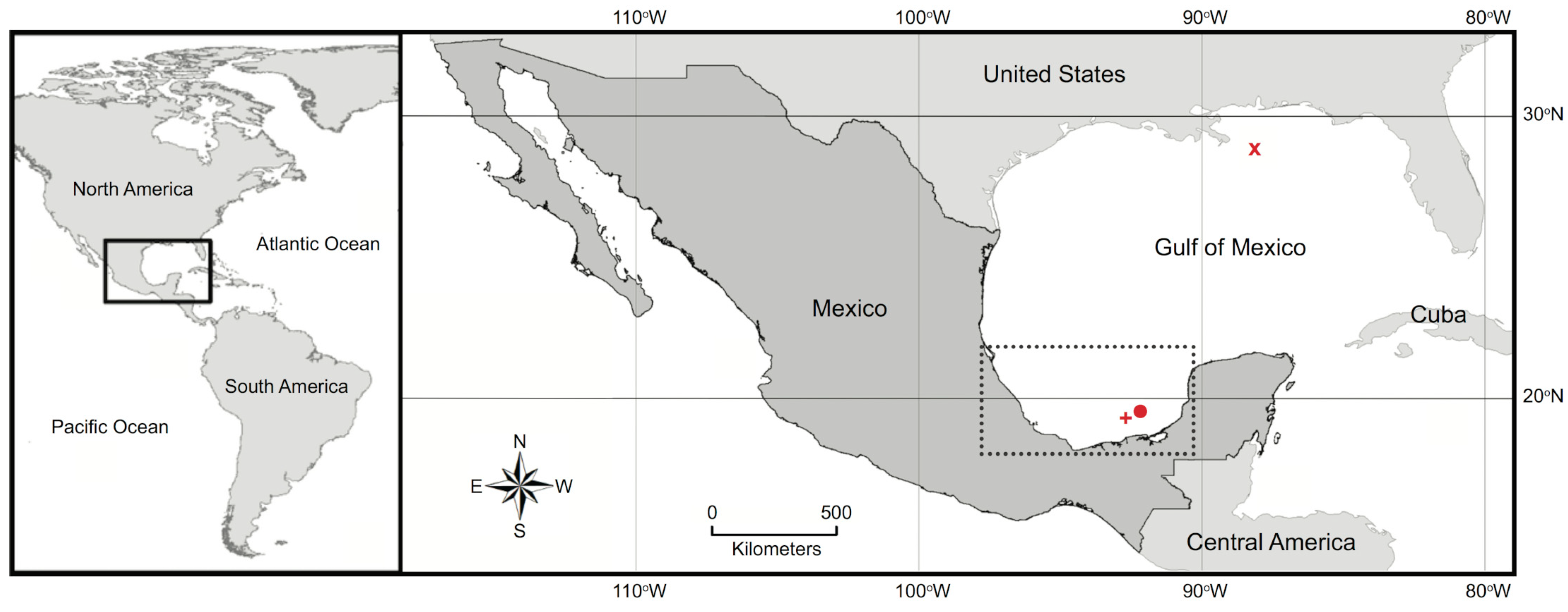
2.1. Dataset
2.2. Proven Technique
2.3. Concepts for Discriminating the Oil-Slick Category
2.3.1. Concept 1: SAR Signature
- SAR calibrated products: back-scattered radar beam measurements given in amplitude (amp) or in decibel (dB), both with or without the application of a despeckle filter [58].
2.3.2. Concept 2: Explored Attributes
2.3.3. Concept 3: Data Transformations
2.3.4. Concept 4: Feature Selection Methods
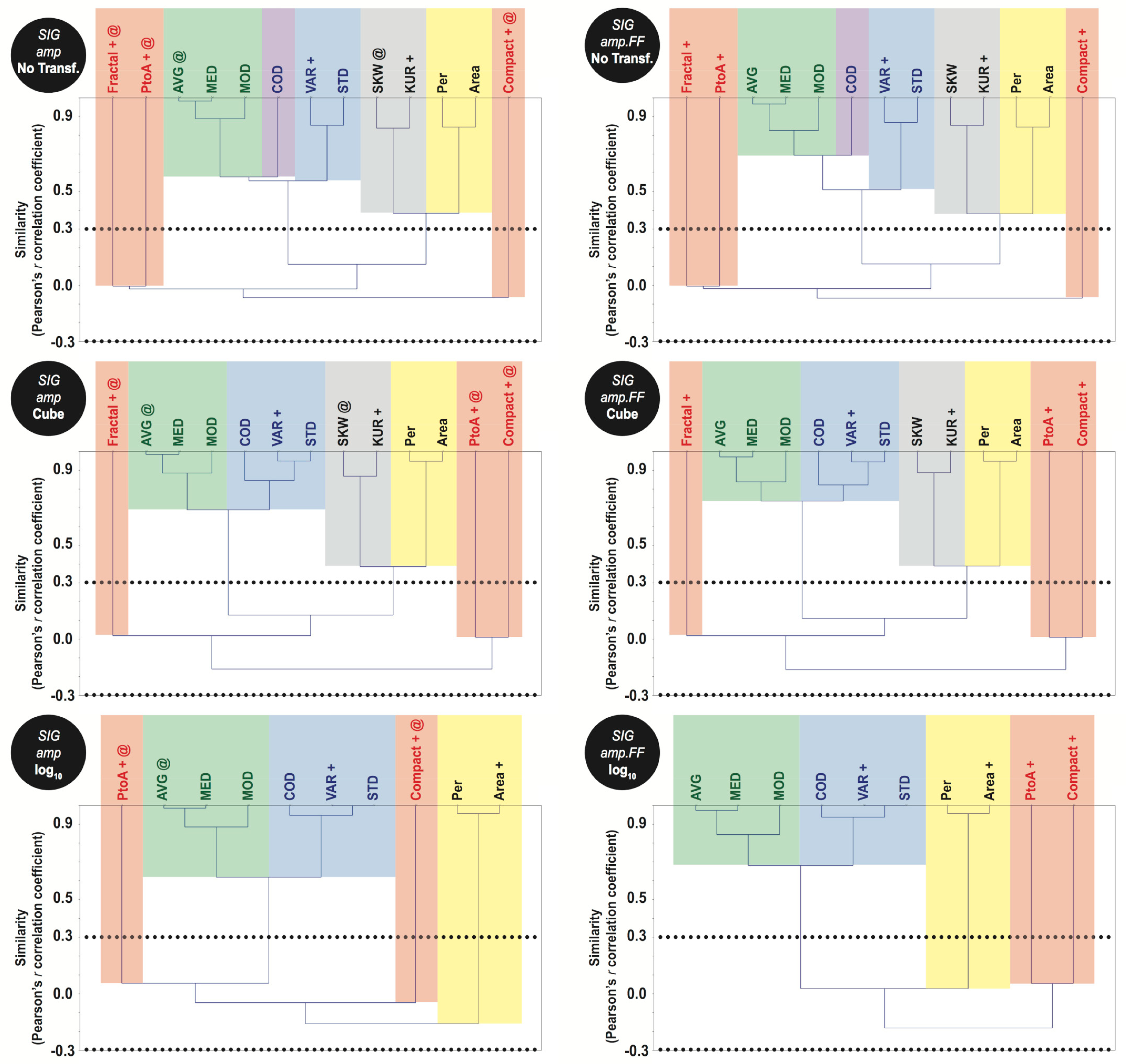
- Unweighted Pair Group Method with Arithmetic Mean (UPGMA): Semi-automated method exploring rooted-tree diagrams (i.e., dendrograms). Its attribute selection process forms groups based on a similarity measure (e.g., Pearson’s r correlation coefficient) in which each element of the matrix undergoes a simple linear two-by-two correlation. This method is adjustable to the user’s needs as groups of correlated variables are relative to a user-defined cut-off to select them, that is, a phenon line (e.g., r = 0.5 and 0.9), which is a horizontal line draw across the dendrograms [67,68,69].
- Principal Component Analysis (PCA): Linear transformation approach used to select the most relevant principal component (PC) axes. The PCs’ scores were the ones used as input to the LDA.
- Do nothing—i.e., all variables were directly inserted onto the LDA;
- Using all variables straight to PCAs without passing thought the UPGMA selection;
- Same approach as used in the initial exploratory analysis [29,30] but using only the UPGMA analyses as it offers more control in the attribute selection process than the CFS. This time, the application of a stricter similarity phenon threshold (i.e., r = 0.3, instead of 0.5 or 0.9) guarantees variables are deemed to have no significant statistical correlation from one another [70]. This leads to using the values of the attributes directly to the LDA; instead of the PCs’ scores. This alternative circumvents the application of PCAs and simplifies the seep–spill discrimination process; and
- The sole and strict UPGMA cut-off but this time with PCA.
2.3.5. Concept 5: Linear Discriminant Analysis (LDA)
2.4. Exploratory Data Analysis
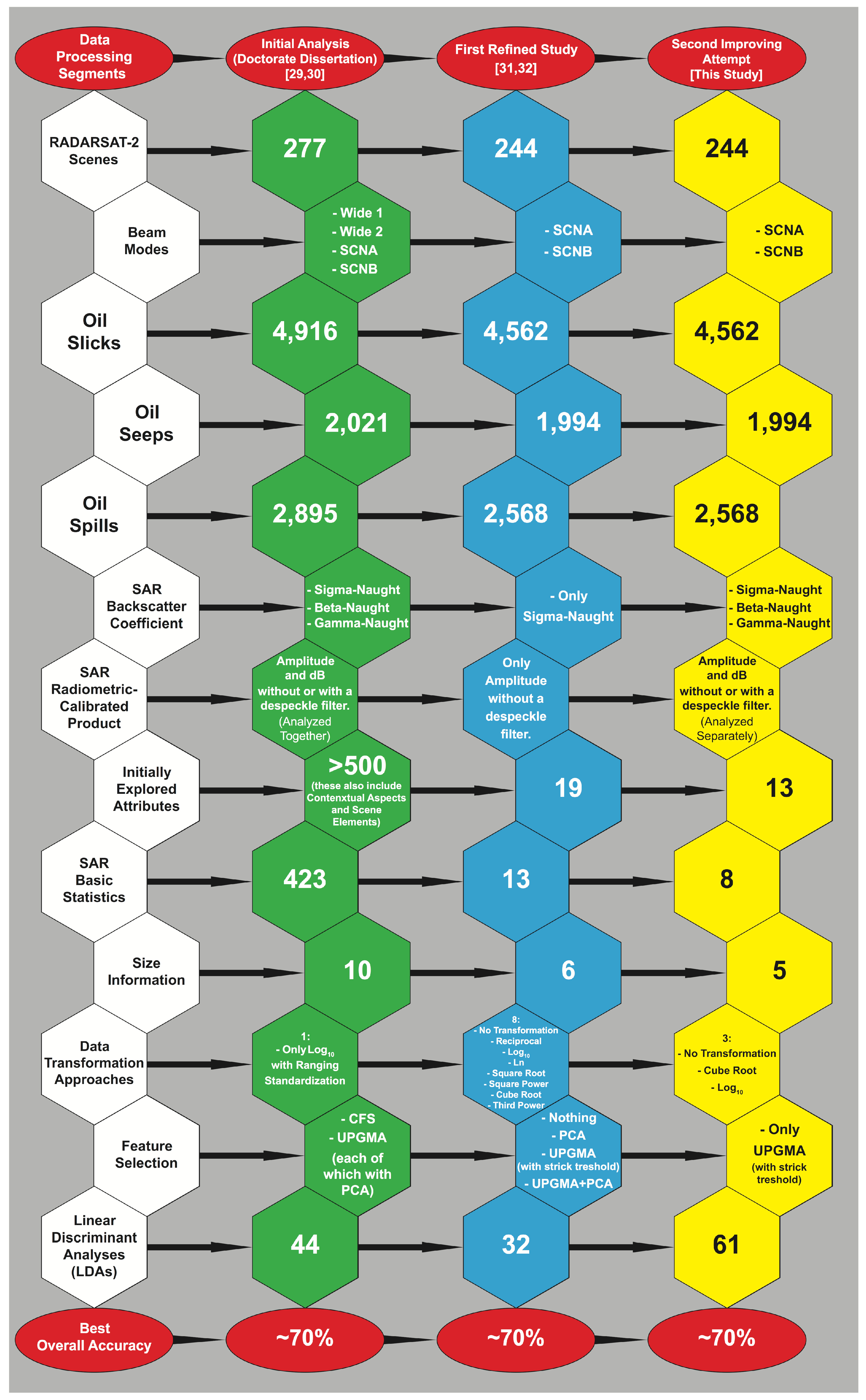
- SAR Signature: To verify which combination of SAR backscatter coefficients with SAR calibrated products provides the finest discrimination accuracy, we separately perform a complete analysis exploring the full SAR signature set (12)—i.e., SIG.amp, SIG.amp.FF, SIG.dB, SIG.dB.FF, BET.amp, BET.amp.FF, BET.dB, BET.dB.FF, GAM.amp, GAM.amp.FF, GAM.dB, and GAM.dB.FF; respectively for σ°, β°, and γ°, given in amp and in dB, with or without a despeckle filter (FF; for Frost filter [62]). This differs from the initial exploratory analysis that analyzed all calibrated products together for each backscatter coefficient [29,30].
- Explored Attributes: We apply the minimum value-scaling filter, and because we also intend to reduce dimensionality, histograms and correlation matrices are examined in an attempt to reduce the number of variables included in our analyses.
- Data Transformations: To evaluate the impact of the two best non-linear transformations found in the first refined study (i.e., cube root and log10) we compare them with the original data with no transformation.
- Linear Discriminant Analysis (LDA): Our LDA-based algorithms involve an analysis of a number of combinations of the three backscatter coefficients, each of which is calculated from the four calibrated products and the three data transformations (36 instances). We also investigate the standalone use of the size information with the tested transformations (3 instances); these are referred to as size only. We also consider 22 extra combinations using several of the main 39–data instances analyzed together—“hybrid schemes”—resembling those used by [75,76]. Therefore, we investigate 61–dataset combinations. To this matter, due to the outsized amount of two-by-two tables analyzed in our current research, these dataset combinations are evaluated based on Table 3, a condensed form of the classic confusion matrix design. We use this abridged-table format to simplify the visualization of our outcomes. The exploratory nature of our analyses focuses on exploring all 4562 oil slicks to train our LDA-based algorithms.
3. Results
3.1. Explored Attributes
- Area (Area);
- Perimeter (Per);
- Ratio between Per and Area (PtoA [78]);
- Compact index (4.π.Area/Per2 [28]);
- Fractal index (2.ln(Per/4)/ln(Area) [79]);
- Average (AVG);
- Median (MED);
- Mode (MOD);
- Standard deviation (STD);
- Variance (VAR);
- Coefficient of dispersion (COD: the third interquartile minus the first, divided by their sum);
- Skewness (SKW); and
- Kurtosis (KUR).
3.2. Feature Selection Methods
- Two variables are selected in only one instance: size only log-transformed (1).
- Three attributes are chosen in eight instances: size only with no transformation and log10 (2), and dB and dB.FF log-transformed (6).
- Four variables are selected in nine instances: cube-dB (3), and amp and amp.FF log-transformed (6).
- Five attributes are accounted in the largest set of instances (fifteen): amp and amp.FF with no transformation (6), and all cube-transformed ones (9) not including dB.
- Six variables are selected in six instances: when no transformation is applied to dB and dB.FF (6).
3.3. Linear Discriminant Analysis (LDA)
4. Discussion
- Three hierarchy-accuracy groups are formed, ruled by data transformation: log10, cube root, and no transformation. While the SAR calibrated products influence a second grouping within the data transformation (dB owing a superior performance), a third grouping is formed within the second but accounting for the SAR backscatter coefficients (better accuracies are found with γ°);
- Even though the LDAs of the not-transformed original data have a good overall accuracy (GAM.dB.FF: 65.67%), their specificity and positive predictive values of ~50% prevent them from discriminating successfully between seeps and spills. This follows from the fact that normal distributions are a fundamental assumption of the LDA method [64,71,72]; and
- The combination of size information and SAR basic statistics variables is more successful in categorizing slicks into seeps or spills. However, a comparison of our current results with those of the first refined study (Table 7) indicates that the choice of different variables within these two types of attributes (i.e., oil-slicks’ size and SAR information) produces small changes in the discrimination power—e.g., log10 SIG.amp (68.52% (only size with VAR and KUR) against 68.50% (only size with AVG and SKW)) or only size cube-transformed information (67.62% (PtoA, Compact, and Fractal) against 67.60% (PtoA and Compact only)).
Recommendations for Future Work
5. Conclusions
- Although the three backscatter coefficients have similar success at categorizing seeped and spilled oil (independently of the applied calibrated product or data transformation), γ° is somewhat superior.
- The discrimination power of the four calibrated products is rather independent of backscatter coefficient but varies to some extent within data transformation. When log10 is applied, dB (68.85%: GAM) is followed by dB.FF (68.72%: GAM) and by two amp forms. A baffling pecking order is observed with cube root, but even though it lacks a defined hierarchy pattern, amp.FF reaches better accuracy levels (68.35%: GAM) and amp the lowest (67.98%: GAM). With the not-transformed original data, dB.FF effectiveness is followed by dB, then by the two amp forms with no definite pattern; however, these have little practical meaning—see point 3 below.
- The data transformation exerts the most influence over the seep–spill discrimination, dictating the performance of our optimal linear models. Among the tested ones, the highest overall accuracy is the log-transformed (68.85%: GAM.dB), though the cube root has slightly more balanced seep–spill discrimination capabilities and is as successful: 68.35% (GAM.amp.FF). If the data is not normalized, the top overall accuracy is 65.67% (GAM.dB.FF); nevertheless, its LDAs are incapable of separating seeps from spills, as its specificity and positive predictive values are void (~50%).
- Concerning the use of different attributes describing the oil-slicks’ signature, a comparison with the first refined study (SIG.amp) demonstrates that even though different size and SAR signatures have been used between both of our investigations (AVG and SKW against VAR and KUR; and PtoA and Compact against PtoA, Compact, and Fractal, respectively, for the refined study and our research), the discrimination improvement is disappointingly small. Although, there is an improvement once other backscatter coefficients and calibrated products are investigated—e.g., cube root size only (67.62%) against cube root GAM.amp.FF (68.35%); the latter accounts for the same size information as the former, plus VAR and KUR.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jernelov, A.; Lindén, O. Ixtoc I: A case study of the world’s largest oil spill. AMBIO 1981, 10, 299–306. [Google Scholar]
- Patton, J.S.; Rigler, M.W.; Boehm, P.D.; Fiest, D.L. Ixtoc I oil spill: Flaking of surface mousse in the Gulf of Mexico. Nature 1981, 290, 235–238. [Google Scholar] [CrossRef]
- NOAA (National Oceanic and Atmospheric Administration). Proceedings of the Symposium on Prerliminary Results from the September 1979 Research/Pierce Ixtoc-1 Cruise, Department of Commerce, Miami, FL, USA, 9–10 June 1980.
- NOAA (National Oceanic and Atmospheric Administration). The Ixtoc-1 Oil Spill: The Federal Scientific Response; Hooper, C.H., Ed.; Department of Commerce: Boulder, CO, USA, 1981.
- Soto, L.A.; Botello, A.V.; Licea-Duán, S.; Lizárraga-Partida, M.L.; Yáñez-Arancibia, A. The environmental legacy of the Ixtoc-I oil spill in Campeche Sound, southwestern Gulf of Mexico. Front. Mar. Sci. 2014, 1, 1–9. [Google Scholar] [CrossRef]
- Sun, S.; Hu, C.; Tunnell, J.W., Jr. Surface oil footprint and trajectory of the Ixtoc-I oil spill determined from Landsat/MSS and CZCS observations. Mar. Pollut. Bull. 2015, 101, 632–641. [Google Scholar] [CrossRef] [PubMed]
- Leifer, I.; Lehr, W.J.; Simecek-Beatty, D.; Bradley, E.; Clark, R.; Dennison, P.; Hu, Y.; Matheson, S.; Jones, C.E.; Holt, B.; et al. Review—State of the art satellite and airborne marine oil spill remote sensing: Application to the BP Deepwater Horizon oil spill. Remote Sens. Environ. 2012, 124, 185–209. [Google Scholar] [CrossRef]
- Garcia-Pineda, O.; Holmes, J.; Rissing, M.; Jones, R.; Wobus, C.; Svejkovsky, J.; Hess, M. Detection of oil near shorelines during the Deepwater Horizon oil spill using synthetic aperture radar (SAR). Remote Sens. 2017, 9, 567. [Google Scholar] [CrossRef]
- Boufadel, M.C.; Gao, F.; Zhao, L.; Özgökmen, T.; Miller, R.; King, T.; Robinson, B.; Lee, K.; Leifer, I. Was the Deepwater Horizon well discharge churn flow? Implications on the estimation of the oil discharge and droplet size distribution. Geophys. Res. Lett. 2018, 45, 2396–2403. [Google Scholar] [CrossRef]
- MPB (Marine Pollution Bulletin). The 1991 Gulf War: Coastal and Marine Environmental Consequences. Special issue examining the consequences of the 1991 Gulf War. Mar. Pollut. Bull. 1993, 27, 380. [Google Scholar]
- Jernelov, A. The threats from oil spills: Now, then, and in the future. AMBIO A J. Hum. Environ. 2010, 39, 353–366. [Google Scholar] [CrossRef]
- Hu, C.; Feng, L.; Holmes, J.; Swayze, G.A.; Leifer, I.; Melton, C.; Garcia, O.; MacDonald, I.; Hess, M.; Muller-Karger, F.; et al. Remote sensing estimation of surface oil volume during the 2010 Deepwater Horizon oil blowout in the Gulf of Mexico: Scaling up AVIRIS observations with MODIS measurements. J. Appl. Remote Sens. 2018, 12, 026008. [Google Scholar] [CrossRef]
- Hu, C.; Li, X.; Pichel, W.G.; Muller-Karger, F.E. Detection of natural oil slicks in the NW Gulf of Mexico using MODIS imagery. Geophys. Res. Lett. 2009, 36, L01604. [Google Scholar] [CrossRef]
- MacDonald, I.R.; Reilly, J.F., Jr.; Beat, S.E.; Venkataramaiah, R.; Sassen, R.; Guinasso, N.L., Jr.; Amos, J. Remote sensing inventory of active oil seeps and chemosynthetic communities in the Northern Gulf of Mexico. In Hydrocarbon Migration and its Near-Surface Expression; Schumacher, D., Abrams, M.A., Eds.; American Association of Petroleum Geologists: Tulsa, OK, USA, 1996; Chapter 3; pp. 27–37. [Google Scholar]
- Garcia-Pineda, O.; MacDonald, I.; Zimmer, B.; Shedd, B.; Roberts, H. Remote-sensing evaluation of geophysical anomaly sites in the outer continental slope, northern Gulf of Mexico. Deep Sea Res. Part II Top. Stud. Oceanogr. 2010, 57, 1859–1869. [Google Scholar] [CrossRef]
- WHOI (Woods Hole Oceanographic Institution). 2015 Natural Oil Seeps. Available online: https://www.whoi.edu/know-your-ocean/ocean-topics/seafloor-below/natural-oil-seeps/ (accessed on 26 June 2019).
- Villarón, R.M. Geoquímica de reservatórios do campo Taratunich da área marinha de Campeche, México. M.Sc. Thesis, Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil, 1998; p. 126. [Google Scholar]
- Miranda, F.P.; Quintero-Marmol, A.M.; Pedroso, E.C.; Beisl, C.H.; Welgan, P.; Morales, L.M. Analysis of RADARSAT-1 data for offshore monitoring activities in the Cantarell Complex, Gulf of Mexico, using the unsupervised semivariogram textural classifier (USTC). Can. J. Remote Sens. 2004, 30, 424–436. [Google Scholar] [CrossRef]
- Li, X.; Li, C.; Yang, Z.; Pichel, W. SAR imaging of ocean surface oil seep trajectories induced by near inertial oscillation. Remote Sens. Environ. 2013, 130, 182–187. [Google Scholar] [CrossRef]
- Ozgokmen, T.M.; Beron-Vera, F.J.; Bogucki, D.; Chen, S.; Dawson, C.; Dewar, W.; Griffa, A.; Haus, B.K.; Haza, A.C.; Huntley, H.; et al. Research overview of the Consortium for Advanced Research on Transport of Hydrocarbon in the Environment (CARTHE). In Proceedings of the International Oil Spill Conference, Long Beach, CA, USA, 15–18 May 2014; pp. 544–560. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, X.; Xu, Q.; Garcia-Pineda, O.; Andersen, O.B.; Pichel, W.G. SAR observation and model tracking of an oil spill event in coastal waters. Mar. Pollut. Bull. 2011, 62, 350–363. [Google Scholar] [CrossRef] [PubMed]
- Mano, M.F.; Beisl, C.H.; Landau, L. Identifying oil seep areas at seafloor using oil inverse modeling. In Proceedings of the AAPG International Conference & Exhibition, Milan, Italy, 23–26 October 2011. [Google Scholar]
- Jackson, C.R.; Apel, J.R. Synthetic Aperture Radar Marine User’s Manual; NOAA/NESDIS, Office of Research and Applications: Washington, DC, USA, 2004; Available online: http://www.sarusersmanual.com (accessed on 26 June 2018).
- Haykin, S.; Puthusserypady, S. Chaotic dynamics of sea clutter. Chaos 1997, 7, 777–808. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Pineda, O.; MacDonald, I.; Zimmer, B. Synthetic aperture radar image processing using the Supervised Textural-Neural Network Classification Algorithm. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS ’08), Boston, MA, USA, 8–11 July 2008; Volume IV, pp. 1265–1268. [Google Scholar]
- Garcia-Pineda, O.; Zimmer, B.; Howard, M.; Pichel, W.; Li, X.; MacDonald, I.R. Using SAR images to delineate ocean oil slicks with a texture-classifying neural network algorithm (TCNNA). Can. J. Remote Sens. 2009, 35, 411–421. [Google Scholar] [CrossRef]
- Bentz, C.M.; Lorenzzetti, J.A.; Kampel, M. Multi-sensor synergistic analysis of mesoscale oceanic features: Campos Basin, south-eastern Brazil. Int. J. Remote Sens. 2004, 25, 4835–4841. [Google Scholar] [CrossRef]
- Bentz, C.M. Reconhecimento automático de eventos ambientais costeiros e oceânicos em imagens de radares orbitais. Ph.D. Dissertation, COPPE, Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil, 2006; p. 115. [Google Scholar]
- Carvalho, G.A. Multivariate data analysis of satellite-derived measurements to distinguish natural from man-made oil slicks on the sea surface of Campeche Bay (Mexico). Ph.D. Dissertation, COPPE, Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil, 2015; p. 285. Available online: http://www.coc.ufrj.br/index.php?option=com_content&view=article&id=4618:gustavo-de-araujocarvalho (accessed on 26 June 2019).
- Carvalho, G.A.; Minnett, P.J.; de Miranda, F.P.; Landau, L.; Paes, E.T. Exploratory data analysis of synthetic aperture radar (SAR) measurements to distinguish the sea surface expressions of naturally-occurring oil seeps from human-related oil spills in Campeche Bay (Gulf of Mexico). ISPRS Int. J. Geo.Inf. 2017, 6, 379. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Minnett, P.J.; Paes, E.T.; Miranda, F.P.; Landau, L. Refined analysis of RADARSAT-2 measurements to discriminate two petrogenic oil-slick categories: seeps versus spills. J. Mar. Sci. Eng. 2018, 6, 153. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Minnett, P.J.; Paes, E.T.; Miranda, F.P.; Landau, L. RADARSAT-2 measurements to investigate oil seeps from oil spills: A refined discrimination strategy. In Proceedings of the XIX Brazilian Remote Sensing Symposium (SBSR), Santos, São Paulo, Brazil, 14–17 April 2019; Volume 17, p. 4, ISBN 978-85-17-00097-3. Available online: https://proceedings.science/sbsr-2019/papers/radarsat-2-measurements-to-investigate-oil-seeps-from-oil-spills--a-refined-discrimination-strategy (accessed on 26 June 2019).
- Carvalho, G.A.; Landau, L.; Miranda, F.P.; Minnett, P.; Moreira, F.; Beisl, C. The use of RADARSAT-derived information to investigate oil slick occurrence in Campeche Bay, Gulf of Mexico. In Proceedings of the XVII Brazilian Remote Sensing Symposium (SBSR), João Pessoa, Brazil, 25–29 April 2015; pp. 1184–1191. Available online: http://www.dsr.inpe.br/sbsr2015/files/p0217.pdf (accessed on 26 June 2019).
- Carvalho, G.A.; Minnett, P.J.; Miranda, F.P.; Landau, L.; Moreira, F. The use of a RADARSAT-derived long-term dataset to investigate the sea surface expressions of human-related oil spills and naturally-occurring oil seeps in Campeche Bay. Can. J. Remote Sens. 2016, 42, 307–321. [Google Scholar] [CrossRef]
- Attema, E.; Davidson, M.; Snoeij, P.; Rommen, B.; Floury, N. Sentinel-1 mission overview. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS ’09), Cape Town, South Africa, 12–17 July 2009; pp. 36–69. [Google Scholar] [CrossRef]
- Panetti, A.; Torres, R.; Lokas, S.; Bruno, C.; Croci, R.; L’Abbate, M.; Marcozzi, M.; Pietropaolo, A.; Venditti, P. GMES Sentinel-1: Mission and satellite system overview. In Proceedings of the 9th European Conference on synthetic aperture radar, EUSAR, Nuremberg, Germany, 23–26 April 2012; pp. 162–165, ISBN 978-3-8007-3404-7. [Google Scholar]
- Potin, P.; Rosich, B.; Miranda, N.; Grimont, P.; Shurmer, I.; O’Connell, A.; Krassenburg, M.; Gratadour, J.B. Sentinel-1 Constellation Mission Operations Status. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS ’18), Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Thompson, A.A. Overview of the RADARSAT Constellation Mission. Can. J. Remote Sens. 2015, 41, 401–407. [Google Scholar] [CrossRef]
- Dabboor, M.; Iris, S.; Singhroy, V. The RADARSAT Constellation Mission in Support of Environmental Applications. Proceedings 2018, 2, 323. [Google Scholar] [CrossRef]
- Zuhlke, M.; Fomferra, N.; Brockmann, C.; Peters, M.; Veci, L.; Malik, J.; Regner, P. SNAP (Sentinel Application Platform) and the ESA Sentinel 3 Toolbox. In Proceedings of the Sentinel-3 for Science Workshop, Venice, Italy, 2–5 June 2015; p. 21, ISBN 978-92-9221-298-8. [Google Scholar]
- Pottier, E. Recent advances in the development of the open source Toolbox for Polarimetric and Interferometric Polarimetric SAR Data Processing: The PolSARpro v4.1.5 Software. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS ’10), Honolulu, HI, USA, 25–30 July 2010; pp. 2527–2530. [Google Scholar] [CrossRef]
- Hammer, Ø.; Harper, D.A.T.; Ryan, P.D. PAST: PAleontological STatistics software package for education and data analysis. Palaeontol. Electron. 2001, 4, 1–9. [Google Scholar]
- Hammer, Ø. PAST: Multivariate Statistics. 2015. Available online: http://folk.uio.no/ohammer/past/multivar.html (accessed on 26 June 2019).
- Hammer, Ø. PAST: PAleontological STatistics, Reference Manual; Version 3.23; University of Oslo: Oslo, Norway, 2019; p. 271. Available online: http://folk.uio.no/ohammer/past/past3manual.pdf (accessed on 26 June 2019).
- Thrasher, J.; Fleet, A.J.; Hay, S.H.; Hovland, M.; Düppenbecker, S. Understanding geology as the key to using seepage in exploration: Spectrum of seepage styles. In Hydrocarbon Migration and its Near-Surface Expression, AAPG Memoir 66; Schumacher, D., Abrams, M.A., Eds.; Association of Petroleum Geologists: Tulsa, OK, USA, 1996; Chapter 17; pp. 223–241. [Google Scholar]
- Mendoza, A.; Miranda, F.; Bannerman, K.; Pedroso, E.; Herrera, M. Satellite environmental monitoring of oil spills in the south Gulf of Mexico. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 3–6 May 2004. Paper No. Oct 16410. [Google Scholar]
- Quintero-Marmol, A.M.; Pedroso, E.C.; Beisl, C.H.; Caceres, R.G.; Miranda, F.P.; Bannerman, K.; Welgan, P.; Castillo, O.L. Operational applications of RADARSAT-1 for the monitoring of natural oil seeps in the South Gulf of Mexico. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS ’03), Toulouse, France, 21–25 July 2003; pp. 2744–2746. [Google Scholar] [CrossRef]
- Quintero-Marmol, A.M.; Miranda, F.P.; Goodman, R.; Bannerman, K.; Pedroso, E.C.; Rodriguez, M.H. Emanacion natural de Cantarell: Laboratorio natural para experimentos de derrames de petroleo. In Proceedings of the International Oil Spill Conference (IOSC), Miami, FL, USA, 17 May 2005; pp. 1039–1044. [Google Scholar] [CrossRef]
- Bannerman, K.; Rodriguez, M.H.; Miranda, F.P.; Pedroso, C.E.; Cáceres, R.G.; Castillo, O.L. Operational applications of RADARSAT-2 for the environmental monitoring of oil slicks in the southern Gulf of Mexico. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS ’09), Cape Town, South Africa, 12–17 July 2009; pp. iii-381–iii-383. [Google Scholar] [CrossRef]
- Parashar, S.; Langham, E.; McNally, J.; Ahmed, S. RADARSAT mission requirements and concept. Can. J. Remote Sens. 1993, 19, 280–288. [Google Scholar] [CrossRef]
- Morena, L.C.; James, K.V.; Beck, J. An introduction to the RADARSAT-2 mission. Can. J. Remote Sens. 2004, 30, 221–234. [Google Scholar] [CrossRef]
- MDA (MacDonald, Dettwiler and Associates Ltd.). RADARSAT-2 Product Description; Technical Report RN-SP-52-1238, Issue/Revision: 1/13; MDA: Richmond, BC, Canada, 2016; p. 91. [Google Scholar]
- Martins, L.R.; Coutinho, P.N. The Brazilian continental margin. Earth-Sci. Rev. 1981, 17, 87–107. [Google Scholar] [CrossRef]
- Jennerjahn, T.C.; Knoppers, B.A.; de Souza, W.F.L.; Carvalho, C.E.V.; Mollenhauer, G.; Hobner, M.; Ittekkot, V. The tropical Brazilian continental margin. In Carbon and Nutrient Fluxes in Continental Margins; Liu, K.K., Atkinson, L., Quiñones, R., Talaue-McManus, L., Eds.; Springer: Berlin, Germany, 2010; pp. 427–442. [Google Scholar]
- Freeman, A. Radiometric calibration of SAR image data. In Proceedings of the XVII Congress for Photogrammetry and Remote Sensing, Washington, DC, USA, 2–14 August 1992; pp. 212–222. [Google Scholar]
- Laur, H.; Bally, P.; Meadows, P.; Sanchez, J.; Schaettler, B.; Lopinto, E.; Esteban, D. ERS SAR Calibration: Derivation of the Backscattering Coefficient Sigma-Naught in ESA ERS SAR PRI Products; Document No.: ES-TN-RS-PM-HL09; ESA (European Space Agency): Paris, France, 1998; p. 51. [Google Scholar]
- Shepherd, N. Extraction of Beta Nought and Sigma Nought from RADARSAT CDPF Products; Technical Report, Revision 4, AS97-5001; Altrix Systems: Ottawa, ON, Canada, 2000; 16p. [Google Scholar]
- MDA (MacDonald, Dettwiler and Associates Ltd.). RADARSAT-2 Product Definition; Technical Report RN-RP-51-2713, Issue/Revision: 1/10; MDA: Richmond, BC, Canada, 2011; p. 83. [Google Scholar]
- Roriz, C.E.D. Detecção de exsudações de óleo utilizando imagens do satélite RADARSAT-1 na porção offshore do delta do Niger. M.Sc. Thesis, COPPE, Universidade Federal do Rio de Janeiro (UFRJ), Rio de Janeiro, Brazil, 2006; p. 267. [Google Scholar]
- Cotton, P.D.; Carter, D.J.T. Cross calibration of TOPEX, ERS-I, and Geosat wave heights. J. Geophys. Res. 1994, 99, 25025–25033. [Google Scholar] [CrossRef]
- Ebuchi, N.; Kawamura, H. Validation of wind speeds and significant wave heights observed by the TOPEX altimeter around Japan. J. Oceanogr. 1994, 50, 479–487. [Google Scholar] [CrossRef]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. A model for radar images and its application to adaptive digital filtering of multiplicative noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, 4, 157–166. [Google Scholar] [CrossRef]
- McLachlan, G. Discriminant Analysis and Statistical Pattern Recognition; A Whiley-Interescience Publication; John Wiley & Sons; Inc.: Queensland, Australia, 1992; ISBN 0-471-61531-5. [Google Scholar]
- Valentin, J.L. Ecologia Numérica—Uma Introdução à Análise Multivariada de Dados Ecológicos, 2nd ed.; Editora Interciência: Rio de Janeiro, Brazil, 2012; p. 153. ISBN 978-85-7193-230-2. [Google Scholar]
- Hall, M.A. Correlation-based feature selection for machine learning. Ph.D. Dissertation, Department of Computer Science, The University of Waikato, Hamilton, New Zealand, 1999; p. 178. [Google Scholar]
- Bouckaert, R.R.; Frank, E.; Hall, M.; Kirby, R.; Reutemann, P.; Seewald, A.; Scuse, D. WEKA Manual for Version 3-6-0; The University of Waikato: Hamilton, New Zealand, 2008; p. 212. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. The Comparison of dendrograms by objective methods. Taxon 1962, 11, 33–40. [Google Scholar] [CrossRef]
- Sneath, P.H.A.; Sokal, R.R. Numerical Taxonomy—The Principles and Practice of Numerical Classification; W.H. Freeman and Company: San Francisco, CA, USA, 1973; p. 573. ISBN 0-7167-0697-0. [Google Scholar]
- Legendre, P.; Legendre, L. Numerical Ecology. In Developments in Environmental Modelling, 3rd ed.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2012; p. 990. ISBN 978-0444538680. [Google Scholar]
- Zar, H.J. Biostatistical Analysi, 5th ed.; Pearson New International Edition; Pearson: Upper Saddle River, NJ, USA, 2014; ISBN 1-292-02404-6. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1994; ISBN 0023527617. [Google Scholar]
- Lohninger, H. Teach./Me Data Analysis (Text.-Only Light Edition); Springer: Berlin, Germany; New York, NY, USA; Tokyo, Japan, 1999; ISBN 3-540-14743-8. [Google Scholar]
- Congalton, R.G. A review of assessing the accuracy of classification of remote sensed data. Remote Sens. Environ. 1991, 37, 35–46. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Carvalho, G.A. The Use of Satellite-Based Ocean Color Measurements for Detecting the Florida Red Tide (Karenia Brevis). M.Sc. Thesis, RSMAS/MPO, University of Miami (UM), Miami, FL, USA, 2008; p. 156. Available online: http://scholarlyrepository.miami.edu/oa_theses/116/ (accessed on 26 June 2019).
- Carvalho, G.A.; Minnett, P.J.; Fleming, L.E.; Banzon, V.F.; Baringer, W. Satellite remote sensing of harmful algal blooms: A new multi-algorithm method for detecting the Florida Red Tide (Karenia brevis). Harmful Algae 2010, 9, 440–448. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, G.A.; Minnett, P.J.; Banzon, V.F.; Baringer, W.; Heil, C.A. Long-term evaluation of three satellite ocean color algorithms for identifying harmful algal blooms (Karenia brevis) along the west coast of Florida: A matchup assessment. Remote Sens. Environ. 2011, 115, 1–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fiscella, B.; Giancaspro, A.; Nirchio, F.; Pavese, P.; Trivero, P. Oil spill monitoring in the Mediterranean Sea using ERS SAR data. In Proceedings of the Envisat Symposium (ESA), Göteborg, Sweden, 16–20 October 2010; p. 9. [Google Scholar]
- Pisano, A. Development of Oil Spill Detection Techniques for Satellite Optical Sensors and Their Application to Monitor Oil Spill Discharge in the Mediterranean Sea. Ph.D. Dissertation, Università di Bologna, Bologna, Italy, 2011; p. 146. [Google Scholar]
- Brekke, C.; Solberg, A.H.S. Review: Oil spill detection by satellite remote sensing. Remote Sens. Environ. 2005, 95, 13. [Google Scholar] [CrossRef]
- Bevilacqua, L.; Barros, M.M.; Galeão, A.C.R.N. Geometry, dynamics and fractals. J. Br. Soc. Mech. Sci. Eng. 2008, 30, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Silva, G.; de Miranda, F.P.; Vieira, J.A.; Rocha, A.C. Detecção e caracterização de alvos na imagem RADARSAT-1 da superfície do mar no Golfo do México utilizando diagramas de espaço de estado defasados. In Proceedings of the XIX Brazilian Remote Sensing Symposium (SBSR), Santos, São Paulo, Brazil, 14–17 April 2019. [Google Scholar]

| LDA Oil Seeps | LDA Oil Spills | Known Oil Slicks | |
|---|---|---|---|
| Known oil seeps | A | B | A + B |
| Known oil spills | C | D | C + D |
| LDA oil slicks | A + C | B + D | A + B + C + D |
| Diagonal of Table 1 | A | = | Correctly identified oil seeps |
| D | = | Correctly identified oil spills | |
| A + D | = | Correctly identified oil slicks | |
| Off-Diagonal of Table 1 | C | = | Misidentified oil seeps |
| B | = | Misidentified oil spills | |
| C + B | = | Misidentified oil slicks | |
| A + B + C + D | = | Known oil slicks (i.e., 4562) | |
| Horizontal Analysis of Table 1 | A + B | = | Known oil seeps (i.e., 1994) |
| C + D | = | Known oil spills (i.e., 2568) | |
| A/(A + B) | = | Sensitivity | |
| D/(C + D) | = | Specificity | |
| B/(A + B) | = | False negative | |
| C/(C + D) | = | False positive | |
| Vertical Analysis of Table 1 | A + C | = | LDA classified oil seeps |
| B + D | = | LDA classified oil spills | |
| A/(A + C) | = | Positive predictive value | |
| D/(B + D) | = | Negative predictive value | |
| C/(A + C) | = | Inverse of the positive predictive value | |
| B/(B + D) | = | Inverse of the negative predictive value | |
| (A + D)/(A + B + C + D) | = | Overall accuracy | |
| Oil Seeps | Oil Spills | Oil Slicks | |||
|---|---|---|---|---|---|
| Correctly Identified oil seeps | Sensitivity | Correctly Identified oil spills | Specificity | Correctly Identified oil slicks | Overall accuracy |
| Positive predictive value | Negative predictive value | ||||
 |
| Hierarchy | Data Transformation | Oil-Slicks’ Signature | Oil Seeps | Oil Spills | Oil Slicks | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | log10 | Gamma-naught | dB | 1293 | 64.84% | 1848 | 71.96% | 3141 | 68.85% |
| 64.23% | 72.50% | ||||||||
| 2 | log10 | Beta-naught | dB | 1292 | 64.79% | 1848 | 71.96% | 3140 | 68.83% |
| 64.21% | 72.47% | ||||||||
| 3 | log10 | Sigma-naught | dB | 1292 | 64.79% | 1845 | 71.85% | 3137 | 68.76% |
| 64.12% | 72.44% | ||||||||
| 4 | log10 | Gamma-naught | dB.FF | 1293 | 64.84% | 1842 | 71.73% | 3135 | 68.72% |
| 64.04% | 72.43% | ||||||||
| 5 | log10 | Sigma-naught | dB.FF | 1292 | 64.79% | 1838 | 71.57% | 3130 | 68.61% |
| 63.90% | 72.36% | ||||||||
| 6 | log10 | Size only | 1288 | 64.59% | 1841 | 71.69% | 3129 | 68.59% | |
| 63.92% | 72.28% | ||||||||
| 7 | log10 | Beta-naught | dB.FF | 1288 | 64.59% | 1840 | 71.65% | 3128 | 68.57% |
| 63.89% | 72.27% | ||||||||
| 8 | log10 | Sigma-naught | amp.FF | 1321 | 66.25% | 1806 | 70.33% | 3127 | 68.54% |
| 63.42% | 72.85% | ||||||||
| 9 | log10 | Sigma-naught | amp | 1323 | 66.35% | 1803 | 70.21% | 3126 | 68.52% |
| 63.36% | 72.88% | ||||||||
| 10 | log10 | Beta-naught | amp | 1324 | 66.40% | 1800 | 70.09% | 3123 | 68.48% |
| 63.29% | 72.87% | ||||||||
| 11 | log10 | Gamma-naught | amp | 1320 | 66.20% | 1803 | 70.21% | 3124 | 68.46% |
| 63.31% | 72.79% | ||||||||
| 12 | log10 | Gamma-naught | amp.FF | 1320 | 66.20% | 1802 | 70.17% | 3122 | 68.44% |
| 63.28% | 72.78% | ||||||||
| 13 | log10 | Beta-naught | amp.FF | 1320 | 66.20% | 1799 | 70.05% | 3119 | 68.37% |
| 63.19% | 72.75% | ||||||||
| 14 | Cube root | Gamma-naught | amp.FF | 1409 | 70.66% | 1709 | 66.55% | 3118 | 68.35% |
| 62.13% | 74.50% | ||||||||
| 15 | Cube root | Sigma-naught | amp.FF | 1410 | 70.71% | 1706 | 66.43% | 3116 | 68.30% |
| 62.06% | 74.50% | ||||||||
| 16 | Cube root | Gamma-naught | dB.FF | 1384 | 69.41% | 1729 | 67.33% | 3113 | 68.24% |
| 62.26% | 73.92% | ||||||||
| 17 | Cube root | Beta-naught | dB | 1393 | 69.86% | 1720 | 66.98% | 3113 | 68.24% |
| 62.16% | 74.11% | ||||||||
| 18 | Cube root | Beta-naught | amp.FF | 1409 | 70.66% | 1703 | 66.32% | 3112 | 68.22% |
| 61.96% | 74.43% | ||||||||
| 19 | Cube root | Gamma-naught | dB | 1391 | 69.76% | 1719 | 66.94% | 3110 | 68.17% |
| 62.10% | 74.03% | ||||||||
| 20 | Cube root | Sigma-naught | dB.FF | 1378 | 69.11% | 1730 | 67.37% | 3108 | 68.13% |
| 62.18% | 73.74% | ||||||||
| 21 | Cube root | Beta-naught | dB.FF | 1385 | 69.46% | 1722 | 67.06% | 3107 | 68.11% |
| 62.08% | 73.87% | ||||||||
| 22 | Cube root | Sigma-naught | dB | 1390 | 69.70% | 1719 | 66.90% | 3109 | 68.10% |
| 62.10% | 74.00% | ||||||||
| 23 | Cube root | Sigma-naught | amp | 1405 | 70.46% | 1701 | 66.24% | 3106 | 68.08% |
| 61.84% | 74.28% | ||||||||
| 24 | Cube root | Beta-naught | amp | 1402 | 70.31% | 1699 | 66.16% | 3101 | 67.98% |
| 61.73% | 74.16% | ||||||||
| 25 | Cube root | Gamma-naught | amp | 1404 | 70.41% | 1697 | 66.08% | 3101 | 67.98% |
| 61.71% | 74.20% | ||||||||
| 26 | Cube root | Size only | 1400 | 70.21% | 1685 | 65.62% | 3085 | 67.62% | |
| 61.71% | 73.94% | ||||||||
| 27 | No transformation | Gamma-naught | dB.FF | 1563 | 78.39% | 1433 | 55.80% | 2996 | 65.67% |
| 57.93% | 76.88% | ||||||||
| 28 | No transformation | Beta-naught | dB.FF | 1560 | 78.23% | 1426 | 55.53% | 2986 | 65.45% |
| 57.74% | 76.67% | ||||||||
| 29 | No transformation | Sigma-naught | dB.FF | 1557 | 78.08% | 1427 | 55.57% | 2984 | 65.41% |
| 57.71% | 76.56% | ||||||||
| 30 | No transformation | Gamma-naught | dB | 1559 | 78.18% | 1410 | 57.91% | 2969 | 65.08% |
| 57.38% | 76.42% | ||||||||
| 31 | No transformation | Sigma-naught | dB | 1555 | 77.98% | 1407 | 54.79% | 2962 | 64.93% |
| 57.25% | 76.22% | ||||||||
| 32 | No transformation | Beta-naught | dB | 1554 | 77.93% | 1403 | 54.63% | 2957 | 64.82% |
| 57.15% | 76.13% | ||||||||
| 33 | No transformation | Gamma-naught | amp.FF | 1580 | 79.24% | 1354 | 52.73% | 2934 | 64.31% |
| 56.55% | 76.58% | ||||||||
| 34 | No transformation | Gamma-naught | amp | 1580 | 79.24% | 1353 | 52.69% | 2933 | 64.29% |
| 56.23% | 76.57% | ||||||||
| 35 | No transformation | Sigma-naught | amp.FF | 1580 | 79.24% | 1353 | 52.69% | 2933 | 64.29% |
| 56.53% | 76.57% | ||||||||
| 36 | No transformation | Sigma-naught | amp | 1579 | 79.19% | 1352 | 52.65% | 2931 | 64.25% |
| 56.49% | 76.51% | ||||||||
| 37 | No transformation | Beta-naught | amp.FF | 1580 | 79.24% | 1351 | 52.61% | 2931 | 64.25% |
| 56.49% | 76.54% | ||||||||
| 38 | No transformation | Beta-naught | amp | 1580 | 79.24% | 1347 | 52.45% | 2927 | 64.16% |
| 56.41% | 76.49% | ||||||||
| 39 | No transformation | Size only | 1574 | 78.94% | 1341 | 52.22% | 2915 | 63.90% | |
| 56.19% | 76.15% | ||||||||
| All Three Transformations | Oil Seeps | Sensitivity | Oil Spills | Specificity | Oil Slicks | Overall Accuracy |
| Maximum | 1580 | 79.24% | 1848 | 71.96% | 3141 | 68.85% |
| Minimum | 1288 | 64.59% | 1341 | 52.22% | 2915 | 63.90% |
| Average | 1424 | 71.40% | 1639 | 63.81% | 3063 | 67.13% |
| Range | 292 | 507 | 226 | |||
| log10 | Oil Seeps | Sensitivity | Oil Spills | Specificity | Oil Slicks | Overall Accuracy |
| Maximum | 1324 | 66.40% | 1848 | 71.96% | 3141 | 68.85% |
| Minimum | 1288 | 64.59% | 1799 | 70.05% | 3119 | 68.37% |
| Average | 1305 | 65.45% | 1824 | 71.04% | 3129 | 68.60% |
| Range | 36 | 49 | 22 | |||
| Cube root | Oil Seeps | Sensitivity | Oil Spills | Specificity | Oil Slicks | Overall Accuracy |
| Maximum | 1410 | 70.71% | 1730 | 67.37% | 3118 | 68.35% |
| Minimum | 1378 | 69.11% | 1685 | 65.62% | 3085 | 67.62% |
| Average | 1397 | 70.06% | 1711 | 66.62% | 3108 | 68.12% |
| Range | 32 | 45 | 33 | |||
| No Transformation | Oil Seeps | Sensitivity | Oil Spills | Specificity | Oil Slicks | Overall Accuracy |
| Maximum | 1580 | 79.24% | 1433 | 55.80% | 2996 | 65.67% |
| Minimum | 1554 | 77.93% | 1341 | 52.22% | 2915 | 63.90% |
| Average | 1569 | 78.70% | 1381 | 53.79% | 2951 | 64.68% |
| Range | 26 | 92 | 81 |
| Hierarchy | Data Transformations | Oil-Slicks’ Signature | Oil Seeps | Oil Spills | Oil Slicks | |||
| 1 | log10 | SIG.amp | 1296 | 64.99% | 1829 | 71.22% | 3125 | 68.50% |
| 63.69% | 72.38% | |||||||
| 2 | Cube root | SIG.amp | 1407 | 70.56% | 1711 | 66.63% | 3118 | 68.35% |
| 62.15% | 74.46% | |||||||
| 3 | No Transformation | SIG.amp | 1570 | 78.74% | 1344 | 52.34% | 2914 | 63.88% |
| 56.19% | 76.02% | |||||||
| Hierarchy | Data Transformations | Size Information | Oil Seeps | Oil Spills | Oil Slicks | |||
| 1 | log10 | PtoA and Compact | 1288 | 64.59% | 1841 | 71.69% | 3129 | 68.59% |
| 63.92% | 72.28% | |||||||
| 1 | Cube root | PtoA and Compact | 1417 | 71.06% | 1667 | 64.91% | 3084 | 67.60% |
| 61.13% | 74.29% | |||||||
| 3 | No Transformation | PtoA and Compact | 1575 | 78.99% | 1338 | 52.10% | 2913 | 63.85% |
| 56.15% | 76.15% | |||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, G.d.A.; Minnett, P.J.; Paes, E.T.; de Miranda, F.P.; Landau, L. Oil-Slick Category Discrimination (Seeps vs. Spills): A Linear Discriminant Analysis Using RADARSAT-2 Backscatter Coefficients (σ°, β°, and γ°) in Campeche Bay (Gulf of Mexico). Remote Sens. 2019, 11, 1652. https://doi.org/10.3390/rs11141652
Carvalho GdA, Minnett PJ, Paes ET, de Miranda FP, Landau L. Oil-Slick Category Discrimination (Seeps vs. Spills): A Linear Discriminant Analysis Using RADARSAT-2 Backscatter Coefficients (σ°, β°, and γ°) in Campeche Bay (Gulf of Mexico). Remote Sensing. 2019; 11(14):1652. https://doi.org/10.3390/rs11141652
Chicago/Turabian StyleCarvalho, Gustavo de Araújo, Peter J. Minnett, Eduardo T. Paes, Fernando P. de Miranda, and Luiz Landau. 2019. "Oil-Slick Category Discrimination (Seeps vs. Spills): A Linear Discriminant Analysis Using RADARSAT-2 Backscatter Coefficients (σ°, β°, and γ°) in Campeche Bay (Gulf of Mexico)" Remote Sensing 11, no. 14: 1652. https://doi.org/10.3390/rs11141652
APA StyleCarvalho, G. d. A., Minnett, P. J., Paes, E. T., de Miranda, F. P., & Landau, L. (2019). Oil-Slick Category Discrimination (Seeps vs. Spills): A Linear Discriminant Analysis Using RADARSAT-2 Backscatter Coefficients (σ°, β°, and γ°) in Campeche Bay (Gulf of Mexico). Remote Sensing, 11(14), 1652. https://doi.org/10.3390/rs11141652






