Micro-Motion Estimation of Maritime Targets Using Pixel Tracking in Cosmo-Skymed Synthetic Aperture Radar Data—An Operative Assessment
Abstract
1. Introduction
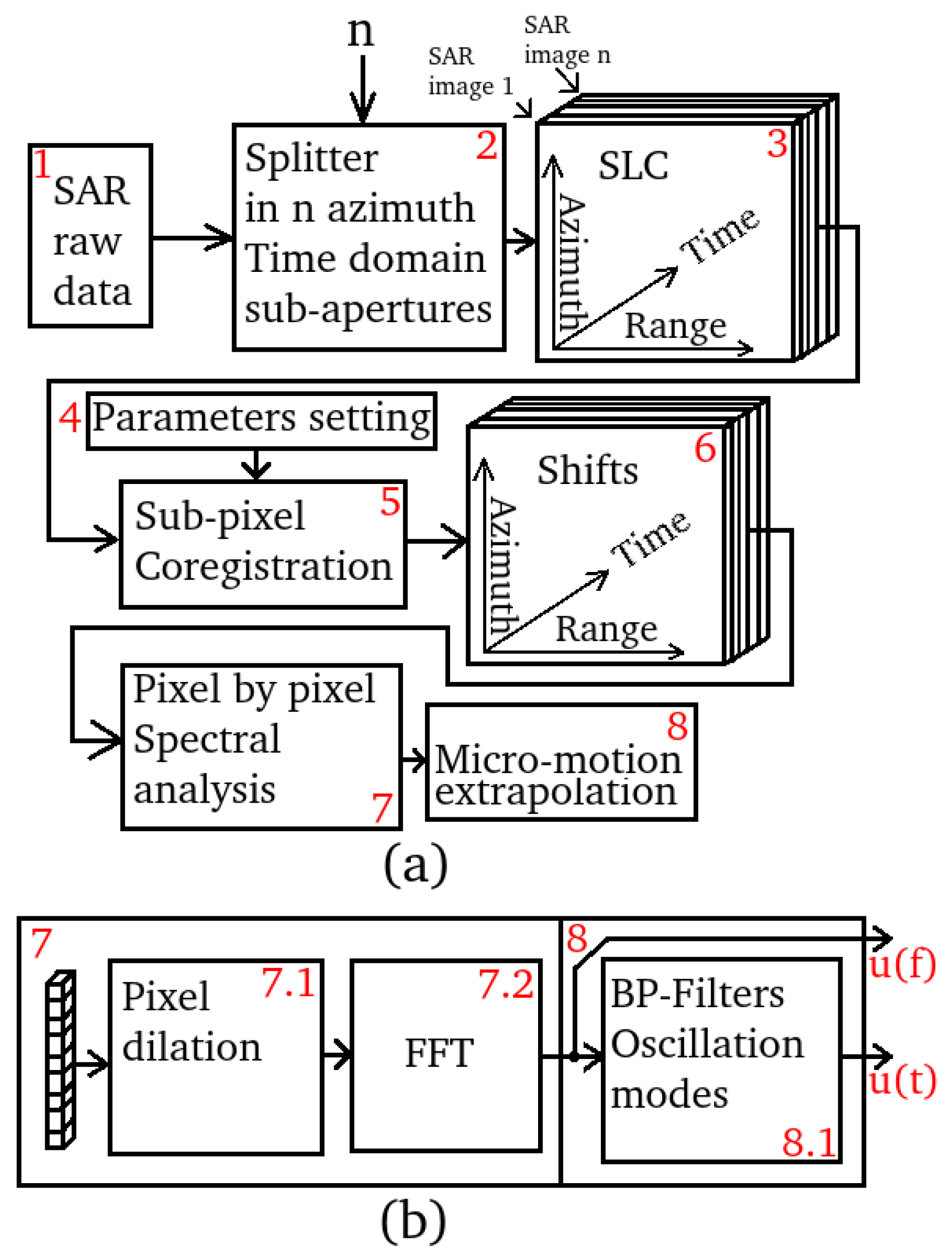
2. Estimation Procedure and Processing Architecture
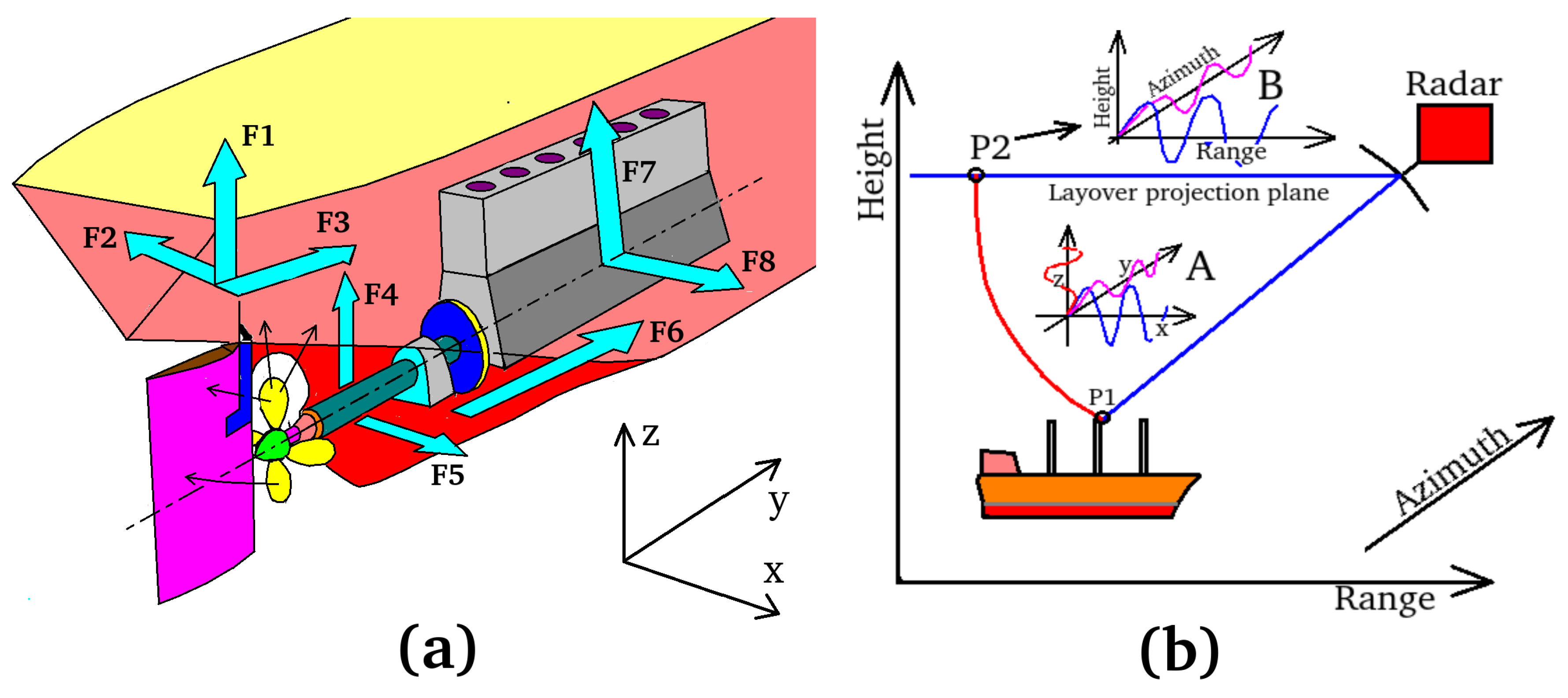
2.1. Computational Model
- Hull beam (keel);
- Main structural substructures;
- Local structural elements.
- On-board equipment (electrical power facilities);
- Main propulsion systems.
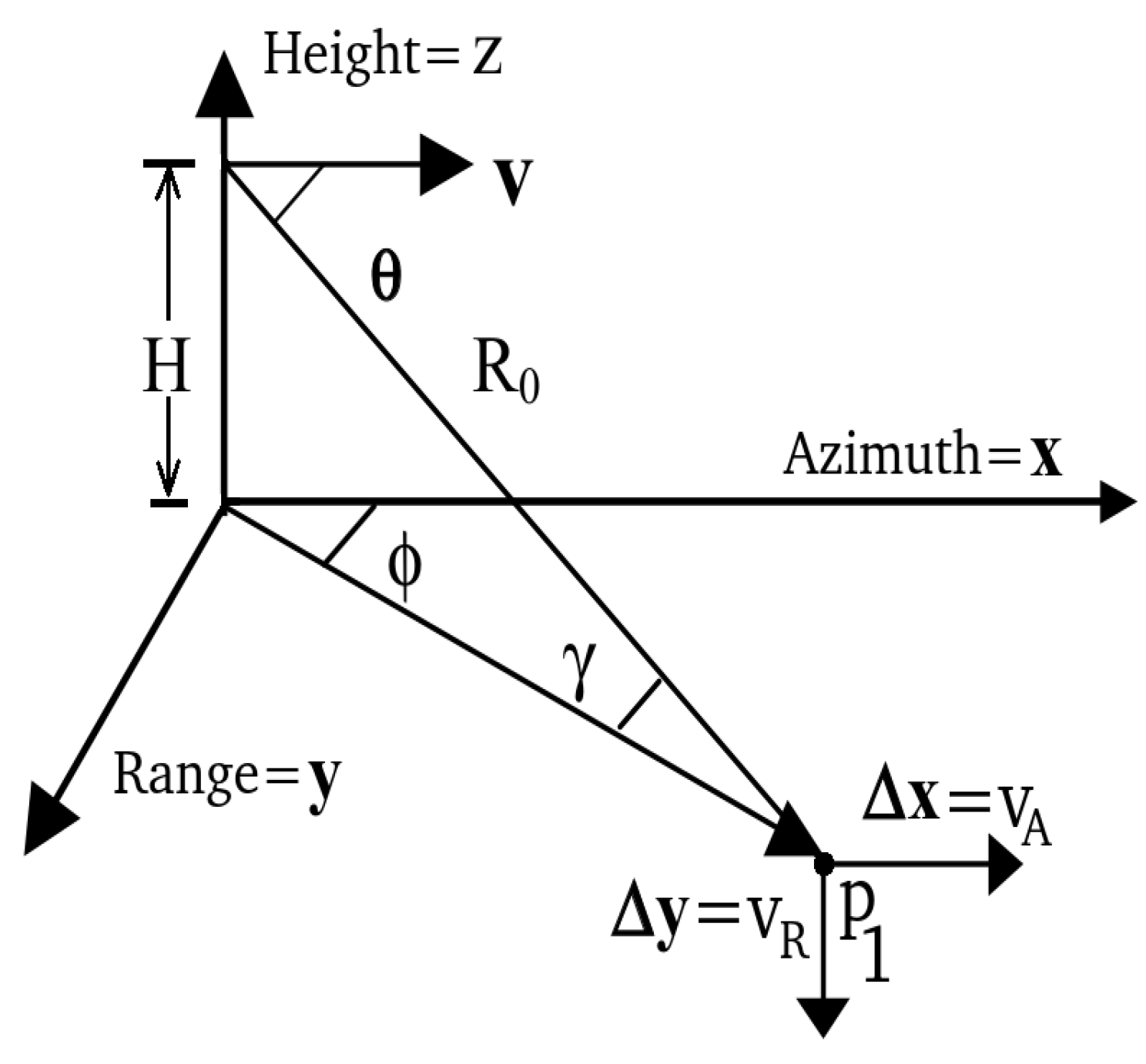
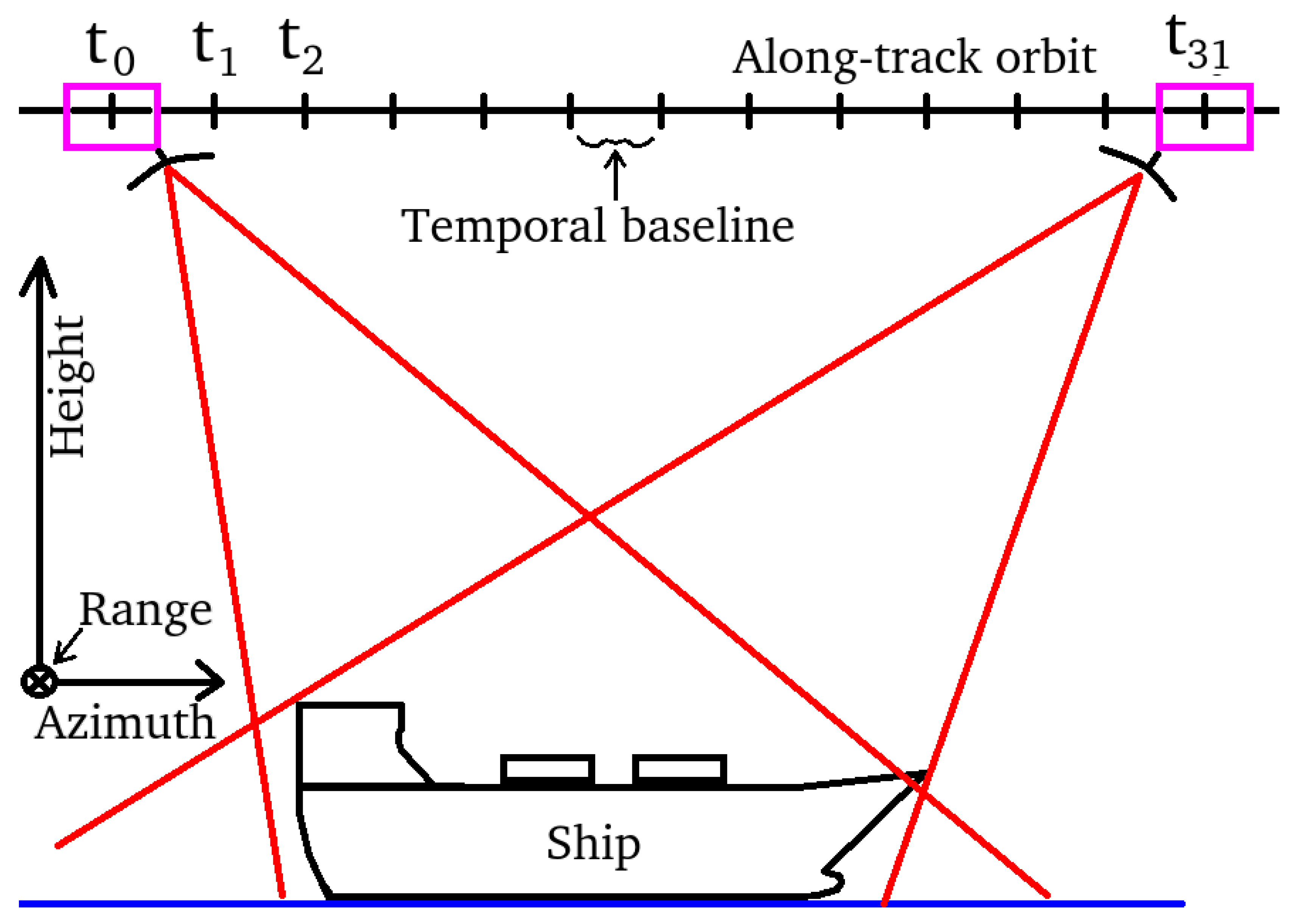
2.2. Estimation Procedure
2.3. Computational Architecture Description
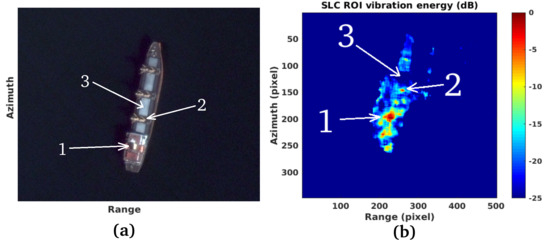
3. Experimental Results
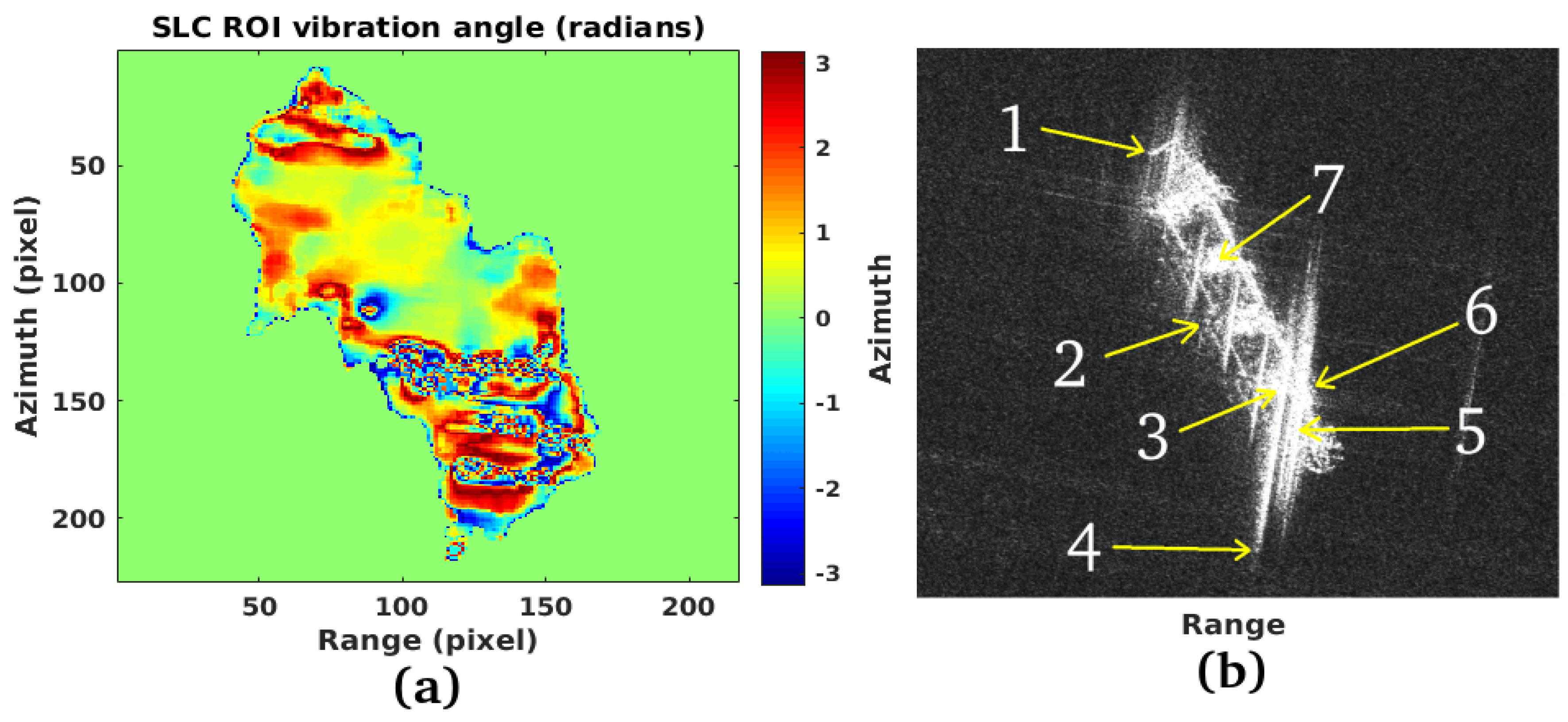
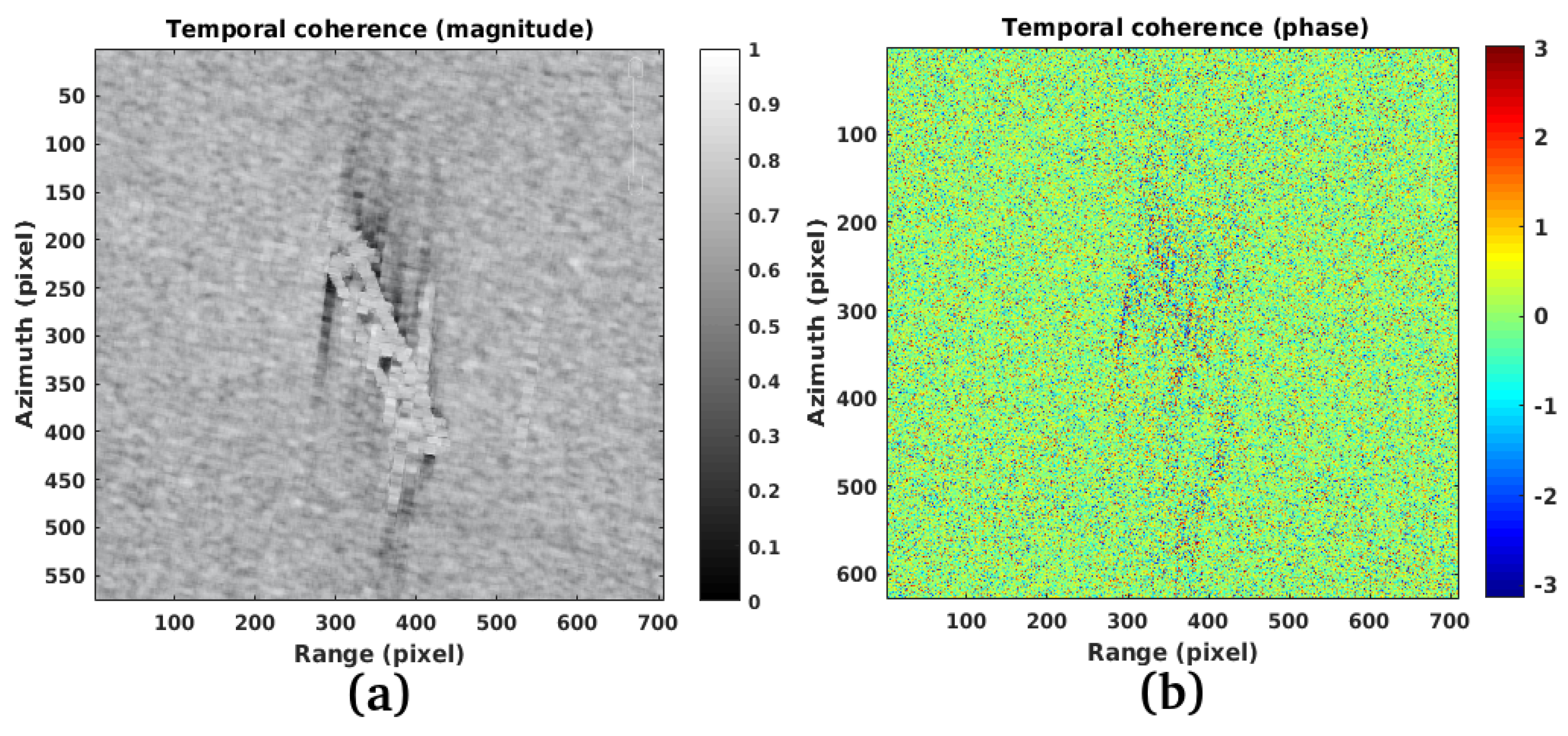
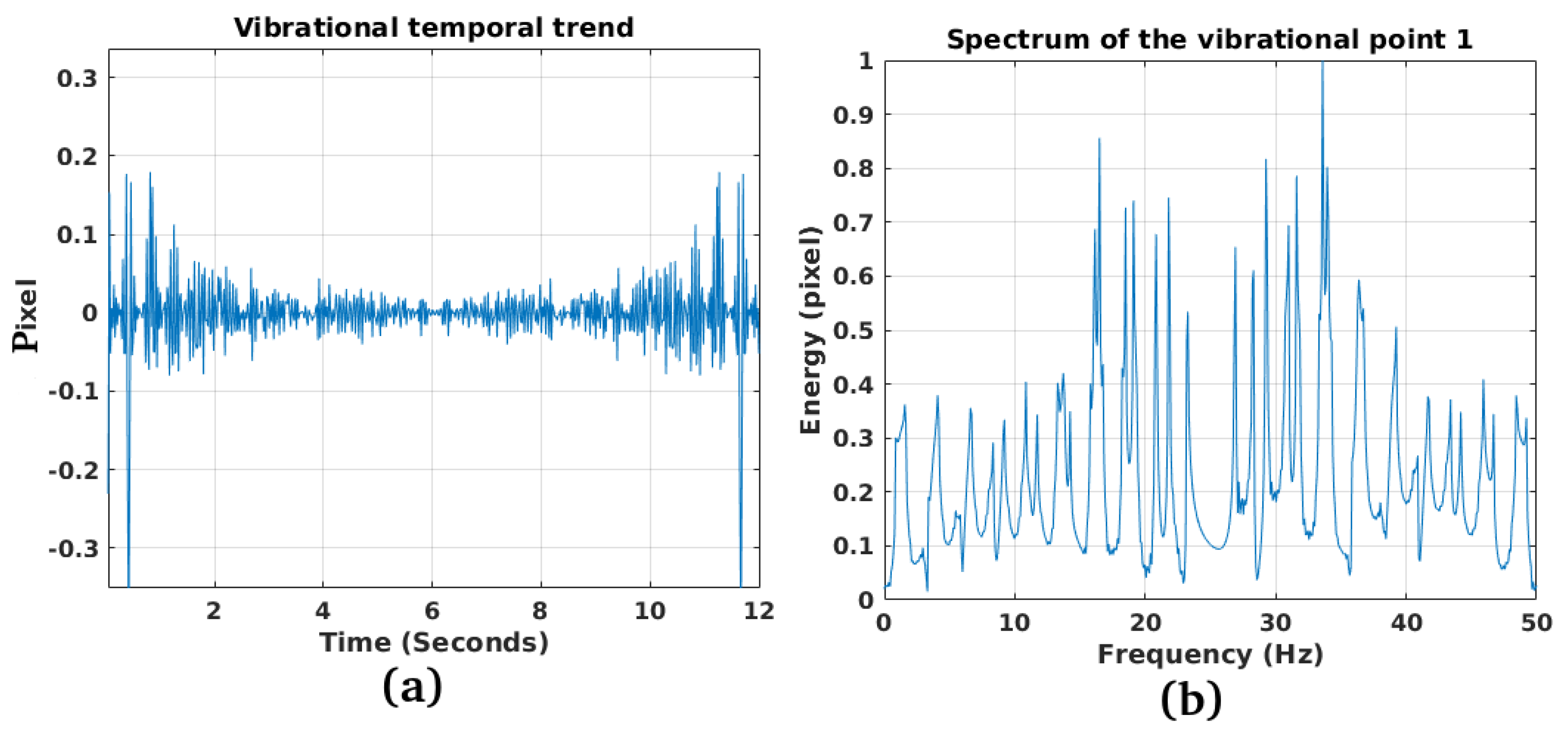
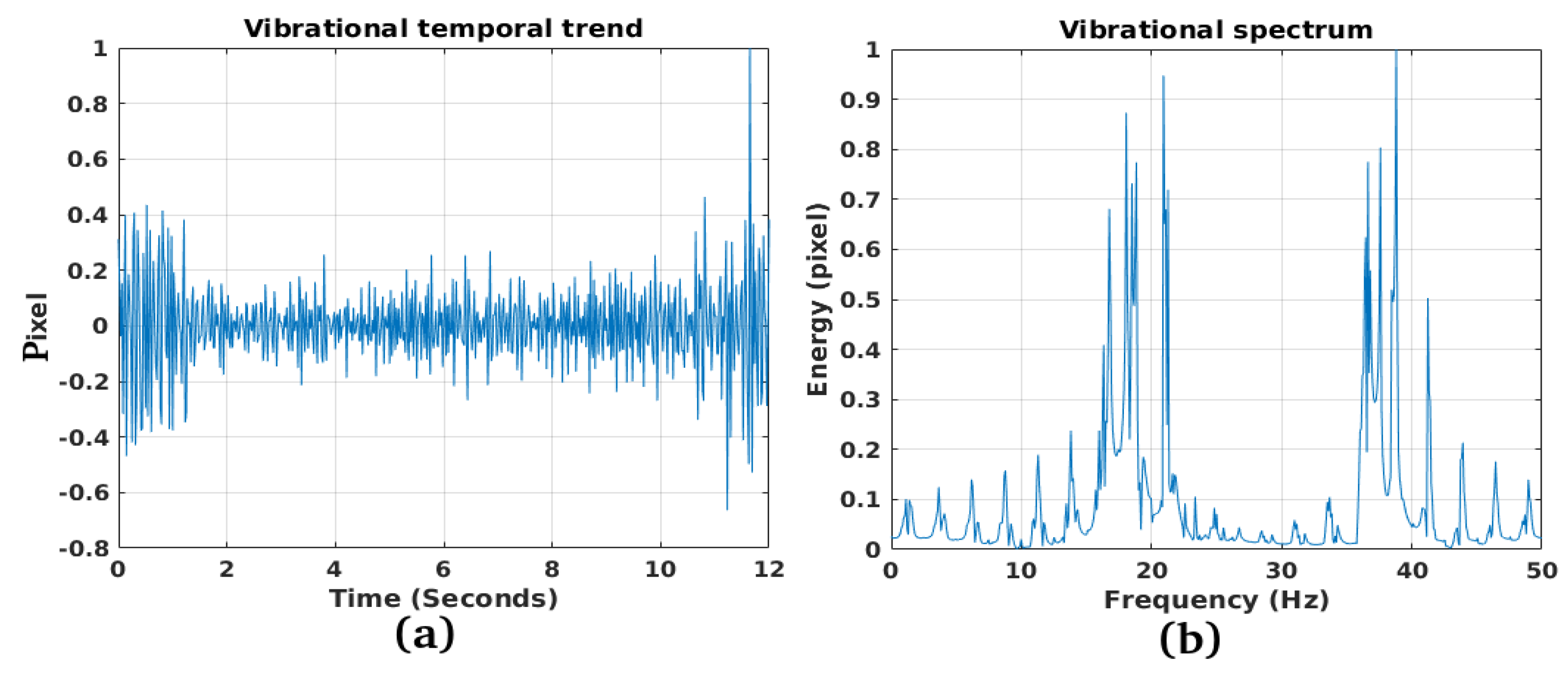
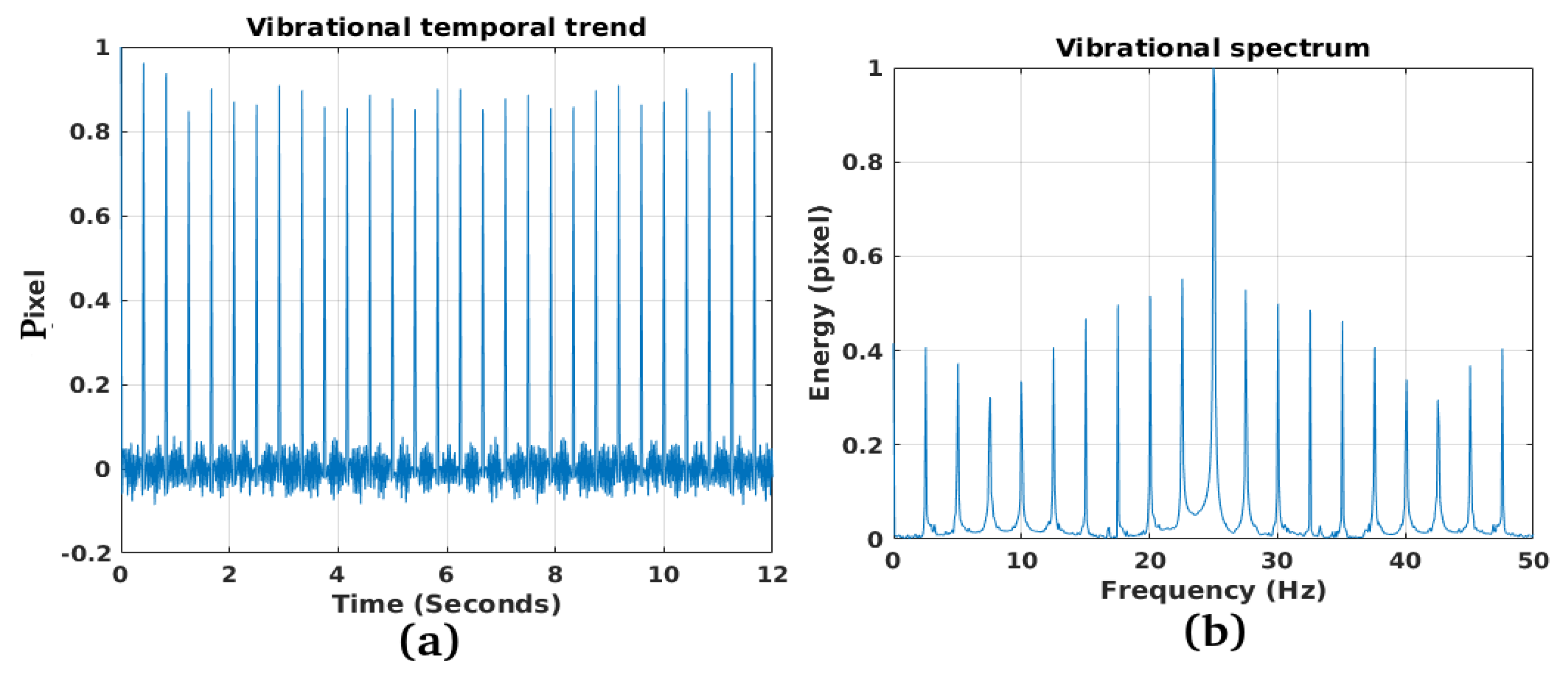
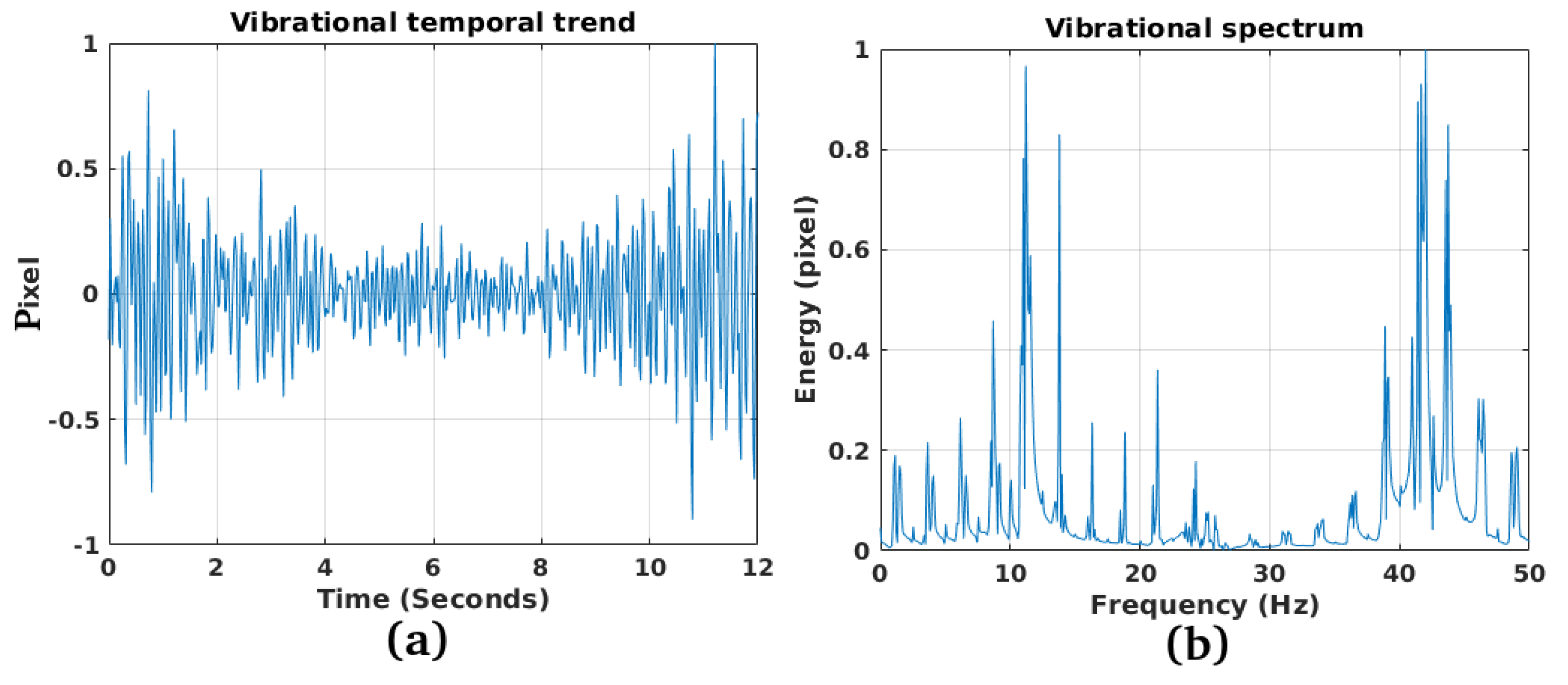
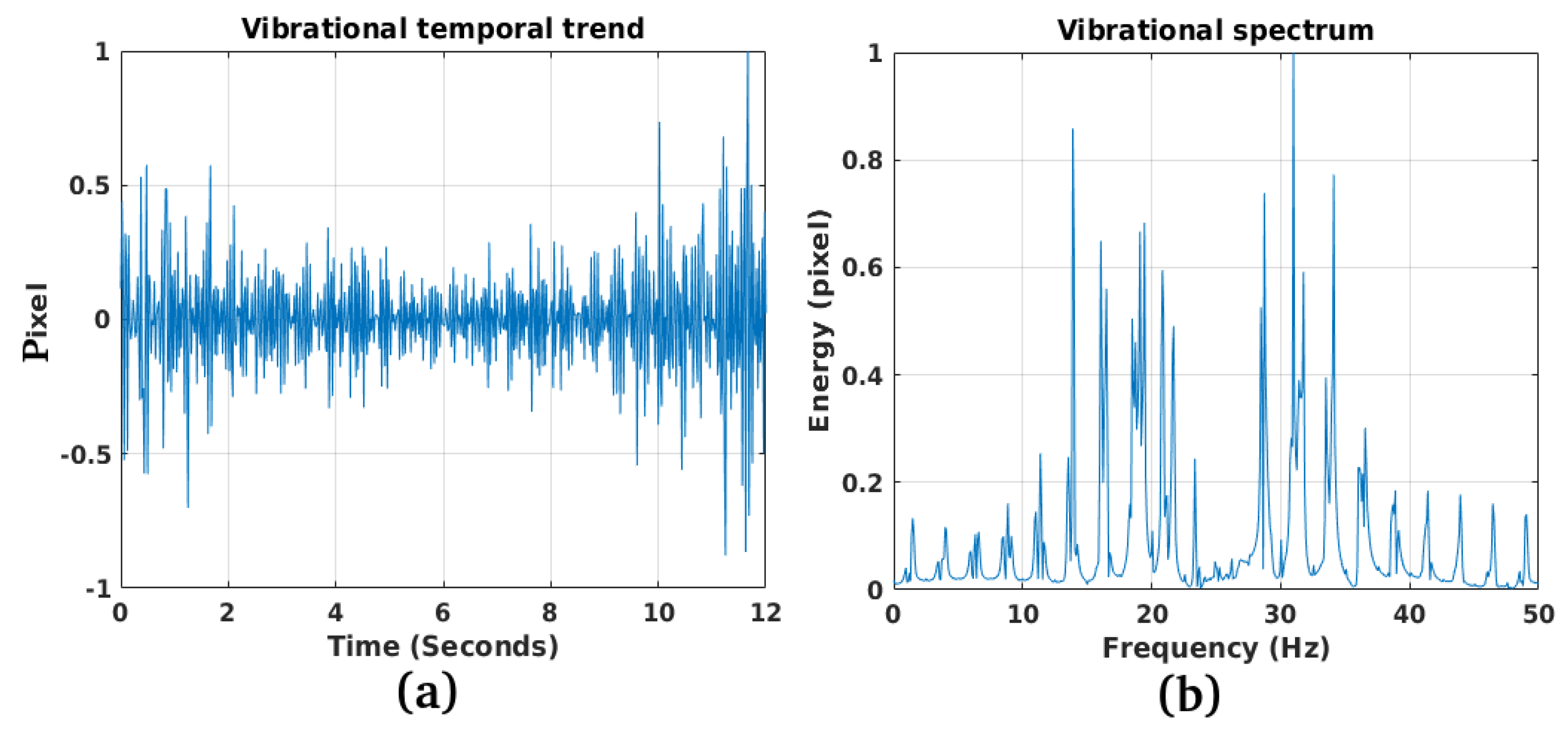
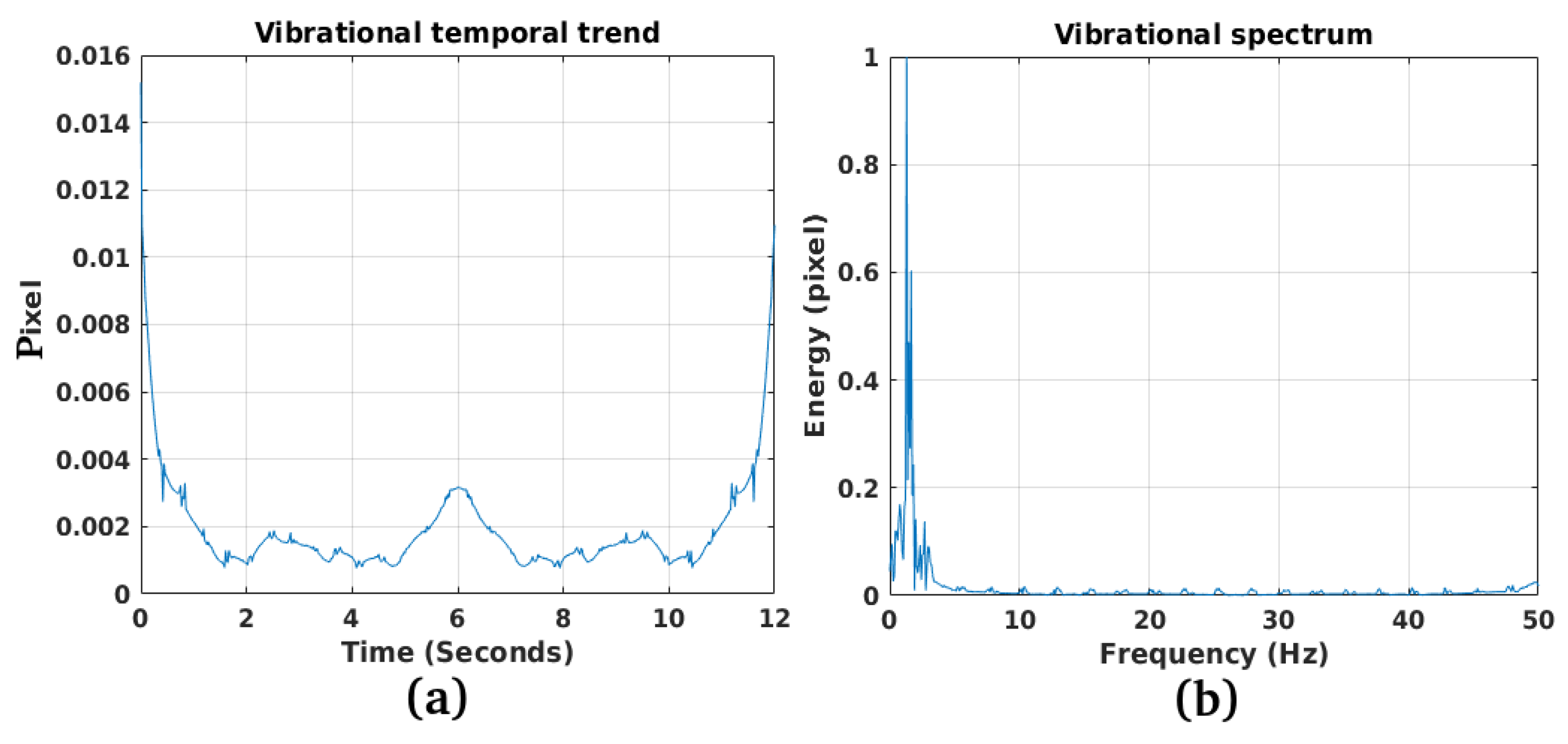
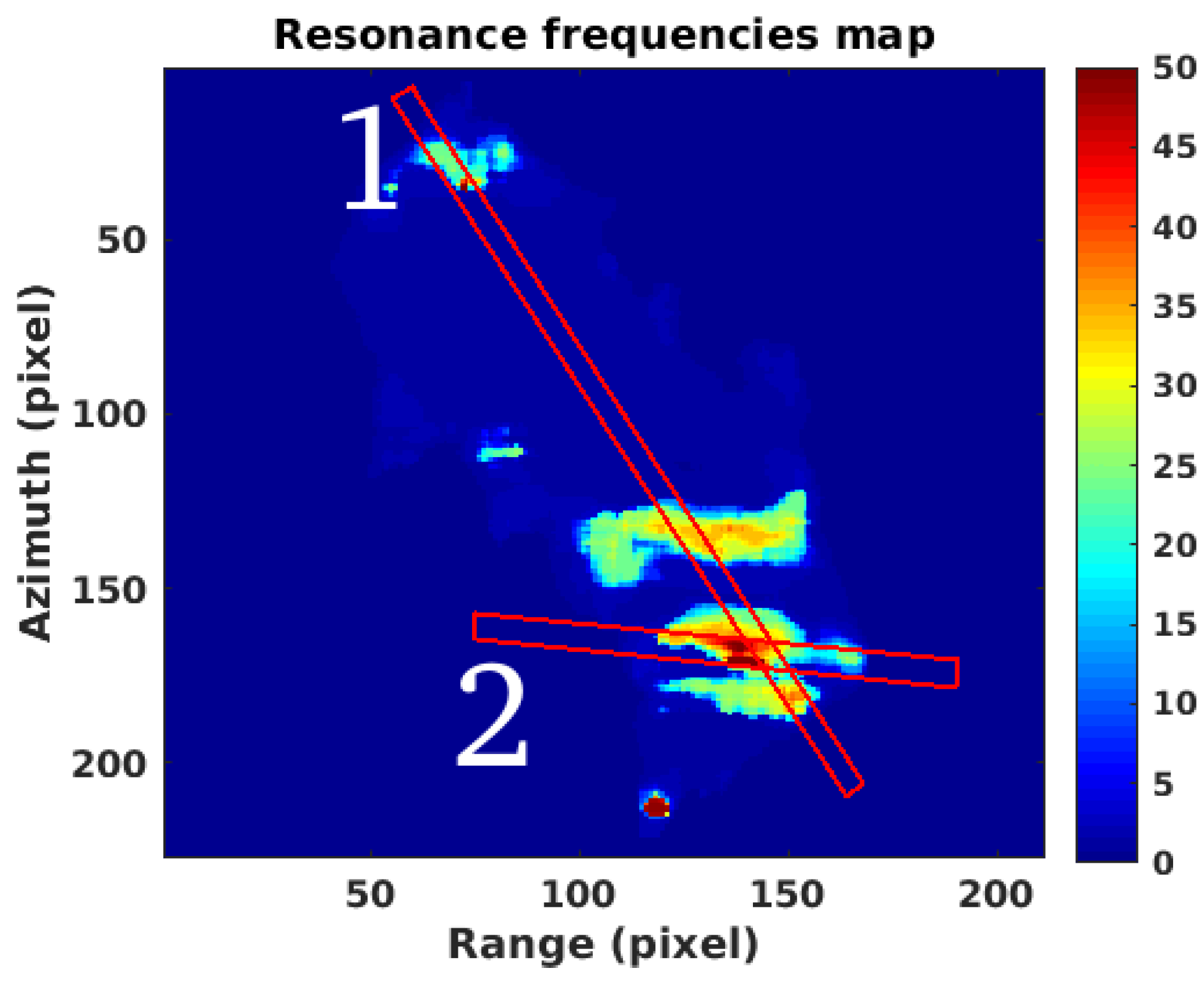
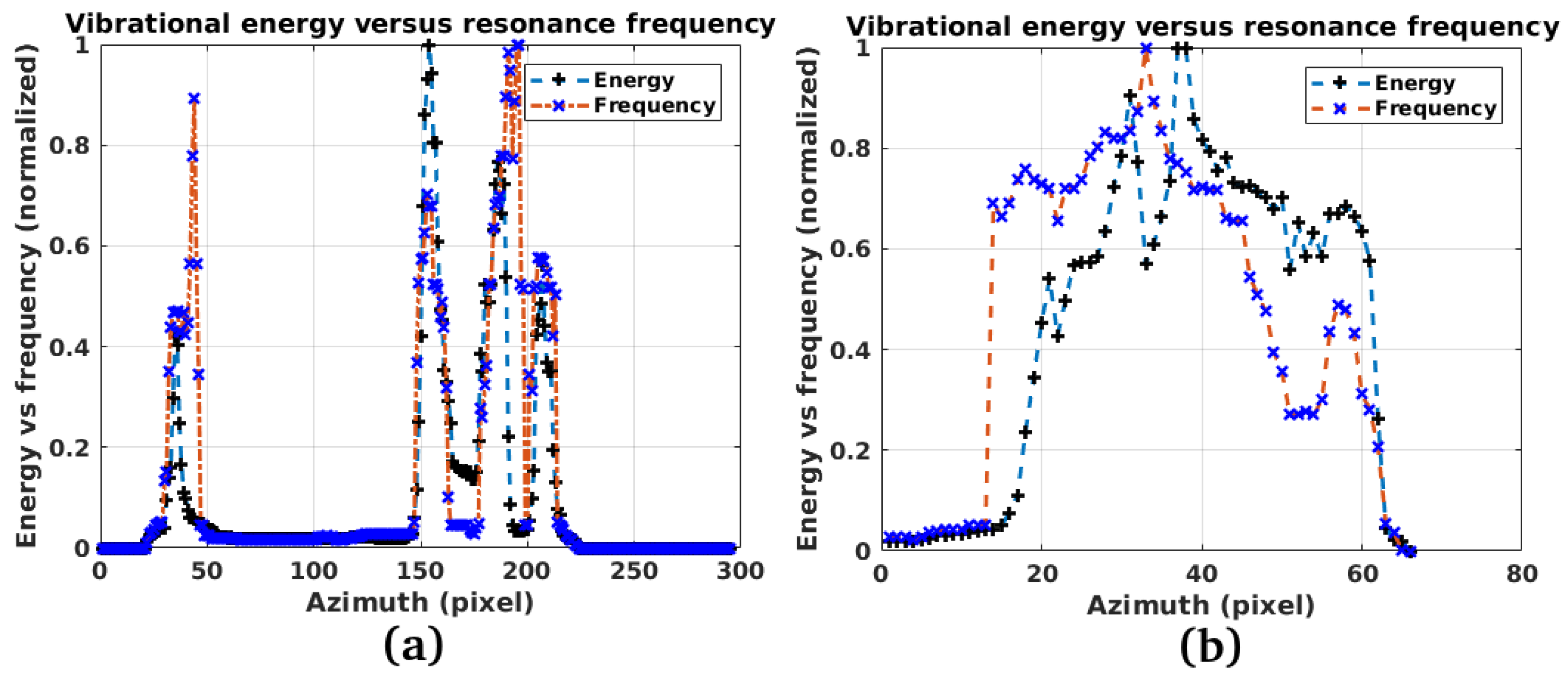
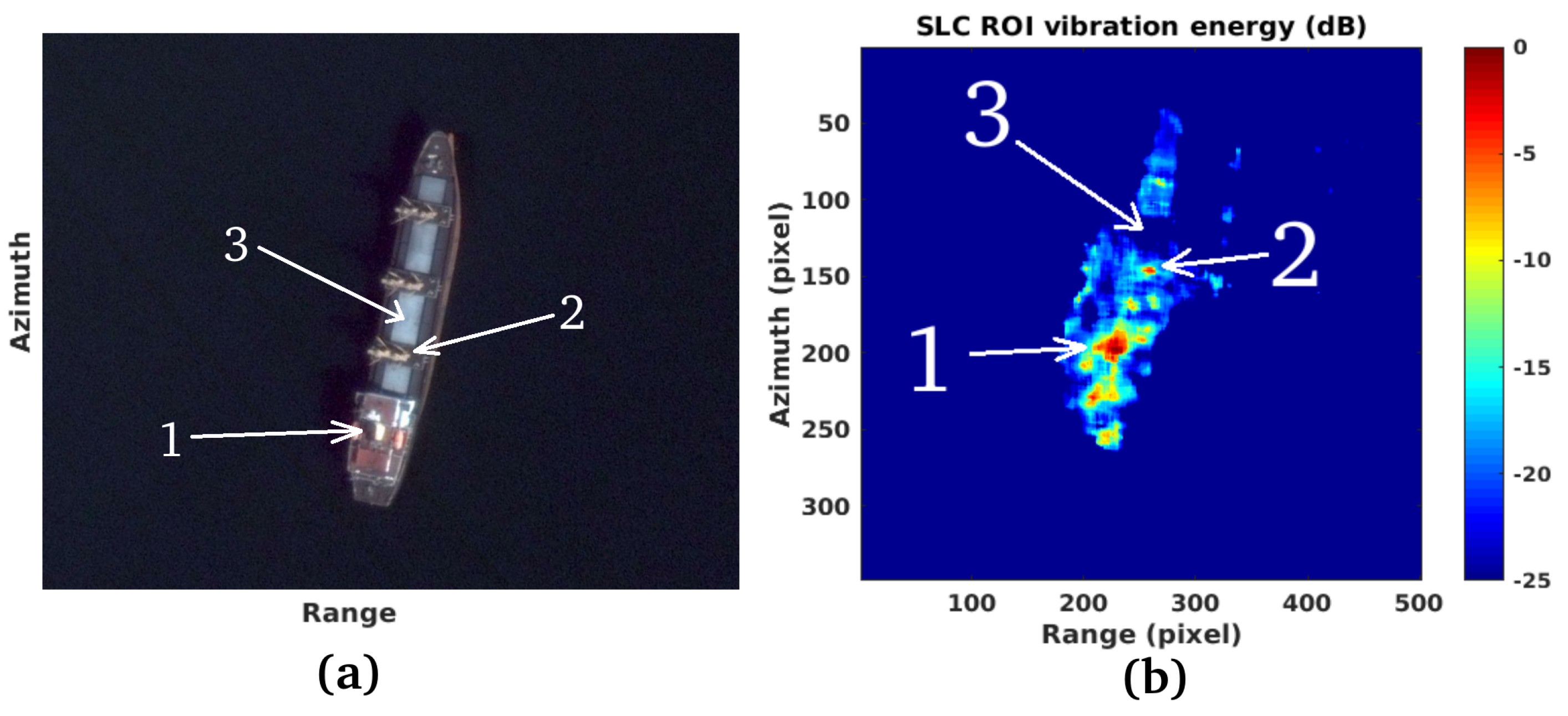
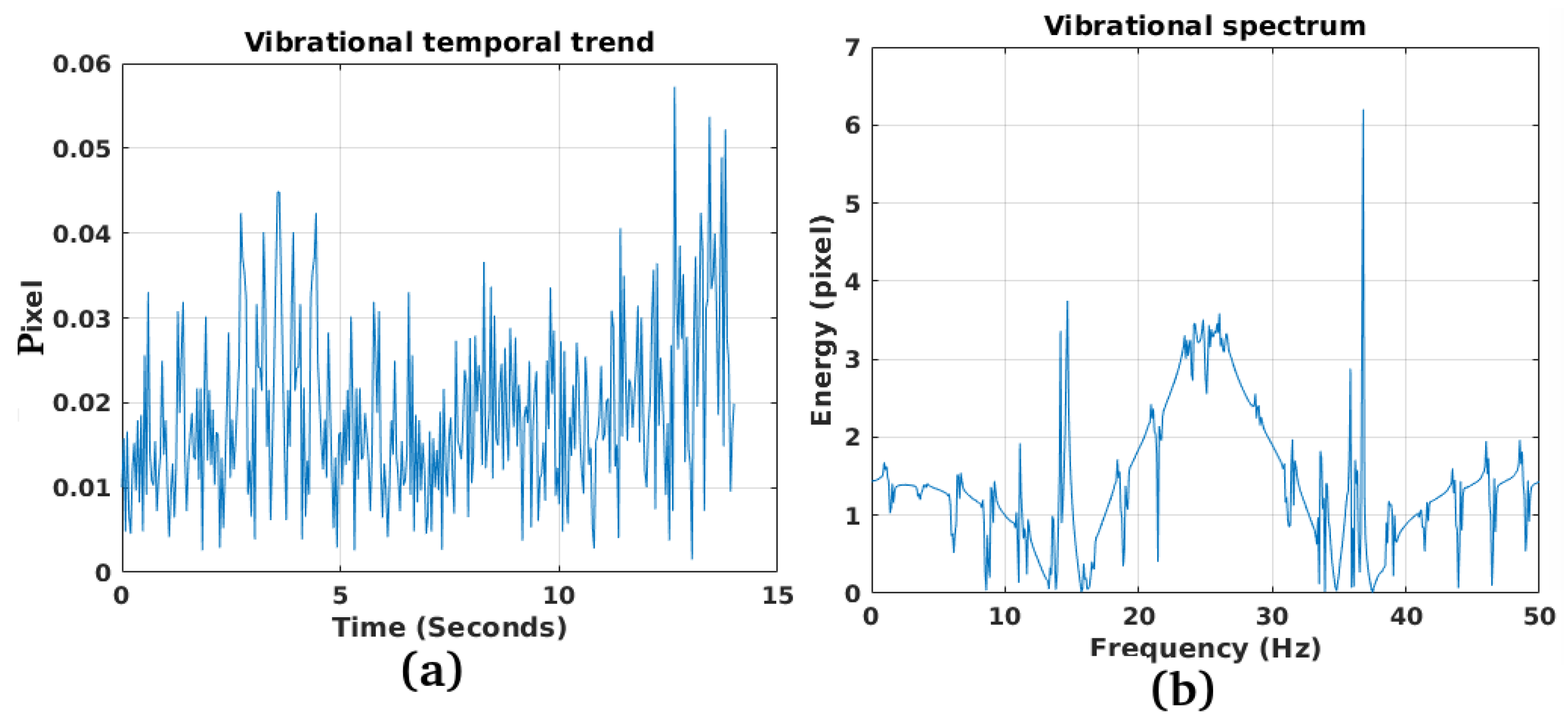
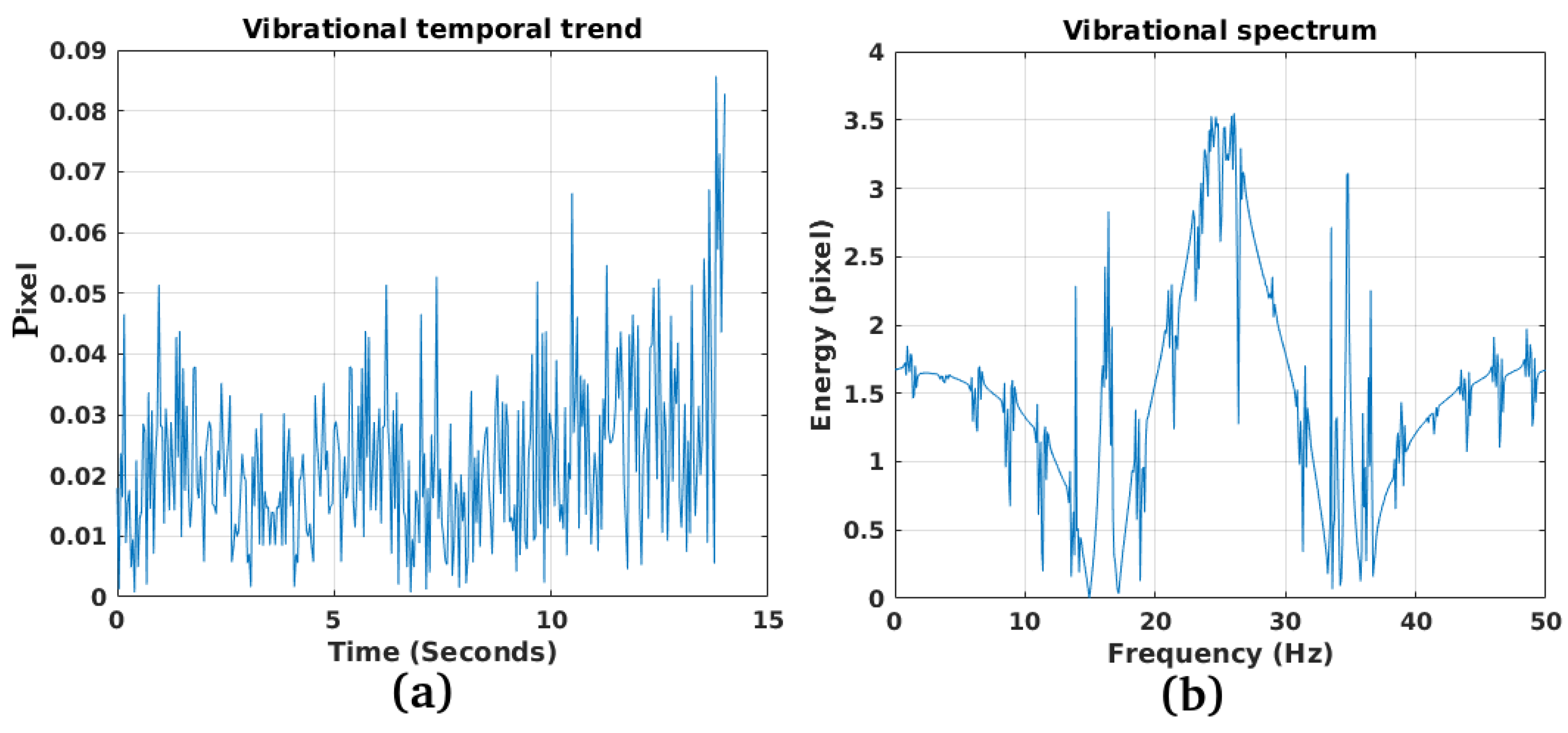
3.1. Study Case 1
3.2. Study Case 2
4. Discussion and Future Assessments
5. Materials and Methods
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SS | Staring Spotlight |
| m-m | micro-motion |
| ROI | Region of Interest |
| MTI | Moving Target Indicator |
| LRSD | Low-Rank plus Sparse Decomposition |
| RT | Radon transform |
| MIMO | Multiple Input Multiple Output |
| SPOT | Pixel Offset Tracking |
| GLRT | Generalized Likelihood Ratio Test |
| LOS | Line of Sight |
| ERS | European remote sensing satellite system |
| CSK | COSMO-SkyMed |
| ATI | Along-Track-Interferometry |
| SAR | Synthetic Aperture Radar |
| ISAR | Interferometric SAR |
| DEM | Digital Elevation Model |
| FFT | Fast Fourier Transform |
| SLC | Single Look Complex |
| BP-Filter | Band Pass Filter |
References
- Filippo, B. COSMO-SkyMed Staring Spotlight SAR Data for Micro-Motion and Inclination Angle Estimation of Ships by Pixel Tracking and Convex Optimization. Remote Sens. 2019, 11, 766. [Google Scholar] [CrossRef]
- Ruegg, M.; Meier, E.; Nuesch, D. Vibration and rotation in millimeter-wave SAR. IEEE Trans. Geosci. Remote Sens. 2007, 45, 293–304. [Google Scholar] [CrossRef]
- Sparr, T.; Krane, B. Micro-Doppler analysis of vibrating targets in SAR. IEE Proc.-Radar Sonar Navig. 2003, 150, 277–283. [Google Scholar] [CrossRef]
- Clemente, C.; Soraghan, J.J. Vibrating target micro-Doppler signature in bistatic SAR with a fixed receiver. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3219–3227. [Google Scholar] [CrossRef]
- Thayaparan, T.; Suresh, P.; Qian, S.; Venkataramaniah, K.; SivaSankaraSai, S.; Sridharan, K.S. Micro-Doppler analysis of a rotating target in synthetic aperture radar. IET Signal Process. 2010, 4, 245–255. [Google Scholar] [CrossRef]
- Deng, B.; Wang, H.Q.; Li, X.; Qin, Y.L.; Wang, J.T. Generalised likelihood ratio test detector for micro-motion targets in synthetic aperture radar raw signals. IET Radar Sonar Navig. 2011, 5, 528–535. [Google Scholar] [CrossRef]
- Stankovic, L.; Thayaparan, T.; Dakovic, M.; Popovic-Bugarin, V. Micro-Doppler removal in the radar imaging analysis. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1234–1250. [Google Scholar] [CrossRef]
- Zhao, G.; Fu, Y.; Nie, L.; Zhuang, Z. Imaging and micro-Doppler analysis of vibrating target in multi-input?multi-output synthetic aperture radar. IET Radar Sonar Navig. 2015, 9, 1360–1365. [Google Scholar] [CrossRef]
- Bandiera, F.; Orlando, D.; Ricci, G. On the CFAR property of GLRT-based direction detectors. IEEE Trans. Signal Process. 2007, 55, 4312–4315. [Google Scholar] [CrossRef]
- Biondi, F. Low rank plus sparse decomposition of synthetic aperture radar data for maritime surveillance. In Proceedings of the 2016 4th International Workshop on Compressed Sensing Theory and its Applications to Radar, Sonar and Remote Sensing (CoSeRa), Aachen, Germany, 19–22 September 2016; pp. 75–79. [Google Scholar]
- Biondi, F. Low-rank plus sparse decomposition and localized radon transform for ship-wake detection in synthetic aperture radar images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 117–121. [Google Scholar] [CrossRef]
- Biondi, F. A Polarimetric Extension of Low-Rank Plus Sparse Decomposition and Radon Transform for Ship Wake Detection in Synthetic Aperture Radar Images. IEEE Geosci. Remote Sens. Lett. 2019, 16, 75–79. [Google Scholar] [CrossRef]
- Casu, F.; Manconi, A.; Pepe, A.; Lanari, R. Deformation time-series generation in areas characterized by large displacement dynamics: The SAR amplitude pixel-offset SBAS technique. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2752–2763. [Google Scholar] [CrossRef]
- Scambos, T.A.; Dutkiewicz, M.J.; Wilson, J.C.; Bindschadler, R.A. Application of image cross-correlation to the measurement of glacier velocity using satellite image data. Remote Sens. Environ. 1992, 42, 177–186. [Google Scholar] [CrossRef]
- Giles, A.B.; Massom, R.A.; Warner, R.C. A method for sub-pixel scale feature-tracking using Radarsat images applied to the Mertz Glacier Tongue, East Antarctica. Remote Sens. Environ. 2009, 113, 1691–1699. [Google Scholar] [CrossRef]
- Wang, Z.; Perissin, D.; Lin, H. Subway tunnels identification through Cosmo-SkyMed PSInSAR analysis in Shanghai. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011. [Google Scholar]
- Perissin, D.; Wang, T. Repeat-pass SAR interferometry with partially coherent targets. IEEE Trans. Geosci. Remote Sens. 2012, 50, 271–280. [Google Scholar] [CrossRef]
- Nitti, D.O.; Hanssen, R.F.; Refice, A.; Bovenga, F.; Nutricato, R. Impact of DEM-assisted coregistration on high-resolution SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1127–1143. [Google Scholar] [CrossRef]
- Biondi, F.; Clemente, C.; Orlando, D. An atmospheric phase screen estimation strategy based on multi-chromatic analysis for differential interferometric synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2019, 1–12. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Near Incidence Angle | |
| Far Incidence Angle | |
| Range Focusing Bandwidth | 250 MHz |
| Azimuth Focusing Bandwidth | 25 kHz |
| Orbit height | 600 km |
| Chirp central frequency | GHz |
| Minimum points for each tile | 50 |
| Acquisition time | 1 June 2014 |
| Acquisition location | Taranto (Italy) |
| Parameter | Value |
|---|---|
| Initial shifts | Coarse cross-correlation |
| Number of points | 4000 |
| Correlation threshold | 0.8 |
| Oversampling factor | 200 |
| Search pixel window | 48 × 48 pixel |
| Points skimming (minimum points) | 30 |
| Use of DEM | No |
| Doppler Centr. Est. Strategy | Polynomials |
| Parameter | Value |
|---|---|
| Satellite Identification | CSK Satellite one |
| Satellite Height: | 627,863.775618 m |
| Location: | Taranto (Italy) |
| Scene Sensing Start UTC: | 2012-07-12 16:47:10.074928684 |
| Scene Sensing Stop UTC: | 2012-07-12 16:47:17.643165988 |
| Azimuth Focusing Bandwidth: | 23,131.019234 Hz |
| Radar Central Frequency: | 9,600,000,000.000000 Hz |
| Radar Wavelength: | 0.031228 Hz |
| Range Focusing Bandwidth: | 247,705,078.125000 Hz |
| Reference Incidence Angle: | 40.000000 Hz |
| Ground Range Instrument Geometric Resolution: | 0.890077 m |
| Range Focusing Bandwidth: | 247,705,078.125000 Hz |
| Scene Centre Geodetic Coordinates: | N E |
| Point Number | Location on the Ship |
|---|---|
| 1 | bow |
| 2 | left-center |
| 3 | bridge area-sterncastle |
| 4 | stern main mast |
| 5 | sterncastle straight side |
| 6 | dashboard straight side |
| 7 | foward-center |
| Point Number | Location on the Ship |
|---|---|
| 1 | top of the funnel |
| 2 | first crane |
| 3 | center |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biondi, F.; Addabbo, P.; Orlando, D.; Clemente, C. Micro-Motion Estimation of Maritime Targets Using Pixel Tracking in Cosmo-Skymed Synthetic Aperture Radar Data—An Operative Assessment. Remote Sens. 2019, 11, 1637. https://doi.org/10.3390/rs11141637
Biondi F, Addabbo P, Orlando D, Clemente C. Micro-Motion Estimation of Maritime Targets Using Pixel Tracking in Cosmo-Skymed Synthetic Aperture Radar Data—An Operative Assessment. Remote Sensing. 2019; 11(14):1637. https://doi.org/10.3390/rs11141637
Chicago/Turabian StyleBiondi, Filippo, Pia Addabbo, Danilo Orlando, and Carmine Clemente. 2019. "Micro-Motion Estimation of Maritime Targets Using Pixel Tracking in Cosmo-Skymed Synthetic Aperture Radar Data—An Operative Assessment" Remote Sensing 11, no. 14: 1637. https://doi.org/10.3390/rs11141637
APA StyleBiondi, F., Addabbo, P., Orlando, D., & Clemente, C. (2019). Micro-Motion Estimation of Maritime Targets Using Pixel Tracking in Cosmo-Skymed Synthetic Aperture Radar Data—An Operative Assessment. Remote Sensing, 11(14), 1637. https://doi.org/10.3390/rs11141637