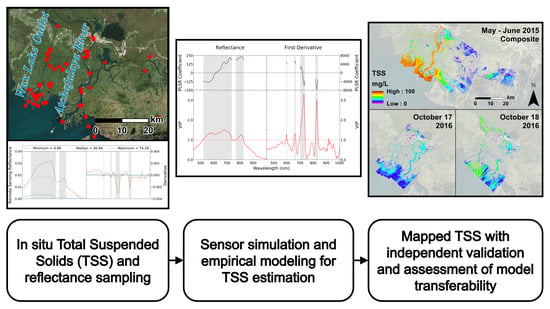
Improving the Transferability of Suspended Solid Estimation in Wetland and Deltaic Waters with an Empirical Hyperspectral Approach
Abstract
1. Introduction
2. Materials and Methods
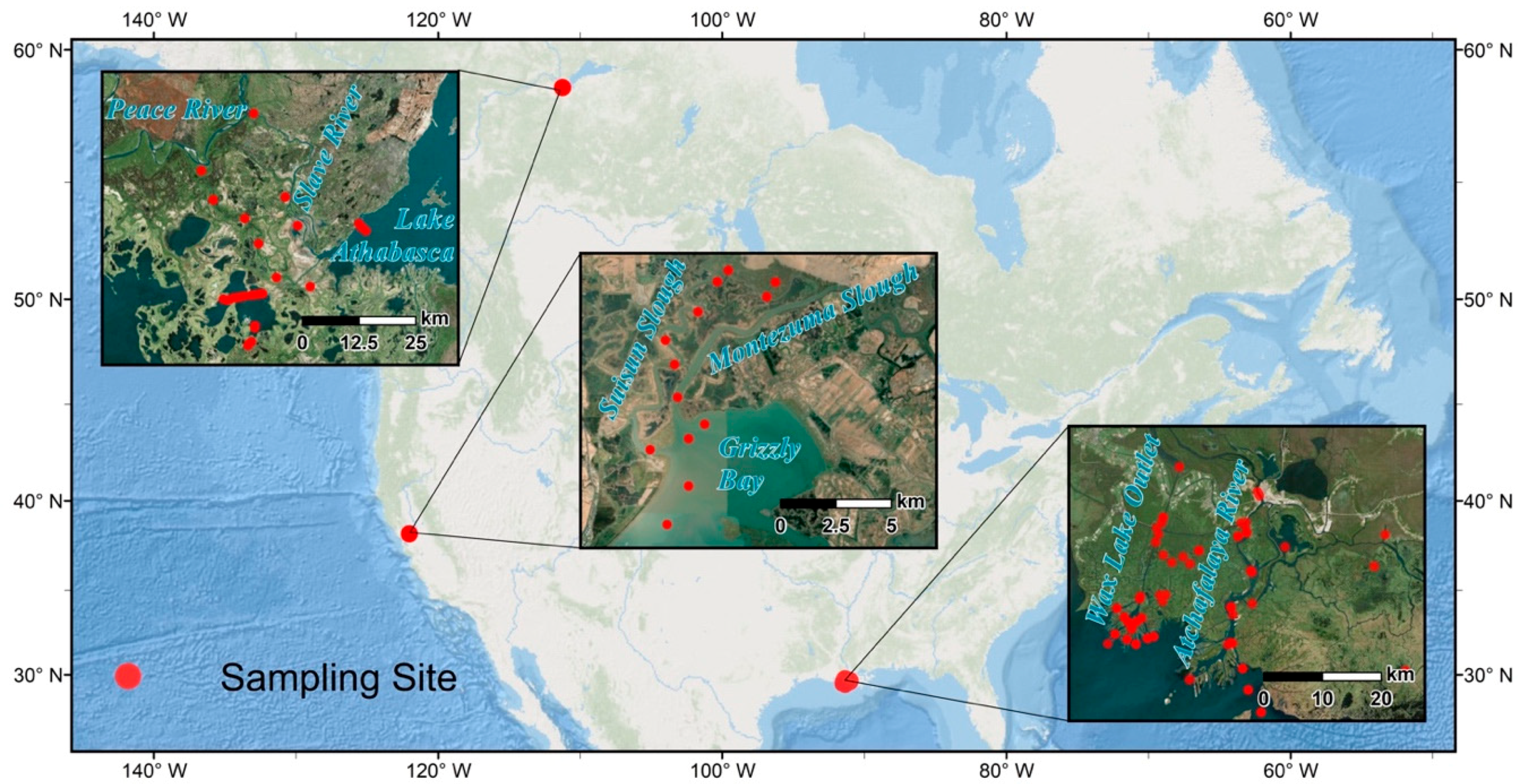
2.1. Airborne Imaging Spectrometer Data Acquisition with AVIRIS-NG
2.2. Field Measurements for Algorithm Development
2.2.1. Total Suspended Solids Measurements
2.2.2. In Situ Spectral Reflectance Measurements
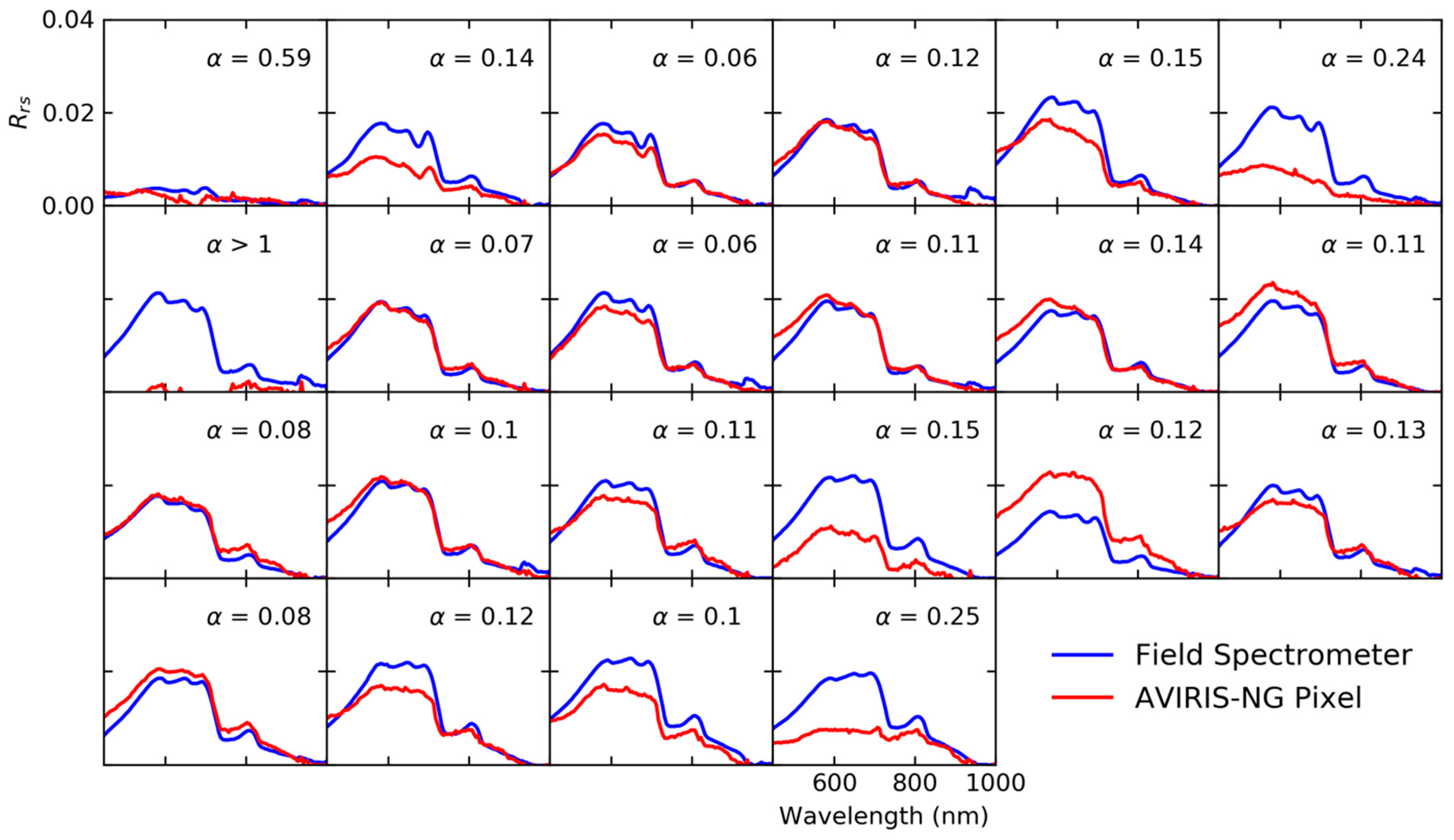
2.2.3. Simulation of AVIRIS-NG and MODIS Remote Sensing Reflectance
2.3. Total Suspended Solids Algorithm Development from Simulated Sensor Data
2.4. Validation
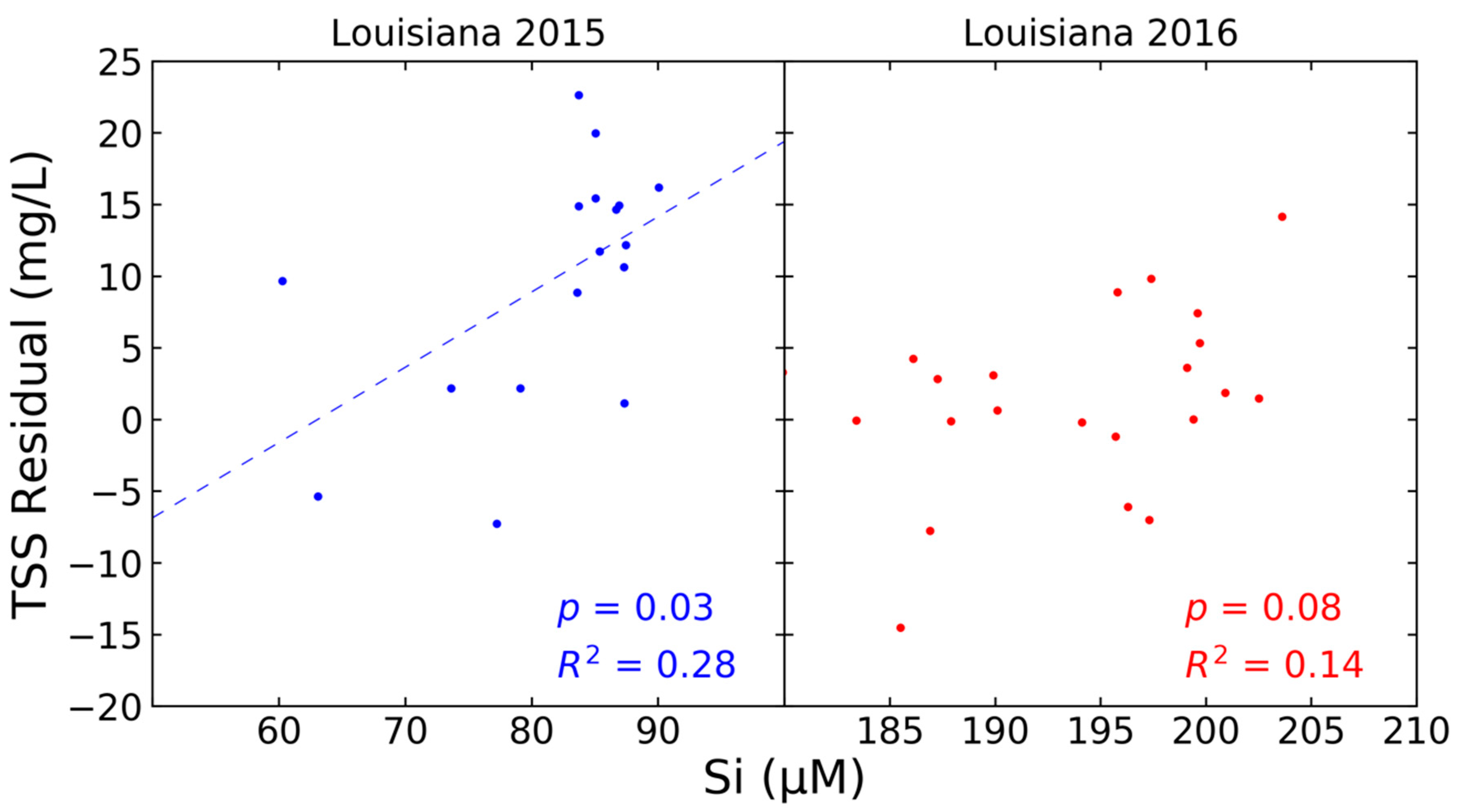
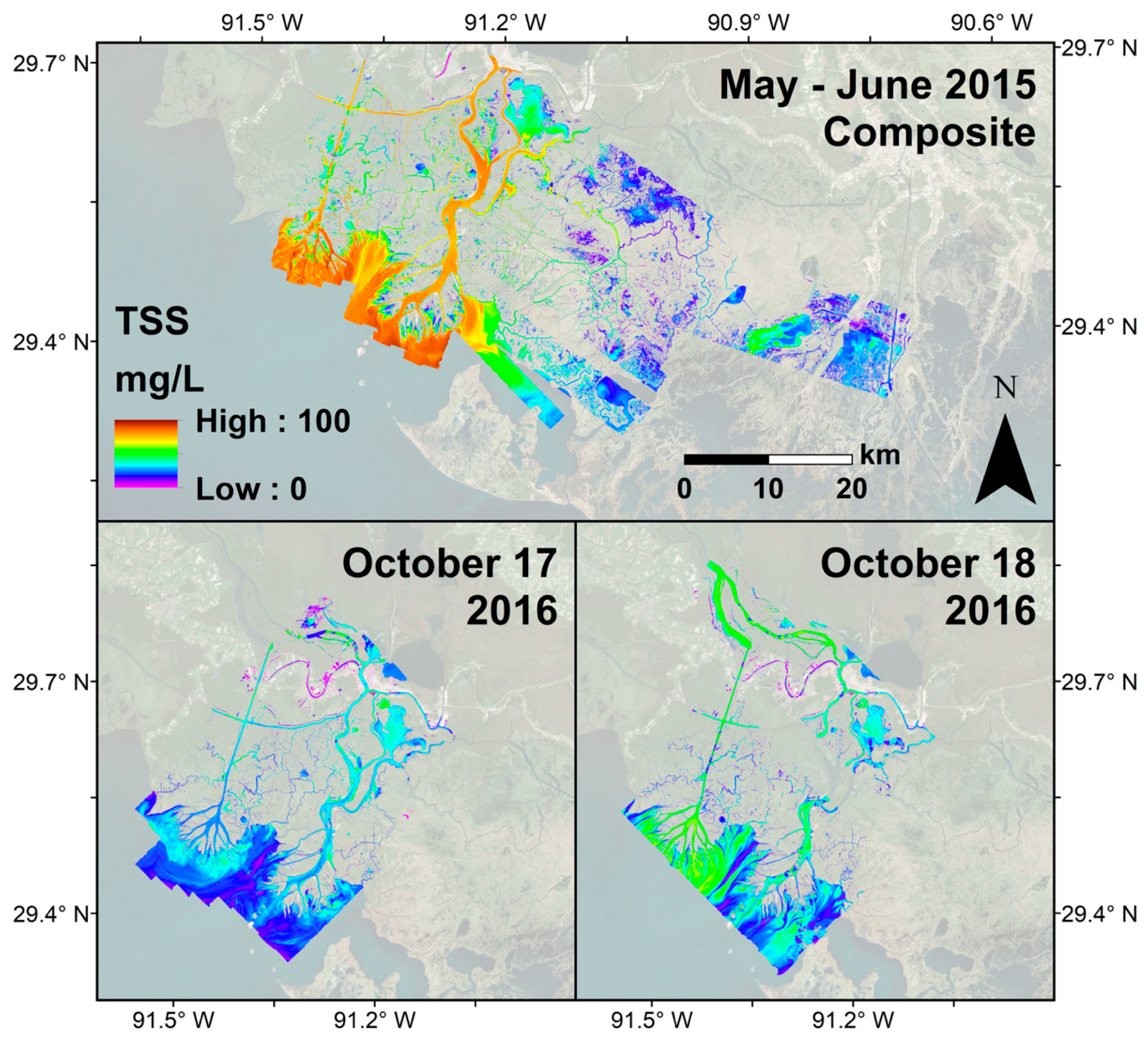
2.4.1. Assessing Model Temporal Transferability: Validation with AVIRIS-NG in Coastal Louisiana
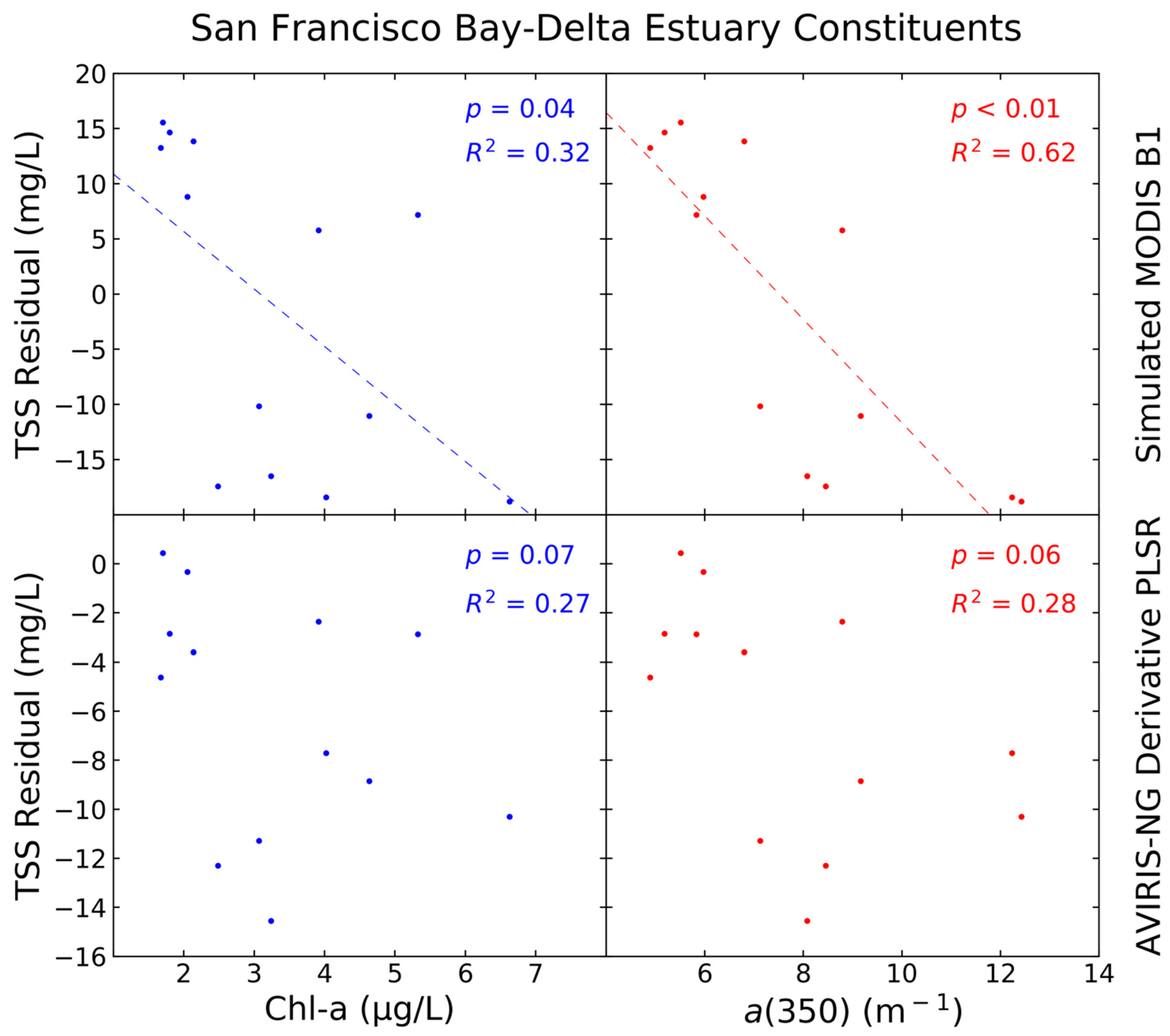
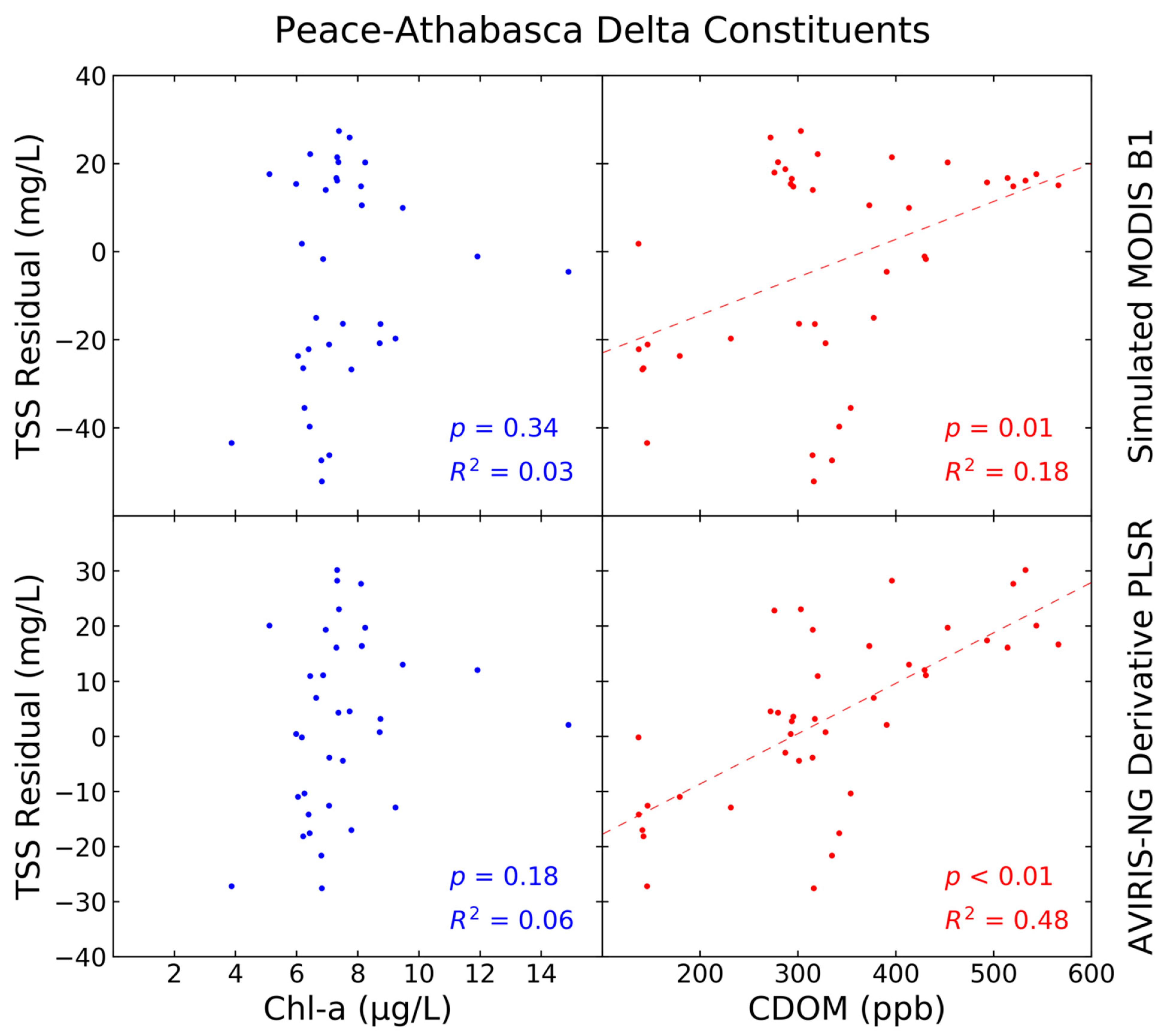
2.4.2. Assessing Model Spatial Transferability: Applications in Grizzly Bay and the Peace–Athabasca Delta
3. Results
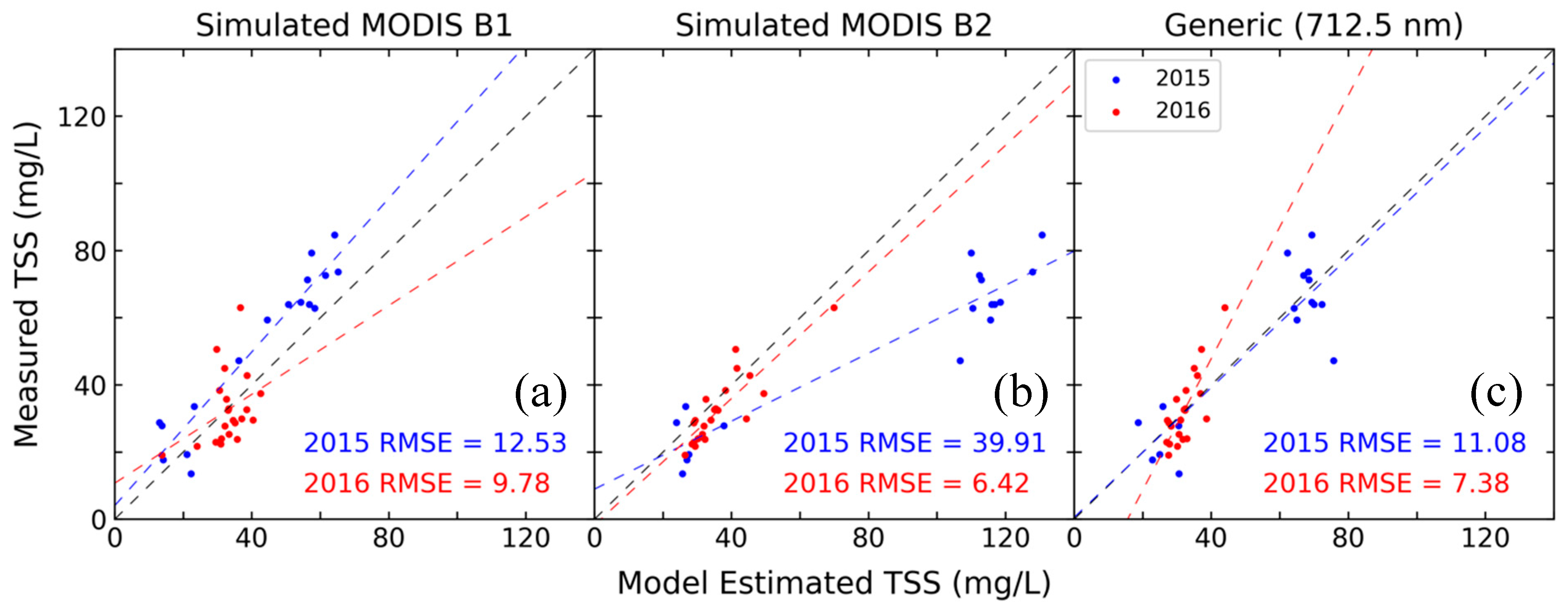
3.1. Simulated MODIS and Generalized Model Assessment
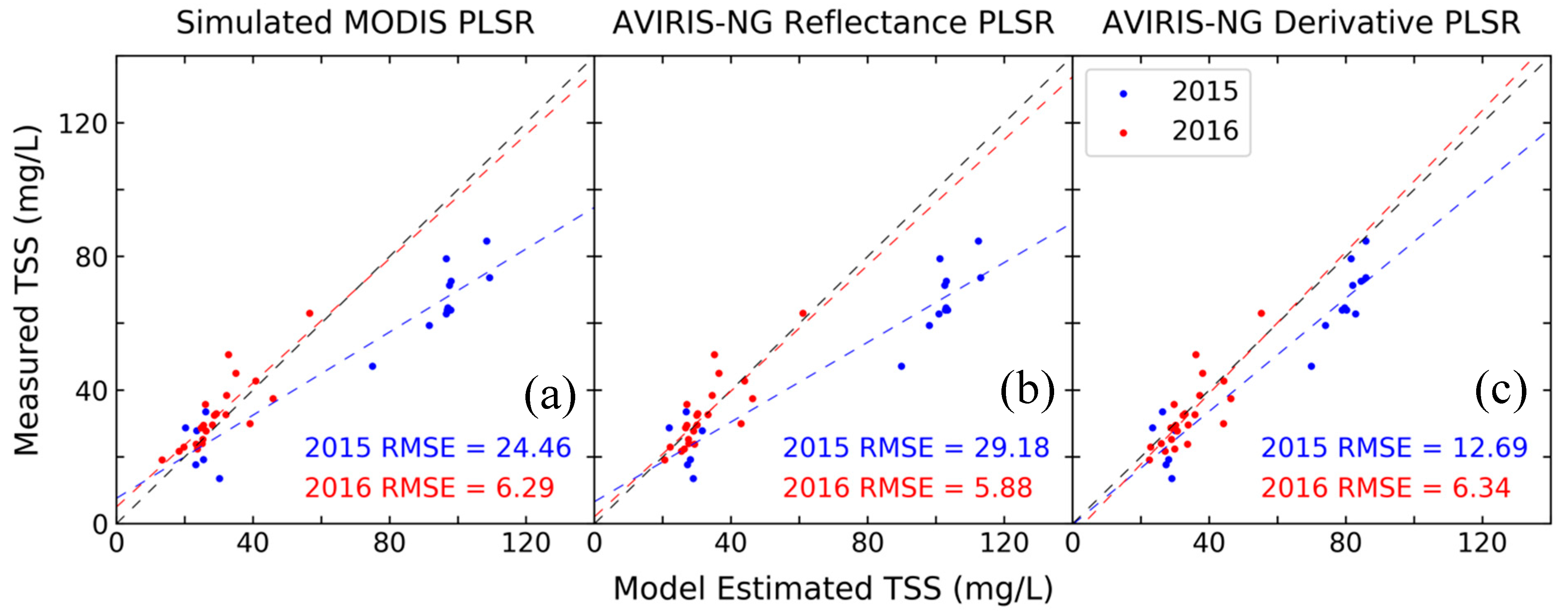
3.2. AVIRIS-NG Assessment
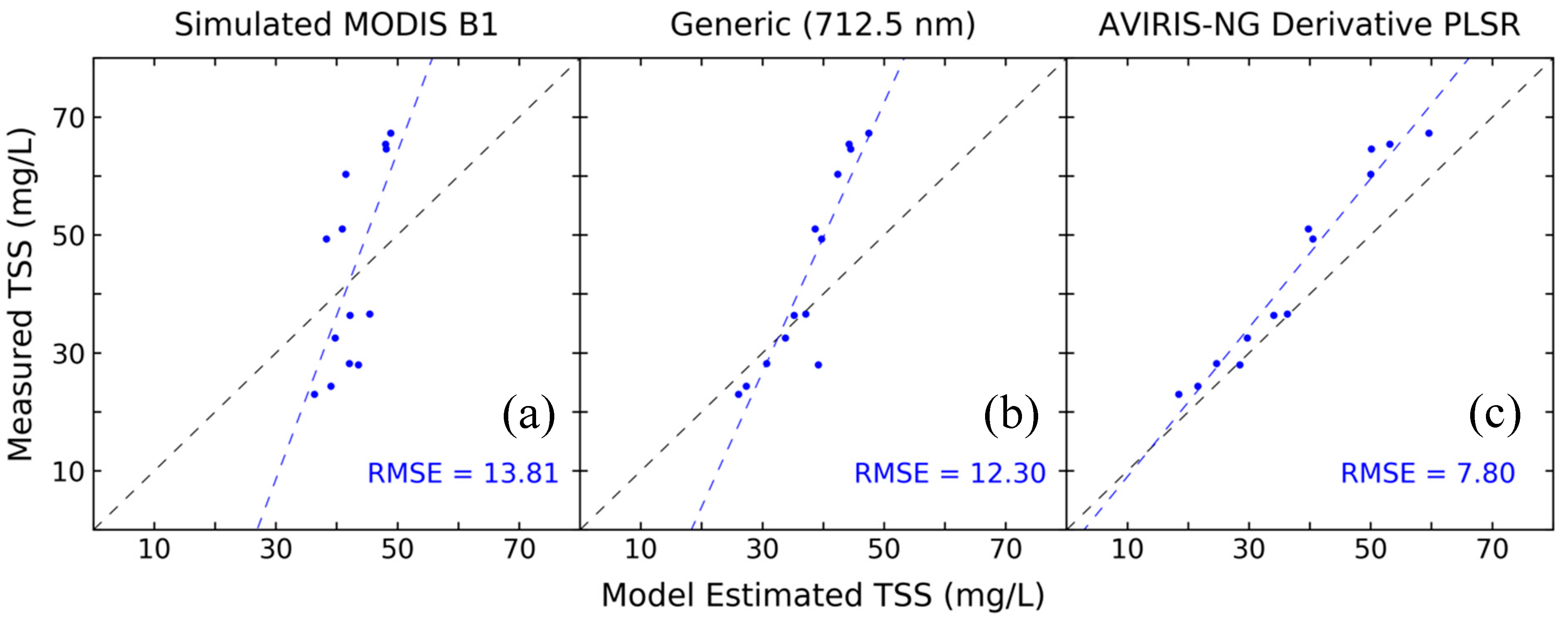
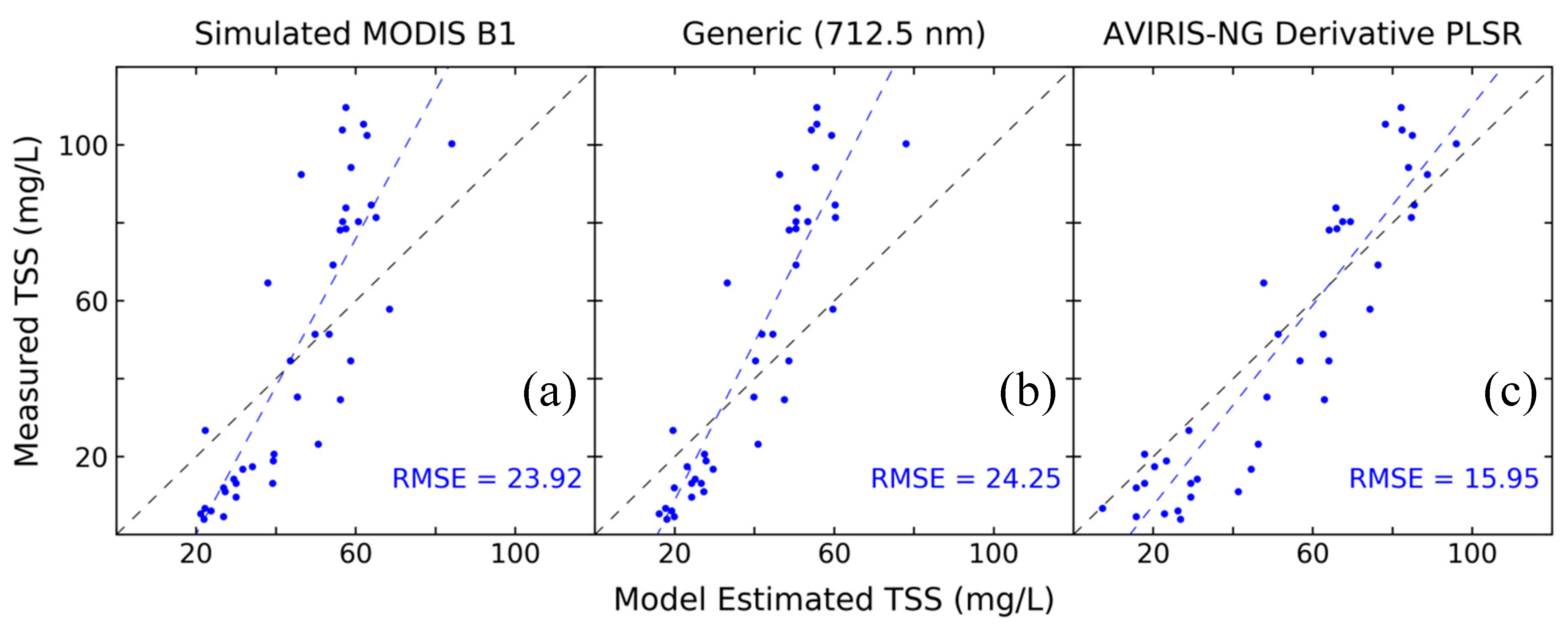
3.3. Independent Imaging Spectroscopy Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Wavelength (nm) | Reflectance Coefficient | Derivative Coefficient |
|---|---|---|
| 521.69 | −114.35 | |
| 526.70 | −121.29 | |
| 531.71 | −126.00 | |
| 536.72 | −128.85 | |
| 541.73 | −131.69 | |
| 546.73 | −133.50 | |
| 551.74 | −133.90 | |
| 556.75 | −134.03 | |
| 561.76 | −133.04 | |
| 566.77 | −130.00 | |
| 571.78 | −125.50 | |
| 576.79 | −119.75 | |
| 581.80 | −110.65 | |
| 586.80 | −100.04 | |
| 591.81 | −86.46 | |
| 596.82 | −63.45 | 4916.79 |
| 601.83 | −36.07 | 4254.01 |
| 606.84 | −21.55 | |
| 611.85 | −11.63 | |
| 616.86 | −1.30 | |
| 621.86 | 7.53 | |
| 626.87 | 16.19 | |
| 631.88 | 22.89 | |
| 636.89 | 28.18 | |
| 641.90 | 33.72 | |
| 646.91 | 41.23 | |
| 651.92 | 53.61 | |
| 656.93 | 77.19 | 5340.10 |
| 661.93 | 105.52 | 5428.36 |
| 666.94 | 128.27 | 4177.92 |
| 671.95 | 144.25 | |
| 676.96 | 153.37 | |
| 681.97 | 154.90 | |
| 686.98 | 142.27 | |
| 691.99 | 129.23 | |
| 696.99 | 129.27 | |
| 702.00 | 141.75 | 1876.78 |
| 707.01 | 163.07 | 2963.11 |
| 712.02 | 187.93 | 2535.39 |
| 717.03 | 208.03 | 662.15 |
| 722.04 | 218.15 | −1707.08 |
| 727.05 | 217.17 | −4655.07 |
| 732.06 | 202.14 | −5867.71 |
| 737.06 | 186.78 | −3510.22 |
| 767.12 | 185.40 | |
| 772.12 | 188.71 | |
| 777.13 | 192.79 | |
| 782.14 | 198.06 | |
| 787.15 | 205.12 | |
| 792.16 | 211.90 | |
| 797.17 | 218.93 | |
| 802.18 | 225.51 | |
| 807.19 | 229.60 | |
| 812.19 | 229.79 | |
| 817.20 | 225.67 | −2548.37 |
| 822.21 | 213.75 | −5553.51 |
| 827.22 | 188.28 | −7608.68 |
| 832.23 | −5955.38 | |
| 837.24 | −3114.65 | |
| Constant | 10.13 | 12.17 |
References
- Morton, R.; Bernier, J.; Barras, J. Evidence of regional subsidence and associated interior wetland loss induced by hydrocarbon production, Gulf Coast region, USA. Environ. Geol. 2006, 50, 261–274. [Google Scholar] [CrossRef]
- Morris, J.T.; Sundareshwar, P.V.; Nietch, C.T.; Kjerfve, B.; Cahoon, D.R. Responses of Coastal Wetlands to Rising Sea Level. Ecology 2002, 83, 2869–2877. [Google Scholar] [CrossRef]
- Burkett, V.R.; Ziklkoski, D.B.; Hart, D.A. Sea-Level Rise and Subsidence: Implications for Flooding in New Orleans, Louisiana. In Proceedings of the U.S. Geological Survey Subsidence Interest Group Conference Technical Meeting, Galveston, TX, USA, 27–29 November 2001; U.S. Geological Survey: Austin, TX, USA, 2003; pp. 63–70. [Google Scholar]
- Ericson, J.P.; Vörösmarty, C.J.; Dingman, S.L.; Ward, L.G.; Meybeck, M. Effective sea-level rise and deltas: Causes of change and human dimension implications. Glob. Planet. Chang. 2006, 50, 63–82. [Google Scholar] [CrossRef]
- Twilley, R.R.; Bentley, S.J.; Chen, Q.; Edmonds, D.A.; Hagen, S.C.; Lam, N.S.N.; Willson, C.S.; Xu, K.; Braud, D.W.; Hampton Peele, R.; et al. Co-evolution of wetland landscapes, flooding, and human settlement in the Mississippi River Delta Plain. Sustain. Sci. 2016, 11, 711–731. [Google Scholar] [CrossRef] [PubMed]
- DeLaune, R.D.; Kongchum, M.; White, J.R.; Jugsujinda, A. Freshwater diversions as an ecosystem management tool for maintaining soil organic matter accretion in coastal marshes. Catena 2013, 107, 139–144. [Google Scholar] [CrossRef]
- Krauss, K.W.; Duberstein, J.A.; Doyle, T.W.; Conner, W.H.; Day, R.H.; Inabinette, L.W.; Whitbeck, J.L. Site condition, structure, and growth of baldcypress along tidal/non-tidal salinity gradients. Wetlands 2009, 29, 505–519. [Google Scholar] [CrossRef]
- Song, C.; White, B.L.; Heumann, B.W. Hyperspectral remote sensing of salinity stress on red (Rhizophora mangle) and white (Laguncularia racemosa) mangroves on Galapagos Islands. Remote Sens. Lett. 2011, 2, 221–230. [Google Scholar] [CrossRef]
- Krauss, K.W.; McKee, K.L.; Lovelock, C.E.; Cahoon, D.R.; Saintilan, N.; Reef, R.; Chen, L. How mangrove forests adjust to rising sea level. New Phytol. 2014, 202, 19–34. [Google Scholar] [CrossRef]
- Glysson, G.D.; Gray, J.R.; Conge, L.M. Adjustment of Total Suspended Solids Data for Use in Sediment Studies. In Proceedings of the ASCE’s 2000 Joint Conference on Water Resources Engineering and Water Resources Planning and Management, Minneapolis, MN, USA, 30 July—2 August 2000; Volume 104. 10p. [Google Scholar]
- Curran, P.; Novo, E.M. The relationship between suspended sediment concentration and remotely sensed spectral radiance: A review. J. Coast. Res. 1988, 4, 351–368. [Google Scholar]
- Griffin, C.G.; Frey, K.E.; Rogan, J.; Holmes, R.M. Spatial and interannual variability of dissolved organic matter in the Kolyma River, East Siberia, observed using satellite imagery. J. Geophys. Res. Biogeosci. 2011, 116, 1–12. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Brezonik, P.L.; Bauer, M.E. Airborne hyperspectral remote sensing to assess spatial distribution of water quality characteristics in large rivers: The Mississippi River and its tributaries in Minnesota. Remote Sens. Environ. 2013, 130, 254–265. [Google Scholar] [CrossRef]
- Fichot, C.G.; Downing, B.D.; Bergamaschi, B.A.; Windham-Myers, L.; Marvin-Dipasquale, M.; Thompson, D.R.; Gierach, M.M. High-Resolution Remote Sensing of Water Quality in the San Francisco Bay-Delta Estuary. Environ. Sci. Technol. 2016, 50, 573–583. [Google Scholar] [CrossRef]
- Miller, R.L.; McKee, B.A. Miller 2004 1 Remote Sensing of Environment. Remote Sens. Environ. 2004, 30, 259–266. [Google Scholar] [CrossRef]
- Warrick, J.A.; Mertes, L.A.K.; Siegel, D.A.; Mackenzie, C. Estimating suspended sediment concentrations in turbid coastal waters of the Santa Barbara Channel with SeaWiFS. Int. J. Remote Sens. 2004, 25, 1995–2002. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Cooper, C.M. Remote sensing techniques for determining water quality: Applications to TMDLs. In Proceedings of the TMDL Science Issues Conference; Water Environment Federation, Alexandria, VA, USA, 4–7 March 2001; pp. 367–375. [Google Scholar]
- Nechad, B.; Ruddick, K.G.; Park, Y. Calibration and validation of a generic multisensor algorithm for mapping of total suspended matter in turbid waters. Remote Sens. Environ. 2010, 114, 854–866. [Google Scholar] [CrossRef]
- Doxaran, D.; Lamquin, N.; Park, Y.J.; Mazeran, C.; Ryu, J.H.; Wang, M.; Poteau, A. Retrieval of the seawater reflectance for suspended solids monitoring in the East China Sea using MODIS, MERIS and GOCI satellite data. Remote Sens. Environ. 2014, 146, 36–48. [Google Scholar] [CrossRef]
- Dogliotti, A.I.; Ruddick, K.G.; Nechad, B.; Doxaran, D.; Knaeps, E. A single algorithm to retrieve turbidity from remotely-sensed data in all coastal and estuarine waters. Remote Sens. Environ. 2015, 156, 157–168. [Google Scholar] [CrossRef]
- Chen, S.; Han, L.; Chen, X.; Li, D.; Sun, L.; Li, Y. Estimating wide range Total Suspended Solids concentrations from MODIS 250-m imageries: An improved method. ISPRS J. Photogramm. Remote Sens. 2015, 99, 58–69. [Google Scholar] [CrossRef]
- Doxaran, D.; Froidefond, J.M.; Lavender, S.; Castaing, P. Spectral signature of highly turbid waters: Application with SPOT data to quantify suspended particulate matter concentrations. Remote Sens. Environ. 2002, 81, 149–161. [Google Scholar] [CrossRef]
- Li, R.-R.; Kaufman, Y.J.; Gao, B.-C.; Davis, C.O. Remote sensing of suspended sediments and shallow coastal waters. IEEE Trans. Geosci. Remote Sens. 2003, 41, 559–566. [Google Scholar]
- Ouillon, S.; Douillet, P.; Andréfouët, S. Coupling satellite data with in situ measurements and numerical modeling to study fine suspended-sediment transport: A study for the lagoon of New Caledonia. Coral Reefs 2004, 23, 109–122. [Google Scholar]
- Han, Z.; Jin, Y.-Q.; Yun, C.-X. Suspended sediment concentrations in the Yangtze River estuary retrieved from the CMODIS data. Int. J. Remote Sens. 2006, 27, 4329–4336. [Google Scholar] [CrossRef]
- Wang, J.J.; Lu, X.X. Estimation of suspended sediment concentrations using Terra MODIS: An example from the Lower Yangtze River, China. Sci. Total Environ. 2010, 408, 1131–1138. [Google Scholar] [CrossRef]
- Pavelsky, T.M.; Smith, L.C. Remote sensing of suspended sediment concentration, flow velocity, and lake recharge in the Peace-Athabasca Delta, Canada. Water Resour. Res. 2009, 45, 1–16. [Google Scholar] [CrossRef]
- Volpe, V.; Silvestri, S.; Marani, M. Remote sensing retrieval of suspended sediment concentration in shallow waters. Remote Sens. Environ. 2011, 115, 44–54. [Google Scholar] [CrossRef]
- Mobley, C.; Boss, E.; Roesler, C. Ocean Optics Web Book. 2010. Available online: http://www.oceanopticsbook.info/ (accessed on 24 October 2017).
- Lee, Z.; Shang, S.; Lin, G.; Chen, J.; Doxaran, D. On the modeling of hyperspectral remote-sensing reflectance of high-sediment-load waters in the visible to shortwave-infrared domain. Appl. Opt. 2016, 55, 1738–1750. [Google Scholar] [CrossRef]
- Dorji, P.; Fearns, P. A quantitative comparison of total suspended sediment algorithms: A case study of the last decade for MODIS and landsat-based sensors. Remote Sens. 2016, 8, 810. [Google Scholar] [CrossRef]
- Tsai, F.; Philpot, W. Derivative analysis of hyperspectral data. Remote Sens. Environ. 1998, 66, 41–51. [Google Scholar] [CrossRef]
- Louchard, E.M.; Reid, R.P.; Stephens, C.F.; Davis, C.O.; Leathers, R.A.; Downes, T.V.; Maffione, R. Derivative analysis of absorption features in hyperspectral remote sensing data of carbonate sediments. Opt. Express 2002, 10, 1573–1584. [Google Scholar] [CrossRef]
- Forget, P.; Broche, P.; Naudin, J.J. Reflectance sensitivity to solid suspended sediment stratification in coastal water and inversion: A case study. Remote Sens. Environ. 2001, 77, 92–103. [Google Scholar] [CrossRef]
- Knaeps, E.; Ruddick, K.G.; Doxaran, D.; Dogliotti, A.I.; Nechad, B.; Raymaekers, D.; Sterckx, S. A SWIR based algorithm to retrieve total suspended matter in extremely turbid waters. Remote Sens. Environ. 2015, 168, 66–79. [Google Scholar] [CrossRef]
- Kromkamp, J.C.; Morris, E.P.; Forster, R.M.; Honeywill, C.; Hagerthey, S.; Paterson, D.M. Relationship of intertidal surface sediment chlorophyll concentration to hyperspectral reflectance and chlorophyll fluorescence. Estuaries Coasts 2006, 29, 183–196. [Google Scholar] [CrossRef]
- Sterckx, S.; Knaeps, E.; Bollen, M.; Trouw, K.; Houthuys, R. Retrieval of Suspended Sediment from Advanced Hyperspectral Sensor Data in the Scheldt Estuary at Different Stages in the Tidal Cycle. Mar. Geod. 2007, 30, 97–108. [Google Scholar] [CrossRef]
- Choe, E.; van der Meer, F.; van Ruitenbeek, F.; van der Werff, H.; de Smeth, B.; Kim, K.W. Mapping of heavy metal pollution in stream sediments using combined geochemistry, field spectroscopy, and hyperspectral remote sensing: A case study of the Rodalquilar mining area, SE Spain. Remote Sens. Environ. 2008, 112, 3222–3233. [Google Scholar] [CrossRef]
- Martínez-Carreras, N.; Krein, A.; Udelhoven, T.; Gallart, F.; Iffly, J.F.; Hoffmann, L.; Pfister, L.; Walling, D.E. A rapid spectral-reflectance-based fingerprinting approach for documenting suspended sediment sources during storm runoff events. J. Soils Sediments 2010, 10, 400–413. [Google Scholar] [CrossRef]
- Chen, Z.; Curran, P.; Hansom, J.D. Derivative reflectance spectroscopy to estimate suspended sediment concentration. Remote Sens. Environ. 1992, 40, 67–77. [Google Scholar] [CrossRef]
- Brando, V.E.; Dekker, A.G. Satellite hyperspectral remote sensing for estimating estuarine and coastal water quality. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1378–1387. [Google Scholar] [CrossRef]
- Senay, G.B.; Shafique, N.A.; Autrey, B.C.; Fulk, F.; Cormier, S.M. The selection of narrow wavebands for optimizing water quality monitoring on the Great Miami River, Ohio using hyperspectral remote sensor data. J. Spat. Hydrol. 2001, 1, 1–22. [Google Scholar]
- Palacios, S.L.; Kudela, R.M.; Guild, L.S.; Negrey, K.H.; Torres-Perez, J.; Broughton, J. Remote sensing of phytoplankton functional types in the coastal ocean from the HyspIRI Preparatory Flight Campaign. Remote Sens. Environ. 2015, 167, 269–280. [Google Scholar] [CrossRef]
- Hamlin, L.; Green, R.O.; Mouroulis, P.; Eastwood, M.; Wilson, D.; Dudik, M.; Paine, C. Imaging spectrometer science measurements for terrestrial ecology: AVIRIS and new developments. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011; pp. 1–8. [Google Scholar]
- Thompson, D.R.; Gao, B.C.; Green, R.O.; Roberts, D.A.; Dennison, P.E.; Lundeen, S.R. Atmospheric correction for global mapping spectroscopy: ATREM advances for the HyspIRI preparatory campaign. Remote Sens. Environ. 2015, 167, 64–77. [Google Scholar] [CrossRef]
- Gao, B.C.; Heidebrecht, K.B.; Goetz, A.F.H. Derivation of scaled surface reflectances from AVIRIS data. Remote Sens. Environ. 1993, 44, 165–178. [Google Scholar] [CrossRef]
- Bue, B.D.; Thompson, D.R.; Eastwood, M.; Green, R.O.; Gao, B.C.; Keymeulen, D.; Sarture, C.M.; Mazer, A.S.; Luong, H.H. Real-Time Atmospheric Correction of AVIRIS-NG Imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6419–6428. [Google Scholar] [CrossRef]
- Morel, A.; Gentili, B. Diffuse reflectance of oceanic waters. III. Implication of bidirectionality for the remote-sensing problem. Appl. Opt. 1996, 35, 4850–4862. [Google Scholar] [CrossRef]
- Environmental Protection Agency. ESS Method 340.2: Total Suspended Solids, Mass Balance (Dried at 103-105 °C) Volatile Suspended Solids (Ignited at 550 °C); Environmental Protection Agency, Environmental Sciences Section: Madison, WI, USA, 1993.
- Gómez, R.A. Spectral Reflectance Analysis of the Caribbean Sea. Geofis. Int. 2014, 53, 385–398. [Google Scholar] [CrossRef][Green Version]
- Östlund, C.; Flink, P.; Strömbeck, N.; Pierson, D.; Lindell, T. Mapping of the water quality of Lake Erken, Sweden, from Imaging Spectrometry and Landsat Thematic Mapper. Sci. Total Environ. 2001, 268, 139–154. [Google Scholar] [CrossRef]
- Tobias, R.D. An introduction to partial least squares regression. In Proceedings of the Twentieth Annual SAS Users Group International Conference, Orlando, FL, USA, 2–5 April 1995. [Google Scholar]
- Carrascal, L.M.; Galván, I.; Gordo, O. Partial least squares regression as an alternative to current regression methods used in ecology. Oikos 2009, 118, 681–690. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Farrés, M.; Platikanov, S.; Tsakovski, S.; Tauler, R. Comparison of the variable importance in projection (VIP) and of the selectivity ratio (SR) methods for variable selection and interpretation. J. Chemom. 2015, 29, 528–536. [Google Scholar] [CrossRef]
- Jensen, D.J.; Simard, M.; Cavanaugh, K.C.; Thompson, D.R. Imaging Spectroscopy BRDF Correction for Mapping Louisiana’s Coastal Ecosystems. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1739–1748. [Google Scholar] [CrossRef]
- Long, C.M.; Pavelsky, T.M. Water Quality and Spectral Reflectance, Peace-Athabasca Delta, Canada, 2010–2011; ORNL DAAC: Oak Ridge, TN, USA, 2012.
- Long, C.M.; Pavelsky, T.M. Remote sensing of suspended sediment concentration and hydrologic connectivity in a complex wetland environment. Remote Sens. Environ. 2013, 129, 197–209. [Google Scholar] [CrossRef]
- Lee, Z.; Mobley, C.D.; Patch, J.S.; Carder, K.L.; Steward, R.G. Hyperspectral remote sensing for shallow waters: Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 3831. [Google Scholar] [CrossRef]
- Walker, N.D.; Rabalais, N.N. Relationships among Satellite Chlorophyll a, River Inputs, and Hypoxia on the Louisiana Continental Shelf, Gulf of Mexico. Estuaries Coasts 2006, 29, 1081–1093. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Pennock, J.R. Calibration of a general optical equation for remote sensing of suspended sediments in a moderately turbid estuary. J. Geophys. Res. 1989, 94, 14363. [Google Scholar] [CrossRef]
- Demetriades-Shah, T.H.; Steven, M.D.; Clark, J.A. High resolution derivative spectra in remote sensing. Remote Sens. Environ. 1990, 33, 55–64. [Google Scholar] [CrossRef]
- Gitelson, A. The peak near 700 nm on radiance spectra of algae and water: Relationships of its magnitude and position with chlorophyll concentration. Int. J. Remote Sens. 2007, 13, 3367–3373. [Google Scholar] [CrossRef]
- Kutser, T.; Paavel, B.; Verpoorter, C.; Ligi, M.; Soomets, T.; Toming, K.; Casal, G. Remote Sensing of Black Lakes and Using 810 nm Reflectance Peak for Retrieving Water Quality Parameters of Optically Complex Waters. Remote Sens. 2016, 8, 497. [Google Scholar] [CrossRef]
- Spyrakos, E.; O’Donnell, R.; Hunter, P.D.; Miller, C.; Scott, M.; Simis, S.G.H.; Neil, C.; Barbosa, C.C.F.; Binding, C.E.; Bradt, S.; et al. Optical types of inland and coastal waters. Limnol. Oceanogr. 2018, 63, 846–870. [Google Scholar] [CrossRef]
- Barras, J.; Beville, S.; Britsch, D.; Hartley, S.; Hawes, S.; Johnston, J.; Kemp, P.; Kinler, Q.; Martucci, A.; Porthouse, J.; et al. Historical and Projected Coastal Louisiana Land Changes: 1978–2050; U.S. Geological Survey: Reston, VA, USA, 2003; Volume 334.
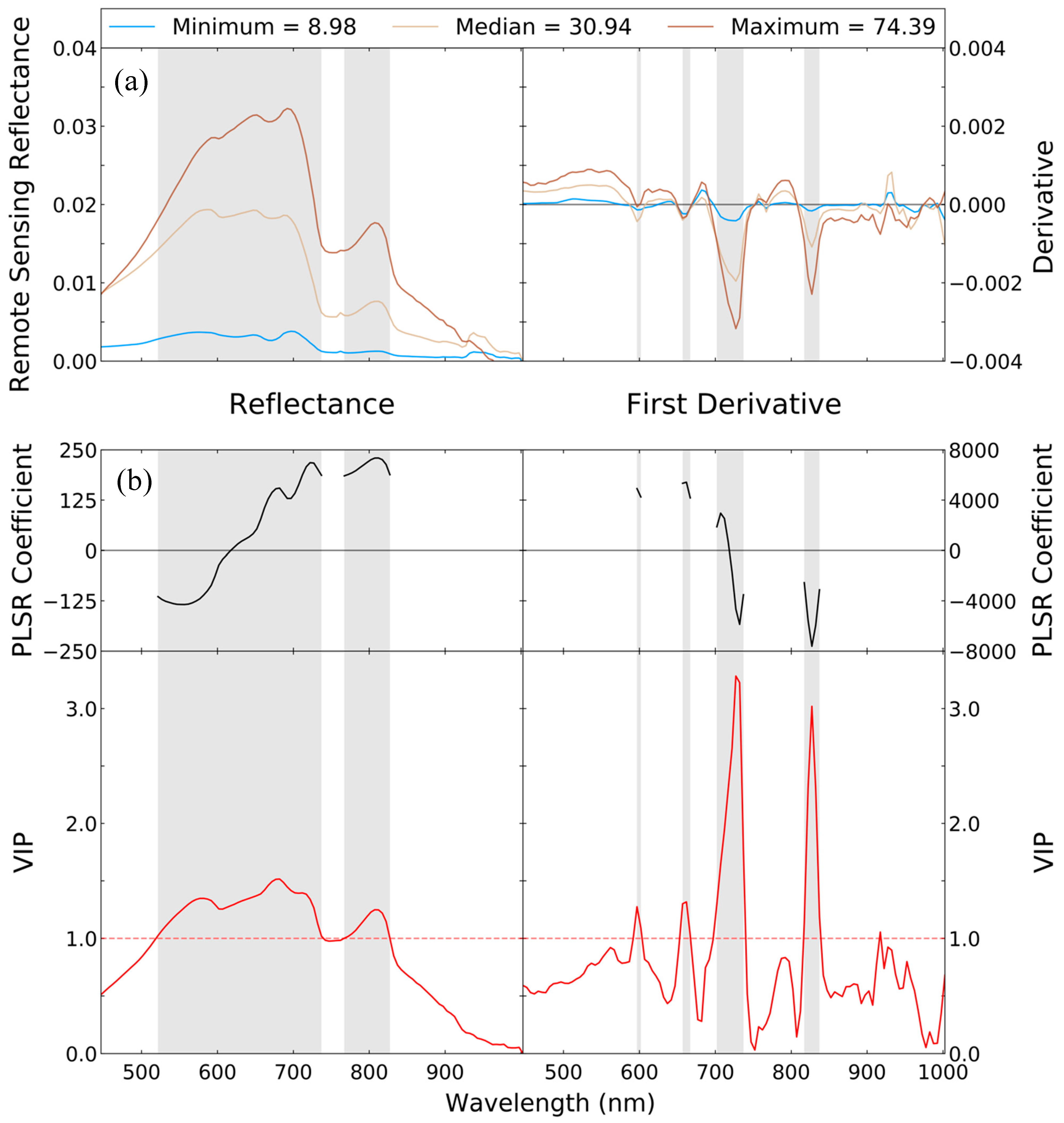

| MODIS Band | Wavelength (nm) | VIP | Coefficient |
|---|---|---|---|
| 8 | 405–420 | 0.35 | |
| 9 | 438–448 | 0.48 | |
| 10 | 483–493 | 0.75 | |
| 11 | 526–536 | 1.05 | −1440.73 |
| 12 | 546–556 | 1.17 | −1546.45 |
| 13 | 662–672 | 1.40 | 1467.11 |
| 14 | 673–683 | 1.48 | 1830.09 |
| 15 | 743–753 | 1.04 | 2273.30 |
| 16 | 862–877 | 0.63 | |
| Constant | 12.64 |
| MODIS Band 1 | MODIS Band 2 | Generic (712.5 nm) [18] | MODIS PLSR | AVIRIS-NG Reflectance PLSR | AVIRIS-NG Derivative PLSR | |
|---|---|---|---|---|---|---|
| Model R2 | 0.53 | 0.80 | - | 0.82 | 0.82 | 0.83 |
| 2015 MRE (%) | 25.51 | 189.00 | 24.28 | 43.83 | 51.01 | 28.88 |
| 2016 MRE (%) | 23.51 | 18.24 | 17.92 | 13.75 | 13.06 | 14.87 |
| 2015 RMSE (mg/L) | 12.53 | 39.91 | 11.08 | 24.46 | 29.18 | 12.69 |
| 2016 RMSE (mg/L) | 9.78 | 6.42 | 7.38 | 6.29 | 5.88 | 6.34 |
| Atchafalaya and Wax Lake Deltas (2015) | Atchafalaya and Wax Lake Deltas (2016) | San Francisco Bay–Delta Estuary [14] | Peace–Athabasca Delta * [57,58] | |
|---|---|---|---|---|
| Instrument | AVIRIS-NG | AVIRIS-NG | PRISM | ASD FieldSpec® 3 |
| Dates | May 7–June 12, 2015 | October 17–18, 2016 | April 28, 2014 | June 24–July 6, 2011 |
| n | 17 | 22 | 13 | 40 |
| TSS Sample Range (mg/L) | 13.53–84.67 | 19.11–62.99 | 23.03–67.29 | 3.93–109.64 |
| Chlorophyll-a Sample Range (µg/L) | - | - | 1.67–6.63 | 3.87–14.89 |
| CDOM Sample Range | - | - | 23.61–56.26 (a(350) (m−1)) | 136.76–566.03 (ppb) |
| RMSE (mg/L) | 12.69 | 6.34 | 7.80 | 15.95 |
| MRE (%) | 28.88 | 14.87 | 13.24 | 76.56 |
| Validation R2 | 0.69 | 0.62 | 0.76 | 0.80 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jensen, D.; Simard, M.; Cavanaugh, K.; Sheng, Y.; Fichot, C.G.; Pavelsky, T.; Twilley, R. Improving the Transferability of Suspended Solid Estimation in Wetland and Deltaic Waters with an Empirical Hyperspectral Approach. Remote Sens. 2019, 11, 1629. https://doi.org/10.3390/rs11131629
Jensen D, Simard M, Cavanaugh K, Sheng Y, Fichot CG, Pavelsky T, Twilley R. Improving the Transferability of Suspended Solid Estimation in Wetland and Deltaic Waters with an Empirical Hyperspectral Approach. Remote Sensing. 2019; 11(13):1629. https://doi.org/10.3390/rs11131629
Chicago/Turabian StyleJensen, Daniel, Marc Simard, Kyle Cavanaugh, Yongwei Sheng, Cédric G. Fichot, Tamlin Pavelsky, and Robert Twilley. 2019. "Improving the Transferability of Suspended Solid Estimation in Wetland and Deltaic Waters with an Empirical Hyperspectral Approach" Remote Sensing 11, no. 13: 1629. https://doi.org/10.3390/rs11131629
APA StyleJensen, D., Simard, M., Cavanaugh, K., Sheng, Y., Fichot, C. G., Pavelsky, T., & Twilley, R. (2019). Improving the Transferability of Suspended Solid Estimation in Wetland and Deltaic Waters with an Empirical Hyperspectral Approach. Remote Sensing, 11(13), 1629. https://doi.org/10.3390/rs11131629