Anomaly Detection in Hyperspectral Imagery Based on Low-Rank Representation Incorporating a Spatial Constraint
Abstract
:1. Introduction
2. Related Work
2.1. LRRSTO Detection Algorithm
2.2. SSC-S Clustering Algorithm
2.3. The Local Summation Anomaly Detection (LSAD) Algorithm
3. Proposed Methods
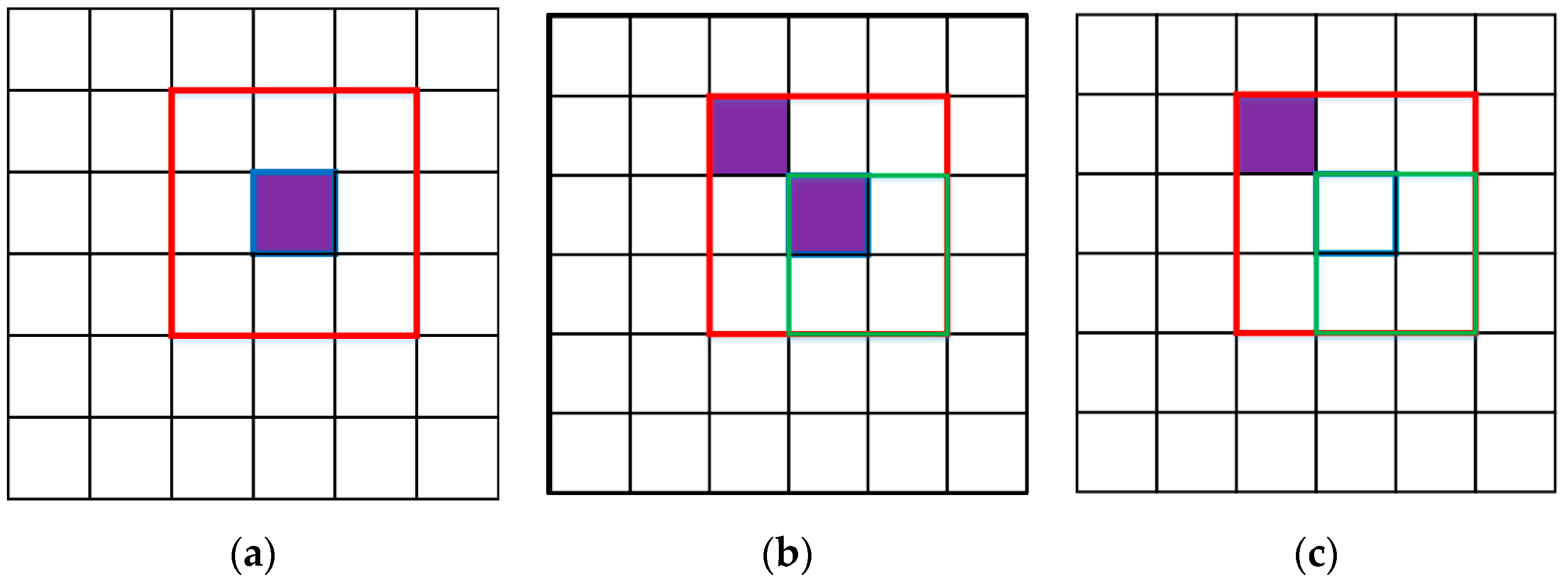
3.1. Single Local Window
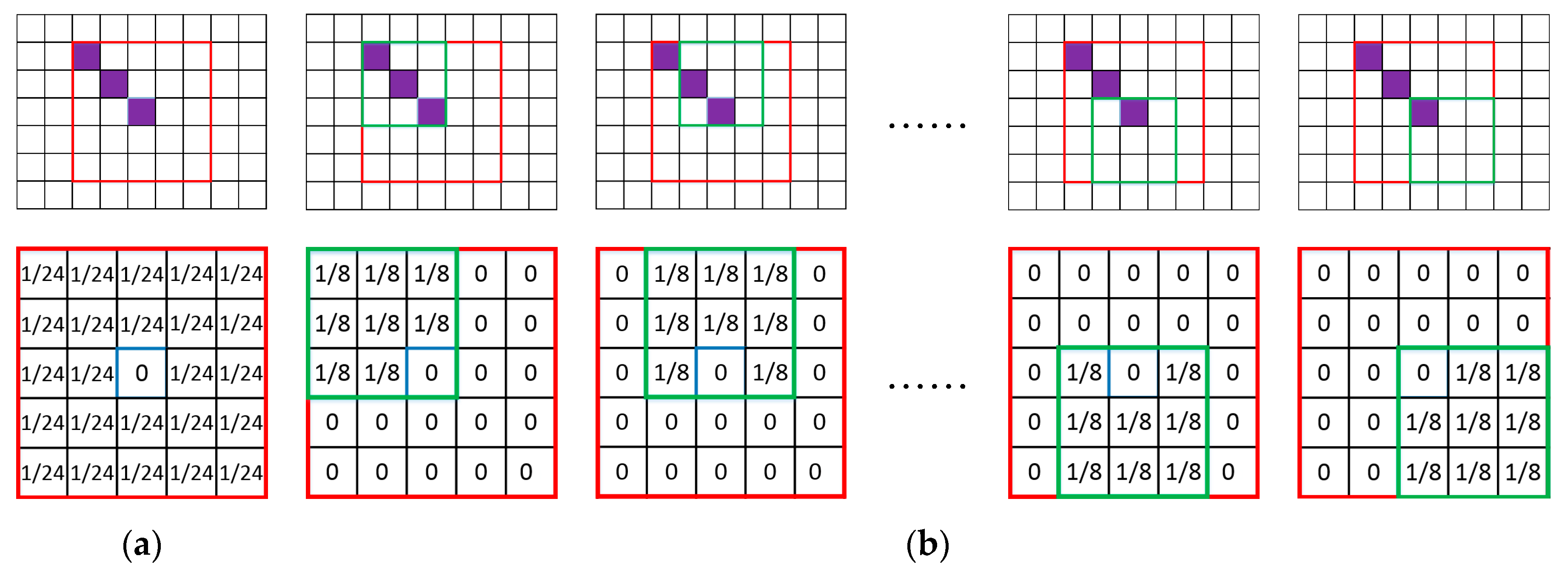
3.2. Multiple Local Background Statistics
| Algorithm 1. Inexact ALM algorithm for MLW_LRRSTO |
| Input: data matrix , size of single local window, parameters and |
| Initialize:, , , , , , , |
| While or |
| Continue (1) update variable (2) update , compose (3) update variable (4) update variable (5) update Lagrange multipliers ; ; ; (6) update penalty parameter where |
| End while |
| Output: the optimal solution |
4. Experiments and Analysis
4.1. Data Description
4.1.1. Simulated Hyperspectral Image
4.1.2. Parameters Analysis
4.1.3. Real Hyperspectral Images
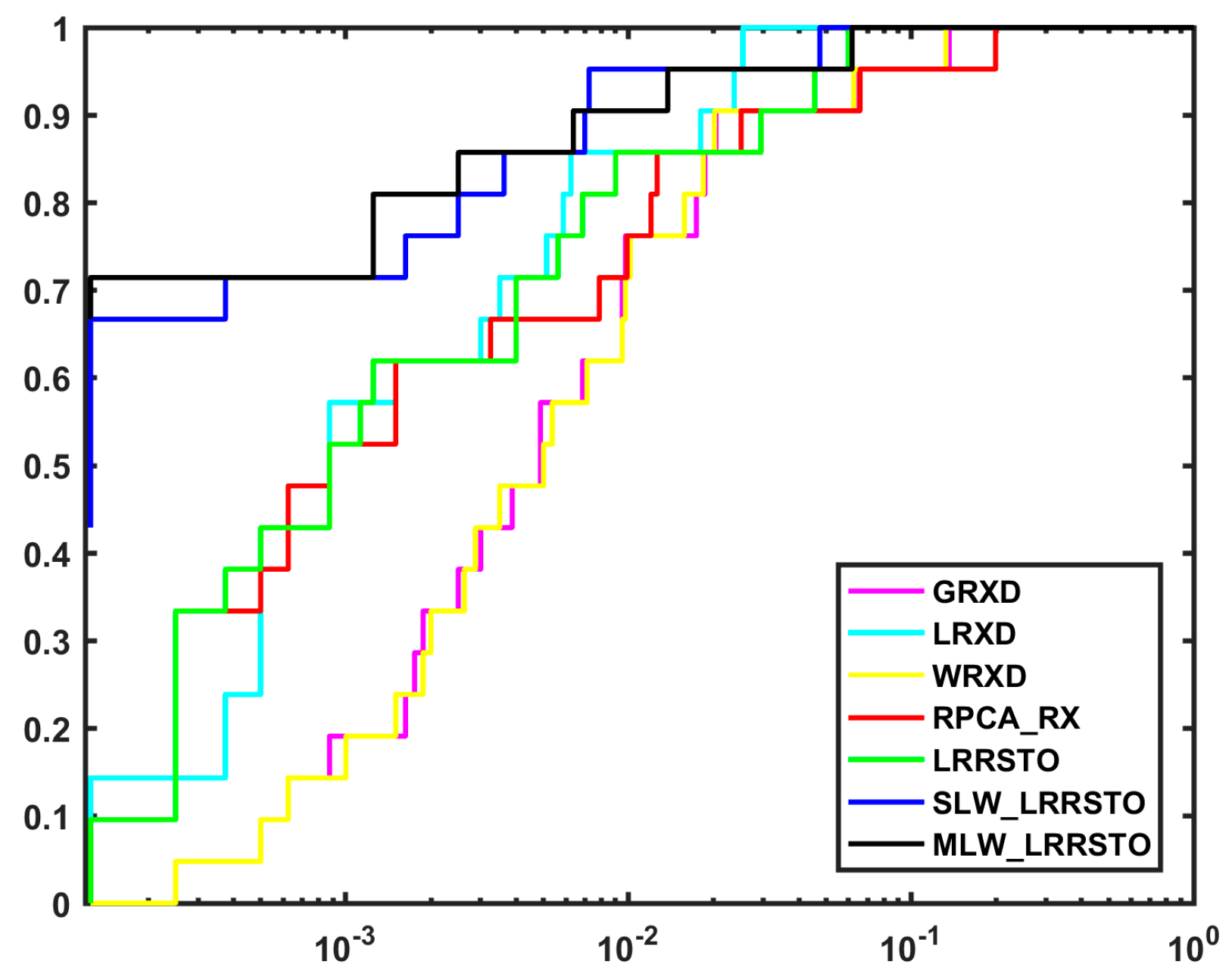
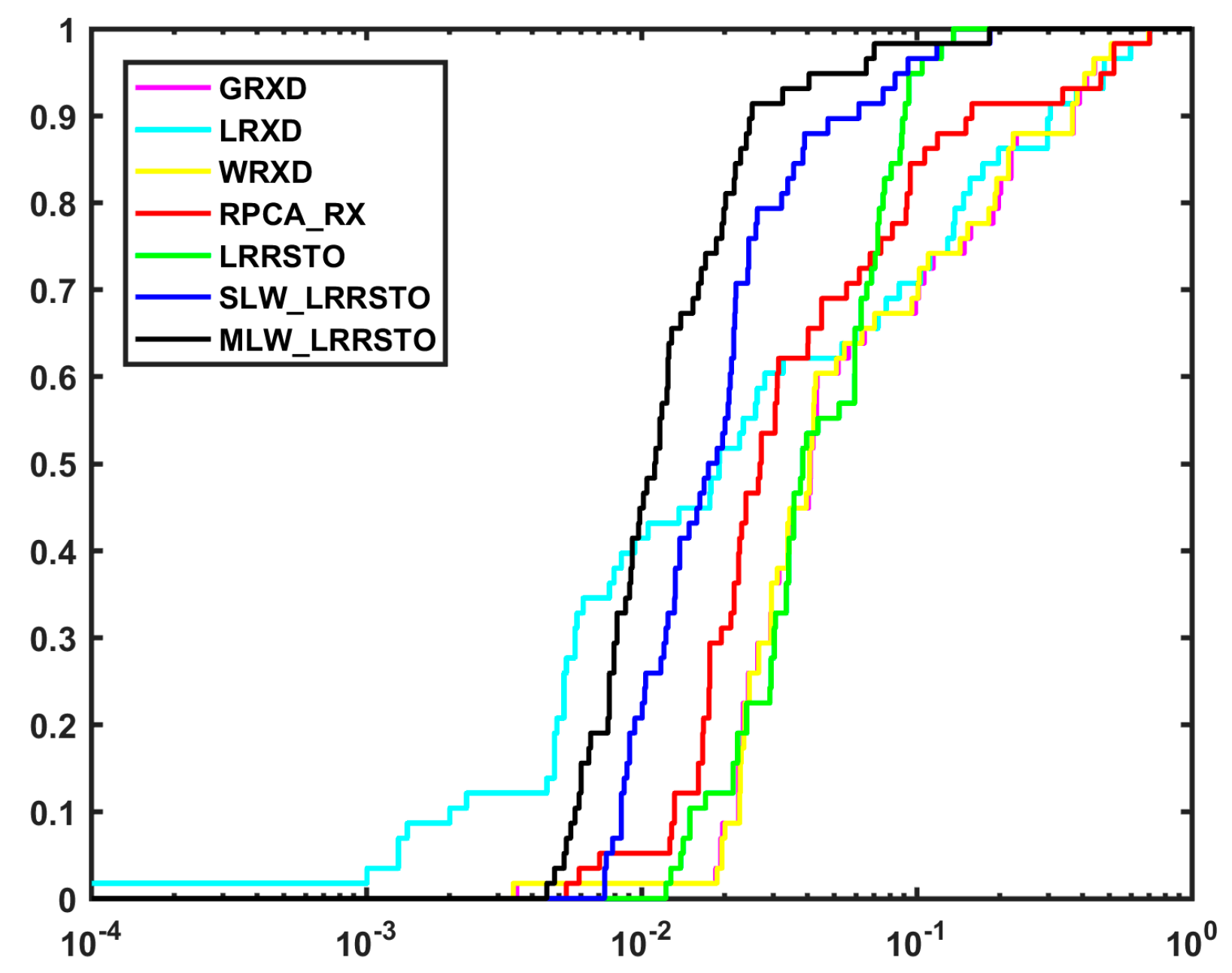
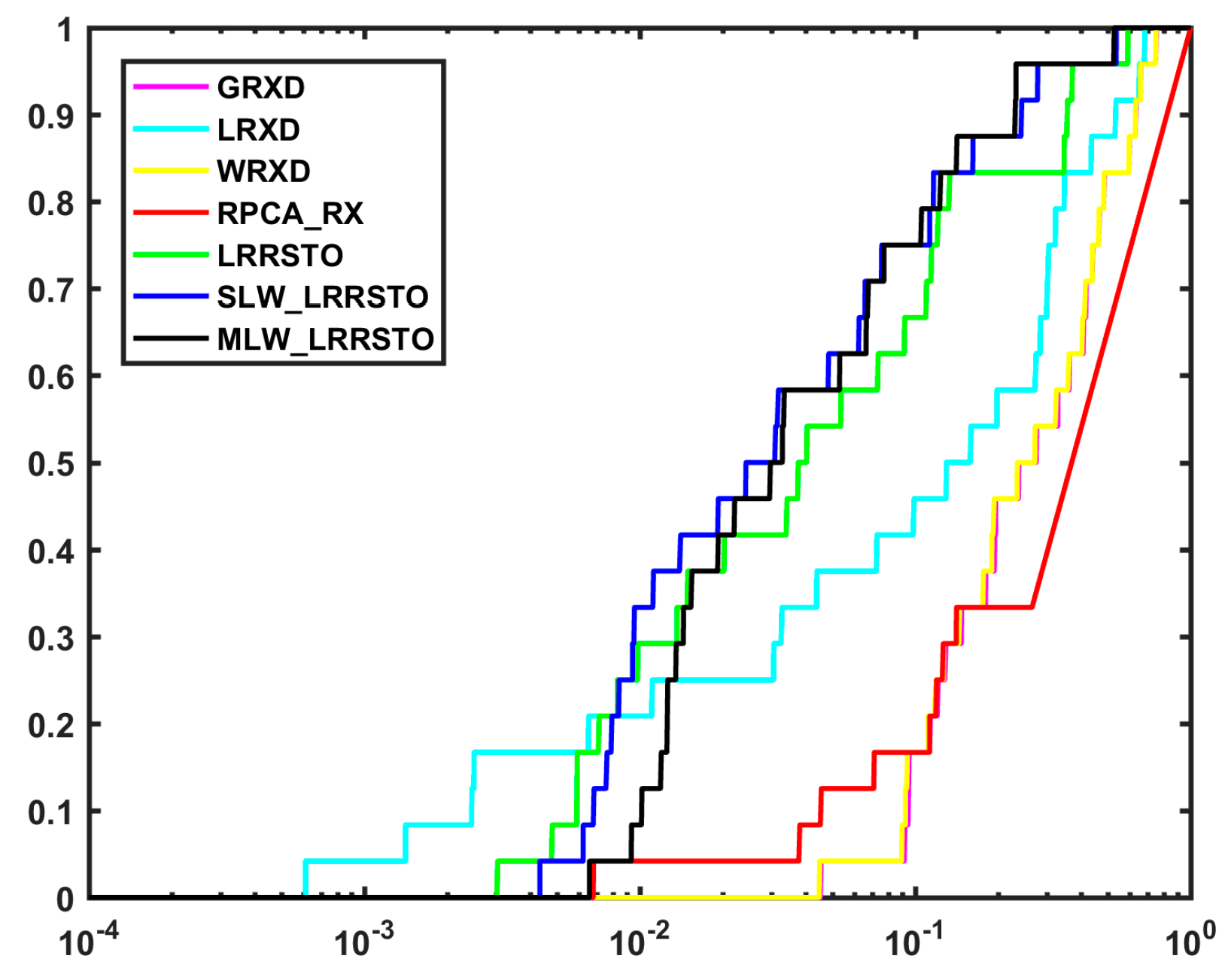
4.2. Detection Performance
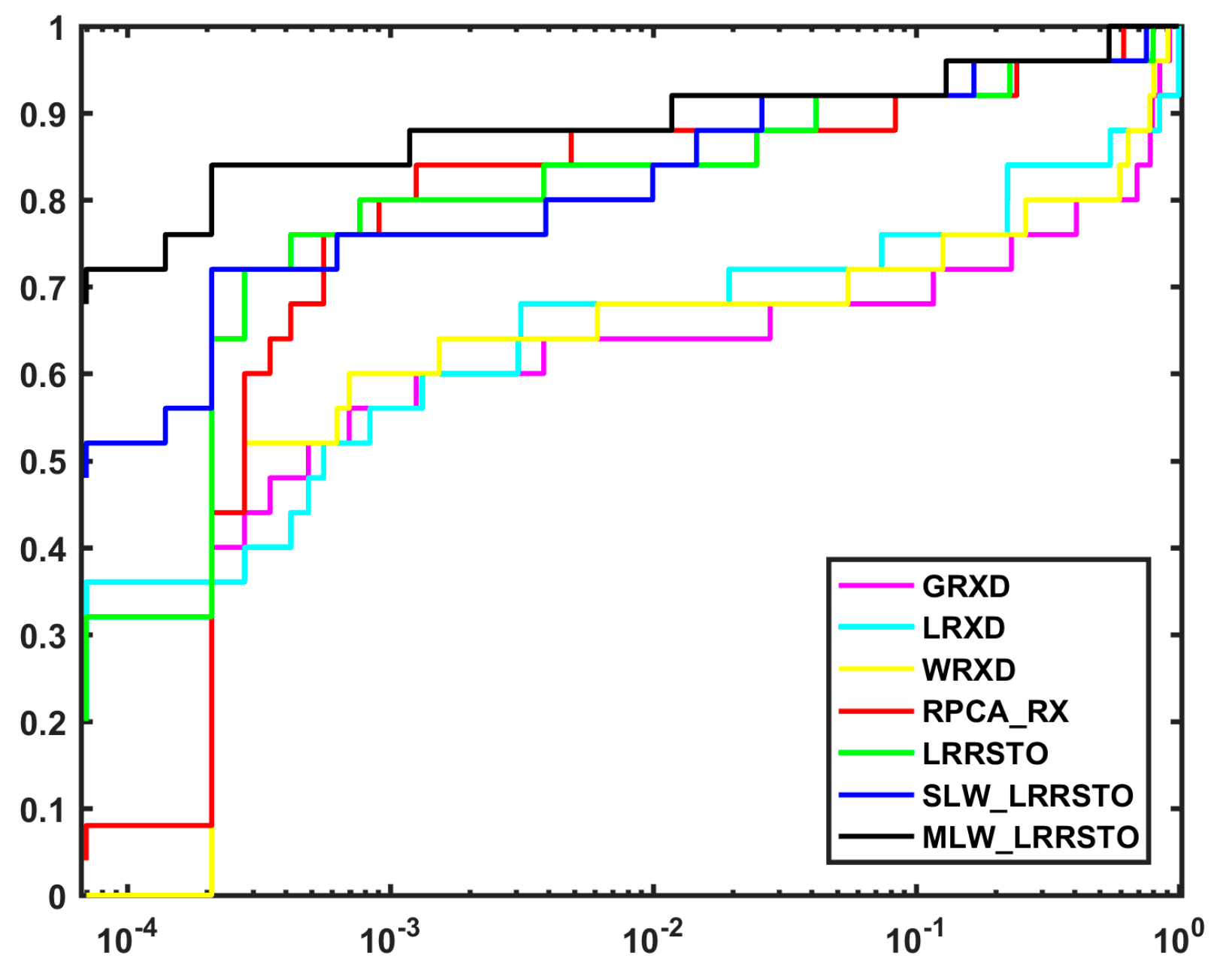
4.2.1. AVIRIS_Salinas Experiment
4.2.2. HYDICE_Urban Experiment
4.2.3. AVIRIS_SanDiego Experiment
4.2.4. Viareggio Experiment
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Niu, Y.; Wang, B. Hyperspectral anomaly detection based on low-rank representation and learned dictionary. Remote Sens. 2016, 8, 289. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Du, Q. Transferred deep learning for anomaly detection in hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 597–601. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral target detection: An overview of current and future challenges. IEEE Signal Process. Mag. 2013, 31, 34–44. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly detection in hyperspectral images based on low-rank and sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1990–2000. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Matteoli, S.; Diani, M.; Corsini, G. Improved estimation of local background covariance matrix for anomaly detection in hyperspectral images. Opt. Eng. 2010, 49, 046201. [Google Scholar] [CrossRef]
- Billor, N.; Hadi, A.S.; Velleman, P.F. BACON: Blocked adaptive computationally efficient outlier nominators. Comput. Stat. Data Anal. 2000, 34, 279–298. [Google Scholar] [CrossRef]
- Imani, M. RX Anomaly detector with rectified background. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1313–1317. [Google Scholar] [CrossRef]
- Yao, X.; Zhao, C. Hyperspectral anomaly detection based on the bilateral filter. Infrared Phys. Technol. 2018, 92, 144–153. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, B.; Ran, Q.; Gao, L.; Li, J.; Plaza, A. Weighted-RXD and linear filter-based RXD: Improving background statistics estimation for anomaly detection in hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2351–2366. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Unsupervised nearest regularized subspace for anomaly detection in hyperspectral imagery. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 1055–1058. [Google Scholar]
- Li, W.; Du, Q. Collaborative representation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1463–1474. [Google Scholar] [CrossRef]
- Philpott, S.; Hankins, C. Simultaneous joint sparsity model for target detection in hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2011, 8, 676–680. [Google Scholar]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification via kernel sparse representation. In Proceedings of the IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 1233–1236. [Google Scholar]
- Wright, J.; Ganesh, A.; Rao, S.; Peng, Y.; Ma, Y. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; pp. 2080–2088. [Google Scholar]
- Chen, S.Y.; Yang, S.; Kalpakis, K.; Chang, C.I. Low-rank decomposition-based anomaly detection. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XIX; SPIE Press: Baltimore, MD, USA, 2013; p. 87430N. [Google Scholar]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Wu, Z.; Wei, Z.; Liu, H.; Xu, X. A novel hyperspectral image anomaly detection method based on low rank representation. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4444–4447. [Google Scholar]
- Zhai, H.; Zhang, H.; Zhang, L.; Li, P.; Plaza, A. A new sparse subspace clustering algorithm for hyperspectral remote sensing imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 43–47. [Google Scholar] [CrossRef]
- Zhang, H.; Zhai, H.; Zhang, L.; Li, P. Spectral–spatial sparse subspace clustering for hyperspectral remote sensing images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3672–3684. [Google Scholar] [CrossRef]
- Elhamifar, E.; Vidal, R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2765–2781. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and spatial classification of hyperspectral data using SVMs and morphological profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef]
- Borghys, D.; Kåsen, I.; Achard, V. Comparative evaluation of hyperspectral anomaly detectors in different types of background. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XVIII; The International Society for Optical Engineering: Baltimore, MD, USA, 2012; p. 83902J. [Google Scholar]
- Du, B.; Zhao, R.; Zhang, L.; Zhang, L. A spectral-spatial based local summation anomaly detection method for hyperspectral images. Signal Process. 2016, 124, 115–131. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, M.; Ma, Y. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices. arXiv 2010, arXiv:1009.5055. [Google Scholar]
- Yuan, Y.; Wang, Q.; Zhu, G. Fast hyperspectral anomaly detection via high-order 2-D crossing filter. IEEE Trans. Geosci. Remote Sens. 2014, 53, 620–630. [Google Scholar] [CrossRef]
- Ma, D.; Yuan, Y.; Wang, Q. A sparse dictionary learning method for hyperspectral anomaly Detection with capped norm. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 648–651. [Google Scholar]
- The Synthetic AVIRIS Salinas Hyperspectral Dataset. Available online: http://www.ehu.eus/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes (accessed on 13 June 2019).
- Stefanou, M.S.; Kerekes, J.P. A method for assessing spectral image utility. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1698–1706. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L.; Ma, L. Hyperspectral anomaly detection by the use of background joint sparse representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2523–2533. [Google Scholar] [CrossRef]
- The Real HYDICE Urban Hyperspectral Dataset. Available online: http://lesun.weebly.com/hyperspectral-data-set.html (accessed on 13 June 2019).
- Zhu, L.; Wen, G. Hyperspectral anomaly detection via background estimation and adaptive weighted sparse representation. Remote Sens. 2018, 10, 272. [Google Scholar]
- Zhao, R.; Du, B.; Zhang, L. Hyperspectral anomaly detection via a sparsity score estimation framework. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3208–3222. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, C. Hyperspectral anomaly detection based on spectral–spatial background joint sparse representation. Eur. J. Remote Sens. 2017, 50, 362–376. [Google Scholar] [CrossRef]
- Acito, N.; Matteoli, S.; Rossi, A.; Diani, M.; Corsini, G. Hyperspectral airborne “Viareggio 2013 Trial” data collection for detection algorithm assessment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2365–2376. [Google Scholar] [CrossRef]
- The “Viareggio 2013 trial” Hyperspectral Dataset. Available online: http://rsipg.dii.unipi.it/ (accessed on 13 June 2019).
- Hanley, J.A.; Mcneil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29. [Google Scholar] [CrossRef]

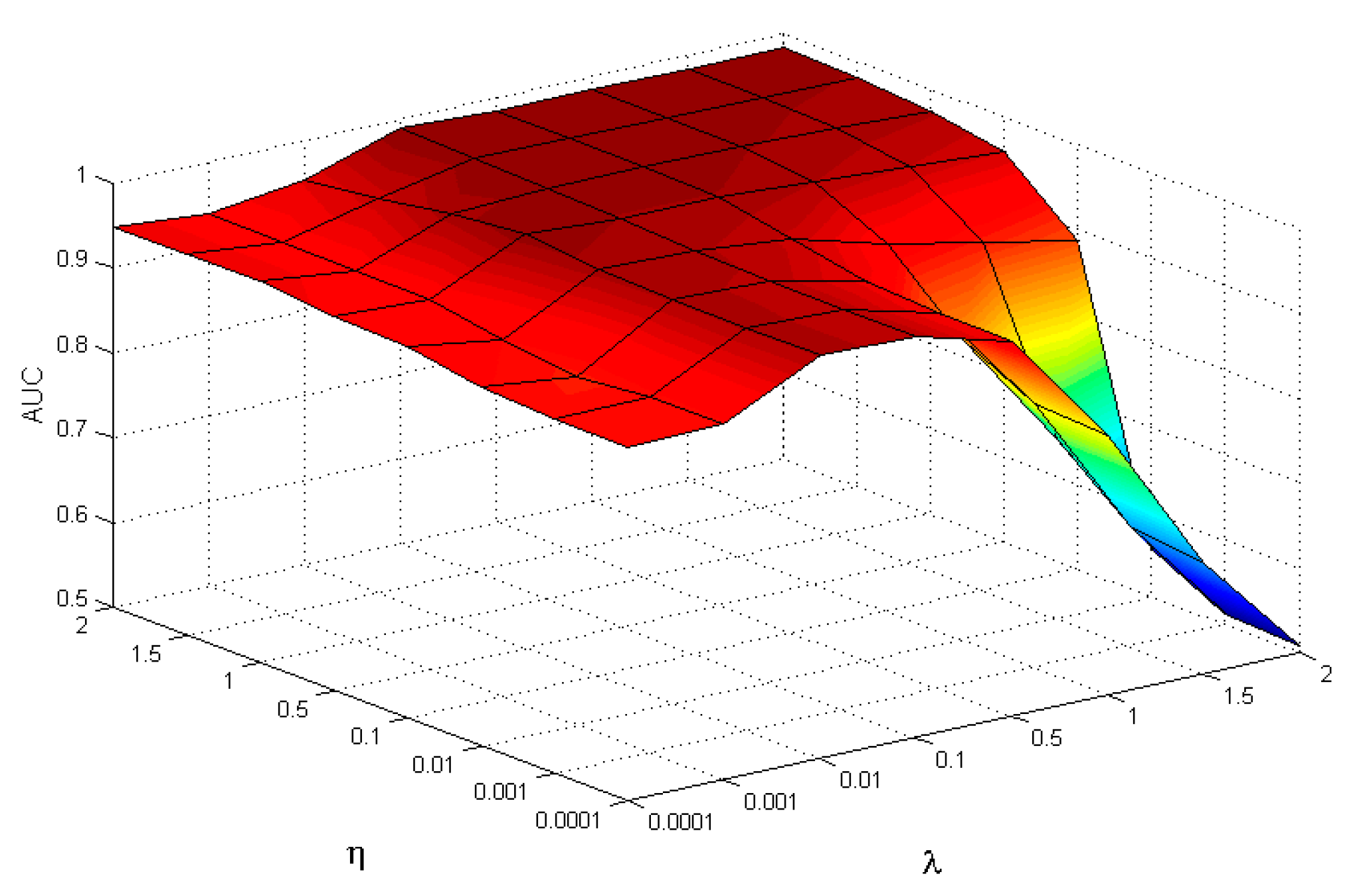



| λ | 0.0001 | 0.001 | 0.01 | 0.1 | 0.5 | 1 | 1.5 | 2 | |
| η | |||||||||
| 0.0001 | 0.9693 | 0.9606 | 0.9516 | 0.9623 | 0.9623 | 0.9622 | 0.9620 | 0.9617 | |
| 0.001 | 0.9694 | 0.9612 | 0.9517 | 0.9623 | 0.9623 | 0.9622 | 0.9620 | 0.9617 | |
| 0.01 | 0.9698 | 0.9666 | 0.9530 | 0.9625 | 0.9623 | 0.9623 | 0.9620 | 0.9618 | |
| 0.1 | 0.9476 | 0.9633 | 0.9640 | 0.9685 | 0.9635 | 0.9627 | 0.9623 | 0.9620 | |
| 0.5 | 0.9482 | 0.9482 | 0.9804 | 0.9774 | 0.9693 | 0.9661 | 0.9645 | 0.9636 | |
| 1 | 0.9486 | 0.9469 | 0.9783 | 0.9794 | 0.9737 | 0.9694 | 0.9673 | 0.9659 | |
| 1.5 | 0.9487 | 0.9463 | 0.9670 | 0.9801 | 0.9760 | 0.9718 | 0.9693 | 0.9677 | |
| 2 | 0.9487 | 0.9460 | 0.9624 | 0.9813 | 0.9777 | 0.9737 | 0.9710 | 0.9692 | |
| Method | Parameters |
|---|---|
| GRXD | — |
| LRXD | (, ) |
| WRXD | — |
| RPCA_RX | |
| LRRSTO | |
| SLW_LRRSTO | |
| MLW_LRRSTO |
| Method | GRXD | LRXD | WRXD | RPCA_RX | LRRSTO | SLW_LRRSTO | MLW_LRRSTO |
|---|---|---|---|---|---|---|---|
| AUC | 0.8073 | 0.8306 | 0.8332 | 0.9619 | 0.9750 | 0.9840 | 0.9854 |
| Time/s | 0.12 | 77.81 | 0.45 | 10.03 | 45.38 | 37.67 | 72.74 |
| Method | GRXD | LRXD | WRXD | RPCA_RX | LRRSTO | SLW_LRRSTO | MLW_LRRSTO |
|---|---|---|---|---|---|---|---|
| AUC | 0.9848 | 0.9953 | 0.9851 | 0.9837 | 0.9881 | 0.9964 | 0.9957 |
| Time/s | 0.06 | 25.48 | 0.21 | 2.34 | 18.43 | 17.72 | 36.78 |
| Method | GRXD | LRXD | WRXD | RPCA_RX | LRRSTO | SLW_LRRSTO | MLW_LRRSTO |
|---|---|---|---|---|---|---|---|
| AUC | 0.8885 | 0.9041 | 0.8901 | 0.9190 | 0.9300 | 0.9621 | 0.9780 |
| Time/s | 0.08 | 42.95 | 0.27 | 3.75 | 25.68 | 24.83 | 50.37 |
| Method | GRXD | LRXD | WRXD | RPCA_RX | LRRSTO | SLW_LRRSTO | MLW_LRRSTO |
|---|---|---|---|---|---|---|---|
| AUC | 0.6884 | 0.7945 | 0.6908 | 0.5509 | 0.8825 | 0.9139 | 0.9172 |
| Time/s | 4.05 | 7153.51 | 13.43 | 863.73 | 1250.67 | 1936.92 | 3589.58 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, K.; Hou, Z.; Ma, D.; Chen, Y.; Du, Q. Anomaly Detection in Hyperspectral Imagery Based on Low-Rank Representation Incorporating a Spatial Constraint. Remote Sens. 2019, 11, 1578. https://doi.org/10.3390/rs11131578
Tan K, Hou Z, Ma D, Chen Y, Du Q. Anomaly Detection in Hyperspectral Imagery Based on Low-Rank Representation Incorporating a Spatial Constraint. Remote Sensing. 2019; 11(13):1578. https://doi.org/10.3390/rs11131578
Chicago/Turabian StyleTan, Kun, Zengfu Hou, Donglei Ma, Yu Chen, and Qian Du. 2019. "Anomaly Detection in Hyperspectral Imagery Based on Low-Rank Representation Incorporating a Spatial Constraint" Remote Sensing 11, no. 13: 1578. https://doi.org/10.3390/rs11131578
APA StyleTan, K., Hou, Z., Ma, D., Chen, Y., & Du, Q. (2019). Anomaly Detection in Hyperspectral Imagery Based on Low-Rank Representation Incorporating a Spatial Constraint. Remote Sensing, 11(13), 1578. https://doi.org/10.3390/rs11131578








