Rangeland Productivity Partitioned to Sub-Pixel Plant Functional Types
Abstract
1. Introduction
2. Materials and Methods
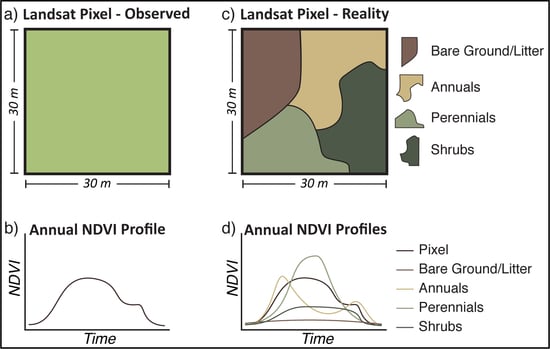
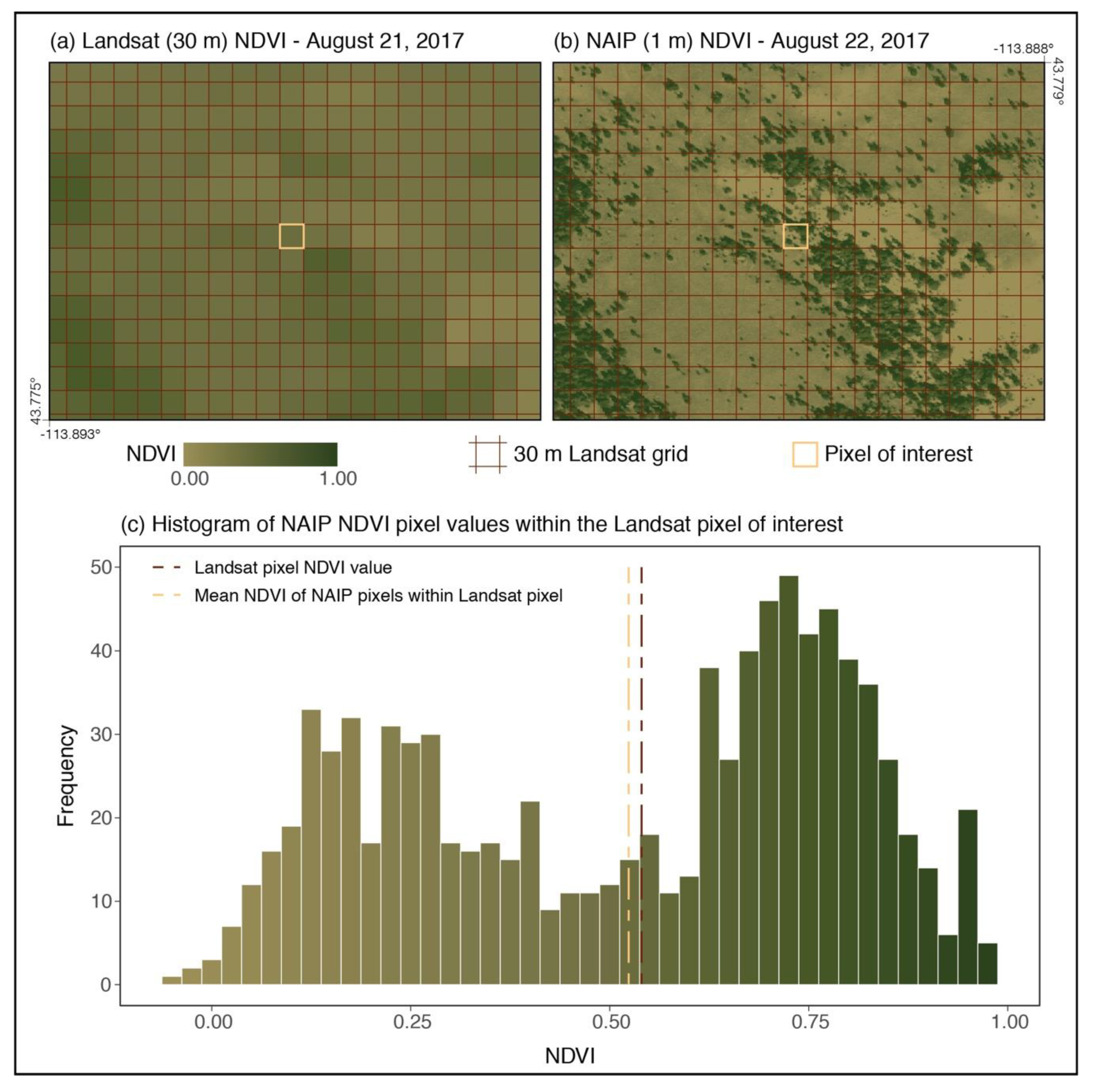
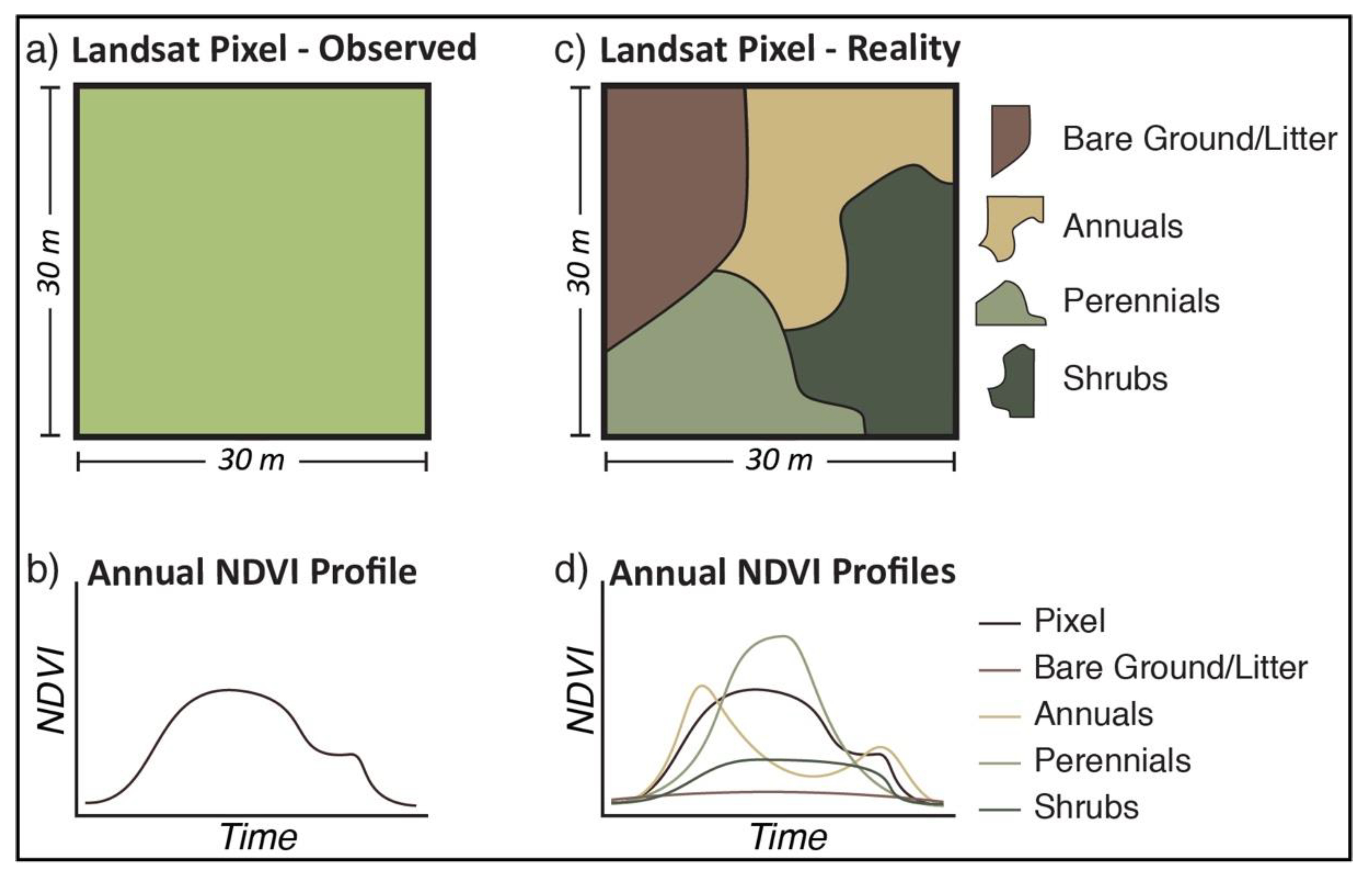
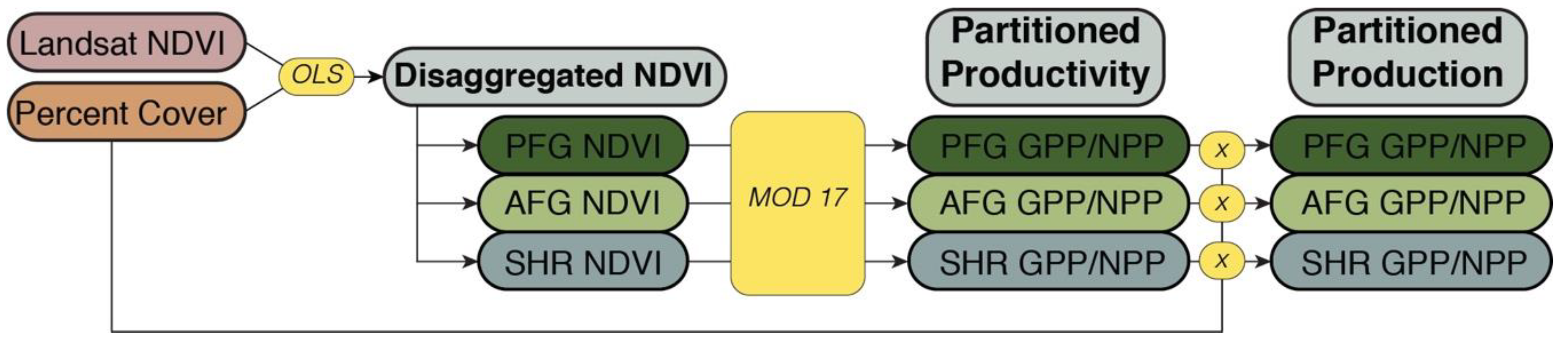
2.1. NDVI Disaggregation
2.2. GPP/NPP Partitioning
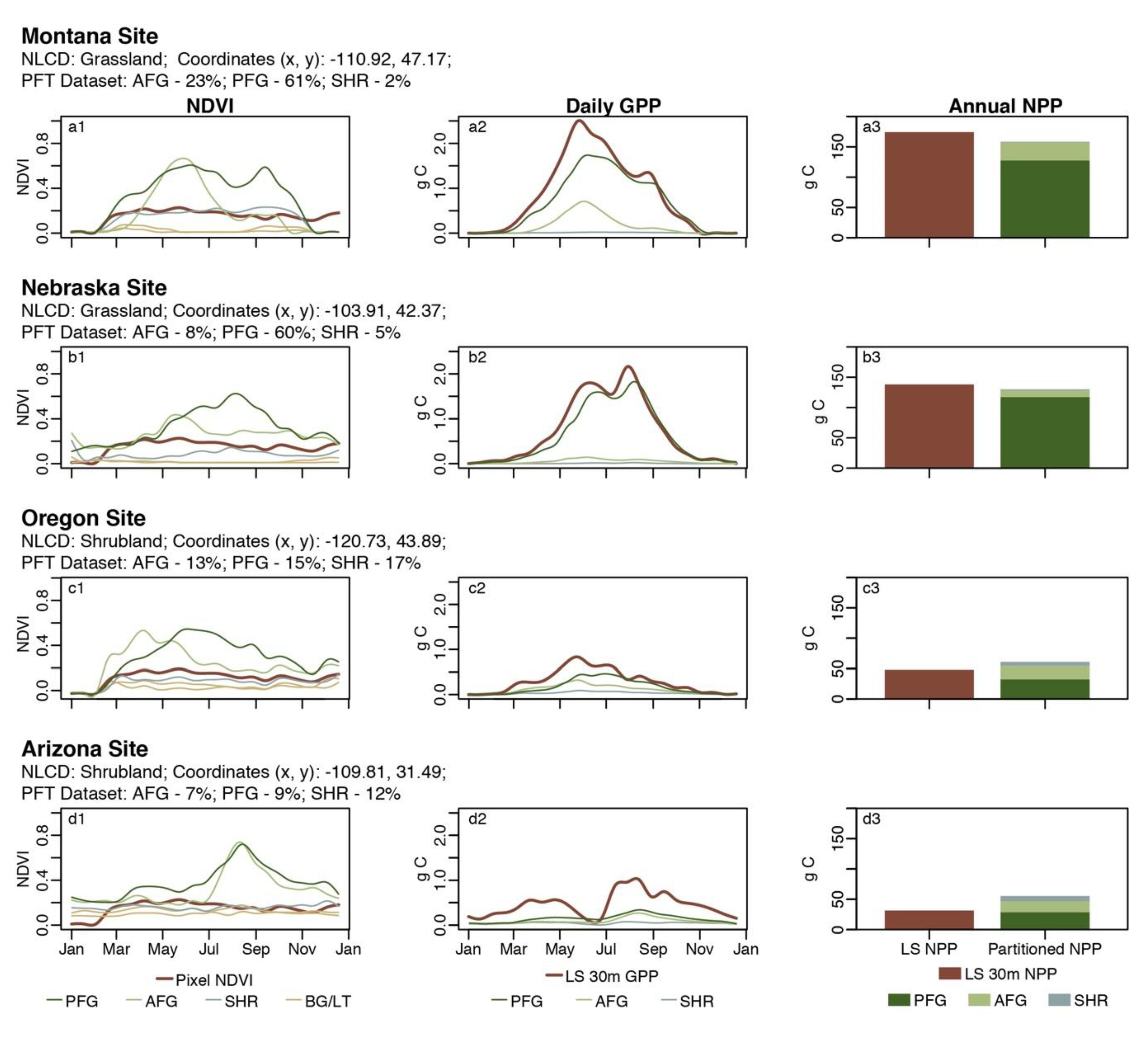
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alkemade, R.; Reid, R.S.; van den Berg, M.; de Leeuw, J.; Jeuken, M. Assessing the impacts of livestock production on biodiversity in rangeland ecosystems. Proc. Natl. Acad. Sci. USA 2013, 110, 20900–20905. [Google Scholar] [CrossRef] [PubMed]
- Sala, O.E.; Yahdjian, L.; Havstad, K.; Aguiar, M.R. Rangeland ecosystem services: Nature’s supply and humans’ demand. In Rangeland Systems: Processes, Management and Challenges; Briske, D.D., Ed.; Springer: Cham, Switzerland, 2017; pp. 467–489. [Google Scholar]
- Havstad, K.; Peters, D.; Allen-Diaz, B.; Bestelmeyer, B.; Briske, D.; Brown, J.; Brunson, M.; Herrick, J.; Johnson, P.; Joyce, L.; et al. The western United States rangelands: A major resource. In Grassland, Quietness and Strength for a New American Agriculture; Wedin, W., Fales, S., Eds.; American Society of Agronomy, Crop Science Society of America, and Soil Science Society of America: Madison, WI, USA, 2009; pp. 75–93. [Google Scholar]
- Veldman, J.W.; Overbeck, G.E.; Negreiros, D.; Mahy, G.; Le Stradic, S.; Fernandes, G.W.; Durigan, G.; Buisson, E.; Putz, F.E.; Bond, W.J. Where tree planting and forest expansion are bad for biodiversity and ecosystem Services. Bioscience 2015, 65, 1011–1018. [Google Scholar] [CrossRef]
- Derner, J.D.; Boutton, T.W.; Briske, D.D. Grazing and ecosystem carbon storage in the North American Great Plains. Plant Soil 2006, 280, 77–90. [Google Scholar] [CrossRef]
- Booker, K.; Huntsinger, L.; Bartolome, J.W.; Sayre, N.F.; Stewart, W. What can ecological science tell us about opportunities for carbon sequestration on arid rangelands in the United States? Glob. Environ. Chang. 2013, 23, 240–251. [Google Scholar] [CrossRef]
- Alcamo, J.; Ash, N.J.; Butler, C.D.; Callicott, J.B.; Capistrano, D.; Carpenter, S.R.; Castilla, J.C.; Chambers, R.; Chopra, K.; Cropper, A.; et al. Millennium Ecosystem Assessment. Ecosystems and Human Well-Being: A Framework for Assessment; World Resources Institute, Island Press: Washington, DC, USA, 2003. [Google Scholar]
- Roy, J.; Mooney, H.A.; Saugier, B. Terrestrial Global Productivity; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Briske, D.D.; Fuhlendorf, S.D.; Smeins, F.E. Vegetation dynamics on rangelands: A critique of the current paradigms. J. Appl. Ecol. 2003, 40, 601–614. [Google Scholar] [CrossRef]
- Frank, D.A.; McNaughton, S.J.; Tracy, B.F. The Ecology of the earth’s grazing ecosystems: Profound functional similarities exist between the Serengeti and Yellowstone. Bioscience 1998, 48, 513–521. [Google Scholar] [CrossRef]
- Fuhlendorf, S.D.; Davis, C.A.; Elmore, R.D.; Goodman, L.E.; Hamilton, R.G. Perspectives on grassland conservation efforts: Should we rewild to the past or conserve for the future? Philos. Trans. R. Soc. Lond. B Biol. Sci. 2018, 373. [Google Scholar] [CrossRef] [PubMed]
- Washington-Allen, R.A.; West, N.E.; Ramsey, R.D.; Efroymson, R.A. A protocol for retrospective remote sensing–based ecological monitoring of rangelands. Rangel. Ecol. Manag. 2006, 59, 19–29. [Google Scholar] [CrossRef]
- West, N.E. History of rangeland monitoring in the USA. Arid Land Res. Manag. 2003, 17, 495–545. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Robinson, N.P.; Allred, B.W.; Smith, W.K.; Jones, M.O.; Moreno, A.; Erickson, T.A.; Naugle, D.E.; Running, S.W. Terrestrial primary production for the conterminous United States derived from Landsat 30 m and MODIS 250 m. Remote Sens. Ecol. Conserv. 2018, 4, 264–280. [Google Scholar] [CrossRef]
- Lillesand, T.; Kiefer, R.W.; Chipman, J. Remote Sensing and Image Interpretation; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Jay, S.; Potter, C.; Crabtree, R.; Genovese, V.; Weiss, D.J.; Kraft, M. Evaluation of modelled net primary production using MODIS and Landsat satellite data fusion. Carbon Balance Manag. 2016, 11, 8. [Google Scholar] [CrossRef] [PubMed]
- Jones, M.O.; Allred, B.W.; Naugle, D.E.; Maestas, J.D.; Donnelly, P.; Metz, L.J.; Karl, J.; Smith, R.; Bestelmeyer, B.; Boyd, C.; et al. Innovation in rangeland monitoring: Annual, 30 m, plant functional type percent cover maps for U.S. rangelands, 1984–2017. Ecosphere 2018, 9, e02430. [Google Scholar] [CrossRef]
- Robinson, N.P.; Allred, B.W.; Jones, M.O.; Moreno, A.; Kimball, J.S.; Naugle, D.E.; Erickson, T.A.; Richardson, A.D. A dynamic Landsat derived normalized difference vegetation index (NDVI) product for the conterminous United States. Remote Sens. 2017, 9, 863. [Google Scholar] [CrossRef]
- Busetto, L.; Meroni, M.; Colombo, R. Combining medium and coarse spatial resolution satellite data to improve the estimation of sub-pixel NDVI time series. Remote Sens. Environ. 2008, 112, 118–131. [Google Scholar] [CrossRef]
- Kerdiles, H.; Grondona, M.O. NOAA-AVHRR NDVI decomposition and subpixel classification using linear mixing in the Argentinean Pampa. Int. J. Remote Sens. 1995, 16, 1303–1325. [Google Scholar] [CrossRef]
- Oleson, K.W.; Sarlin, S.; Garrison, J.; Smith, S.; Privette, J.L.; Emery, W.J. Unmixing multiple land-cover type reflectances from coarse spatial resolution satellite data. Remote Sens. Environ. 1995, 54, 98–112. [Google Scholar] [CrossRef]
- Cherchali, S.; Amram, O.; Flouzat, G. Retrieval of temporal profiles of reflectances from simulated and real NOAA-AVHRR data over heterogeneous landscapes. Int. J. Remote Sens. 2000, 21, 753–775. [Google Scholar] [CrossRef]
- Fortin, J.-P.; Bernier, M.; Lapointe, S.; Gauthier, Y.; De Sève, D.; Beaudoin, S. Estimation of Surface Variables at the Sub-Pixel Level for Use as Input to Climate and Hydrological Models—Final report to Centre National d’Études Spatiales (France); INRS-Eau: Sainte-Foy, QC, Canada, 1998. [Google Scholar]
- Maselli, F. Definition of spatially variable spectral endmembers by locally calibrated multivariate regression analyses. Remote Sens. Environ. 2001, 75, 29–38. [Google Scholar] [CrossRef]
- Zhukov, B.; Oertel, D.; Lanzl, F.; Reinhackel, G. Unmixing-based multisensor multiresolution image fusion. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1212–1226. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2016, 202, 18–27. [Google Scholar] [CrossRef]
- Omernik, J.M.; Griffith, G.E. Ecoregions of the conterminous United States: Evolution of a hierarchical spatial framework. Environ. Manag. 2014, 54, 1249–1266. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: New York, NY, USA, 2009. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robinson, N.P.; Jones, M.O.; Moreno, A.; Erickson, T.A.; Naugle, D.E.; Allred, B.W. Rangeland Productivity Partitioned to Sub-Pixel Plant Functional Types. Remote Sens. 2019, 11, 1427. https://doi.org/10.3390/rs11121427
Robinson NP, Jones MO, Moreno A, Erickson TA, Naugle DE, Allred BW. Rangeland Productivity Partitioned to Sub-Pixel Plant Functional Types. Remote Sensing. 2019; 11(12):1427. https://doi.org/10.3390/rs11121427
Chicago/Turabian StyleRobinson, Nathaniel P., Matthew O. Jones, Alvaro Moreno, Tyler A. Erickson, David E. Naugle, and Brady W. Allred. 2019. "Rangeland Productivity Partitioned to Sub-Pixel Plant Functional Types" Remote Sensing 11, no. 12: 1427. https://doi.org/10.3390/rs11121427
APA StyleRobinson, N. P., Jones, M. O., Moreno, A., Erickson, T. A., Naugle, D. E., & Allred, B. W. (2019). Rangeland Productivity Partitioned to Sub-Pixel Plant Functional Types. Remote Sensing, 11(12), 1427. https://doi.org/10.3390/rs11121427