Evaluation of Leaf N Concentration in Winter Wheat Based on Discrete Wavelet Transform Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Acquisition
2.1.1. Experimental Design
2.1.2. Canopy Spectral Measurement
2.1.3. Leaf Nitrogen Concentration Measurement
2.2. Spectral Transformation
2.3. Analytical Methods
2.3.1. Discrete Wavelet Transform Analysis
2.3.2. Existing Spectral Indices Calculation
2.3.3. Modeling Method
2.3.4. Calibration and Validation
3. Results
3.1. LNC Estimation Models (SR-LNC) Based on Sensitive-Band Reflectance
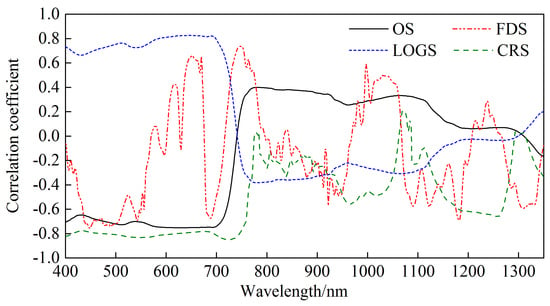
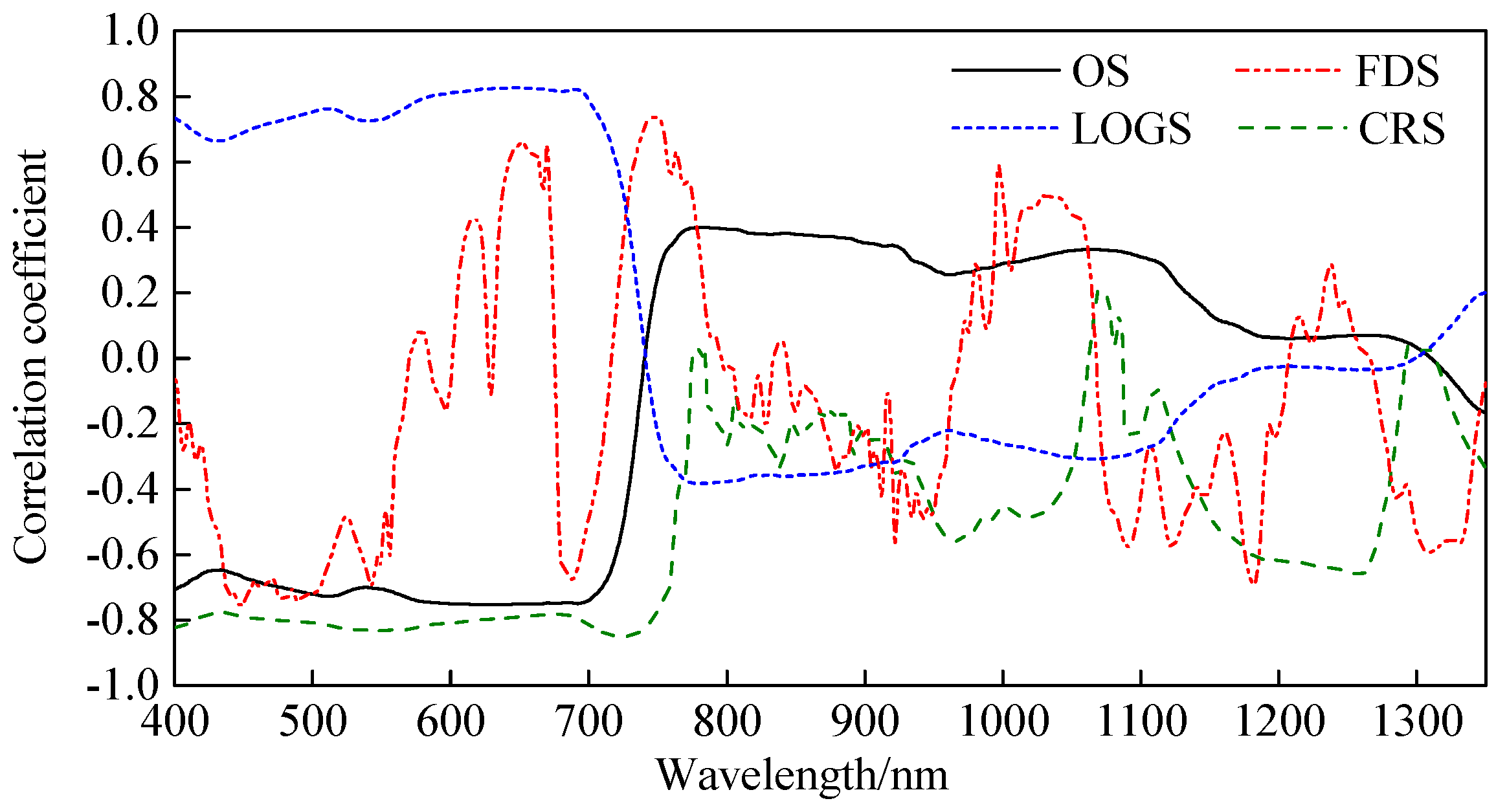
3.1.1. Correlations Between Canopy Spectra and LNC
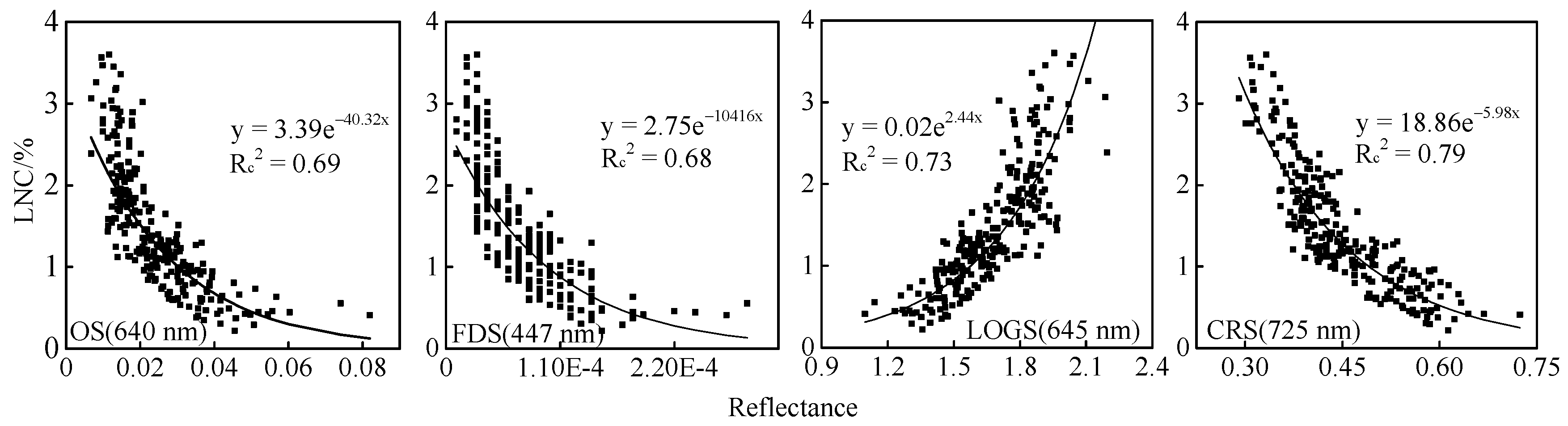
3.1.2. Construction of SR-LNC Estimation Models
3.2. LNC Estimation Models (SI-LNC) Based on Spectral Indices
3.3. LNC Estimation Models (DWT-LNC) Based on DWT Features
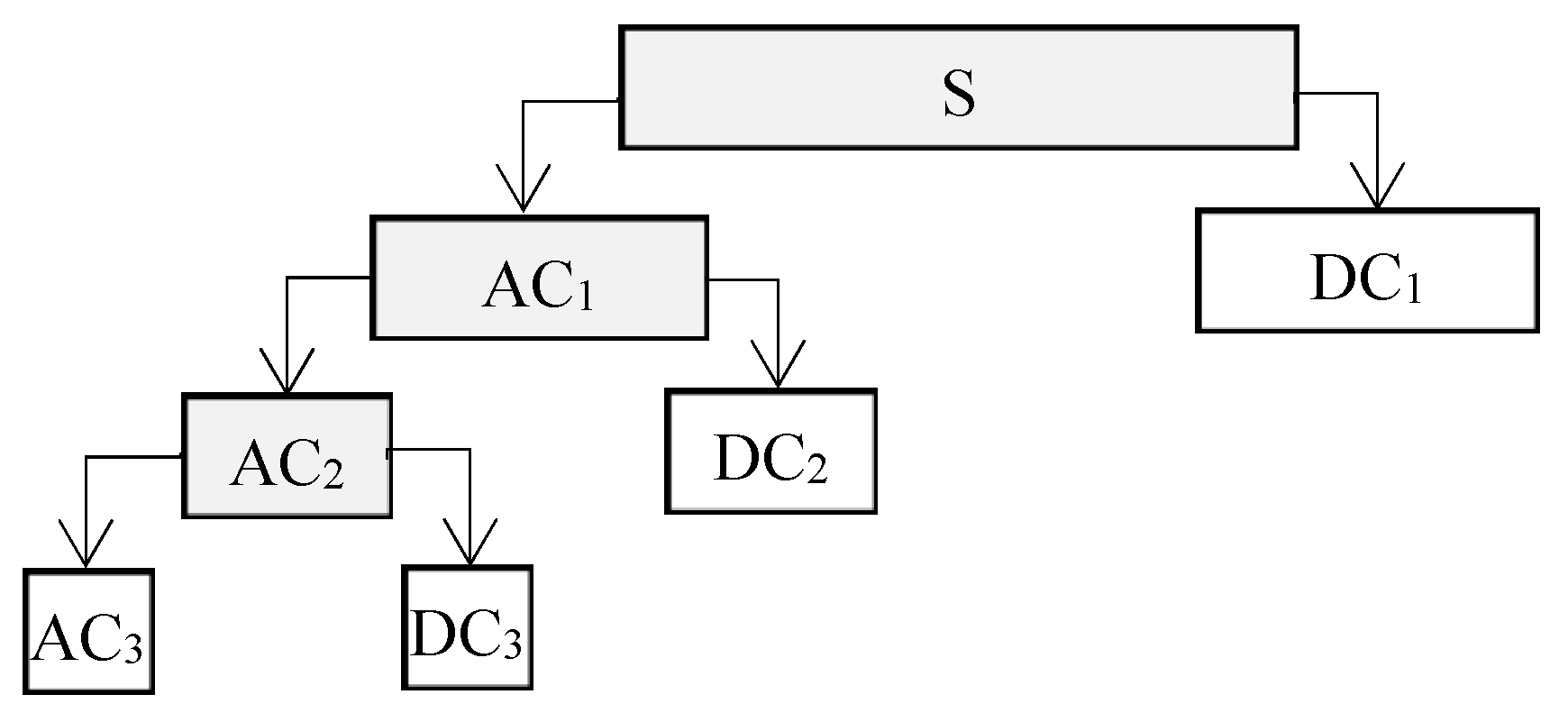
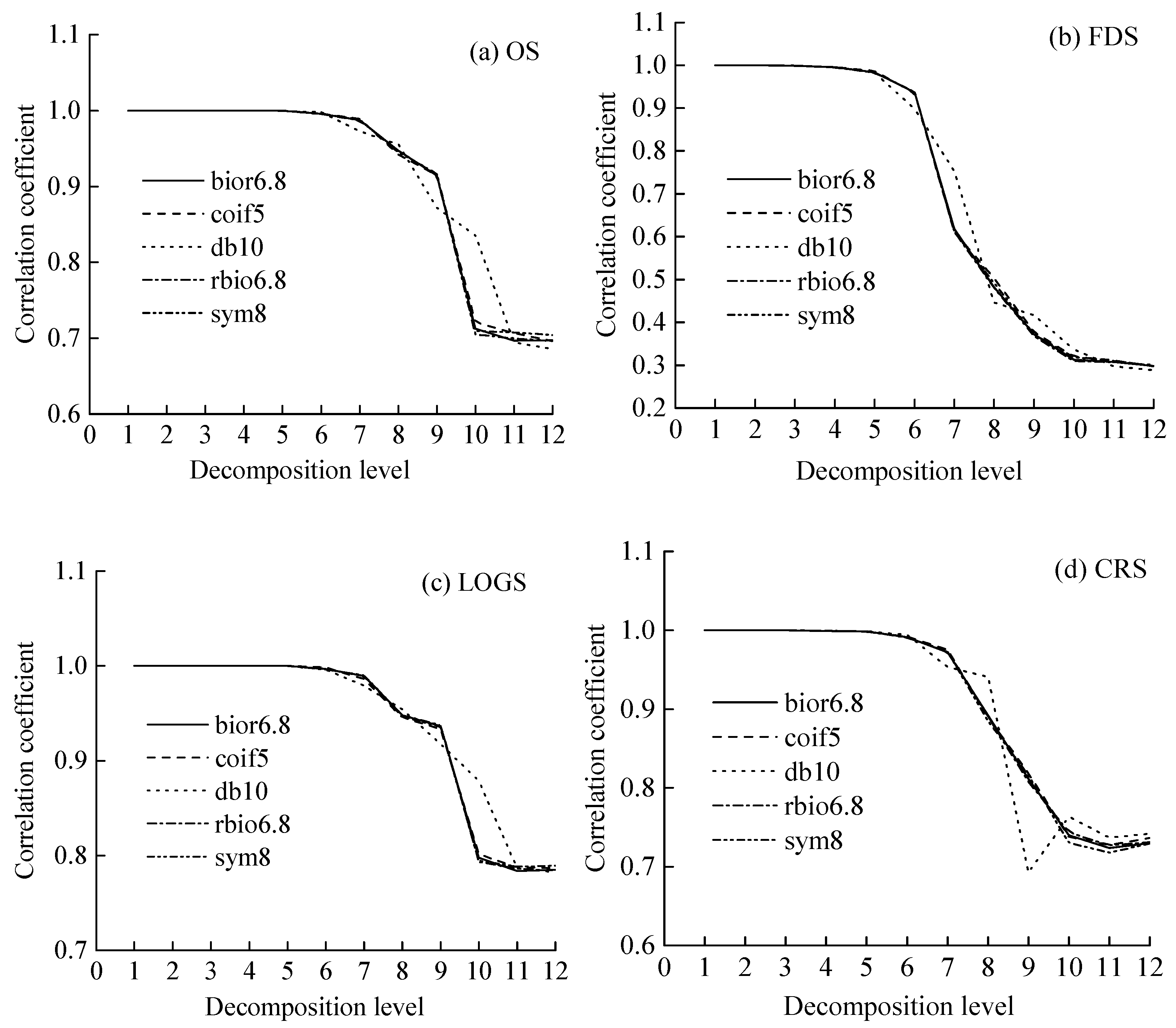
3.3.1. Selection of Optimum Mother Wavelet and Decomposition Level
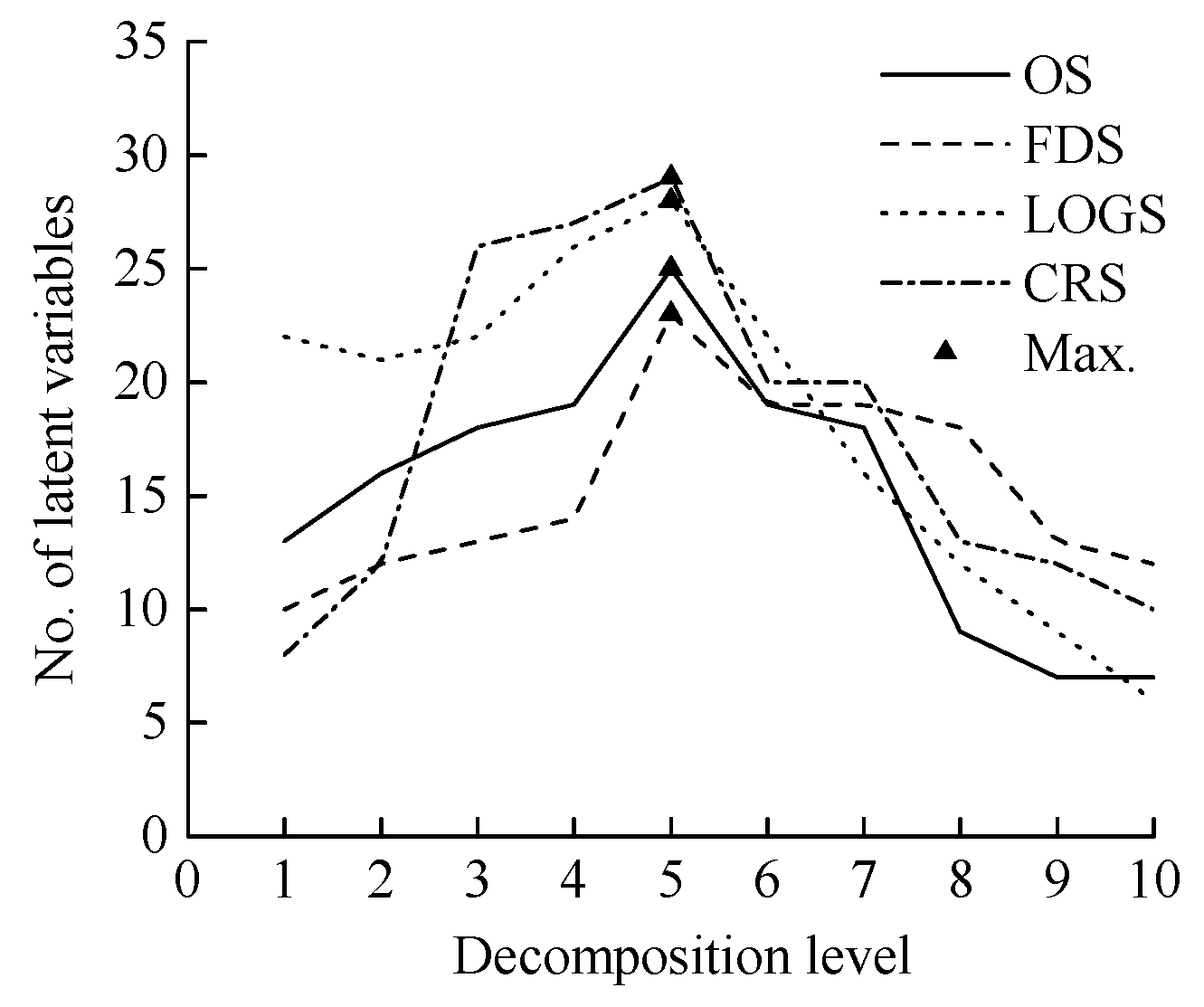
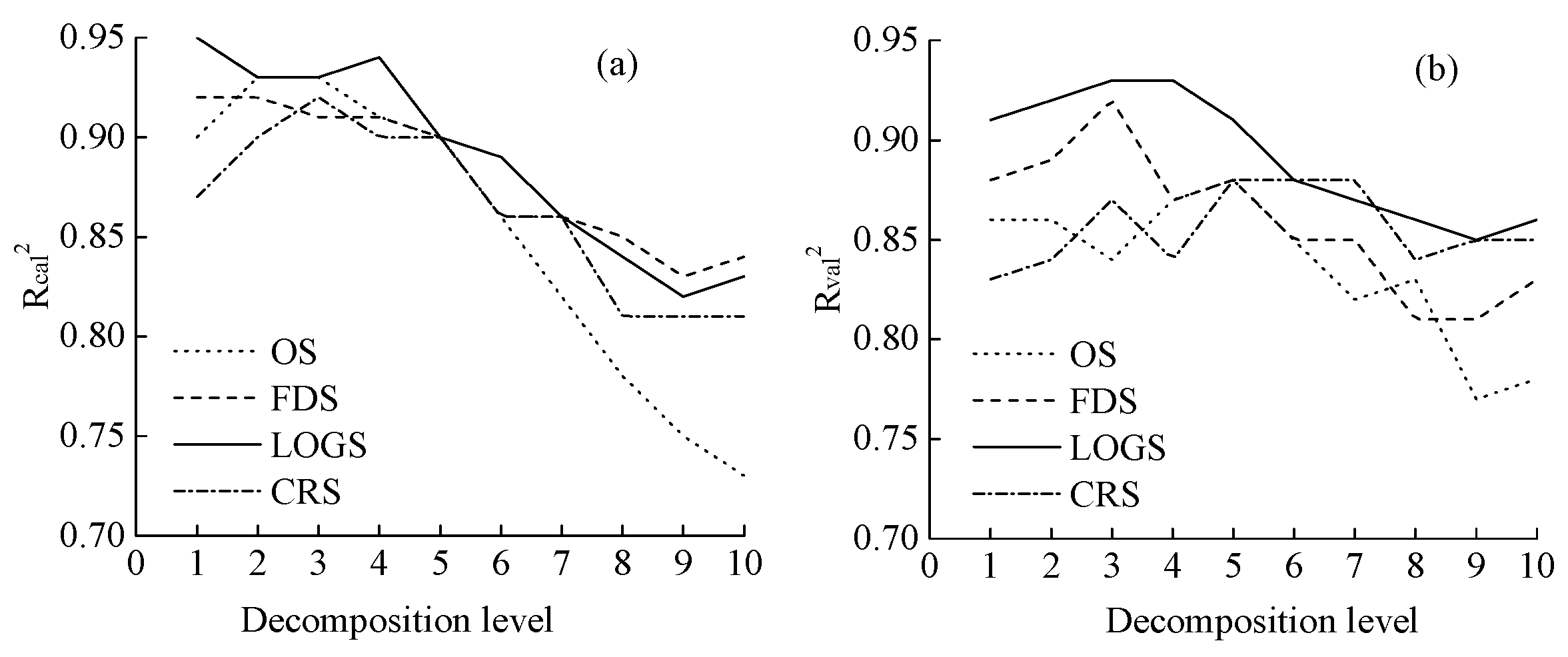
3.3.2. DWT-LNC Models Based on PLS Regression
PLS Regression Using Wavelet ACs
PLS Regression Using Wavelet DCs
PLS Regression Using EVs
3.3.3. DWT-LNC Based on RF Regression
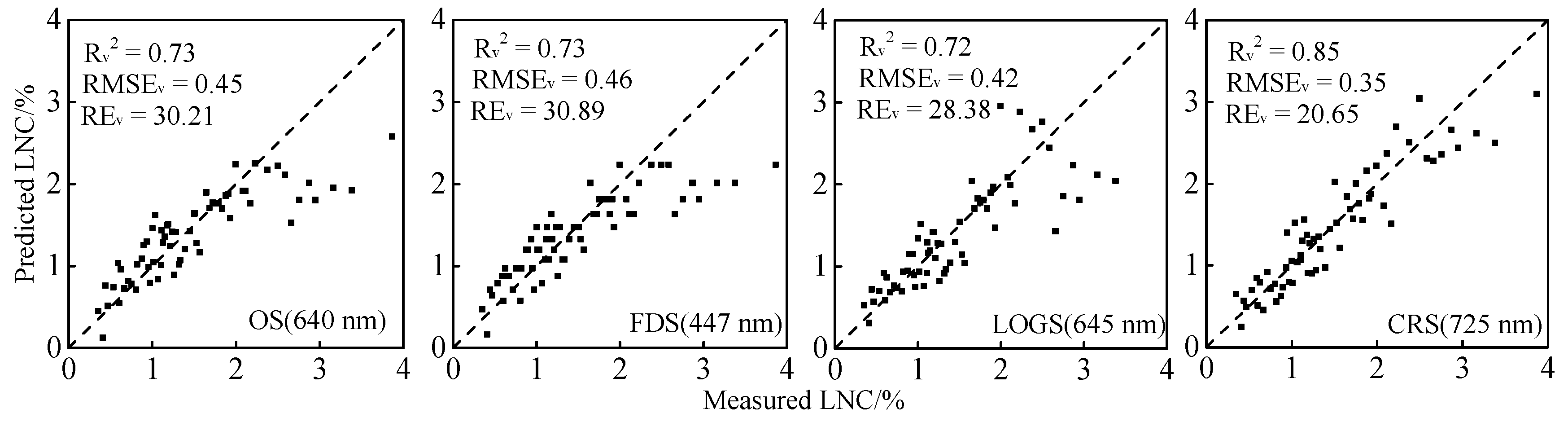
3.4. Estimation Accuracy Comparison
4. Discussion
4.1. Sensitive Band Reflectance and Spectral Transformation
4.2. Relationship Between Spectral Indices and LNC
4.3. Features and Parameters Selection of the DWT Analysis
4.4. Estimation Models of LNC
4.5. Research Challenges
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Singh, B.; Singh, G. Effects of controlled irrigation on water potential, nitrogen uptake and biomass production in Dalbergia sissoo seedlings. Environ. Exp. Bot. 2006, 55, 209–219. [Google Scholar] [CrossRef]
- Wang, H.; Guo, Z.; Shi, Y.; Zhang, Y.; Yu, Z. Impact of tillage practices on nitrogen accumulation and translocation in wheat and soil nitrate-nitrogen leaching in drylands. Soil Till. Res. 2015, 153, 20–27. [Google Scholar] [CrossRef]
- Banedjschafie, S.; Bastani, S.; Widmoser, P.; Mengel, K. Improvement of water use and N fertilizer efficiency by subsoil irrigation of winter wheat. Eur. J. Agron. 2008, 28, 1–7. [Google Scholar] [CrossRef]
- Munoz-Huerta, R.F.; Guevara-Gonzalez, R.G.; Contreras-Medina, L.M.; Torres-Pacheco, I.; Prado-Olivarez, J.; Ocampo-Velazquez, R.V. A review of methods for sensing the nitrogen status in plants: advantages, disadvantages and recent advances. Sensors 2013, 13, 10823–10843. [Google Scholar] [CrossRef]
- Vigneau, N.; Ecarnot, M.; Rabatel, G.; Roumet, P. Potential of field hyperspectral imaging as a non destructive method to assess leaf nitrogen content in Wheat. Field Crop Res. 2011, 122, 25–31. [Google Scholar] [CrossRef]
- Miao, Y.; Mulla, D.J.; Randall, G.W.; Vetsch, J.A.; Vintila, R. Combining chlorophyll meter readings and high spatial resolution remote sensing images for in-season site-specific nitrogen management of corn. Precis. Agric. 2009, 10, 45–62. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Fourty, T.; Baret, F.; Jacquemoud, S.; Schmuck, G.; Verdebout, J. Leaf optical properties with explicit description of its biochemical composition: direct and inverse problems. Remote Sens. Environ. 1996, 56, 104–117. [Google Scholar] [CrossRef]
- Poorter, H.; Evans, J.R. Photosynthetic nitrogen-use efficiency of species that differ inherently in specific leaf area. Oecologia 1998, 116, 26–37. [Google Scholar] [CrossRef]
- Schepers, J.S.; Francis, D.D.; Vigil, M.; Below, F.E. Comparison of corn leaf nitrogen concentration and chlorophyll meter readings. Commun. Soil Sci. Plan. 1992, 23, 2173–2187. [Google Scholar] [CrossRef]
- Kokaly, R.F. Investigating a physical basis for spectroscopic estimates of leaf nitrogen concentration. Remote Sens. Environ. 2001, 75, 153–161. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Vina, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, 93–114. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, H.Y.; Zhang, Y.S.; Qi, S.L.; Heng, Y.R.; Guo, B.B.; Ma, D.Y.; Guo, T.C. Remote detection of canopy leaf nitrogen concentration in winter wheat by using water resistance vegetation indices from in-situ hyperspectral data. Field Crop Res. 2016, 198, 238–246. [Google Scholar] [CrossRef]
- Yoder, B.J.; Pettigrew-Crosby, R.E. Predicting nitrogen and chlorophyll content and concentrations from reflectance spectra (400-2500 nm) at leaf and canopy scales. Remote Sens. Environ. 1995, 53, 199–211. [Google Scholar] [CrossRef]
- Mutanga, O.; Skidmore, A.K.; van Wieren, S. Discriminating tropical grass (Cenchrus ciliaris) canopies grown under different nitrogen treatments using spectroradiometry. ISPRS J. Photogramm. 2003, 57, 263–272. [Google Scholar] [CrossRef]
- Tian, Y.C.; Yao, X.; Yang, J.; Cao, W.X.; Hannaway, D.B.; Zhu, Y. Assessing newly developed and published vegetation indices for estimating rice leaf nitrogen concentration with ground-and space-based hyperspectral reflectance. Field Crop Res. 2011, 120, 299–310. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Zhu, Y.; Takahashi, W. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens. Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
- Feng, W.; Guo, B.B.; Wang, Z.J.; He, L.; Song, X.; Wang, Y.H.; Guo, T.C. Measuring leaf nitrogen concentration in winter wheat using double-peak spectral reflection remote sensing data. Field Crop Res. 2014, 159, 43–52. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Chen, P.; Haboudane, D.; Tremblay, N.; Wang, J.; Vigneault, P.; Li, B. New spectral indicator assessing the efficiency of crop nitrogen treatment in corn and wheat. Remote Sens. Environ. 2010, 114, 1987–1997. [Google Scholar] [CrossRef]
- Yao, X.; Huang, Y.; Shang, G.; Zhou, C.; Cheng, T.; Tian, Y.; Cao, W.; Zhu, Y. Evaluation of six algorithms to monitor wheat leaf nitrogen concentration. Remote Sens. 2015, 7, 14939–14966. [Google Scholar] [CrossRef]
- Wang, H.F.; Huo, Z.G.; Zhou, G.S.; Liao, Q.H.; Feng, H.K.; Wu, L. Estimating leaf SPAD values of freeze-damaged winter wheat using continuous wavelet analysis. Plant Physiol. Bioch. 2016, 98, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Quandt, V.I.; Pacola, E.R.; Pichorim, S.F.; Gamba, H.R.; Sovierzoski, M.A. Pulmonary crackle characterization: approaches in the use of discrete wavelet transform regarding border effect, mother-wavelet selection, and subband reduction. Res. Biomed. Eng. 2015, 31, 148–159. [Google Scholar] [CrossRef]
- Chang, T.; Kuo, C.C. Texture analysis and classification with tree-structured wavelet transform. IEEE Trans. Image Process. 1993, 2, 429–441. [Google Scholar] [CrossRef] [PubMed]
- Bruce, L.M.; Koger, C.H.; Li, J. Dimensionality reduction of hyperspectral data using discrete wavelet transform feature extraction. IEEE Trans. Geosci. Remote 2002, 40, 2331–2338. [Google Scholar] [CrossRef]
- Sahadevan, A.S.; Shrivastava, P.; Das, B.S.; Sarathjith, M.C. Discrete wavelet transform approach for the estimation of crop residue mass from spectral reflectance. IEEE J-STARS 2014, 7, 2490–2495. [Google Scholar] [CrossRef]
- Shi, Y.; Huang, W.; Zhou, X. Evaluation of wavelet spectral features in pathological detection and discrimination of yellow rust and powdery mildew in winter wheat with hyperspectral reflectance data. J. Appl. Remote Sens. 2017, 11, 026025. [Google Scholar] [CrossRef]
- Blackburn, G.A. Wavelet decomposition of hyperspectral data: a novel approach to quantifying pigment concentrations in vegetation. Int. J. Remote Sens. 2007, 28, 2831–2855. [Google Scholar] [CrossRef]
- Peng, J.; Shen, H.; Wu, J.S. Soil moisture retrieving using hyperspectral data with the application of wavelet analysis. Environ. Earth Sci. 2013, 69, 279–288. [Google Scholar] [CrossRef]
- Pu, R.; Gong, P. Wavelet transform applied to EO-1 hyperspectral data for forest LAI and crown closure mapping. Remote Sens. Environ. 2004, 91, 212–224. [Google Scholar] [CrossRef]
- Bremner, J.M. Determination of nitrogen in soil by the Kjeldahl method. J. Agric. Sci. 1960, 55, 11–33. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Dawson, T.P.; Curran, P.J.; Plummer, S.E. LIBERTY-Modeling the effects of leaf biochemical concentration on reflectance spectra. Remote Sens. Environ. 1998, 65, 50–60. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res.-Solid Earth 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; De Colstoun, E.B.; McMurtrey Iii, J.E. Estimating corn leaf chlorophyll concentration from leaf and canopy reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Penuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids / chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Filella, I.; Serrano, L.; Serra, J.; Penuelas, J. Evaluating wheat nitrogen status with canopy reflectance indices and discriminant analysis. Crop Sci. 1995, 35, 1400–1405. [Google Scholar] [CrossRef]
- Barnes, E.M.; Clarke, T.R.; Richards, S.E.; Colaizzi, P.D.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T.; et al. Coincident detection of crop water stress, nitrogen status and canopy density using ground based multispectral data. In Proceedings of the 5th International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Ecarnot, M.; Compan, F.; Roumet, P. Assessing leaf nitrogen content and leaf mass per unit area of wheat in the field throughout plant cycle with a portable spectrometer. Field Crop Res. 2013, 140, 44–50. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: a tutorial. Anal. Chim. ACTA 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Wang, J.; Ding, J.; Abulimiti, A.; Cai, L. Quantitative estimation of soil salinity by means of different modeling methods and visible-near infrared (VIS–NIR) spectroscopy, Ebinur Lake Wetland, Northwest China. PeerJ 2018, 6, e4703. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.T.; Lee, B.W. Assessment of rice leaf growth and nitrogen status by hyperspectral canopy reflectance and partial least square regression. Eur. J. Agron. 2006, 24, 349–356. [Google Scholar] [CrossRef]
- Zhu, Y.; Yao, X.; Tian, Y.; Liu, X.; Cao, W. Analysis of common canopy vegetation indices for indicating leaf nitrogen accumulations in wheat and rice. Int. J. Appl. Earth Obs. 2008, 10, 1–10. [Google Scholar] [CrossRef]
- Jahn, B.R.; Brooksby, P.A.; Upadhyaya, S.K. Wavelet-based spectral analysis for soil nitrate content measurement. Trans. ASAE 2005, 48, 2065–2071. [Google Scholar] [CrossRef]
- Cao, Q.; Miao, Y.; Feng, G.; Gao, X.; Li, F.; Liu, B.; Yue, S.; Cheng, S.; Ustin, S.L.; Khosla, R. Active canopy sensing of winter wheat nitrogen status: An evaluation of two sensor systems. Comput. Electron Agric. 2015, 112, 54–67. [Google Scholar] [CrossRef]
- Ramoelo, A.; Skidmore, A.K.; Schlerf, M.; Mathieu, R.; Heitkonig, I.M. Water-removed spectra increase the retrieval accuracy when estimating savanna grass nitrogen and phosphorus concentrations. ISPRS J. Photogramm. 2011, 66, 408–417. [Google Scholar] [CrossRef]
- Li, F.; Miao, Y.; Feng, G.; Yuan, F.; Yue, S.; Gao, X.; Liu, Y.; Liu, B.; Ustin, S.L.; Chen, X. Improving estimation of summer maize nitrogen status with red edge-based spectral vegetation indices. Field Crop Res. 2014, 157, 111–123. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.K. A new technique for extracting the red edge position from hyperspectral data: The linear extrapolation method. Remote Sens. Environ. 2006, 101, 181–193. [Google Scholar] [CrossRef]
- Diker, K.; Bausch, W.C. Potential use of nitrogen reflectance index to estimate plant parameters and yield of maize. Biosyst. Eng. 2003, 85, 437–447. [Google Scholar] [CrossRef]
- Hunt, E.R.; Daughtry, C.S.T.; Eitel, J.U.; Long, D.S. Remote sensing leaf chlorophyll content using a visible band index. Agron. J. 2011, 103, 1090–1099. [Google Scholar] [CrossRef]
- Wang, W.; Yao, X.; Yao, X.; Tian, Y.; Liu, X.; Ni, J.; Cao, W.; Zhu, Y. Estimating leaf nitrogen concentration with three-band vegetation indices in rice and wheat. Field Crop Res. 2012, 129, 90–98. [Google Scholar] [CrossRef]
- Cocchi, M.; Seeber, R.; Ulrici, A. Multivariate calibration of analytical signals by WILMA (wavelet interface to linear modelling analysis). J. Chemometr. 2003, 17, 512–527. [Google Scholar] [CrossRef]
- Ferwerda, J.G.; Jones, S.D. Continuous wavelet transformations for hyperspectral feature detection. In Progress in Spatial Data Handling; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Blackburn, G.A.; Ferwerda, J.G. Retrieval of chlorophyll concentration from leaf reflectance spectra using wavelet analysis. Remote Sens. Environ. 2008, 112, 1614–1632. [Google Scholar] [CrossRef]
| Category | Index | Formula | Developed by |
|---|---|---|---|
| Chlorophyll indices | mSR705 | (R750 – R445)/(R705 − R445) | [19] |
| MTCI | (R754 − R709)/(R709 − R681) | [35] | |
| SIPI | (R800 − R445)/(R800 − R680) | [36] | |
| NPCI | (R430 − R680)/(R430 + R680) | [36] | |
| Nitrogen indices | NRI | (R570 − R670)/(R570 + R670) | [37] |
| NDRE | (R790 − R720)/(R790 + R720) | [38] | |
| DCNI | (R720 − R700)/(R700 − R670)/(R720 − R670 + 0.03) | [20] | |
| Greenness indices | GNDVI | (R750 − R550)/( R750 + R550) | [39] |
| OSAVI | 1.16(R800−R670)/(R800 + R670 + 0.16) | [40] | |
| MTVI2 | 1.5(1.2(R800 − R550) − 2.5(R670 − R550))/sqrt((2R800 + 1)2 − (6R800 − 5sqrt(R670)) − 0.5) | [41] | |
| Ri is the reflectance at i nm wavelength | |||
| Data Set | No. of Samples | Min | Max | Range | Mean | SD | Variance | Skewness | Kurtosis | CV (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| Whole | 315 | 0.22 | 3.87 | 3.64 | 1.47 | 0.77 | 0.59 | 0.76 | 2.98 | 52.03 |
| Calibration | 252 | 0.22 | 3.60 | 3.38 | 1.46 | 0.76 | 0.58 | 0.73 | 2.88 | 51.88 |
| Validation | 63 | 0.35 | 3.87 | 3.52 | 1.5 | 0.79 | 0.63 | 0.86 | 3.26 | 53.00 |
| Category | Index | Correlation Coefficient | Equation | Rc2 | Rv2 | RMSEv | REv |
|---|---|---|---|---|---|---|---|
| Chlorophyll indices | mSR705 | 0.91 ** | LNC = 0.2702x − 0.6773 | 0.83 | 0.86 | 0.28 | 18.81 |
| MTCI | 0.89 ** | LNC = 0.5454x − 1.0901 | 0.78 | 0.84 | 0.31 | 20.94 | |
| SIPI | 0.79 ** | LNC = 1E − 06e15.28x | 0.71 | 0.69 | 0.57 | 37.80 | |
| NPCI | 0.80 ** | LNC = 1.9583e4.13x | 0.70 | 0.71 | 0.45 | 30.13 | |
| Nitrogen indices | NRI | 0.70 ** | LNC = 6.2342x − 0.5199 | 0.50 | 0.50 | 0.56 | 37.64 |
| NDRE | 0.86 ** | LNC = 0.046e6.28x | 0.80 | 0.85 | 0.30 | 20.27 | |
| DCNI | 0.79 ** | LNC = 0.039x − 0.8904 | 0.63 | 0.74 | 0.41 | 27.06 | |
| Greenness indices | GNDVI | 0.85 ** | LNC = 0.002e8.44x | 0.81 | 0.82 | 0.33 | 21.90 |
| OSAVI | 0.69 ** | LNC = 0.0099e6.61x | 0.55 | 0.54 | 0.55 | 36.61 | |
| MTVI2 | 0.60 ** | LNC = 5.293x − 1.0551 | 0.36 | 0.42 | 0.60 | 40.08 |
| Mother Wavelet | L1 | L2 | L3 | L4 | L5 | L6 | L7 | L8 | L9 | L10 | L11 | L12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bior6.8 | 484 | 250 | 133 | 75 | 46 | 31 | 24 | 20 | 18 | 17 | 17 | 17 |
| coif5 | 490 | 259 | 144 | 86 | 57 | 43 | 36 | 32 | 30 | 29 | 29 | 29 |
| db10 | 485 | 252 | 135 | 77 | 48 | 33 | 26 | 22 | 20 | 19 | 19 | 19 |
| rbio6.8 | 484 | 250 | 133 | 75 | 46 | 31 | 24 | 20 | 18 | 17 | 17 | 17 |
| sym8 | 483 | 249 | 132 | 73 | 44 | 29 | 22 | 18 | 16 | 15 | 15 | 15 |
| OS | FDS | LOGS | CRS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | |
| AC1 | 0.86 | 0.29 | 19.59 | 0.88 | 0.27 | 18.07 | 0.91 | 0.24 | 15.78 | 0.83 | 0.33 | 22.06 |
| AC2 | 0.86 | 0.30 | 19.68 | 0.89 | 0.26 | 17.22 | 0.92 | 0.23 | 15.19 | 0.84 | 0.33 | 22.13 |
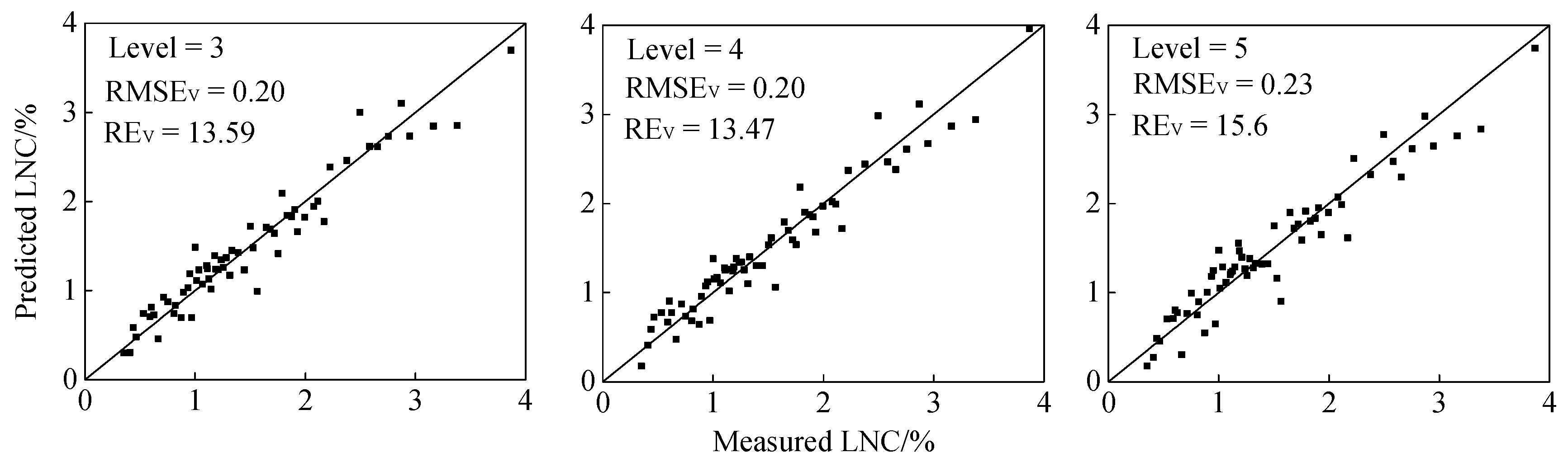
| AC3 | 0.84 | 0.32 | 21.24 | 0.92 | 0.23 | 15.50 | 0.93 | 0.20 | 13.59 | 0.87 | 0.33 | 22.18 |
| AC4 | 0.87 | 0.29 | 19.09 | 0.87 | 0.27 | 18.18 | 0.93 | 0.20 | 13.47 | 0.84 | 0.33 | 22.20 |
| AC5 | 0.88 | 0.28 | 18.45 | 0.88 | 0.29 | 19.49 | 0.91 | 0.23 | 15.60 | 0.88 | 0.28 | 18.37 |
| AC6 | 0.85 | 0.31 | 20.98 | 0.85 | 0.31 | 20.76 | 0.88 | 0.27 | 17.95 | 0.88 | 0.27 | 18.24 |
| AC7 | 0.82 | 0.34 | 22.62 | 0.85 | 0.31 | 20.52 | 0.87 | 0.30 | 20.11 | 0.88 | 0.27 | 17.99 |
| AC8 | 0.83 | 0.33 | 22.28 | 0.81 | 0.31 | 20.84 | 0.86 | 0.30 | 19.83 | 0.84 | 0.31 | 20.87 |
| AC9 | 0.77 | 0.38 | 25.13 | 0.81 | 0.35 | 23.07 | 0.85 | 0.30 | 20.29 | 0.85 | 0.31 | 20.74 |
| AC10 | 0.78 | 0.37 | 24.90 | 0.83 | 0.32 | 21.64 | 0.86 | 0.29 | 19.59 | 0.85 | 0.30 | 20.14 |
| DC | OS | FDS | LOGS | CRS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | |
| DC6 | 0.84 | 0.32 | 21.43 | 0.81 | 0.35 | 23.02 | 0.89 | 0.26 | 17.53 | 0.85 | 0.30 | 20.25 |
| DC7 | 0.83 | 0.33 | 21.75 | 0.77 | 0.38 | 25.19 | 0.89 | 0.27 | 17.73 | 0.84 | 0.32 | 21.41 |
| DC8 | 0.83 | 0.33 | 22.17 | 0.57 | 0.52 | 34.54 | 0.87 | 0.29 | 18.38 | 0.81 | 0.35 | 23.13 |
| DC9 | 0.77 | 0.38 | 25.36 | 0.48 | 0.57 | 38.05 | 0.88 | 0.28 | 18.77 | 0.81 | 0.36 | 23.76 |
| DC10 | 0.76 | 0.39 | 26.17 | 0.39 | 0.62 | 41.63 | 0.88 | 0.28 | 19.55 | 0.77 | 0.38 | 25.53 |
| EV | OS | FDS | LOGS | CRS | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | |
| EV1 | 0.14 | 0.73 | 49.02 | 0.46 | 0.58 | 38.83 | 0.47 | 0.57 | 38.22 | 0.64 | 0.47 | 31.61 |
| EV2 | 0.25 | 0.69 | 46.14 | 0.43 | 0.59 | 39.80 | 0.72 | 0.42 | 28.67 | 0.71 | 0.43 | 28.43 |
| EV3 | 0.19 | 0.71 | 47.34 | 0.41 | 0.61 | 40.58 | 0.71 | 0.44 | 29.36 | 0.72 | 0.41 | 27.66 |
| EV4 | 0.19 | 0.71 | 47.34 | 0.36 | 0.63 | 42.08 | 0.65 | 0.46 | 31.14 | 0.74 | 0.40 | 26.74 |
| EV5 | 0.29 | 0.67 | 44.42 | 0.32 | 0.65 | 43.47 | 0.69 | 0.43 | 29.05 | 0.75 | 0.39 | 26.34 |
| EV6 | 0.74 | 0.42 | 27.93 | 0.65 | 0.47 | 26.41 | 0.81 | 0.34 | 22.85 | 0.75 | 0.39 | 26.41 |
| EV7 | 0.79 | 0.36 | 23.99 | 0.66 | 0.47 | 31.49 | 0.81 | 0.34 | 22.91 | 0.76 | 0.38 | 25.88 |
| EV8 | 0.87 | 0.29 | 19.22 | 0.74 | 0.41 | 27.61 | 0.83 | 0.32 | 21.56 | 0.80 | 0.35 | 23.56 |
| EV9 | 0.87 | 0.29 | 19.15 | 0.76 | 0.40 | 27.02 | 0.84 | 0.32 | 21.35 | 0.81 | 0.34 | 23.19 |
| EV10 | 0.87 | 0.29 | 19.28 | 0.82 | 0.35 | 23.23 | 0.88 | 0.26 | 17.82 | 0.83 | 0.33 | 22.17 |
| OS | FDS | LOGS | CRS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | Rv2 | RMSEv | REv | |
| AC1 | 0.86 | 0.29 | 19.64 | 0.87 | 0.29 | 19.30 | 0.89 | 0.26 | 17.53 | 0.89 | 0.27 | 17.93 |
| AC2 | 0.86 | 0.30 | 19.86 | 0.87 | 0.29 | 19.25 | 0.89 | 0.27 | 17.91 | 0.89 | 0.28 | 18.38 |
| AC3 | 0.87 | 0.29 | 19.34 | 0.87 | 0.29 | 19.20 | 0.89 | 0.26 | 17.21 | 0.88 | 0.28 | 18.41 |
| AC4 | 0.86 | 0.29 | 19.52 | 0.86 | 0.29 | 19.52 | 0.91 | 0.24 | 16.08 | 0.89 | 0.27 | 17.78 |
| AC5 | 0.87 | 0.28 | 18.89 | 0.87 | 0.29 | 19.01 | 0.90 | 0.25 | 16.35 | 0.89 | 0.28 | 18.44 |
| AC6 | 0.86 | 0.28 | 18.91 | 0.86 | 0.29 | 19.44 | 0.86 | 0.28 | 18.40 | 0.88 | 0.29 | 19.25 |
| AC7 | 0.88 | 0.29 | 19.41 | 0.71 | 0.43 | 28.76 | 0.86 | 0.30 | 20.12 | 0.86 | 0.31 | 20.77 |
| AC8 | 0.83 | 0.33 | 21.84 | 0.69 | 0.45 | 29.85 | 0.85 | 0.31 | 20.84 | 0.84 | 0.32 | 21.57 |
| AC9 | 0.85 | 0.31 | 20.67 | 0.64 | 0.49 | 32.45 | 0.80 | 0.36 | 24.02 | 0.81 | 0.35 | 23.27 |
| AC10 | 0.83 | 0.32 | 21.49 | 0.51 | 0.56 | 37.15 | 0.74 | 0.41 | 27.17 | 0.76 | 0.39 | 26.23 |
| EV10 | 0.82 | 0.35 | 23.34 | 0.77 | 0.38 | 25.36 | 0.86 | 0.29 | 19.43 | 0.84 | 0.32 | 21.16 |
| Model | OLS regression | PLS regression | RF regression | ||||
|---|---|---|---|---|---|---|---|
| CRS725 | mSR705 | AC4 | DC6 | EV10 | AC4 | EV10 | |
| RPDc | 1.95 | 2.43 | 3.97 | 2.81 | 2.61 | 3.04 | 2.38 |
| RPDv | 2.26 | 2.82 | 3.95 | 3.04 | 3.04 | 3.29 | 2.72 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Wang, L.; Liu, J.; Wang, Y.; Chang, Q. Evaluation of Leaf N Concentration in Winter Wheat Based on Discrete Wavelet Transform Analysis. Remote Sens. 2019, 11, 1331. https://doi.org/10.3390/rs11111331
Li F, Wang L, Liu J, Wang Y, Chang Q. Evaluation of Leaf N Concentration in Winter Wheat Based on Discrete Wavelet Transform Analysis. Remote Sensing. 2019; 11(11):1331. https://doi.org/10.3390/rs11111331
Chicago/Turabian StyleLi, Fenling, Li Wang, Jing Liu, Yuna Wang, and Qingrui Chang. 2019. "Evaluation of Leaf N Concentration in Winter Wheat Based on Discrete Wavelet Transform Analysis" Remote Sensing 11, no. 11: 1331. https://doi.org/10.3390/rs11111331
APA StyleLi, F., Wang, L., Liu, J., Wang, Y., & Chang, Q. (2019). Evaluation of Leaf N Concentration in Winter Wheat Based on Discrete Wavelet Transform Analysis. Remote Sensing, 11(11), 1331. https://doi.org/10.3390/rs11111331