The Challenge of Spatial Resolutions for GRACE-Based Estimates Volume Changes of Larger Man-Made Lake: The Case of China’s Three Gorges Reservoir in the Yangtze River
Abstract
1. Introduction
2. Data Sources
2.1. GRACE
2.2. Land Surface Models
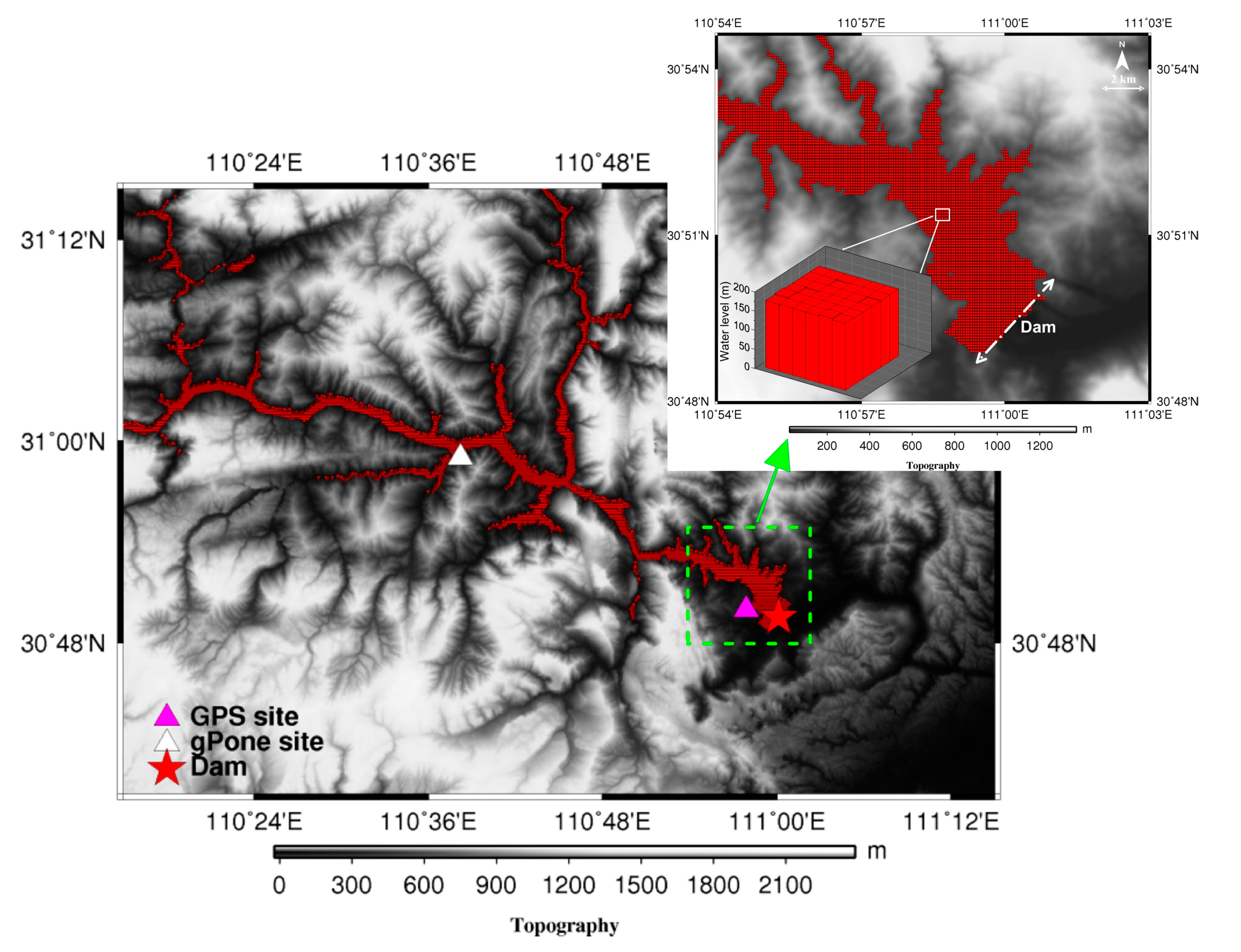
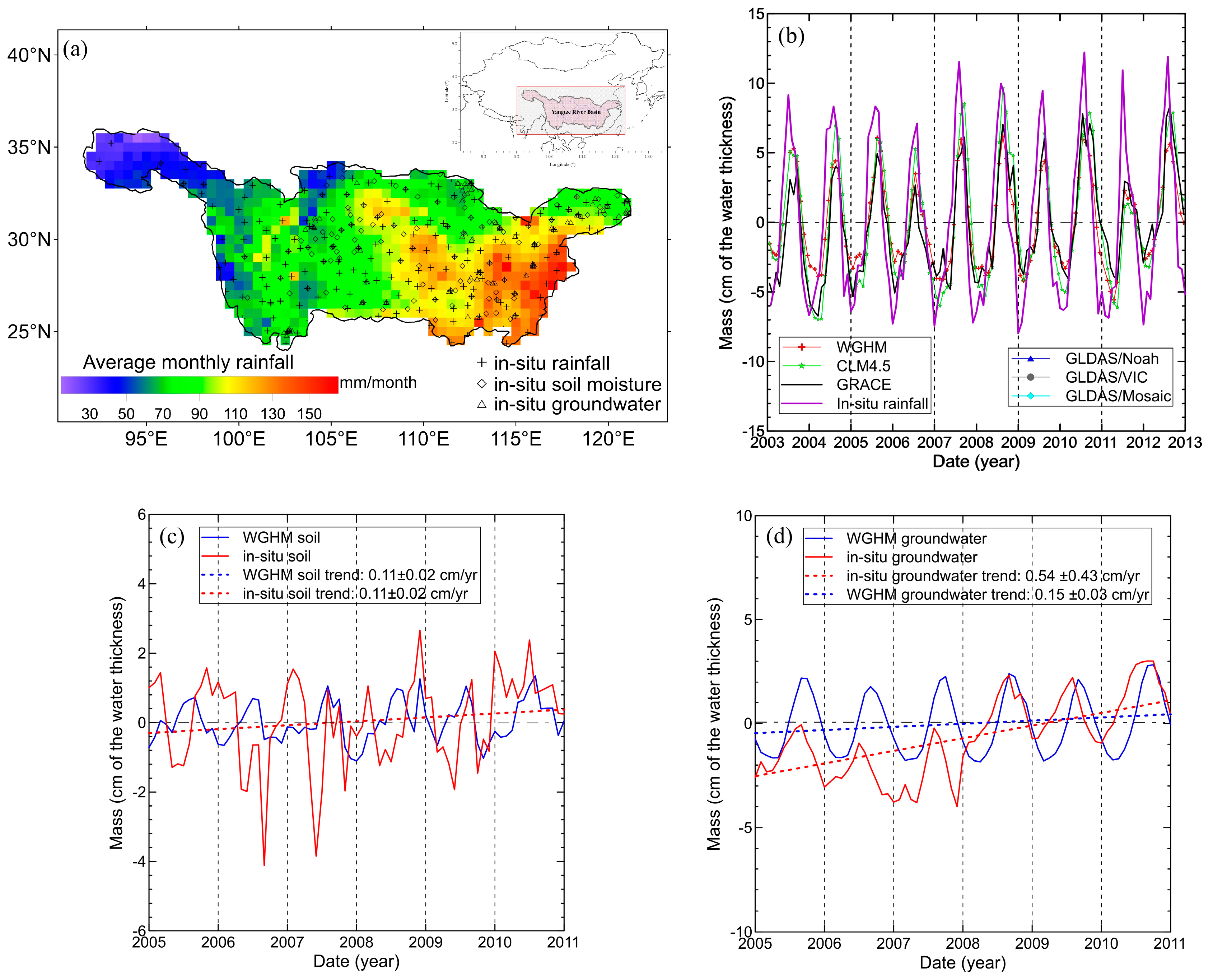
2.3. In-Situ Measurements
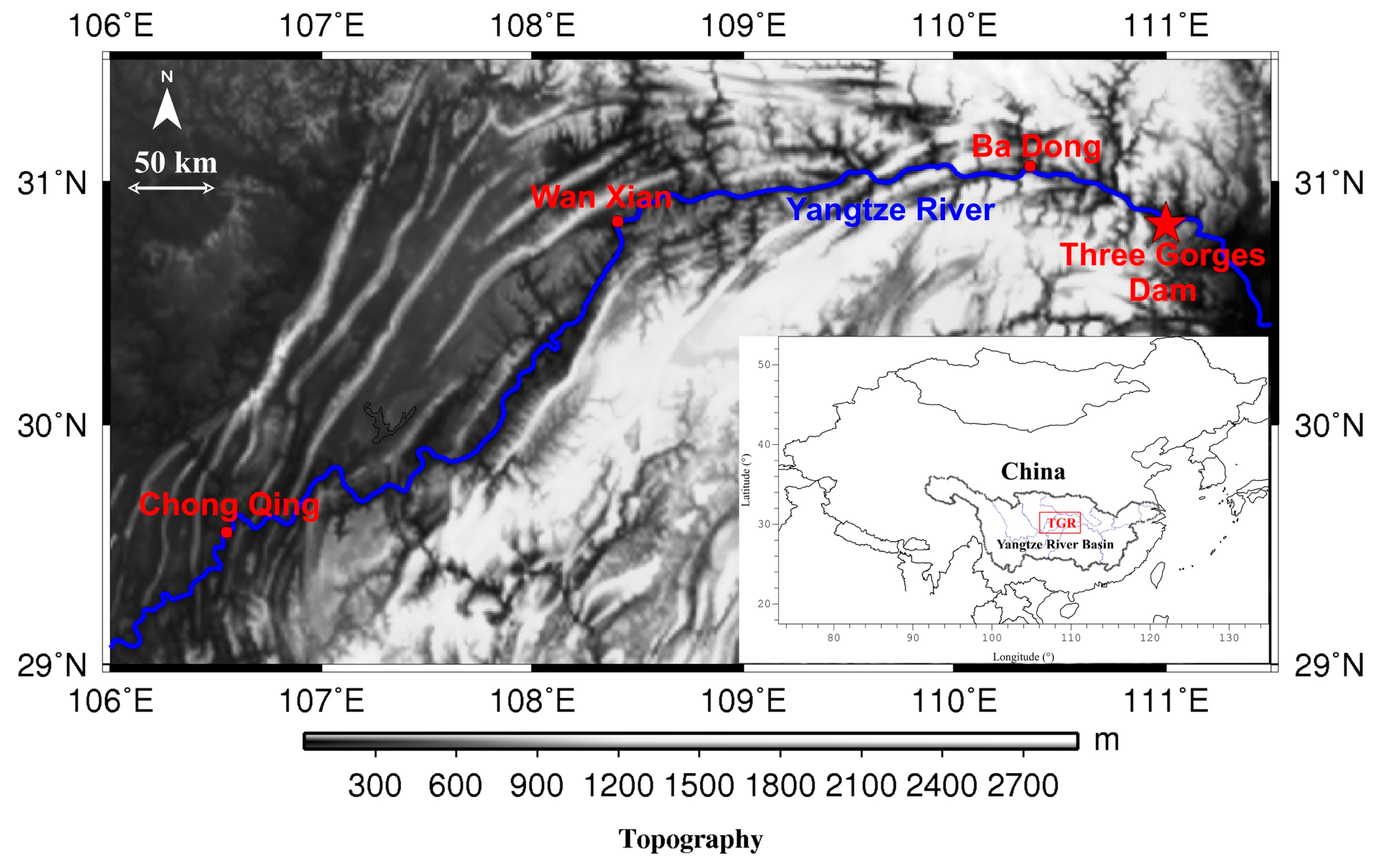
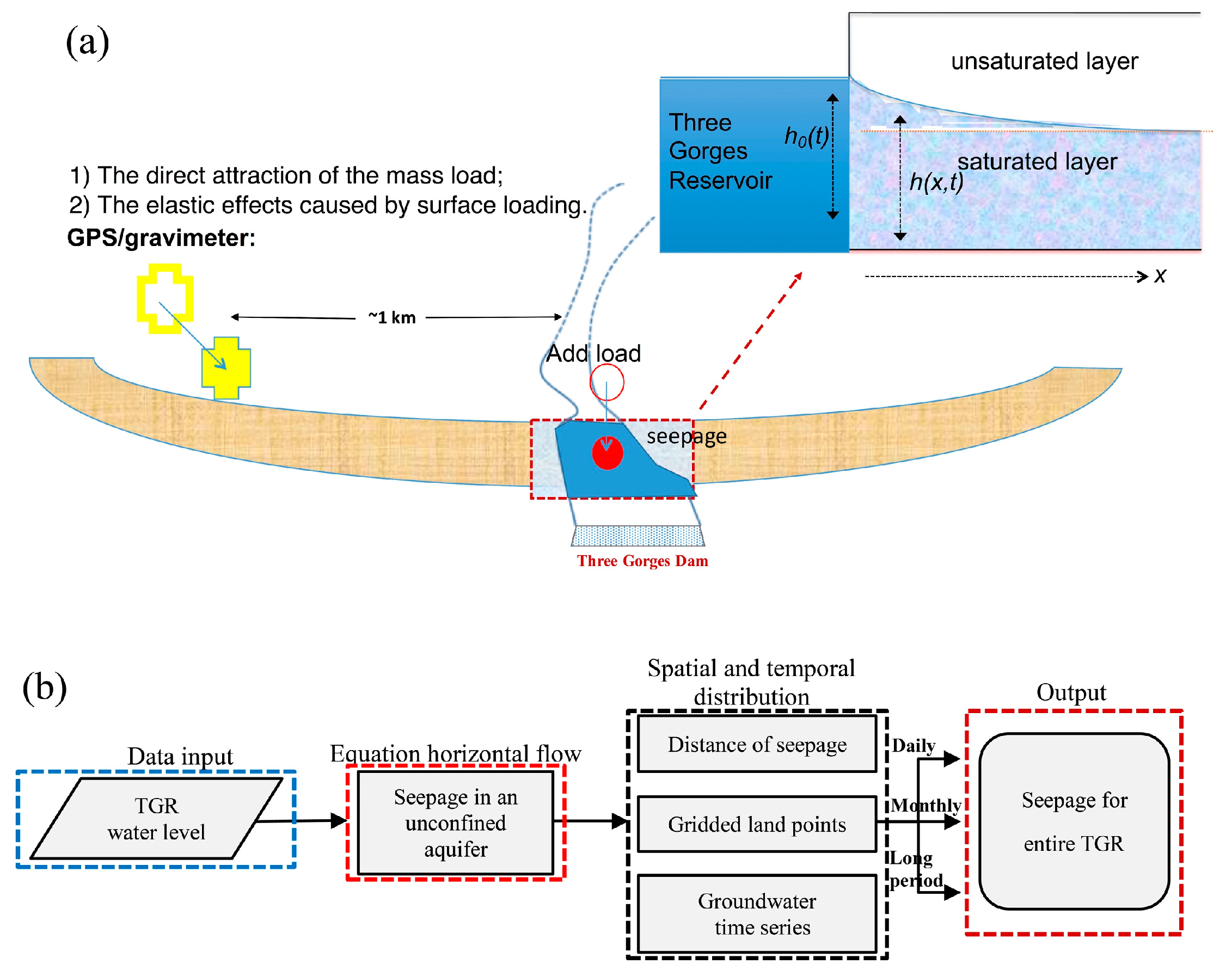
3. Numerical Simulation of the Response to Three Gorges Reservoir Filling
4. Results
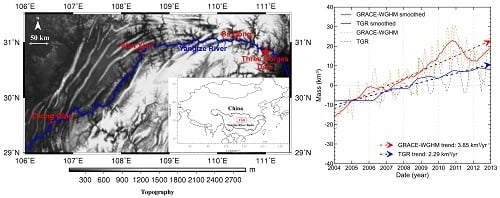
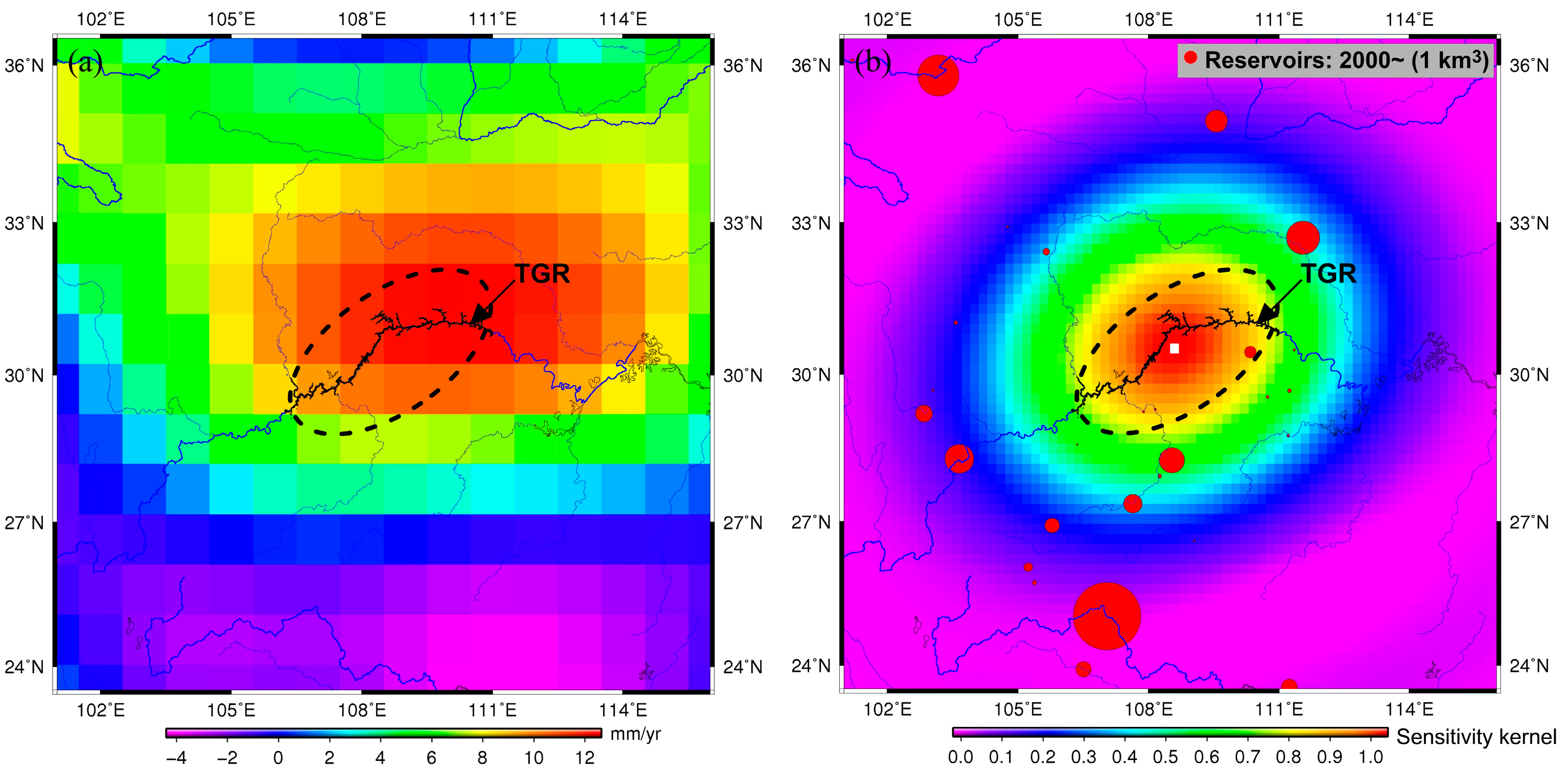
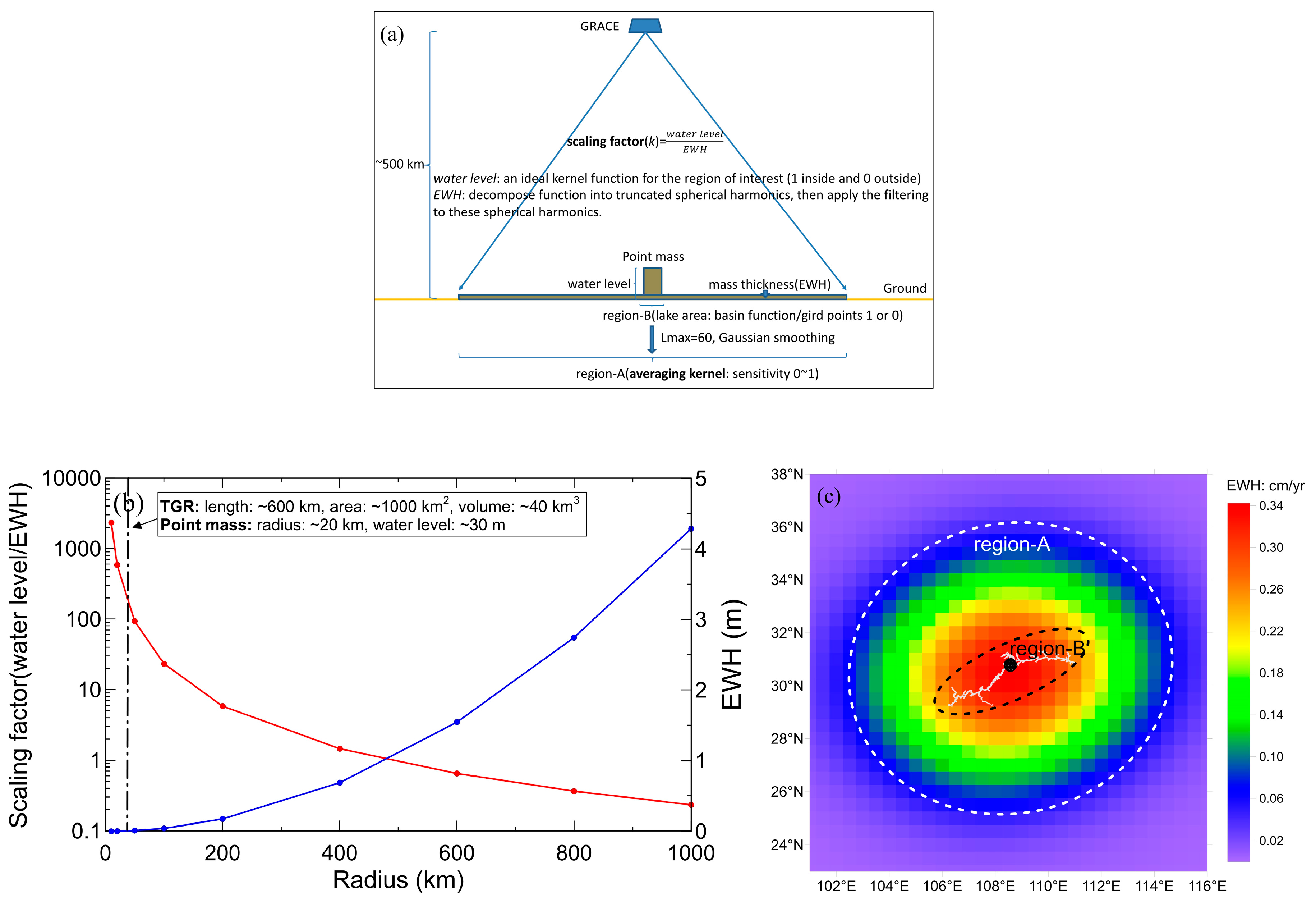
4.1. GRACE Estimated Mass Changes and Sensitivity Kernels
4.2. Assessing Land Surface Models
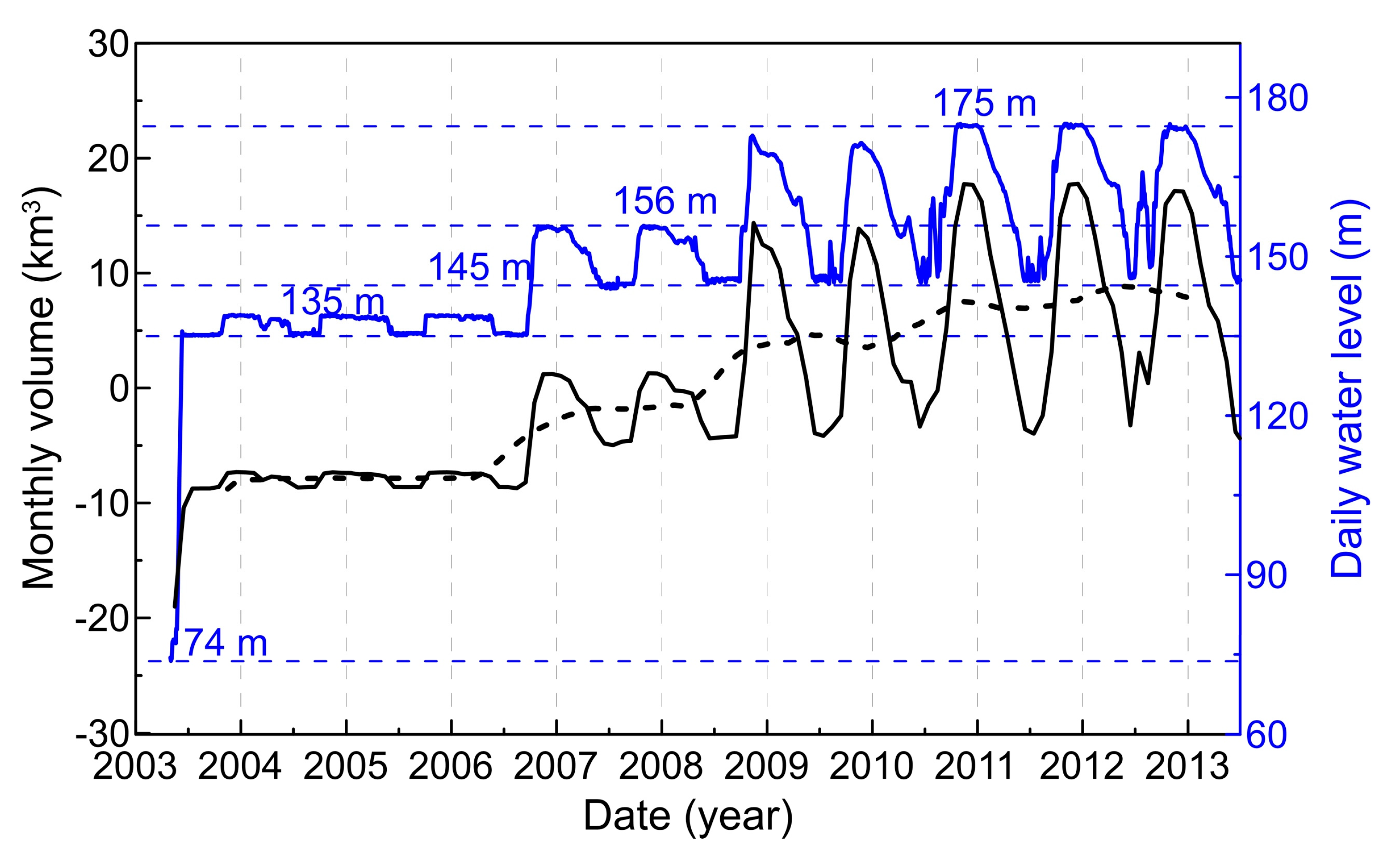
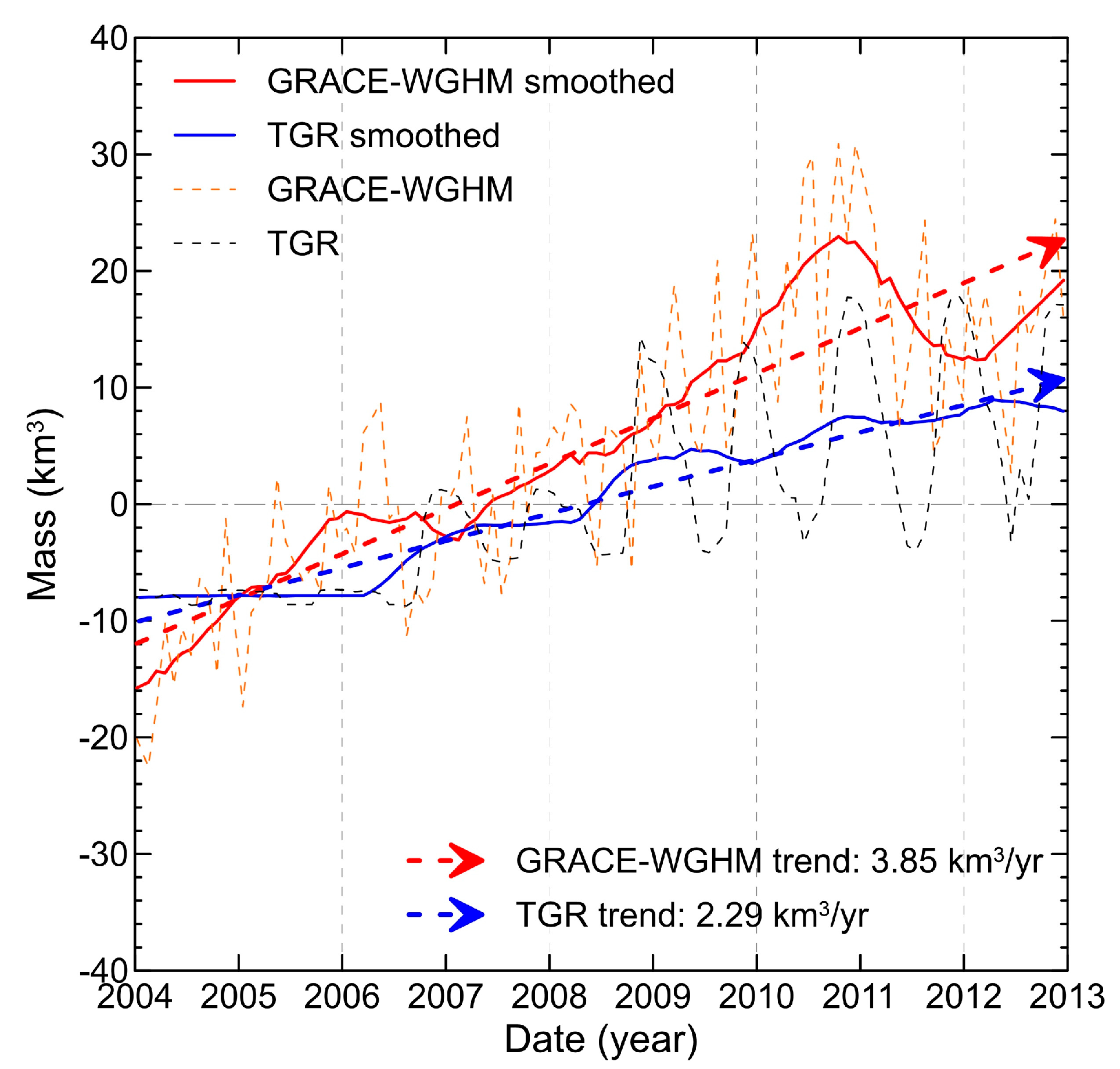
4.3. Time Series of the GRACE-Based Three Gorges Reservoir Volume
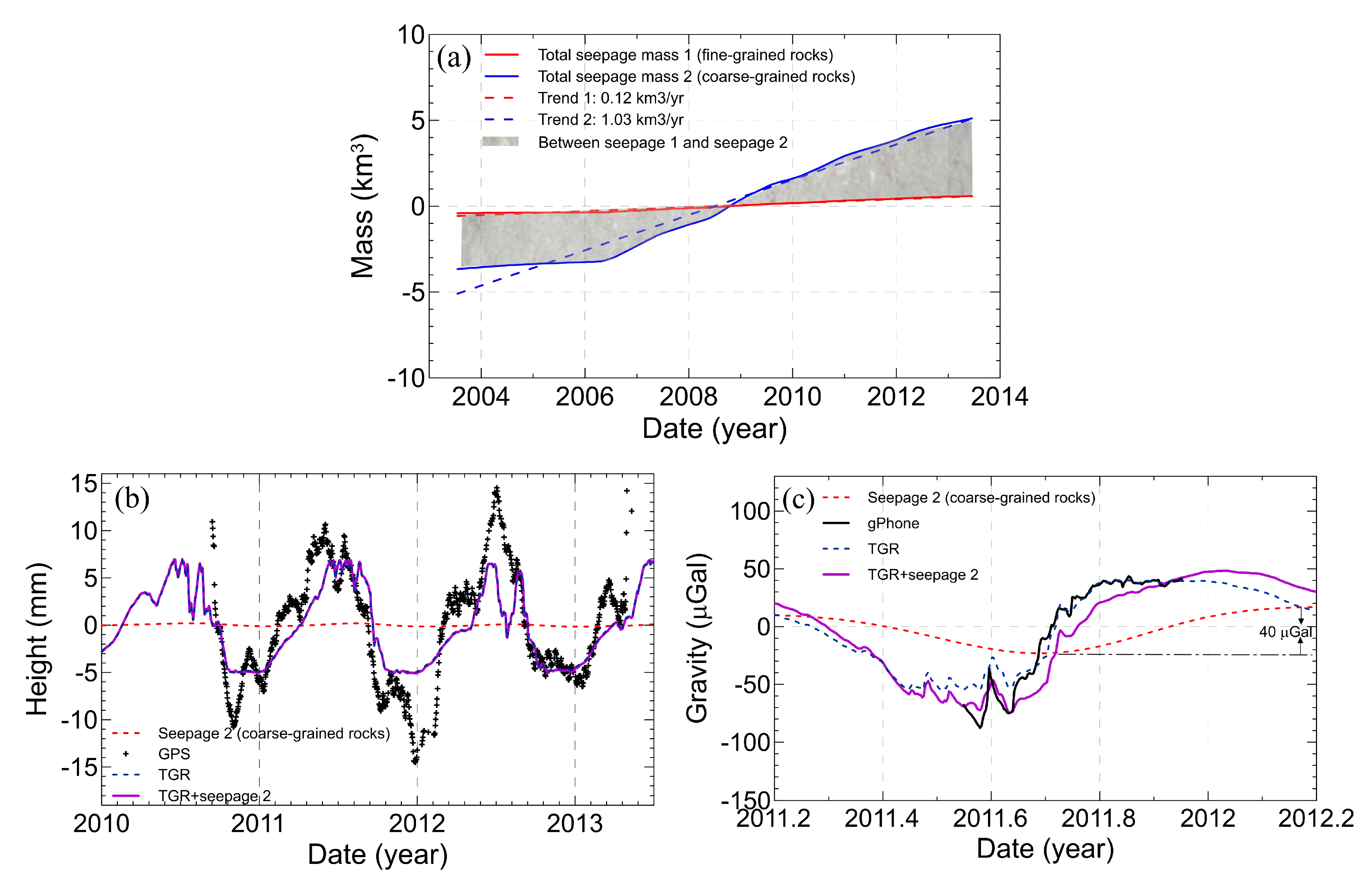
4.4. Reservoir Leakage Due to Three Gorges Reservoir Filling
5. Discussion
5.1. Effects of Small-Scale Mass Change on GRACE Estimates
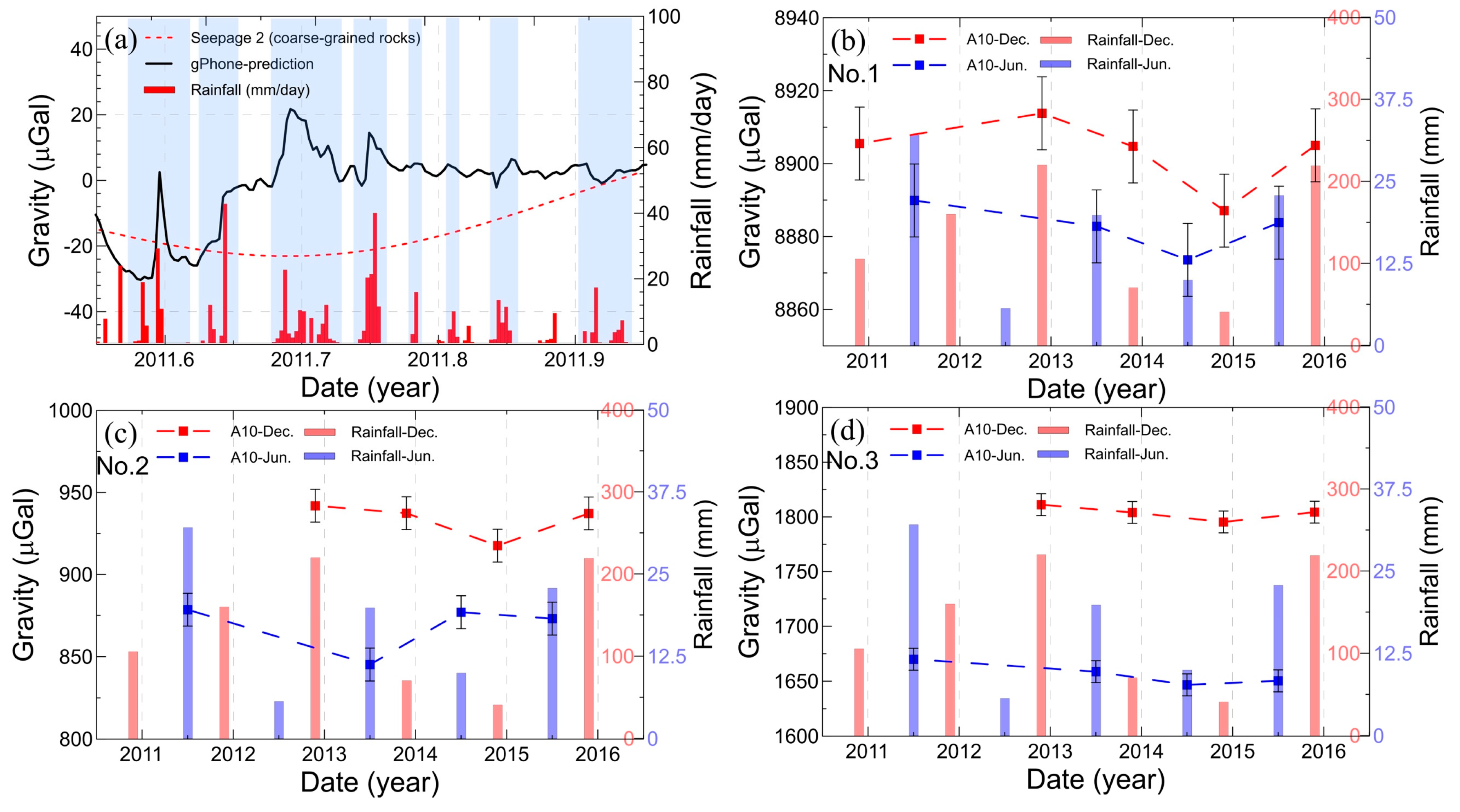
5.2. Short- and Long-Term Surface Gravity Changes
5.3. Contributions of Other Anthropogenic Reservoirs to the GRACE Signal
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Reager, J.T.; Thomas, B.F.; Famiglietti, J.S. River basin flood potential inferred using GRACE gravity observations at several months lead time. Nat. Geosci. 2014, 7, 588–592. [Google Scholar] [CrossRef]
- Velicogna, I.; Sutterley, T.C.; van den Broeke, M.R. Regional acceleration in ice mass loss from Greenland and Antarctica using GRACE time-variable gravity data. J. Geophys. Res. Space Phys. 2014, 41, 8130–8137. [Google Scholar] [CrossRef]
- Yi, S.; Sun, W. Evaluation of glacier changes in high-mountain Asia based on 10 year GRACE RL05 models. J. Geophys. Res. 2014, 119, 2504–2517. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Zhong, M.; Lemoine, J.M.; Biancale, R.; Hsu, H.T.; Xia, J. Evaluation of groundwater depletion in North China using the Gravity Recovery and Climate Experiment (GRACE) data and ground-based measurements. Water Resour. Res. 2013, 49, 2110–2118. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Longuevergne, L.; Long, D. Ground referencing GRACE satellite estimates of groundwater storage changes in the California Central Valley, USA. Water Resour. Res. 2012, 48, W04520. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33, L08402. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Chao, B.F.; Lu, Y.; Hsu, H.T. An effective filtering for GRACE time-variable gravity: Fan filter. Geophys. Res. Lett. 2009, 36, L17311. [Google Scholar] [CrossRef]
- Song, C.; Ke, L.; Huang, B.; Richards, K.S. Can mountain glacier melting explains the grace-observed mass loss in the southeast Tibetan plateau: From a climate perspective? Glob. Planet. Chang. 2015, 124, 1–9. [Google Scholar] [CrossRef]
- Landerer, F.; Swenson, S. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48, W04531. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Global analysis of approaches for deriving total water storage changes from GRACE satellites. Water Resour. Res. 2015, 51, 2574–2594. [Google Scholar] [CrossRef]
- Longuevergne, L.; Wilson, C.R.; Scanlon, B.R.; Cretaux, J.F. GRACE water storage estimates for the Middle East and other regions with significant reservoir and lake storage. Hydrol. Earth Syst. Sci. 2013, 17, 4817–4830. [Google Scholar] [CrossRef]
- Klees, R.; Zapreeva, E.A.; Winsemius, H.C.; Savenije, H.H.G. The bias in GRACE estimates of continental water storage variations. Hydrol. Earth Syst. Sci. 2007, 11, 1227–1241. [Google Scholar] [CrossRef]
- Longuevergne, L.; Scanlon, B.R.; Wilson, C.R. GRACE Hydrological estimates for small basins: Evaluating processing approaches on the High Plains Aquifer, USA. Water Resour. Res. 2010, 46, W11517. [Google Scholar] [CrossRef]
- Vishwakarma, B.D.; Horwath, M.; Devaraju, B.; Groh, A.; Sneeuw, N. A data-driven approach for repairing the hydrological catchment signal damage due to filtering of GRACE products. Water Resour. Res. 2017, 53, 9824–9844. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Monitoring the water balance of Lake Victoria, East Africa, from space. J. Hydrol. 2009, 370, 163–176. [Google Scholar] [CrossRef]
- Becker, M.; LLovel, W.; Cazenave, A.; Güntner, A.; Cretaux, J.F. Recent hydrological behavior of the East African great lakes region inferred from GRACE, satellite altimetry and rainfall observations. C. R. Geosci. 2010, 342, 223–233. [Google Scholar] [CrossRef]
- Wang, Q.; Yi, S.; Sun, W. The changing pattern of lake and its con- tribution to increased mass in the Tibetan Plateau derived from GRACE and ICESat data. Geophys. J. Int. 2016, 207, 528–541. [Google Scholar] [CrossRef]
- Wang, L.; Chen, C.; Thomas, M.; Kaban, M.K.; Güntner, A.; Du, J. Increased water storage of Lake Qinghai during 2004–2012 from GRACE data, hydrological models, radar altimetry and in situ measurements. Geophys. J. Int. 2018, 212, 679–693. [Google Scholar] [CrossRef]
- Boy, J.P.; Chao, B.F. Time-variable gravity signal during the water impoundment of China’s Three-Gorges Reservoir. Geophys. Res. Lett. 2002, 29, 2200. [Google Scholar] [CrossRef]
- Wang, X.; de Linage, C.; Famiglietti, J.; Zender, C.S. Gravity Recovery and Climate Experiment (GRACE) detection of water storage changes in the Three Gorges Reservoir of China and comparison with in situ measurements. Water Resour. Res. 2011, 47, W12502. [Google Scholar] [CrossRef]
- Wang, L.; Chen, C.; Zou, R.; Du, J. Surface gravity and deformation effects of water storage changes in China’s Three Gorges Reservoir constrained by modeled results and in situ measurements. J. Appl. Geophys. 2014, 108, 25–34. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of GRACE and ocean model output. J. Geophys. Res. 2008, 113, B08410. [Google Scholar] [CrossRef]
- Geruo, A.; Wahr, J.; Zhong, S. Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: An application to Glacial Isostatic Adjustment in Antarctica and Canada. Geophys. J. Int. 2013, 192, 557–572. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Joodaki, G.; Wahr, J.; Swenson, S. Estimating the human contribution to groundwater depletion in the Middle East, from GRACE data, land surface models, and well observations. Water Resour. Res. 2014, 50, 2679–2692. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Döll, P.; Kaspar, F.; Lehner, B. A global hydrological model for deriving water availability indicators: Model tuning and validation. J. Hydrol. 2013, 270, 105–134. [Google Scholar] [CrossRef]
- Oleson, K.W.; Lawrence, D.M.; Gordon, B.; Flanner, M.G.; Kluzek, E.; Peter, J.; Levis, S.; Swenson, S.C.; Thornton, E.; Feddema, J.; et al. Technical Description of Version 4.5 of the Community Land Model (CLM); NCAR Tech. Note NCAR/TN-5031STR; National Center for Atmospheric Research: Boulder, CO, USA, 2010; 434p. [Google Scholar]
- Rodriguez, E.; Morris, C.S.; Belz, J.E.; Chapin, E.C.; Martin, J.M.; Daffer, W.; Hensley, S. An Assessment of the SRTM Topographic Products; Technical Report JPL D-31639; Jet Propulsion Laboratory: Pasadena, CA, USA, 2005; 143p.
- Wang, Y.; Liao, M.; Sun, G.; Gong, J. Analysis of the water volume, length, total area and inundated area of the Three Gorges Reservoir, China using the SRTM DEM data. Int. J. Remote Sens. 2005, 26, 4001–4012. [Google Scholar] [CrossRef]
- Wang, X.W.; Chen, Y.; Song, L.; Chen, X.; Xie, H.; Liu, L. Analysis of lengths, water areas and volumes of the Three Gorges Reservoir at different water levels using Landsat images and SRTM DEM data. Q. Int. 2013, 304, 115–125. [Google Scholar] [CrossRef]
- Wang, H.F.; Anderson, M.P. Groundwater Modelling with Finite Difference and Finite Element Methods; Elsevier Publishing: Amsterdam, The Netherlands, 1982; pp. 1–137. [Google Scholar]
- Freeze, A.; Cherry, J. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979; 604p. [Google Scholar]
- Jentzsch, G. Earth Tides and Ocean Tidal Loading, Tidal Phenomena; Springer: Berlin/Heidelberg, Germany, 1997; Volume 66, pp. 145–171. [Google Scholar]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Methods for inferring regional surface-mass anomalies from Gravity Recovery and Climate Experiment (GRACE) measurements of time-variable gravity. J. Geophys. Res. 2002, 107, 2193. [Google Scholar] [CrossRef]
- Wahr, J.; Smeed, D.A.; Leuliette, E.; Swenson, S. Seasonal variability of the Red Sea, from satellite gravity, radar altimetry, and in situ observations. J. Geophys. Res. 2014, 119, 5091–5104. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Institute of China Geological Enviornment Monitoring. China Geological Environment Monitoring: Groundwater Yearbook; Vastplain House: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Ahmed, M.; Sultan, M.; Yan, E.; Wahr, J. Assessing and improving land surface model outputs over Africa using GRACE, field, and remote sensing data. Surv. Geophys. 2016, 37, 529–556. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models, part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Zhang, L.; Dobslaw, H.; Stacke, T.; Güntner, A.; Dill, R.; Thomas, M. Validation of terrestrial water storage variations as simulated by different global numerical models with GRACE satellite observations. Hydrol. Earth Syst. Sci. 2017, 21, 821–837. [Google Scholar] [CrossRef]
- Hunger, M.; Döll, P. Value of river discharge data for global-scale hydrological modeling. Hydrol. Earth Syst. Sci. 2008, 12, 841–861. [Google Scholar] [CrossRef]
- Ministry of Water Resources of China (MWR). China Water Resources Bulletin; MWR: Beijing, China, 2014. [Google Scholar]
| Correlation Coefficients with In-Situ (with 95% Confidence Bounds) | NSE with In-Situ | Trend (cm/Year) | Annual Amplitude (cm) | Annual Phase (Year) | |
|---|---|---|---|---|---|
| GRACE | 0.75 | 0.55 | 0.37 | 4.07 | 0.62 |
| GLDAS/Noah | 0.66 | 0.35 | 0.03 | 1.89 | 0.63 |
| GLDAS/VIC | 0.50 | 0.24 | −0.04 | 1.28 | 0.73 |
| GLDAS/Mosaic | 0.51 | 0.22 | −0.40 | 2.58 | 0.65 |
| WGHM | 0.85 | 0.64 | 0.00 | 3.94 | 0.62 |
| CLM4.5 | 0.73 | 0.52 | 0.14 | 5.18 | 0.60 |
| Reservoir_Name | Lat. (°) | Long. (°) | Start_Volume (km3) | Final_Volume (km3) | Increase of_Volume (km3) | Start T_Start (year) | Finish T_End (year) | Kernel Weight |
|---|---|---|---|---|---|---|---|---|
| Yinzidu | 28.59 | 106.36 | 0.21 | 0.53 | 0.32 | 2001 | 2003 | 0.6 |
| Hanpingzui | 32.91 | 104.75 | 0 | 0.51 | 0.51 | 2002 | 2004 | 0.2 |
| Jiangkou | 29.24 | 107.88 | 0 | 0.51 | 0.51 | 2002 | 2004 | 1.0 |
| Hongjiadu | 26.92 | 105.78 | 1.59 | 4.95 | 3.36 | 2001 | 2005 | 0.2 |
| Sanbanxi | 26.60 | 109.05 | 3.66 | 4.09 | 0.43 | 2005 | 2006 | 0.2 |
| Zipingpu | 31.02 | 103.56 | 0.22 | 1.11 | 0.89 | 2005 | 2006 | 0.2 |
| Pengshui | 29.29 | 108.15 | 0.93 | 1.44 | 0.51 | 2006 | 2007 | 1.0 |
| Zaoshi | 29.66 | 111.23 | 0.66 | 1.44 | 0.78 | 2004 | 2007 | 0.6 |
| Shuibuya | 30.44 | 110.33 | 1.93 | 4.58 | 2.65 | 2007 | 2009 | 1.0 |
| Danjiangkou | 32.70 | 111.54 | 17.50 | 29.05 | 11.55 | 2005 | 2009 | 0.5 |
| Goupintan | 27.37 | 107.63 | 1.41 | 5.56 | 4.15 | 2004 | 2011 | 0.4 |
| Silin | 27.93 | 108.25 | 0.88 | 1.65 | 0.77 | 2009 | 2012 | 0.6 |
| Xiludu | 28.29 | 103.64 | 6.34 | 12.91 | 6.57 | 2007 | 2013 | 0.1 |
| The total mass # | 12.78 km3 | |||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Kaban, M.K.; Thomas, M.; Chen, C.; Ma, X. The Challenge of Spatial Resolutions for GRACE-Based Estimates Volume Changes of Larger Man-Made Lake: The Case of China’s Three Gorges Reservoir in the Yangtze River. Remote Sens. 2019, 11, 99. https://doi.org/10.3390/rs11010099
Wang L, Kaban MK, Thomas M, Chen C, Ma X. The Challenge of Spatial Resolutions for GRACE-Based Estimates Volume Changes of Larger Man-Made Lake: The Case of China’s Three Gorges Reservoir in the Yangtze River. Remote Sensing. 2019; 11(1):99. https://doi.org/10.3390/rs11010099
Chicago/Turabian StyleWang, Linsong, Mikhail K. Kaban, Maik Thomas, Chao Chen, and Xian Ma. 2019. "The Challenge of Spatial Resolutions for GRACE-Based Estimates Volume Changes of Larger Man-Made Lake: The Case of China’s Three Gorges Reservoir in the Yangtze River" Remote Sensing 11, no. 1: 99. https://doi.org/10.3390/rs11010099
APA StyleWang, L., Kaban, M. K., Thomas, M., Chen, C., & Ma, X. (2019). The Challenge of Spatial Resolutions for GRACE-Based Estimates Volume Changes of Larger Man-Made Lake: The Case of China’s Three Gorges Reservoir in the Yangtze River. Remote Sensing, 11(1), 99. https://doi.org/10.3390/rs11010099