UAV Remote Sensing for Biodiversity Monitoring: Are Forest Canopy Gaps Good Covariates?
Abstract
1. Introduction
2. Materials and Methods
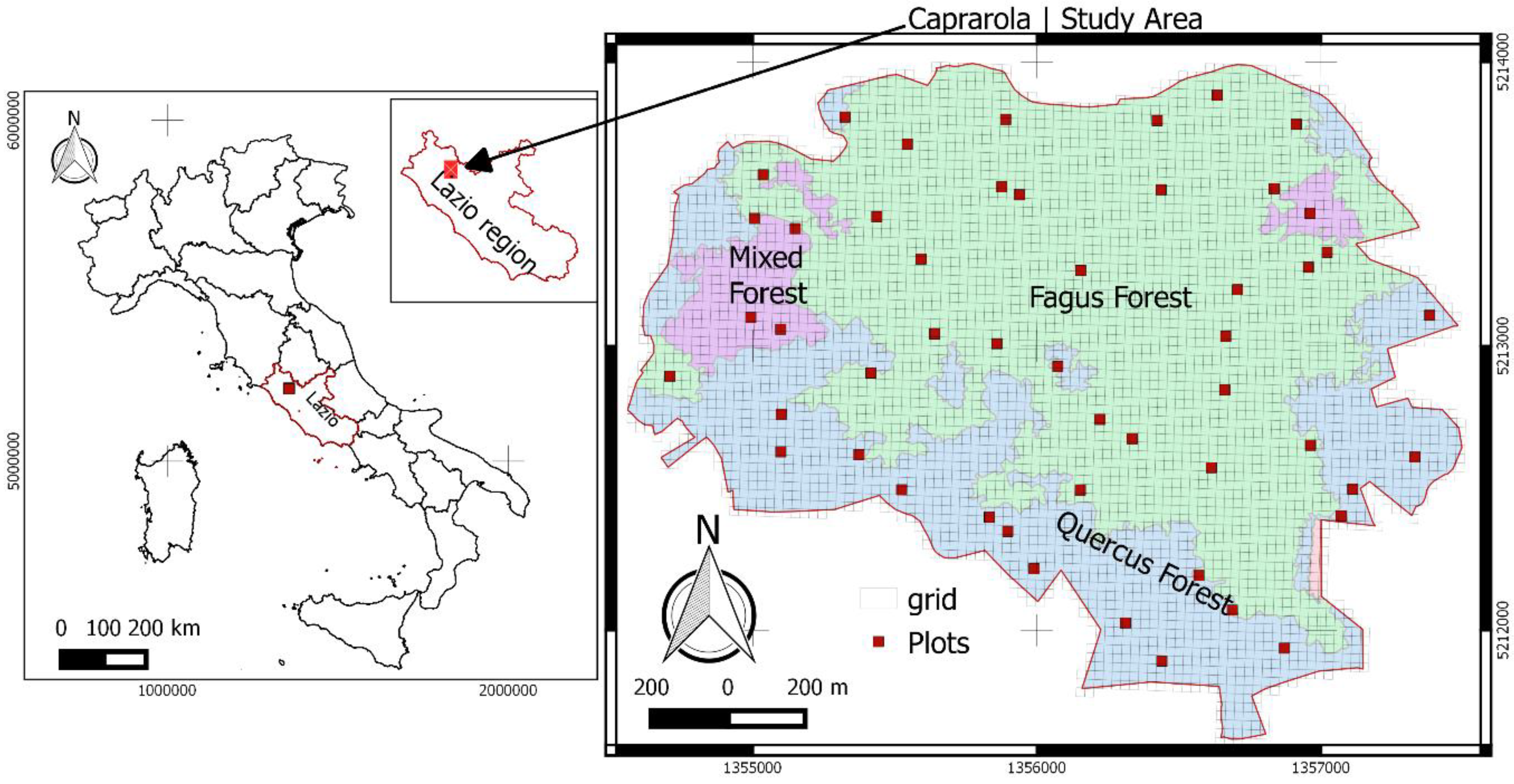
2.1. Study Site
2.2. Field Data Processing
2.3. UAV Data
2.4. Methods
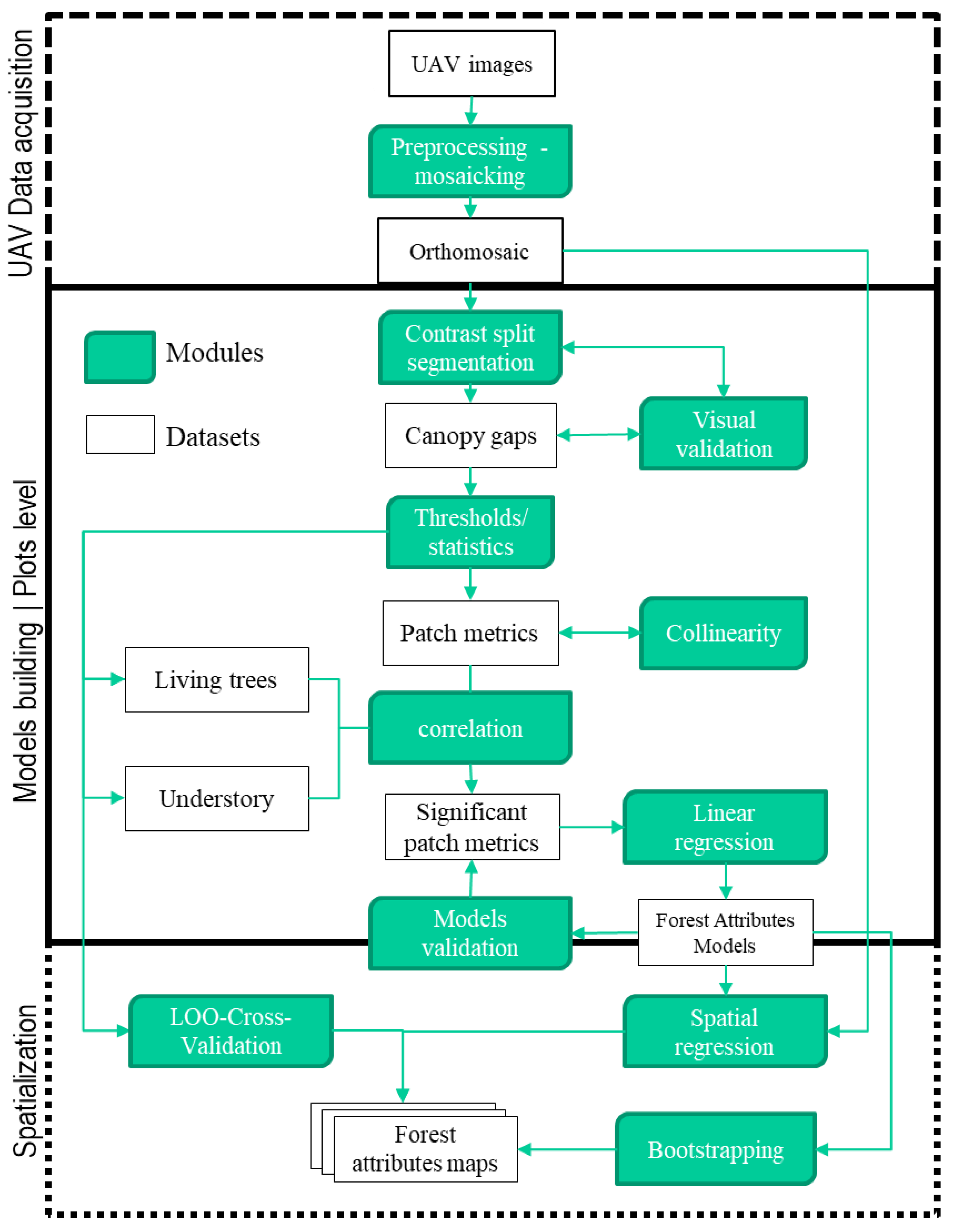
2.4.1. Image Processing and Variable Selection
2.4.2. Statistical Analysis
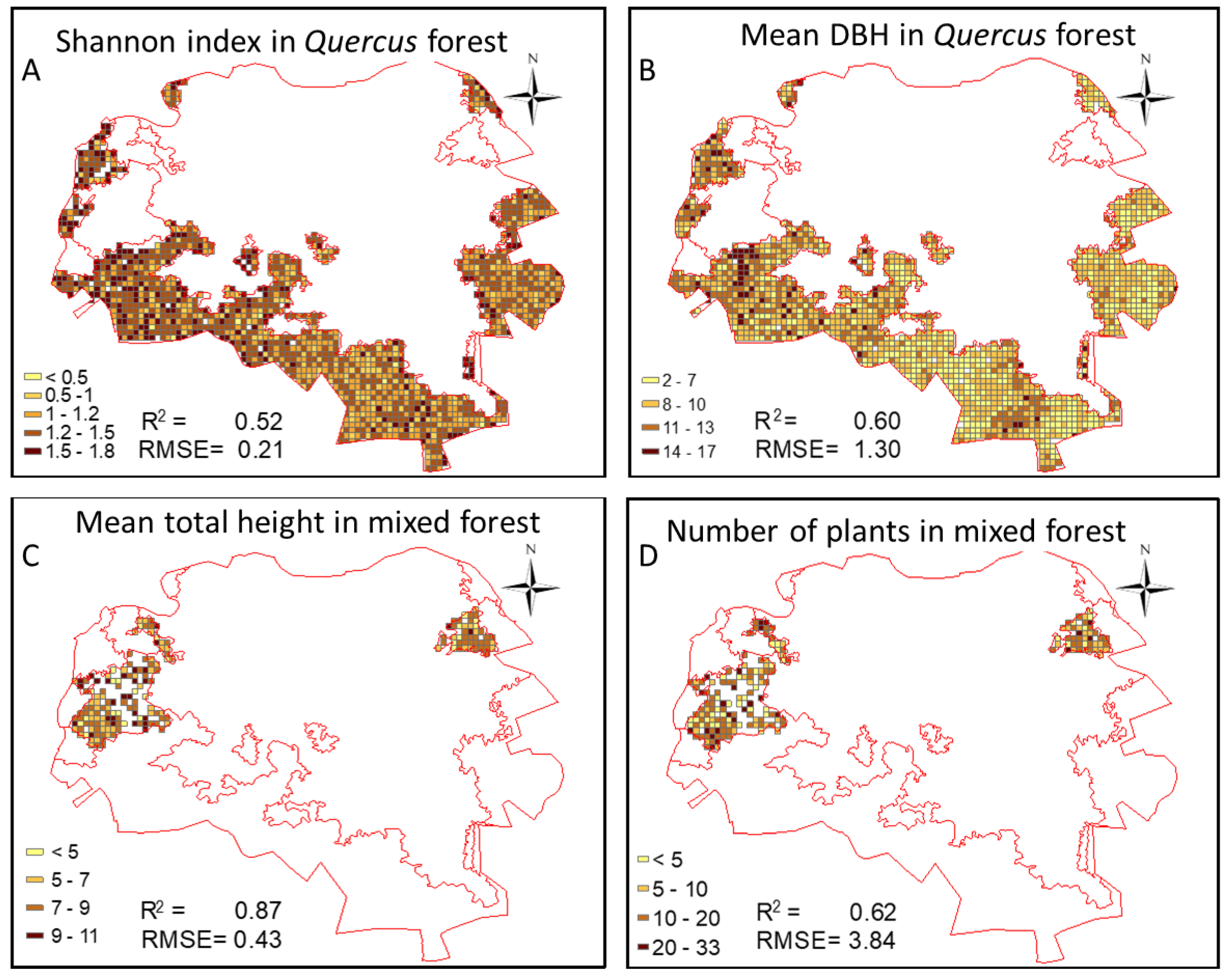
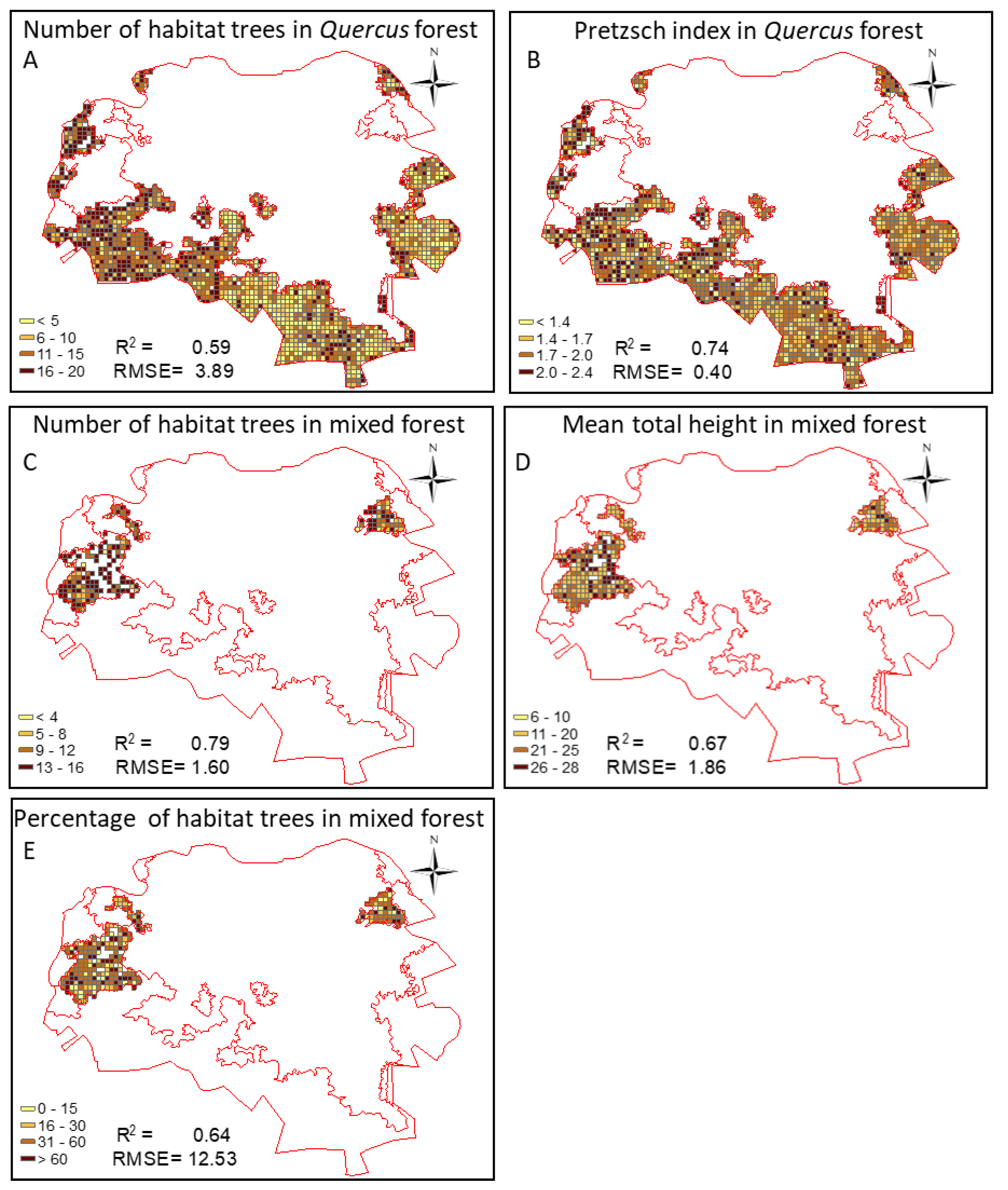
3. Results
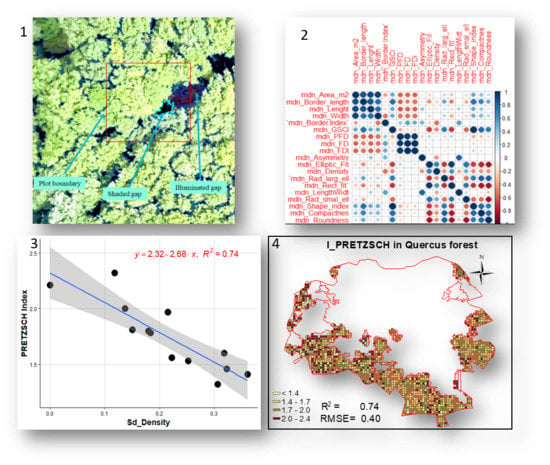
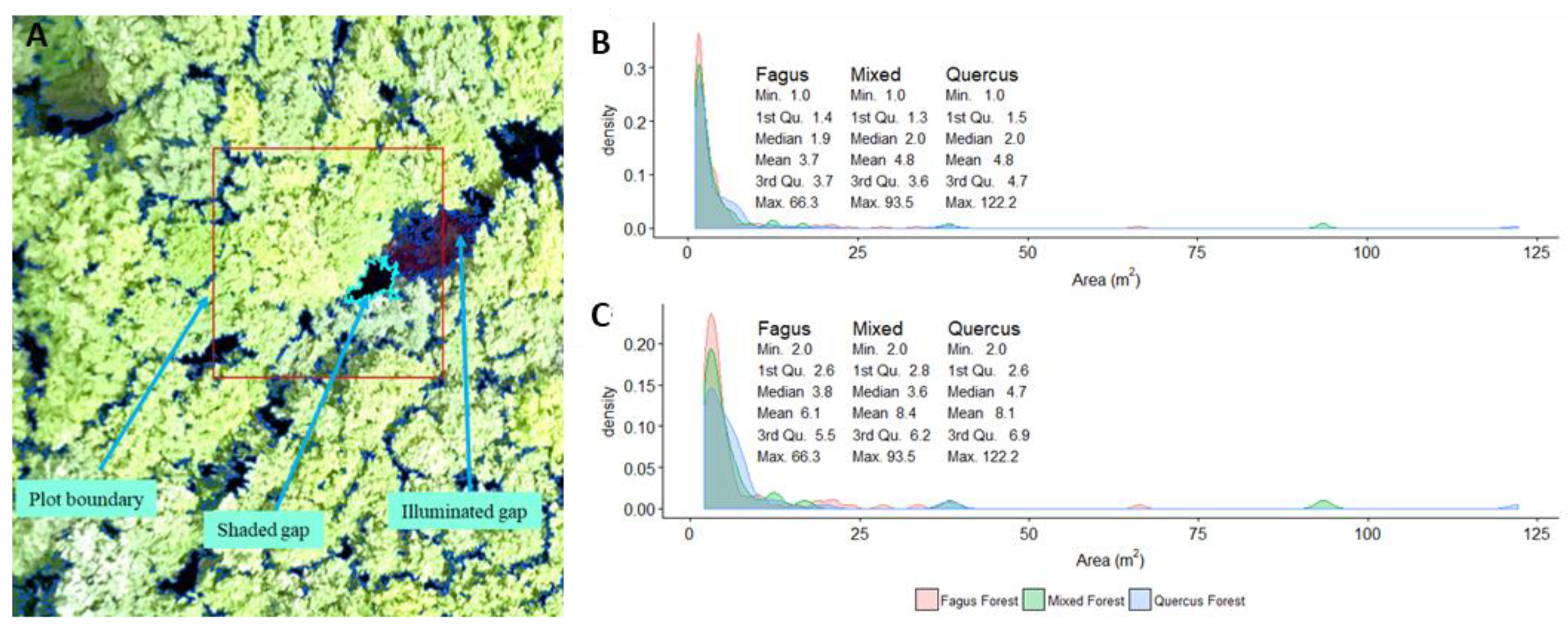
3.1. Canopy Gaps Mapping
3.2. Correlation between Gap Metrics and Understory Variables
3.3. Correlations between Gap Metrics and Living Tree Variables
3.4. Quality Assessment
4. Discussion
4.1. Mapping Forest Canopy Gaps
4.2. Modeling Understory Variables through Canopy Gaps Covariates
4.3. Modeling Living Trees Biodiversity through Canopy Gaps Covariates
4.4. Comparison with Other Studies and Implications
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Patch Metric | Formula | Values Range | Description |
|---|---|---|---|
| Border length () | [0, ∞) | Is basically the perimeter of the gap | |
| Length () | [0, ∞) | is the total number of pixels contained in the patch v is the length-width ratio of an image object v | |
| Length/Width () | - | [0, ∞) | The length-to-width ratio of an image object |
| Width () | [0, ∞) | The width of an image object is calculated using the length-to-width ratio | |
| Asymmetry | - | [0,1] | The Asymmetry feature describes the relative length of an image object, compared to a regular polygon. An ellipse is approximated around a given image object, which can be expressed by the ratio of the lengths of its minor and the major axes. The feature value increases with this asymmetry |
| Border Index | [1, ∞) 1 = ideal | The Border Index feature describes how jagged an image object is; the more jagged, the higher its border index. This feature is similar to the Shape Index feature, but the Border Index feature uses a rectangular approximation instead of a square. The smallest rectangle enclosing the image object is created, and the border index is calculated as the ratio between the border lengths of the image object and the smallest enclosing rectangle | |
| Compactness | - | [0, ∞) 1 = ideal | The Compactness feature describes how compact an image object is. It is similar to Border Index, but is based on area. However, the more compact an image object is, the smaller its border appears. The compactness of an image object is the product of the length and the width, divided by the number of pixels |
| Density | - | [0, depending on shape of image object] | The Density feature describes the distribution in space of the pixels of an image object. In eCognition Developer 9.0, the most “dense” shape is a square; the more an object is shaped like a filament, the lower its density. The density is calculated by the number of pixels forming the image object divided by its approximated radius, based on the covariance matrix |
| Elliptic Fit | - | [0,1]; 1 = complete fitting, 0 = <50% fit. | The Elliptic Fit feature describes how well an image object fits into an ellipse of similar size and proportions. While 0 indicates no fit, 1 indicates a perfect fit. The calculation is based on an ellipse with the same area as the selected image object. The proportions of the ellipse are equal to the length to the width of the image object. The area of the image object outside the ellipse is compared with the area inside the ellipse that is not filled by the image object |
| Radius of Largest Enclosed Ellipse () | - | [0, ∞) | The Radius of Largest Enclosed Ellipse feature describes how similar an image object is to an ellipse. The calculation uses an ellipse with the same area as the object and is based on the covariance matrix. This ellipse is scaled down until it is totally enclosed by the image object. The ratio of the radius of this largest enclosed ellipse to the radius of the original ellipse is returned as a feature value |
| Radius of Smallest Enclosing Ellipse () | - | [0, ∞) | The Radius of Smallest Enclosing Ellipse feature describes how much the shape of an image object is similar to an ellipse. The calculation is based on an ellipse with the same area as the image object and based on the covariance matrix. This ellipse is enlarged until it encloses the image object in total. The ratio of the radius of this smallest enclosing ellipse to the radius of the original ellipse is returned as a feature value |
| Rectangular Fit | - | [0,1] ; where 1 is a perfect rectangle. | The Rectangular Fit feature describes how well an image object fits into a rectangle of similar size and proportions. While 0 indicates no fit, 1 indicates for a complete fitting image object. The calculation is based on a rectangle with the same area as the image object. The proportions of the rectangle are equal to the proportions of the length to width of the image object. The area of the image object outside the rectangle is compared with the area inside the rectangle |
| Roundness | [0, ∞); 0 = ideal | The Roundness feature describes how similar an image object is to an ellipse. It is calculated by the difference of the enclosing ellipse and the enclosed ellipse | |
| Shape Index | [1,∞) ; 1 = ideal | The Shape index describes the smoothness of an image object border. The smoother the border of an image object is, the lower its shape index | |
| Gap shape complexity index (GSCI) | [1,∞) ; 1 = perfect circle | It is the ratio of a gap’s perimeter to the perimeter of a circular gap of the same area | |
| Patch fractal dimension (PFD) | - | - | |
| Fractal dimension (FD) | - | - | |
| fractal dimension index (FDI) | - | - |
Appendix B. Correlations with understory data
| N_PLANTS | N_SPECIES | I_SHANNON | I_PIELOU | MEAN_DBH | MEAN_HTOT | V_TOT | G_TOT | |
|---|---|---|---|---|---|---|---|---|
| Mdn_GSCI | Sd_Rect.fit | Sd_Rect.fit | Sd_Density | Avg_Rect.fit | Mdn_B. Index | Mdn_Asy | Avg_Asy | |
| Threshold | 1 m2 | 2 m2 | 2 m2 | 1 m2 | 1 m2 | 2 m2 | 1 m2 | 1 m2 |
| Pearson | 0.73 | −0.66 | −0.75 | −0.64 | 0.79 | −0.58 | −0.64 | −0.57 |
| Spearman | 0.70 | −0.73 | −0.88 | −0.68 | 0.75 | −0.67 | −0.57 | −0.55 |
| N_PLANTS | N_SPECIES | I_SHANNON | I_PIELOU | MEAN_DBH | MEAN_HTOT | G_TOT | V_TOT | |
|---|---|---|---|---|---|---|---|---|
| Avg_Round. | Mdn_RSE | Mdn_RSE | Avg_RLE | Sum_width | Avg_Asym. | Sd_Asym. | Avg_Comp. | |
| Threshold | 2 m2 | 1 m2 | 1 m2 | 2 m2 | 2 m2 | 2 m2 | 2 m2 | 2 m2 |
| Pearson | −0.81 | 0.73 | 0.69 | 0.71 | −0.78 | 0.94 | 0.72 | −0.67 |
| Spearman | −0.83 | 0.70 | 0.70 | 0.75 | −0.70 | 0.92 | 0.72 | −0.77 |
| N_SPECIES | I_SHANNON | I_PIELOU | MEAN_HTOT | |
|---|---|---|---|---|
| Cv_Round | Sd_Round | Mdn_PFD | Cv_Lenght | |
| Threshold | 1 m2 | 1 m2 | 1 m2 | 2 m2 |
| Pearson | −0.43 | 0.50 | 0.74 | 0.52 |
| Spearman | −0.45 | 0.56 | 0.87 | 0.57 |
Appendix C. Correlations with living trees data
| N_SPECIES | I_SHANNON | I_MARGALEF | I_PRETZSCH | MEAN_DBH | MEAN_HTOT | HAB | %HAB | |
|---|---|---|---|---|---|---|---|---|
| Sd_rect_fit | Cv_Density | Sd_rect_fit | Sd_Density | Sum_Rect.fit | Mdn_Rect.fit | Sum_Rect.fit | Sum_RLE | |
| Threshold | 2 m2 | 2 m2 | 2 m2 | 2 m2 | 1 m2 | 1 m2 | 2 m2 | 2 m2 |
| Pearson | −0.68 | −0.64 | −0.71 | −0.87 | 0.61 | 0.59 | −0.79 | −0.71 |
| Spearman | −0.72 | −0.61 | −0.74 | −0.90 | 0.70 | 0.56 | −0.70 | −0.64 |
| MEAN_DBH | MEAN_HTOT | HAB | %HAB | |
|---|---|---|---|---|
| Avg_Round. | Sd_Asym. | Cv_Length | Avg_RSE | |
| Threshold | 2 m2 | 1 m2 | 2 m2 | 1 m2 |
| Pearson | 0.74 | −0.84 | −0.90 | −0.83 |
| Spearman | 0.82 | −0.95 | −0.92 | −0.92 |
| 2m | HAB | %HAB |
|---|---|---|
| Cv_PFD | Avg_RSE | |
| Pearson | 0.43 | −0.38 |
| Spearman | 0.50 | −0.39 |
References
- Muscolo, A.; Bagnato, S.; Sidari, M.; Mercurio, R. A review of the roles of forest canopy gaps. J. For. Res. 2014, 25, 725–736. [Google Scholar] [CrossRef]
- Karsten, R.J.; Jovanovic, M.; Meilby, H.; Perales, E.; Reynel, C. Regeneration in canopy gaps of tierra-firme forest in the Peruvian Amazon: Comparing reduced impact logging and natural, unmanaged forests. For. Ecol. Manag. 2013, 310, 663–671. [Google Scholar] [CrossRef]
- Stan, A.B.; Daniels, L.D. Growth releases across a natural canopy gap-forest gradient in old-growth forests. For. Ecol. Manag. 2014, 313, 98–103. [Google Scholar] [CrossRef]
- Feldmann, E.; Drößler, L.; Hauck, M.; Kucbel, S.; Pichler, V.; Leuschner, C. Canopy gap dynamics and tree understory release in a virgin beech forest, Slovakian Carpathians. For. Ecol. Manag. 2018, 415–416, 38–46. [Google Scholar] [CrossRef]
- Amir, A.A. Canopy gaps and the natural regeneration of Matang mangroves. For. Ecol. Manag. 2012, 269, 60–67. [Google Scholar] [CrossRef]
- Muscolo, A.; Settineri, G.; Bagnato, S.; Mercurio, R.; Sidari, M. Use of canopy gap openings to restore coniferous stands in Mediterranean environment. iFor. Biogeosci. For. 2017, 10, 322–327. [Google Scholar] [CrossRef]
- Čater, M.; Diaci, J.; Roženbergar, D. Gap size and position influence variable response of Fagus sylvatica L. and Abies alba Mill. For. Ecol. Manag. 2014, 325, 128–135. [Google Scholar] [CrossRef]
- Getzin, S.; Nuske, R.S.; Wiegand, K. Using unmanned aerial vehicles (UAV) to quantify spatial gap patterns in forests. Remote Sens. 2014, 6, 6988–7004. [Google Scholar] [CrossRef]
- Nagendra, H. Using remote sensing to assess biodiversity. Int. J. Remote Sens. 2001, 22, 2377–2400. [Google Scholar] [CrossRef]
- Tang, L.; Shao, G. Drone remote sensing for forestry research and practices. J. For. Res. 2015, 26, 791–797. [Google Scholar] [CrossRef]
- Giannetti, F.; Chirici, G.; Gobakken, T.; Naesset, E.; Travaglini, D.; Puliti, S. A new set of DTM-independent metrics for forest growing stock prediction using UAV photogrammetric data. Remote Sens. Environ. 2018, 213, 195–205. [Google Scholar] [CrossRef]
- Torresan, C.; Berton, A.; Carotenuto, F.; Di Gennaro, S.F.; Gioli, B.; Matese, A.; Miglietta, F.; Vagnoli, C.; Zaldei, A.; Wallace, L. Forestry applications of UAVs in Europe: a review. Int. J. Remote Sens. 2017, 38, 2427–2447. [Google Scholar] [CrossRef]
- Puliti, S.; Olerka, H.; Gobakken, T.; Næsset, E. Inventory of Small Forest Areas Using an Unmanned Aerial System. Remote Sens. 2015, 7, 9632–9654. [Google Scholar] [CrossRef]
- Dandois, J.P.; Ellis, E.C. High spatial resolution three-dimensional mapping of vegetation spectral dynamics using computer vision. Remote Sens. Environ. 2013, 136, 259–276. [Google Scholar] [CrossRef]
- Fardusi, M.J.; Chianucci, F.; Barbati, A. Concept to practices of geospatial information tools to assist forest management & planning under precision forestry framework: A review. Ann. Silvic. Res. 2017, 41, 3–14. [Google Scholar] [CrossRef]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- Zahawi, R.A.; Dandois, J.P.; Holl, K.D.; Nadwodny, D.; Reid, J.L.; Ellis, E.C. Using lightweight unmanned aerial vehicles to monitor tropical forest recovery. Biol. Conserv. 2015, 186, 287–295. [Google Scholar] [CrossRef]
- Alonzo, M.; Andersen, H.E.; Morton, D.; Cook, B. Quantifying Boreal Forest Structure and Composition Using UAV Structure from Motion. Forests 2018, 9, 119. [Google Scholar] [CrossRef]
- Messinger, M.; Asner, G.P.; Silman, M. Rapid assessments of amazon forest structure and biomass using small unmanned aerial systems. Remote Sens. 2016, 8, 1–15. [Google Scholar] [CrossRef]
- Chianucci, F.; Disperati, L.; Guzzi, D.; Bianchini, D.; Nardino, V.; Lastri, C.; Rindinella, A.; Corona, P. Estimation of canopy attributes in beech forests using true colour digital images from a small fixed-wing UAV. Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 60–68. [Google Scholar] [CrossRef]
- Lisein, J.; Michez, A.; Claessens, H.; Lejeune, P. Discrimination of deciduous tree species from time series of unmanned aerial system imagery. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, J.R.K.; Nieberding, F.; Prinz, T.; Knoth, C. Analysis of unmanned aerial system-based CIR images in forestry-a new perspective to monitor pest infestation levels. Forests 2015, 6, 594–612. [Google Scholar] [CrossRef]
- Hall, R.J.; Castilla, G.; White, J.C.; Cooke, B.J.; Skakun, R.S. Remote sensing of forest pest damage: a review and lessons learned from a Canadian perspective. Can. Entomol. 2016, 148, S296–S356. [Google Scholar] [CrossRef]
- Michez, A.; Piégay, H.; Lisein, J.; Claessens, H.; Lejeune, P. Classification of riparian forest species and health condition using multi-temporal and hyperspatial imagery from unmanned aerial system. Environ. Monit. Assess. 2016, 188, 146. [Google Scholar] [CrossRef] [PubMed]
- Myers, D.; Ross, C.M.; Liu, B. A Review of Unmanned Aircraft System (UAS) Applications for Agriculture. 2015 ASABE Int. Meet. 2015, 1. [Google Scholar] [CrossRef]
- Lisein, J.; Linchant, J.; Lejeune, P.; Bouche, P.; Vermeulen, C. Aerial surveys using an Unmanned Aerial System (UAS): Comparison of different methods for estimating the surface area of sampling strips. Trop. Conserv. Sci. 2013, 6, 506–520. [Google Scholar] [CrossRef]
- Colomina, I.; Molina, P. Unmanned aerial systems for photogrammetry and remote sensing: A review. J. Photogramm. Remote Sens. 2014, 7, 9632–9654. [Google Scholar] [CrossRef]
- Sandbrook, C. The social implications of using drones for biodiversity conservation. Ambio 2015, 44, 636–647. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Hu, J.; Lian, J.; Fan, Z.; Ouyang, X.; Ye, W. Seeing the forest from drones: Testing the potential of lightweight drones as a tool for long-term forest monitoring. Biol. Conserv. 2016, 198, 60–69. [Google Scholar] [CrossRef]
- Anderson, K.; Gaston, K.J. Lightweight unmanned aerial vehicles will revolutionize spatial ecology. Front. Ecol. Environ. 2013, 11, 138–146. [Google Scholar] [CrossRef]
- Paneque-Gálvez, J.; McCall, M.K.; Napoletano, B.M.; Wich, S.A.; Koh, L.P. Small drones for community-based forest monitoring: An assessment of their feasibility and potential in tropical areas. Forests 2014, 5, 1481–1507. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Watson, C. An automated technique for generating georectified mosaics from ultra-high resolution Unmanned Aerial Vehicle (UAV) imagery, based on Structure from Motion (SFM) point clouds. Remote Sens. 2012, 4, 1392–1410. [Google Scholar] [CrossRef]
- Zielewska-Büttner, K.; Adler, P.; Ehmann, M.; Braunisch, V. Automated Detection of Forest Gaps in Spruce Dominated Stands using Canopy Height Models Derived from Stereo Aerial Imagery. Remote Sens. 2016, 8, 1–21. [Google Scholar] [CrossRef]
- Betts, H.D.; Brown, L.J.; Stewart, G.H. Forest canopy gap detection and characterisation by the use of high- resolution Digital Elevation Models. N. Z. J. Ecol. 2005, 29, 95–103. [Google Scholar]
- Seidel, D.; Ammer, C.; Puettmann, K. Describing forest canopy gaps efficiently, accurately, and objectively: New prospects through the use of terrestrial laser scanning. Agric. For. Meteorol. 2015, 213, 23–32. [Google Scholar] [CrossRef]
- Bonnet, S.; Gaulton, R.; Lehaire, F.; Lejeune, P. Canopy gap mapping from airborne laser scanning: An assessment of the positional and geometrical accuracy. Remote Sens. 2015, 7, 11267–11294. [Google Scholar] [CrossRef]
- Getzin, S.; Wiegand, K.; Schöning, I. Assessing biodiversity in forests using very high-resolution images and unmanned aerial vehicles. Methods Ecol. Evol. 2012, 3, 397–404. [Google Scholar] [CrossRef]
- Turner, D.; Lucieer, A.; Wallace, L. Direct georeferencing of ultrahigh-resolution UAV imagery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2738–2745. [Google Scholar] [CrossRef]
- Czapski, P.; Kacprzak, M.; Kotlarz, J.; Mrowiec, K.; Kubiak, K.; Tkaczyk, M. Preliminary analysis of the forest health state based on multispectral images acquired by Unmanned Aerial Vehicle. Folia For. Pol. 2015, 57, 138–144. [Google Scholar] [CrossRef]
- Scoppola, A.; Caporali, C. Mesophilous woods with Fagus sylvatica L. of Northern Latium (Tyrrenian Central Italy): Synecology and syntaxonomy. Plant Biosyst. 1998, 132, 151–168. [Google Scholar] [CrossRef]
- Winter, S.; Möller, G.C. Microhabitats in lowland beech forests as monitoring tool for nature conservation. For. Ecol. Manag. 2008, 255, 1251–1261. [Google Scholar] [CrossRef]
- Assmann, E. The Principles of Forest Yield Study; Pergamon Press: Oxford, UK, 1970. [Google Scholar]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Pielou, E.C. Ecological Diversity; Wiley: New York, NY, USA, 1975. [Google Scholar]
- Clifford, H.T.; Stephenson, W. An Introduction to Numerical Classification; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Agisoft PhotoScan User Manual: Professional Edition, Version 1.3. 2017. Available online: http://www.agisoft.com/pdf/photoscan-pro_1_3_en.pdf (accessed on 11 April 2017).
- Kachamba, D.; Ørka, O.H.; Gobakken, T.; Eid, T.; Mwase, W. Biomass Estimation Using 3D Data from Unmanned Aerial Vehicle Imagery in a Tropical Woodland. Remote Sens. 2016, 8, 968. [Google Scholar] [CrossRef]
- Lisein, J.; Pierrot-Deseilligny, M.; Bonnet, S.; Lejeune, P. A photogrammetric workflow for the creation of a forest canopy height model from small unmanned aerial system imagery. Forests 2013, 4, 922–944. [Google Scholar] [CrossRef]
- Puliti, S.; Gobakken, T.; Ørka, H.O.; Næsset, E. Assessing 3D point clouds from aerial photographs for species-specific forest inventories. Scand. J. For. Res. 2017, 32, 68–79. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Malenovsky, Z.; Turner, D.; Vopenka, P. Assessment of forest structure using two UAV techniques: A comparison of airborne laser scanning and structure from motion (SfM) point clouds. Forests 2016, 7, 1–16. [Google Scholar] [CrossRef]
- Dezso, B.; Fekete, I.; Gera, D.; Giachetta, R.; László, I.; Benczúr, A.; Dezs, B.; Fekete, I.; Gera, D.; Giachetta, R.; et al. Object-based image analysis in remote sensing applications using various segmentation techniques. Ann. Univ. Sci. Budapest. Sect. Comp. 2012, 37, 103–120. [Google Scholar]
- Trimble Germany GmbH. Trimble Segmentation Algorithms: 9.01. Trimble Germany GmbH: Munich, Germany, 2014. Available online: https://www.scribd.com/document/332173213/Reference-Book (accessed on 31 August 2018).
- Koukoulas, S.; Blackburn, G.A. Quantifying the spatial properties of forest canopy gaps using LiDAR imagery and GIS. Int. J. Remote Sens. 2004, 25, 3049–3072. [Google Scholar] [CrossRef]
- Moser, D.; Zechmeister, H.G.; Plutzar, C.; Sauberer, N.; Wrbka, T.; Grabherr, G. Landscape patch shape complexity as an effective measure for plant species richness in rural landscapes. Landsc. Ecol. 2002, 17, 657–669. [Google Scholar] [CrossRef]
- Eysenrode, D.S.; Bogaert, J.; Van Hecke, P.; Impens, I. Influence of tree-fall orientation on canopy gap shape in an Ecuadorian rain forest. J. Trop. Ecol. 1998, 14, 865–869. [Google Scholar] [CrossRef]
- Saura, S.; Carballal, P. Discrimination of native and exotic forest patterns through shape irregularity indices: An analysis in the landscapes of Galicia, Spain. Landsc. Ecol. 2004, 19, 647–662. [Google Scholar] [CrossRef]
- Busing, R.T. Canopy cover and tree regeneration in old-growth cove forests of the Appalachian Mountains. Vegetatio 1994, 115, 19–27. [Google Scholar]
- Main-Knorn, M.; Moisen, G.G.; Healey, S.P.; Keeton, W.S.; Freeman, E.A.; Hostert, P. Evaluating the remote sensing and inventory-based estimation of biomass in the western carpathians. Remote Sens. 2011, 3, 1427–1446. [Google Scholar] [CrossRef]
- Legendre, P.; Legendre, L. Development in Environmental Modelling: Numerical Ecology; Elsevier: Amsterdam, The Netherlands, 1983. [Google Scholar]
- James, G.; Witen, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning with Applications in R; Castilla, G., Fienberg, S., Olkin, I., Eds.; Springer: New York, NY, USA, 2013; ISBN 978-1-4614-7138-7. [Google Scholar]
- Hauke, J.; Kossowski, T. Comparison of values of Pearson’s and Spearman’s correlation coefficients on the same sets of data. Quaest. Geogr. 2011, 30, 87–93. [Google Scholar] [CrossRef]
- Møller, A.P.; Jennions, M.D. How much variance can be explained by ecologists and evolutionary biologists? Oecologia 2002, 132, 492–500. [Google Scholar] [CrossRef] [PubMed]
- Mura, M.; McRoberts, R.E.; Chirici, G.; Marchetti, M. Statistical inference for forest structural diversity indices using airborne laser scanning data and the k-Nearest Neighbors technique. Remote Sens. Environ. 2016, 186, 678–686. [Google Scholar] [CrossRef]
- Lyons, M.B.; Keith, D.A.; Phinn, S.R.; Mason, T.J.; Elith, J. A comparison of resampling methods for remote sensing classification and accuracy assessment. Remote Sens. Environ. 2018, 208, 145–153. [Google Scholar] [CrossRef]
- McRoberts, R.E.; Magnussen, S.; Tomppo, E.O.; Chirici, G. Parametric, bootstrap, and jackknife variance estimators for the k-Nearest Neighbors technique with illustrations using forest inventory and satellite image data. Remote Sens. Environ. 2011, 115, 3165–3174. [Google Scholar] [CrossRef]
- Rao, J.N.K. Jackknife and Bootstrap Methods for Small Area Estimation. 2007. Available online: https://ww2.amstat.org/sections/srms/Proceedings/y2007/Files/JSM2007-000358.pdf (accessed on 11 July 2018).
- Efron, B.; Tibshirani, R. Improvements on cross-validation: The 632 plus bootstrap method. J. Am. Stat. Assoc. 1997, 92, 548. [Google Scholar] [CrossRef]
- Boyd, D.S.; Hill, R.A.; Hopkinson, C.; Baker, T.R. Landscape-scale forest disturbance regimes in southern Peruvian. Ecol. Appl. 2013, 23, 1588–1602. [Google Scholar] [CrossRef] [PubMed]
- Senécal, J.F.; Doyon, F.; Messier, C. Tree death not resulting in gap creation: An investigation of canopy dynamics of northern temperate deciduous forests. Remote Sens. 2018, 10, 121. [Google Scholar] [CrossRef]
- Senécal, J.F.; Doyon, F.; Messier, C. Management implications of varying gap detection height thresholds and other canopy dynamics processes in temperate deciduous forests. For. Ecol. Manag. 2018, 410, 84–94. [Google Scholar] [CrossRef]
- Vepakomma, U.; St-Onge, B.; Kneeshaw, D. Spatially explicit characterization of boreal forest gap dynamics using multi-temporal lidar data. Remote Sens. Environ. 2008, 112, 2326–2340. [Google Scholar] [CrossRef]
- Schliemann, S.A.; Bockheim, J.G. Methods for studying treefall gaps: A review. For. Ecol. Manag. 2011, 261, 1143–1151. [Google Scholar] [CrossRef]
- Hobi, M.L.; Ginzler, C.; Commarmot, B.; Bugmann, H. Gap pattern of the largest primeval beech forest of Europe revealed by remote sensing. Ecosphere 2015, 6, 76. [Google Scholar] [CrossRef]
- Brokaw, N.V.L. The Definition of Treefall Gap and Its Effect on Measures of Forest Dynamics. Biotropica 1982, 14, 158. [Google Scholar] [CrossRef]
- White, J.C.; Tompalski, P.; Coops, N.C.; Wulder, M.A. Comparison of airborne laser scanning and digital stereo imagery for characterizing forest canopy gaps in coastal temperate rainforests. Remote Sens. Environ. 2018, 208, 1–14. [Google Scholar] [CrossRef]
- Kane, V.R.; Gersonde, R.F.; Lutz, J.A.; McGaughey, R.J.; Bakker, J.D.; Franklin, J.F. Patch dynamics and the development of structural and spatial heterogeneity in Pacific Northwest forests. Can. J. For. Res. 2011, 41, 2276–2291. [Google Scholar] [CrossRef]
- Asner, G.P.; Kellner, J.R.; Kennedy-Bowdoin, T.; Knapp, D.E.; Anderson, C.; Martin, R.E. Forest Canopy Gap Distributions in the Southern Peruvian Amazon. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Zielewska-Büttner, K.; Adler, P.; Petersen, M.; Braunisch, V. Parameters Influencing Forest Gap Detection Using Canopy Height Models Derived From Stereo Aerial Imagery. Publ. DGPF 2016, 25, 405–416. [Google Scholar]
- Perroy, R.L.; Sullivan, T.; Stephenson, N. Assessing the impacts of canopy openness and flight parameters on detecting a sub-canopy tropical invasive plant using a small unmanned aerial system. ISPRS J. Photogramm. Remote Sens. 2017, 125, 174–183. [Google Scholar] [CrossRef]
- Lombard, L.; Ismail, R.; Poona, N. Modelling forest canopy gaps using LiDAR-derived variables. Geocarto Int. 2017, 6049, 1–15. [Google Scholar] [CrossRef]
- Ma, L.; Zheng, G.; Wang, X.; Li, S.; Lin, Y.; Ju, W. Retrieving forest canopy clumping index using terrestrial laser scanning data. Remote Sens. Environ. 2018, 210, 452–472. [Google Scholar] [CrossRef]
- Barbati, A.; Chirici, G.; Corona, P.; Montaghi, A.; Travaglini, D. Area-based assessment of forest standing volume by field measurements and airborne laser scanner data. Int. J. Remote Sens. 2009, 30, 5177–5194. [Google Scholar] [CrossRef]
- Popma, J.; Bongers, F. The effect of canopy gaps on growth and morphology of seedlings of rain forest species. Oecologia 1988, 75, 625–632. [Google Scholar] [CrossRef] [PubMed]
- Garbarino, M.; Borgogno Mondino, E.; Lingua, E.; Nagel, T.A.; Dukic, V.; Govedar, Z.; Motta, R. Gap disturbances and regeneration patterns in a Bosnian old-growth forest: a multispectral remote sensing and ground-based approach. Ann. For. Sci. 2012, 69, 617–625. [Google Scholar] [CrossRef]
- Runkle, J.R. Patterns of Disturbance in Some Old-Growth Mesic Forests of Eastern North America. Ecology 1982, 63, 1533–1546. [Google Scholar] [CrossRef]
- Franklin, J.F.; Spies, T.A.; Pelt, R.V.; Carey, A.B.; Thornburgh, D.A.; Berg, D.R.; Lindenmayer, D.B.; Harmon, M.E.; Keeton, W.S.; Shaw, D.C.; Bible, K.; Chen, J. Disturbances and structural development of natural forest ecosystems with silvicultural implications, using Douglas-fir forests as an example. For. Ecol. Manag. 2002, 155, 399–423. [Google Scholar] [CrossRef]
- Larrieu, L.; Paillet, Y.; Winter, S.; Bütler, R.; Kraus, D.; Krumm, F.; Lachat, T.; Michel, A.K.; Regnery, B.; Vandekerkhove, K. Tree related microhabitats in temperate and Mediterranean European forests: A hierarchical typology for inventory standardization. Ecol. Indic. 2018, 84, 194–207. [Google Scholar] [CrossRef]
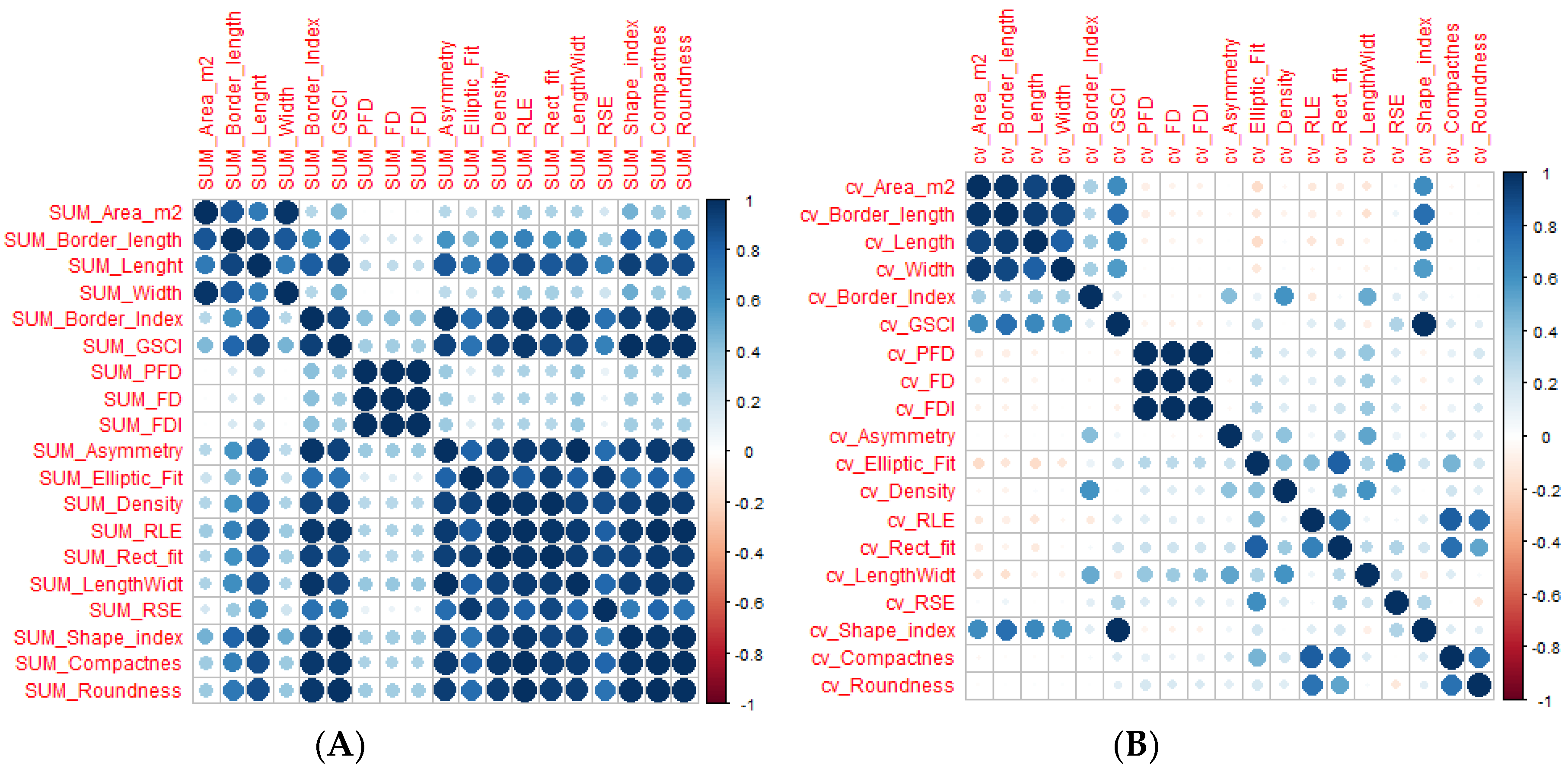
| Indices | Formulae | Range of Variation | Description |
|---|---|---|---|
| Shannon index () | [0,ln(S)] | The Shannon index expresses the frequency of the i-th species in a community; its values generally lie between 0 and 3.5; higher values correspond to higher species diversity. Its maximum value (MAX_SHANNON) is given by the natural logarithm of the number of species found in the test area and occurs when all species are equally present. | |
| Pielou index () | [0,1] | The Pielou index measures the relative abundance of species groups. The index can take values between 1 (all species are equally abundant) and 0 (there is only one species). | |
| Pretzsch index () | [0,ln(SxZ)] | The Pretzsch index summarizes and quantifies species diversity and the vertical distribution of species in a forest. The index is lowest in one-story pure forests, whereas it rises for pure forests with two or more stories. Peak values are reached in mixed woodlands with heterogeneous structures. | |
| Margalef index () | [0,∞) | It quantifies the presence of a number of species in a community. It also depends on the number of plants found in the sampling area. The index value increases with increasing species diversity. |
| Normal Distributed Variables | ||
| Variables | ANOVA | TUKEY |
| Pielou index (I_PIELOU) | no significant difference | |
| Mean total height (MEAN_HTOT) | no significant difference | |
| Variables Non Normal | ||
| Variables | KRUSKAL-WALLIS | MANN-WHITNEY |
| Number of plants (N_PLANTS) | *** | (1 vs. 2) ***; (2 vs. 3) ** |
| Number of species (N_SPECIES) | *** | (1 vs. 2) ***; (1 vs. 3) ** |
| Shannon index (I_SHANNON) | *** | (1 vs. 2) ***; (1 vs. 3) ** |
| Mean DBH (MEAN_DBH) | no significant difference | |
| Total basal area (G_TOT) | *** | (1 vs. 2) *** |
| Total volume (V_TOT) | ** | (1 vs. 2) ** |
| Quercus Forest | |||||||||||||||||||
| N_PLANTS | N_SPECIES | I_SHANNON | I_PIELOU | ||||||||||||||||
| N = 13 | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | |||
| Linear regr. | Linear regr. | Linear regr | Linear regr | ||||||||||||||||
| Intercept | −28.85 | 16.8 | Intercept | 7.21 | 0.71 | 0.000 | Intercept | 1.70 | 0.13 | 0.000 | Intercept | 1.02 | 0.10 | 0.000 | |||||
| Mdn_GSCI | 18.61 | 5.24 | 0.49 | 0.005 | Sd_rect.fit | −20.66 | 7.02 | 0.39 | 0.013 | Sd_rect.fit | −4.83 | 1.28 | 0.52 | 0.003 | Sd_Density | −1.10 | 0.41 | 0.34 | 0.021 |
| MEAN_DBH | MEAN_HTOT | V_TOT | G_TOT | ||||||||||||||||
| N = 13 | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | |||
| Linear regr. | Linear regr | Linear regr | Linear regr | ||||||||||||||||
| Intercept | −23.27 | 7.38 | 0.009 | Intercept | 9.54 | 1.04 | Intercept | 5.34 | 1.48 | 0.004 | Intercept | 1.05 | 0.35 | 0.012 | |||||
| Avg_rect.fit | 48.39 | 11.43 | 0.60 | 0.001 | Mdn_B.Index | −56.61 | 24.15 | 0.27 | 0.039 | Mdn_Asym. | −6.60 | 2.36 | 0.36 | 0.018 | Avg_Asym | −1.36 | 0.59 | 0.26 | 0.041 |
| Mixed forest | |||||||||||||||||||
| N_PLANTS | N_SPECIES | I_SHANNON | I_PIELOU | ||||||||||||||||
| N = 9 | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | |||
| Linear regr. | Linear regr | Linear regr | Linear regr | ||||||||||||||||
| Intercept | 47.02 | 9.62 | 0.002 | Intercept | 0.86 | 0.93 | Intercept | 0.11 | 0.35 | Intercept | 0.1 | 0.3 | |||||||
| Avg_Round. | −23.79 | 6.40 | 0.62 | 0.007 | Mdn_RSE | 8.29 | 2.92 | 0.47 | 0.025 | Mdn_RSE | 2.73 | 1.08 | 0.40 | 0.040 | Avg_RLE | 0.42 | 0.17 | 0.43 | 0.045 |
| MEAN_DBH | MEAN_HTOT | G_TOT | V_TOT | ||||||||||||||||
| N = 9 | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | |||
| Linear regr. | Linear regr | Linear regr | Linear regr. | ||||||||||||||||
| Intercept | 9.70 | 0.82 | 0.000 | Intercept | 0.90 | 0.82 | Intercept | −0.02 | 0.05 | Intercept | 3.48 | 1.23 | 0.026 | ||||||
| Sum_width | −0.00 | 0.00 | 0.51 | 0.018 | avg_Asym | 10.39 | 1.40 | 0.87 | 0.000 | Sd_Asym. | 0.59 | 0.21 | 0.45 | 0.027 | Avg_Comp | −1.16 | 0.48 | 0.37 | 0.048 |
| Fagus forest | |||||||||||||||||||
| N_SPEIES | I_SHANNON | I_PIELOU | MEAN_HTOT | ||||||||||||||||
| N = 28 | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | |||
| Linear regr. | Linear regr | Linear regr | Linear regr | ||||||||||||||||
| Intercept | 3.13 | 0.77 | 0.000 | Intercept | 1.01 | 0.29 | 0.002 | Intercept | 0.26 | 0.18 | Intercept | 5.46 | 1.40 | 0.000 | |||||
| Cv_Round. | −6.02 | 2.64 | 0.15 | 0.033 | Sd_Round. | −1.85 | 0.72 | 0.21 | 0.018 | Mdn_PFD. | 0.06 | 0.02 | 0.48 | 0.022 | Cv_Length | 11.14 | 4.20 | 0.23 | 0.016 |
| Variables with Normal Distribution | ||
| Variables | ANOVA | TUKEY |
| Number of plants (N_PLANTS) | *** | (1 vs. 2) ***; (2 vs. 3) *** |
| Pretzsch index (I_PRETZSCH) | *** | (1 vs. 2) ***; (1 vs. 3) *** |
| Total basal area (G_TOT) | no significant difference | |
| Total volume (V_TOT) | no significant difference | |
| Number of habitat trees (HAB) | * | (1 vs. 2) ** |
| Percentage of habitat trees (%_HAB) | ** | (1 vs. 2)* |
| Non Normal Distributed Variables | ||
| Variables | KRUSKAL-WALLIS | MANN-WHITNEY |
| Number of species (N_SPECIES) | *** | (1 vs. 2) ***; (1 vs. 3) *** |
| Margalef index (I_MARGALEF) | *** | (1 vs. 2) ***; (1 vs. 3) *** |
| Shannon index (I_SHANNON) | *** | (1 vs. 2) ***; (1 vs. 3) *** |
| Mean diameter at breast height (MEAN_DBH) | *** | (1 vs. 2) ***; (2 vs. 3) *** |
| Mean total height (MEAN_HTOT) | ** | (1 vs. 2)** |
| Quercus forest | |||||||||||||||||||
| N_SPECIES | I_SHANNON | I_MARGLEF | I _ PRETZSCH | ||||||||||||||||
| N = 13 | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | |||
| Linear regr. | Linear regr | Linear regr | Linear regr | ||||||||||||||||
| Intercept | 8.13 | 0.71 | 0.000 | Intercept | 1.81 | 0.14 | 0.000 | Intercept | 1.94 | 0.18 | 0.000 | Intercept | 2.32 | 0.1 | 0.000 | ||||
| Sd_Rect.fit | −21.46 | 7.04 | 0.41 | 0.011 | Cv_Density | −2.61 | 0.95 | 0.35 | 0.019 | Sd_Rect.fit | −6.02 | 1.80 | 0.46 | 0.006 | Sd_Density | −2.68 | 0.45 | 0.74 | 0.000 |
| MEAN_DBH | MEAN_HTOT | HAB | %HAB | ||||||||||||||||
| N = 13 | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | |||
| Linear regr. | Linear regr | Linear regr | Linear regr | ||||||||||||||||
| Intercept | 11.30 | 3.42 | 0.007 | Intercept | −15.73 | 11.99 | Intercept | 20.54 | 2.44 | 0.000 | Intercept | 41.87 | 5.45 | 0.000 | |||||
| Sum_rect.fit | 1.29 | 0.50 | 0.32 | 0.02 | Mdn_rect.fit | 45.41 | 18.68 | 0.29 | 0.033 | Sum_rect.fit | −3.10 | 0.73 | 0.59 | 0.001 | Sum_RLE | −1.86 | 0.54 | 0.47 | 0.006 |
| Mixed forest | |||||||||||||||||||
| MEAN_DBH | MEAN_HTOT | HAB | %HAB | ||||||||||||||||
| N = 9 | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | |||
| Linear regr. | Linear regr | Linear regr | Linear regr | ||||||||||||||||
| Intercept | −10.86 | 13.32 | Intercept | 27.74 | 2.70 | 0.000 | Intercept | 14.34 | 1.20 | 0.000 | Intercept | 108.24 | 17.54 | 0.000 | |||||
| Avg_Round | 25.92 | 8.86 | 0.49 | 0.022 | Sd_Asym. | −49.06 | 11.72 | 0.67 | 0.004 | Cv_Length | −14.01 | 2.51 | 0.79 | 0.000 | Avg_RSE | −208.99 | 53.19 | 0.64 | 0.005 |
| Fagus forest | |||||||||||||||||||
| HAB | %HAB | ||||||||||||||||||
| N = 28 | B | SE (B) | R2 | p-value | B | SE (B) | R2 | p-value | |||||||||||
| Linear regr. | Linear regr | ||||||||||||||||||
| Intercept | 4.00 | 1.21 | 0.003 | Intercept | 61.35 | 7.88 | 0.000 | ||||||||||||
| cv_PFD | 11.82 | 5.23 | 0.15 | 0.034 | Avg_RSE | −58.21 | 27.71 | 0.11 | 0.045 | ||||||||||
| Forest Types | Parameters | Bootstrap R2 | Standard Error (95%) | R2 | Bias | |
|---|---|---|---|---|---|---|
| Understory | mixed | Mean total height | 0.877 | 0.006 | 0.872 | −0.005 |
| Number of plants | 0.623 | 0.016 | 0.616 | −0.007 | ||
| Mean DBH | 0.507 | 0.022 | 0.515 | 0.008 | ||
| Quercus | Mean DBH | 0.577 | 0.017 | 0.600 | 0.024 | |
| Shannon index | 0.576 | 0.010 | 0.523 | −0.053 | ||
| Living trees | Quercus | Pretzsch index | 0.755 | 0.008 | 0.738 | −0.016 |
| Number of habitat trees | 0.554 | 0.018 | 0.586 | 0.032 | ||
| mixed | Mean total height | 0.682 | 0.012 | 0.674 | −0.008 | |
| Number of habitat trees | 0.757 | 0.014 | 0.790 | 0.032 | ||
| Percentage of habitat trees | 0.627 | 0.019 | 0.644 | 0.017 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bagaram, M.B.; Giuliarelli, D.; Chirici, G.; Giannetti, F.; Barbati, A. UAV Remote Sensing for Biodiversity Monitoring: Are Forest Canopy Gaps Good Covariates? Remote Sens. 2018, 10, 1397. https://doi.org/10.3390/rs10091397
Bagaram MB, Giuliarelli D, Chirici G, Giannetti F, Barbati A. UAV Remote Sensing for Biodiversity Monitoring: Are Forest Canopy Gaps Good Covariates? Remote Sensing. 2018; 10(9):1397. https://doi.org/10.3390/rs10091397
Chicago/Turabian StyleBagaram, Martin B., Diego Giuliarelli, Gherardo Chirici, Francesca Giannetti, and Anna Barbati. 2018. "UAV Remote Sensing for Biodiversity Monitoring: Are Forest Canopy Gaps Good Covariates?" Remote Sensing 10, no. 9: 1397. https://doi.org/10.3390/rs10091397
APA StyleBagaram, M. B., Giuliarelli, D., Chirici, G., Giannetti, F., & Barbati, A. (2018). UAV Remote Sensing for Biodiversity Monitoring: Are Forest Canopy Gaps Good Covariates? Remote Sensing, 10(9), 1397. https://doi.org/10.3390/rs10091397