Using Dual-Polarization Interferograms to Correct Atmospheric Effects for InSAR Topographic Mapping
Abstract
1. Introduction
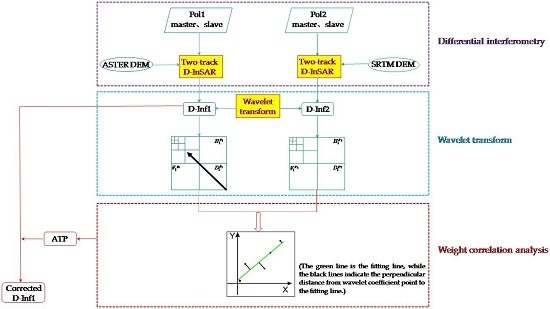
2. Methodology
2.1. Phase in the Differential Interferograms
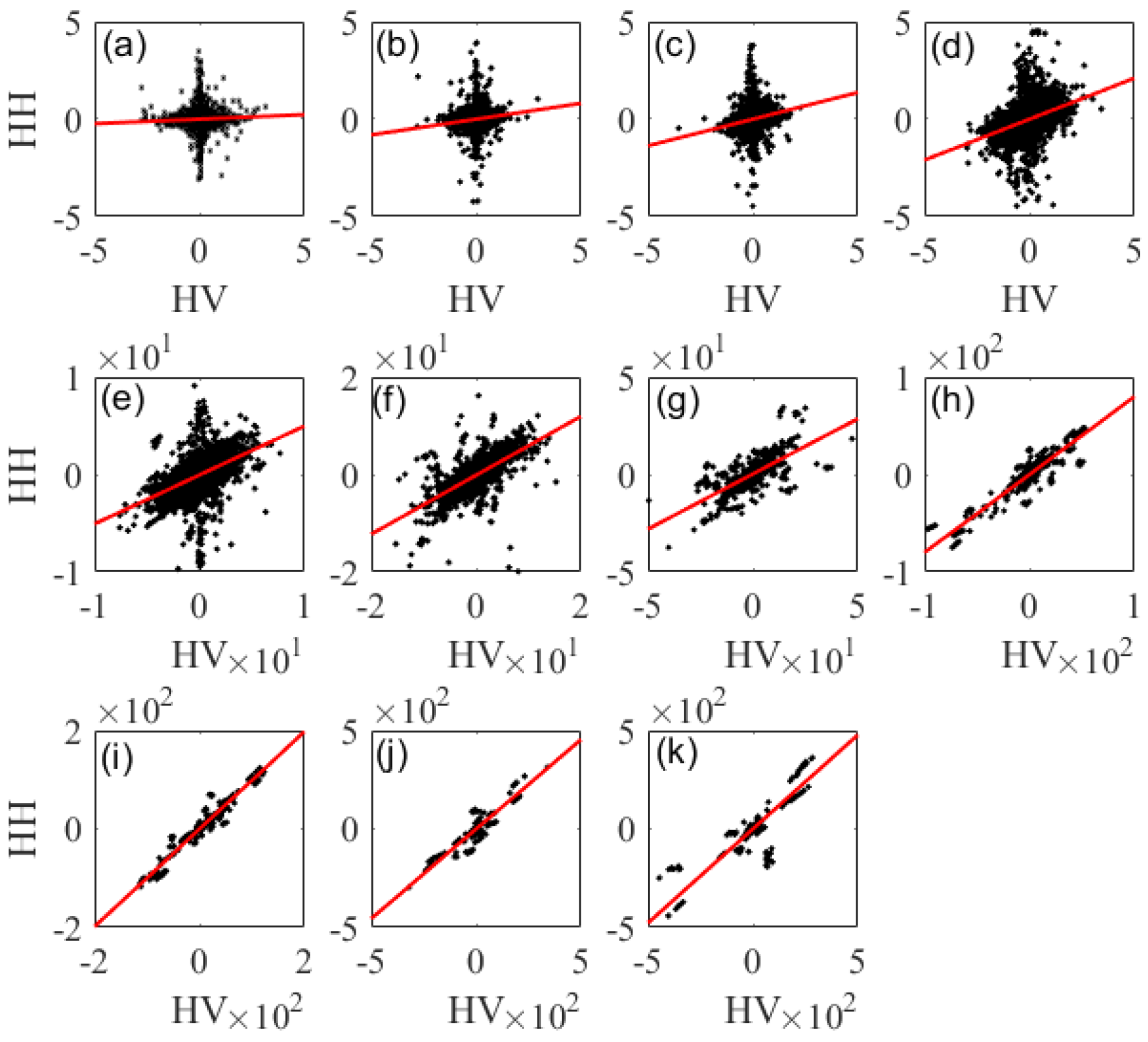
2.2. Estimation of the Atmospheric Effects
3. Experiments and Analysis
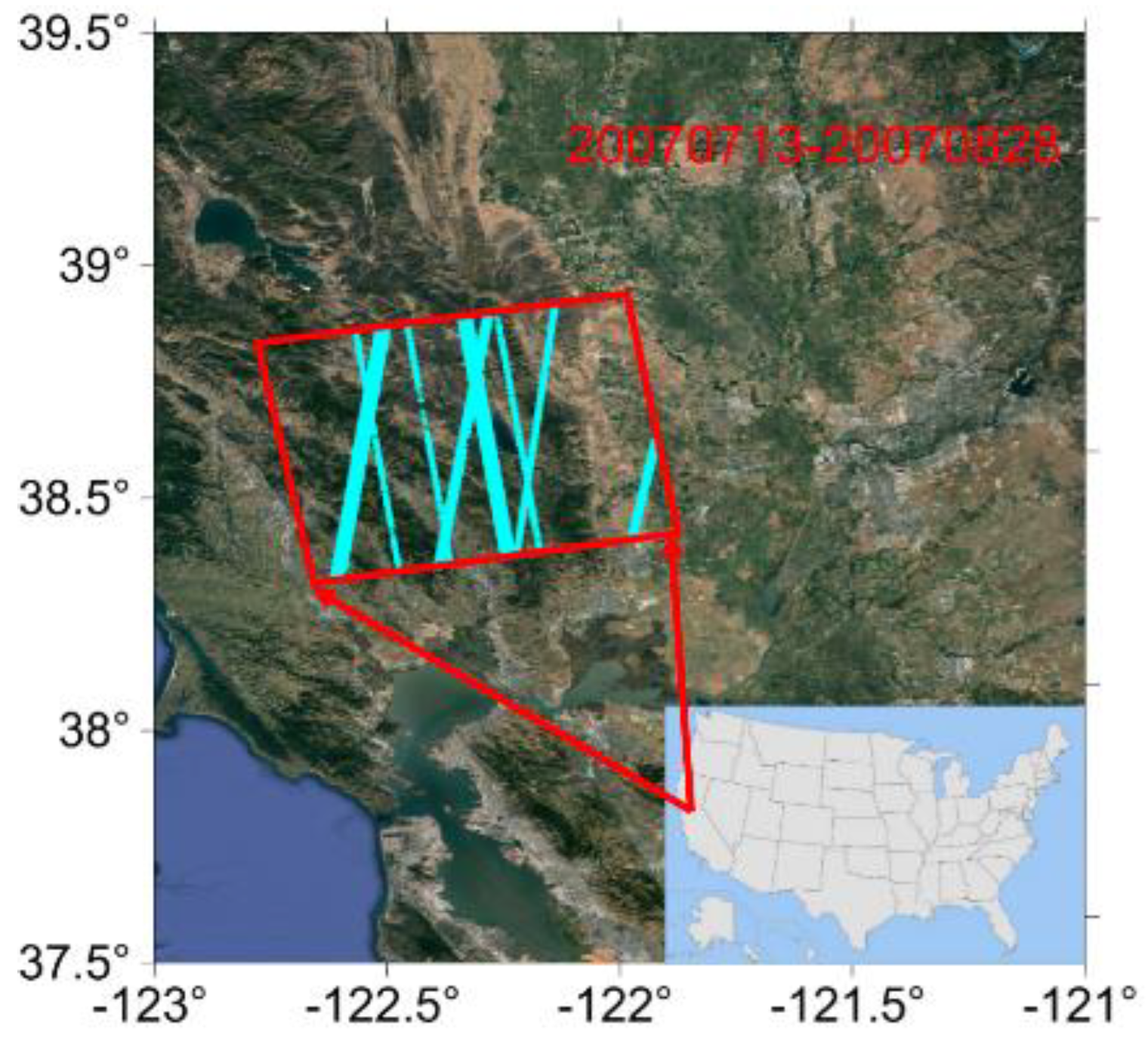
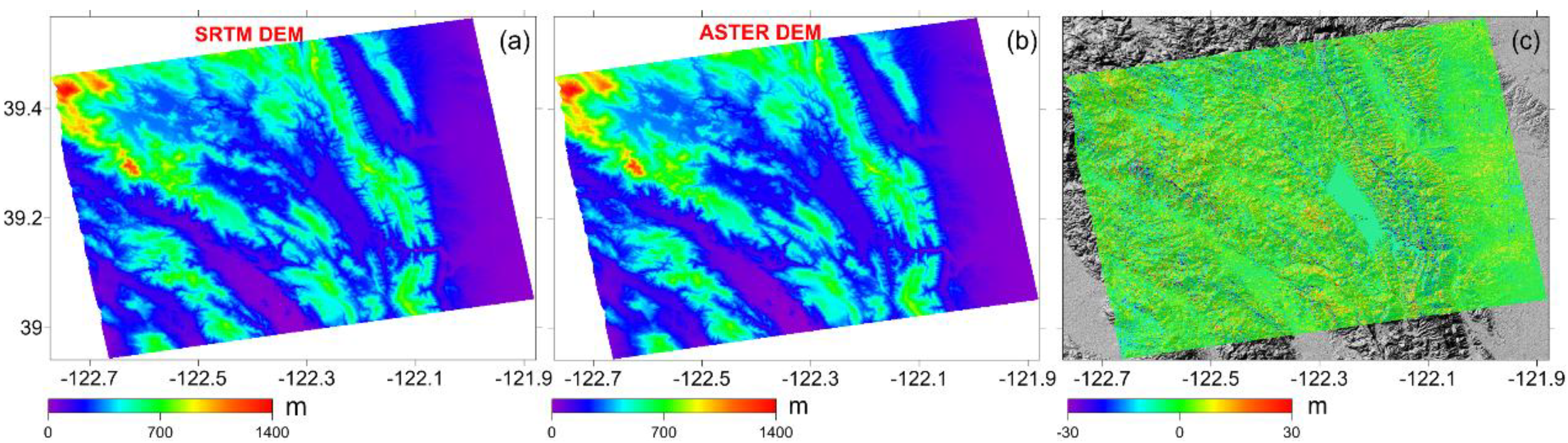
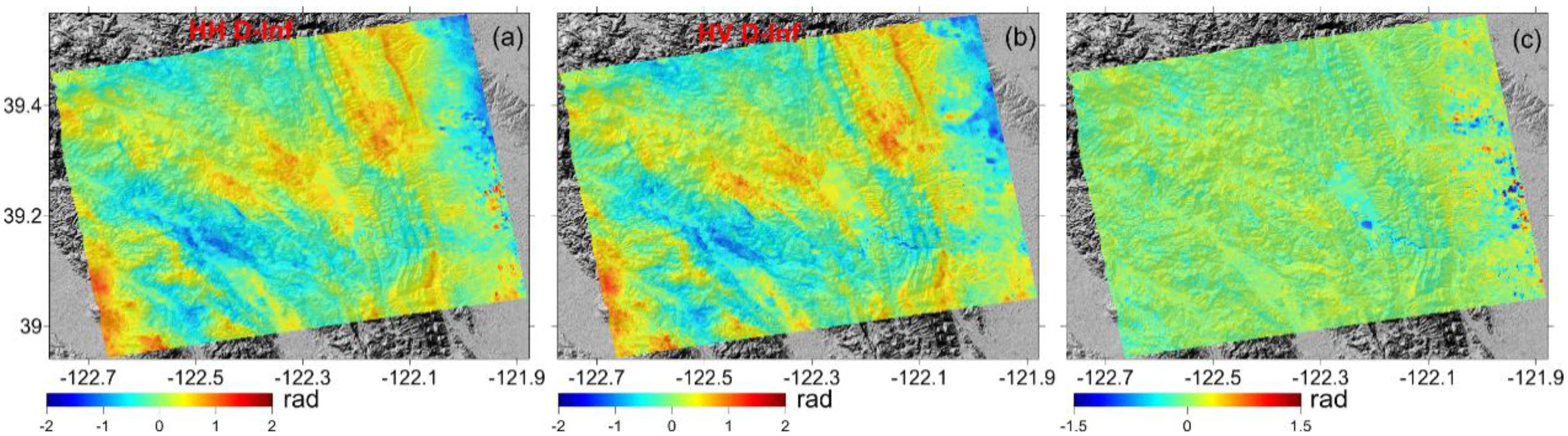
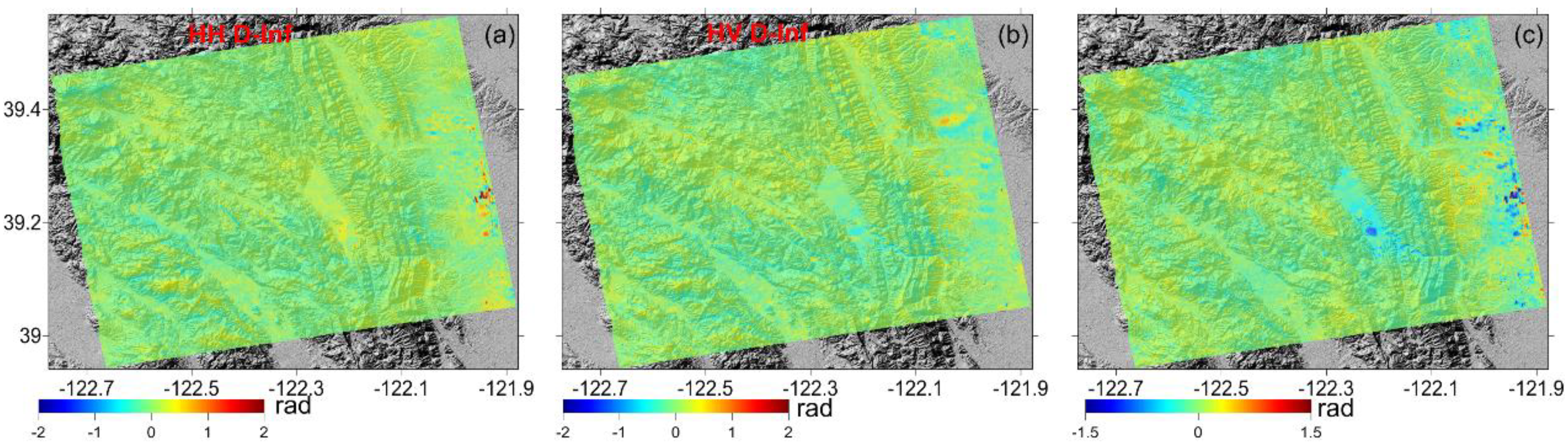
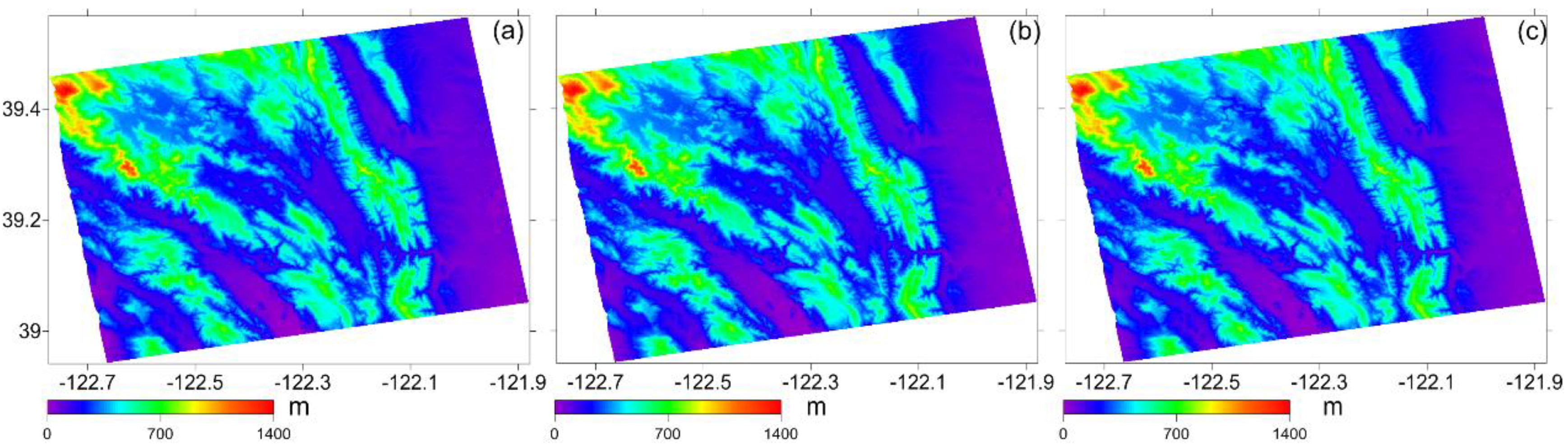
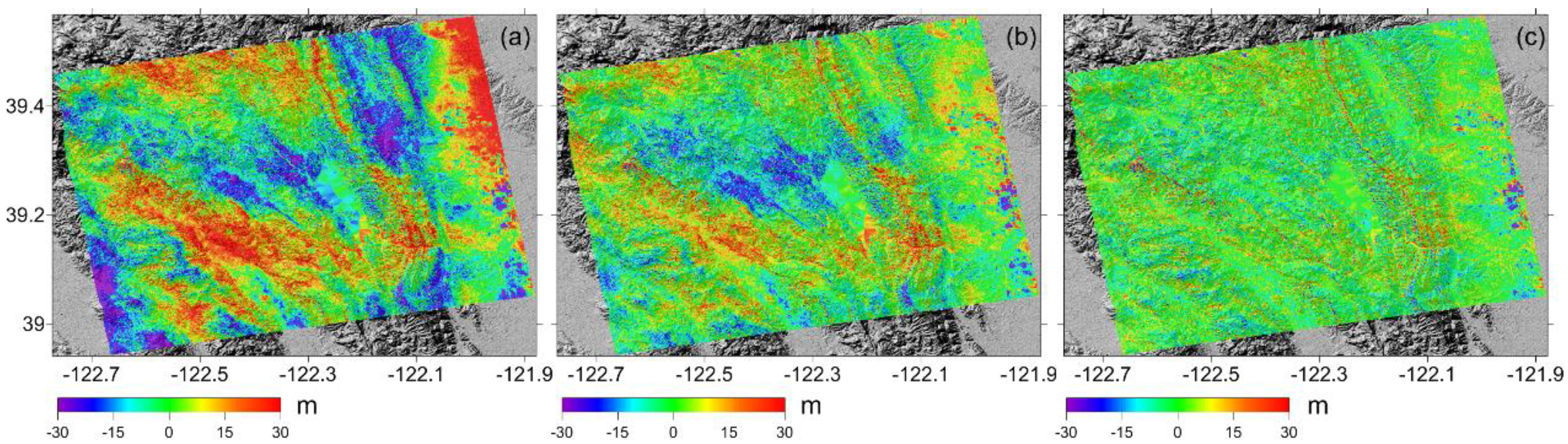
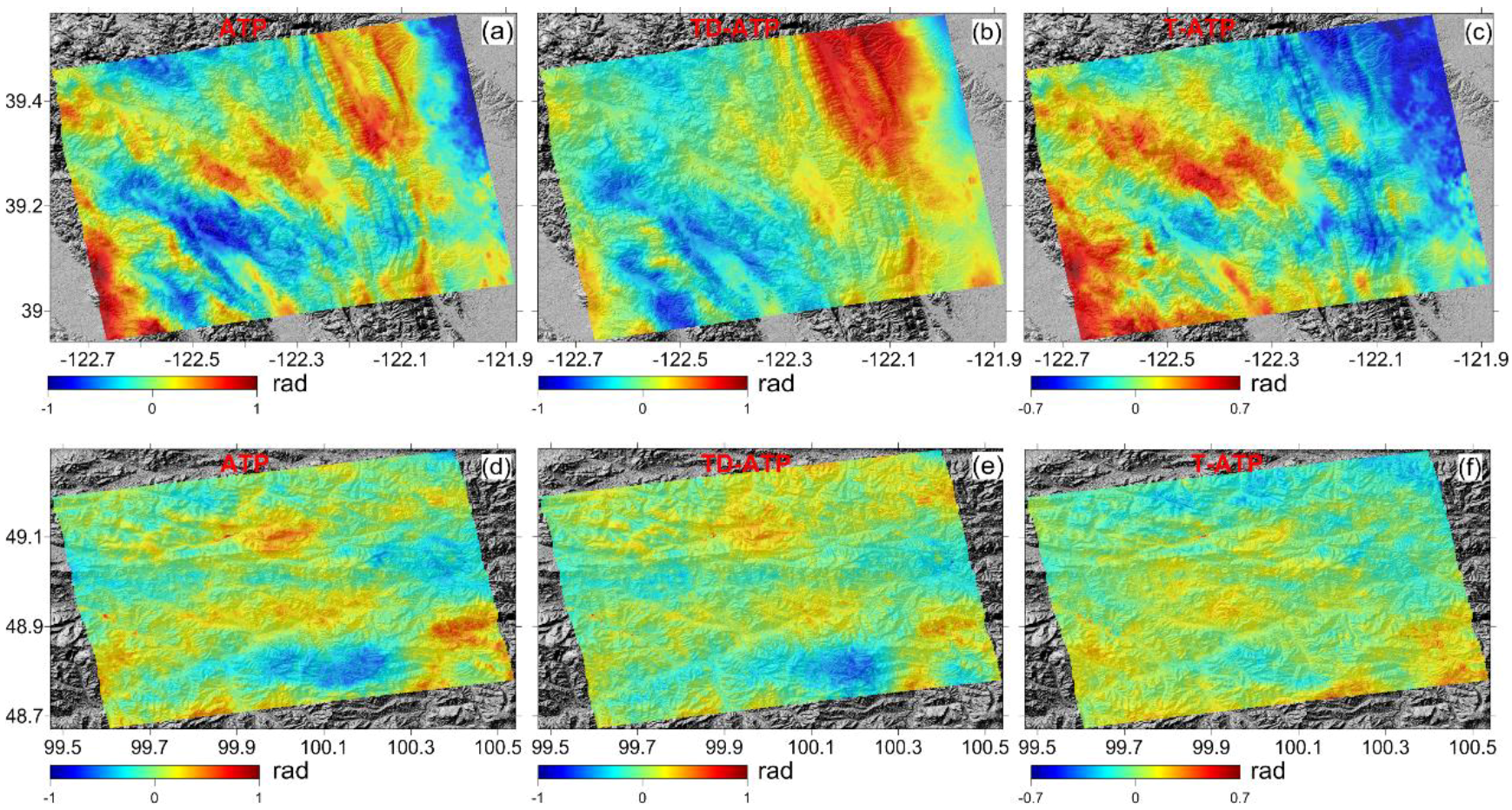
3.1. San Francisco Test Site
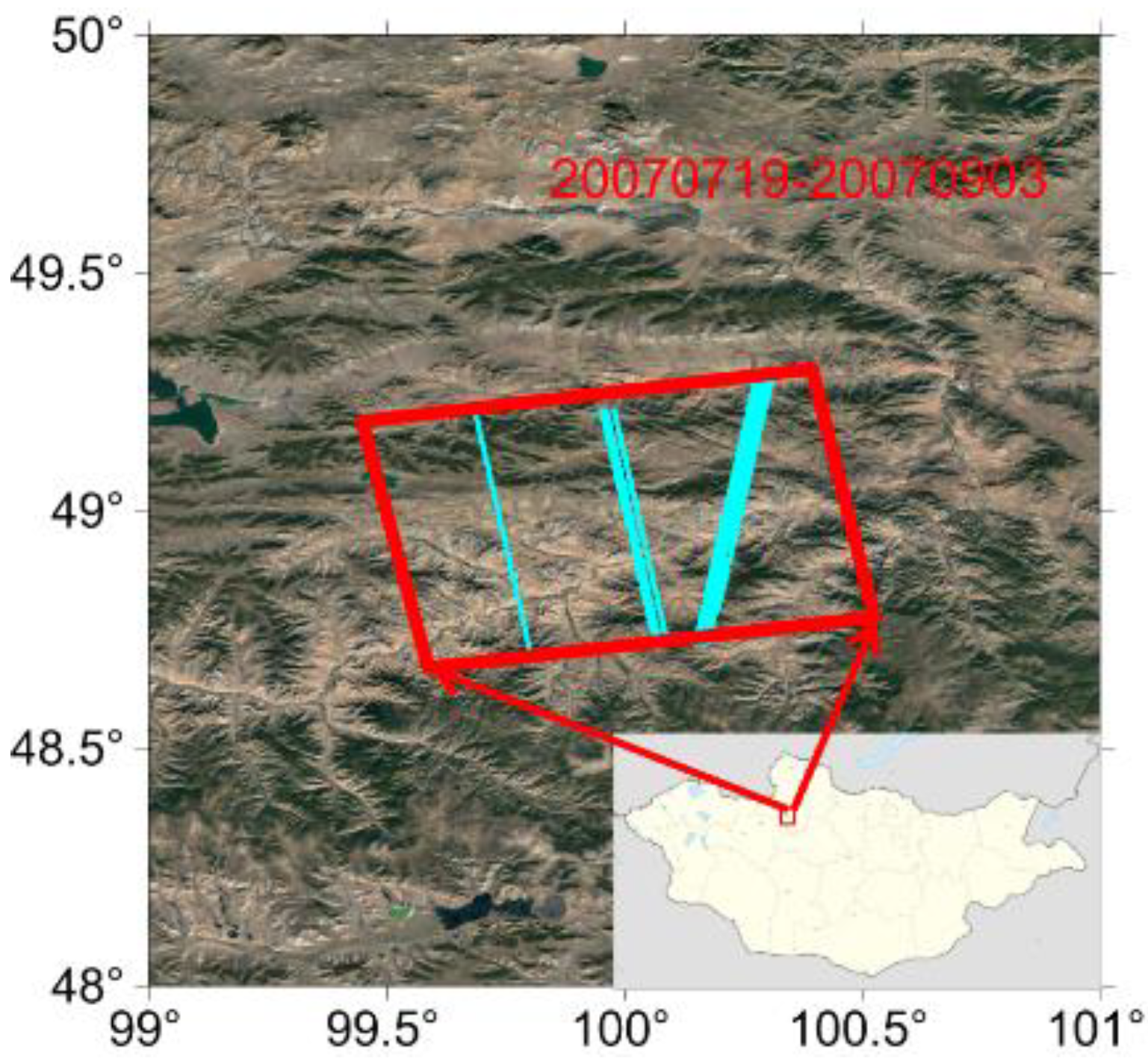
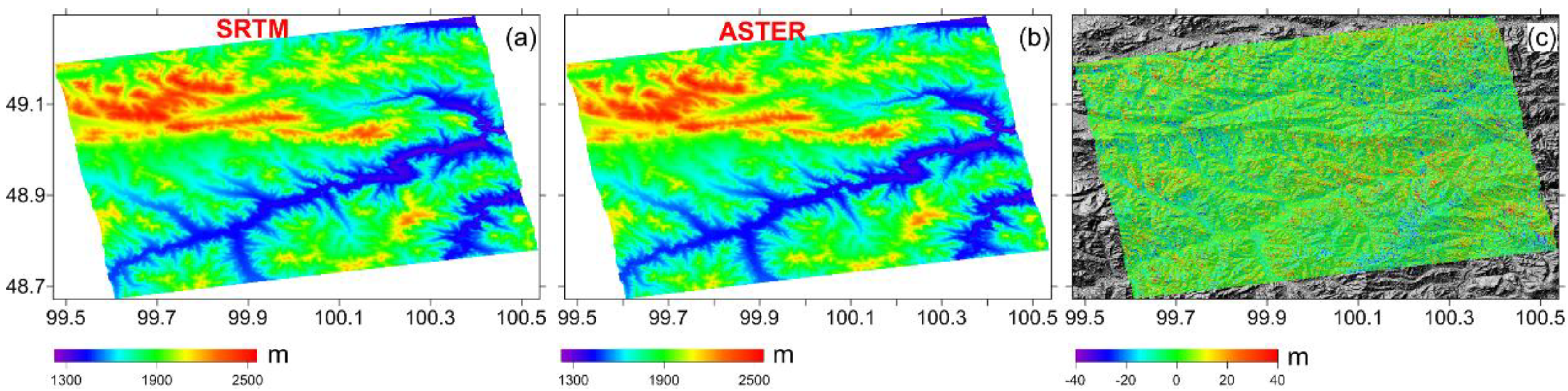
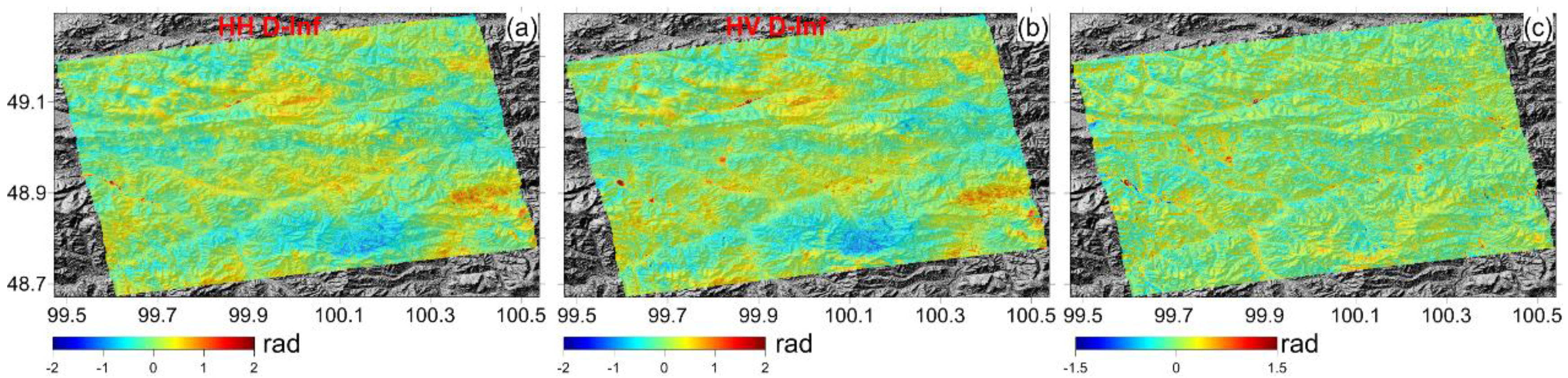
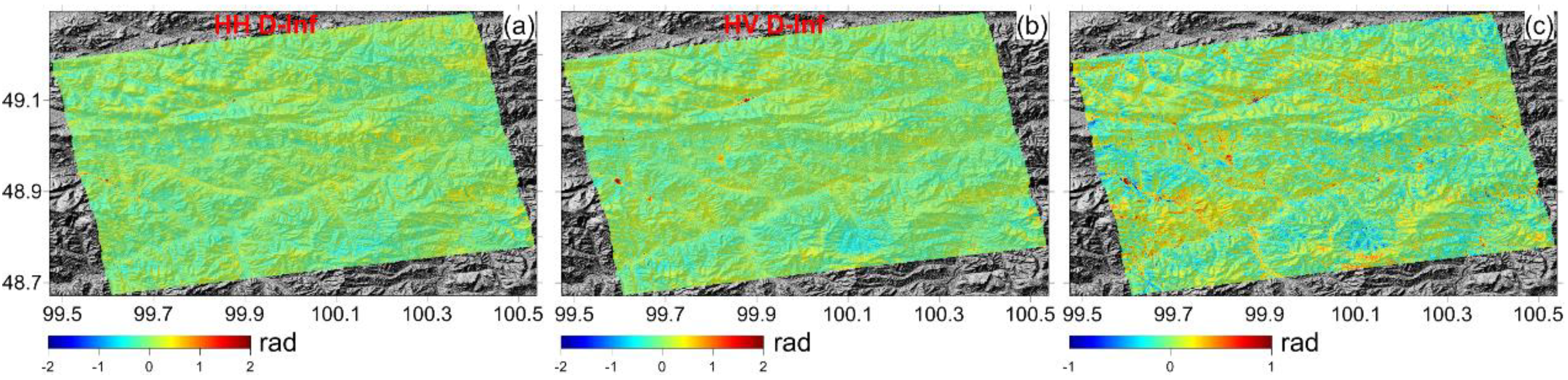
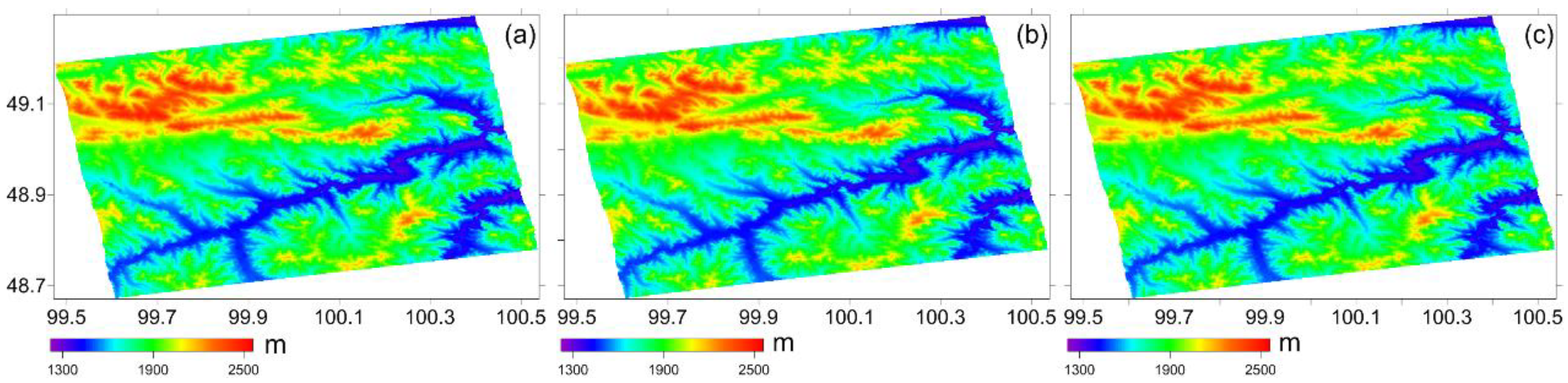
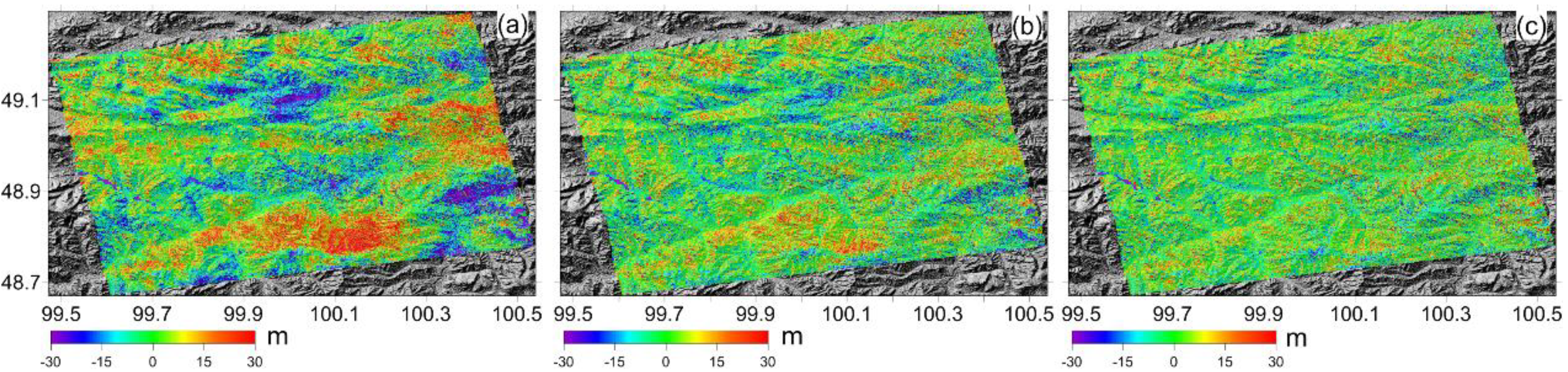
3.2. Moron Test Site
4. Discussion
4.1. Summary of the MRWCA Method
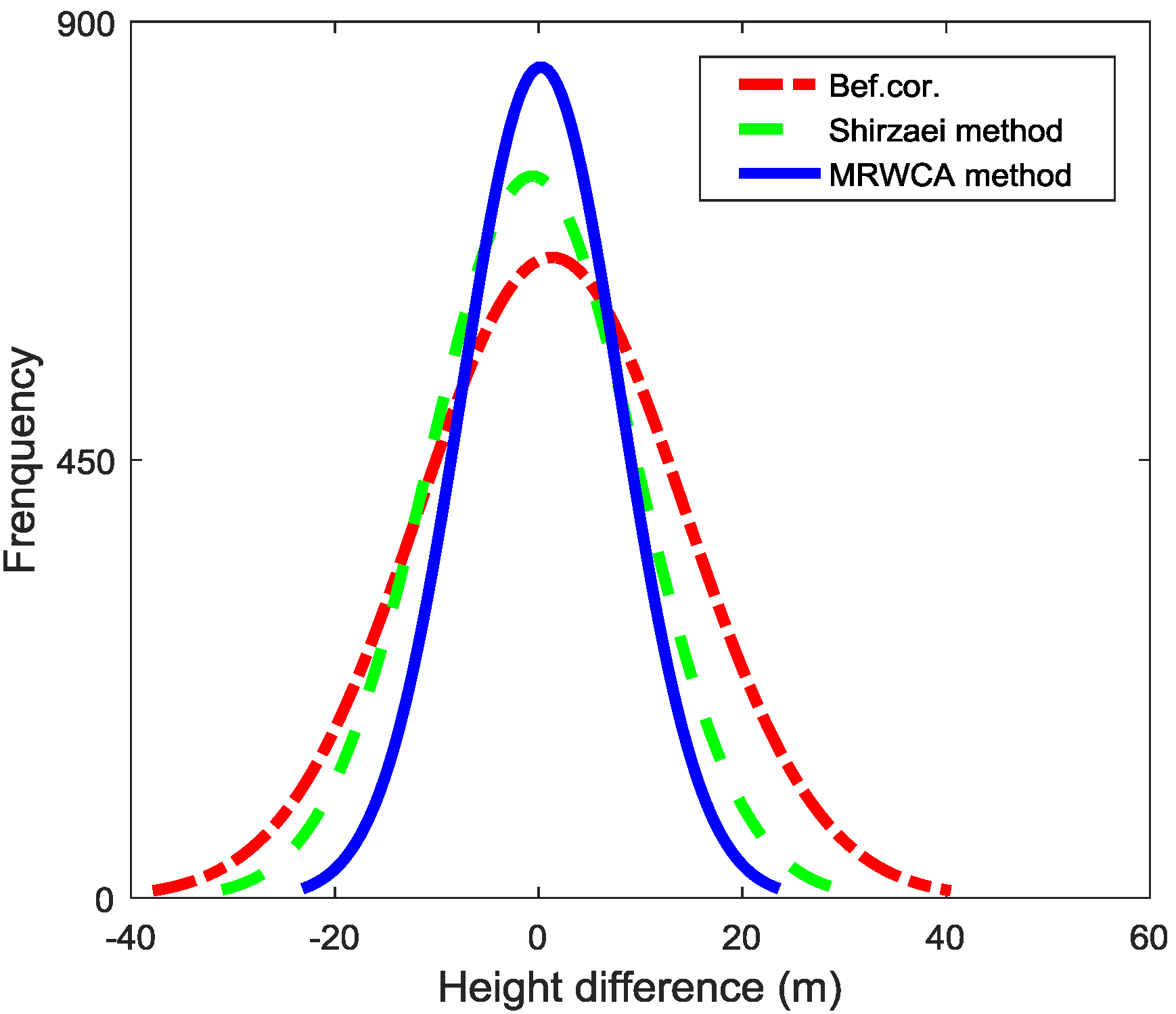
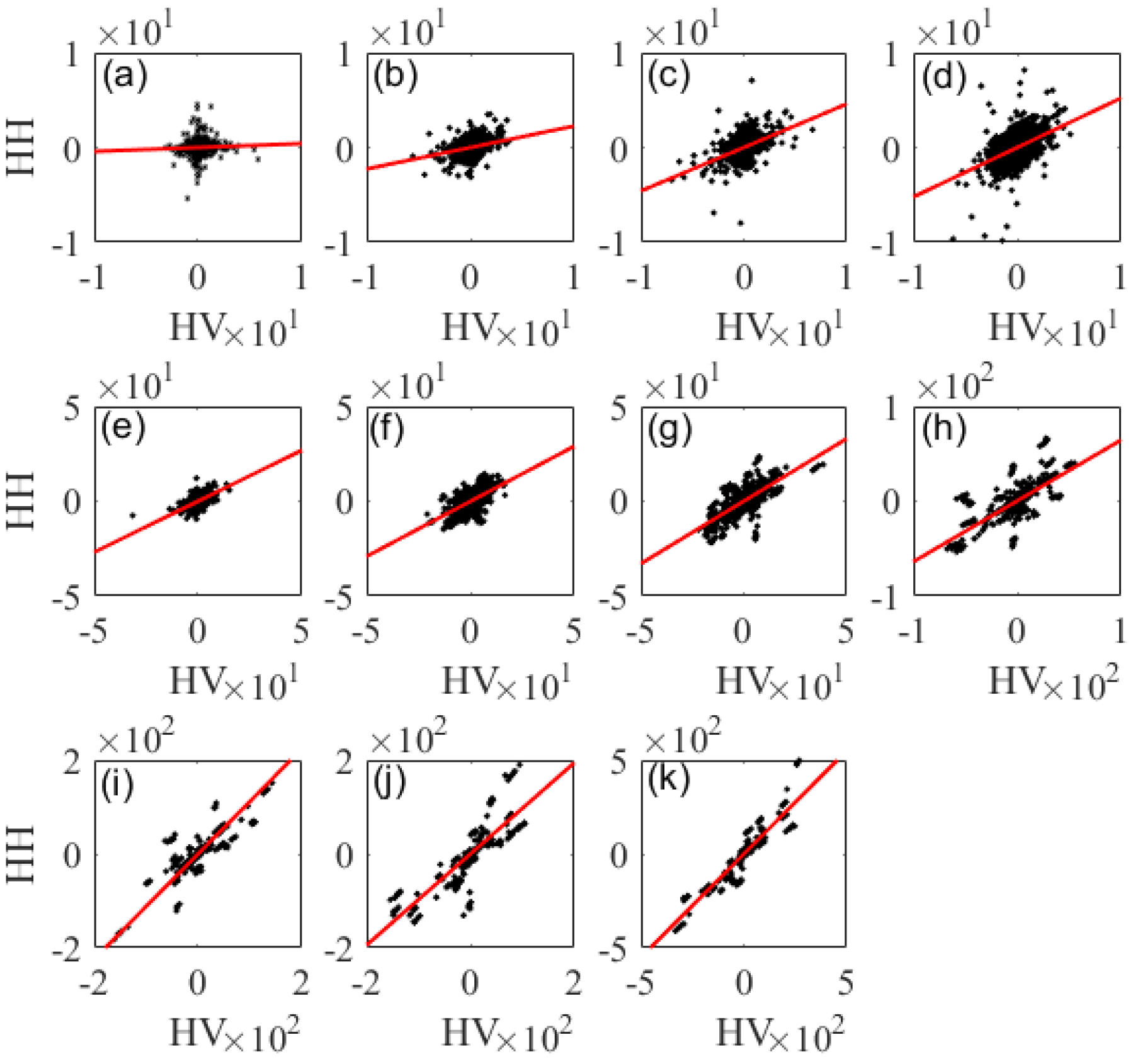
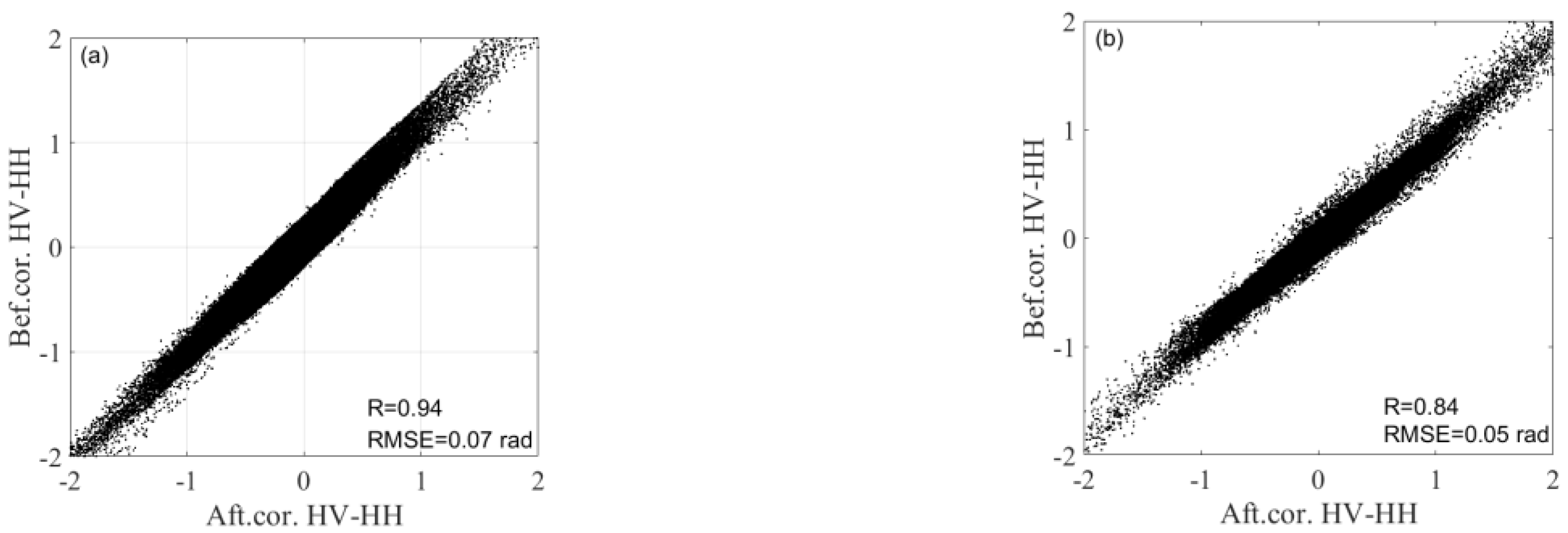
4.2. Self-Consistency Checking between Differences Maps before and after MRWCA Method Correction
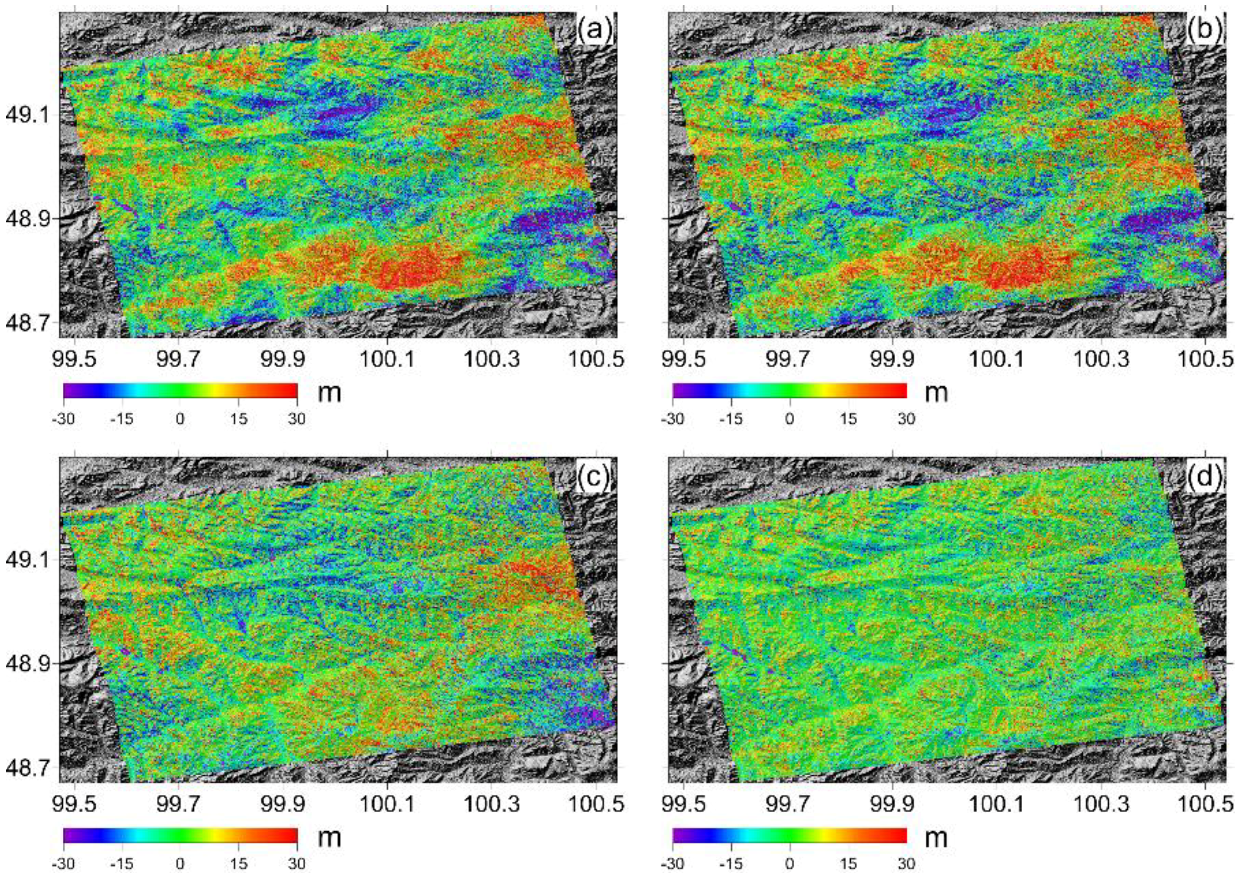
4.3. Effects of Different Decomposition Scales on ATP Correction
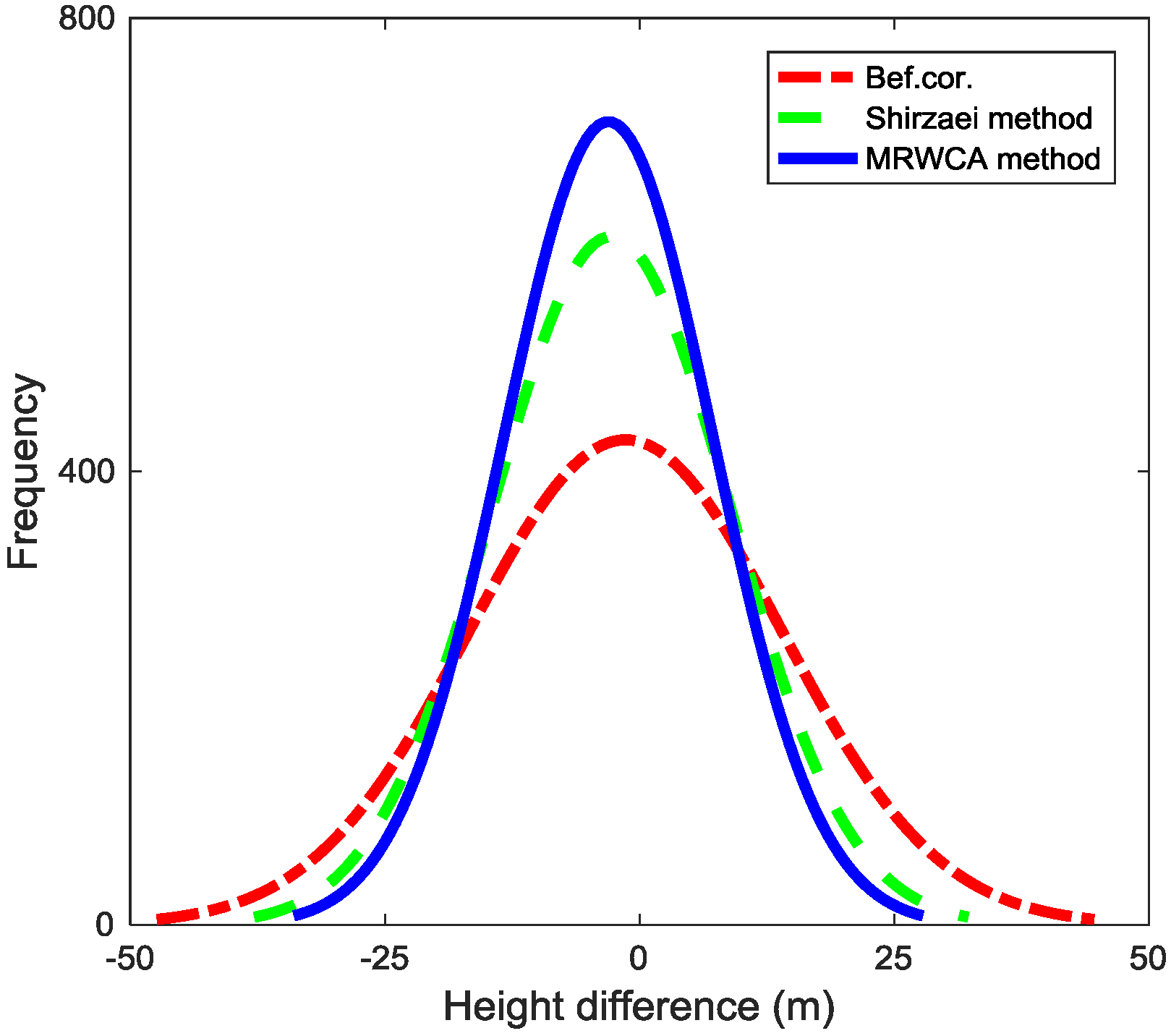
4.4. Comparison with the Existing Method
4.5. Potential and Limits of MRWCA Method in Atmospheric Correction
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, J.; Li, Z.W.; Zhu, J.J.; Ding, X.L.; Wang, C.C.; Feng, G.C.; Sun, Q. Measuring three-dimensional surface displacements from combined InSAR and GPS data based on BFGS method. Chin. J. Geophys. 2013, 56, 117–126. [Google Scholar]
- Zebker, H.A.; Werner, C.L.; Rosen, P.A.; Hensley, S. Accuracy of topographic maps derived from ERS-1 interferometric radar. IEEE Trans. Geosci. Remote Sens. 1994, 32, 823–836. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Multibaseline InSAR DEM reconstruction: The wavelet approach. IEEE Trans. Geosci. Remote Sens. 1999, 37, 705–715. [Google Scholar] [CrossRef]
- Liao, M.S.; Jiang, H.J.; Wang, Y.; Wang, T.; Zhang, L. Improved topographic mapping through high-resolution SAR interferometry with atmospheric effect removal. ISPRS J. Photogramm. Remote Sens. 2013, 80, 72–79. [Google Scholar] [CrossRef]
- Shirzaei, M.; Bürgmann, R. Topography correlated atmospheric delay correction in radar interferometry using wavelet transforms. Geophys. Res. Lett. 2012, 39, 1305–1310. [Google Scholar] [CrossRef]
- Li, Z.H.; Fielding, E.J.; Cross, P.; Muller, J.-P. Interferometric synthetic aperture radar atmospheric correction: GPS topography-dependent turbulence model. J. Geophys. Res. Solid Earth 2006, 111, B02404. [Google Scholar] [CrossRef]
- Li, Z.H.; Muller, J.-P.; Cross, P.; Fielding, E.J. Interferometric synthetic aperture radar (InSAR) atmospheric correction: GPS, moderate resolution imaging spectroradiometer (MODIS), and InSAR integration. J. Geophys. Res. Solid Earth 2005, 110, B03410. [Google Scholar] [CrossRef]
- Li, Z.H.; Fielding, E.J.; Cross, P.; Muller, J.-P. Interferometric synthetic aperture radar atmospheric correction: Medium resolution imaging spectrometer and advanced synthetic aperture radar integration. Geophys. Res. Lett. 2006, 33, 272–288. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Zebker, H.A.; Webb, F.H.; Fielding, E.J. Surface deformation and coherence measurements of Kilauea Volcano, Hawaii, from SIR-C radar interferometry. J. Geophys. Res.: Planets 1996, 101, 23109–23125. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Ishitsuka, K.; Matsuoka, T.; Tamura, M. Persistent Scatterer Selection Incorporating Polarimetric SAR Interferograms Based on Maximum Likelihood Theory. IEEE Trans. Geosci. Remote Sens. 2016, 55, 38–50. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry Data Interpretation and Error Analysis; Kluwer: Norwell, MA, USA, 2001. [Google Scholar]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Shanker, P.; Zebker, H. Persistent scatterer selection using maximum likelihood estimation. Geophys. Res. Lett. 2007, 34, 315–324. [Google Scholar] [CrossRef]
- Xu, B.; Li, Z.W.; Wang, Q.J.; Jiang, M.; Zhu, J.J.; Ding, X.L. A Refined Strategy for Removing Composite Errors of SAR Interferogram. IEEE Geosci. Remote Sens. Lett. 2013, 11, 143–147. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Levin, D. The approximation power of moving least-squares. Math. Comp. 1998, 67, 1517–1531. [Google Scholar] [CrossRef]
- Shim, J.S. Analysis of Total Electron Content (TEC) Variations in the Low- and Middle-Latitude Ionosphere. Ph.D. Thesis, Utah State University, Logan, UT, USA, 2009. [Google Scholar]
- Satgé, F.; Bonnet, M.-P.; Timouk, F.; Calmant, S.; Pillco, R.; Molina, J.; Lavado-Casimiro, W.; Arsen, A.; Crétaux, J.; Garnier, J. Accuracy assessment of SRTM v4 and ASTER GDEM v2 over the Altiplano watershed using ICESat/GLAS data. Int. J. Remote Sens. 2015, 36, 465–488. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Xie, H.; Kang, S.; Yi, D.; Ackley, S.F. Monitoring lake level changes on the Tibetan plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ. 2011, 115, 1733–1742. [Google Scholar] [CrossRef]
- Bhang, K.; Schwartz, F.W.; Braun, A. Verification of the vertical error in C-band SRTM DEM using ICESat and Landsat-7, Otter Tail County, MN. IEEE Trans. Geosci. Remote Sens. 2007, 45, 36–44. [Google Scholar] [CrossRef]
- Hirano, A.; Welch, R.; Lang, H. Mapping from ASTER stereo image data: DEM validation and accuracy assessment. ISPRS J. Photogramm. 2003, 57, 356–370. [Google Scholar] [CrossRef]
- Li, Z.W.; Ding, X.L.; Huang, C.; Zhu, J.J.; Chen, Y.L. Improved filtering parameter determination for the Goldstein radar interferogram filter. ISPRS J. Photogramm. 2008, 63, 621–634. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost function in nonlinear optimization. J. Opt. Soc. Am. A 2001, 18, 338–351. [Google Scholar] [CrossRef]
- Costantini, M.; Rosen, P.A. A generalized phase unwrapping approach for sparse data. In Proceedings of the 1999 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Hamburg, Germany, 28 June–2 July 1999. [Google Scholar]
- Marghany, M. DInSAR technique for three-dimensional coastal spit simulation from radarsat-1 fine mode data. Acta Geophysica 2013, 61, 478–493. [Google Scholar] [CrossRef]
- Imperatore, P.; Pepe, A. Topological characterization and advanced noise filtering techniques for phase unwrapping of interferometric data-stacks. Remote Sens. Environ. 2016. [Google Scholar] [CrossRef]
- Shirzaei, M. A Wavelet-Based Multitemporal DInSAR Algorithm for Monitoring Ground Surface Motion. IEEE Geosci. Remote Sens. Lett. 2013, 10, 456–460. [Google Scholar] [CrossRef]
- Neelmeijer, J.; Schöne, T.; Dill, R.; Klemann, V.; Motagh, M. Ground Deformations around the Toktogul Reservoir, Kyrgyzstan, from Envisat ASAR and Sentinel-1 Data—A Case Study about the Impact of Atmospheric Corrections on InSAR Time Series. Remote Sens. 2018, 10, 462. [Google Scholar] [CrossRef]
- Beiranvand Pour, A.; Hashim, M. Application of PALSAR-2 remote sensing data for landslide hazard mapping in Kelantan river basin, Peninsular Malaysia. Int. Arch. Photogramm. Remote Sens. Spat. Inf. 2016, 37, 012067. [Google Scholar]
- Moreira, A.; Krieger, G.; Hajnsek, I.; Papathanassiou, K. Tandem-L: A highly innovative bistatic SAR mission for global observation of dynamic processes on the earth’s surface. IEEE Geosci. Remote Sens. Mag. 2015, 3, 8–23. [Google Scholar] [CrossRef]
- Freeman, A. Calibration of linearly polarized polarimetric SAR data subject to Faraday rotation. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1617–1624. [Google Scholar] [CrossRef]
- Dubois-Fernandez, P.C.; Souyris, J.C.; Angelliaume, S.; Garestier, F. The Compact Polarimetry Alternative for Spaceborne SAR at Low Frequency. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3208–3222. [Google Scholar] [CrossRef]
- Jung, H.S.; Lee, D.T.; Lu, Z.; Won, J.S. Ionospheric correction of SAR interferograms by multiple-aperture interferometry. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3191–3199. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Chen, C. Measurement and mitigation of the ionosphere in L-band Interferometric SAR data. In Proceedings of the IEEE Radar Conference, Washington, DC, USA, 10–14 May 2010. [Google Scholar] [CrossRef]
- Gomba, G.; Parizzi, A.; Zan, F.D.; Eineder, M.; Bamler, R. Toward Operational Compensation of Ionospheric Effects in SAR Interferograms: The Split-Spectrum Method. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1446–1461. [Google Scholar] [CrossRef]
- Fattahi, H.; Simons, M.; Agram, P. InSAR time-series estimation of the ionospheric phase delay: An extension of the split range-spectrum technique. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1–13. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Fu, H.; Zhu, J.; Zhou, C.; Zuo, T. Using Dual-Polarization Interferograms to Correct Atmospheric Effects for InSAR Topographic Mapping. Remote Sens. 2018, 10, 1310. https://doi.org/10.3390/rs10081310
Liu Z, Fu H, Zhu J, Zhou C, Zuo T. Using Dual-Polarization Interferograms to Correct Atmospheric Effects for InSAR Topographic Mapping. Remote Sensing. 2018; 10(8):1310. https://doi.org/10.3390/rs10081310
Chicago/Turabian StyleLiu, Zhiwei, Haiqiang Fu, Jianjun Zhu, Cui Zhou, and Tingying Zuo. 2018. "Using Dual-Polarization Interferograms to Correct Atmospheric Effects for InSAR Topographic Mapping" Remote Sensing 10, no. 8: 1310. https://doi.org/10.3390/rs10081310
APA StyleLiu, Z., Fu, H., Zhu, J., Zhou, C., & Zuo, T. (2018). Using Dual-Polarization Interferograms to Correct Atmospheric Effects for InSAR Topographic Mapping. Remote Sensing, 10(8), 1310. https://doi.org/10.3390/rs10081310