Using Near-Infrared-Enabled Digital Repeat Photography to Track Structural and Physiological Phenology in Mediterranean Tree–Grass Ecosystems
Abstract
1. Introduction
2. Materials and Methods
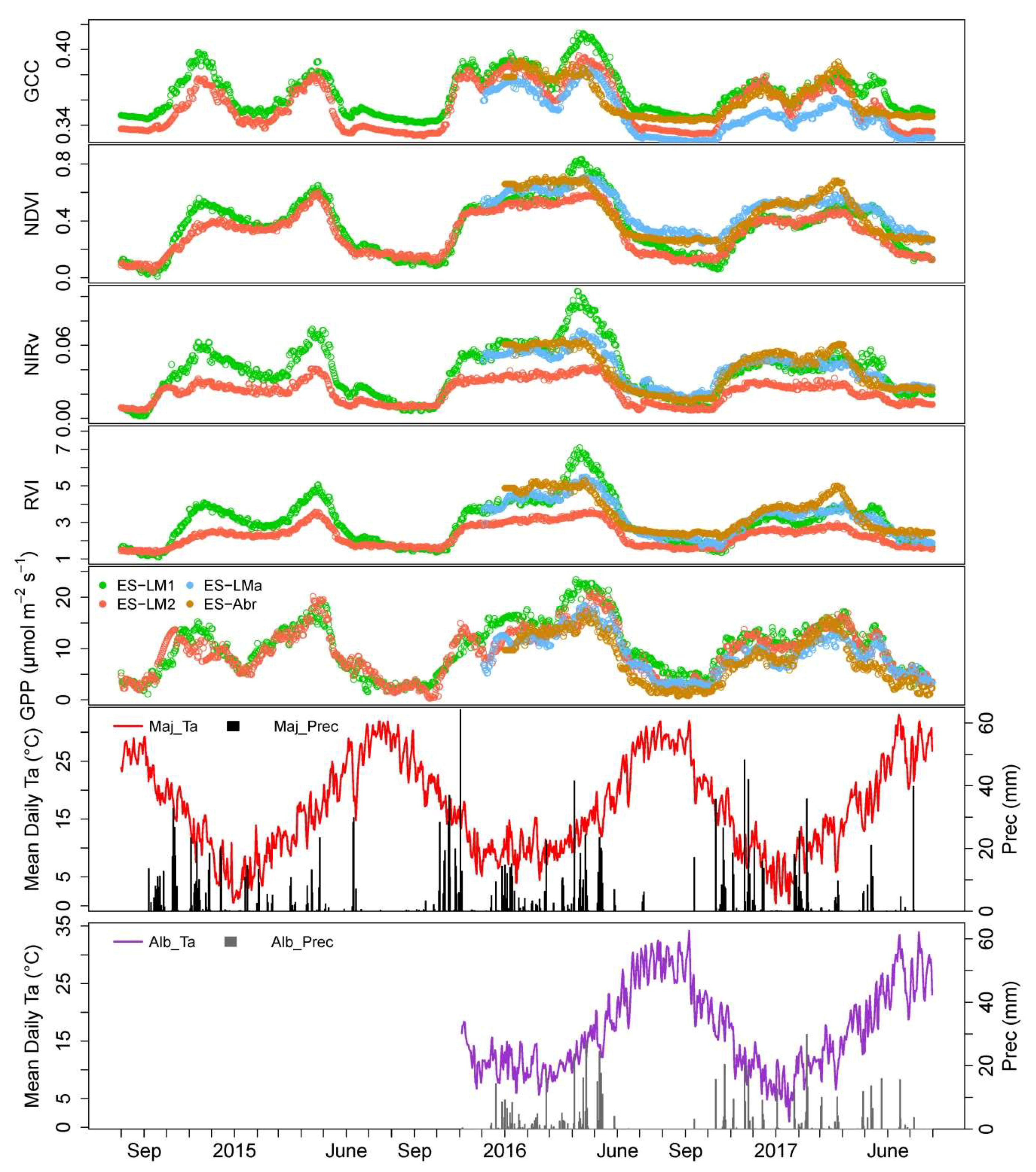
2.1. Sites Description, Instrument Set-Up, and Data Sources
2.2. EC Data Processing and Flux Partitioning to GPP
2.3. Calculation of Vegetation Indexes from PhenoCam
2.4. Data Filtering and to Compute Daily VIs and GPP
- We discarded VIs measured with PAR below 600 µmol m−2 s−1. This procedure was used, on one hand, to filter out the VI values measured during adverse meteorological conditions (i.e., rainy, foggy, or overcast half-hours [34,48]), and on the other hand, Petach et al. [29] suggests to apply a threshold on PAR to reduce the variability of CamNDVI due to changes in illumination conditions. Here, we selected a more conservative threshold than Petach et al. [29].
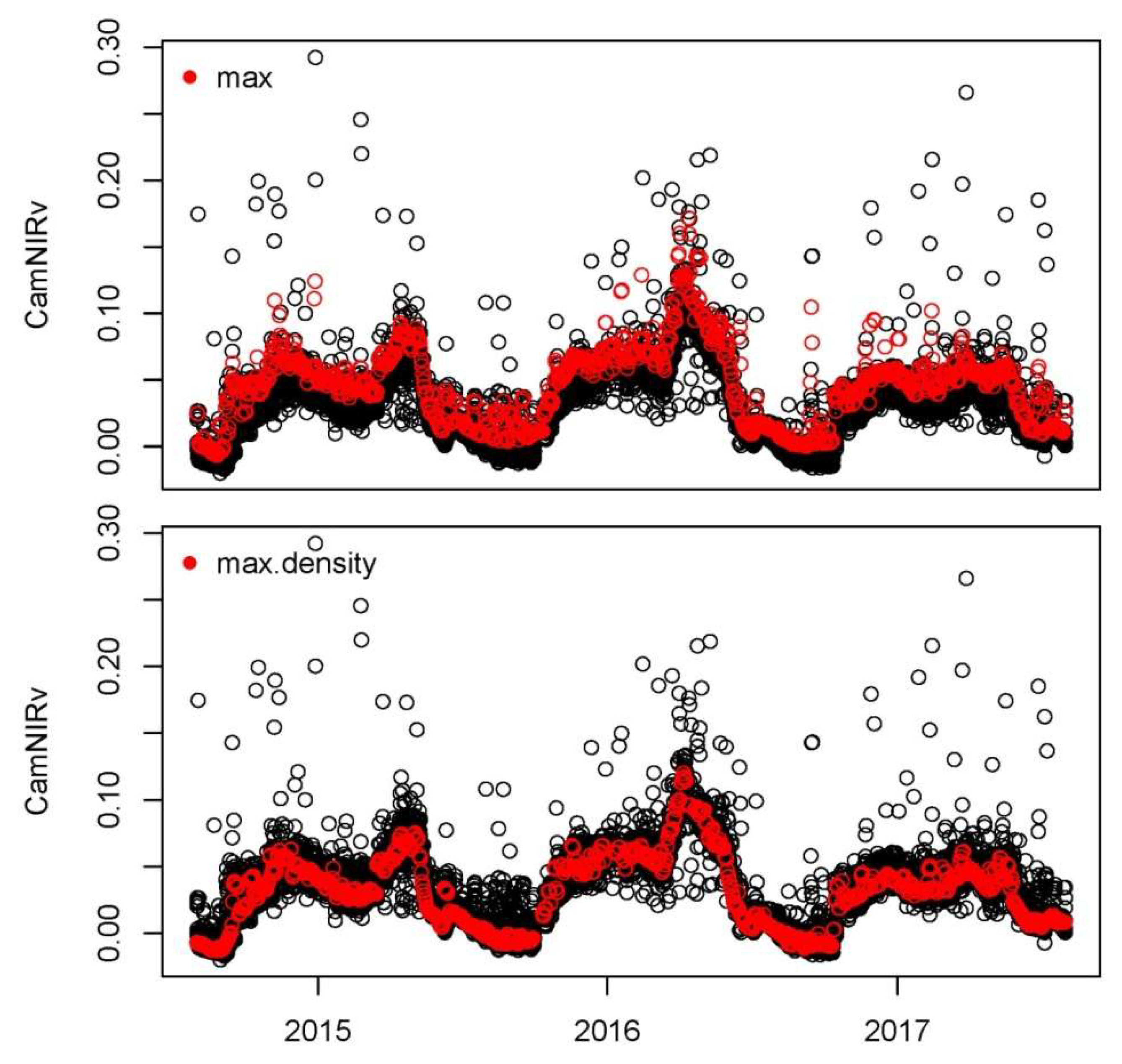
- A max.density filter method was developed to filter and retrieve daily VIs. We constructed the probability density function (PDF) of VIs in 3-day moving windows (30 observations), and assigned the value that has highest probability density as the filtered daily value. We did not apply the widely used max method [22,36], which uses the 90th percentile of the VIs value from a 3-day moving window as the filtered daily value. This is because the variability of NIRDN is larger compared to other channels (i.e., RDN, GDN, BDN) in the PhenoCam, which would result in large variability of VIs (i.e., CamNDVI, CamNIRv and CamRVI) that is especially obvious for Mediterranean ecosystems compared to other ecosystems (some comparison using data retrieved from [34], results are not shown in this study). Hence, we chose to apply the max.density filter to retrieve time series of VIs with less variability, which were not always retrieved by applying max filter in our study. We used an example to demonstrate the better filter performance of max.density compare to max filter methods in our study (Figure A1).
- Daily VIs were gap-filled using the Singular Spectrum Analysis (SSA) method implemented in the “spectral.methods” R package [60].
- Similar to the processing of VIs, the daily GPP was derived from half-hourly data following the step (2) and step (3).
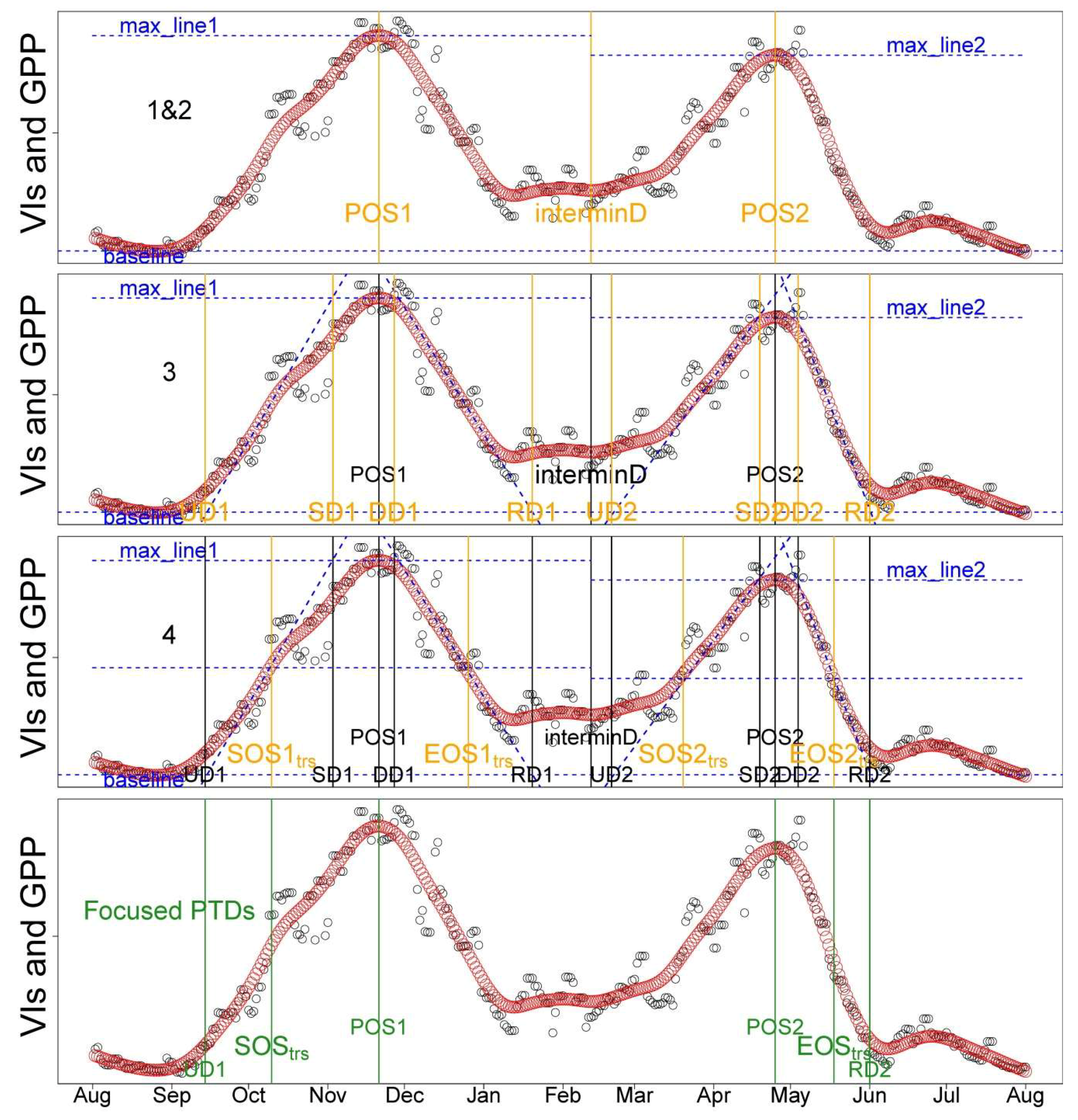
2.5. Phenological Transition Dates (PTDs) Extraction
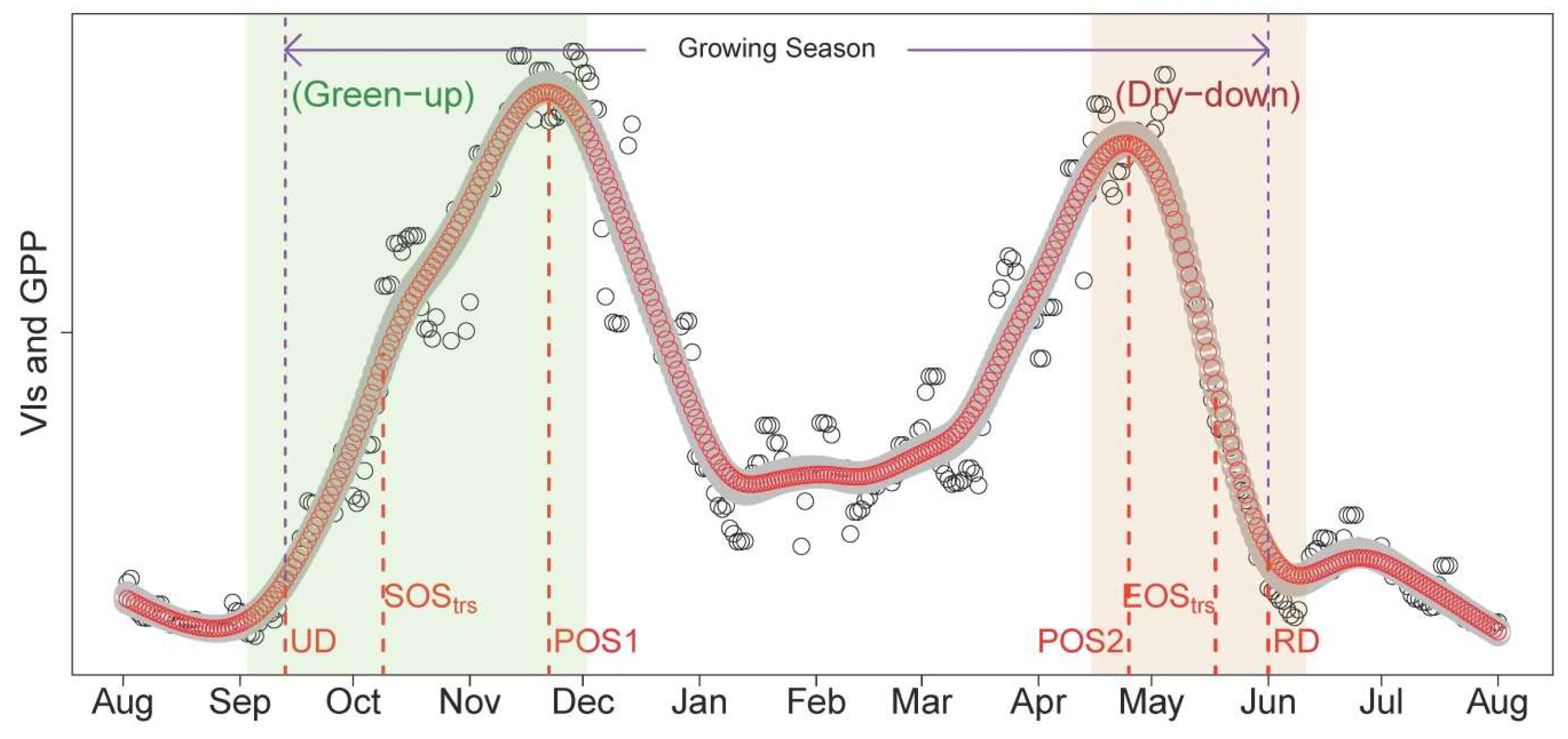
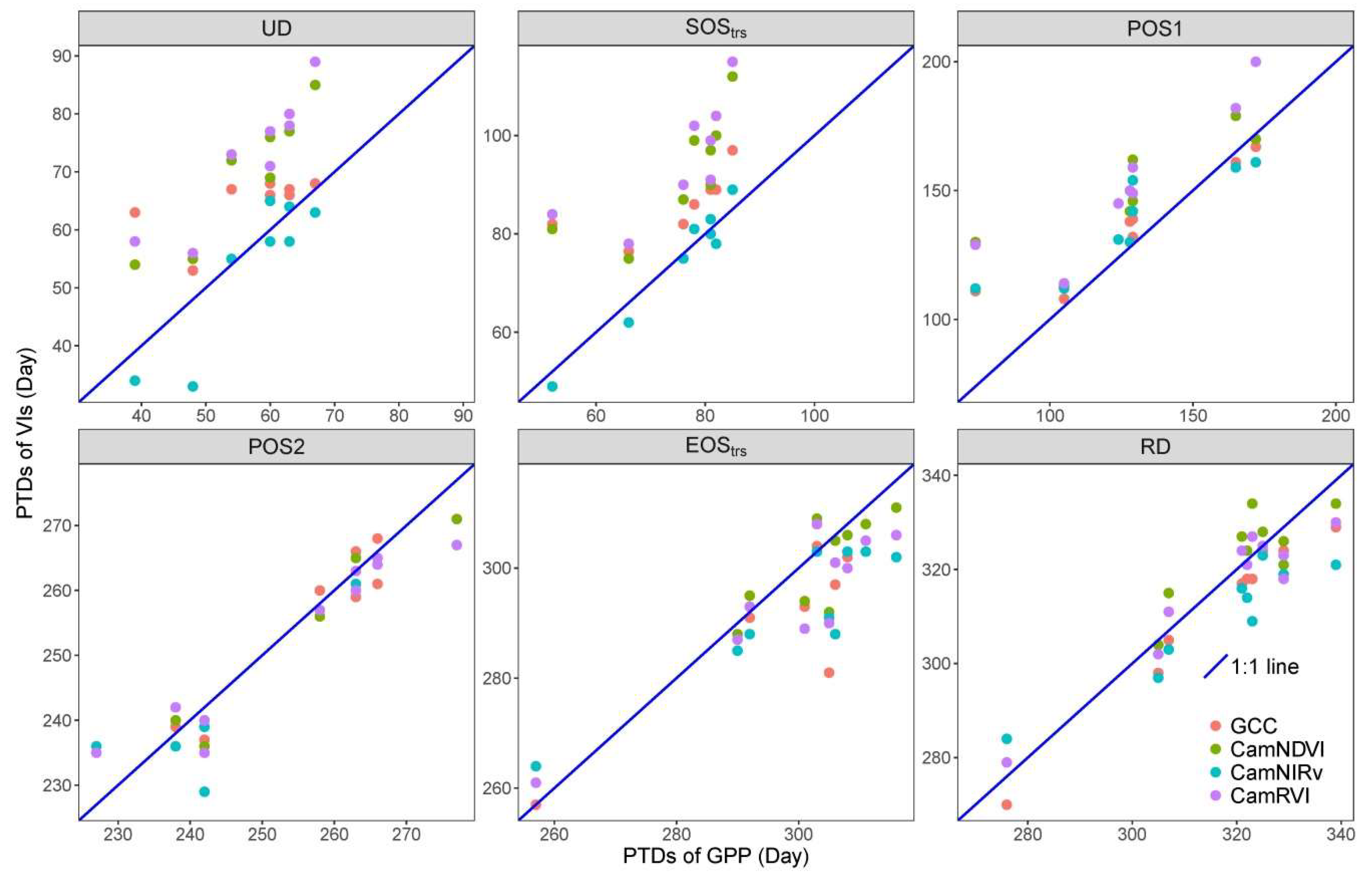
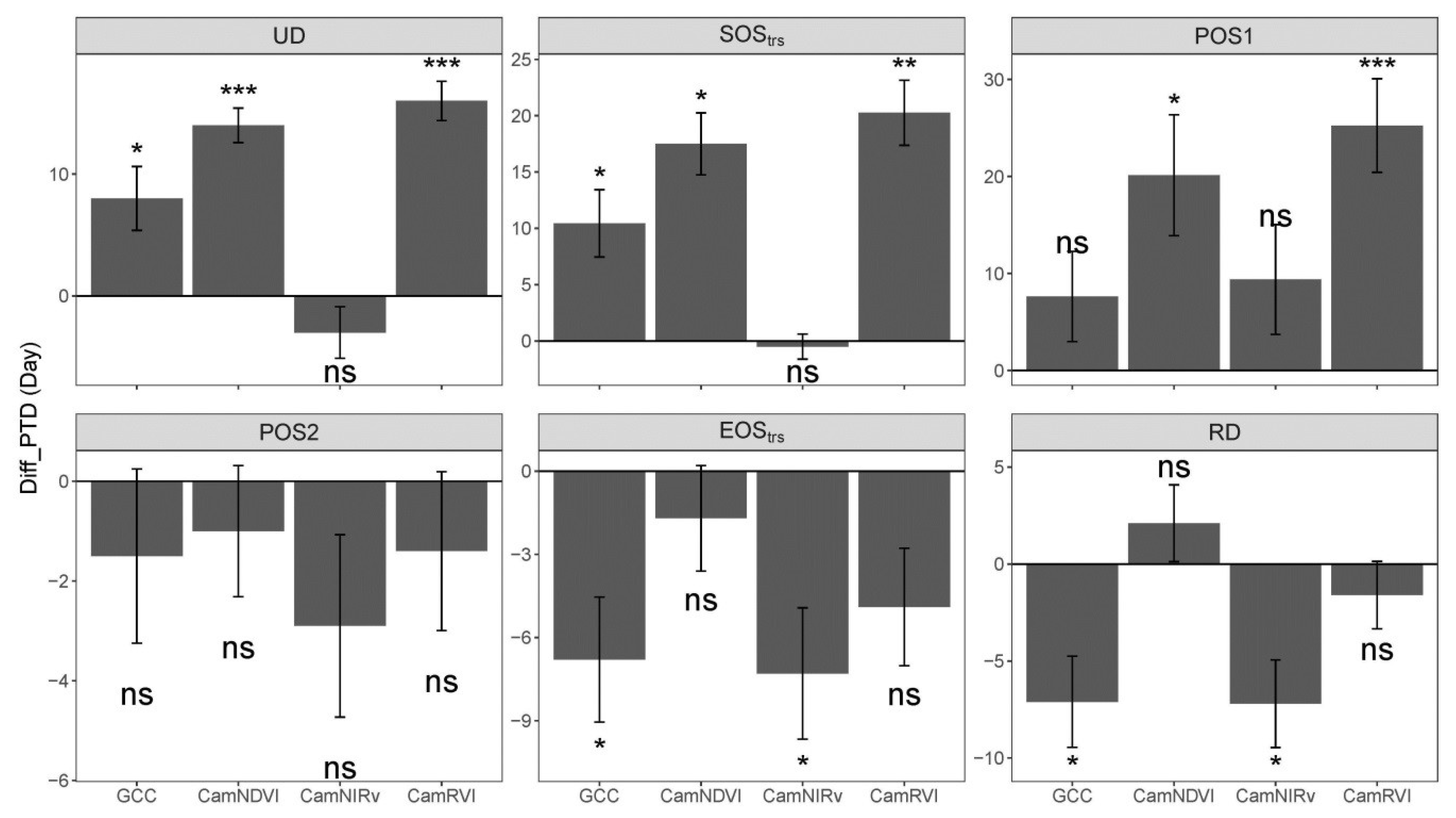
- Data were smoothed using the spline method [20,36]; PTDs were extracted using the derivatives of smoothed seasonal cycle [61] and applying thresholds (i.e., 50%) of amplitude of VIs [62]. As the start and end of the season are extremely important to characterize the phenology, we defined two sets of PTDs in the start (UD, SOStrs; Table 2) and end of season (RD, EOStrs; Table 2) for intercomparison and better characterizing the phenology. These two sets of PTDs are derived based on different perception and methodology. UD and RD are retrieved as the intersection dates between steepest slope and minimum value in the Green-up and Dry-down periods, respectively [61]. In contrast, SOStrs and EOStrs are retrieved by using the thresholds of 50% amplitude [62]; i.e., they are defined when 50% of amplitudes are reached in the Green-up and Dry-down periods, respectively. Other extracted PTDs and the phenological periods analyzed in this study were summarized in Figure 2 and Table 2. The detailed procedures and corresponding code related to the extraction of PTDs are provided in Appendix B.
- Uncertainty of extracted PTDs was assessed by extracting PTDs repeatedly (100 times) from an ensemble of time series constructed by summing original data and random noise as described by Filippa et al. [36].
2.6. Statistical Analysis
3. Results
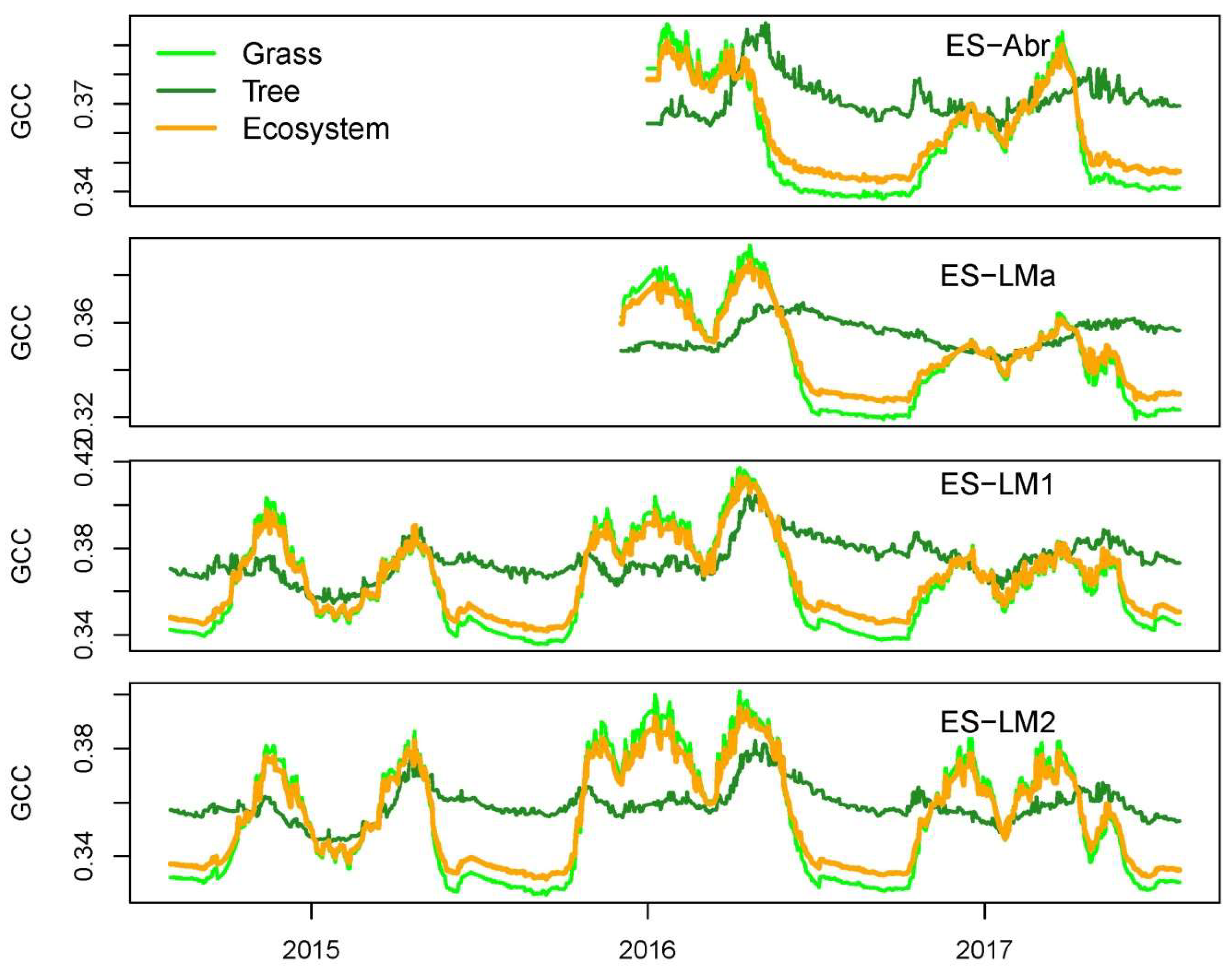
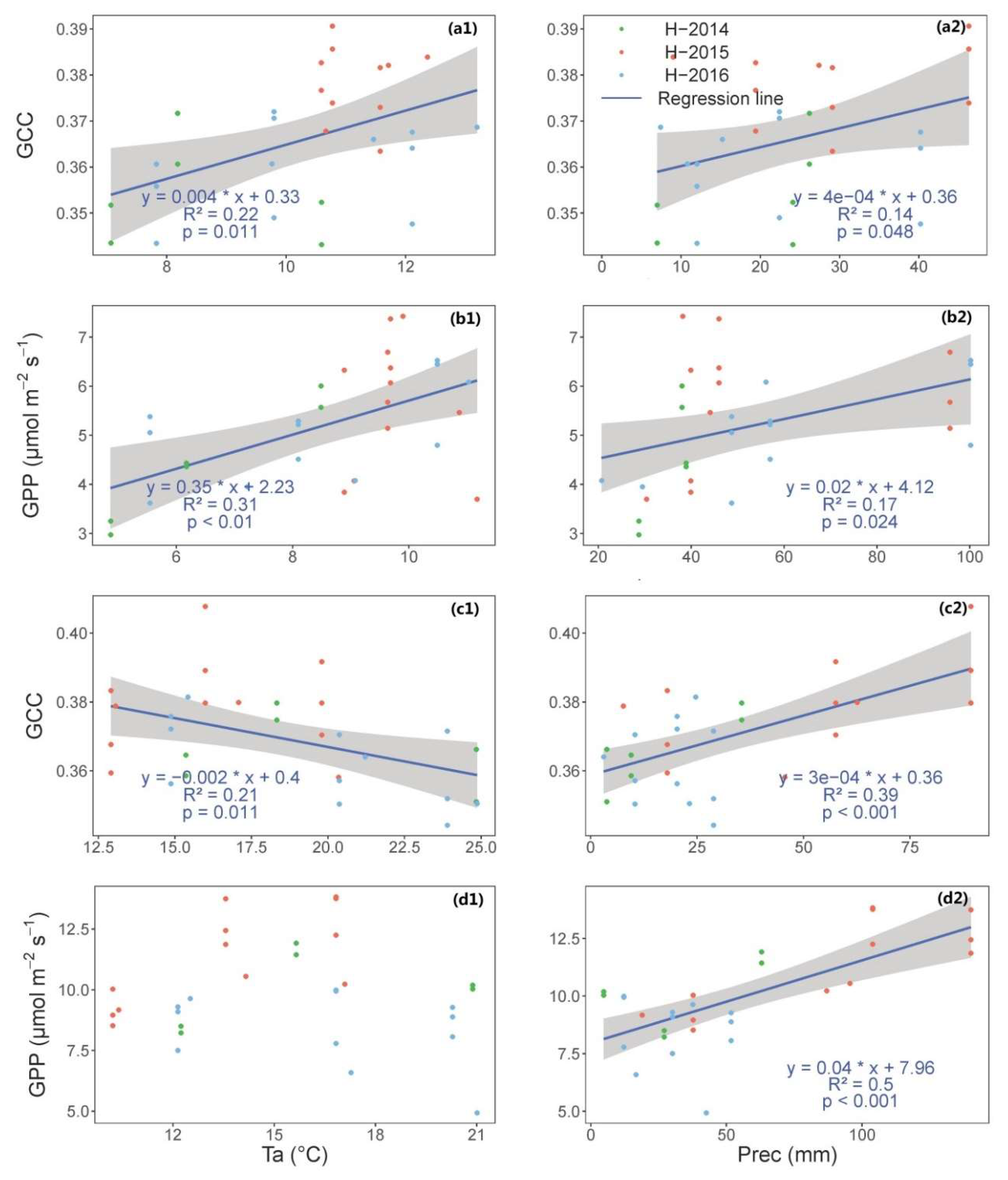
3.1. Time Series of VIs (GCC, CamNDVI, CamNIRv, CamRVI), GPP, and Their Relationship with Meteorological Conditions
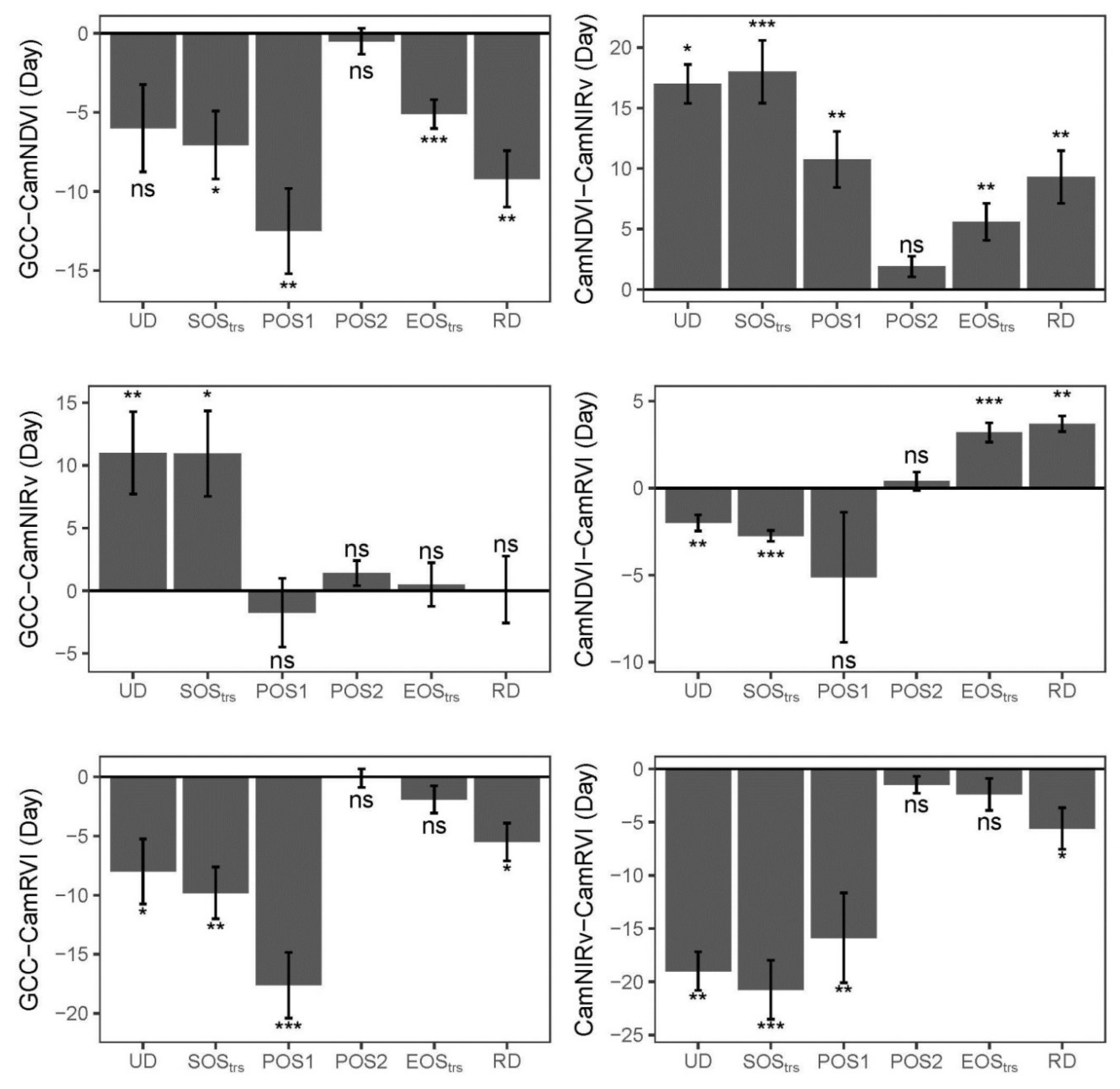
3.2. Comparison of Phenological Transition Dates (PTDs) Derived from Different VIs
3.3. Comparison of Phneological Transition Dates (PTDs) Derived from VIs and GPP
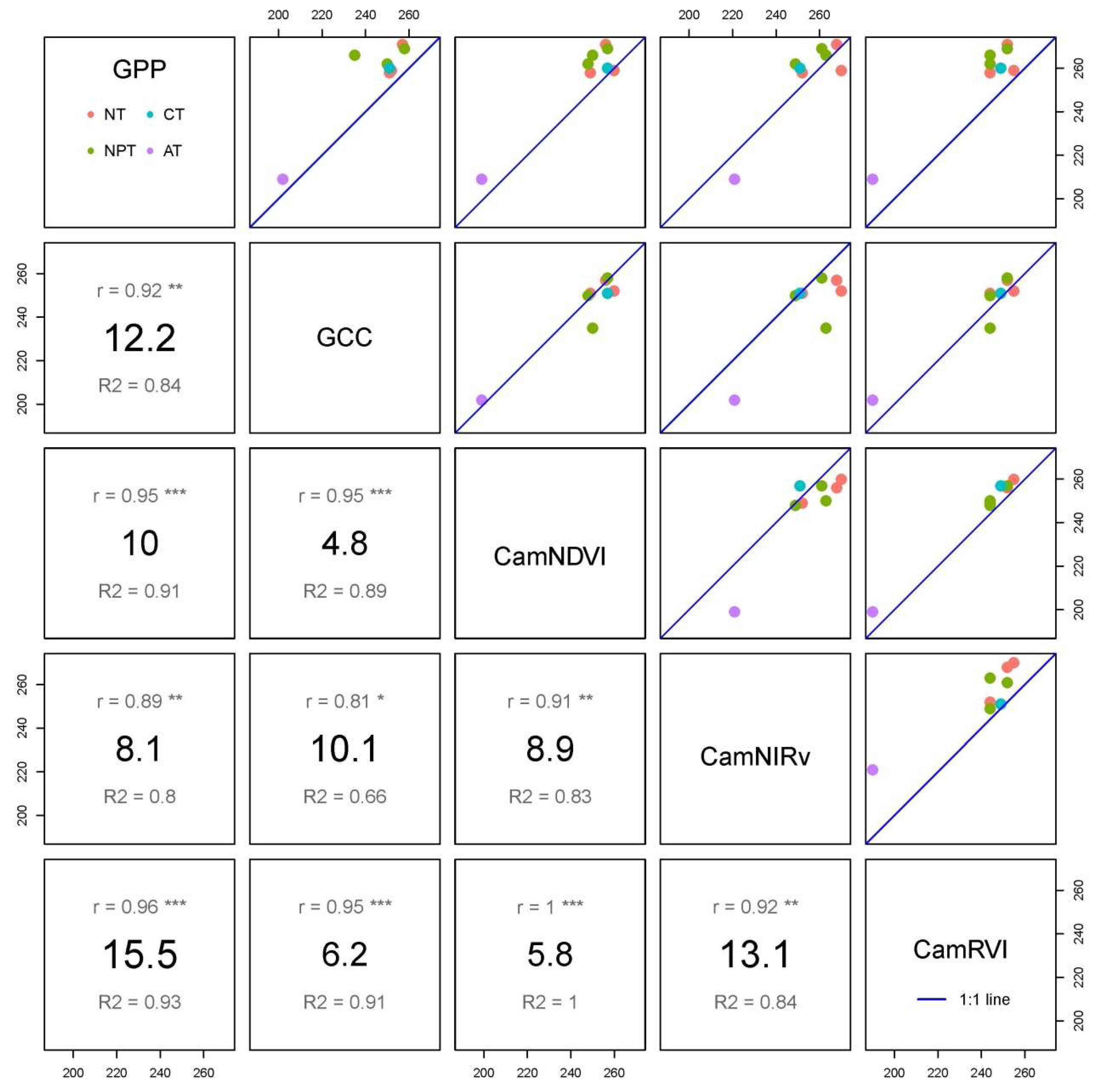
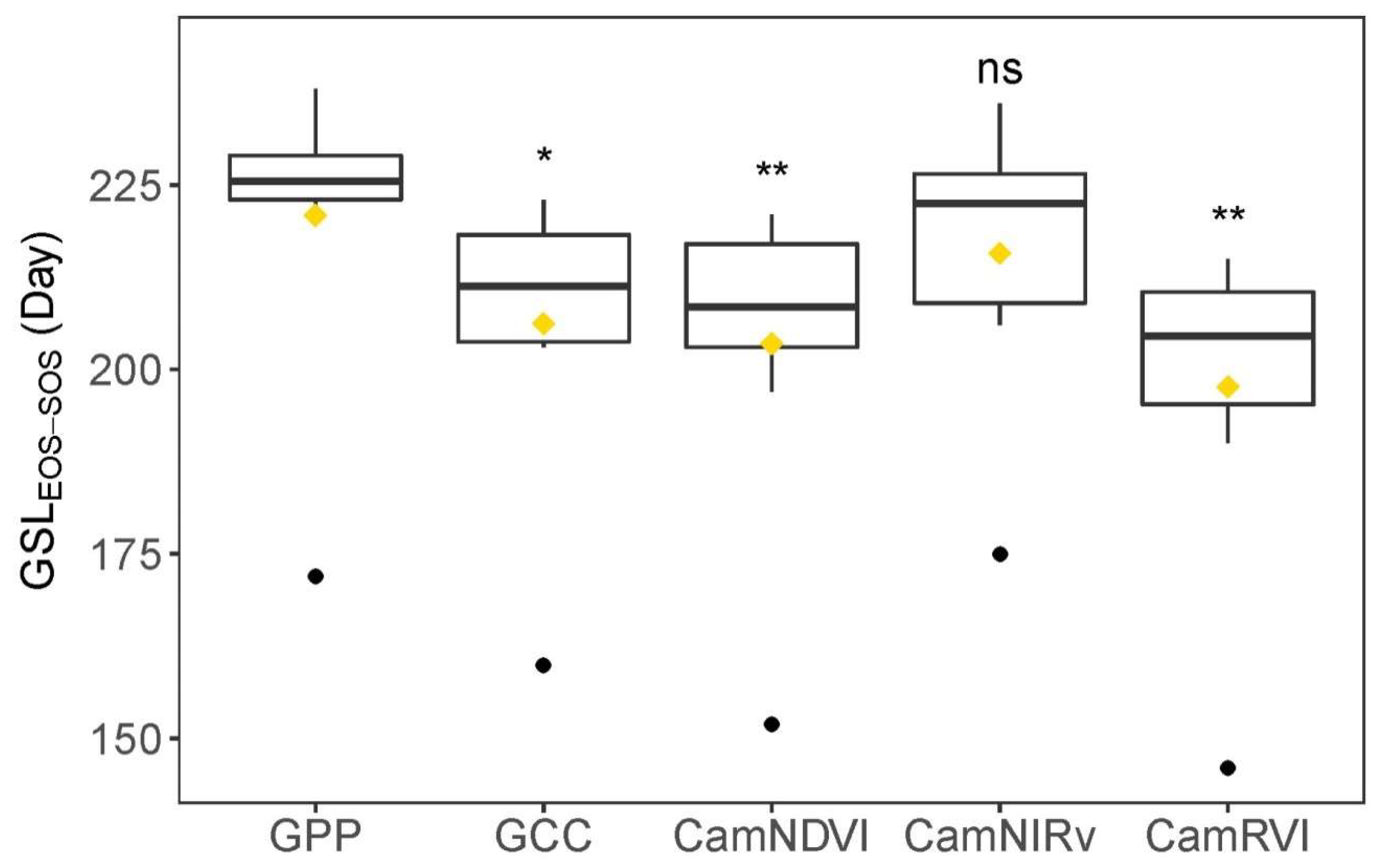
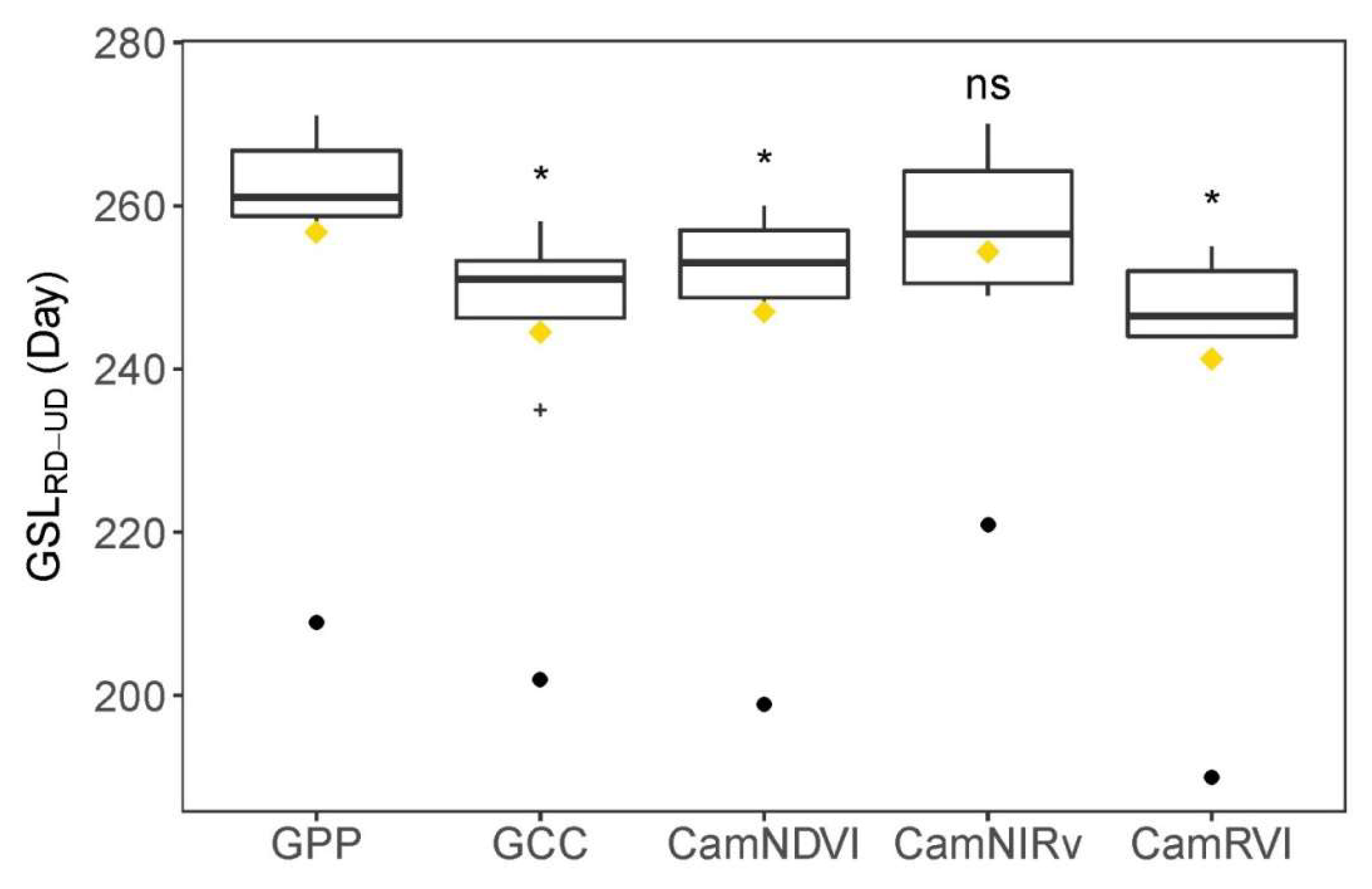
3.4. Comparison of Growing Season Length (GSL)-Derived VIs and GPP
4. Discussion
4.1. Characterizing Variatoin and Drivers of Structural and Physiological Phenology
4.2. Utilizing Different PhenoCam-Based VIs to Represent Structural Phenology
4.3. Combing Different PhenoCam-Based VIs to Represent Physiological Phenology
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
| Autumn | Winter | Spring | Summer | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (September–November) | (December–February) | (March–May) | (June–July) | |||||||||
| Ta | Prec | GPP | Ta | Prec | GPP | Ta | Prec | GPP | Ta | Prec | GPP | |
| (°C) | (mm) | (µmol m−2 s−1) | (°C) | (mm) | (µmol m−2 s−1) | (°C) | (mm) | (µmol m−2 s−1) | (°C) | (mm) | (µmol m−2 s−1) | |
| Hydro-2014 | 17.5 | 333.4 | 4.7 | 6.4 | 105.6 | 4.3 | 16.3 | 94.9 | 9.4 | 27.5 | 67.7 | 4.2 |
| Hydro-2015 | 16.8 | 296.0 | 3.6 | 9.4 | 181.6 | 5.7 | 13.5 | 281.7 | 11.7 | 26.4 | 14.1 | 7.0 |
| Hydro-2016 | 17.2 | 272.7 | 3.6 | 8.0 | 205.9 | 5.2 | 16.4 | 94.0 | 8.9 | 27.3 | 46.4 | 4.2 |
| Green-Up Period | Dry-Down Period | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GCC | CamNDVI | CamNIRv | CamRVI | GCC | CamNDVI | CamNIRv | CamRVI | |||||||||
| Stats | UD | SOStrs | UD | SOStrs | UD | SOStrs | UD | SOStrs | EOStrs | RD | EOStrs | RD | EOStrs | RD | EOStrs | RD |
| N | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| MAE (day) | 8.0 | 13.1 | 14 | 17.5 | 4.8 | 2.8 | 16 | 20.2 | 7.0 | 7.1 | 4.9 | 5.5 | 8.7 | 8.8 | 6.9 | 4.4 |
| RMSE (day) | 10.6 | 10.4 | 14.5 | 19 | 6.3 | 3.3 | 16.6 | 21.6 | 9.6 | 10.0 | 6.0 | 6.3 | 10.2 | 9.9 | 8.0 | 5.5 |
| r | 0.61 | 0.64 | 0.94 | 0.77 | 0.91 | 0.98 | 0.91 | 0.75 | 0.90 | 0.91 | 0.94 | 0.94 | 0.91 | 0.95 | 0.92 | 0.95 |
| p-value | * | * | *** | * | ns | ns | *** | ** | * | * | ns | ns | * | * | ns | ns |
Appendix B. The Procedures and Code for Extracting Phenological Transition Dates (PTDs)
- Try to find interminD. The linking point of two peaks (interminD) is the minimum between the two peaks between the Julian day of the year (Doy) 150–250.
- Once we found the interminD, the time series is split into two parts and for each part the main PTDs are computed. The date of POS is calculated by determining the date at which the maximum value of the time series (using f(t) to refer to the time series hereafter) is reached. Baseline and maxline are the minimum and maximum value in each part of f(t), respectively.
- The maximum and minimum of the first derivative of the f(t) (f’(t)) represent the maximum slopes of the upward and downward period (dashed lines). The intersections between these lines and the baseline are defined as upward day (UD) and recession day (RD). UD stands for the value when the f(t) begins to increase during the Green-up period. RD stands for the value when the f(t) stops decreasing during the Dry-down period. The intersections between these lines and maxline are the saturating day (SD) and downward day (DD). The SD indicates when the plants begin to reach full greenness or maximum photosynthesis, while DD stands for the date when plants begin to senesce [61].
- SOStrs and EOStrs are retrieved by computing the date when the value reaches 50% of the maximum in the upward and downward period, respectively [62].
References
- Dubé, P.; Perry, L.P.; Vittum, M. Instructions for Phenological Observations: Lilac and Honeysuckle; Bulletin/Vermont Agricultural Experiment Station: Burlington, NJ, USA, 1984. [Google Scholar]
- Lieth, H. Purposes of a phenology book. In Phenology and Seasonality Modeling; Springer: Berlin, Germany, 1974; pp. 3–19. [Google Scholar]
- Hollinger, D.Y.; Ollinger, S.; Richardson, A.; Meyers, T.; Dail, D.; Martin, M.; Scott, N.; Arkebauer, T.; Baldocchi, D.; Clark, K.; et al. Albedo estimates for land surface models and support for a new paradigm based on foliage nitrogen concentration. Glob. Chang. Boil. 2010, 16, 696–710. [Google Scholar] [CrossRef]
- Keenan, T.F.; Gray, J.; Friedl, M.A.; Toomey, M.; Bohrer, G.; Hollinger, D.Y.; Munger, J.W.; O’Keefe, J.; Schmid, H.P.; Wing, I.S.; et al. Net carbon uptake has increased through warming-induced changes in temperate forest phenology. Nat. Clim. Chang. 2014, 4, 598–604. [Google Scholar] [CrossRef]
- Peñuelas, J.; Rutishauser, T.; Filella, I. Phenology feedbacks on climate change. Science 2009, 324, 887. [Google Scholar] [CrossRef] [PubMed]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Forkel, M.; Migliavacca, M.; Thonicke, K.; Reichstein, M.; Schaphoff, S.; Weber, U.; Carvalhais, N. Co-dominant water control on global inter-annual variability and trends in land surface phenology and greenness. Glob. Chang. Boil. 2015, 21, 3414–3435. [Google Scholar] [CrossRef] [PubMed]
- Randerson, J.T.; Hoffman, F.M.; Thornton, P.E.; Mahowald, N.M.; Lindsay, K.; Lee, Y.H.; Nevison, C.D.; Doney, S.C.; Bonan, G.; Stöckli, R.; et al. Systematic assessment of terrestrial biogeochemistry in coupled climate–carbon models. Glob. Chang. Boil. 2009, 15, 2462–2484. [Google Scholar] [CrossRef]
- Richardson, A.D.; Anderson, R.S.; Arain, M.A.; Barr, A.G.; Bohrer, G.; Chen, G.; Chen, J.M.; Ciais, P.; Davis, K.J.; Desai, A.R.; et al. Terrestrial biosphere models need better representation of vegetation phenology: Results from the North American Carbon Program Site Synthesis. Glob. Chang. Boil. 2012, 18, 566–584. [Google Scholar] [CrossRef]
- Migliavacca, M.; Sonnentag, O.; Keenan, T.F.; Cescatti, A.; O’Keefe, J.; Richardson, A.D. On the uncertainty of phenological responses to climate change, and implications for a terrestrial biosphere model. Biogeosciences 2012, 9, 2063–2083. [Google Scholar] [CrossRef]
- Tang, J.; Körner, C.; Muraoka, H.; Piao, S.; Shen, M.; Thackeray, S.J.; Yang, X. Emerging opportunities and challenges in phenology: A review. Ecosphere 2016, 7, e01436. [Google Scholar] [CrossRef]
- Menzel, A. Phenology: Its importance to the global change community. Clim. Chang. 2002, 54, 379–385. [Google Scholar] [CrossRef]
- Basler, D.; Körner, C. Photoperiod sensitivity of bud burst in 14 temperate forest tree species. Agric. For. Meteorol. 2012, 165, 73–81. [Google Scholar] [CrossRef]
- Fu, Y.H.; Zhao, H.; Piao, S.; Peaucelle, M.; Peng, S.; Zhou, G.; Ciais, P.; Huang, M.; Menzel, A.; Peñuelas, J.; et al. Declining global warming effects on the phenology of spring leaf unfolding. Nature 2015, 526, 104–107. [Google Scholar] [CrossRef] [PubMed]
- Menzel, A. A 500 year pheno-climatological view on the 2003 heatwave in Europe assessed by grape harvest dates. Meteorol. Z. 2005, 14, 75–77. [Google Scholar] [CrossRef]
- Menzel, A.; Sparks, T.H.; Estrella, N.; Koch, E.; Aasa, A.; Ahas, R.; Alm-KÜBler, K.; Bissolli, P.; BraslavskÁ, O.G.; Briede, A.; et al. European phenological response to climate change matches the warming pattern. Glob. Chang. Boil. 2006, 12, 1969–1976. [Google Scholar] [CrossRef]
- Richardson, A.D.; Klosterman, S.; Toomey, M. Near-surface sensor-derived phenology. In Phenology: An Integrative Environmental Science; Springer: Berlin, Germany, 2013; pp. 413–430. [Google Scholar]
- Hufkens, K.; Friedl, M.; Sonnentag, O.; Braswell, B.H.; Milliman, T.; Richardson, A.D. Linking near-surface and satellite remote sensing measurements of deciduous broadleaf forest phenology. Remote Sens. Environ. 2012, 117, 307–321. [Google Scholar] [CrossRef]
- Ide, R.; Oguma, H. Use of digital cameras for phenological observations. Ecol. Inform. 2010, 5, 339–347. [Google Scholar] [CrossRef]
- Migliavacca, M.; Galvagno, M.; Cremonese, E.; Rossini, M.; Meroni, M.; Sonnentag, O.; Cogliati, S.; Manca, G.; Diotri, F.; Busetto, L.; et al. Using digital repeat photography and eddy covariance data to model grassland phenology and photosynthetic CO2 uptake. Agric. For. Meteorol. 2011, 151, 1325–1337. [Google Scholar] [CrossRef]
- Motohka, T.; Nasahara, K.N.; Oguma, H.; Tsuchida, S. Applicability of green-red vegetation index for remote sensing of vegetation phenology. Remote Sens. 2010, 2, 2369–2387. [Google Scholar] [CrossRef]
- Sonnentag, O.; Hufkens, K.; Teshera-Sterne, C.; Young, A.M.; Friedl, M.; Braswell, B.H.; Milliman, T.; O’Keefe, J.; Richardson, A.D. Digital repeat photography for phenological research in forest ecosystems. Agric. For. Meteorol. 2012, 152, 159–177. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Y.; Tan, Z.; Song, Q.; Liang, N.; Yu, L.; Zhao, J. Using digital cameras for comparative phenological monitoring in an evergreen broad-leaved forest and a seasonal rain forest. Ecol. Inform. 2012, 10, 65–72. [Google Scholar] [CrossRef]
- Brown, T.B.; Hultine, K.R.; Steltzer, H.; Denny, E.G.; Denslow, M.W.; Granados, J.; Henderson, S.; Moore, D.; Nagai, S.; SanClements, M.; et al. Using phenocams to monitor our changing Earth: Toward a global phenocam network. Front. Ecol. Environ. 2016, 14, 84–93. [Google Scholar] [CrossRef]
- Keller, M.; Schimel, D.S.; Hargrove, W.W.; Hoffman, F.M. A continental strategy for the National Ecological Observatory Network. Front. Ecol. Environ. 2008, 6, 282–284. [Google Scholar] [CrossRef]
- Nasahara, K.N.; Nagai, S. Review: Development of an in situ observation network for terrestrial ecological remote sensing: The Phenological Eyes Network (PEN). Ecol. Res. 2015, 30, 211–223. [Google Scholar] [CrossRef]
- Richardson, A.D.; Braswell, B.H.; Hollinger, D.Y.; Jenkins, J.P.; Ollinger, S.V. Near-surface remote sensing of spatial and temporal variation in canopy phenology. Ecol. Appl. 2009, 19, 1417–1428. [Google Scholar] [CrossRef] [PubMed]
- Wingate, L.; Ogée, J.; Cremonese, E.; Filippa, G.; Mizunuma, T.; Migliavacca, M.; Moisy, C.; Wilkinson, M.; Moureaux, C.; Wohlfahrt, G.; et al. Interpreting canopy development and physiology using a European phenology camera network at flux sites. Biogeosciences 2015, 12, 5995–6015. [Google Scholar] [CrossRef]
- Petach, A.R.; Toomey, M.; Aubrecht, D.M.; Richardson, A.D. Monitoring vegetation phenology using an infrared-enabled security camera. Agric. For. Meteorol. 2014, 195, 143–151. [Google Scholar] [CrossRef]
- Moore, C.E.; Beringer, J.; Evans, B.; Hutley, L.B.; Tapper, N.J. Tree–grass phenology information improves light use efficiency modelling of gross primary productivity for an Australian tropical savanna. Biogeosciences 2017, 14, 111–129. [Google Scholar] [CrossRef]
- Richardson, A.D.; Black, T.A.; Ciais, P.; Delbart, N.; Friedl, M.A.; Gobron, N.; Hollinger, D.Y.; Kutsch, W.L.; Longdoz, B.; Luyssaert, S.; et al. Influence of spring and autumn phenological transitions on forest ecosystem productivity. Philos. Trans. R. Soc. B Boil. Sci. 2010, 365, 3227–3246. [Google Scholar] [CrossRef] [PubMed]
- Toomey, M.; Friedl, M.A.; Frolking, S.; Hufkens, K.; Klosterman, S.; Sonnentag, O.; Baldocchi, D.D.; Bernacchi, C.J.; Biraud, S.C.; Bohrer, G.; et al. Greenness indices from digital cameras predict the timing and seasonal dynamics of canopy-scale photosynthesis. Ecol. Appl. 2015, 25, 99–115. [Google Scholar] [CrossRef] [PubMed]
- Richardson, A.D.; Hollinger, D.Y.; Dail, D.B.; Lee, J.T.; Munger, J.W.; O’Keefe, J. Influence of spring phenology on seasonal and annual carbon balance in two contrasting New England forests. Tree Physiol. 2009, 29, 321–331. [Google Scholar] [CrossRef] [PubMed]
- Filippa, G.; Cremonese, E.; Migliavacca, M.; Galvagno, M.; Sonnentag, O.; Humphreys, E.; Hufkens, K.; Ryu, Y.; Verfaillie, J.; di Cella, U.M.; et al. NDVI derived from near-infrared-enabled digital cameras: Applicability across different plant functional types. Agric. For. Meteorol. 2018, 249, 275–285. [Google Scholar] [CrossRef]
- Yang, H.; Yang, X.; Heskel, M.; Sun, S.; Tang, J. Seasonal variations of leaf and canopy properties tracked by ground-based NDVI imagery in a temperate forest. Sci. Rep. 2017, 7, 1267. [Google Scholar] [CrossRef] [PubMed]
- Filippa, G.; Cremonese, E.; Migliavacca, M.; Galvagno, M.; Forkel, M.; Wingate, L.; Tomelleri, E.; di Cella, U.M.; Richardson, A.D. Phenopix: AR package for image-based vegetation phenology. Agric. For. Meteorol. 2016, 220, 141–150. [Google Scholar] [CrossRef]
- Elmore, A.J.; Guinn, S.M.; Minsley, B.J.; Richardson, A.D. Landscape controls on the timing of spring, autumn, and growing season length in mid-Atlantic forests. Glob. Chang. Boil. 2012, 18, 656–674. [Google Scholar] [CrossRef]
- Graham, E.A.; Riordan, E.C.; Yuen, E.M.; Estrin, D.; Rundel, P.W. Public Internet-connected cameras used as a cross-continental ground-based plant phenology monitoring system. Glob. Chang. Boil. 2010, 16, 3014–3023. [Google Scholar] [CrossRef]
- Klosterman, S.; Hufkens, K.; Gray, J.; Melaas, E.; Sonnentag, O.; Lavine, I.; Mitchell, L.; Norman, R.; Friedl, M.; Richardson, A. Evaluating remote sensing of deciduous forest phenology at multiple spatial scales using PhenoCam imagery. Biogeosciences 2014, 11, 4305–4320. [Google Scholar] [CrossRef]
- Liang, L.; Schwartz, M.D.; Fei, S. Validating satellite phenology through intensive ground observation and landscape scaling in a mixed seasonal forest. Remote Sens. Environ. 2011, 115, 143–157. [Google Scholar] [CrossRef]
- Badgley, G.; Field, C.B.; Berry, J.A. Canopy near-infrared reflectance and terrestrial photosynthesis. Sci. Adv. 2017, 3, e1602244. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.M. Evaluation of vegetation indices and a modified simple ratio for boreal applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Liu, Y.; Hill, M.J.; Zhang, X.; Wang, Z.; Richardson, A.D.; Hufkens, K.; Filippa, G.; Baldocchi, D.D.; Ma, S.; Verfaillie, J.; et al. Using data from Landsat, MODIS, VIIRS and PhenoCams to monitor the phenology of California oak/grass savanna and open grassland across spatial scales. Agric. For. Meteorol. 2017, 237–238, 311–325. [Google Scholar] [CrossRef]
- Moore, C.E.; Beringer, J.; Evans, B.; Hutley, L.B.; Tapper, N.J. Tree-grass phenology information improves light use efficiency modelling of gross primary productivity for an Australian tropical savanna. Biogeosciences 2017, 14, 111–129. [Google Scholar] [CrossRef]
- Beringer, J.; Hutley, L.B.; Abramson, D.; Arndt, S.K.; Briggs, P.; Bristow, M.; Canadell, J.G.; Cernusak, L.A.; Eamus, D.; Edwards, A.C.; et al. Fire in Australian savannas: From leaf to landscape. Glob. Chang. Boil. 2015, 21, 62–81. [Google Scholar] [CrossRef] [PubMed]
- Grace, J.; Jose, J.S.; Meir, P.; Miranda, H.S.; Montes, R.A. Productivity and carbon fluxes of tropical savannas. J. Biogeogr. 2006, 33, 387–400. [Google Scholar] [CrossRef]
- Hanan, N.; Hill, M. Savannas in a Changing Earth System: The NASA Terrestrial Ecology Tree-Grass Project. White Paper for the NASA Terrestrial Ecology Program; Earth Science Division: Washington, DC, USA, 2012. [Google Scholar]
- Migliavacca, M.; Reichstein, M.; Richardson, A.D.; Mahecha, M.D.; Cremonese, E.; Delpierre, N.; Galvagno, M.; Law, B.E.; Wohlfahrt, G.; Andrew Black, T.; et al. Influence of physiological phenology on the seasonal pattern of ecosystem respiration in deciduous forests. Glob. Chang. Boil. 2015, 21, 363–376. [Google Scholar] [CrossRef] [PubMed]
- Perez-Priego, O.; El-Madany, T.S.; Migliavaca, M.; Kowalski, A.S.; Jung, M.; Carrara, A.; Kolle, O.; Martín, M.P.; Pacheco-Labrador, J.; Moreno, G.; et al. Evaluation of eddy covariance latent heat fluxes with independent lysimeter and sapflow estimates in a Mediterranean savannah ecosystem. Agric. For. Meteorol. 2017, 236, 87–99. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Oncley, S.P.; Stage, S.A. Sonic anemometer tilt correction algorithms. Bound.-Lay. Meteorol. 2001, 99, 127–150. [Google Scholar] [CrossRef]
- Moncrieff, J.; Clement, R.; Finnigan, J.; Meyers, T. Averaging, detrending, and filtering of eddy covariance time series. In Handbook of Micrometeorology; Springer: Berlin, Germany, 2004; pp. 7–31. [Google Scholar]
- Moncrieff, J.B.; Massheder, J.; De Bruin, H.; Elbers, J.; Friborg, T.; Heusinkveld, B.; Kabat, P.; Scott, S.; Soegaard, H.; Verhoef, A. A system to measure surface fluxes of momentum, sensible heat, water vapour and carbon dioxide. J. Hydrol. 1997, 188, 589–611. [Google Scholar] [CrossRef]
- Mauder, M.; Foken, T. Documentation and Instruction Manual of the Eddy-Covariance Software Package TK3; University of Bayreuth: Bayreuth, Germany, 2011. [Google Scholar]
- Rebmann, C.; Göckede, M.; Foken, T.; Aubinet, M.; Aurela, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Carrara, A.; Cescatti, A.; et al. Quality analysis applied on eddy covariance measurements at complex forest sites using footprint modelling. Theor. Appl. Clim. 2005, 80, 121–141. [Google Scholar] [CrossRef]
- Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Kutsch, W.; Longdoz, B.; Rambal, S.; Valentini, R.; Vesala, T.; et al. Towards a standardized processing of Net Ecosystem Exchange measured with eddy covariance technique: Algorithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Boil. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Wutzler, T.; Lucas-Moffat, A.; Migliavacca, M.; Knauer, J.; Sickel, K.; Šigut, L.; Menzer, O.; Reichstein, M. Basic and extensible post-processing of eddy covariance flux data with REddyProc. Biogeosci. Discuss. 2018. [Google Scholar] [CrossRef]
- Pacheco-Labrador, J.; El-Madany, T.S.; Martín, M.P.; Migliavacca, M.; Rossini, M.; Carrara, A.; Zarco-Tejada, P.J. Spatio-Temporal Relationships between Optical Information and Carbon Fluxes in a Mediterranean Tree-Grass Ecosystem. Remote Sens. 2017, 9, 608. [Google Scholar] [CrossRef]
- EI-Madany, T.S.; Reichstein, M.; Perez-Priego, O.; Carrara, A.; Moreno, G.; Martín, M.P.; Pacheco-Labrador, J.; Wohlfahrt, G.; Nieto, H.; Weber, U.; et al. Drivers of spatio-temporal variability of carbon dioxide and energy fluxes in a Mediterranean savanna ecosystem. Agric. For. Meteorol. 2018, 262, 258–278. [Google Scholar] [CrossRef]
- Von Buttlar, J.; Zscheischler, J.; Mahecha, M.D. An extended approach for spatiotemporal gapfilling: Dealing with large and systematic gaps in geoscientific datasets. Nonlinear Process. Geophys. 2014, 21, 203–215. [Google Scholar] [CrossRef]
- Gu, L.; Post, W.M.; Baldocchi, D.D.; Black, T.A.; Suyker, A.E.; Verma, S.B.; Vesala, T.; Wofsy, S.C. Characterizing the seasonal dynamics of plant community photosynthesis across a range of vegetation types. In Phenology of Ecosystem Processes; Springer: Berlin, Germany, 2009; pp. 35–58. [Google Scholar]
- White, M.A.; Thornton, P.E.; Running, S.W. A continental phenology model for monitoring vegetation responses to interannual climatic variability. Glob. Biogeochem. Cycles 1997, 11, 217–234. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing 2014 [Internet]; R Foundation for Statistical Computing: Vienna, Austria, 2015. [Google Scholar]
- Baldocchi, D.D.; Xu, L.; Kiang, N. How plant functional-type, weather, seasonal drought, and soil physical properties alter water and energy fluxes of an oak–grass savanna and an annual grassland. Agric. For. Meteorol. 2004, 123, 13–39. [Google Scholar] [CrossRef]
- Moreno, G.; Cubera, E. Impact of stand density on water status and leaf gas exchange in Quercus ilex. For. Ecol. Manag. 2008, 254, 74–84. [Google Scholar] [CrossRef]
- Rolo, V.; Moreno, G. Interspecific competition induces asymmetrical rooting profile adjustments in shrub-encroached open oak woodlands. Trees 2012, 26, 997–1006. [Google Scholar] [CrossRef]
- Ward, D.; Wiegand, K.; Getzin, S. Walter’s two-layer hypothesis revisited: Back to the roots! Oecologia 2013, 172, 617–630. [Google Scholar] [CrossRef] [PubMed]
- Hatfield, J.L.; Prueger, J.H. Temperature extremes: Effect on plant growth and development. Weather Clim. Extremes 2015, 10, 4–10. [Google Scholar] [CrossRef]
- Allard, V.; Ourcival, J.; Rambal, S.; Joffre, R.; Rocheteau, A. Seasonal and annual variation of carbon exchange in an evergreen Mediterranean forest in southern France. Glob. Chang. Boil. 2008, 14, 714–725. [Google Scholar] [CrossRef]
- Diodato, N.; Bellocchi, G. Modelling vegetation greenness responses to climate variability in a Mediterranean terrestrial ecosystem. Environ. Monit. Assess. 2008, 143, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Baldocchi, D.D.; Xu, L.; Hehn, T. Inter-annual variability in carbon dioxide exchange of an oak/grass savanna and open grassland in California. Agric. For. Meteorol. 2007, 147, 157–171. [Google Scholar] [CrossRef]
- Sippel, S.; El-Madany, T.S.; Migliavacca, M.; Mahecha, M.D.; Carrara, A.; Flach, M.K.T.; Thonicke, K.; Vossbeck, M.; Reichstein, M. Warm Winter, Wet Spring and an Extreme Response in Ecosystem Functioning on the Iberian Peninsula. Special issue: Explaining Extreme Events from a Climate Perspective. Bull. Am. Meteor. Soc. 2018, 98, 80–85. [Google Scholar] [CrossRef]
- Choler, P.; Sea, W.; Briggs, P.; Raupach, M.; Leuning, R. A simple ecohydrological model captures essentials of seasonal leaf dynamics in semi-arid tropical grasslands. Biogeosciences 2010, 7, 907–920. [Google Scholar] [CrossRef]
- Hufkens, K.; Keenan, T.F.; Flanagan, L.B.; Scott, R.L.; Bernacchi, C.J.; Joo, E.; Brunsell, N.A.; Verfaillie, J.; Richardson, A.D. Productivity of North American grasslands is increased under future climate scenarios despite rising aridity. Nat. Clim. Chang. 2016, 6, 710–714. [Google Scholar] [CrossRef]
- Keenan, T.; Darby, B.; Felts, E.; Sonnentag, O.; Friedl, M.; Hufkens, K.; O’Keefe, J.; Klosterman, S.; Munger, J.W.; Toomey, M.; et al. Tracking forest phenology and seasonal physiology using digital repeat photography: A critical assessment. Ecol. Appl. 2014, 24, 1478–1489. [Google Scholar] [CrossRef] [PubMed]
- Ryu, Y.; Lee, G.; Jeon, S.; Song, Y.; Kimm, H. Monitoring multi-layer canopy spring phenology of temperate deciduous and evergreen forests using low-cost spectral sensors. Remote Sens. Environ. 2014, 149, 227–238. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.; Mustard, J.F. Beyond leaf color: Comparing camera-based phenological metrics with leaf biochemical, biophysical, and spectral properties throughout the growing season of a temperate deciduous forest. J. Geophys. Res. Biogeosci. 2014, 119, 181–191. [Google Scholar] [CrossRef]
- Migliavacca, M.; Perez-Priego, O.; Rossini, M.; El-Madany, T.S.; Moreno, G.; van der Tol, C.; Rascher, U.; Berninger, A.; Bessenbacher, V.; Burkart, A.; et al. Plant functional traits and canopy structure control the relationship between photosynthetic CO2 uptake and far-red sun-induced fluorescence in a Mediterranean grassland under different nutrient availability. New Phytol. 2017, 214, 1078–1091. [Google Scholar] [CrossRef] [PubMed]
- Viña, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Vrieling, A.; Meroni, M.; Darvishzadeh, R.; Skidmore, A.K.; Wang, T.; Zurita-Milla, R.; Oosterbeek, K.; O’Connor, B.; Paganini, M. Vegetation phenology from Sentinel-2 and field cameras for a Dutch barrier island. Remote Sens. Environ. 2018, 215, 517–529. [Google Scholar] [CrossRef]
- Linderholm, H.W. Growing season changes in the last century. Agric. For. Meteorol. 2006, 137, 1–14. [Google Scholar] [CrossRef]
- Churkina, G.; Schimel, D.; Braswell, B.H.; Xiao, X. Spatial analysis of growing season length control over net ecosystem exchange. Glob. Chang. Boil. 2005, 11, 1777–1787. [Google Scholar] [CrossRef]
- White, M.; Running, S.; Thornton, P. The impact of growing-season length variability on carbon assimilation and evapotranspiration over 88 years in the eastern US deciduous forest. Int. J. Biometeorol. 1999, 42, 139–145. [Google Scholar] [CrossRef] [PubMed]
- Yengoh, G.T.; Dent, D.; Olsson, L.; Tengberg, A.E.; Tucker, C.J., III. Use of the Normalized Difference Vegetation Index (NDVI) to Assess Land Degradation at Multiple Scales: Current Status, Future Trends, and Practical Considerations; Springer: Berlin, Germany, 2015. [Google Scholar]
- Peng, Y.; Gitelson, A.A. Application of chlorophyll-related vegetation indices for remote estimation of maize productivity. Agric. For. Meteorol. 2011, 151, 1267–1276. [Google Scholar] [CrossRef]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Yang, J.; Tian, H.; Pan, S.; Chen, G.; Zhang, B.; Dangal, S. Amazon droughts and forest responses: Largely reduced forest photosynthesis but slightly increased canopy greenness during the extreme drought of 2015/2016. Glob. Chang. Boil. 2018. [Google Scholar] [CrossRef] [PubMed]
| Site | VIs | N | Intercept | Slope | R2 |
|---|---|---|---|---|---|
| ES-LM1 | NDVI | 4000 | 0.60 | 1.51 | 0.69 |
| NIRv | 3282 | 0.06 | 0.01 | 0.60 | |
| RVI | 3389 | −2.03 | 6.61 | 0.54 | |
| ES-LM2 | NDVI | 4340 | 0.56 | 1.12 | 0.77 |
| NIRv | 4223 | 0.04 | 0.01 | 0.55 | |
| RVI | 4268 | −0.14 | 3.55 | 0.57 | |
| ES-LMa | NDVI | 3549 | 0.67 | 0.89 | 0.89 |
| NIRv | 3522 | 0.06 | 0.01 | 0.73 | |
| RVI | 3515 | −0.20 | 5.17 | 0.84 | |
| ES-Abr | NDVI | 3560 | 0.64 | 1.18 | 0.83 |
| NIRv | 3361 | 0.06 | 0.01 | 0.82 | |
| RVI | 3564 | −0.78 | 5.39 | 0.80 |
| Terms | Description | |
|---|---|---|
| Phenological Transition Dates (PTDs) | UD | Upturn day in the green up period in the autumn |
| SOStrs | When 50% of amplitude in the green up period in the autumn is reached | |
| POS1 | When the first peak of season is reached | |
| POS2 | When the second peak of season is reached | |
| EOStrs | When 50% of amplitude in the senescent period in the summer is reached | |
| RD | Recession day at the end of senescent period in the summer | |
| Phenological periods | Green-up | Greenness/GPP increasing period in the autumn (including UD, SOStrs, and POS1) |
| Dry-down | Greenness/GPP decreasing period in the summer (including POS2, EOStrs and RD) | |
| GSLRD-UD | Growing season length defined in the hydrological year (day length between UD and RD) | |
| GSLEOS-SOS | Growing season length defined for comparison with GSLRD-UD (day length between EOStrs and SOStrs, which is widely used in land surface phenology) |
| Site | VIs-GPP | N | r |
|---|---|---|---|
| ES-LM1 | GCC | 1096 | 0.90 |
| CamNDVI | 1096 | 0.91 | |
| CamNIRv | 1096 | 0.93 | |
| CamRVI | 1096 | 0.91 | |
| ES-LM2 | GCC | 1096 | 0.86 |
| CamNDVI | 1096 | 0.87 | |
| CamNIRv | 1096 | 0.87 | |
| CamRVI | 1096 | 0.87 | |
| ES-LMa | GCC | 607 | 0.89 |
| CamNDVI | 607 | 0.90 | |
| CamNIRv | 607 | 0.85 | |
| CamRVI | 607 | 0.90 | |
| ES-Abr | GCC | 635 | 0.86 |
| CamNDVI | 635 | 0.91 | |
| CamNIRv | 635 | 0.86 | |
| CamRVI | 635 | 0.91 |
| Season Summary | ||||||||
|---|---|---|---|---|---|---|---|---|
| GCC | CamNDVI | CamNIRv | CamRVI | |||||
| Stats | Green-Up | Dry-Down | Green-Up | Dry-Down | Green-Up | Dry-Down | Green-Up | Dry-Down |
| N | 24 | 30 | 24 | 30 | 24 | 30 | 24 | 30 |
| MAE (day) | 9.4 | 6.3 | 17.4 | 4.6 | 7.0 | 7.4 | 20.5 | 5.0 |
| RMSE (day) | 12.8 | 8.6 | 20.4 | 5.5 | 11.0 | 8.9 | 22.7 | 6.3 |
| p-value | *** | *** | *** | ns | ns | *** | *** | * |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; El-Madany, T.S.; Filippa, G.; Ma, X.; Ahrens, B.; Carrara, A.; Gonzalez-Cascon, R.; Cremonese, E.; Galvagno, M.; Hammer, T.W.; et al. Using Near-Infrared-Enabled Digital Repeat Photography to Track Structural and Physiological Phenology in Mediterranean Tree–Grass Ecosystems. Remote Sens. 2018, 10, 1293. https://doi.org/10.3390/rs10081293
Luo Y, El-Madany TS, Filippa G, Ma X, Ahrens B, Carrara A, Gonzalez-Cascon R, Cremonese E, Galvagno M, Hammer TW, et al. Using Near-Infrared-Enabled Digital Repeat Photography to Track Structural and Physiological Phenology in Mediterranean Tree–Grass Ecosystems. Remote Sensing. 2018; 10(8):1293. https://doi.org/10.3390/rs10081293
Chicago/Turabian StyleLuo, Yunpeng, Tarek S. El-Madany, Gianluca Filippa, Xuanlong Ma, Bernhard Ahrens, Arnaud Carrara, Rosario Gonzalez-Cascon, Edoardo Cremonese, Marta Galvagno, Tiana W. Hammer, and et al. 2018. "Using Near-Infrared-Enabled Digital Repeat Photography to Track Structural and Physiological Phenology in Mediterranean Tree–Grass Ecosystems" Remote Sensing 10, no. 8: 1293. https://doi.org/10.3390/rs10081293
APA StyleLuo, Y., El-Madany, T. S., Filippa, G., Ma, X., Ahrens, B., Carrara, A., Gonzalez-Cascon, R., Cremonese, E., Galvagno, M., Hammer, T. W., Pacheco-Labrador, J., Martín, M. P., Moreno, G., Perez-Priego, O., Reichstein, M., Richardson, A. D., Römermann, C., & Migliavacca, M. (2018). Using Near-Infrared-Enabled Digital Repeat Photography to Track Structural and Physiological Phenology in Mediterranean Tree–Grass Ecosystems. Remote Sensing, 10(8), 1293. https://doi.org/10.3390/rs10081293







