1. Introduction
Image fusion can be defined as the fusion of two or more images of different properties or modalities such that the fused image has the same properties as the source images, e.g., spatial and spectral resolution, and is thus more informative. The fusion process must, as best as possible, preserve the salient information found in each source image, and it must avoid introducing spectral and/or spatial distortion into the fused image.
One of the earliest and most established types of image fusion in remote sensing is so-called pansharpening [
1,
2]. There, a multispectral (MS) image of high spectral resolution but low spatial resolution is fused with a single band panchromatic (PAN) image of high spatial resolution to yield a high spatial resolution MS image, which has the same spatial resolution as the PAN image and the same spectral resolution of the original MS image. By performing this kind of image fusion, more use is made of the available data, and this can be useful for many applications such as classification [
3], target detection, snow cover analysis [
4], etc. In recent years, more fusion scenarios are becoming possible, such as the fusion of hyperspectral (HS) images and PAN images, referred to as hypersharpening [
5,
6,
7,
8,
9,
10] to yield HS images of high spatial resolution and the fusion of MS and HS images [
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22] to yield high spatial resolution HS images. Both MS/HS fusion and hypersharpening can be seen as extensions of the pansharpening problem, where the source images have more bands.
What all these fusion problems have in common is that there is significant spectral overlap between the low and high spatial resolution source images. For example, in pansharpening, the PAN image is a wide-band image of a single channel which means that the PAN sensor is sensitive to a wide band of the electromagnetic spectrum. The spectral response of the MS sensor has a significant overlap with the spectral response of the PAN sensor. Recently, more advanced MS sensors have been developed, which acquire images from more spectral bands covering a wider band of the electromagnetic spectrum. The Sentinel-2 constellation of satellites operated by the European Space Agency (ESA), and the Worldview-3 and Worldview-4 satellites operated by DigitalGlobe (Westminster, CA, USA), are examples of such sensors. They typically acquire images in the visible, near-infrared (NIR) and shortwave infrared (SWIR) regions of the electromagnetic spectrum, and at different spatial resolution. For example, the Sentinel-2 sensor acquires four bands at 10 m resolution (ground sampling distance), six bands at 20 m resolution and three bands at 60 m resolution.
Since all the acquired images show the same scene, this presents an opportunity for single sensor image fusion or super-resolution, i.e., to enhance the resolution of the coarse resolution bands using information from the finer bands. However, due to the lack of spectral overlap between bands, this problem is more challenging than the pansharpening problem. A widely used constraint in pansharpening is that a linear combination of the fused bands gives an approximation to the PAN image. This constraint makes the problem easier to solve. However, in the single sensor case, this assumption is false since the bands are spectrally disjoint.
Several methods have been developed to fuse spectrally disjoint images. In [
23], the 90 m resolution thermal bands of the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) were sharpened using data from the 15 m resolution Visible Near Infrared (VNIR) bands using a method based on Generalized Laplacian Pyramid (GLP) [
24]. The 20 m bands of Sentinel-2 were sharpened in [
25] using geostatical stochastic simulation and genetic programming. The 500 m resolution bands of the Moderate Resolution Imaging Spectroradiometer (MODIS) were upscaled to 250 m resolution in [
26] using area-to-point regression kriging (ATPRK). Wavelet multiresolution analysis was used to enhance the 500 m bands using the 250 m bands in [
4]. Sentinel-2 super-resolution was performed in [
27] by solving a convex deconvolution problem in a lower dimensional subspace and using a roughness penalty as a regularizer, and its extension was given in [
28], by using cyclic decent on a manifold. A two-stage method for Sentinel-2 fusion was given in [
29] that separates band-dependent geometrical information from band specific reflectance and then applies this model to the lower resolution bands while preserving their reflectance using spectral unmixing techniques.
Recently, deep learning based methods have been demonstrated to outperform traditional signal processing approaches in areas such as speech and pattern recognition [
30]. These are methods based on deep neural networks, and specifically in pattern recognition and related fields [
31,
32], the so-called convolutional neural network (CNN) has been shown to be effective. Deep learning methods have been used to solve the pansharpening problem [
33,
34,
35], multispectral/hyperspectral image fusion [
11], and super-resolution [
36]. In [
37], the authors trained a deep residual neural network to super-resolve Sentinel-2 images using extensive training data with global coverage. In this study, we focus more on the single image case and provide a study of how the performance of the network is affected by several important hyperparameters of the method. It is not meant to find an optimal set of the hyperparameters, but rather to study the effects of each hyperparameter on the quantitative quality metric values. However, hyperparameter tuning for deep learning algorithms is an important issue, and several methods have been proposed to automate this task. In [
38,
39], particle swarm optimization was used, Ref. [
40] used greedy sequential algorithms using the expected improvement criterion, Ref. [
41] used the Covariance Matrix Adaptation Evolution Strategy (CMA-ES), Ref. [
42] used Bayesian optimization based on Gaussian Processes, and, finally, Ref. [
43] extrapolated learning curves to speed up the task of parameter selection.
Residual neural networks (ResNets) [
44] have recently been shown to give good performance in image recognition tasks. The residual design allows deeper networks to be trained more easily and there is indeed evidence that deeper networks perform better than shallower nets [
30].
In this paper, we propose a method for single sensor image fusion based on a deep residual neural network architecture. The network consists of a number of residual blocks, where each residual block contains two convolutional (conv) layers. The last layer in each block is an element-wise sum layer where the output of the layer preceding the block is added to its output. Apart from the residual blocks, there is also an important residual aspect to the network inspired by the fusion model. The upscaled coarse part of the input is added to the last layer of the network, relieving it from having to learn the low-pass structure of the image. The lack of high-resolution reference during training is circumvented by reducing the resolution of the observed data before training, by the resolution ratio between the coarse and fine bands. Therefore, the observed coarse bands can be used as the reference or target during training. This strategy is inspired by Wald’s protocol [
45], and is commonly used in image fusion in remote sensing to evaluate the performance of fusion methods. The assumption being made here is that the relationship learned between the reduced resolution level and the observed level also applies to the higher level [
46].
We perform several experiments using real Sentinel-2 datasets and compare the proposed method to three state-of-the-art methods for single sensor fusion. These are the model-based Super-Resolution for Multispectral Multiresolution Estimation (SupReME) method from [
27], the Area-To-Point Regression Kriging (ATPRK) method from [
47] and the Superres method from [
29].
The outline of this paper is as follows. In
Section 2, we give a brief overview of residual networks and describe the proposed method in detail. In
Section 3, we discuss implementation issues, choice of hyperparameters, experimental results, and finally, in
Section 4, the conclusions are drawn.
2. The ResNet
Recently, deep and very deep CNNs have been demonstrated to perform significantly better than shallower networks in many image recognition tasks [
30,
48,
49]. In general, deep networks are difficult to train due to the problem of vanishing/exploding gradients [
50,
51], however this has currently been largely mitigated by techniques such as batch-normalization [
52], self normalizing networks [
53] and better initialization techniques [
51,
54]. Still, a problem remains with training deep networks. With an increasing number of layers, the accuracy of the network saturates and then starts decreasing. This phenomenon is known as degradation [
44] and is not caused by overfitting of the network. Once the network accuracy becomes saturated, adding more layers will only result in higher training error.
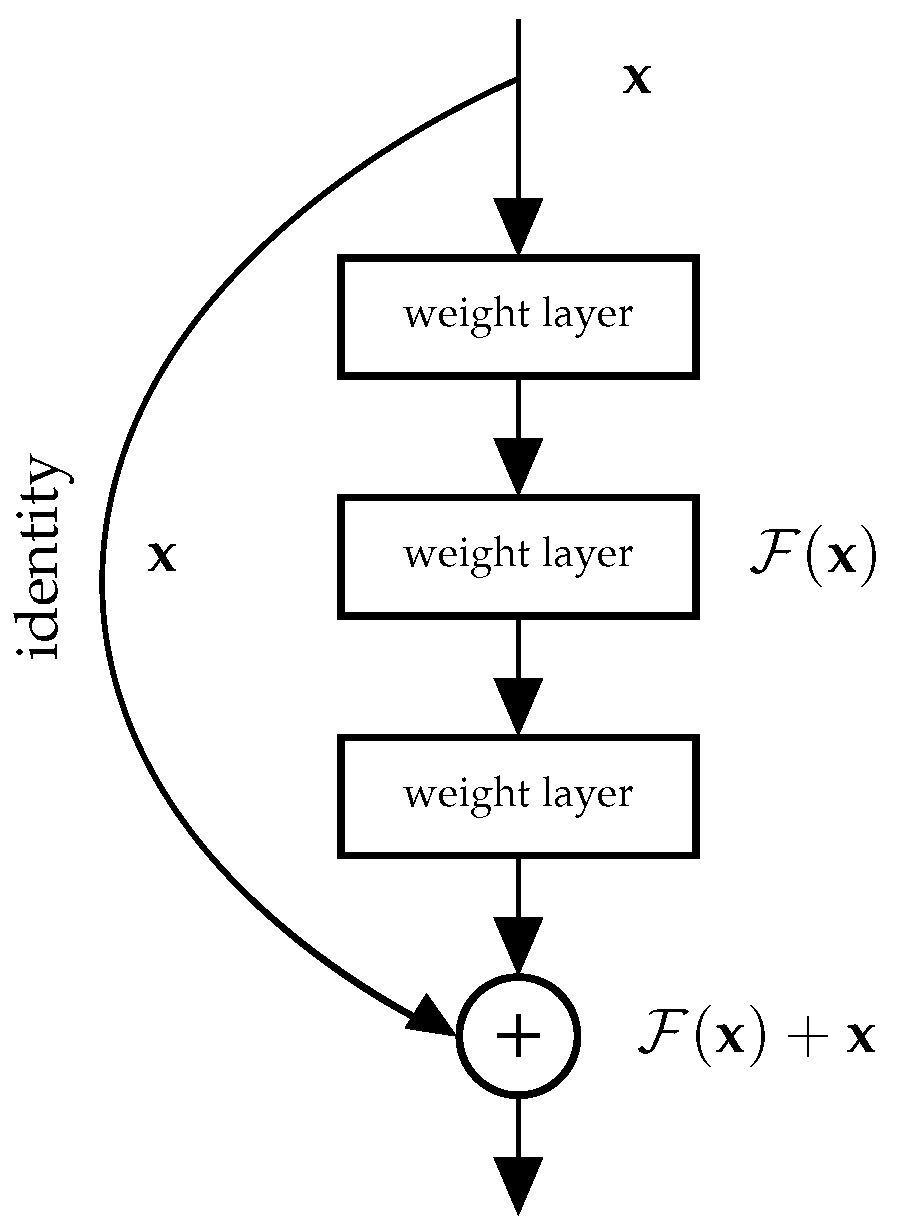
A solution to this problem is the deep residual learning framework or ResNets [
44]. The main idea behind ResNets is that, instead of letting a stack of layers learn the desired mapping
, shortcut connections are constructed which skip over the stack and are added to the output of the previous layers. The shortcut connection is the identity mapping, and it forces the “skipped” layers to fit a residual mapping,
, which is easier to optimize. In this way, the originally desired mapping has been transformed into
. This is illustrated in
Figure 1.
In this paper, we use the following notation: the observed fine bands are denoted by and observed coarse bands are denoted by , where is the dimension of the fine resolution bands, is the number of fine resolution bands, is the number of coarse resolution bands and r is the resolution ratio between the fine and coarse resolution bands. Filtering and subsequent downsampling by the factor r, i.e., decimation, is denoted by the operator and upsampling by a factor r and subsequent filtering is denoted by . Finally, square brackets denote the concatenation of matrices along the spectral dimension, i.e., . Note that the first two dimensions of the matrices need to be the same. The operators and operate band-wise.
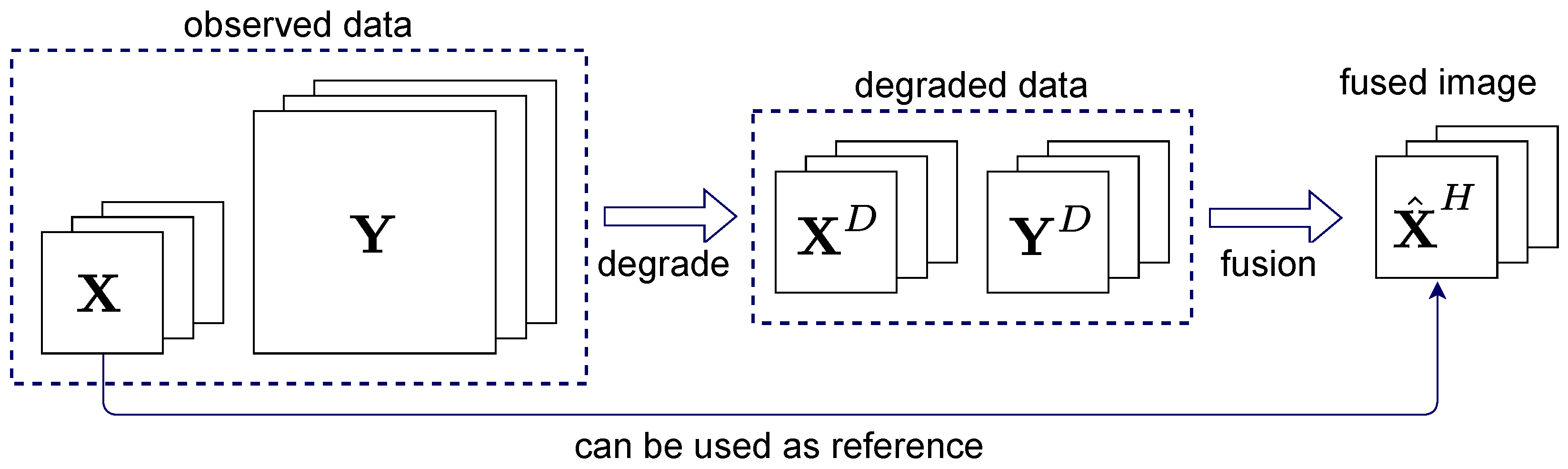
Since there is no high-resolution reference image available, the data need to be degraded in resolution before training to be able to use the observed coarse bands as the reference. This approach, depicted in
Figure 2, is the most widely used method for quantitative evaluation of image fusion methods such as pansharpening. We denote the spatially degraded fine and coarse bands by
and
, respectively, where the operator
degrades their spatial dimensions by the factor
r, which is the resolution ratio between the fine and coarse bands. Since
is smaller than
by a factor of
r along each spatial dimension, it needs to be interpolated to the same size as
. We denote the interpolated degraded coarse bands by
and the degraded fine bands by
. Now,
,
and
, i.e., the observed coarse bands, have the same spatial size.
To make the training of the network computationally feasible, the input images are divided into many small overlapping patches of suitable size. Thus, the input to the network are patches of the stacked degraded bands, i.e., patches of , denoted by , where M is the number of patches and p is the patch-size. The target patches during training come from and are denoted by . As all the bands have the same size, the ith patch covers the same part of the scene for all the images, i.e., , and .
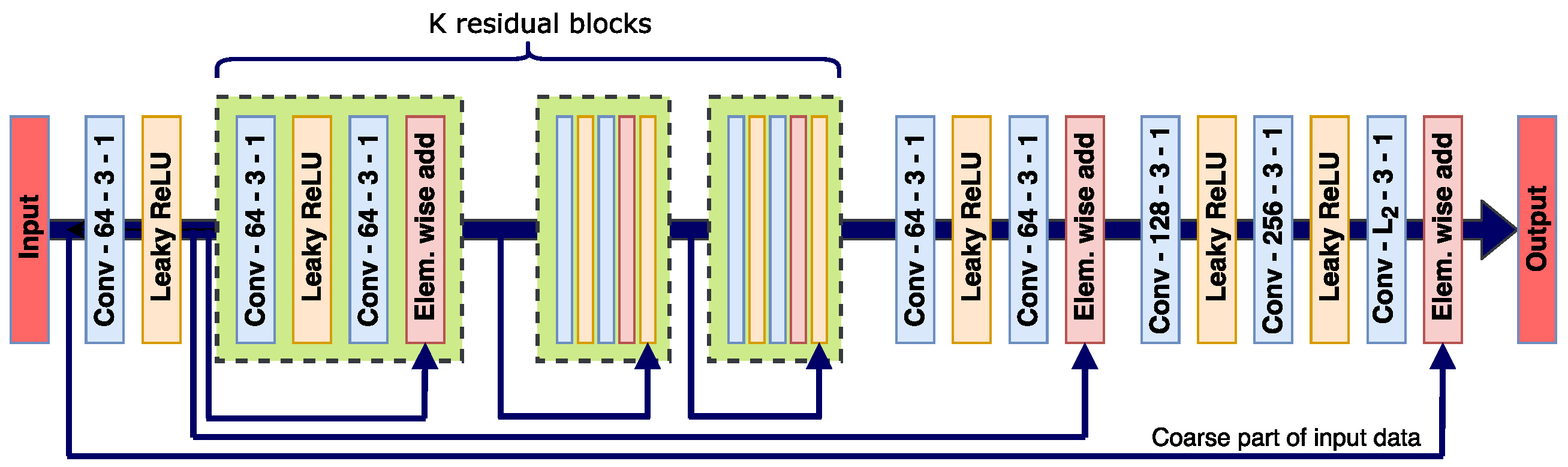
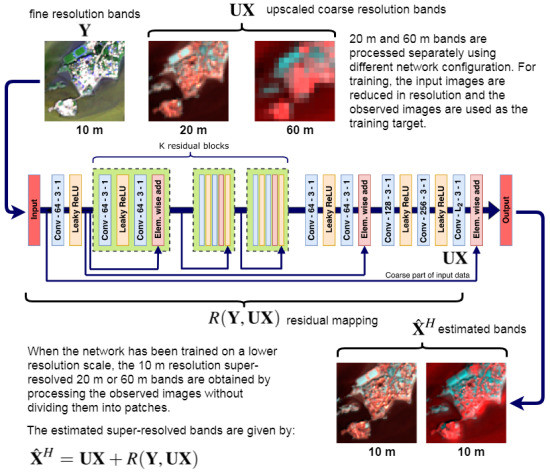
We can formulate the fusion problem as
where the estimated fused image is denoted by
and
is the mapping from the fine bands
and the upscaled coarse bands
, i.e., the input bands. Thus, the residuals
are fine details that are added to
, which can be viewed as the low-pass component of the fused image
. In this framework, the residual mapping
is learned by the network during training. The design of the network is shown in
Figure 3. The network is residual on two-levels. First, we have the residual blocks that are designed as shown in
Figure 1. Each residual block consists of a conv layer with leaky rectified linear unit (ReLU) activation. activation [
55], followed by another conv layer with linear activation and finally an element-wise sum layer where the output of the layer preceding the residual block is added to the output of its last conv layer. There are a total of
K residual blocks in the network, where the parameter
K is a tuning parameter of the method. Aside from the residual blocks themselves, there are two other skip connections, one that skips the entire stack of residual blocks and one that skips from the input layer to the output layer of the network. Only the coarse part of the input, i.e., the part
is added via the skip connection. This design reflects the model given in Equation (
1). The last skip connection effectively enforces the residual nature of the fusion process according to the model.
2.1. Training
The key idea of the method is to degrade the resolution of the input images
and
before training to use the observed coarse bands
as the training targets. The input and target images are split into
M overlapping patches of size
pixels with a shift of one pixel between patches such that the patches completely cover the source images. The training and target patches are then obtained by randomly sampling
M patches from the input and target images without replacement. The input to the network are then
M stacked patches of
and
, i.e.,
. The target patches are
. The loss function of the network is given by
where
is the prediction of the network for the
ith patch,
are the network parameters and
M is the number of patches.
An important factor in the method is how the decimation and interpolation of the bands is performed, i.e., the operators
and
. For downsampling, we use the GLP filters described in [
56], which are implemented in the Scikit-image Python library [
57] as the function
pyramid_reduce. The parameter
of the Gaussian filter is chosen as
, which is the default value of this parameter. For interpolation of the bands, we use spline interpolation of order 5. This is implemented in the Scikit-image function
rescale. The CNN was implemented using the high level Keras [
58] deep learning library, which is now a part of Tensorflow 1.4 [
59].
2.2. Testing
The main hypothesis behind the method is that the relationship learned by the network between the data at the reduced scale, i.e., between and also holds for and the hypothetical fine resolution image , which are the coarse bands at the next higher resolution scale, i.e., the scale of . When the network has been trained, the entire stack of the input images at the observed resolution scale is processed at once to yield the high-resolution bands .
3. Experiment Results
3.1. Data
The Sentinel-2 constellation is a part of ESA’s Copernicus Programme and consists of the twin Sentinel-2A and Sentinel-2B polar-orbiting satellites that are located in the same orbit, phased at 180 to each other. Built by Airbus DS (Ottobrunn, Germany) and operated by the ESA, these satellites were designed to deliver global coverage of high-resolution multi-spectral imagery with high revisit frequency and provide observation data for the next generation of operational products such as land-cover change-detection maps, managing of natural disasters and forest monitoring. Each satellite is provided with a multi-spectral instrument (MSI) that has a total of 13 spectral channels in the visible/NIR and SWIR range. The MSI splits the incoming reflected light at a filter and focuses it onto two distinct focal plane assemblies/detectors. There is a separate detector for visible and NIR bands (VNIR) and another one for SWIR bands. Stripe filters mounted on top of the detectors separate each spectral band into individual wavelengths. The data are acquired on 13 spectral bands in the VNIR and SWIR range. There are four bands in the visible and NIR range at a 10 m resolution (ground sampling distance), six bands in the NIR and SWIR range at 20 m resolution and three bands at a 60 m resolution in the visible NIR and SWIR ranges. The radiometric resolution of all bands is 12 bits per pixel, i.e., there are 4096 possible light intensity values. Finally, the temporal resolution, i.e., the revisit frequency of the combined constellation is five days and ten days for a single satellite.
The MSI products are compilations of granules of a fixed size. For ortho-rectified products such as Level-1C products, the granules are 100 km ortho-images in UTM/WGS84 projection. All data in this paper come from a single Level-1C product which means that the data have been converted from radiances into top-of-atmosphere (TOA) reflectances and projected into cartographic coordinates using a digital elevation model (DEM) and then resampled at constant ground sampling distance of 10 m, 20 m or 60 m depending on the native resolution of the respective spectral bands.
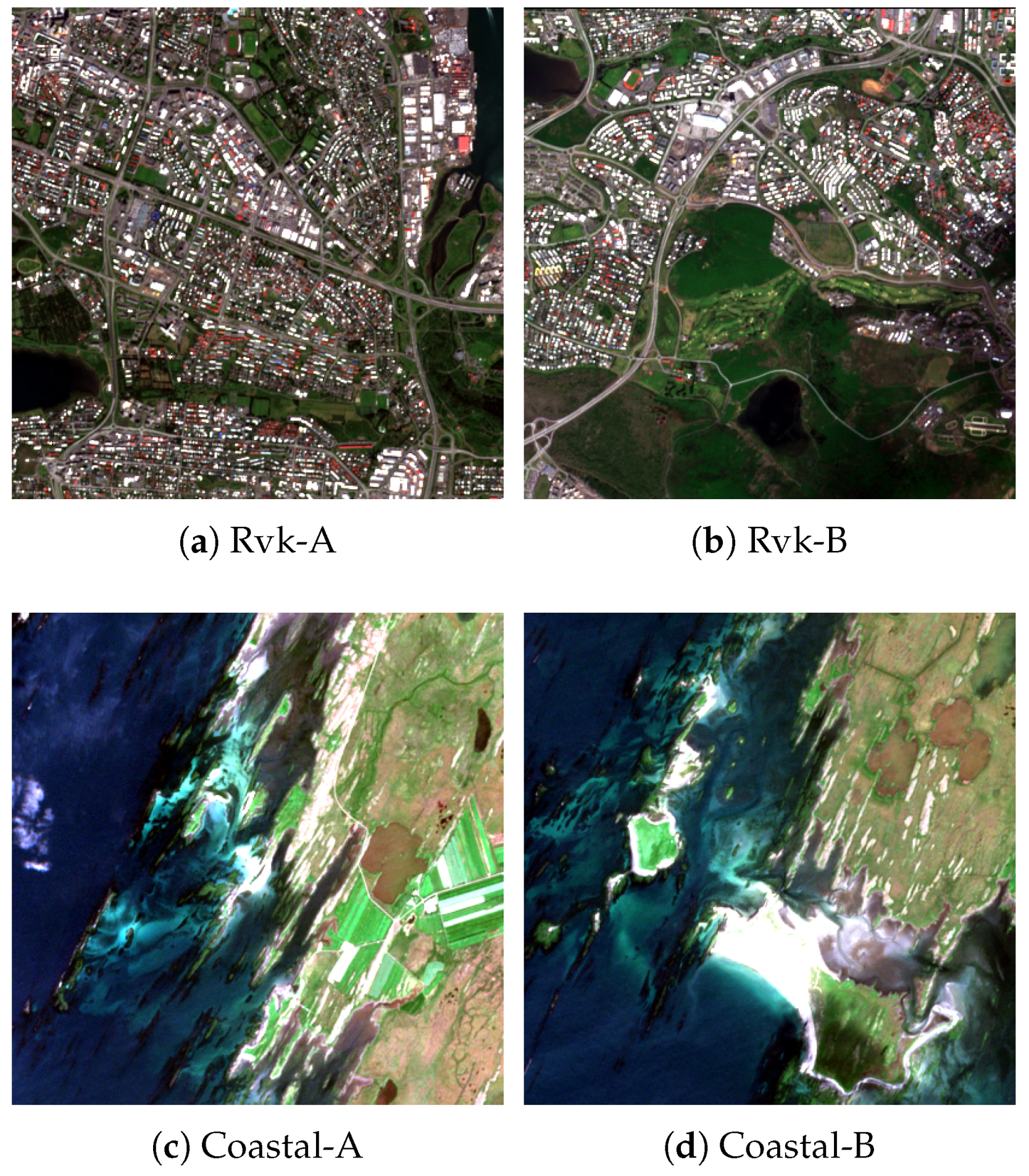
The dataset used is a 100 km by 100 km tile showing part of western Iceland, including the capital Reykjavik and the fjords of Hvalfjörður and Borgarfjörður. The acquisition date is 27 July 2017, and it is almost cloud free. From this image, we have made four smaller ones for 20 m super-resolution of size 408 by 408 pixels at 10 m resolution that translates to 4.08 km by 4.08 km and one large data set of size 3452 by 3452 pixels, i.e., 34.52 km by 34.52 km, which is used for experiments involving the super-resolution of 60 m bands. The datasets come in pairs of similar images denoted by A and B. One pair is of a rural coastal area north of Borgarfjörður (
N,
W), and the other pair shows part of the capital of Iceland, Reykjavik (
N,
W). The datasets are referred to as Coastal-A, Coastal-B, and Rvk-A, Rvk-B, and they are shown as RGB color images in
Figure 4.
3.2. Experiment Methodology
Two end-user scenarios can be envisioned for the proposed method. The first one is a single image approach, where the network is trained and tested on the same image. This means that, if the user is interested in super-resolving a specific image, he/she would need to train the network specifically for that image. The second scenario is to pre-train the network on a large number of different scenes such that it can generalize well-enough to make training for specific images unnecessary. This is the approach in [
37], where a deep residual network was trained on a large number of different images. In this paper, the focus will be on the single image approach. However, we do experiments where we train on one image and test on another image. The experiments are divided into experiments involving 20 m bands, and experiments involving the 60 m bands. Experiments, where we try to estimate the effect of different network parameters such as the number of residual blocks or the patch-size, are based on 40 m to 20 m super-resolution. To test the generalization capacity of the method, we train on one image, referred to as image A and test on another similar image, referred to as image B.
3.3. Quality Metrics and Reduced Resolution Evaluation
To be able to evaluate the fused image quantitatively, a reference image is needed. Obviously, such a reference image is not available. However, in image fusion such as pansharpening, it is common practice to reduce the observed data in resolution by a factor that is equal to the resolution factor between the higher resolution bands and the lower resolution bands. In this way, the observed lower resolution bands can be used as the reference image for the fusion. This is the method that is used for the training of the network. The drawback is however that, obviously, the reduced resolution image fusion problem is not the same problem as the fusion at the observed resolution scale. By degrading the observed data, information is lost. However, this method enables the comparison of image fusion methods since it can give an idea of their relative performance as measured by quantitative quality evaluation metrics. The experiments are divided into 40 m to 20 m super-resolution, and 360 m to 60 m super-resolution and the main focus will be on super-resolution of the 20 m bands.
By using the reduced resolution method, we can use standard performance metrics or indices to evaluate the quality of the estimated high-resolution images. For this purpose, we use the following quality indices: signal-to-reconstruction error (SRE), Erreur Relative Globale Adimensionnelle de Synthese (ERGAS) and Spectral Angle Mapper (SAM).
The SRE is the ratio of the power of the signal to the error, and it is given in decibels by
where
denotes the reference image,
denotes the estimated image,
is the mean of
and
N is the number of pixels in each band.
ERGAS [
60] calculates the amount of spectral/spatial distortion in the enhanced image based on the mean square error (MSE) and is given by
where
is the ratio of high-resolution pixels to low-resolution pixels,
denotes the number of bands and
denotes pixel
n of band
l.
Finally, SAM calculates the spectral similarity between two vectors as an angle. The value of SAM for the entire image is the average of all the angles for each pixel. It is given in degrees by
For ERGAS and SAM, the optimal value is 0, while higher values are better for the SRE.
The data are degraded in resolution by first filtering each band with a Gaussian filter, with the standard deviation parameter chosen as , then filtering again with a moving average filter with kernel size and finally downsampling by factor r.
3.4. 20 m Bands—Study of the Effect of Network Parameters
In this part of the experiments, we investigate the effect of various network hyperparameters, such as the number of training patches, the number of training epochs, the number of residual blocks K, and the patch size. We train on the image A and test on both images A and B.
The results of all the experiments are the values of the quantitative quality metrics for both train and test datasets for each value of the parameter under study. The default value of the parameters are as follows: the number of training patches is 500, the number of residual blocks is 24, the size of patches is pixels, and the number of epochs is 200. For a single experiment where one parameter is varied, the random seed for the random patches selected for training is kept fixed to see the effects of that parameter better.
3.4.1. Effect of the Number of Training Patches
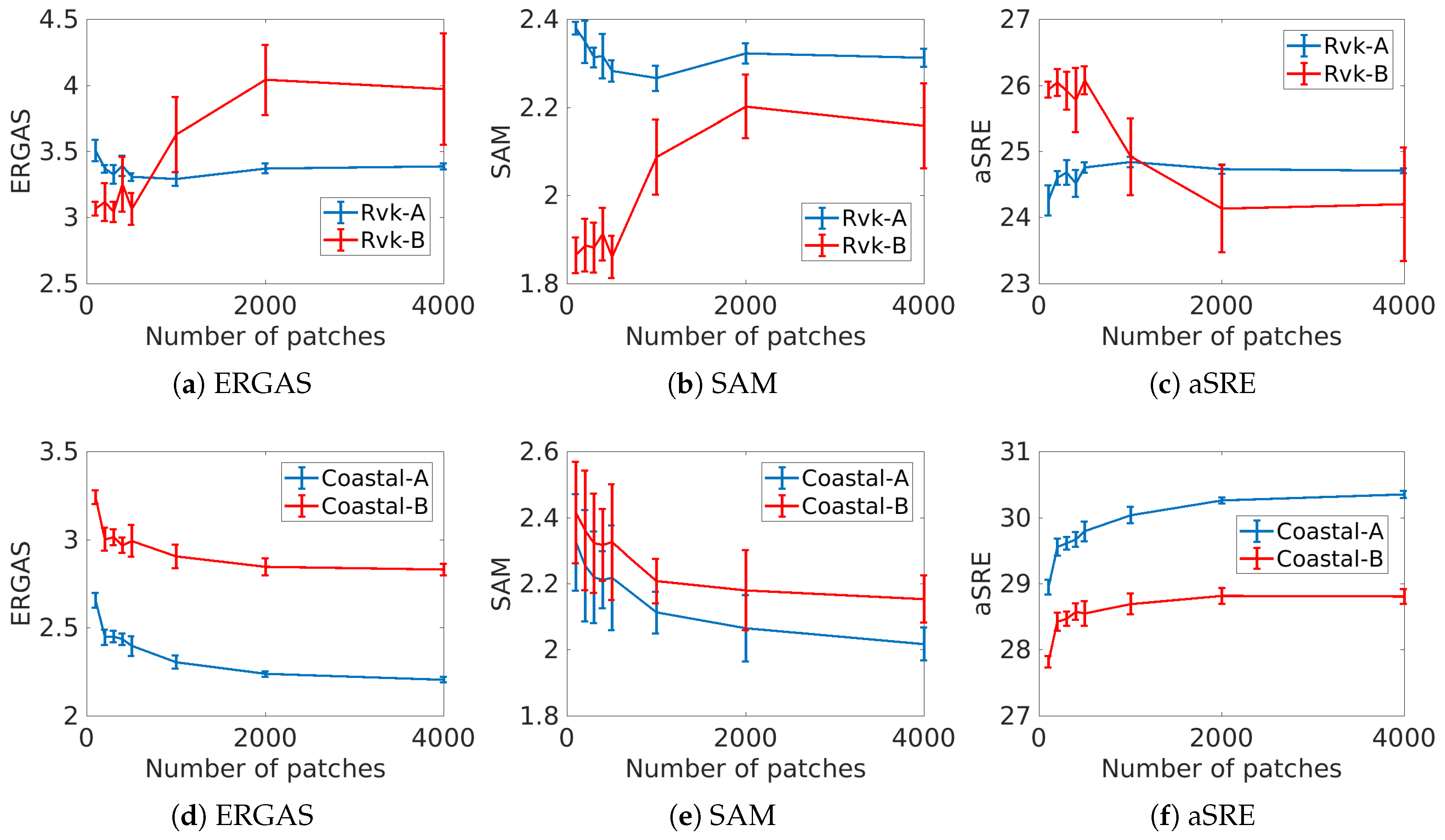
In this experiment, we estimate the effect of the number of training patches on the values of the quantitative quality metrics. The number of patches varies from 100 to 4000 in increments of 100 and 1000 patches. For each number of patches, 30 trials are performed, and the results of the experiment are the mean of the test metrics for both A and B images. The results are shown in
Figure 5. For the urban Rvk datasets, all evaluation metrics reach an optimal value at 1000 or fewer training patches for the train image A and test image B. Using more than 1000 patches results in worse performance and especially so for the test image. This is a clear sign of overfitting of the network when the number of training patches increases. For the coastal data set, the behavior is very different. Using more training patches gives better results according to all the metrics. It seems that overfitting is much less of an issue for the coastal images than for the urban images, but it is not clear why that is so. These results indicate that the optimal number of training patches is largely scene dependent.
3.4.2. Effect of the Number of Training Epochs
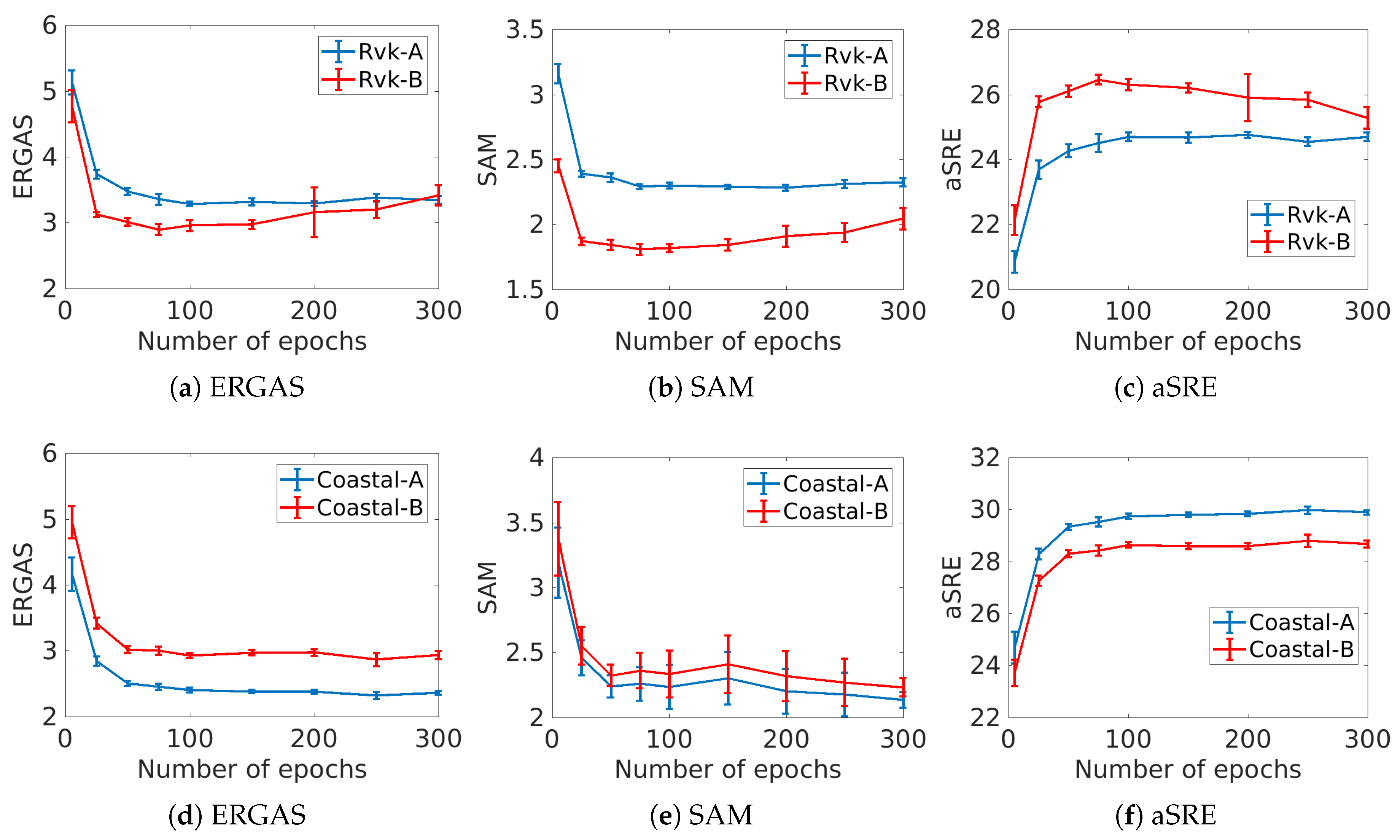
Now, we consider how the evaluation metrics change as a function of the number of epochs used to train the network. The setup of the experiment is the same as before, and now only the number of training epochs varies from 15 to 100 in increments of 25 epochs and from 100 to 300 in increments of 50 epochs. The results are shown in
Figure 6. For the urban Reykjavik dataset, the performance metrics for both A and B images indicate optimal performance is reached at around 100 epochs of training. Training for a higher number of epochs does not improve the performance of the network. For the coastal dataset, the best results are obtained at 250 epochs for ERGAS and aSRE and at 300 epochs for SAM. This experiment reveals that the network converges quickly and that, when the training data is limited, training the network for a large number of epochs does not improve the performance, even if the cost function is still decreasing. Note that the network is trained at a lower resolution scale than used when predicting the fused image and the relation between the network loss and the values of the metrics is not strictly linear.
3.4.3. Effect of the Number of Residual Blocks
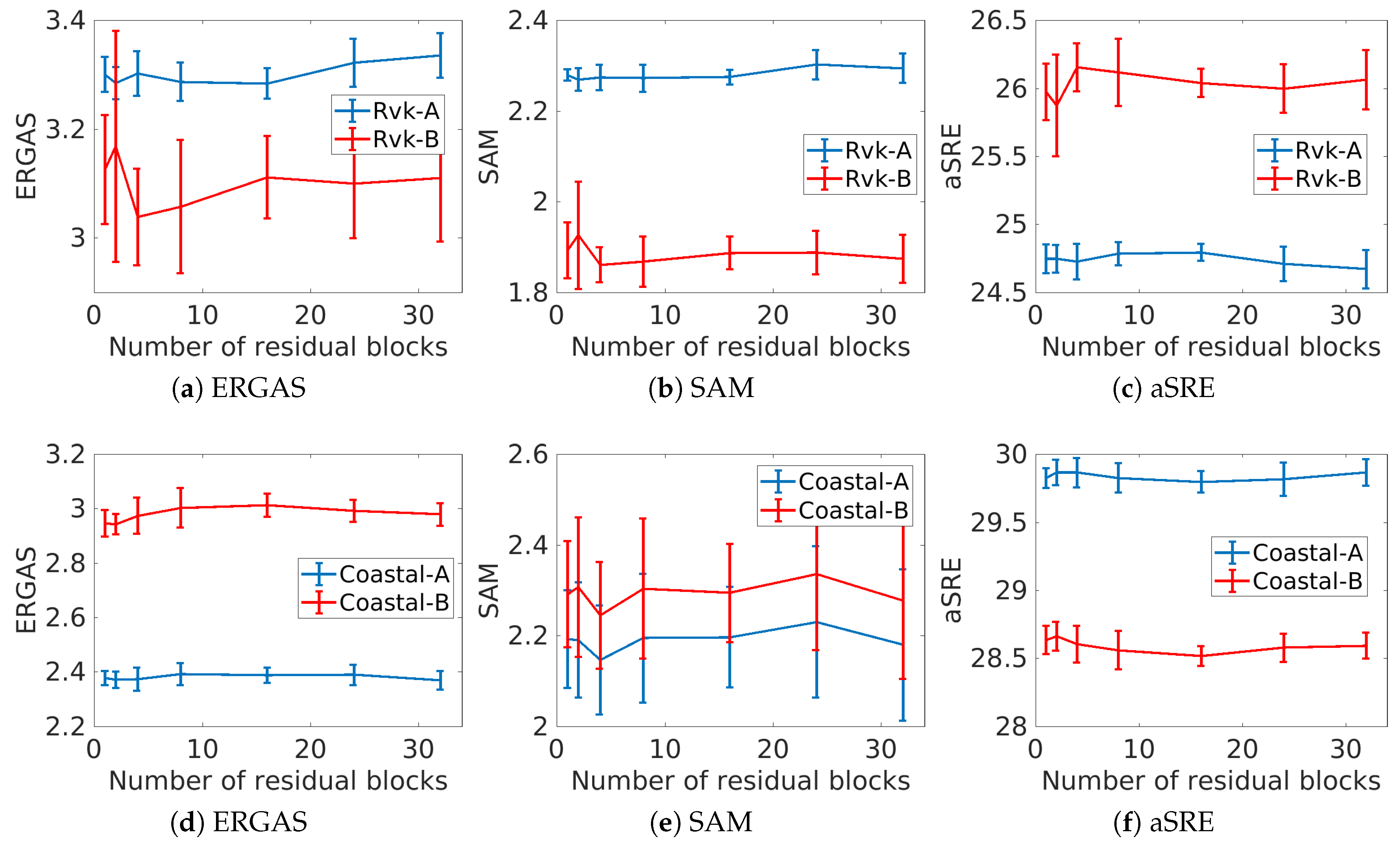
The number of residual blocks is an important tuning parameter; in this experiment, we estimate the effect of the network depth in terms of the number of residual blocks on the values of the quantitative quality metrics. The network was trained on the A images for the following values of
K, i.e., number of residual blocks: 2, 4, 8, 16, 24, 32, and 40. Each residual block contains four layers, i.e., two conv layers, one Leaky ReLU activation layer and one element-wise sum layer. Aside from the residual blocks, the network has six conv layers, and thus the network depth in terms of the number of conv layers varies from eight conv layers to 70 conv layers. For each value of
K, 30 trials were performed using patch size of 16 by 16 pixels, and the number of patches was set to 500 for the Rvk dataset and 2000 for the Coastal dataset. After training on the A image in each trial, the network was tested on both the A and B images. The test results are shown in
Figure 7. The results indicate that, for the urban Reykjavik image, best results for the evaluation metrics are obtained with a low number of residual blocks. For the single image case, i.e., image A, the optimal number of
K is eight, and it is the same for the test image B. For the coastal images, four to eight residual blocks are optimal. Perhaps the most surprising result of this experiment is that the performance of the network is not very sensitive to the network depth.
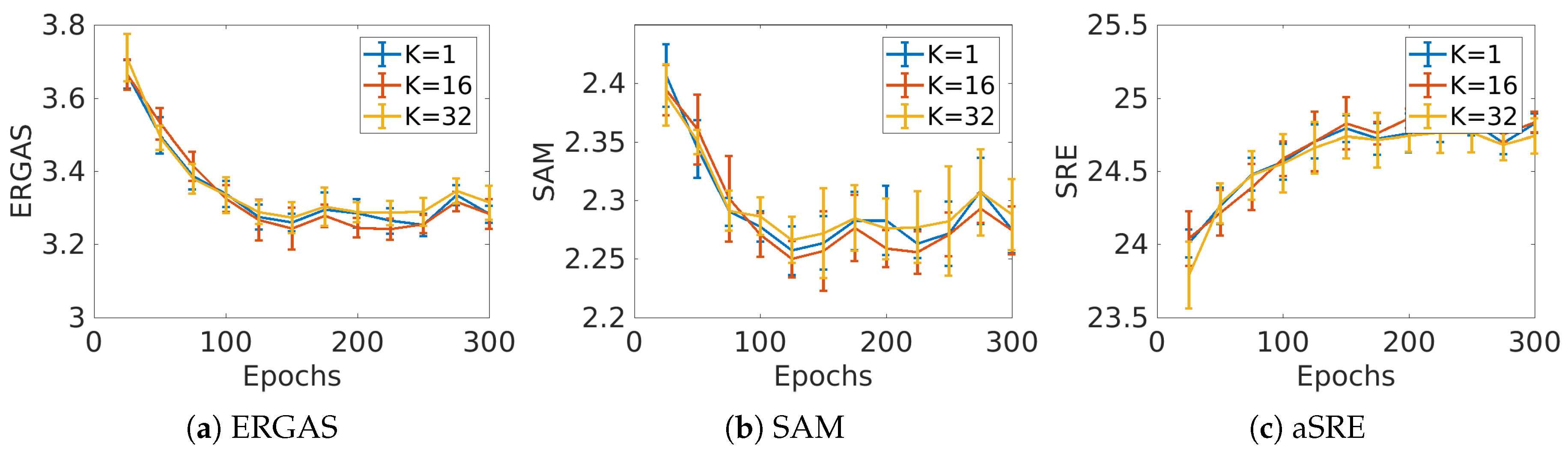
Figure 8 shows a plot of the evaluation metrics as a function of number of epochs for the Rvk-A dataset. There are three cases, i.e., the number of residual blocks
K is 1, 16, and 32. This plot shows that there seems to be no relation between convergence speed and number of residual blocks. Actually, 32 residual blocks give worse performance than one.
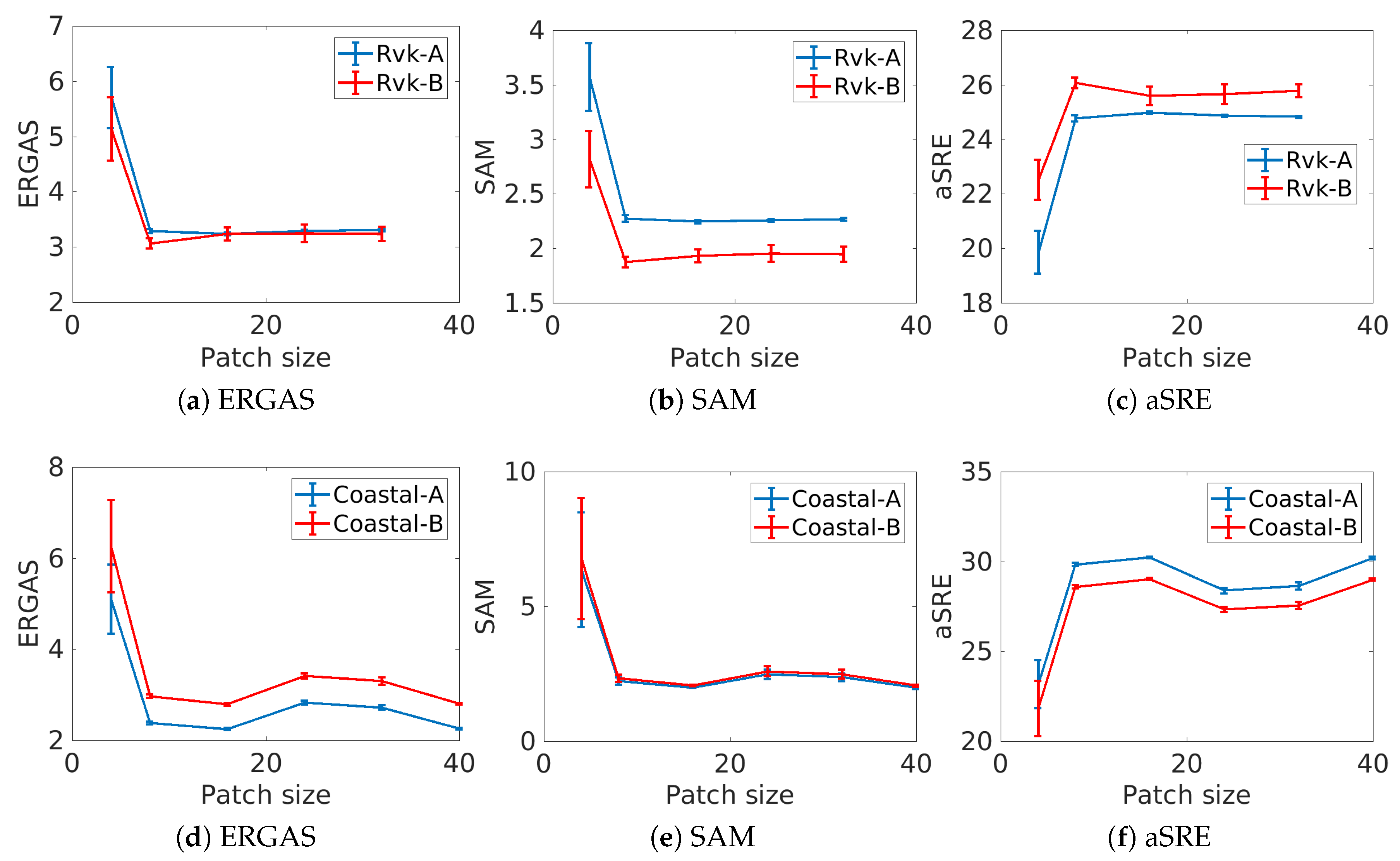
3.4.4. Effect of the Patch Size
In this experiment, the effect of the size of the training patches is investigated. As before, the other hyperparameters are kept fixed and 30 trials are run for each patch size of
,
,
,
,
, and
pixels, respectively. The network is trained on the image A and tested on both images A and B. The results are summarized in
Figure 9. For the Reykjavik image A, a patch size of 16 gives the optimal results, while for the B image, eight pixels gives the best results. For the coastal images,
pixels and
pixels give the best results. A large patch size increases the computational cost of the algorithm significantly, and therefore it is beneficial to keep it as small as possible. According to
Figure 9, the optimal patch size for performance and computational complexity is 16 by 16 pixels. Minimal improvement is gained by increasing the patch size beyond that.
3.5. 20 m Bands—Comparison to State-of-the Art
We compare the proposed method to the CNN based method in [
11], the SupReME method [
27], the ATPRK method [
47], and the Superres method [
29]. The CNN based method, which we refer to as ConvNet, is based on a three convolutional layer network, which has no skip connections. The size of the filters is 3 by 3 pixels, and there are 32, 64, and 128 filters in each layer, respectively. This method serves as a baseline neural network method for the comparison. The SupReME method depends on solving a deconvolution problem in a lower dimensional subspace. The ATPRK method is based on area-to-point regression kriging of coarse residuals between fine and coarse bands, which are obtained by regression modeling. Finally, the Superres method tries to propagate band-independent details from the fine bands to the coarse bands using spectral unmixing.
For the experiments, we use the same four datasets as in previous experiments, i.e., the Coastal and Rvk pairs of datasets. The hyperparameters of the proposed methods were chosen according to the results of the previous experiments, i.e., the patch size was selected as 16 by 16 pixels, the number of training epochs is 200, and the number of residual blocks was set to 24. This also applies to the ConvNet method. Results of the quantitative evaluation of all methods and datasets are summarized in
Table 1. The best results are highlighted using a bold typeface.
It is evident that the neural network based methods considerably outperform the other methods, with ResNet showing the best performance in every dataset but Rvk-A, where the ConvNet method gives slightly better results for some of the bands. Of the remaining methods, the ATPRK method performs clearly worst in every dataset. The Superres method gives the third best results and SupReME comes fourth. Interestingly, the performance gap between the proposed method and the SupReME method is considerably larger for the coastal datasets than the urban datasets.
Figure 10 shows a visual comparison of the results for the Coastal-A dataset for all bands and methods. A quick glance at the results in
Figure 10 reveals that the ATPRK method gives results that are clearly worse than the other methods. It is more difficult to discern the differences between the other methods, but scrutiny of the images shows that the proposed method gives images that are indeed the closest to the reference.
The residuals for each band are shown in
Figure 11. The ATPRK and Superres methods have the largest residuals while the proposed method and the ConvNet method produced images whose residuals have the least structure.
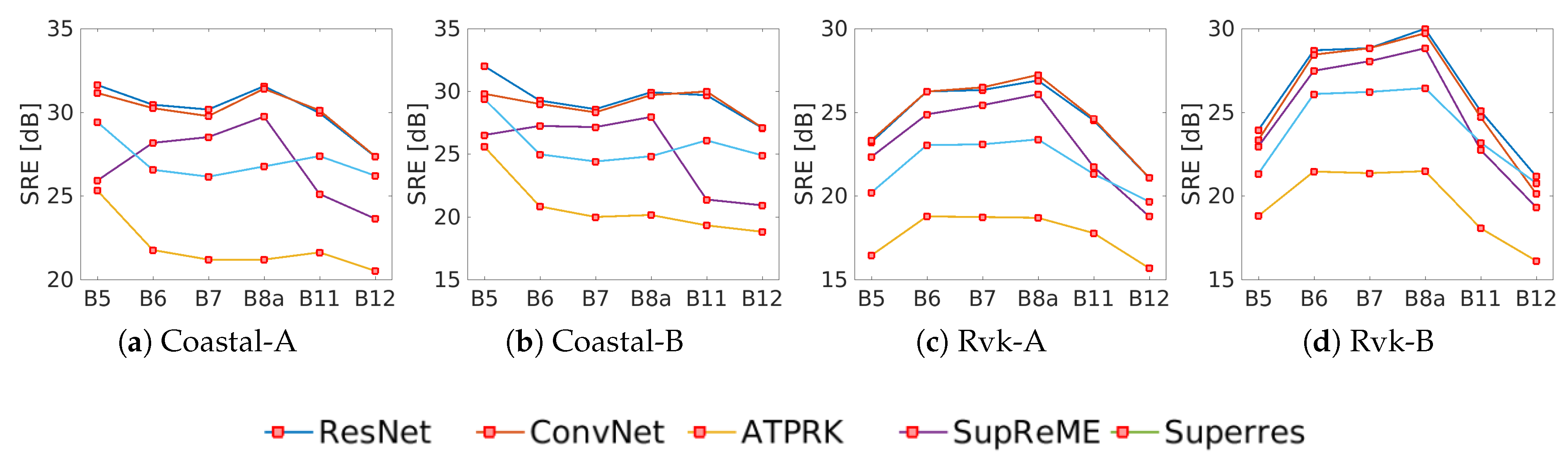
Finally,
Figure 12 shows the SRE values for each band, for all methods and all the datasets. For the Coastal datasets in sub-figures (a) and (b), respectively, the CNN based methods give results that are substantially better than the other methods used in the comparison. Interestingly, the SupReME method shows a trend in the band-wise SRE values that is different from what the other methods show. For the urban datasets in (c) and (d), all methods show a similar trend, and now the SupReME method performs relatively better compared to ResNet.
3.6. 60 m Bands
For the sharpening of the 60 m bands, we use the same network architecture as the 20 m bands. In order to be able to use the observed 60 m bands as targets during training, the input image has to be downgraded in resolution by a factor of 6 and now the input also contains the 60 m bands, thus the network uses information from both the 10 m bands and the 20 m bands to produce the sharpened 60 m bands. After downgrading by factor 6, the 60 m, 20 m, and 10 m bands are at resolution 360 m, 120 m, and 60 m, respectively. For all input bands to be of the same size, the downgraded 60 m and 20 m bands need to be interpolated by a factor of 6 and 3, respectively. To be able to quantitatively evaluate the fusion performance, a reference image is needed. As with the 20 m sharpening, this can be achieved by reducing the observed image by a factor of 6 and using the observed 60 m bands as the reference. This means that the input to the network during training has been downgraded in resolution by a factor of 36. Thus, the only difference between the proposed method for 20 m and 60 m super-resolution is that for the latter, the 60 m bands are added to the input, during training, the input data are downgraded by a factor of 6 instead of 2, and now the observed 60 m bands serve as targets.
The dataset is a 3452 by 3452 pixel subset of the same Level-1C product as for the previous datasets. It shows a part of the western coast of Iceland, including the fjord of Borgarfjörður and its surroundings. An RGB rendering of the data set is shown in
Figure 13.
For this experiment, we use the same network parameters as for the 20 m bands. The number of residual blocks is 24, the batch size is 48, and the patch size is 16 by 16 pixels. For ResNet, the number of training epochs was set to 200, while for ConvNet the number of epochs was set to 500, and the batch size was set to 16. For the SupReME method, the dimension of the subspace was chosen as 7, and the value of the regularization parameter was determined by performing a simple linear search of 30 values. The ATPRK method cannot do sharpening of the 60 m bands and the Superres method is limited to the sharpening of the 20 m bands in reduced resolution mode; therefore, these methods are not included in this experiment.
The results are summarized in
Table 2. The results for the neural network based methods is the mean of 30 trials. The proposed method gives the best results with the ConvNet method giving the second best results. The performance difference between the two methods is larger than for the super-resolution of the 20 m bands. This also applies to the SupReME method, which now performs relatively worse. The SAM value for SupReME is more than twice higher than for the proposed method, and the average SRE value is lower by almost 6 dB.
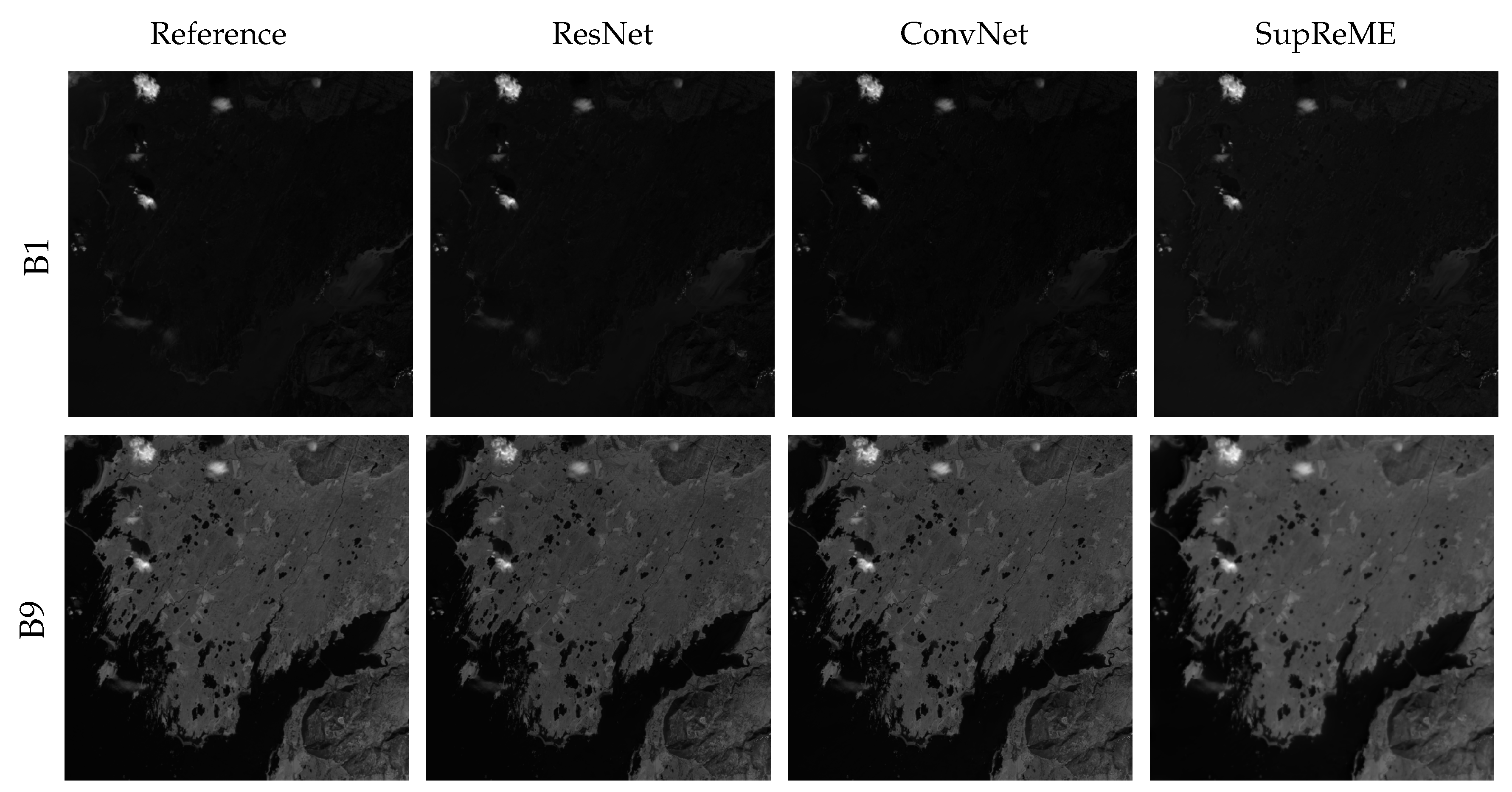
Figure 14 shows band B1 and B9 obtained using all methods as well as the reference. The images produced by the two CNN based methods look noticeably sharper and more detailed than the images obtained using the SupReME method. This applies especially to band B9. The corresponding residual plots are shown in
Figure 15 and there one can see that the residuals for the SupReME method contain more information and structure than for the proposed method, especially for band B9. Finally, visual results for 60 m to 10 m super-resolution are shown in
Figure 16, where a subset of the dataset showing the town of Borgarnes in the western part of Iceland. The results are shown in false color using band B1 as the red and blue channels and B9 as the green channel. The colors in the image obtained using the proposed method look closer to the colors in the observed bands B1 and B9 than for the SupReME method, where the colors look darker. In addition, the details obtained using the proposed method seem more natural, and there are fewer artifacts, such as ringing around sharp edges, which are visible in the SupReME results.