SLALOM: An All-Surface Snow Water Path Retrieval Algorithm for the GPM Microwave Imager
Abstract
1. Introduction
2. Materials and Methods
2.1. GMI-CPR Database
2.2. Complementary Dataset
3. SLALOM Algorithm
3.1. Snowfall Detection
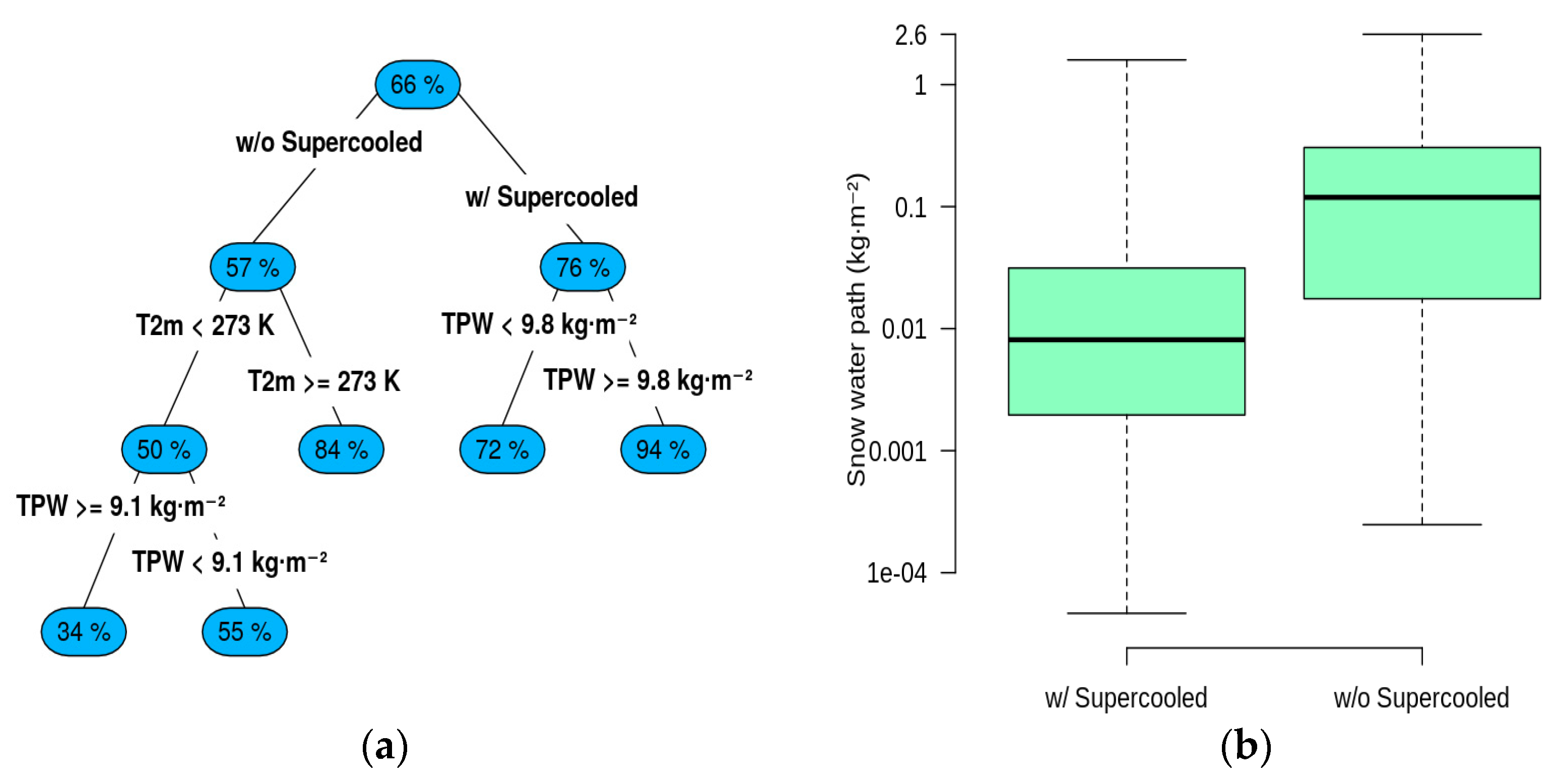
3.2. Supercooled Droplets Detection
3.3. SWP Retrieval
4. Algorithm Evaluation
5. Results
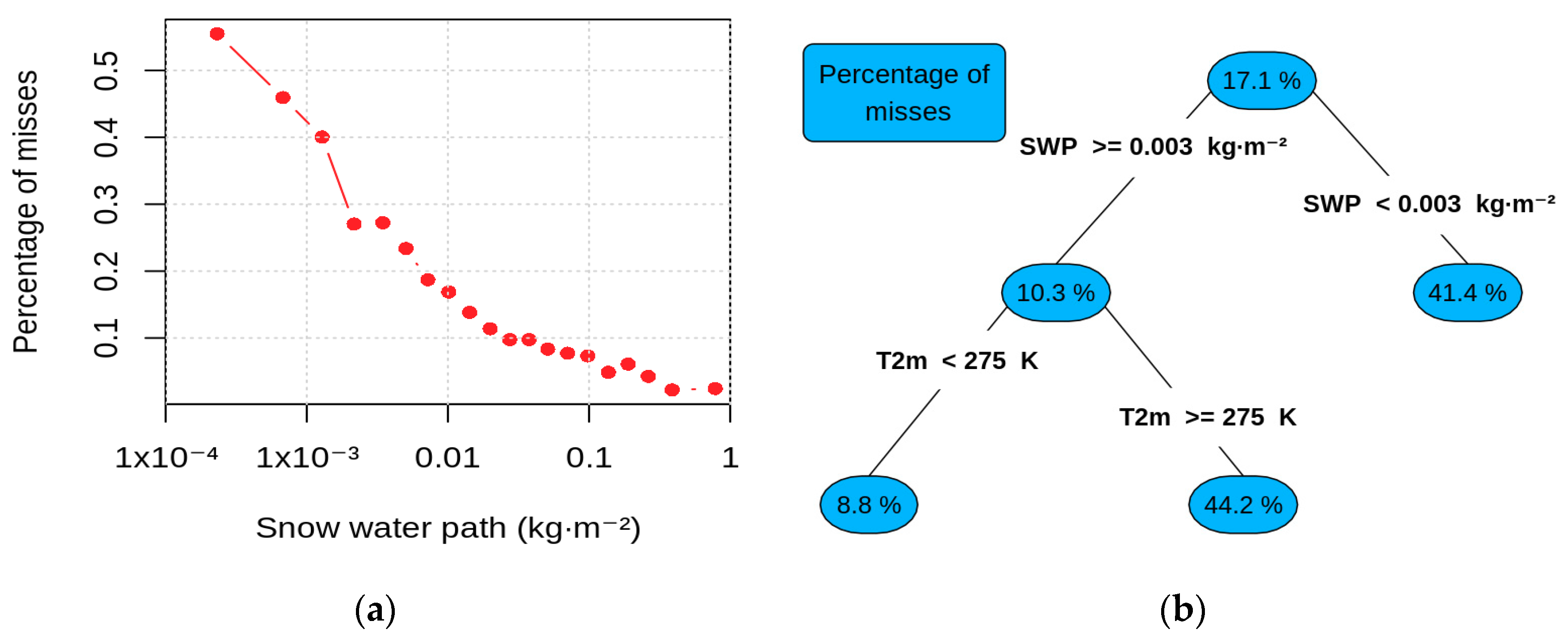
5.1. Snowfall Detection Module
5.2. Supercooled Droplets Detection Module
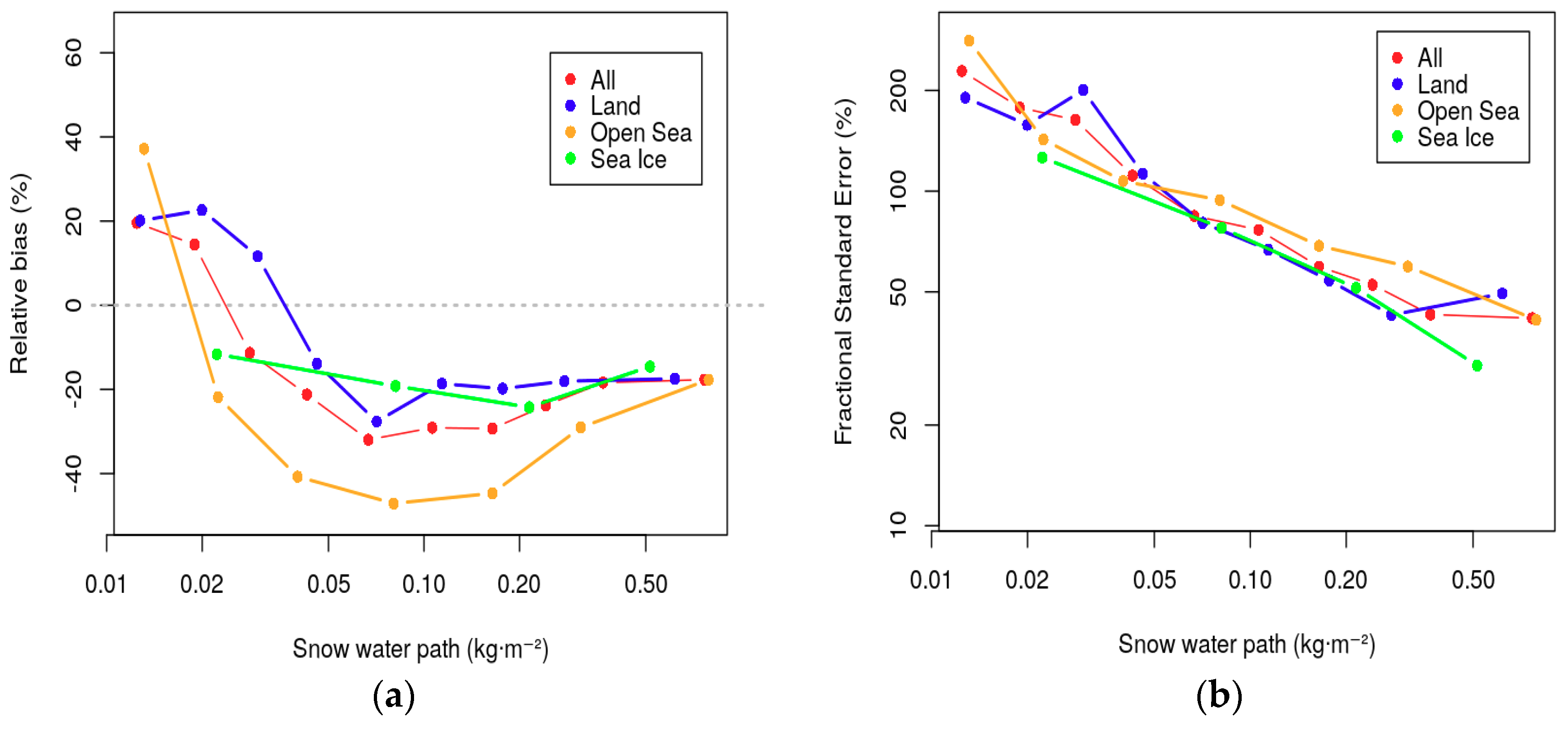
5.3. Snow Retrieval
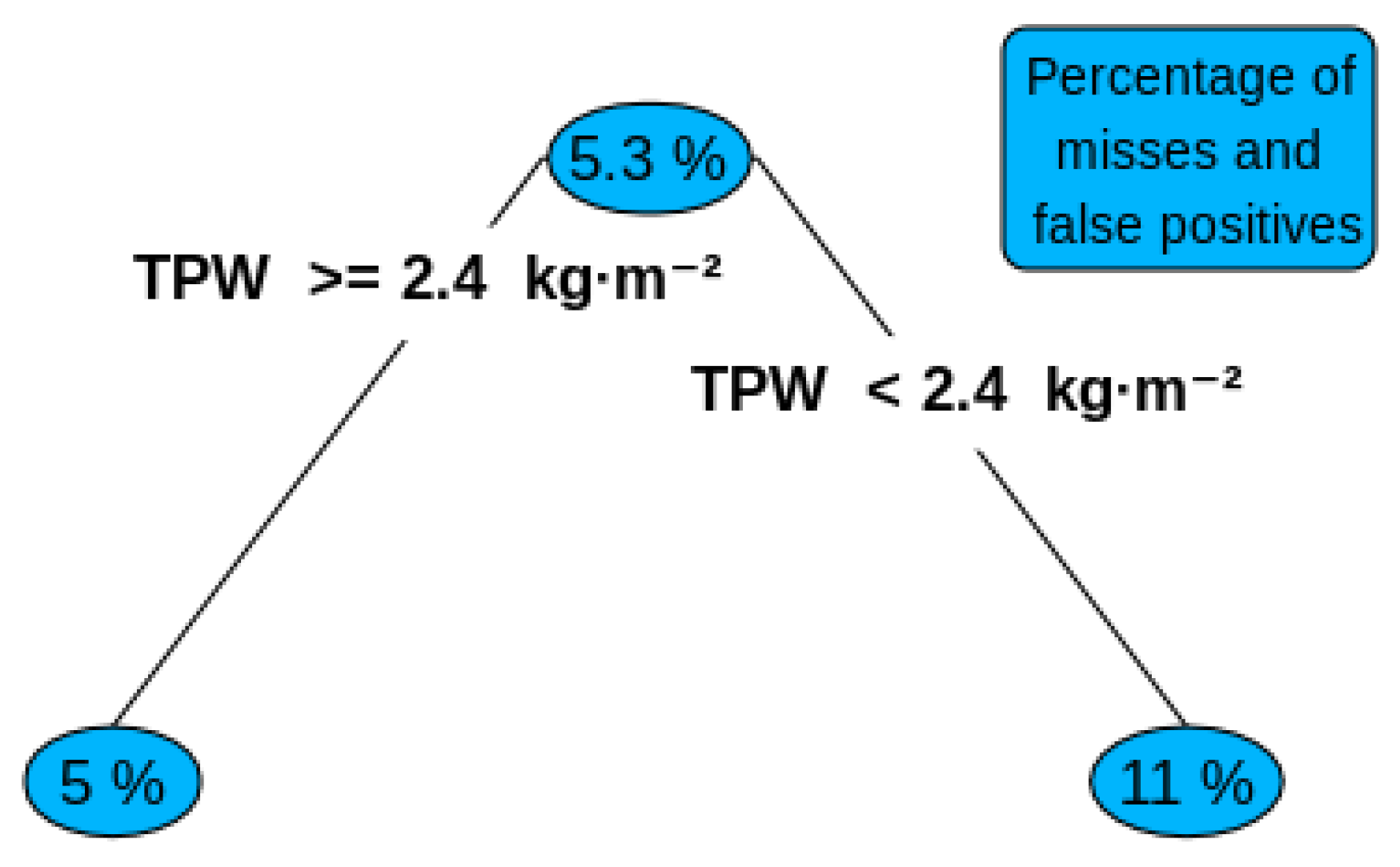
5.4. Full Algorithm Evaluation and Sensitivity Test
6. Applications of SLALOM Algorithm
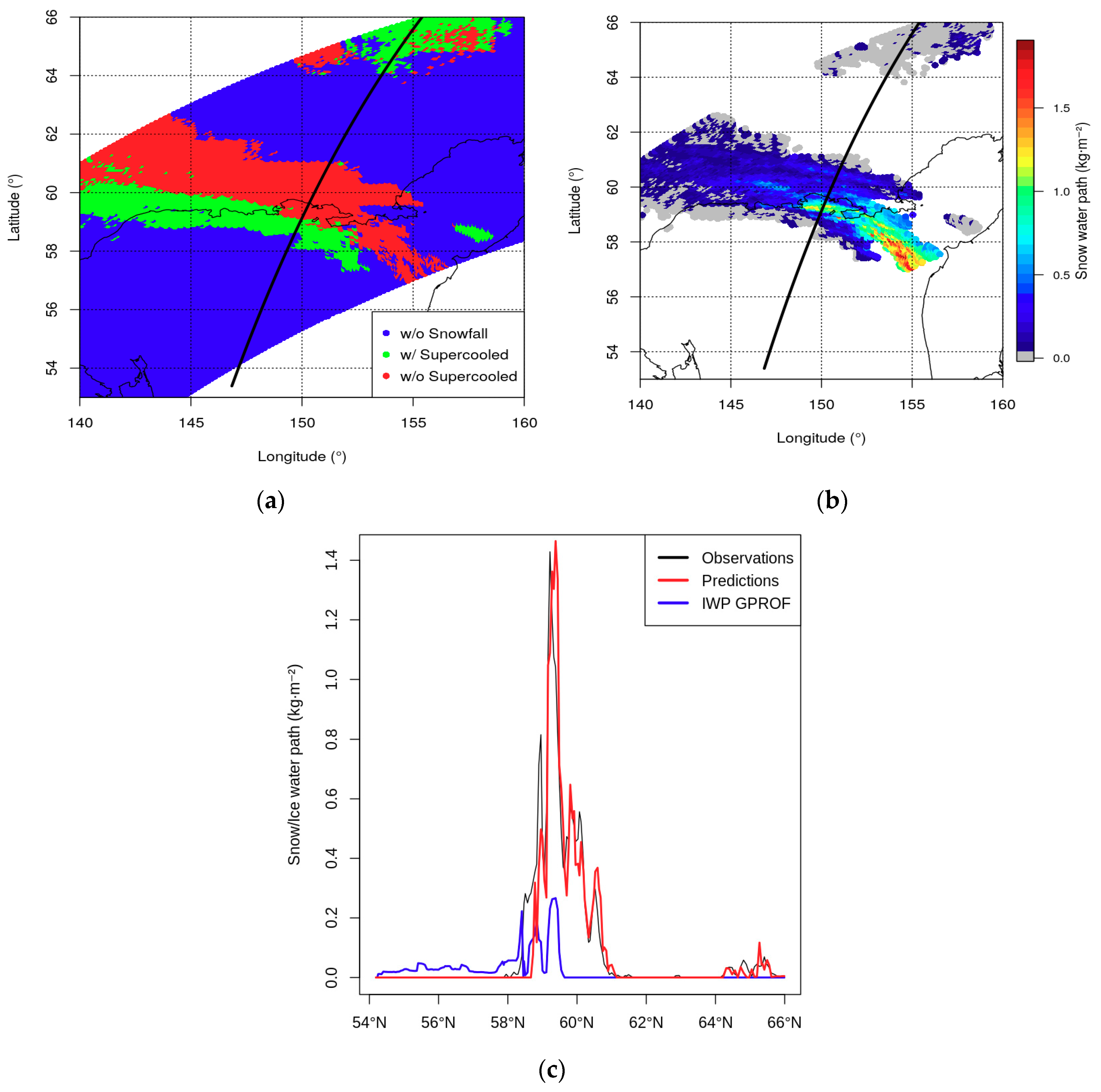
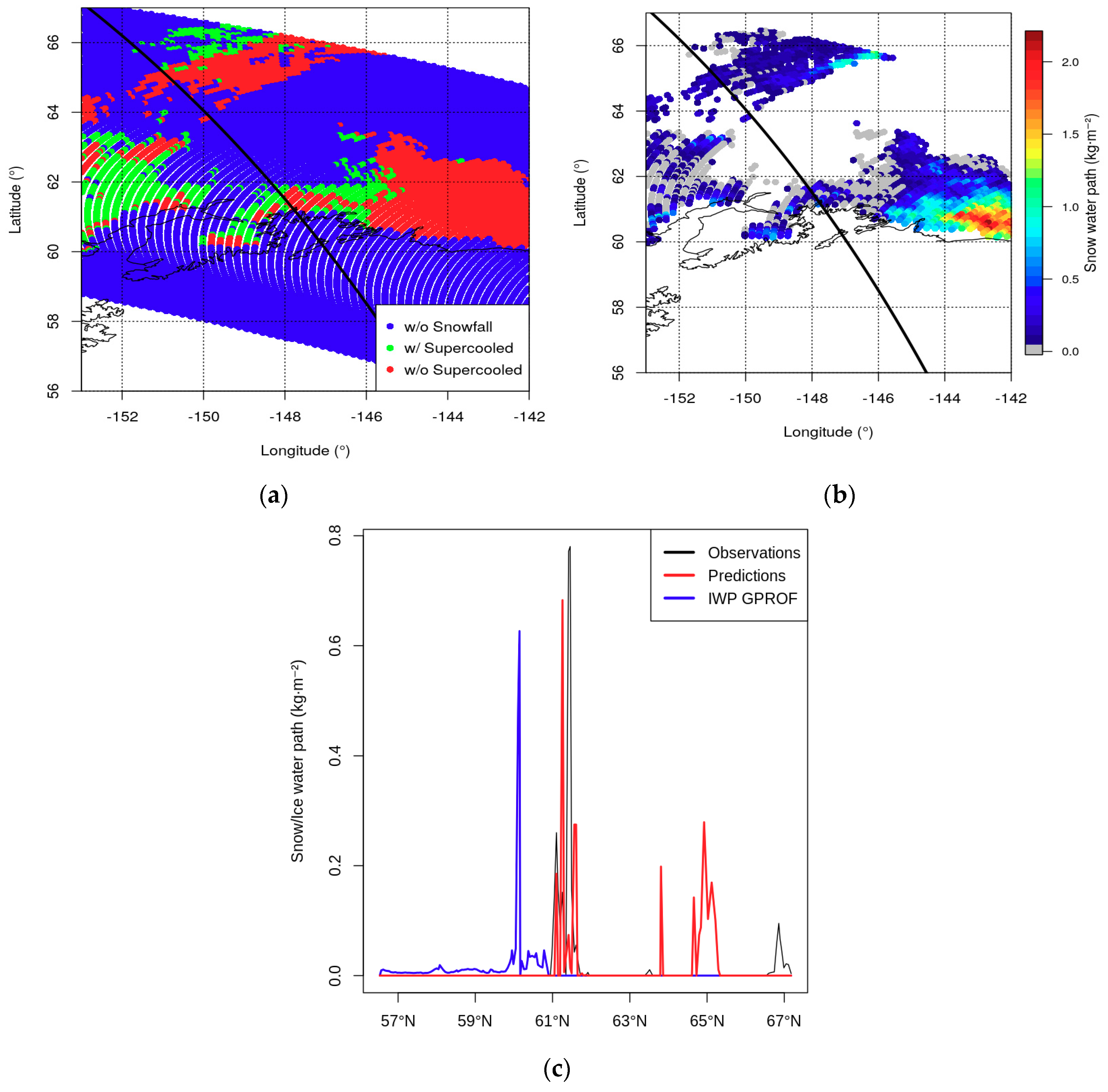
6.1. Case Studies
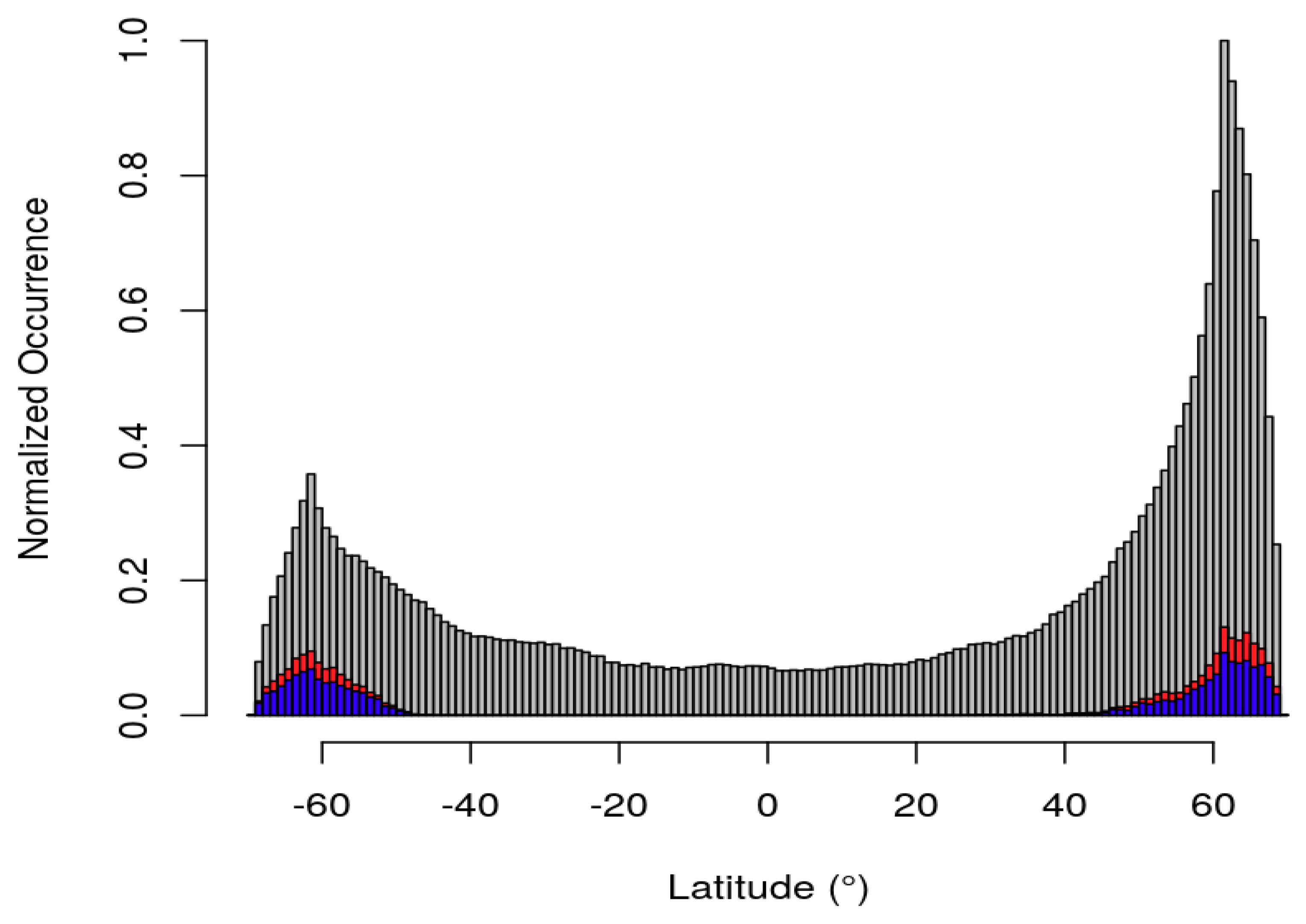
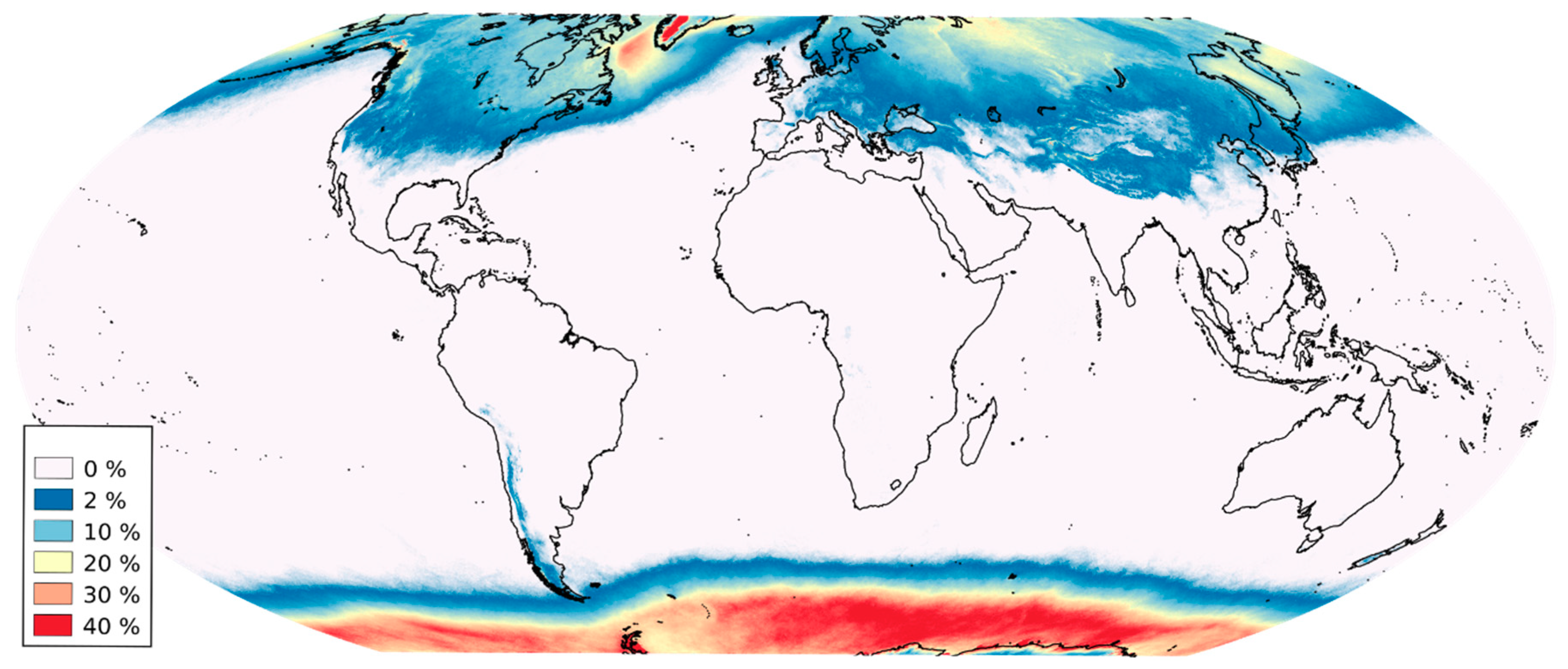
6.2. Climatology of Snowfall Occurrence
7. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Tools
References
- Knowles, N.; Dettinger, M.D.; Cayan, D.R. Trends in snowfall versus rainfall in the Western United States. J. Clim. 2006, 19, 4545–4559. [Google Scholar] [CrossRef]
- Feng, S.; Hu, Q. Changes in winter snowfall/precipitation ratio in the contiguous United States. J. Geophys. Res. Atmos. 2007, 112, D15109. [Google Scholar] [CrossRef]
- Levizzani, V.; Laviola, S.; Cattani, E. Detection and measurement of snowfall from space. Remote Sens. 2011, 3, 145–166. [Google Scholar] [CrossRef]
- Behrangi, A.; Christensen, M.; Richardson, M.; Lebsock, M.; Stephens, G.; Huffman, G.J.; Bolvin, D.; Adler, R.F.; Gardner, A.; Lambrigtsen, B.; et al. Status of high-latitude precipitation estimates from observations and reanalyses. J. Geophys. Res.-Atmos. 2016, 121, 4468–4486. [Google Scholar] [CrossRef] [PubMed]
- Skofronick-Jackson, G.M.; Kim, M.J.; Weinman, J.A.; Chang, D.E. A physical model to determine snowfall over land by microwave radiometry. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1047–1058. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.M.; Johnson, B.T.; Munchak, S.J. Detection thresholds of falling snow from satellite-borne active and passive sensors. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4177–4189. [Google Scholar] [CrossRef]
- Stephens, G.L.; Vane, D.G.; Boain, R.J.; Mace, G.G.; Sassen, K.; Wang, Z.E.; Illingworth, A.J.; O’Connor, E.J.; Rossow, W.B.; Durden, S.L.; et al. The cloudsat mission and the a-train—A new dimension of space-based observations of clouds and precipitation. Bull. Am. Meteorol. Soc. 2002, 83, 1771–1790. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Kulie, M.S.; Bennartz, R. Utilizing spaceborne radars to retrieve dry snowfall. J. Appl. Meteorol. Climatol. 2009, 48, 2564–2580. [Google Scholar] [CrossRef]
- Hiley, M.J.; Kulie, M.S.; Bennartz, R. Uncertainty analysis for CloudSat snowfall retrievals. J. Appl. Meteorol. Climatol. 2011, 50, 399–418. [Google Scholar] [CrossRef]
- Kulie, M.S.; Milani, L.; Wood, N.B.; Tushaus, S.A.; Bennartz, R.; L’Ecuyer, T.S. A shallow cumuliform snowfall census using spaceborne radar. J. Hydrometeorol. 2016, 17, 1261–1279. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Kulie, M.; Behrangi, A.; Stepanian, P.M.; Cao, Q.; You, Y.; Zhang, J.; Hu, J.; Zhang, X. Comparison of snowfall estimates from the NASA CloudSat cloud profiling radar and NOAA/NSSL multi-radar multi-sensor system. J. Hydrol. 2016, 541, 862–872. [Google Scholar] [CrossRef]
- Milani, L.; Kulie, M.S.; Casella, D.; Dietrich, S.; L’Ecuyer, T.S.; Panegrossi, G.; Porcù, F.; Sanò, P.; Wood, N.B. CloudSat snowfall estimates over Antarctica and the Southern Ocean: An assessment of independent retrieval methodologies and multi-year snowfall analysis. Atmos. Res. 2018, 213, 121–135. [Google Scholar] [CrossRef]
- Casella, D.; Panegrossi, G.; Sano, P.; Marra, A.C.; Dietrich, S.; Johnson, B.T.; Kulie, M.S. Evaluation of the GPM-DPR snowfall detection capability: Comparison with CloudSat-CPR. Atmos. Res. 2017, 197, 64–75. [Google Scholar] [CrossRef]
- Bennartz, R.; Bauer, P. Sensitivity of microwave radiances at 85–183 GHz to precipitating ice particles. Radio Sci. 2003, 38. [Google Scholar] [CrossRef]
- Liu, G.; Seo, E.-K. Detecting snowfall over land by satellite high-frequency microwave observations: The lack of scattering signature and a statistical approach. J. Geophys. Res.-Atmos. 2013, 118, 1376–1387. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Johnson, B.T. Surface and atmospheric contributions to passive microwave brightness temperatures for falling snow events. J. Geophys. Res.-Atmos. 2011, 116, D02213. [Google Scholar] [CrossRef]
- Gong, J.; Wu, D.L. Microphysical properties of frozen particles inferred from Global Precipitation Measurement (GPM) Microwave Imager (GMI) polarimetric measurements. Atmos. Chem. Phys. 2017, 17, 2741–2757. [Google Scholar] [CrossRef]
- Liu, G.S.; Curry, J.A. Precipitation characteristics in Greenland-Iceland-Norwegian Seas determined by using satellite microwave data. J. Geophys. Res.-Atmos. 1997, 102, 13987–13997. [Google Scholar] [CrossRef]
- Kongoli, C.; Pellegrino, P.; Ferraro, R.R.; Grody, N.C.; Meng, H. A new snowfall detection algorithm over land using measurements from the Advanced Microwave Sounding Unit (AMSU). Geophys. Res. Lett. 2003, 30, 1756. [Google Scholar] [CrossRef]
- Surussavadee, C.; Staelin, D.H. Satellite retrievals of arctic and equatorial rain and snowfall rates using millimeter wavelengths. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3697–3707. [Google Scholar] [CrossRef]
- Noh, Y.-J.; Liu, G.; Jones, A.S.; Haar, T.H.V. Toward snowfall retrieval over land by combining satellite and in situ measurements. J. Geophys. Res.-Atmos. 2009, 114, D24205. [Google Scholar] [CrossRef]
- Kongoli, C.; Meng, H.; Dong, J.; Ferraro, R. A snowfall detection algorithm over land utilizing high-frequency passive microwave measurements-Application to ATMS. J. Geophys. Res.-Atmos. 2015, 120, 1918–1932. [Google Scholar] [CrossRef]
- Kongoli, C.; Meng, H.; Dong, J.; Ferraro, R. A hybrid snowfall detection method from satellite passive microwave measurements and global forecast weather models. Q. J. R. Meteorol. Soc. 2018. [Google Scholar] [CrossRef]
- You, Y.; Wang, N.-Y.; Ferraro, R. A prototype precipitation retrieval algorithm over land using passive microwave observations stratified by surface condition and precipitation vertical structure. J. Geophys. Res.-Atmos. 2015, 120, 5295–5315. [Google Scholar] [CrossRef]
- You, Y.; Wang, N.-Y.; Ferraro, R.; Rudlosky, S. Quantifying the snowfall detection performance of the GPM microwave imager channels over land. J. Hydrometeorol. 2017, 18, 729–751. [Google Scholar] [CrossRef]
- Kummerow, C.D.; Randel, D.L.; Kulie, M.; Wang, N.-Y.; Ferraro, R.; Joseph Munchak, S.; Petkovic, V. The evolution of the Goddard profiling algorithm to a fully parametric scheme. J. Atmos. Ocean. Technol. 2015, 32, 2265–2280. [Google Scholar] [CrossRef]
- Sims, E.M.; Liu, G. A parameterization of the probability of snow–rain transition. J. Hydrometeorol. 2015, 16, 1466–1477. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Munchak, S.J.; Ringerud, S.; Petersen, W.; Lott, B. Falling snow estimates from the global precipitation measurement (gpm) mission. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; IEEE: New York, NY, USA, 2017; pp. 2724–2727, ISBN 978-1-5090-4951-6. [Google Scholar]
- Prigent, C.; Aires, F.; Rossow, W.B. Land surface microwave emissivities over the globe for a decade. Bull. Am. Meteorol. Soc. 2006, 87, 1573–1584. [Google Scholar] [CrossRef]
- Foster, J.L.; Skofronick-Jackson, G.; Meng, H.; Wang, J.R.; Riggs, G.; Kocin, P.J.; Johnson, B.T.; Cohen, J.; Hall, D.K.; Nghiem, S.V. Passive microwave remote sensing of the historic February 2010 snowstorms in the Middle Atlantic region of the USA. Hydrol. Process. 2012, 26, 3459–3471. [Google Scholar] [CrossRef]
- Turk, F.J.; Haddad, Z.S.; Kirstetter, P.; You, Y.; Ringerud, S. An observationally based method for stratifying a priori passive microwave observations in a Bayesian-based precipitation retrieval framework. Q. J. R. Meteorol. Soc. 2017. [Google Scholar] [CrossRef]
- Ebtehaj, A.M.; Kummerow, C.D. Microwave retrievals of terrestrial precipitation over snow-covered surfaces: A lesson from the GPM satellite. Geophys. Res. Lett. 2017, 44, 6154–6162. [Google Scholar] [CrossRef]
- Petty, G. Physical retrievals of over-ocean rain rate from multichannel microwave imagery. 1: Theoretical characteristics of normalized polarization and scattering indexes. Meteorol. Atmos. Phys. 1994, 54, 79–99. [Google Scholar] [CrossRef]
- Bennartz, R.; Petty, G.W. The sensitivity of microwave remote sensing observations of precipitation to ice particle size distributions. J. Appl. Meteorol. 2001, 40, 345–364. [Google Scholar] [CrossRef]
- Kulie, M.S.; Bennartz, R.; Greenwald, T.J.; Chen, Y.; Weng, F. Uncertainties in microwave properties of frozen precipitation implications for remote sensing and data assimilation. J. Atmos. Sci. 2010, 67, 3471–3487. [Google Scholar] [CrossRef]
- Petty, G.W.; Huang, W. Microwave backscatter and extinction by soft ice spheres and complex snow aggregates. J. Atmos. Sci. 2010, 67, 769–787. [Google Scholar] [CrossRef]
- Kuo, K.-S.; Olson, W.S.; Johnson, B.T.; Grecu, M.; Tian, L.; Clune, T.L.; van Aartsen, B.H.; Heymsfield, A.J.; Liao, L.; Meneghini, R. The microwave radiative properties of falling snow derived from nonspherical ice particle models. Part I: An extensive database of simulated pristine crystals and aggregate particles, and their scattering properties. J. Appl. Meteorol. Climatol. 2016, 55, 691–708. [Google Scholar] [CrossRef]
- Olson, W.S.; Tian, L.; Grecu, M.; Kuo, K.-S.; Johnson, B.T.; Heymsfield, A.J.; Bansemer, A.; Heymsfield, G.M.; Wang, J.R.; Meneghini, R. The microwave radiative properties of falling snow derived from nonspherical ice particle models. Part II: Initial testing using radar, radiometer and in situ observations. J. Appl. Meteorol. Climatol. 2016, 55, 709–722. [Google Scholar] [CrossRef]
- Kneifel, S.; Loehnert, U.; Battaglia, A.; Crewell, S.; Siebler, D. Snow scattering signals in ground-based passive microwave radiometer measurements. J. Geophys. Res.-Atmos. 2010, 115, D16214. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, G.; Seo, E.-K.; Fu, Y. Liquid water in snowing clouds: Implications for satellite remote sensing of snowfall. Atmos. Res. 2013, 131, 60–72. [Google Scholar] [CrossRef]
- Johnson, B.T.; Olson, W.S.; Skofronick-Jackson, G. The microwave properties of simulated melting precipitation particles: Sensitivity to initial melting. Atmos. Meas. Tech. 2016, 9, 9–21. [Google Scholar] [CrossRef]
- Panegrossi, G.; Rysman, J.-F.; Casella, D.; Marra, A.C.; Sano, P.; Kulie, M.S. CloudSat-based assessment of GPM microwave imager snowfall observation capabilities. Remote Sens. 2017, 9, 1263. [Google Scholar] [CrossRef]
- Panegrossi, G.; Rysman, J.-F.; Casella, D.; Sano, P.; Marra, A.C.; Dietrich, S.; Kulie, M.S. Exploitation of GPM/CloudSat coincidence dataset for global snowfall retrieval. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Valencia, Spain, 23–27 July 2018; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Draper, D.W.; Newell, D.A.; Wentz, F.J.; Krimchansky, S.; Skofronick-Jackson, G.M. The global precipitation measurement (GPM) microwave imager (GMI): Instrument overview and early on-orbit performance. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 3452–3462. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Berg, W.; Kidd, C.; Kirschbaum, D.B.; Petersen, W.A.; Huffman, G.J.; Takayabu, Y.N. Global precipitation measurement (GPM): Unified precipitation estimation from space. In Remote Sensing of Clouds and Precipitation; Andronache, C., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 175–193. ISBN 978-3-319-72583-3. [Google Scholar]
- Turk, J. CloudSat-GPM coincidence dataset (version 1C). In NASA Technical Report; California Institute of Technology: Pasadena, CA, USA, 2016. [Google Scholar]
- Xie, X.; Loehnert, U.; Kneifel, S.; Crewell, S. Snow particle orientation observed by ground-based microwave radiometry. J. Geophys. Res.-Atmos. 2012, 117, D02206. [Google Scholar] [CrossRef]
- Battaglia, A.; Delanoë, J. Synergies and complementarities of CloudSat-CALIPSO snow observations. J. Geophys. Res.-Atmos. 2013, 118, 721–731. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Spreen, G.; Kaleschke, L.; Heygster, G. Sea ice remote sensing using AMSR-E 89-GHz channels. J. Geophys. Res.-Oceans 2008, 113, C02S03. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liu, J.; Wu, S.Y.; Zidek, J.V. On segmented multivariate regression. Stat. Sin. 1997, 7, 497–525. [Google Scholar]
- Breiman, L. Classification and Regression Trees; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; ISBN 978-0-12-385022-5. [Google Scholar]
- Adhikari, A.; Liu, C.; Kulie, M.S. Global distribution of snow precipitation features and their properties from 3 years of GPM observations. J. Clim. 2018, 31, 3731–3754. [Google Scholar] [CrossRef]
- Wood, N.B.; L’Ecuyer, T.S.; Heymsfield, A.J.; Stephens, G.L.; Hudak, D.R.; Rodriguez, P. Estimating snow microphysical properties using collocated multisensor observations. J. Geophys. Res. Atmos. 2014, 119, 8941–8961. [Google Scholar] [CrossRef]
- Sano, P.; Panegrossi, G.; Casella, D.; Marra, A.C.; D’Adderio, L.P.; Rysman, J.-F.; Dietrich, S. The passive microwave neural network precipitation retrieval (PNPR) algorithm for the conical scanning GMI radiometer. Remote Sens. 2018, 10, 1122. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.; Kulie, M.S.; Milani, L.; Munchak, S.J.; Wood, N.B.; Levizzani, V. Satellite estimation of falling snow: A global precipitation measurement (GPM) core observatory perspective. Rev. J. Appl. Meteorol. Climatol. (under review).
- RCoreTeam. R: A Language and Environment for Statistical Computing; RCoreTeam: Vienna, Austria, 2013. [Google Scholar]
- Fischer, B. rhdf5-HDF5 interface for R. In R# Package Version; RCoreTeam: Vienna, Austria, 2015; Volume 2. [Google Scholar]
- Pierce, D. ncdf4: Interface to Unidata netCDF (Version 4 or Earlier) Format Data Files. R Package 2012. Available online: http://CRAN. R-project. org/package = ncdf4 (accessed on 31 January 2018).
- Therneau, T.; Atkinson, B.; Ripley, B. RPART: Recursive Partitioning and Regression Trees. In R Package Version 4.1–10; RCoreTeam: Vienna, Austria, 2015. [Google Scholar]
- Dowle, M.; Short, T.; Lianoglou, S.; Saporta, R.; Srinivasan, A.; Antonyan, E. Data. Table: Extension of Data. Frame. 2014. Available online: https://cran.r-project.org/web/packages/data.table/index.html (accessed on 31 January 2018).
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A. Caret: Classification and regression training. 2016. In R Package Version; RCoreTeam: Vienna, Austria, 2017; Volume 4. [Google Scholar]
- Hothorn, T.; Hornik, K.; Zeileis, A. Unbiased recursive partitioning: A conditional inference framework. J. Comput. Graph. Stat. 2006, 15, 651–674. [Google Scholar] [CrossRef]
- Zeileis, A.; Hothorn, T.; Hornik, K. Model-based recursive partitioning. J. Comput. Graph. Stat. 2008, 17, 492–514. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting linear mixed-effects models using lme4. arXiv. 2014. arXiv Preprint:1406.5823. Available online: https://arxiv.org/abs/1406.5823 (accessed on 31 January 2018).
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S-PLUS; Springer Science & Business Media: New York, NY, USA, 2013; ISBN 978-1-4757-3121-7. [Google Scholar]
- Zambrano-Bigiarini, M. hydroGOF: Goodness-of-fit functions for comparison of simulated and observed hydrological time series. In R Package Version 0.3-8; RCoreTeam: Vienna, Austria, 2014. [Google Scholar]
- Ripley, B. Tree: Classification and regression trees. In R Package Version; RCoreTeam: Vienna, Austria, 2005; Available online: http://CRAN.R-project.org/package=tree (accessed on 31 January 2018).
- Elseberg, J.; Magnenat, S.; Siegwart, R.; Nüchter, A. Comparison of nearest-neighbor-search strategies and implementations for efficient shape registration. J. Softw. Eng. Robot. 2012, 3, 2–12. [Google Scholar]
- Tierney, L.; Rossini, A.J.; Li, N.; Sevcikova, H. Snow: Simple network of workstations. R Package Version 0.3-3; RCoreTeam: Vienna, Austria, 2008; Available online: http://CRAN.R-project.org/package=snow (accessed on 31 January 2018).
- Knaus, J. Snowfall: Easier cluster computing (based on snow). In R Package Version; RCoreTeam: Vienna, Austria, 2010; Volume 1. [Google Scholar]
- Muggeo, V.M. Estimating regression models with unknown break-points. Stat. Med. 2003, 22, 3055–3071. [Google Scholar] [CrossRef] [PubMed]
- Muggeo, V.M. Segmented: An R package to fit regression models with broken-line relationships. R news 2008, 8, 20–25. [Google Scholar]
- Adler, D.; Murdoch, D.; Nenadic, O.; Urbanek, S.; Chen, M.; Gebhardt, A.; Bolker, B.; Csardi, G.; Strzelecki, A.; Senger, A. Rgl: 3D visualization using OpenGL. In R Package Version 0.95; RCoreTeam: Vienna, Austria, 2016; Volume 1441. [Google Scholar]


| Surface | Correlation | Bias | RMSE |
|---|---|---|---|
| All | 0.88 | −16% | 0.1 kg∙m−2 |
| Land | 0.85 | −13% | 0.1 kg∙m−2 |
| Open Sea | 0.88 | −21% | 0.12 kg∙m−2 |
| Sea ice | 0.92 | −15% | 0.08 kg∙m−2 |
| Configuration | Correlation | Bias | RMSE |
|---|---|---|---|
| SLALOM | 0.86 | −20% | 0.04 kg∙m−2 |
| SLALOM w/o Sc | 0.86 | −18% | 0.04 kg∙m−2 |
| SLALOM w/o Env | 0.61 | −49% | 0.13 kg∙m−2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rysman, J.-F.; Panegrossi, G.; Sanò, P.; Marra, A.C.; Dietrich, S.; Milani, L.; Kulie, M.S. SLALOM: An All-Surface Snow Water Path Retrieval Algorithm for the GPM Microwave Imager. Remote Sens. 2018, 10, 1278. https://doi.org/10.3390/rs10081278
Rysman J-F, Panegrossi G, Sanò P, Marra AC, Dietrich S, Milani L, Kulie MS. SLALOM: An All-Surface Snow Water Path Retrieval Algorithm for the GPM Microwave Imager. Remote Sensing. 2018; 10(8):1278. https://doi.org/10.3390/rs10081278
Chicago/Turabian StyleRysman, Jean-François, Giulia Panegrossi, Paolo Sanò, Anna Cinzia Marra, Stefano Dietrich, Lisa Milani, and Mark S. Kulie. 2018. "SLALOM: An All-Surface Snow Water Path Retrieval Algorithm for the GPM Microwave Imager" Remote Sensing 10, no. 8: 1278. https://doi.org/10.3390/rs10081278
APA StyleRysman, J.-F., Panegrossi, G., Sanò, P., Marra, A. C., Dietrich, S., Milani, L., & Kulie, M. S. (2018). SLALOM: An All-Surface Snow Water Path Retrieval Algorithm for the GPM Microwave Imager. Remote Sensing, 10(8), 1278. https://doi.org/10.3390/rs10081278








