The Salinity Retrieval Algorithms for the NASA Aquarius Version 5 and SMAP Version 3 Releases
Abstract
1. Introduction
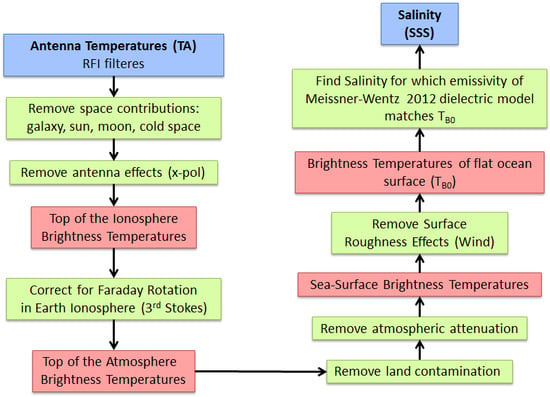
2. Major Steps of the Salinity Retrieval Algorithm
2.1. Basic Algorithm Flow
2.2. Ancillary Inputs
2.2.1. Sea Surface Temperature (SST)
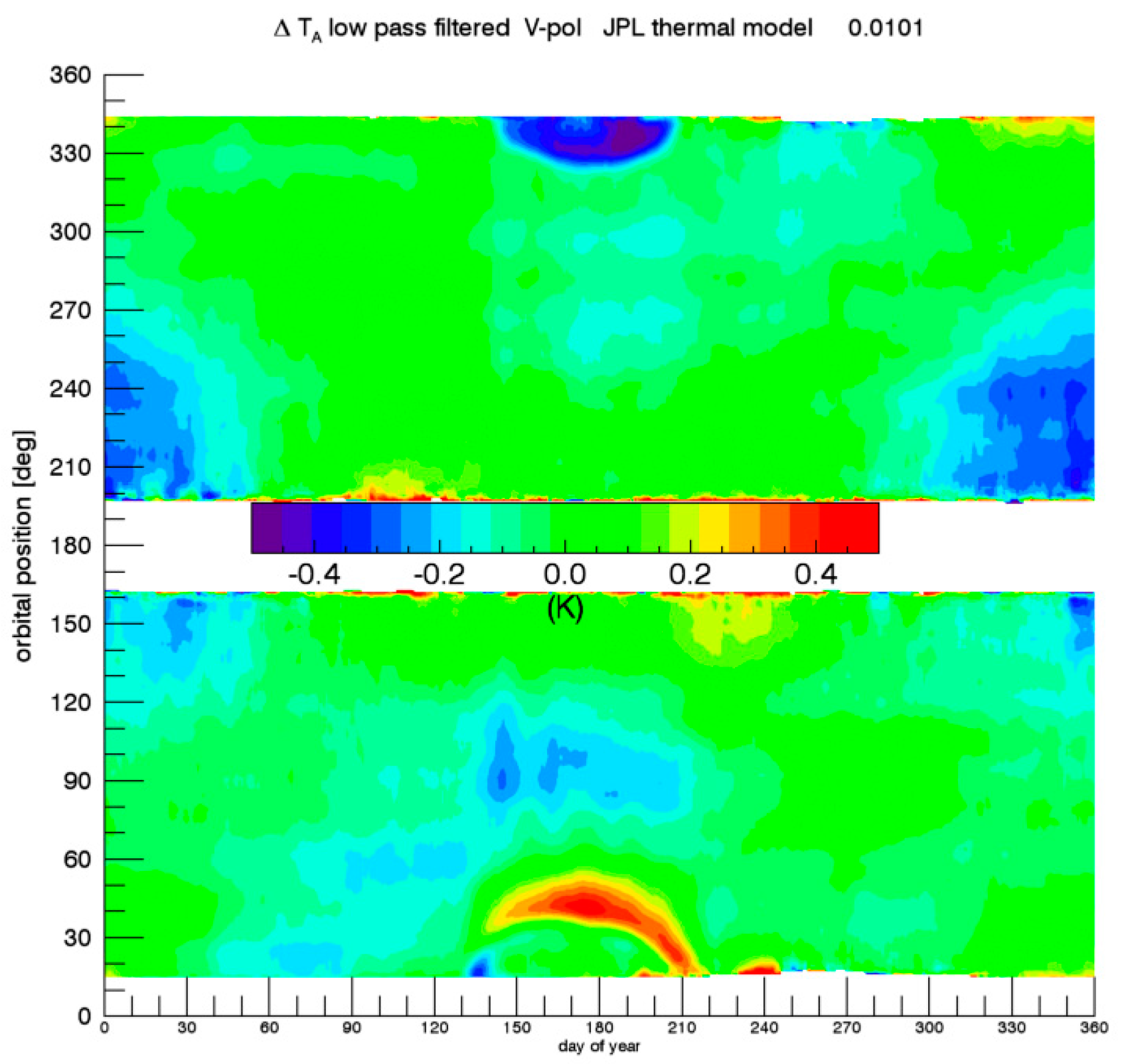
2.2.2. Atmospheric Profiles
2.2.3. Wind Speed Background Field
2.2.4. Wind Direction
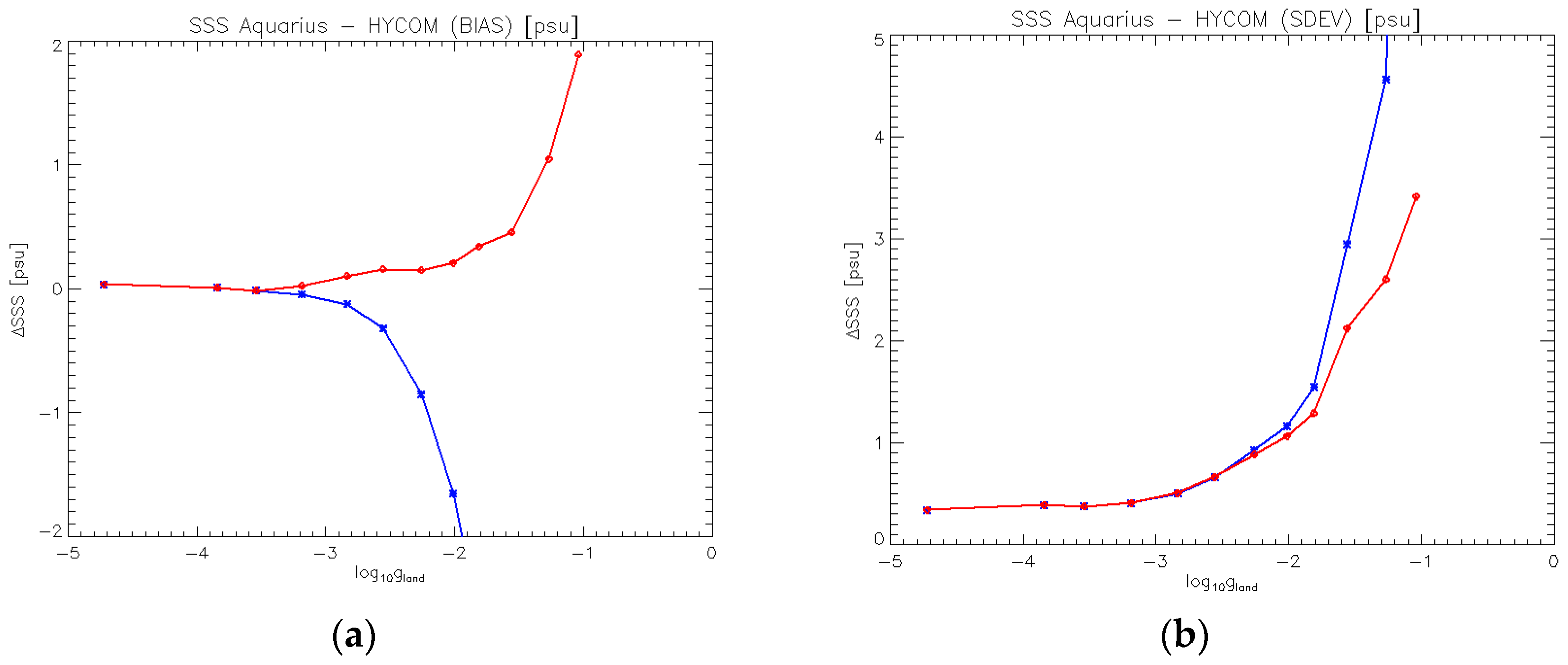
2.2.5. Land Mask
2.2.6. Rain Rate and Rain Flagging
2.3. Forward Model and Expected TA
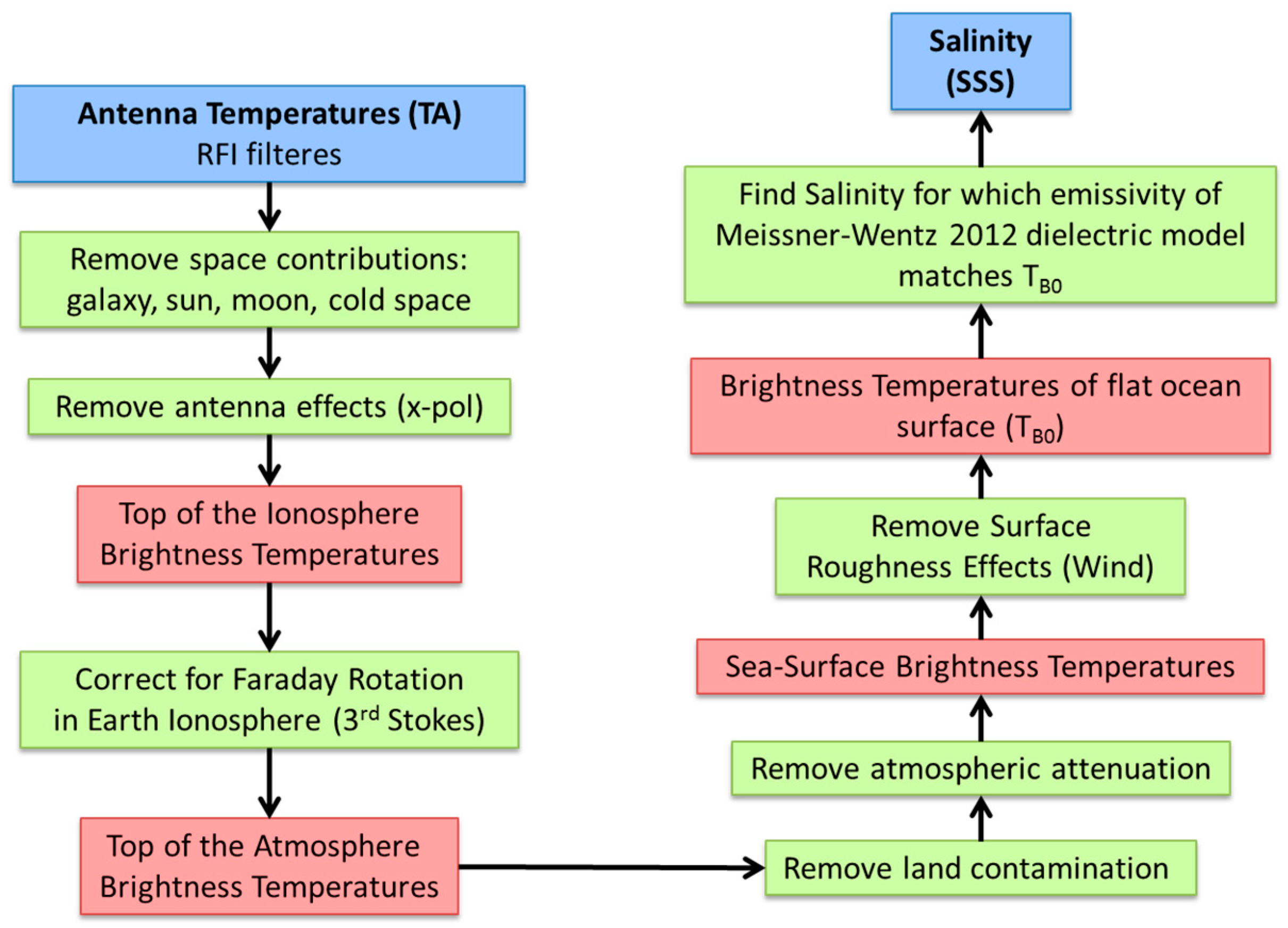
3. Surface Roughness Correction
4. Atmospheric Absoprtion Correction
4.1. Atmospheric Absoprtion and Correction Algorithm
4.2. Oxygen Absorption Model
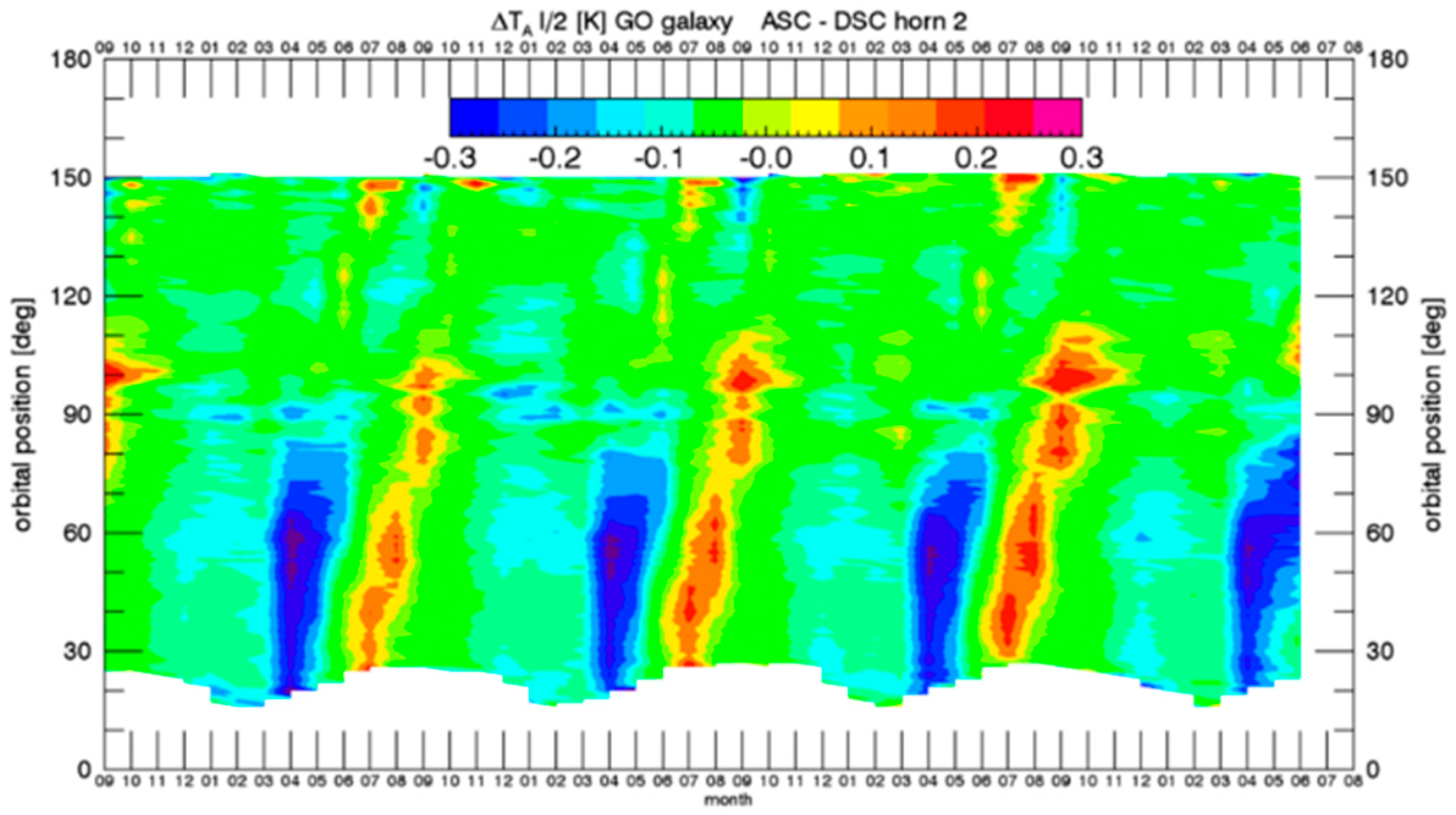
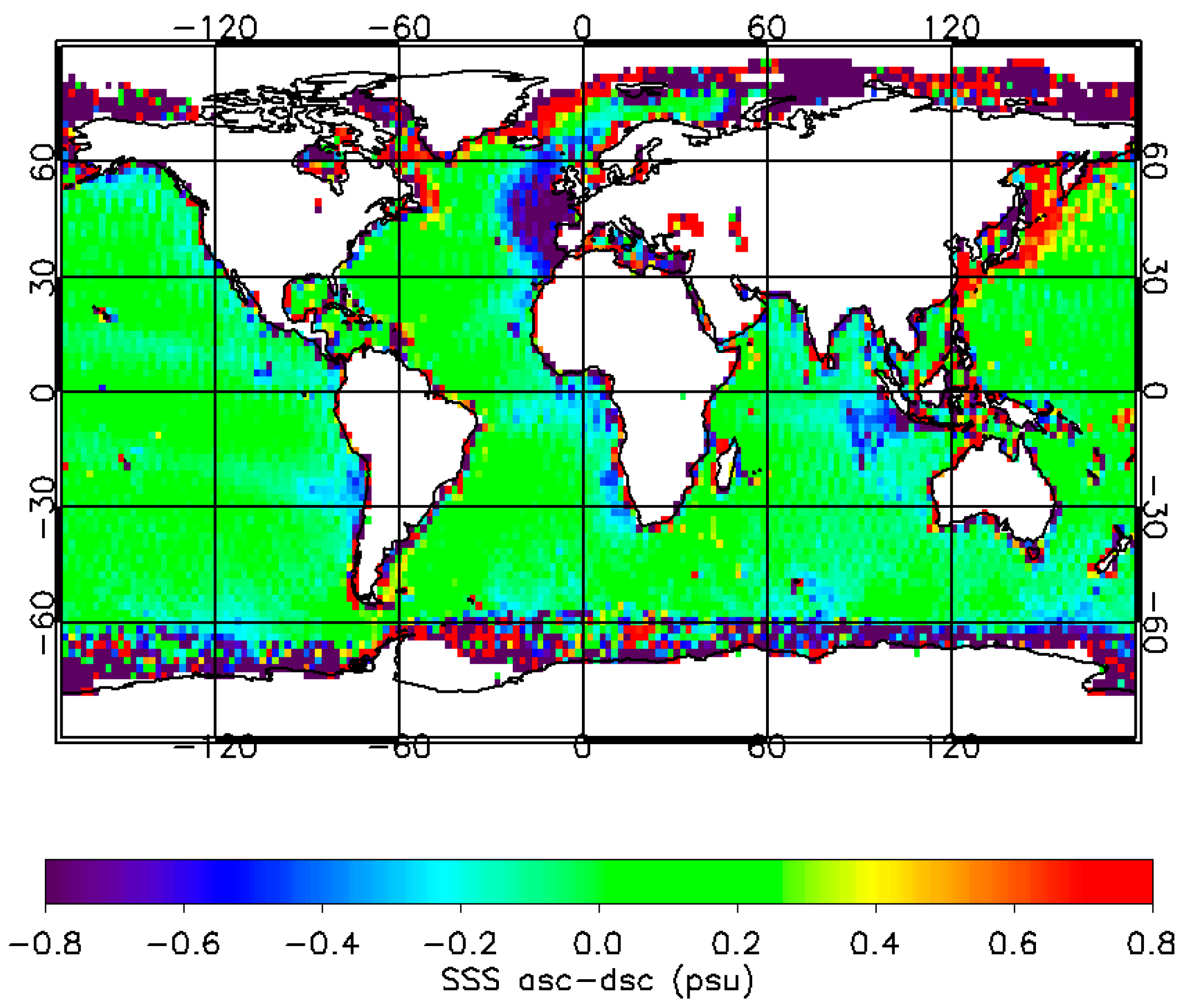
5. Reflected Galaxy Correction
5.1. Geometric Optics Model
5.2. SMAP Fore—Aft Analysis
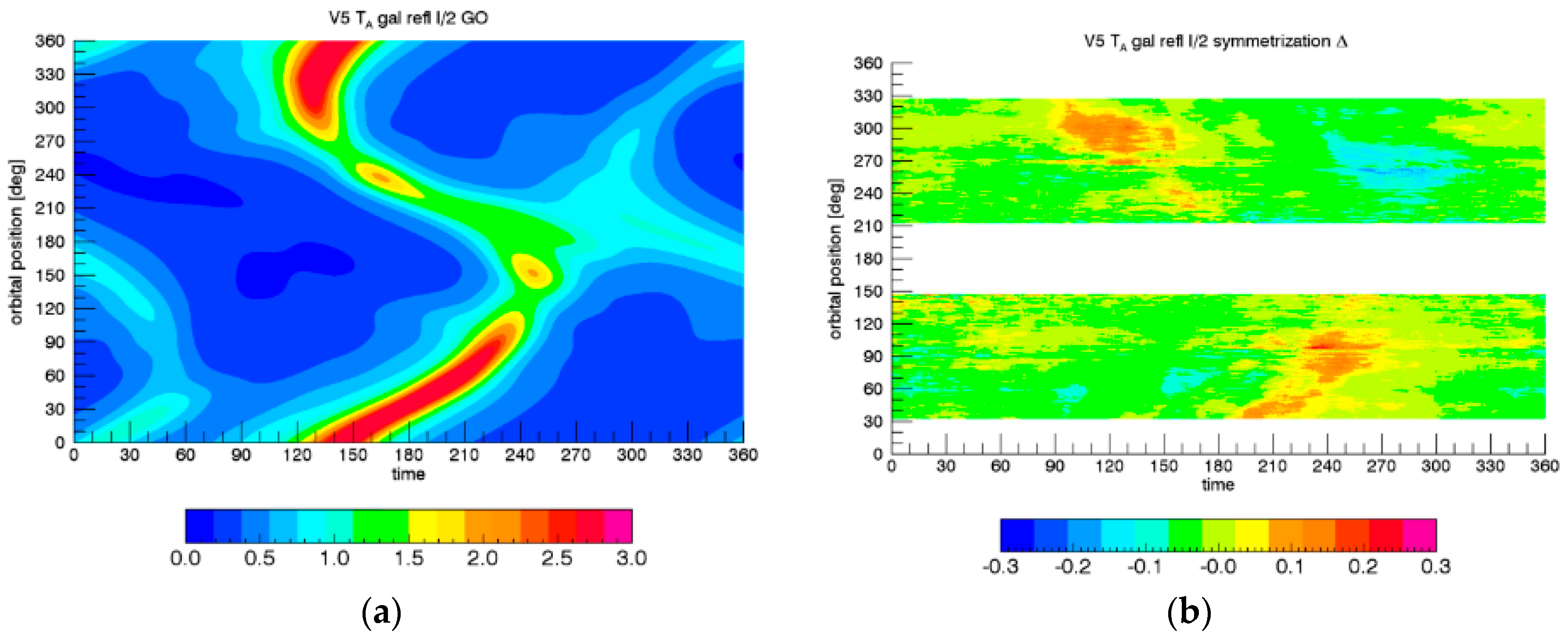
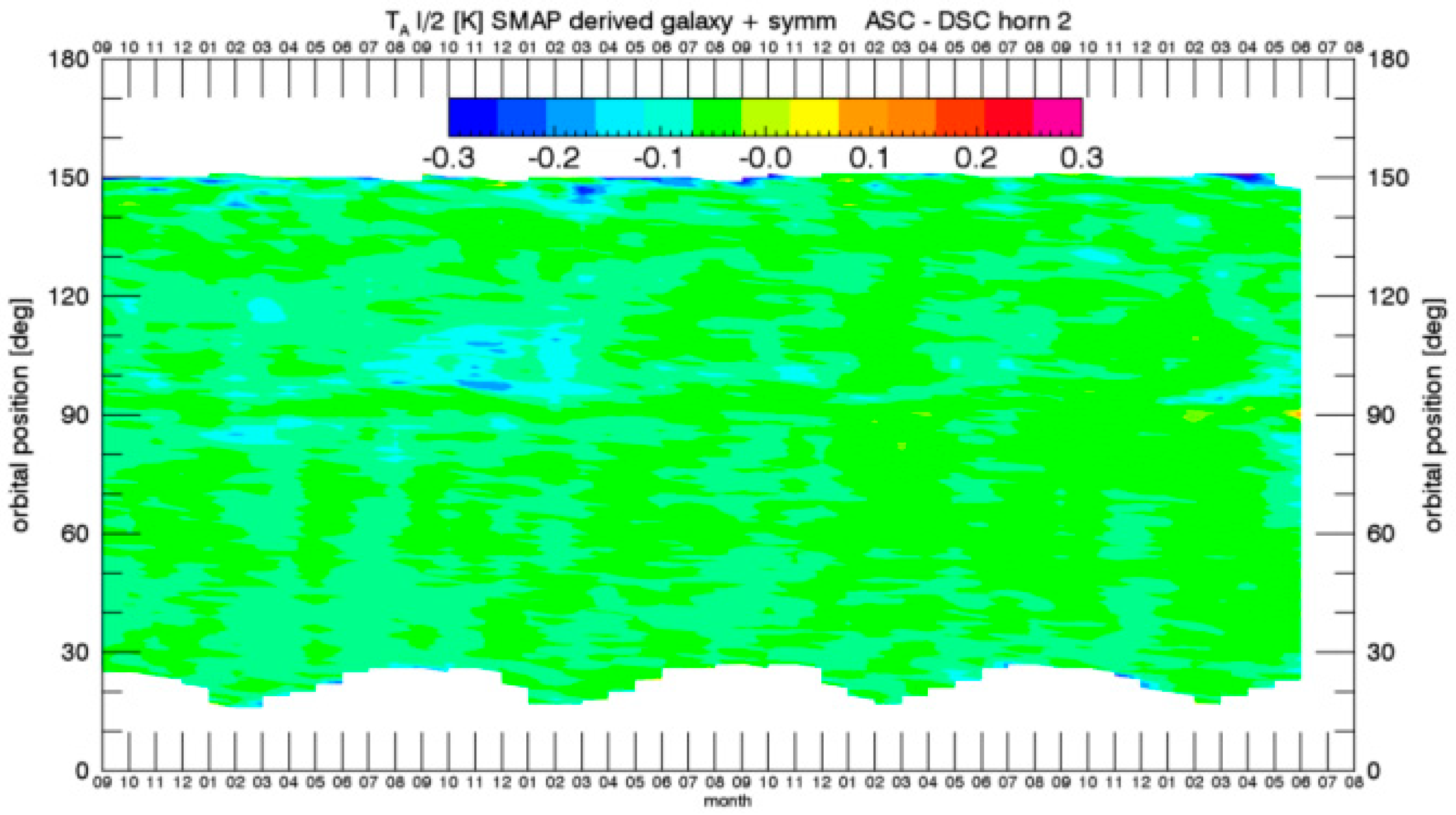
5.3. Emprirical Zonal Symmetrization
- The value of the variance of the slope distribution is not completely correct, even after effectively increasing the roughness by adding 2 m/s to the wind speed based on the SMAP fore—aft results.
- Errors in the antenna gain patterns used to derive the tables of the GO model.
- Other ocean roughness effects, which cause reflection of galactic radiation but cannot be modeled with an ensemble of tilted facets (e.g., Bragg scattering at short waves, breaking waves and/or foam, and net directional roughness features on a large scale).
- There are no zonal ascending—descending biases in ocean salinity on weekly or larger time scales.
- The residual zonal ascending—descending biases that are observed are all due to the inadequacies (either over or under correction) in the GO model calculation for the reflected galactic radiation.
- The size of the residual ascending—descending biases is proportional to the strength of the reflected galactic radiation.
- Assume that lies in the ascending swath and therefore lies in the descending swath. If there is no reflected galactic radiation in the ascending swath, i.e., , then and . That means that the symmetrization term and thus the whole empirical correction vanishes, and therefore: .
- If, on the other hand, there is no reflected galactic radiation in the descending swath, i.e., , then and . That implies and thus .
- The zonal average of is symmetric: .
- If the reflected galactic radiation is the same in ascending and descending swaths , then and thus the global average (sum of ascending and descending swaths) does not change after adding the symmetrization term: .
- If the zonal averages are already symmetric , then the symmetrization term and thus the whole empirical correction vanishes, and therefore: . That means that our method will not introduce any additional ascending—descending biases that were not already there.
6. Correction for Sidelobe Intrusion from Land Surfaces
7. Ocean Target Calibration and Calibration Drift Correction
8. Error Sources and Formal Uncertainty Estimation
8.1. Methodology
- The computational/algorithm part, i.e., running each retrieval algorithm with the perturbed parameter values.
- Obtaining a realistic error model for all the uncertainties that are involved. This part is done offline and its results are fed into the perturbed retrievals.
- Uncertainties that fluctuate on larger time and spatial scales (1 month, >100 km) are treated as systematic uncertainties.
- Uncertainties that fluctuate on shorter time and length scales are treated as random uncertainties.
8.2. Error Sources
8.2.1. NEDT
8.2.2. Wind Speed
8.2.3. Wind Direction
8.2.4. SST
8.2.5. Reflected Galaxy
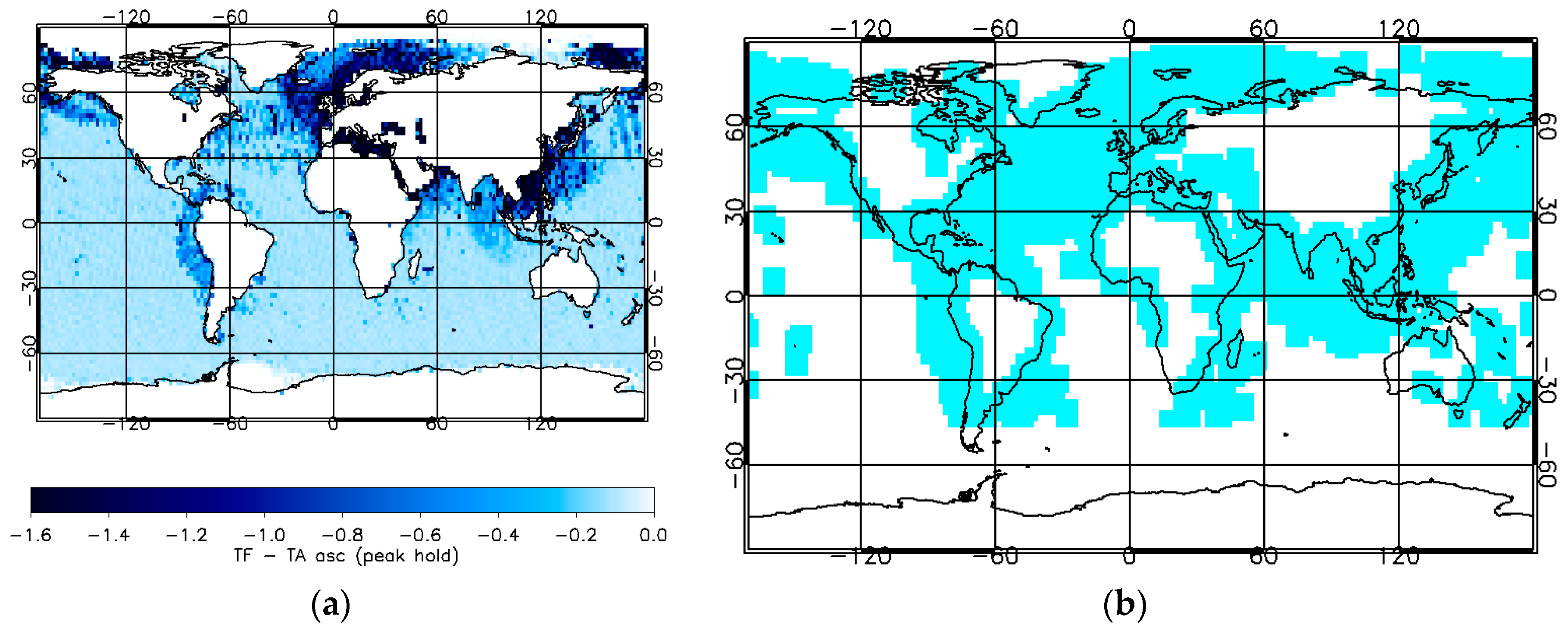
8.2.6. Land Contamination
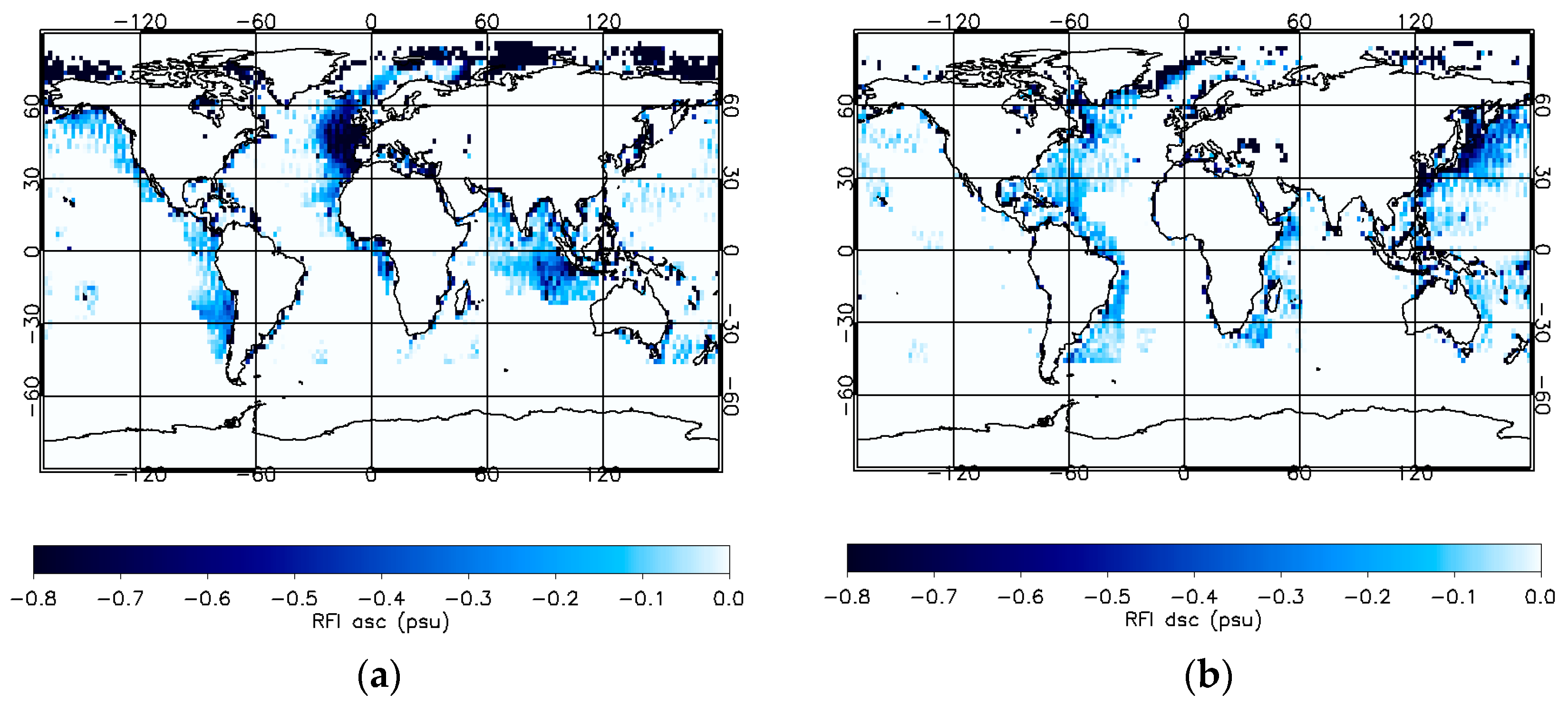
8.2.7. Undetected RFI
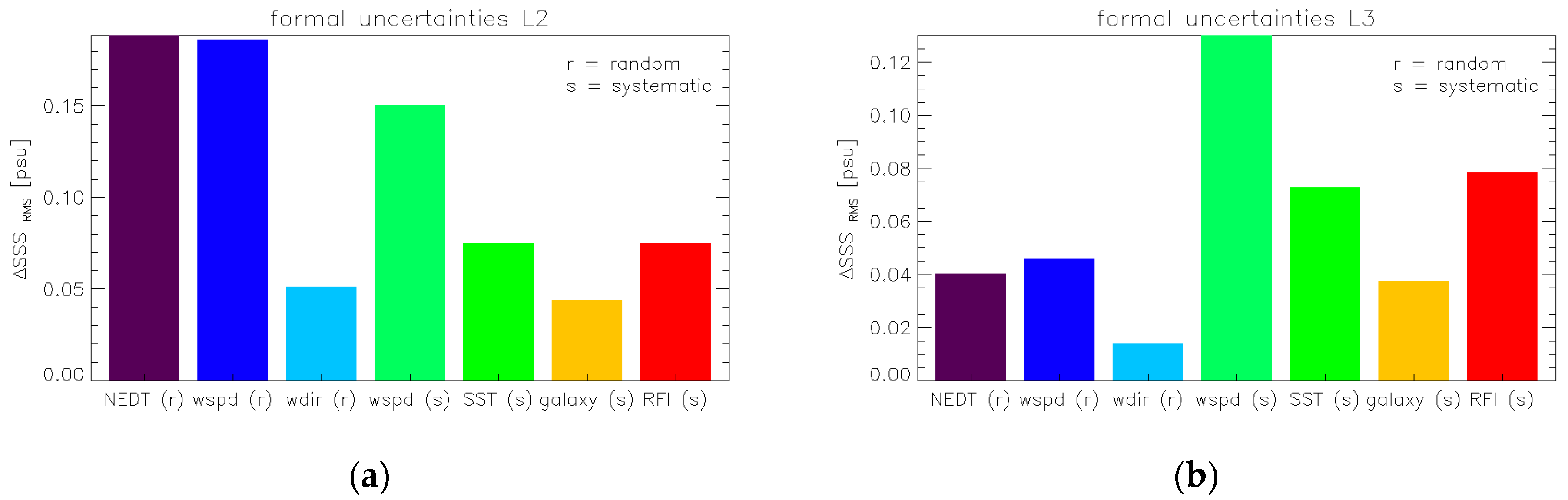
8.3. Error Allocations at Level 2 and Level 3
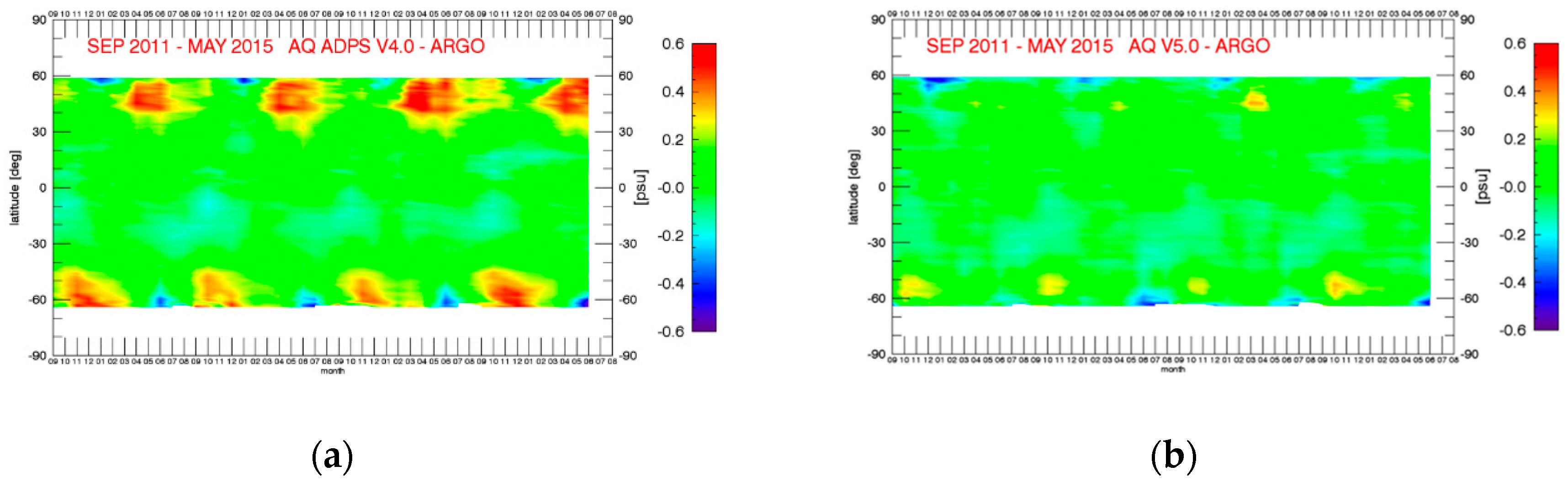
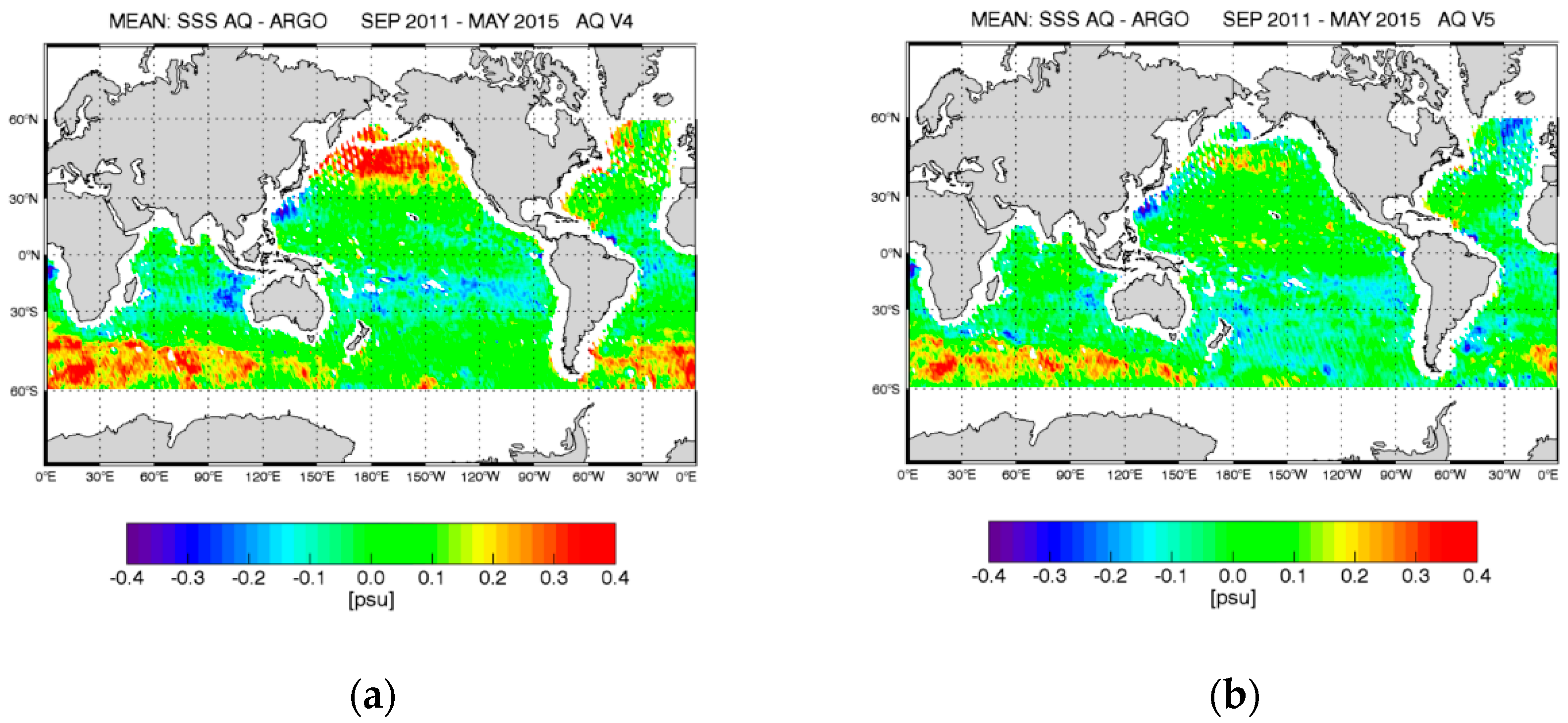
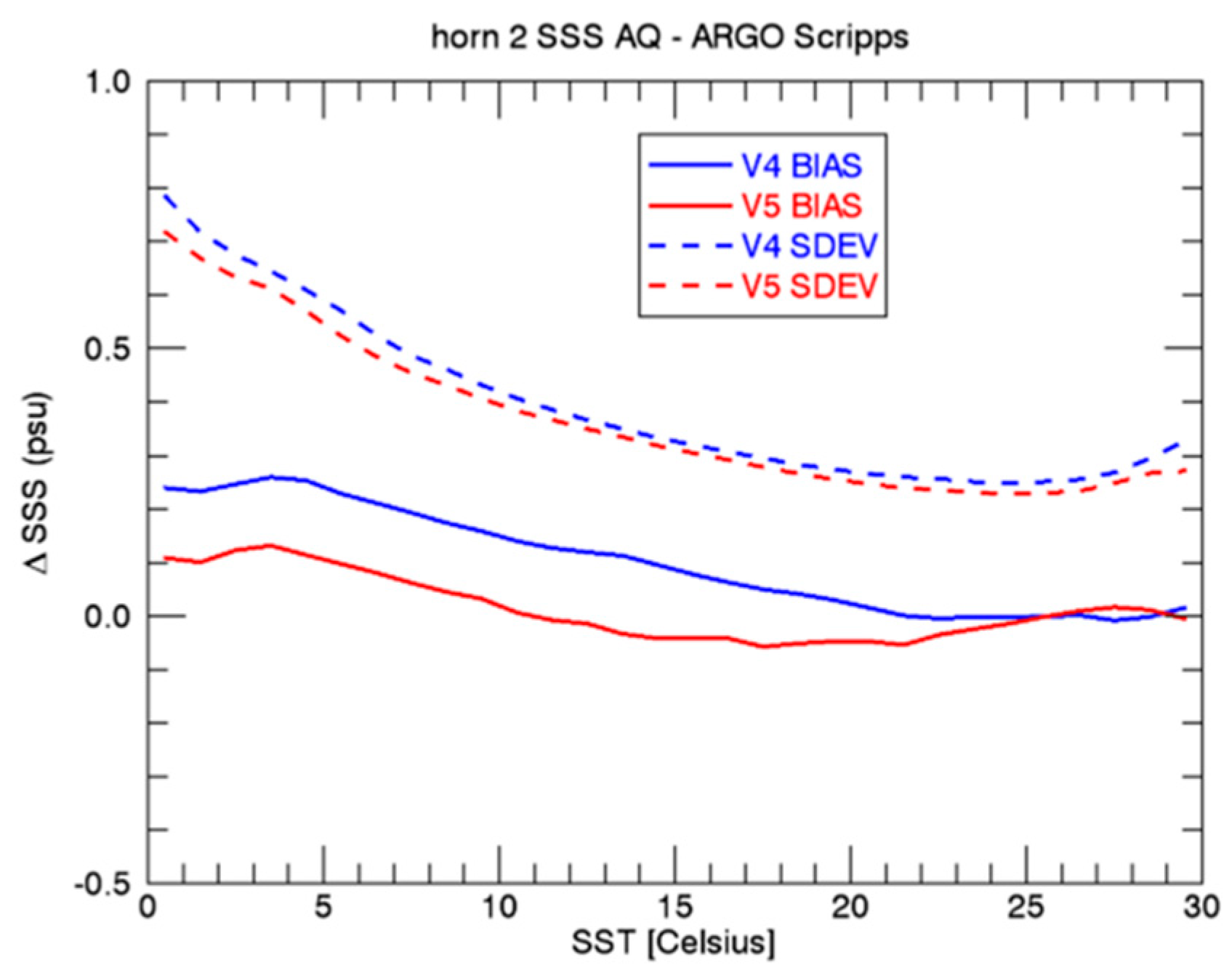
9. Validation and Improvements from Previous Releases
10. Adaption to Version 3 SMAP Salinity Retrievals
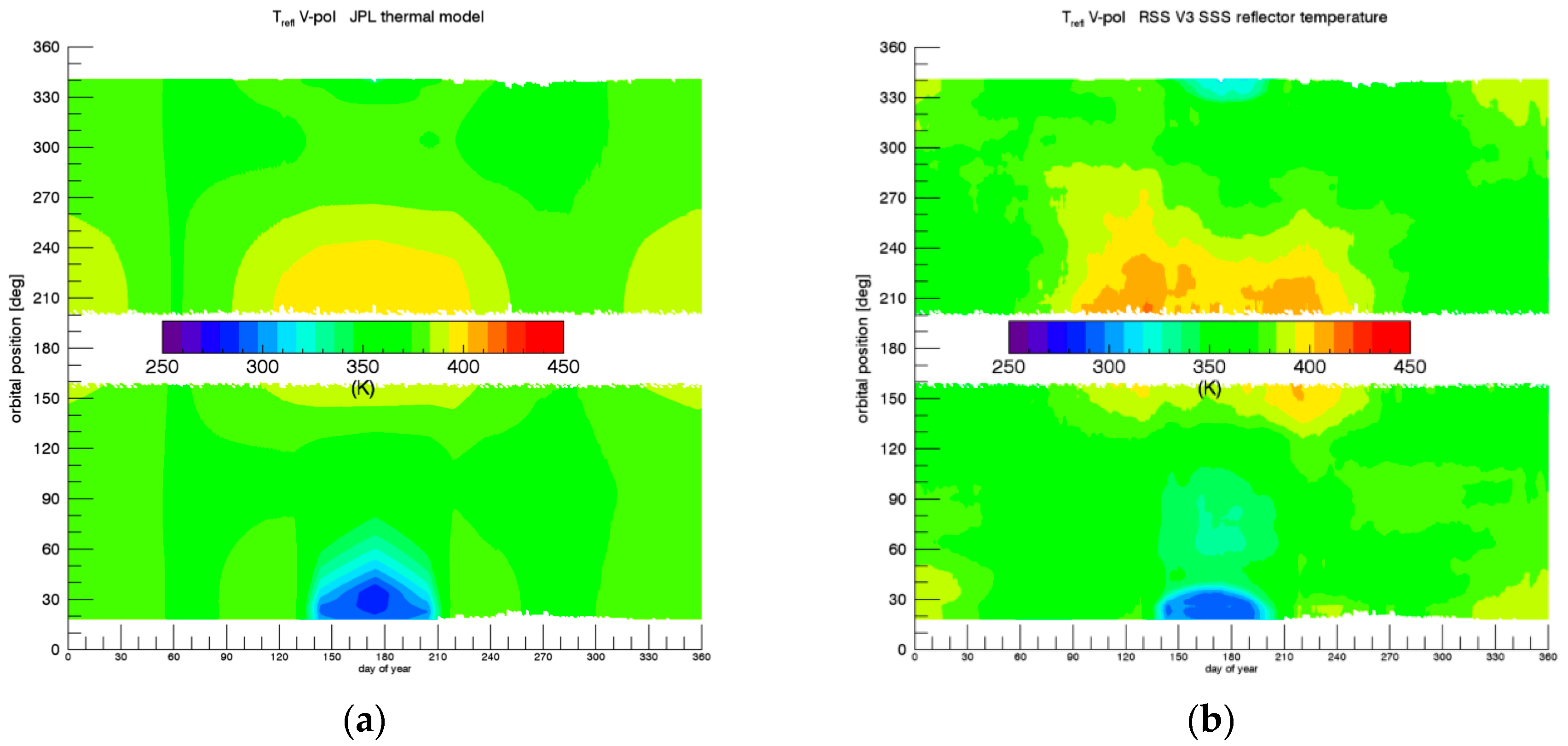
10.1. SMAP Emissive Reflector
10.2. SMAP Surface Roughness Correction
11. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Le Vine, D.; Lagerloef, G.; Colomb, F.; Yueh, S.; Pellerano, F. Aquarius: An instrument to monitor sea surface salinity from space. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2040–2050. [Google Scholar] [CrossRef]
- Aquarius Official Release Level 2 Sea Surface Salinity & Wind Speed Data V5.0. Available online: https://podaac.jpl.nasa.gov/dataset/AQUARIUS_L2_SSS_V5 (accessed on 10 July 2018).
- Meissner, T.; Wentz, F.; Le Vine, D. Aquarius Salinity Retrieval Algorithm Theoretical Basis Document (ATBD), End of Mission Version; RSS Technical Report 120117. 1 December 2017. Available online: http://podaac-ftp.jpl.nasa.gov/allData/aquarius/docs/v5/AQ-014-PS-0017_Aquarius_ATBD-EndOfMission.pdf (accessed on 10 July 2018).
- Le Vine, D.; Dinnat, E.; Meissner, T.; Yueh, S.; Wentz, F.; Torrusio, S.; Lagerloef, G. Status of Aquarius/SAC-D and Aquarius salinity retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 5401–5415. [Google Scholar] [CrossRef]
- Entekhabi, D.; Joku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Peng, J.; Misra, S.; Piepmeier, J.R.; Dinnat, E.P.; Hudson, D.; Le Vine, D.M.; De Amici, G.; Mohammed, P.N.; Bindlish, R.; Yueh, S.H.; et al. Soil Moisture Active/Passive L-Band microwave radiometer postlaunch calibration. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5339–5354. [Google Scholar] [CrossRef]
- RSS SMAP Level 2C Sea Surface Salinity V2.0 Validated Dataset. Available online: https://podaac.jpl.nasa.gov/dataset/SMAP_RSS_L2_SSS_V2 (accessed on 10 July 2018).
- Misra, S.; Ruf, C. Detection of radio-frequency interference for the Aquarius radiometer. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3123–3128. [Google Scholar] [CrossRef]
- Le Vine, D.; de Matthaeis, P.; Ruf, C.; Chen, D. Aquarius RFI Detection and Mitigation Algorithm: Assessment and Examples. IEEE Geosci. Remote Sens. 2014, 52, 4574–4584. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F. The complex dielectric constant of pure and sea water from microwave satellite observations. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1836–1849. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F. The emissivity of the ocean surface between 6 and 90 GHz over a large range of wind speeds and Earth incidence angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3004–3026. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.; Ricciardulli, L. The emission and scattering of L-band microwave radiation from rough ocean surfaces and wind speed measurements from Aquarius. J. Geophys. Res. Oceans 2014, 119. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.; Scott, J.; Vasquez-Cuervo, J. Sensitivity of ocean surface salinity measurements from spaceborne L-Band radiometers to ancillary sea surface temperature. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7105–7111. [Google Scholar] [CrossRef]
- Boutin, J.; Chao, Y.; Asher, W.E.; Delcroix, T.; Drucker, R.; Drushka, K.; Kolodziejczyk, N.; Lee, T.; Reul, N.; Reverdin, G.; et al. Satellite and in situ salinity: Understanding near-surface stratification and subfootprint variability. Bull. Am. Meteorol. Soc. 2016, 97, 1391–1407. [Google Scholar] [CrossRef]
- Santos-Garcia, A.; Jacob, M.; Jones, W.L.; Asher, W.; Hejazin, Y.; Ebrahimi, H.; Rabolli, M. Investigation of rain effects on Aquarius sea surface salinity measurements. J. Geophys. Res. Oceans 2014, 119, 7605–7624. [Google Scholar] [CrossRef]
- Joyce, R.; Janowiak, J.; Arkin, P.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Wentz, F.; Meissner, T. Algorithm Theoretical Basis Document (ATBD), Version 2, AMSR Ocean Algorithm, RSS Tech. Report 121599A-1. Available online: http://images.remss.com/papers/rsstech/2000_121599A-1_Wentz_AMSR_Ocean_Algorithm_ATBD_Version2.pdf (accessed on 10 July 2018).
- Wentz, F.; Meissner, T. Atmospheric absorption model for dry air and water vapor at microwave frequencies below 100 GHz derived from spaceborne radiometer observations. Radio Sci. 2016, 51, 381–391. [Google Scholar] [CrossRef]
- Liebe, H.; Rosenkranz, P.; Hufford, G. Atmospheric 60-GHz oxygen spectrum: New laboratory measurements and line parameters. J. Quant. Spectrosc. Radiat. Transf. 1992, 48, 629–643. [Google Scholar] [CrossRef]
- Le Vine, D.; Abraham, S. Galactic noise and passive microwave remote sensing from space at L-band. IEEE Trans. Geosci. Remote Sens. 2004, 42, 119–129. [Google Scholar] [CrossRef]
- Dinnat, E.; Le Vine, D.; Abraham, S.; Floury, N. Map of Sky Background Brightness Temperature at L-Band. Available online: https://podaac-tools.jpl.nasa.gov/drive/files/allData/aquarius/L3/mapped/galaxy/2018 (accessed on 7 July 2018).
- Wentz, F. The forward scattering of microwave solar radiation from a water surface. Radio Sci. 1978, 13, 131–138. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Measurement of the roughness of the sea surface from photographs of the sun’s glitter. J. Opt. Soc. Am. 1954, 44, 838–850. [Google Scholar] [CrossRef]
- Piepmeier, J. Calibration of passive microwave polarimeters that use hybrid coupler-based correlators. IEEE Trans. Geosci. Remote Sens. 2004, 43, 391–400. [Google Scholar] [CrossRef]
- Misra, S.; Brown, S. Enabling the extraction of climate-scale temporal salinity variations from Aquarius: An instrument based long-term radiometer drift correction. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2913–2923. [Google Scholar] [CrossRef]
- Dinnat, E.; Le Vine, D. Cold sky calibration (CSC) biases and time Series with hardware-only wiggle correction. Presented at the Aquarius Cal/Val Meeting, Santa Rosa, CA, USA, 9–11 January 2017; Available online: https://aquarius.umaine.edu/cgi/meetings.htm (accessed on 7 July 2018).
- Meissner, T. Assessment of Uncertainties in Aquarius Salinity Retrievals, RSS Technical Report 061015. 10 June 2015. Available online: http://podaac-ftp.jpl.nasa.gov/allData/aquarius/docs/v4/AQ-014-PS-0017_AquariusATBD_uncertainties_Addendum5_DatasetVersion4.0.pdf (accessed on 7 July 2018).
- Meissner, T.; Wentz, F.; Le Vine, D.; Lee, T. Estimate of uncertainties in the Aquarius salinity retrievals. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5324–5327. Available online: http://images.remss.com/papers/rssconf/Meissner_igarss_2015_Milan_AquariusErrors.pdf (accessed on 7 July 2018). [CrossRef]
- Wentz, F.; Ricciardulli, L.; Gentemann, C.; Meissner, T.; Hilburn, K.; Scott, J. Remote Sensing Systems Coriolis WindSat Environmental Suite on 0.25 deg Grid, Version 7.0.1, Remote Sensing Systems. Santa Rosa, CA, 2013. Available online: www.remss.com/missions/windsat (accessed on 7 July 2018).
- Yu, T.-W.; Gerald, V.M. Evaluation of NCEP operational model forecasts of surface wind and pressure fields over the oceans. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction. 2004. Available online: http://polar.ncep.noaa.gov/mmab/papers/tn233/mmab233.pdf (accessed on 7 July 2018).
- Ricciardulli, L.; Meissner, T.; Wentz, F. Towards a climate data record of satellite ocean vector winds. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 2067–2069. Available online: http://images.remss.com/papers/rssconf/ricciardulli_igarss_2012_munich.pdf (accessed on 7 July 2018). [CrossRef]
- Aquarius Salinity Validation Analysis (Data Version 5.0). Available online: https://podaac.jpl.nasa.gov/dataset/AQUARIUS_L2_SSS_V5?ids=SpatialCoverage:TemporalResolution&values=Global:Weekly (accessed on 7 July 2018).
- Kao, H.-Y.; Lagerloef, G.; Lee, T.; Melnichenko, O.; Meissner, T.; Hacker, P. Assessment of Aquarius Sea Surface Salinity Data using Aquarius Validation Data System (AVDS) and other statistical methods. Remote Sens. 2018. submitted. [Google Scholar]
- Piepmeier, J.; Mohammed, P.; Peng, J.; Kim, E.; De Amici, G.; Ruf, C. SMAP L1B Radiometer Half-Orbit Time-Ordered Brightness Temperatures; Version 3; CRID 13080; NSIDC: Boulder, CO, USA, 2016. [Google Scholar] [CrossRef]
- Atlas, R.; Hoffman, R.; Ardizzone, J.; Leidner, S.M.; Jusem, J.; Smith, D.; Gombos, D. A cross-calibrated, multiplatform ocean surface wind velocity product for meteorological and oceanographic applications. Bull. Am. Meteorol. Soc. 2011, 92, 157–174. [Google Scholar] [CrossRef]
- Wentz, F.; Scott, J.; Hoffman, R.; Leidner, M.; Atlas, R.; Ardizzone, J. Remote Sensing Systems Cross-Calibrated Multi-Platform (CCMP) 6-Hourly Ocean Vector Wind Analysis Product on 0.25 deg Grid; Version 2.0; Remote Sensing Systems: Santa Rosa, CA, USA, 2015; Available online: http://www.remss.com/measurements/ccmp (accessed on 7 July 2018).
- Ricciardulli, L.; National Center for Atmospheric Research Staff (Eds.) The Climate Data Guide: CCMP: Cross-Calibrated Multi-Platform Wind Vector Analysis. 2017. Available online: https://climatedataguide.ucar.edu/climate-data/ccmp-cross-calibrated-multi-platform-wind-vector-analysis (accessed on 7 July 2018).


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meissner, T.; Wentz, F.J.; Le Vine, D.M. The Salinity Retrieval Algorithms for the NASA Aquarius Version 5 and SMAP Version 3 Releases. Remote Sens. 2018, 10, 1121. https://doi.org/10.3390/rs10071121
Meissner T, Wentz FJ, Le Vine DM. The Salinity Retrieval Algorithms for the NASA Aquarius Version 5 and SMAP Version 3 Releases. Remote Sensing. 2018; 10(7):1121. https://doi.org/10.3390/rs10071121
Chicago/Turabian StyleMeissner, Thomas, Frank J. Wentz, and David M. Le Vine. 2018. "The Salinity Retrieval Algorithms for the NASA Aquarius Version 5 and SMAP Version 3 Releases" Remote Sensing 10, no. 7: 1121. https://doi.org/10.3390/rs10071121
APA StyleMeissner, T., Wentz, F. J., & Le Vine, D. M. (2018). The Salinity Retrieval Algorithms for the NASA Aquarius Version 5 and SMAP Version 3 Releases. Remote Sensing, 10(7), 1121. https://doi.org/10.3390/rs10071121