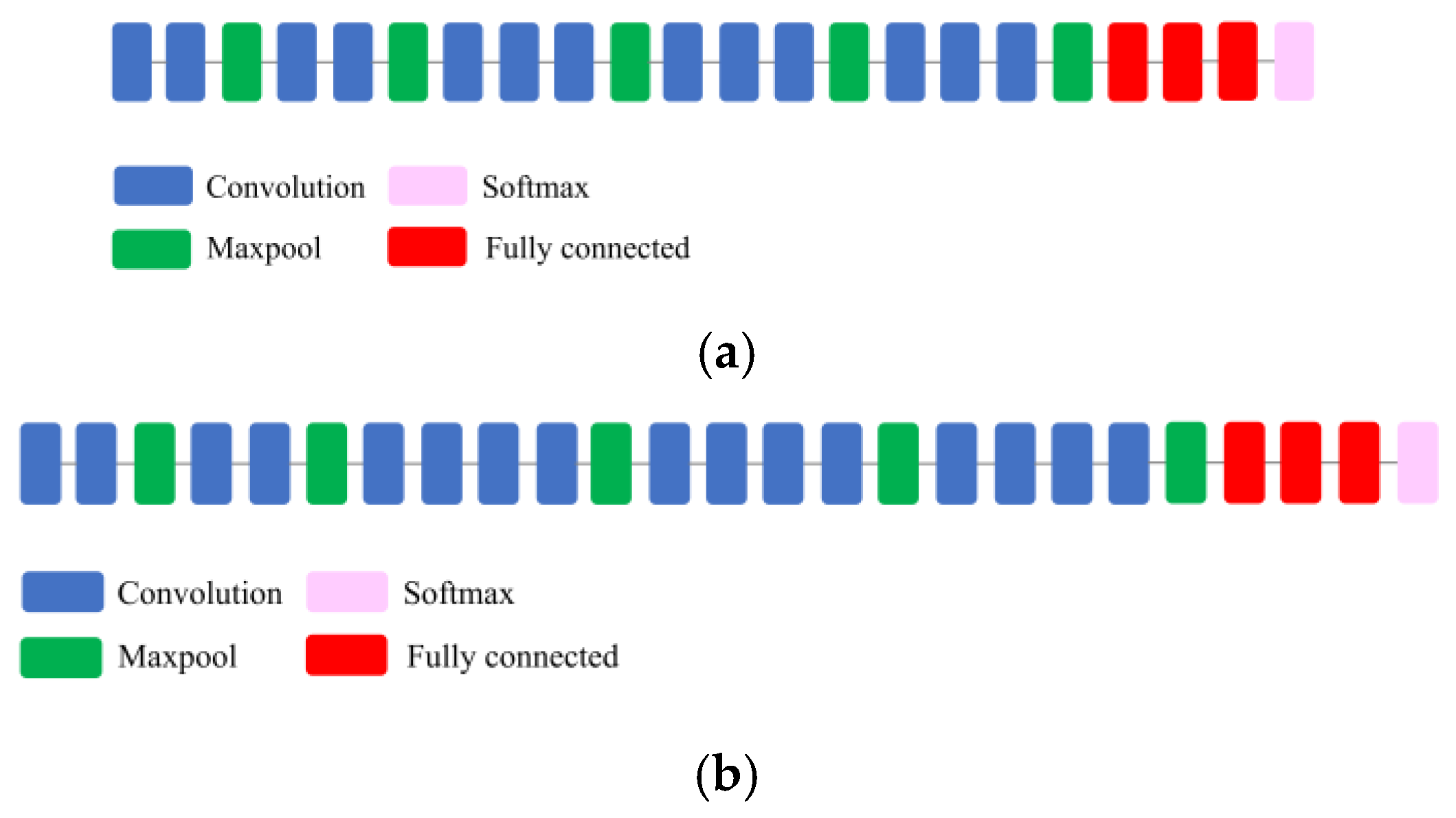
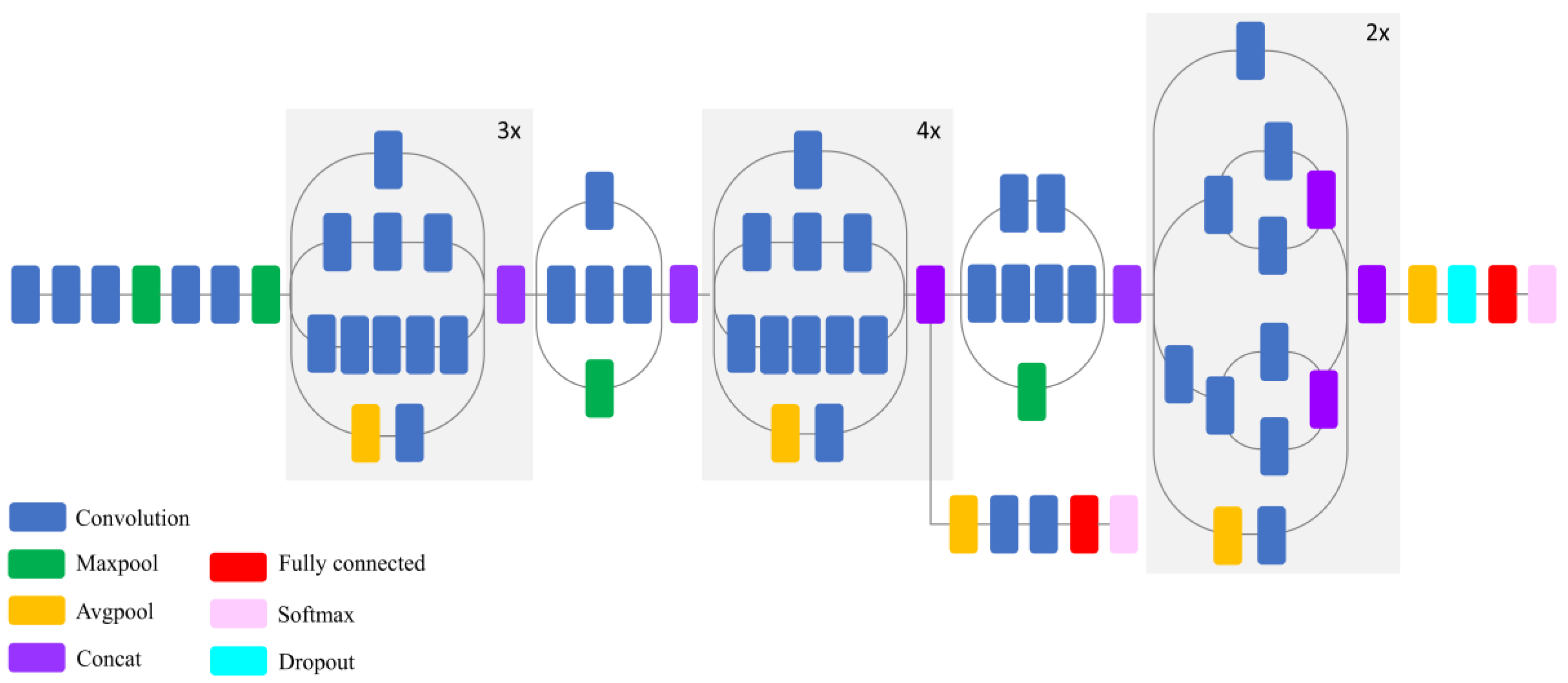
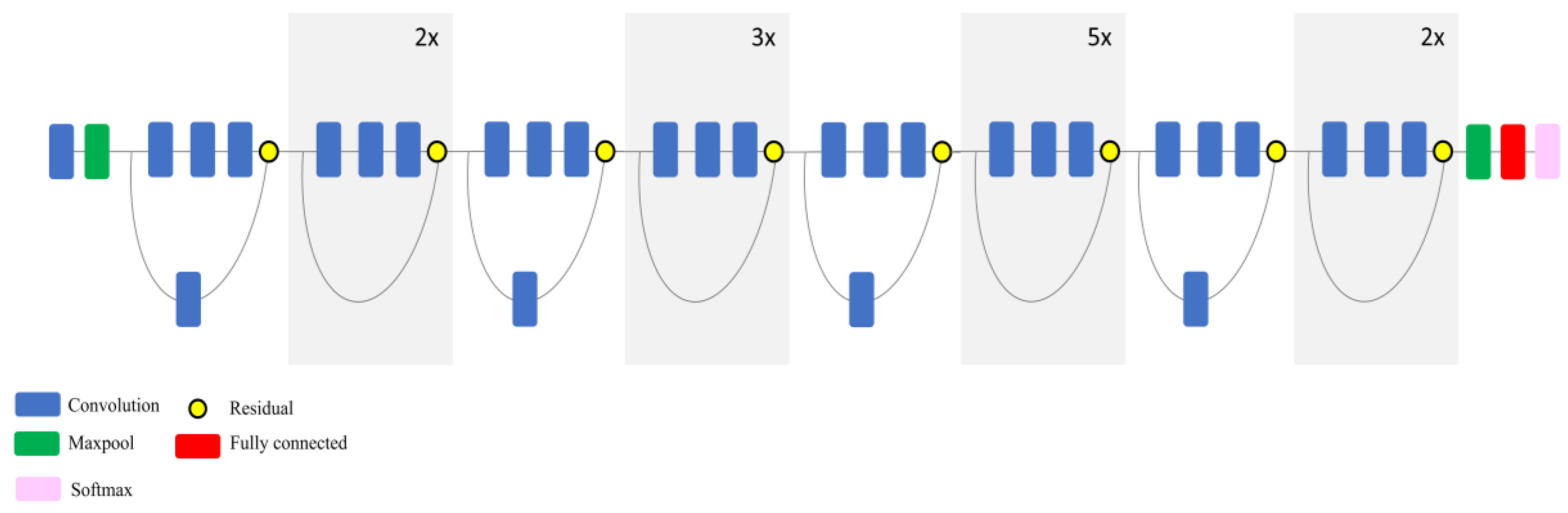
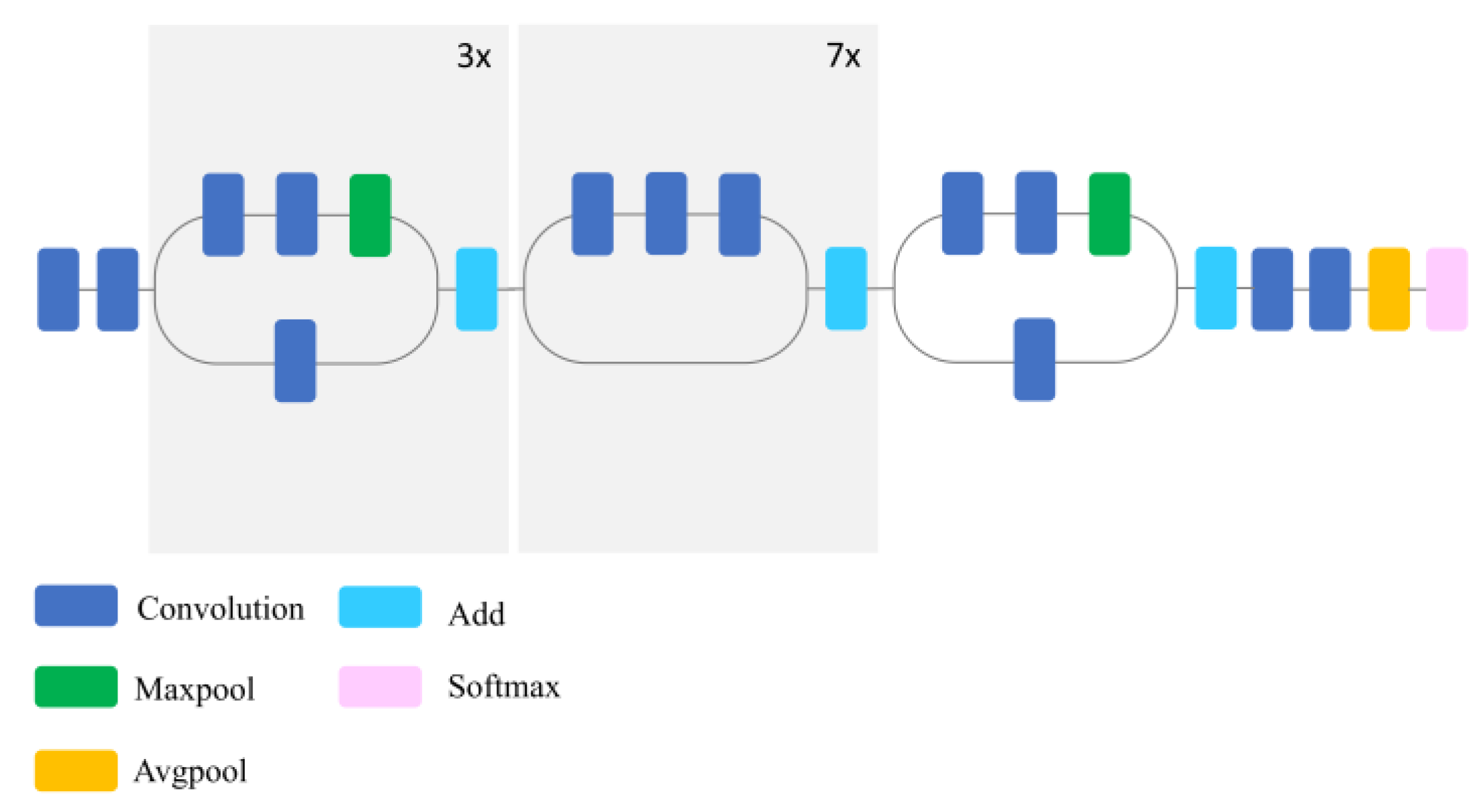
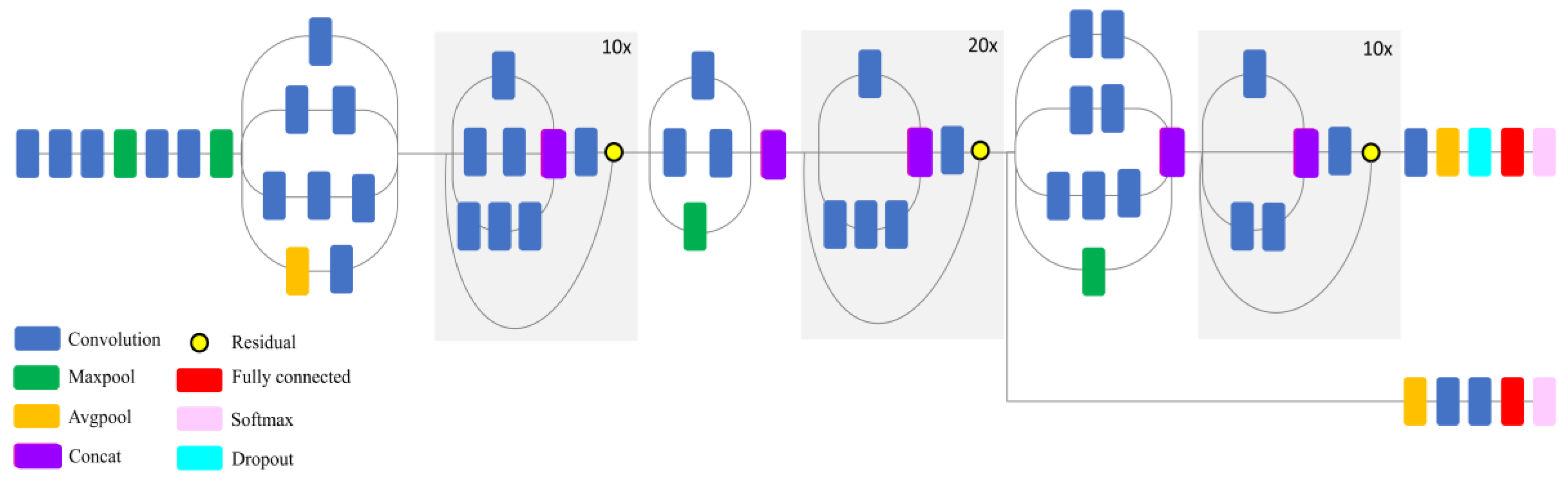
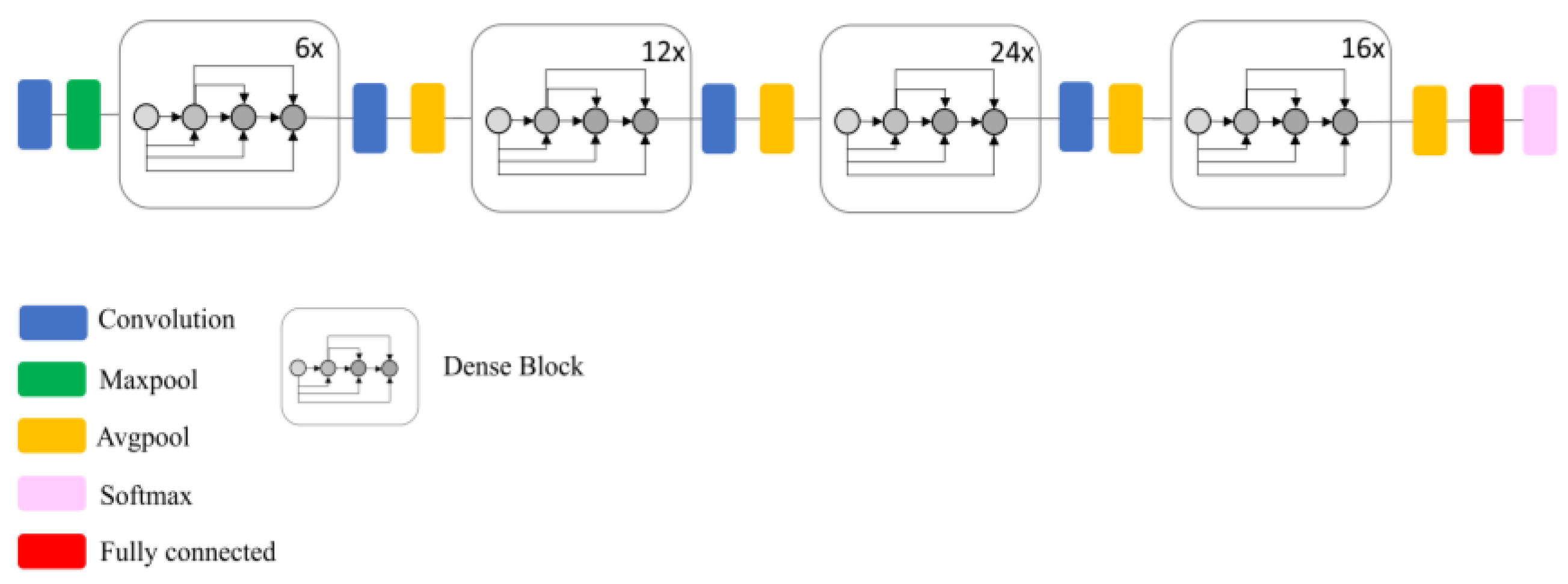
1. Introduction
Wetlands are transitional zones between terrestrial and aquatic systems that support a natural ecosystem of a variety of plant and animal species, adapted to wet conditions [
1]. Flood- and storm-damage protection, water quality improvement and renovation, greenhouse gas reduction, shoreline stabilization, and aquatic productivity are only a handful of the advantages associated with wetlands. Unfortunately, wetlands have undergone variations due to natural processes, such as changes in temperature and precipitation caused by climate change, coastal plain subsidence and erosion, as well as human-induced disturbances such as industrial and residential development, agricultural activities, and runoff from lawns and farms [
1].
Knowledge of the spatial distribution of these valuable ecosystems is crucial in order to characterize ecosystem processes and to monitor the subsequent changes over time [
2]. However, the remoteness, vastness, and seasonally dynamic nature of most wetland ecosystems make conventional methods of data acquisition (e.g., surveying) labor-intensive and costly [
3,
4]. Fortunately, remote sensing, as a cost- and time-efficient tool, addresses the limitations of conventional techniques by providing valuable ecological data to characterize wetland ecosystems and to monitor land cover changes [
5,
6]. Optical remote sensing data have shown to be promising tools for wetland mapping and monitoring. This is because biomass concentration, leaf water content, and vegetation chlorophyll—all important characteristics of wetland vegetation—can be determined using optical satellite images [
7]. In particular, optical remote sensing sensors collect spectral information of ground targets at various points of the electromagnetic spectrum, such as visible and infrared, which is of great benefit for wetland vegetation mapping [
7]. Therefore, several studies reported the success of wetland mapping using optical satellite imagery [
8,
9,
10,
11].
Despite the latest advances in remote sensing tools, such as the availability of high spatial and temporal resolution satellite data and object-based image analysis tools [
12], the classification accuracy of complex land cover, such as wetland ecosystems, is insufficient [
5]. This could be attributed to the spectral similarity of wetland vegetation types, making the exclusive use of spectral information insufficient for the classification of heterogeneous land cover classes. In addition, several studies reported the significance of incorporating both spectral and spatial information for land cover mapping [
1,
13]. Thus, spatial features may augment spectral information and thereby contribute to the success of complex land cover mapping. Accordingly, several experiments were carried out to incorporate both spectral and spatial features into a classification scheme. These studies were based on the Markov Random Field (MRF) model [
14], the Conditional Random Field (CRF) model [
15], and Composite Kernel (CK) methods [
16]. However, in most cases, the process of extracting a large number of features, the feature engineering process [
17], for the purpose of supervised classification is time intensive, and requires broad and profound knowledge to extract amenable features. Furthermore, classification based on hand-crafted spatial features primarily relies on low-level features, resulting in insufficient classification results in most cases and a poor capacity for generalization [
13].
Most recently, Deep Learning (DL), a state-of-the-art machine learning tool, has been placed in the spotlight in the field of computer vision and, subsequently, in remote sensing [
18]. This is because these advanced machine learning algorithms address the primary limitations of the conventional shallow-structured machine learning tools, such as Support Vector Machine (SVM) and Random Forest (RF) [
19]. Deep Belief Net (DBN) [
20], Stacked Auto-Encoder (SAE) [
21], and deep Convolutional Neural Network (CNN) [
22,
23] are current deep learning models, of which the latter is most well-known. Importantly, CNN has led to a series of breakthroughs in several remote sensing applications, such as classification [
15], segmentation [
24], and object detection [
25], due to its superior performance in a variety of applications relative to shallow-structured machine learning tools. CNNs are characterized by multi-layered interconnected channels, with a high capacity for learning the features and classifiers from data spontaneously given their deep architecture, their capacity to adjust parameters jointly, and to classify simultaneously [
26]. One of the ubiquitous characteristics of such a configuration is its potential to encode both spectral and spatial information into the classification scheme in a completely automated workflow [
26]. Accordingly, the complicated, brittle, and multistage feature engineering procedure is replaced with a simple end-to-end deep learning workflow [
17].
Notably, there is a different degree of abstraction for the data within multiple convolutional layers, wherein low-, mid-, and high-level information is extracted in a hierarchical learning framework at the initial, intermediate, and final layers, respectively [
26]. This configuration omits the training process from scratch in several applications since the features in the initial layers are generic filters (e.g., edge) and, accordingly, are less dependent on the application. However, the latest layers are related to the final application and should be trained according to the given data and classification problem. This also addresses the poor generalization capacity of shallow-structured machine learning tools, which are site- and data-dependent, suggesting the versatility of CNNs [
17].
Although the advent of CNN dates back to as early as the 1980s, when LeCun designed a primary convolutional neural network known as LeNet to classify handwritten digits, it gained recognition and was increasingly applied around 2010 [
27]. This is attributable to the advent of more powerful hardware, larger datasets (e.g., ImageNet) [
28], and new ideas, which consequently improved network architecture [
23]. The original idea of deep CNNs [
27] has been further developed by Krizhevsky and his colleagues, who designed a breakthrough CNN, known as AlexNet, a pioneer of modern deep CNNs, with multiple convolutional and max-pooling layers that provide deeper feature-learning at different spatial scales [
22]. Subsequent successes have been achieved since 2014, when VGG [
29], GoogLeNet (i.e., Inception network) [
23], ResNet [
30], and Xception [
31] were introduced in the ImageNet Large-Scale Visual Recognition Challenge (ILSVRC).
The intricate tuning process, heavy computational burden, high tendency of overfitting, and the empirical nature of model establishment are the main limitations associated with deep CNNs [
26]. Although some studies have argued that all deep learning methods have a black-box nature, it is not completely true for CNN [
17]. This is because the features learned by CNNs can be visualized and, in particular, they are an illustration of visual concepts. There are three different strategies for employing current CNNs: A full-training network, a pre-trained network as a feature extractor, and fine-tuning of a pre-trained network. In the first case, a network is trained from scratch with random weights and biases to extract particular features for the dataset of interest. However, the limited number of training samples constrains the efficiency of this technique due to the overfitting problem. The other two strategies are more useful when a limited amount of training samples is available [
26,
32].
In cases of limited training data, a stacked auto-encoder (SAE) is also useful to learn the features from a given dataset using an unsupervised learning network [
33]. In such a network, the deconstruction error between the input data at the encoding layer and its reconstruction at the decoding layer is minimized [
34]. SAE networks are characterized by a relatively simple structure relative to deep CNNs and they have a great capacity for fast image interpretation. In particular, they convert raw data to an abstract representation using a simple non-linear model and they integrate features using an optimization algorithm. This results in a substantial decrease of redundant information between the features while achieving a strong generalization capacity [
35].
Despite recent advances in deep CNNs, their applications in remote sensing have been substantially limited to the classification of very high spatial resolution aerial and satellite imagery from a limited number of well-known datasets, owing to the similar characteristics of these data to object recognition in computer vision. However, acquiring high spatial resolution imagery may be difficult, especially on a large scale. Accordingly, less research has been carried out on the classification of medium and high spatial resolution satellite imagery in different study areas. Furthermore, the capacity of CNNs has been primarily investigated for the classification of urban areas, whereas there is limited research examining the potential of state-of-the-art classification tools for complex land cover mapping. Complex land cover units, such as wetland vegetation, are characterized by high intra- and low inter-class variance, resulting in difficulties in their discrimination relative to typical land cover classes. Thus, an environment with such highly heterogeneous land cover is beneficial for evaluating the capacity of CNNs for the classification of remote sensing data. Finally, the minimal application of well-known deep CNNs in remote sensing may be due to the limitation of input bands. Specifically, these convnets are designed to work with three input bands (e.g., Red, Green, and Blue), making them inappropriate for most remote sensing data. This indicates the significance of developing a pipeline compatible with multi-channel satellite imagery.
The main goals of this study were, therefore, to: (1) Eliminate the limitation of the number of input bands by developing a pipeline in Python with the capacity to operate with multi-layer remote sensing imagery; (2) examine the power of deep CNNs for the classification of spectrally similar wetland classes; (3) investigate the generalization capacity of existing CNNs for the classification of multispectral satellite imagery (i.e., a different dataset than those they were trained for); (4) explore whether full-training or fine-tuning is the optimal strategy for exploiting the pre-existing convnets for wetland mapping; and (5) compare the efficiency of the most well-known deep CNNs, including DenseNet121, InceptionV3, VGG16, VGG19, Xception, ResNet50, and InceptionResNetV2, for wetland mapping in a comprehensive and elaborate analysis. Thus, this study contributes to the use of the state-of-the-art classification tools for complex land cover mapping using multispectral remote sensing data.
3. Results and Discussion
In this study, fine-tuning was employed for pre-existing, well-known convnets, which were trained based on the ImageNet dataset.
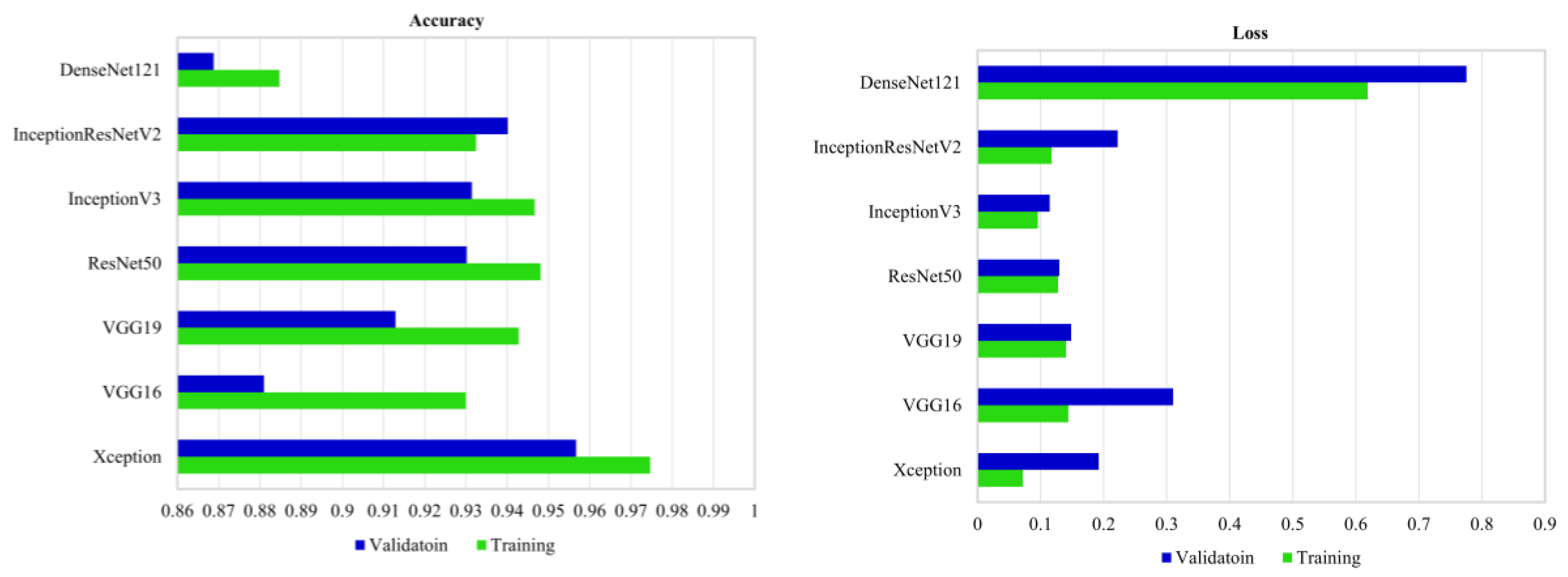
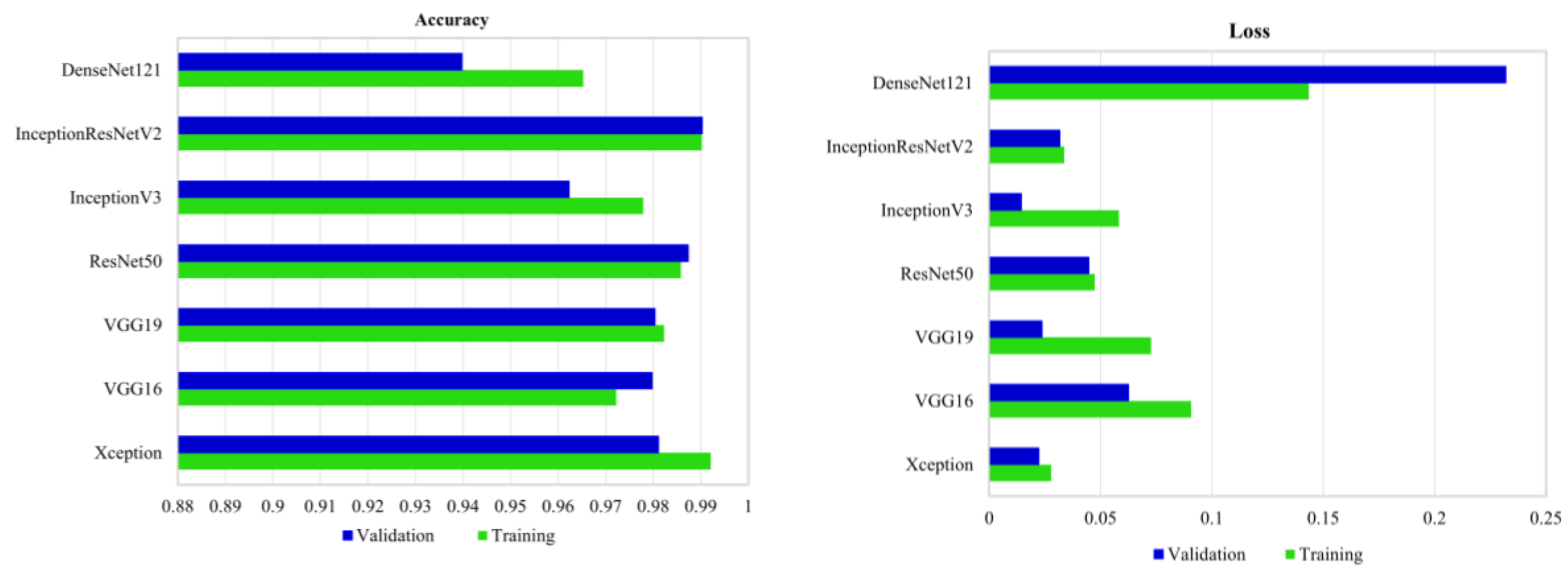
Figure 9 demonstrates the validation and training accuracy and loss in the case of fine-tuning of convnets using the three selected bands of RapidEye imagery.
As shown, DenseNet121 has the lowest validation accuracy, followed by VGG16. Conversely, the Xception network has the highest validation accuracy, followed by InceptionResNetV2. The two convnets, namely InceptionV3 and ResNet50, show relatively equal validation accuracies.
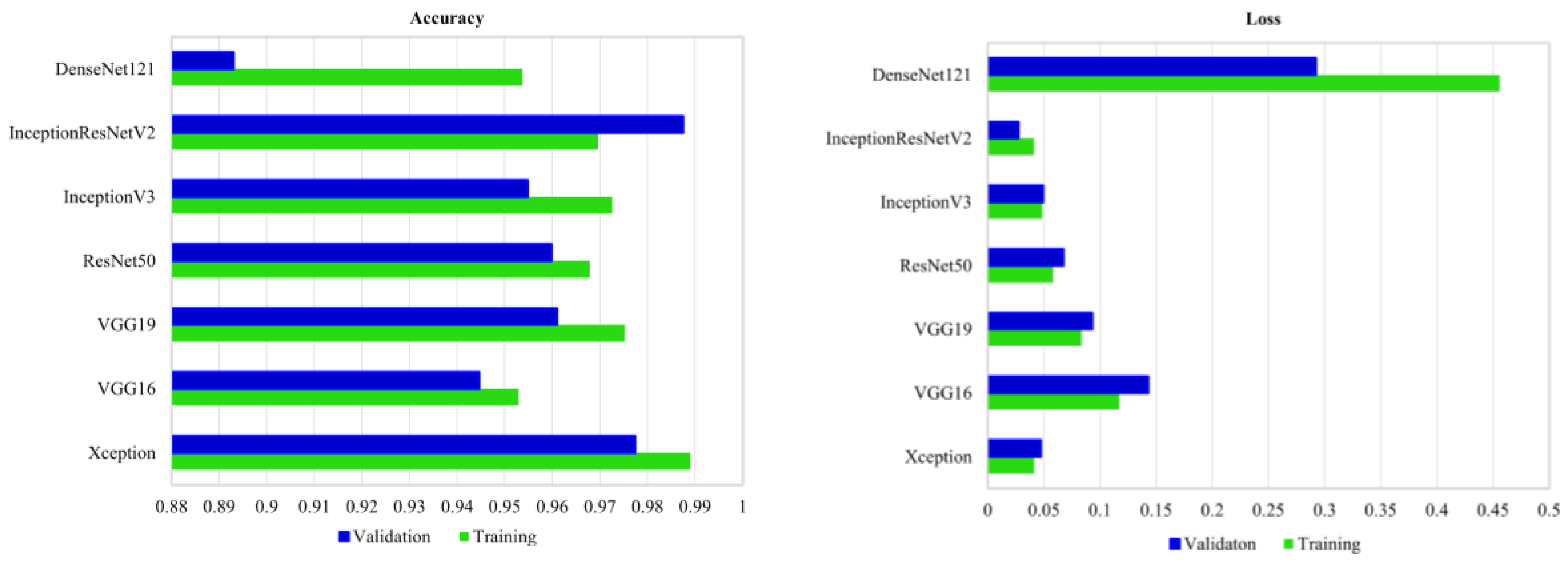
Figure 10 shows the validation and training accuracy and loss in the case of training convnets from scratch when three bands of RapidEye imagery were employed.
As shown, all convnets, excluding DensNet121, perform very well for wetland classification when validation accuracies are compared. In particular, three convnets, including InceptionResNetV2, Xception, and VGG19, have higher training and validation accuracies relative to the other well-known convnets. Conversely, DenseNet121 has the lowest validation accuracy, suggesting that this network is less suitable for complex land cover mapping relative to the other convnets.
Figure 11 shows the validation and training accuracy and loss in the case of training convnets from scratch when five bands of RapidEye imagery were employed.
The effects of increasing the number of bands are readily apparent by comparing
Figure 10 and
Figure 11. Specifically, an increase in the number of bands improves classification accuracy in all cases. For example, the validation accuracy for DenseNet121 was lower than 90% when only three bands were employed. However, by increasing the number of bands, the validation accuracy reached to 94% for DenseNet121. InceptionResNetV2 again exhibited the highest validation accuracy, followed by ResNet50, Xception, and VGG19. Thus, the results indicate the significance of incorporating more spectral information for the classification of spectrally similar wetland classes (see
Figure 10 and
Figure 11).
One of the most interesting aspects of the results obtained in this study is that the full-training strategy had better classification results relative to fine-tuning in all cases. Previous studies reported the superiority of fine-tuning relative to full-training for classification of very high resolution aerial imagery, although full-training was found to be more accurate relative to fine-tuning for classification of multi-spectral satellite data [
26,
45]. In particular, Nogueira et al. (2017) evaluated the efficiency of fine-tuning and full-training strategies of some well-known deep CNNs (e.g., AlexNet and GoogLeNet) for classification of three well-known datasets, including UCMerced land-use [
46], RS19 dataset [
47], and Brazilian Coffee Scenes [
48]. The fine-tuning strategy yielded a higher accuracy for the first two datasets, likely due to their similarity with the ImageNet dataset, which was originally used for training deep CNNs. However, the full-training strategy had similar [
26] or better results [
45] relative to the fine-tuning for the Brazilian Coffee Scenes. This is because the latter dataset is multi-spectral (SPOT), containing finer and more homogeneous textures, wherein the patterns visually overlap substantially and, importantly, differ from the objects commonly found within the ImageNet dataset [
26]. The results obtained from the latter dataset are similar to those found in our study. In particular, there is a significant difference between the original training datasets of these convnets and our dataset. Fine-tuning is an optimal solution when the edges and local structures within the dataset of interest are similar to those for which the networks were trained. However, the texture, color, edges, and local structures of the typical objects found in the ImageNet dataset differ from the objects found in the wetland classes. Moreover, our dataset is intrinsically different from the ImageNet dataset used for pre-training. In particular, our dataset has five spectral bands, namely red, green, blue, red-edge, and near-infrared, all of which are essential for classifying spectrally similar wetland classes. However, the ImageNet dataset has only the red, green, and blue bands [
45]. This could explain the differences between validation accuracies obtained in the case of full-training and fine-tuning (see
Figure 9 and
Figure 10). Nevertheless, the results obtained from fine-tuning are still very promising, taking into account the complexity of wetland classes and the high classification accuracy obtained in most cases. In particular, an average validation accuracy of greater than 86% was achieved in all cases (see
Figure 9), suggesting the generalizability and versatility of pre-trained deep convnets for the classification of various land cover types. It is also worth noting that fine-tuning was employed on the top three layers of convnets in this study. However, the results could be different upon including more layers in the fine-tuning procedure.
Having obtained higher accuracies via full-training of five bands, the classification results obtained from this strategy were selected for further analysis. These classification results were also compared with the results obtained from two conventional machine learning tools (i.e., SVM and RF). For this purpose, a total number of eight features were used as input features for both the SVM and RF classifiers. These features were Normalized Difference Vegetation Index (NDVI), Normalized Difference Water Index (NDWI), Red-edge Normalized Difference Vegetation Index (ReNDVI), and all the original spectral bands of the RapidEye image.
Table 2 represents the overall accuracy, Kappa coefficient, and F1-score using different CNNs (full-training of five bands), RF, and SVM for wetland classification in this study.
As seen in
Table 2, SVM and RF have the lowest classification accuracies and F1-scores relative to all deep convnets in this study. Among deep convnets, InceptionResNetV2 has the highest classification accuracy, 96.17%, as well as the highest F1-score, 93.66%, followed by ResNet50 and Xception with overall accuracies of 94.81% and 93.57%, as well as F1-scores of 91.39% and 89.55%, respectively. Conversely, DenseNet121 and InceptionV3 have the lowest overall accuracies, 84.78% and 86.14%, as well as F1-scores, 72.61% and 75.09%, respectively. VGG19 was found to be more accurate than VGG16 by about 3% (OA), presumably due to the deeper structure of the former convnet. These results are in general agreement with [
49], which reported the superiority of ResNet relative to GoogLeNet (Inception), VGG16, and VGG19 for the classification of four public remote sensing datasets (e.g., UCM, WHU-RS19). InceptionResNetV2 benefits from integrating two well-known deep convnets, Inception and ResNet, which positively contribute to the most accurate result in this study. This also suggests that the extracted features from different convnets are supplementary and improve the model’s classification efficiency. The results demonstrated that deeper networks (e.g., InceptionResNetV2) have a greater efficiency in extracting varying degrees of abstraction and representation within the hierarchical learning scheme [
50]. In particular, they are more efficient in separating the input space into more detailed regions, owing to their deeper architecture, that contributes to a better separation of complex wetland classes.
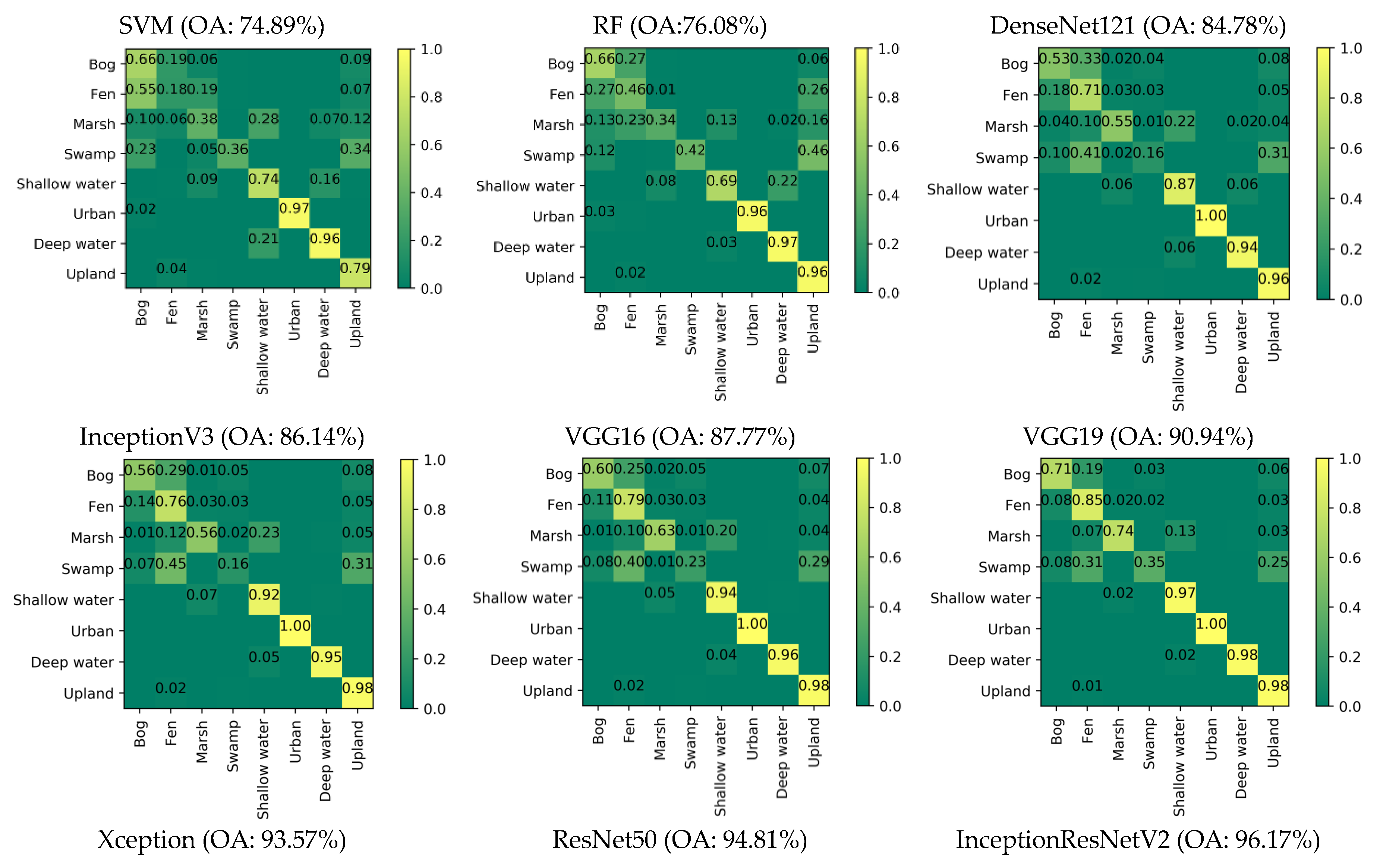
As shown in
Figure 12, all deep networks were successful in classifying non-wetland classes, including urban, deep water, and upland classes, with an accuracy greater than 94% in all cases. SVM and RF also correctly classified the non-wetland classes with an accuracy exceeding 96% in most cases (excluding upland). Interestingly, all deep networks correctly classified the urban class with an accuracy of 100%, suggesting the robustness of the deep learning features for classification of complex human-made structures (e.g., buildings and roads). This observation fits well with [
13]. However, the accuracy of the urban class did not exceed 97% when either RF or SVM was employed.
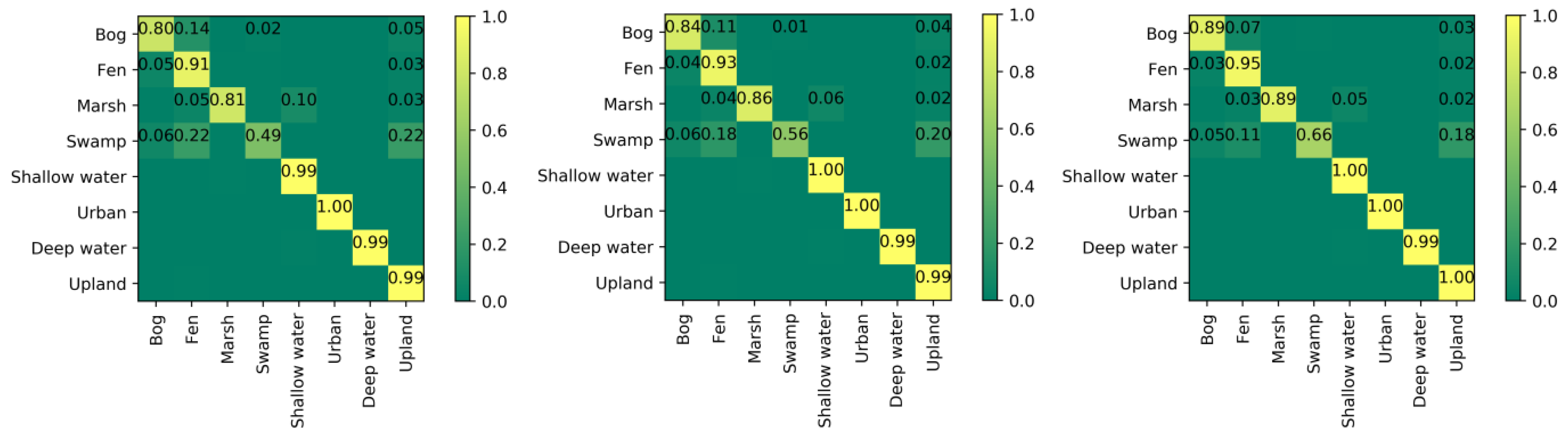
The confusion matrices demonstrate that, by using the last three networks, a significant improvement was achieved in the accuracy of both overall and individual classes. In particular, InceptionResNetV2 correctly classified non-wetland classes with an accuracy of 99% for deep water and 100% for both urban and upland classes. ResNet50 and Xception were also successful in distinguishing non-wetland classes with an accuracy of 100% for urban and 99% for both deep water and upland. One possible explanation for why the highest accuracies were obtained for these classes is the availability of larger amounts of training samples for non-wetland classes relative to wetland classes.
Although RF and SVM, as well as the convnets, performed very well in distinguishing non-wetland classes, the difference in accuracy between the two groups (i.e., conventional classifiers versus deep networks) was significant for wetland classes. This was particularly true for the last three convnets compared to SVM and RF. Specifically, the three networks of InceptionResNetV2, ResNet50, and Xception were successful in classifying all wetland classes with accuracies exceeding 80%, excluding the swamp wetland. This contrasts with the results obtained from SVM and RF, wherein the accuracies were lower than 74% for all wetland classes. Overall, the swamp wetland had the lowest accuracy among all classes using the deep convnets. As the effectiveness of these networks largely depends on the numbers of the training samples, the lowest accuracy of the swamp wetland could be attributable to the low availability of training samples for this class.
A large degree of confusion was observed between herbaceous wetlands, namely marsh, bog, and fen (especially between bog and fen), when DenseNet121, InceptionV3, and VGG16 were employed. The largest confusion between bog and fen is possibly due to the very similar visual features of these classes (see
Figure 8). These two classes are both peatland dominated with different species of Sphagnum in bogs and Graminoid in fens. According to field biologist reports, these two classes were adjacent successional classes with a heterogeneous nature and were hardly distinguished from each other during the in-situ field data collection.
Overall, confusion was more pronounced among the first four deep networks, whereas it was significantly reduced when the last three networks were employed (see
Figure 12). This suggests that the last three networks and, especially, InceptionResNetV2, are superior for distinguishing confusing wetland classes relative to the other convnets. For example, the classes of bog and fen were correctly classified with accuracies of greater than 89% when InceptionResNetV2 was used. Both Xception and ResNet50 were also found to successfully classify these two classes with accuracies of higher than 80%. Overall, the wetland classification accuracies obtained from these three networks were strongly positive for several spectrally and spatially similar wetland classes (e.g., bog, fen, and marsh) and demonstrate a large number of correctly classified pixels.
Cropped images of the classified maps obtained from SVM, RF, DenseNet121, and InceptionResNetV2 are depicted in
Figure 13. As shown, the classified maps obtained from convnets better resemble the real ground features. Both classified maps, obtained from convnets (
Figure 13d,e) show a detailed distribution of all land cover classes; however, the classified map obtained from InceptionResNetV2 (
Figure 13e) is more accurate when it is compared with optical imagery (
Figure 13a). For example, in the classified map obtained from DenseNet121, the fen class was misclassified as bog and upland classes in some cases (
Figure 13d). This, too, occurred between shallow water and deep water; however, this was not the case when InceptionResNetV2 was employed. In particular, most land cover classes obtained from InceptionResNetV2 are accurate representations of ground features. This conclusion was based on the confusion matrix (see
Figure 12) and further supported by a comparison between the classified map and the optical data (
Figure 13a, e).
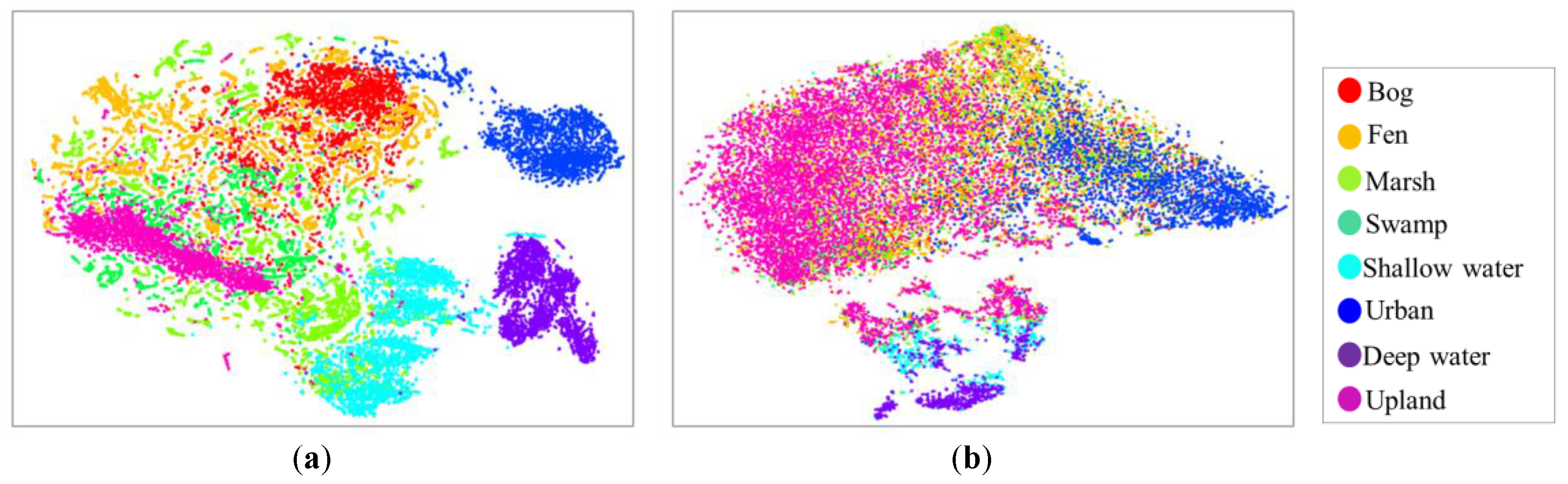
Figure 14 shows two-dimensional features extracted from the last layer of the InceptionResNetV2 (a) and DenseNet121 (b) using the two-dimensional t-SNE algorithm [
51]. The features from InceptionResNetV2 demonstrate a clear semantic clustering. In particular, most classes are clearly separated from each other; however, the feature clusters of bog and fen show some degree of confusion. Conversely, the features from DenseNet121 only generate a few visible clusters (e.g., upland and urban), while other features corresponding to wetland classes overlap with each other, suggesting a large degree of confusion.
4. Conclusions
Wetlands are characterized by complex land cover with high intra-class variability and low inter-class disparity, posing several challenges to conventional machine learning tools in classification tasks. To date, the discrimination of such complex land cover classes using conventional classifiers heavily relies on a large number of hand-crafted features incorporated into the classification scheme. In this research, we used state-of-the-art deep learning tools, deep Convolutional Neural Networks, to classify such a heterogeneous environment to address the problem of extracting a large number of hand-crafted features. Two different strategies of employing pre-existing convnets were investigated: Full-training and fine-tuning. The potential of the most well-known deep convnets, currently employed for several computer vision tasks, including DenseNet121, InceptionV3, VGG16, VGG19, Xception, ResNet50, and InceptionResNetV2, was examined in a comprehensive and elaborate framework using multispectral RapidEye optical data for wetland classification.
The results of this study revealed that the incorporation of high-level features learned by a hierarchical deep framework is very efficient for the classification of complex wetland classes. Specifically, the results illustrate that the full-training of pre-existing convnets using five bands is more accurate than both full-training and fine-tuning using three bands, suggesting that the extra multispectral bands provide complementary information. In this study, InceptionResNetV2 consistently outperformed all other convnets for the classification of wetland and non-wetland classes with a state-of-the-art overall classification accuracy of about 96%, followed by ResNet50 and Xception, with accuracies of about 94% and 93%, respectively. The impressive performance of InceptionResNetV2 suggests that an integration of the Inception and ResNet modules is an effective architecture for complex land cover mapping using multispectral remote sensing images. The individual class accuracy illustrated that confusion occurred between wetland classes (herbaceous wetlands), although it was less pronounced when InceptionResNetV2, ResNet50, and Xception were employed. The swamp wetland had the lowest accuracy in all cases, potentially because the lowest number of training samples was available for this class. It is also worth noting that all deep convnets were very successful in classifying non-wetland classes in this study.
The results of this study demonstrate the potential for the full exploitation of pre-existing deep convnets for the classification of multispectral remote sensing data, which are significantly different than large datasets (e.g., ImageNet) currently employed in computer vision. Given the similarity of wetland classes across Canada, the deep trained networks in this study provide valuable baseline information and tools, and will substantially contribute to the success of wetland mapping in this country using state-of-the-art remote sensing data.