Accuracy Assessment of Primary Production Models with and without Photoinhibition Using Ocean-Colour Climate Change Initiative Data in the North East Atlantic Ocean
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Region
2.2. Simulated In Situ 14C Primary Production Measurements (PPeu)
2.3. Satellite Data
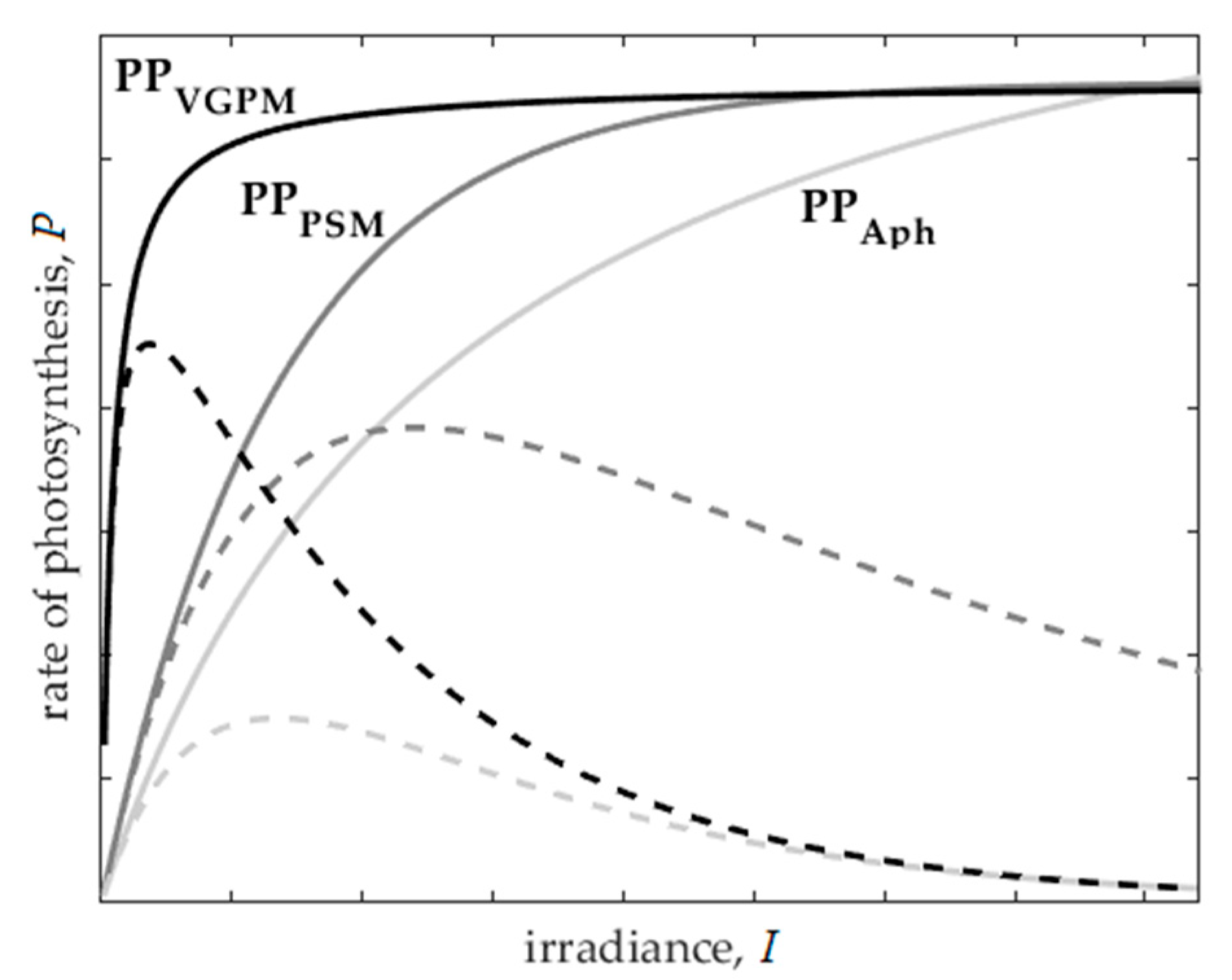
2.4. Satellite Models of Primary Production
2.5. Implementation of Photoinhibition in the Primary Production Models
2.6. Validation Statistics
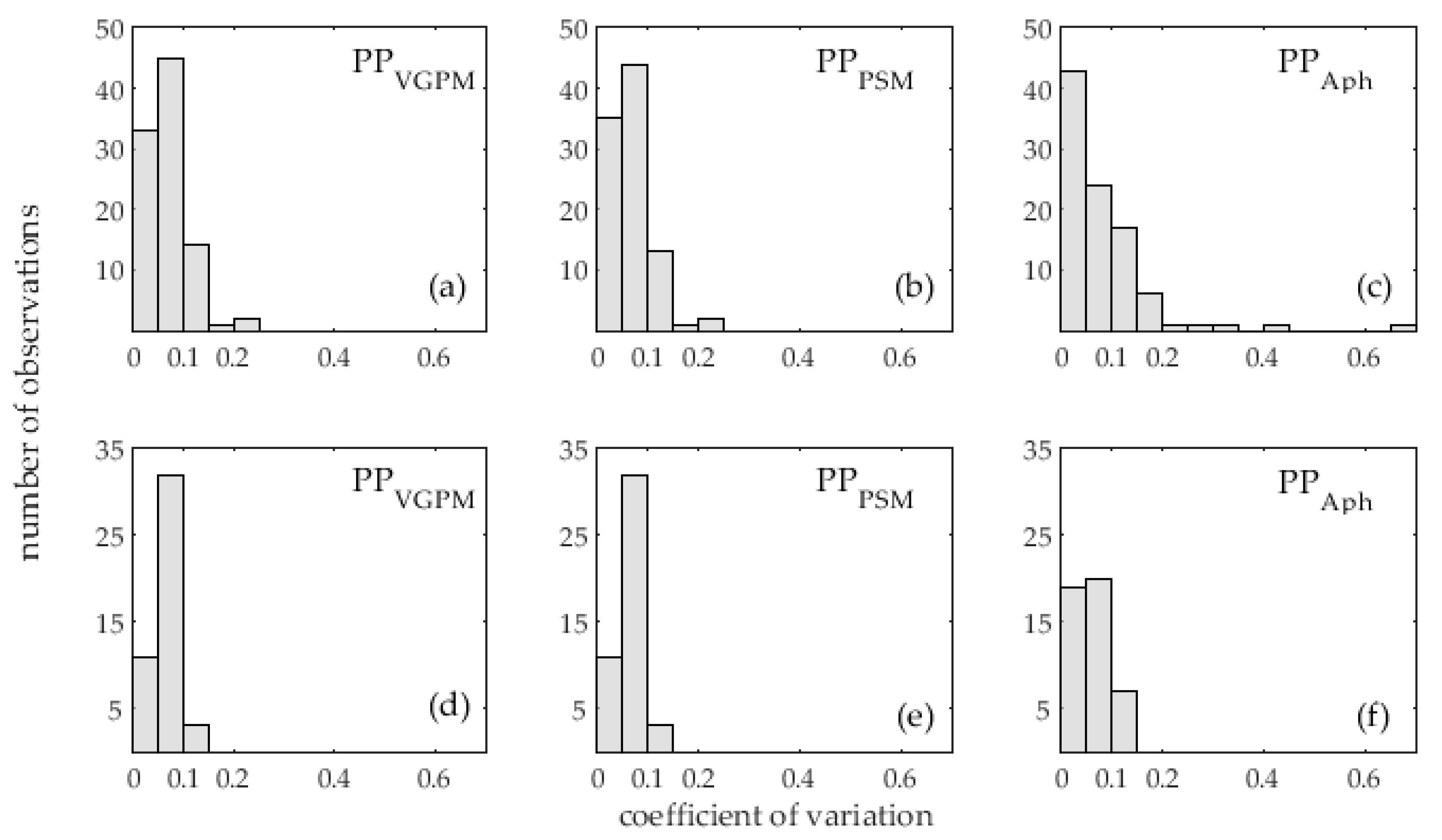
2.7. Sensitivity Analysis
3. Results
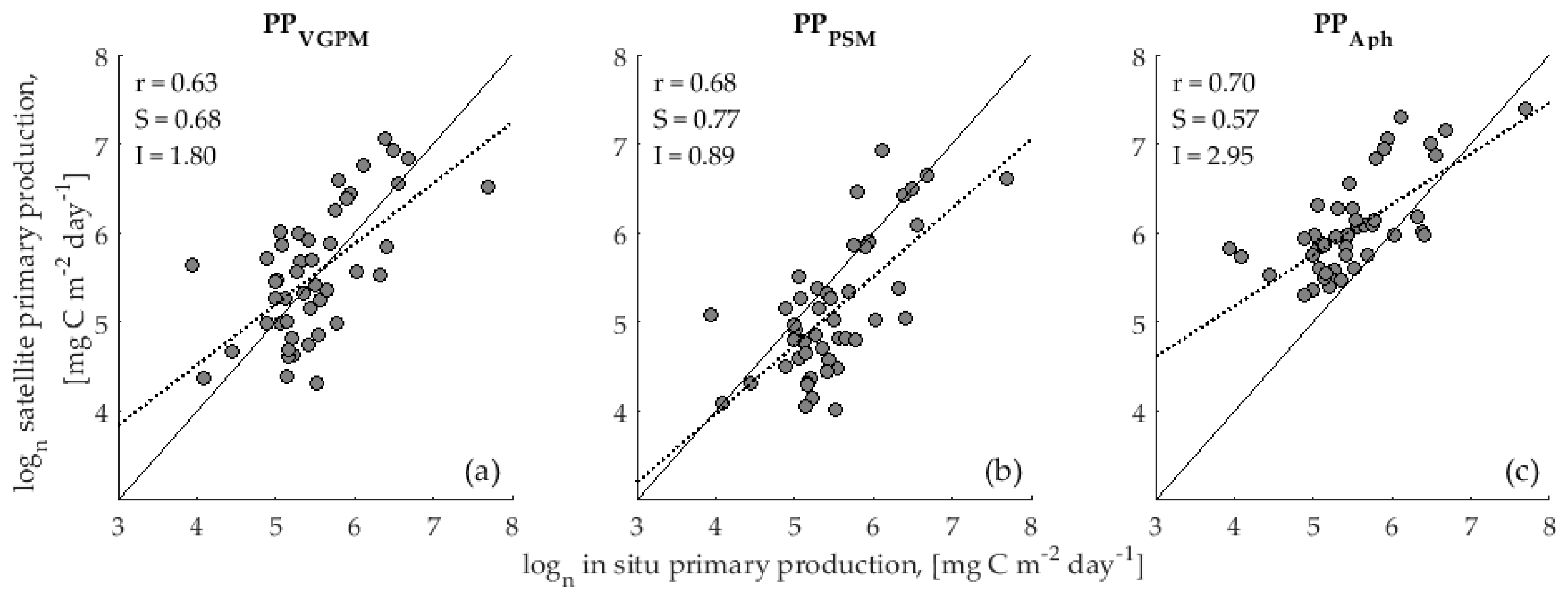
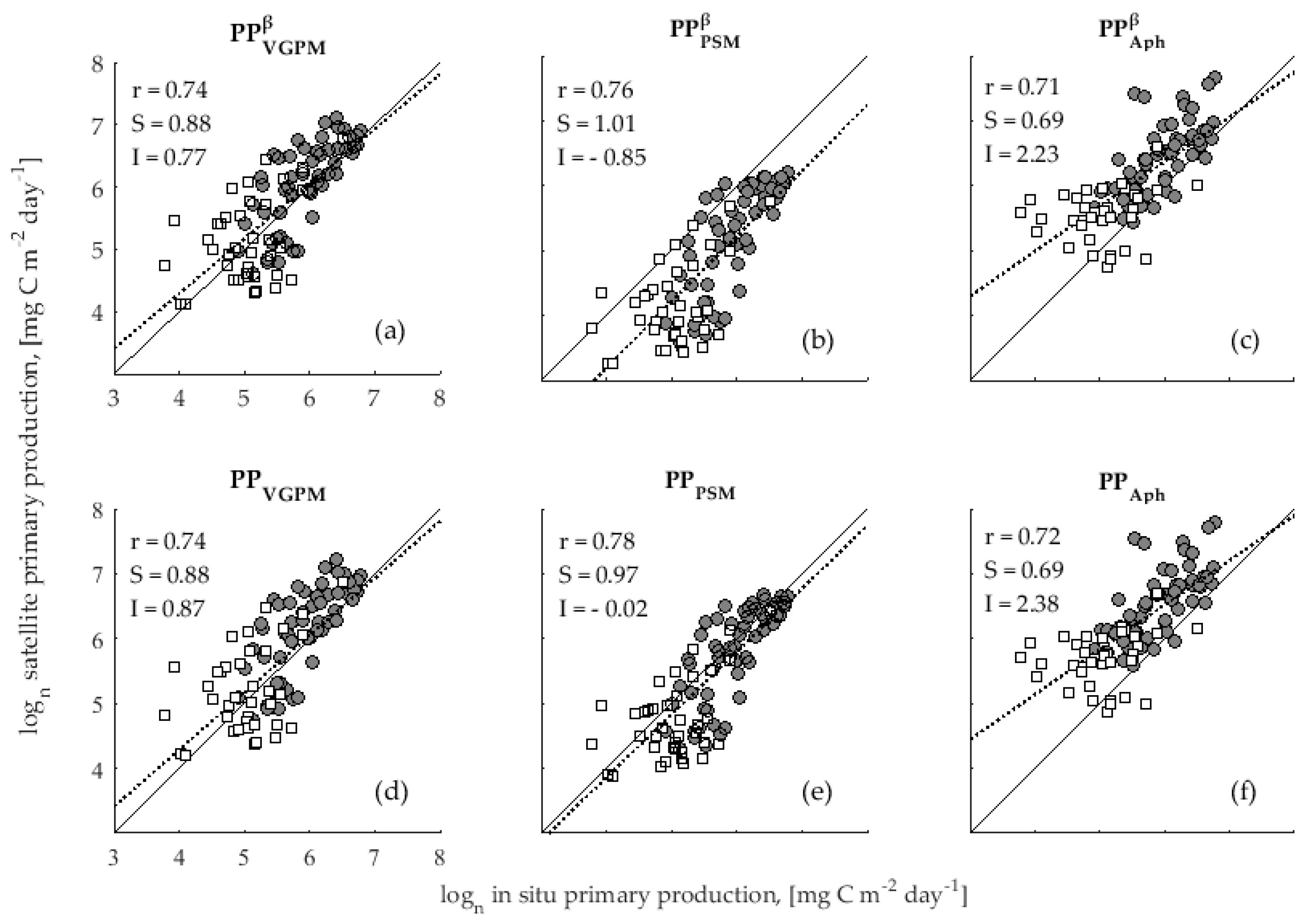
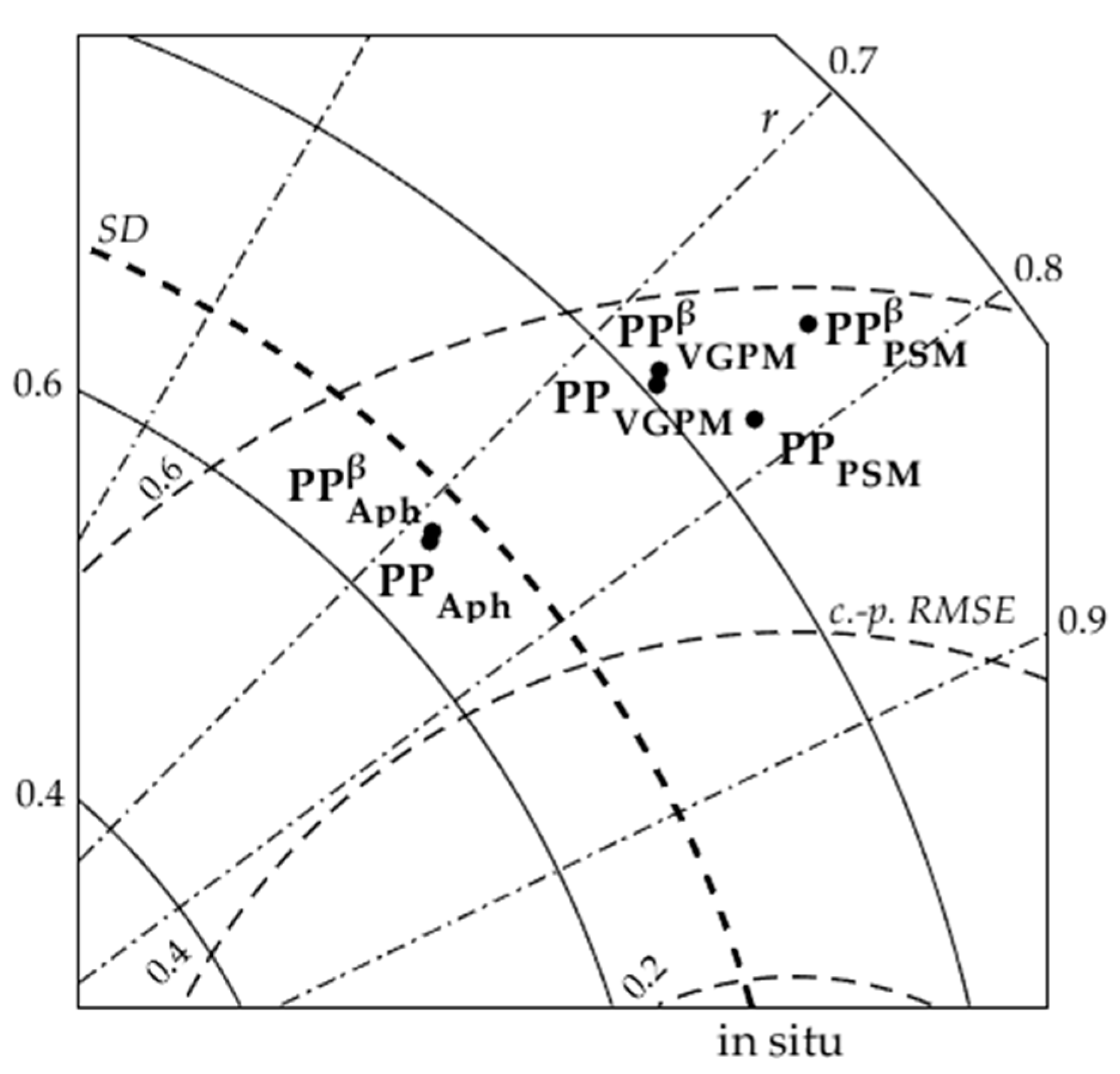
3.1. Accuracy Assessment of Primary Production Models
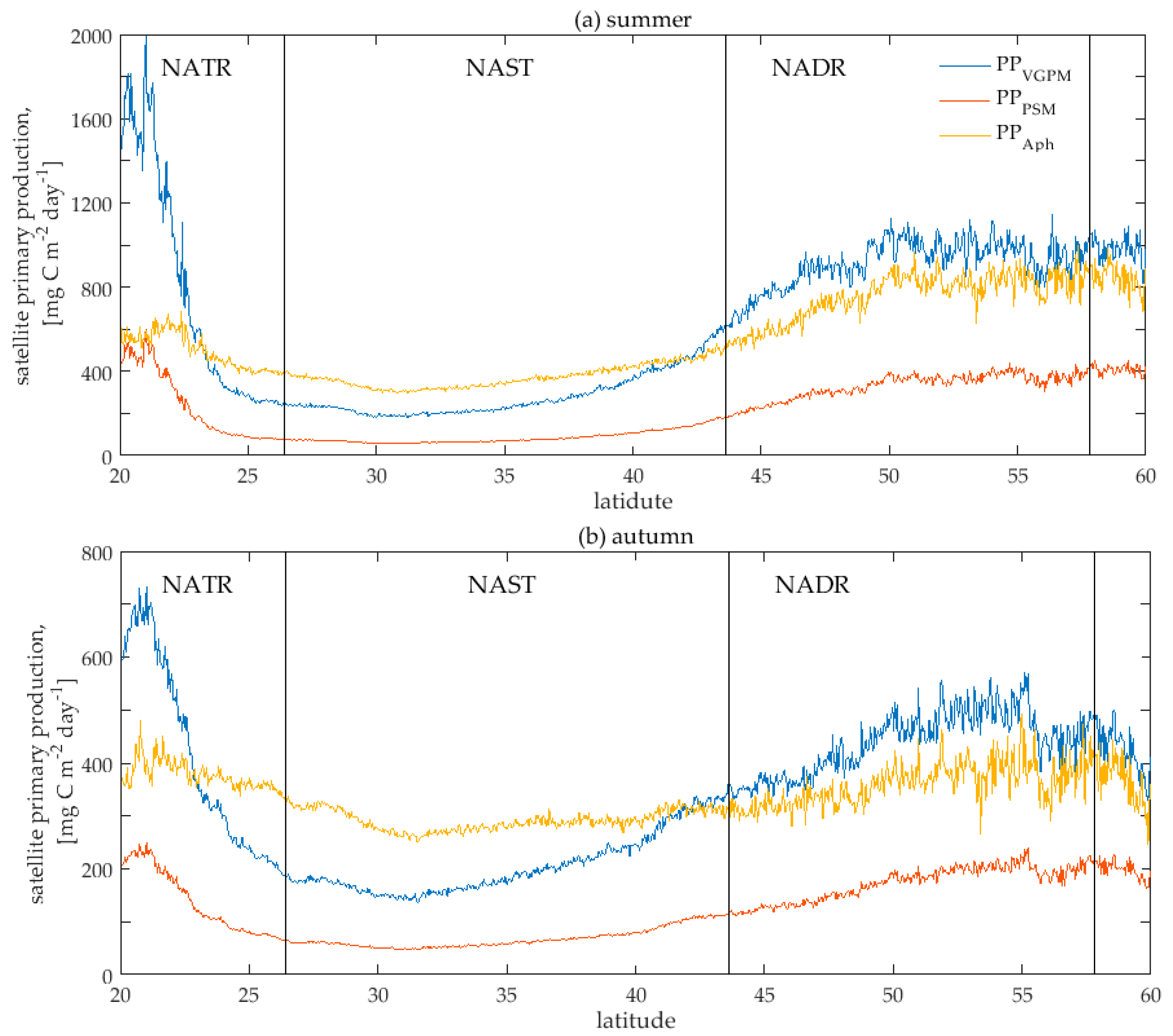
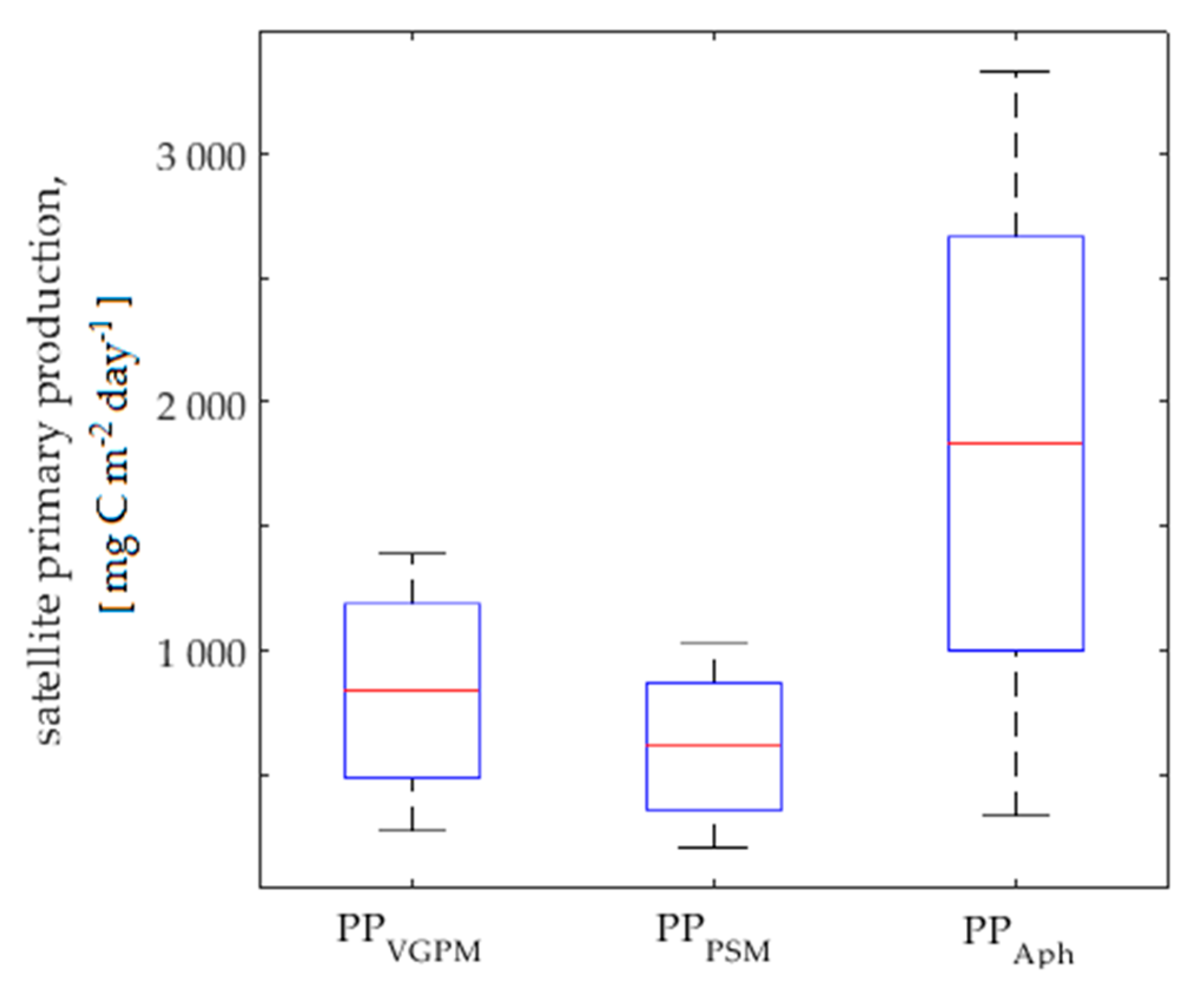
3.2. Satellite Primary Production Images
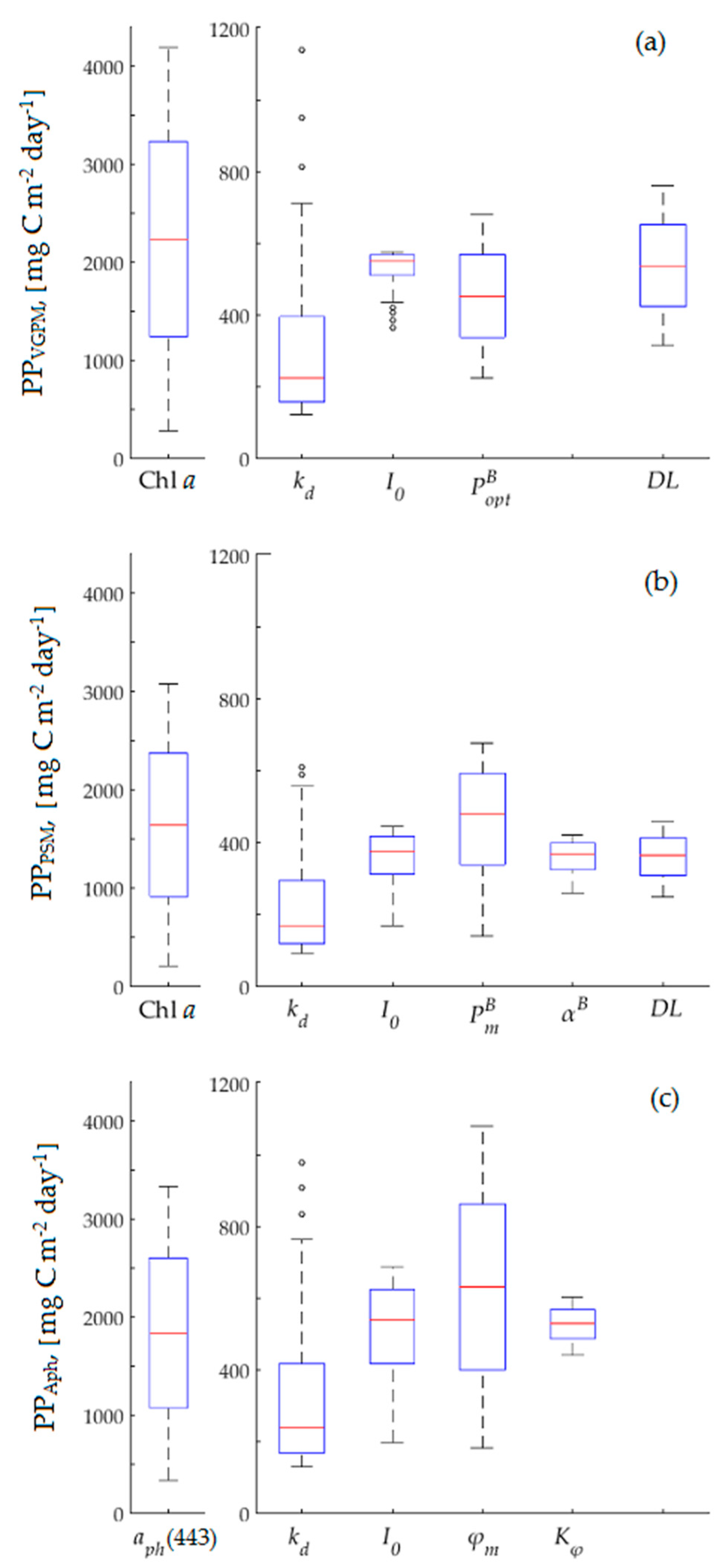
3.3. Model Sensitivity Analysis
4. Discussion
4.1. Validation of Primary Production Models
4.2. Effect of Photoinhibition in Primary Production Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| (a) Mathematical Equations for the Models | ||
| Model | ||
| PPβPSM | ||
| PPPSM | ||
| PPβAph | ||
| PPAph | ||
| (b) Mathematical Representation of Photoinhibition | ||
| Model | Photoinhibition Term | Reference |
| PPPSM | [43] | |
| PPAph | [32] | |
| PPVGPM | this paper | |
Appendix B
| (a) Daily, N = 46 | 1 | 2 | 3 | 4 | 5 | 6 | ||
| r | p-Level | Centre-Pattern RMSE | S | I | Bias | RMSE | APD, % | |
| PPβVGPM | 0.63 | p < 0.001 | 0.60 | 0.68 | 1.73 | −0.04 | 0.60 | 9.2 |
| PPVGPM | 0.63 | p < 0.001 | 0.60 | 0.68 | 1.80 | 0.05 | 0.61 | 9.3 |
| PPβPSM | 0.69 | p < 0.001 | 0.57 | 0.79 | 0.16 | −0.99 | 1.15 | 18.8 |
| PPPSM | 0.68 | p < 0.001 | 0.57 | 0.77 | 0.89 | −0.38 | 0.68 | 9.9 |
| PPβAph | 0.71 | p < 0.001 | 0.48 | 0.56 | 2.86 | 0.42 | 0.63 | 9.8 |
| PPAph | 0.70 | p < 0.001 | 0.48 | 0.57 | 2.95 | 0.56 | 0.74 | 11.8 |
| (b) Eight day composites, N = 46 | ||||||||
| PPβVGPM | 0.65 | p < 0.001 | 0.56 | 0.66 | 1.80 | −0.06 | 0.57 | 8.6 |
| PPVGPM | 0.66 | p < 0.001 | 0.56 | 0.67 | 1.86 | 0.03 | 0.56 | 8.6 |
| PPβPSM | 0.69 | p < 0.001 | 0.57 | 0.79 | 0.16 | −0.99 | 1.15 | 18.8 |
| PPPSM | 0.73 | p < 0.001 | 0.49 | 0.75 | 0.98 | −0.40 | 0.64 | 9.5 |
| PPβAph | 0.75 | p < 0.001 | 0.45 | 0.53 | 3.00 | 0.40 | 0.60 | 9.4 |
| PPAph | 0.73 | p < 0.001 | 0.46 | 0.54 | 3.09 | 0.53 | 0.70 | 11.4 |
| All Stations, N = 95 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| SD | r | r2 | S | I | bias | RMSE | Centre-Pattern RMSE | APD, % | ANOVA, F | ANOVA, p | |
| In situ PPeu | 0.68 | ||||||||||
| PPβVGPM | 0.81 | 0.74 | 0.54 | 0.88 | 0.77 | 0.13 | 0.57 | 0.56 | 9 | 1.4 | 0.237 |
| PPVGPM | 0.81 | 0.74 | 0.55 | 0.88 | 0.87 | 0.21 | 0.59 | 0.55 | 9 | 3.9 | 0.051 |
| PPβPSM | 0.90 | 0.76 | 0.58 | 1.01 | −0.85 | −0.78 | 0.97 | 0.58 | 15 | 45.6 | 0.000 |
| PPPSM | 0.84 | 0.78 | 0.61 | 0.97 | −0.02 | −0.21 | 0.56 | 0.52 | 8 | 3.6 | 0.060 |
| PPβAph | 0.66 | 0.71 | 0.51 | 0.69 | 2.23 | 0.51 | 0.71 | 0.50 | 11 | 27.0 | 0.000 |
| PPAph | 0.65 | 0.72 | 0.52 | 0.69 | 2.38 | 0.64 | 0.81 | 0.50 | 13 | 44.2 | 0.000 |
| NADR, N = 28 | |||||||||||
| In situ PPeu | 0.54 | ||||||||||
| PPβVGPM | 0.35 | 0.73 | 0.53 | 0.47 | 3.70 | 0.48 | 0.61 | 0.38 | 9 | 15.1 | 0.000 |
| PPVGPM | 0.35 | 0.74 | 0.54 | 0.48 | 3.69 | 0.55 | 0.66 | 0.37 | 10 | 19.5 | 0.000 |
| PPβPSM | 0.43 | 0.79 | 0.62 | 0.62 | 1.91 | −0.40 | 0.52 | 0.34 | 7 | 9.1 | 0.004 |
| PPPSM | 0.43 | 0.82 | 0.67 | 0.64 | 2.25 | 0.10 | 0.33 | 0.32 | 5 | 0.5 | 0.468 |
| PPβAph | 0.37 | 0.80 | 0.63 | 0.54 | 3.18 | 0.41 | 0.53 | 0.34 | 8 | 10.4 | 0.002 |
| PPAph | 0.38 | 0.80 | 0.65 | 0.56 | 3.18 | 0.52 | 0.62 | 0.33 | 9 | 16.7 | 0.000 |
| NAST, N = 40 | |||||||||||
| In situ PPeu | 0.57 | ||||||||||
| PPβVGPM | 0.55 | 0.52 | 0.27 | 0.51 | 2.59 | 0.07 | 0.55 | 0.55 | 9 | 0.32 | 0.572 |
| PPVGPM | 0.56 | 0.54 | 0.29 | 0.53 | 2.57 | 0.17 | 0.57 | 0.54 | 10 | 1.68 | 0.199 |
| PPβPSM | 0.49 | 0.51 | 0.26 | 0.44 | 1.88 | −0.97 | 1.10 | 0.52 | 19 | 65.16 | 0.000 |
| PPPSM | 0.50 | 0.55 | 0.30 | 0.48 | 2.29 | −0.34 | 0.61 | 0.51 | 10 | 7.76 | 0.008 |
| PPβAph | 0.42 | 0.42 | 0.17 | 0.31 | 4.06 | 0.55 | 0.78 | 0.55 | 14 | 23.80 | 0.000 |
| PPAph | 0.44 | 0.43 | 0.19 | 0.34 | 4.06 | 0.70 | 0.89 | 0.55 | 16 | 36.57 | 0.000 |
| NATR, N = 14 | |||||||||||
| In situ PPeu | 0.33 | ||||||||||
| PPβVGPM | 0.66 | 0.51 | 1.49 | −3.22 | −0.49 | 0.68 | 0.46 | 11 | 5.78 | 0.024 | |
| PPVGPM | 0.66 | 0.51 | 1.49 | −3.13 | −0.39 | 0.61 | 0.47 | 10 | 3.58 | 0.069 | |
| PPβPSM | 0.62 | 0.57 | 1.44 | −3.89 | −1.44 | 1.50 | 0.42 | 26 | 54.11 | 0.000 | |
| PPPSM | 0.63 | 0.54 | 1.44 | −3.22 | −0.77 | 0.88 | 0.43 | 14 | 15.14 | 0.001 | |
| All Summer Stations, N = 56 | |||||||||||
| In situ PPeu | 0.49 | ||||||||||
| PPβVGPM | 0.68 | 0.73 | 0.54 | 1.01 | 0.07 | 0.14 | 0.48 | 0.46 | 7 | 1.5 | 0.218 |
| PPVGPM | 0.66 | 0.73 | 0.53 | 0.98 | 0.35 | 0.23 | 0.51 | 0.45 | 7 | 4.3 | 0.041 |
| PPβPSM | 0.80 | 0.76 | 0.58 | 1.25 | −2.20 | −0.74 | 0.91 | 0.54 | 13 | 33.9 | 0.000 |
| PPPSM | 0.72 | 0.76 | 0.58 | 1.11 | −0.84 | −0.17 | 0.50 | 0.47 | 7 | 2.1 | 0.146 |
| PPβAph | 0.55 | 0.67 | 0.45 | 0.76 | 1.94 | 0.50 | 0.66 | 0.43 | 9 | 24.9 | 0.000 |
| PPAph | 0.53 | 0.66 | 0.44 | 0.72 | 2.32 | 0.64 | 0.77 | 0.42 | 11 | 43.0 | 0.000 |
| ARCT, N = 12 | |||||||||||
| In situ PPeu | 0.40 | ||||||||||
| PPβPSM | 0.28 | 0.56 | 0.45 | 3.01 | −0.37 | 0.47 | 0.30 | 7 | 6.3 | 0.020 | |
| PPPSM | 0.28 | 0.55 | 0.46 | 3.37 | 0.09 | 0.31 | 0.30 | 4 | 0.4 | 0.547 | |
| NADR, N = 22 | |||||||||||
| In situ PPeu | 0.39 | ||||||||||
| PPβVGPM | 0.30 | 0.57 | 0.40 | 4.09 | 0.39 | 0.52 | 0.34 | 7 | 13.3 | 0.001 | |
| PPVGPM | 0.29 | 0.55 | 0.40 | 4.22 | 0.46 | 0.58 | 0.34 | 8 | 18.9 | 0.000 | |
| PPβPSM | 0.34 | 0.53 | 0.53 | 2.45 | −0.47 | 0.57 | 0.33 | 8 | 16.9 | 0.000 | |
| PPPSM | 0.32 | 0.59 | 0.50 | 3.14 | 0.05 | 0.32 | 0.31 | 5 | 0.2 | 0.669 | |
| PPβAph | 0.28 | 0.58 | 0.46 | 3.68 | 0.33 | 0.45 | 0.30 | 6 | 9.7 | 0.003 | |
| PPAph | 0.28 | 0.62 | 0.45 | 3.88 | 0.45 | 0.54 | 0.30 | 8 | 18.6 | 0.000 | |
| NATR, N = 6 | |||||||||||
| In situ PPeu | 0.19 | ||||||||||
| PPβVGPM | 0.21 | 0.81 | 0.80 | 0.57 | −0.50 | 0.52 | 0.15 | 9 | 15.4 | 0.003 | |
| PPVGPM | 0.21 | 0.81 | 0.76 | 0.93 | −0.39 | 0.42 | 0.16 | 7 | 9.2 | 0.012 | |
| All Autumn Stations, N = 38 | |||||||||||
| In situ PPeu | 0.55 | ||||||||||
| PPβVGPM | 0.68 | 0.41 | 0.16 | 0.50 | 2.64 | 0.10 | 0.69 | 0.68 | 12 | 0.5 | 0.477 |
| PPVGPM | 0.67 | 0.41 | 0.17 | 0.50 | 2.70 | 0.18 | 0.69 | 0.67 | 12 | 1.6 | 0.213 |
| PPβPSM | 0.65 | 0.47 | 0.22 | 0.54 | 1.42 | −0.87 | 1.07 | 0.62 | 18 | 38.6 | 0.000 |
| PPPSM | 0.61 | 0.50 | 0.25 | 0.55 | 1.97 | −0.28 | 0.65 | 0.58 | 11 | 4.4 | 0.039 |
| NATR, N = 8 | |||||||||||
| In situ PPeu | 0.38 | ||||||||||
| PPβVGPM | 0.84 | 0.69 | 1.67 | −4.29 | −0.48 | 0.77 | 0.60 | 12 | 1.9 | 0.190 | |
| PPVGPM | 0.85 | 0.69 | 1.69 | −4.29 | −0.39 | 0.72 | 0.60 | 12 | 1.2 | 0.286 | |
| PPβPSM | 0.77 | 0.64 | 1.53 | −4.38 | −1.38 | 1.48 | 0.53 | 25 | 18.0 | 0.001 | |
| PPPSM | 0.78 | 0.69 | 1.58 | −4.00 | −0.72 | 0.90 | 0.54 | 13 | 4.8 | 0.046 | |
References
- Falkowski, P. Ocean productivity from space. Nature 1988, 335, 205. [Google Scholar] [CrossRef]
- Steemann Nielsen, E. The use of radio-active carbon (C14) for measuring organic production in the sea. ICES J. Mar. Sci. 1952, 18, 117–140. [Google Scholar] [CrossRef]
- Smith, R.C.; Eppley, R.W.; Baker, K.S. Correlation of primary production as measured aboard ship in southern California coastal waters and as estimated from satellite chlorophyll images. Mar. Biol. 1982, 66, 281–288. [Google Scholar] [CrossRef]
- Eppley, R.W.; Stewart, E.; Abbott, M.R.; Owen, R.W. Estimating ocean production from satellite-derived chlorophyll: Insights from the Eastropac data set. Oceanol. Acta Spec. Issue 1987, SP, 109–113. [Google Scholar]
- Antoine, D.; André, J.M.; Morel, A. Oceanic primary production: 2. Estimation at global scale from satellite (coastal zone color scanner) chlorophyll. Glob. Biogeochem. Cycles 1996, 10, 57–69. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Falkowski, P.G. Photosynthetic rates derived from satellite-based chlorophyll concentration. Limnol. Oceanogr. 1997, 42, 1–20. [Google Scholar] [CrossRef]
- Tilstone, G.; Smyth, T.; Poulton, A.; Hutson, R. Measured and remotely sensed estimates of primary production in the Atlantic Ocean from 1998 to 2005. Deep Sea Res. Part II Top. Stud. Oceanogr. 2009, 56, 918–930. [Google Scholar] [CrossRef]
- Joo, H.; Son, S.; Park, J.W.; Kang, J.J.; Jeong, J.Y.; Lee, C.I.; Kang, C.K.; Lee, S.H. Long-Term pattern of primary productivity in the East/Japan sea based on ocean color data derived from MODIS-Aqua. Remote Sens. 2016, 8, 25. [Google Scholar] [CrossRef]
- Campbell, J.; Antoine, D.; Armstrong, R.; Arrigo, K.; Balch, W.; Barber, R.; Behrenfeld, M.; Bidigare, R.; Bishop, J.; Carr, M.-E.; et al. Comparison of algorithms for estimating ocean primary production from surface chlorophyll, temperature, and irradiance. Glob. Biogeochem. Cycles 2002, 16. [Google Scholar] [CrossRef]
- Carr, M.E.; Friedrichs, M.A.; Schmeltz, M.; Aita, M.N.; Antoine, D.; Arrigo, K.R.; Asanuma, I.; Aumont, O.; Barber, R.; Behrenfeld, M.; et al. A comparison of global estimates of marine primary production from ocean color. Deep Sea Res. Part II Top. Stud. Oceanogr. 2006, 53, 741–770. [Google Scholar] [CrossRef]
- Friedrichs, M.A.; Carr, M.E.; Barber, R.T.; Scardi, M.; Antoine, D.; Armstrong, R.A.; Asanuma, I.; Behrenfeld, M.J.; Buitenhuis, E.T.; Chai, F.; et al. Assessing the uncertainties of model estimates of primary productivity in the tropical Pacific Ocean. J. Mar. Syst. 2009, 76, 113–133. [Google Scholar] [CrossRef]
- Saba, V.S.; Friedrichs, M.A.M.; Carr, M.-E.; Antoine, D.; Armstrong, R.A.; Asanuma, I.; Aumont, O.; Bates, N.R.; Behrenfeld, M.J.; Bennington, V.; et al. Challenges of modeling depth-integrated marine primary productivity over multiple decades: A case study at BATS and HOT. Glob. Biogeochem. Cycles 2010, 24. [Google Scholar] [CrossRef]
- Saba, V.S.; Friedrichs, M.A.M.; Antoine, D.; Armstrong, R.A.; Asanuma, I.; Behrenfeld, M.J.; Ciotti, A.M.; Dowell, M.; Hoepffner, N.; Hyde, K.J.W.; et al. An evaluation of ocean color model estimates of marine primary productivity in coastal and pelagic regions across the globe. Biogeosciences 2011, 8, 489–503. [Google Scholar] [CrossRef]
- Tilstone, G.H.; Taylor, B.H.; Blondeau-Patissier, D.; Powell, T.; Groom, S.B.; Rees, A.P.; Lucas, M.I. Comparison of new and primary production models using SeaWiFS data in contrasting hydrographic zones of the northern North Atlantic. Remote Sens. Environ. 2015, 156, 473–489. [Google Scholar] [CrossRef]
- Balch, W.; Evans, R.; Brown, J.; Feldman, G.; McClain, C.; Esaias, W. The remote sensing of ocean primary productivity: Use of a new data compilation to test satellite algorithms. J. Geophys. Res. Oceans 1992, 97, 2279–2293. [Google Scholar] [CrossRef]
- Berthon, J.F.; Morel, A. Validation of a spectral light-photosynthesis model and use of the model in conjunction with remotely sensed pigment observations. Limnol. Oceanogr. 1992, 37, 781–796. [Google Scholar] [CrossRef]
- Petrenko, D.; Pozdnyakov, D.; Johannessen, J.; Counillon, F.; Sychov, V. Satellite-derived multi-year trend in primary production in the Arctic Ocean. Int. J. Remote Sens. 2013, 34, 3903–3937. [Google Scholar] [CrossRef]
- Dierssen, H.M.; Smith, R.C. Bio-optical properties and remote sensing ocean color algorithms for Antarctic Peninsula waters. J. Geophys. Res. Oceans 2000, 105, 26301–26312. [Google Scholar] [CrossRef]
- IOCCG. Remote Sensing of Ocean Colour in Coastal, and Other Optically-Complex Waters; Sathyendranath, S., Ed.; Reports of the International Ocean-Colour Coordinating; IOCCG: Dartmouth, NS, Canada, 2000. [Google Scholar]
- Volpe, G.; Santoleri, R.; Vellucci, V.; d’Alcalà, M.R.; Marullo, S.; d’Ortenzio, F. The colour of the Mediterranean Sea: Global versus regional bio-optical algorithms evaluation and implication for satellite chlorophyll estimates. Remote Sens. Environ. 2007, 107, 625–638. [Google Scholar] [CrossRef]
- Campbell, J.W.; O’Reilly, J.E. Role of satellites in estimating primary productivity on the northwest Atlantic continental shelf. Cont. Shelf Res. 1988, 8, 179–204. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S. Oceanic primary production: Estimation by remote sensing at local and regional scales. Science 1988, 241, 1613–1620. [Google Scholar] [CrossRef] [PubMed]
- Platt, T.; Caverhill, C.; Sathyendranath, S. Basin-scale estimates of primary production by remote sensing: The North Atlantic. J. Geophys. Res. 1991, 96, 15147–15159. [Google Scholar] [CrossRef]
- Gregg, W.W.; Conkright, M.E. Global seasonal climatologies of ocean chlorophyll: Blending in situ and satellite data for the Coastal Zone Color Scanner era. J. Geophys. Res. Oceans 2001, 106, 2499–2515. [Google Scholar] [CrossRef]
- Milutinović, S.; Bertino, L. Assessment and propagation of uncertainties in input terms through an ocean-color-based model of primary productivity. Remote Sens. Environ. 2011, 115, 1906–1917. [Google Scholar] [CrossRef]
- Balch, W.M.; Byrne, C.F. Factors affecting the estimate of primary production from space. J. Geophys. Res. Oceans 1994, 99, 7555–7570. [Google Scholar] [CrossRef]
- Finenko, Z.Z.; Suslin, V.V.; Churilova, T.Y. The regional model to calculate the Black Sea primary production using satellite color scanner SeaWiFS. Mar. Ecol. J. 2009, 8, 81–106. (In Russian) [Google Scholar]
- Dogliotti, A.I.; Lutz, V.A.; Segura, V. Estimation of primary production in the southern Argentine continental shelf and shelf-break regions using field and remote sensing data. Remote Sens. Environ. 2014, 140, 497–508. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Falkowski, P.G. A consumer’s guide to phytoplankton primary productivity models. Limnol. Oceanogr. 1997, 42, 1479–1491. [Google Scholar] [CrossRef]
- Peterson, D.H.; Perry, M.J.; Bencala, K.E.; Talbot, M.C. Phytoplankton productivity in relation to light intensity: A simple equation. Estuar. Coast. Shelf Sci. 1987, 24, 813–832. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S. Modelling Marine Primary Production; IOCCG: Halifax, NS, Canada, 2002; 280p. [Google Scholar]
- Lee, Z.P.; Carder, K.L.; Marra, J.; Steward, R.G.; Perry, M.J. Estimating primary production at depth from remote sensing. Appl. Opt. 1996, 35, 463–474. [Google Scholar] [CrossRef] [PubMed]
- Lee, Z.; Lance, V.P.; Shang, S.; Vaillancourt, R.; Freeman, S.; Lubac, B.; Hargreaves, B.R.; Castillo, C.D.; Miller, R.; Twardowski, M.; et al. An assessment of optical properties and primary production derived from remote sensing in the Southern Ocean (SO GasEx). J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems, 3rd ed.; Cambridge University Press: Cambridge, UK, 2011; 649p. [Google Scholar]
- Longhurst, A. Seasonal cycles of pelagic production and consumption. Prog. Oceanogr. 1995, 36, 77–167. [Google Scholar] [CrossRef]
- Vedernikov, V.I.; Gagarin, V.I.; Demidov, A.B.; Burenkov, V.I.; Stunzhas, P.A. Primary production and chlorophyll distributions in the subtropical and tropical waters of the Atlantic ocean in the autumn of 2002. Oceanology 2007, 47, 386–399. [Google Scholar] [CrossRef]
- Tilstone, G.H.; Lange, P.K.; Misra, A.; Brewin, R.J.W.; Cain, T. Microphytoplankton photosynthesis, primary production and potential export production in the Atlantic Ocean. Prog. Oceanogr. 2017, 158, 109–129. [Google Scholar] [CrossRef]
- IOC. Protocols for the Joint Global Ocean Flux Study (JGOFS) Core Measurements; UNESCO: Paris, France, 1994. [Google Scholar]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Lizon, F.; Seuront, L.; Lagadeuc, Y. Photoadaptation and primary production study in tidally mixed coastal waters using a Lagrangian model. Mar. Ecol. Prog. Ser. 1998, 169, 43–54. [Google Scholar] [CrossRef]
- Lee, Z.; Marra, J.; Perry, M.J.; Kahru, M. Estimating oceanic primary productivity from ocean color remote sensing: A strategic assessment. J. Mar. Syst. 2015, 149, 50–59. [Google Scholar] [CrossRef]
- Kahru, M.; Jacox, M.G.; Lee, Z.; Kudela, R.M.; Manzano-Sarabia, M.; Mitchell, B.G. Optimized multi-satellite merger of primary production estimates in the California Current using inherent optical properties. J. Mar. Syst. 2015, 147, 94–102. [Google Scholar] [CrossRef]
- Platt, T.G.; Gallegos, C.L.; Harrison, W.G. Photoinhibition of photosynthesis in natural assemblages of marine phytoplankton. J. Mar. Res. 1980, 38, 687–701. [Google Scholar]
- Kiefer, D.A.; Mitchell, B.G. A simple, steady state description of phytoplankton growth based on absorption cross section and quantum efficiency. Limnol. Oceanogr. 1983, 28, 770–776. [Google Scholar] [CrossRef]
- Morel, A. Available, usable, and stored radiant energy in relation to marine photosynthesis. Deep Sea Res. 1978, 25, 673–688. [Google Scholar] [CrossRef]
- Rabinovich, E. Photosynthesis; Foreign Lit: Moscow, Russia, 1953; Volume 2, 652p. (In Russian) [Google Scholar]
- Marra, J.; Ho, C.; Trees, C. An Alternative Algorithm for the Calculation of Primary Productivity from Remote Sensing Data; Lamont Doherty Earth Observatory Technical Report (LDEO-2003-1); LDEO: Palisades, NY, USA, 2003. [Google Scholar]
- Bannister, T.T. Production equations in terms of chlorophyll concentration, quantum yield, and upper limit to production. Limnol. Oceanogr. 1974, 19, 1–12. [Google Scholar] [CrossRef]
- Laws, E.A.; Bannister, T.T. Nutrient- and light-limited growth of Thalassiosira fluviatilis in continuous culture, with implications for phytoplankton growth in the ocean. Limnol. Oceanogr. 1980, 25, 457–473. [Google Scholar] [CrossRef]
- Babin, M.; Morel, A.; Claustre, H.; Bricaud, A.; Kolber, Z.; Falkowski, P.G. Nitrogen- and irradiance-dependent variations of the maximum quantum yield of carbon fixation in eutrophic, mesotrophic and oligotrophic marine systems. Deep Sea Res. Part I Oceanogr. Res. Pap. 1996, 43, 1241–1272. [Google Scholar] [CrossRef]
- Morel, A.; Antoine, D.; Babin, M.; Dandonneau, Y. Measured and modeled primary production in the northeast Atlantic (EUMELI JGOFS program): The impact of natural variations in photosynthetic parameters on model predictive skill. Deep Sea Res. Part I Oceanogr. Res. Pap. 1996, 43, 1273–1304. [Google Scholar] [CrossRef]
- Kyewalyanga, M.N.; Platt, T.; Sathyendranath, S.; Lutz, V.A.; Stuart, V. Seasonal variations in physiological parameters of phytoplankton across the North Atlantic. J. Plankton Res. 1998, 20, 17–42. [Google Scholar] [CrossRef]
- Suggett, D.; Kraay, G.; Holligan, P.; Davey, M.; Aiken, J.; Geider, R. Assessment of photosynthesis in a spring cyanobacterial bloom by use of a fast repetition rate fluorometer. Limnol. Oceanogr. 2001, 46, 802–810. [Google Scholar] [CrossRef]
- Smyth, T.J.; Tilstone, G.H.; Groom, S.B. Integration of radiative transfer into satellite models of ocean primary production. J. Geophys. Res. Oceans 2005, 110. [Google Scholar] [CrossRef]
- Picart, S.S.; Sathyendranath, S.; Dowell, M.; Moore, T.; Platt, T. Remote sensing of assimilation number for marine phytoplankton. Remote Sens. Environ. 2014, 146, 87–96. [Google Scholar] [CrossRef]
- Johnson, Z. Regulation of Marine Photosynthetic Efficiency by Photosystem II. Ph.D. Thesis, Graduate School of Duke University, Durham, NC, USA, 2000; 189p. [Google Scholar]
- Morel, A.; Huot, Y.; Gentili, B.; Werdell, P.J.; Hooker, S.B.; Franz, B.A. Examining the consistency of products derived from various ocean color sensors in open ocean (Case 1) waters in the perspective of a multi-sensor approach. Remote Sens. Environ. 2007, 111, 69–88. [Google Scholar] [CrossRef]
- Emery, W.J.; Tomson, R.E. Data Analysis Methods in Physical Oceanography; Gulf Professional Publishing: Houston, TX, USA, 2001; 638p. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Barnes, M.; Tilstone, G.H.; Smyth, T.J.; Suggett, D.; Kromkamp, J.; Astoreca, R.; Lancelot, C. Absorption based algorithm of primary production for total and size-fractionated phytoplankton in coastal waters. Mar. Ecol. Prog. Ser. 2014, 504, 73–89. [Google Scholar] [CrossRef]
- Tilstone, G.H.; Smyth, T.J.; Gowen, R.J.; Martinez-Vicente, V.; Groom, S.B. Inherent optical properties of the Irish Sea and their effect on satellite primary production algorithms. J. Plankton Res. 2005, 27, 1–22. [Google Scholar] [CrossRef]
- Curl, H.; Small, L.F. Variations in photosynthetic assimilation ratios in natural, marine phytoplankton communities. Limnol. Oceanogr. 1965, 10, R67–R73. [Google Scholar] [CrossRef]
- O’Reilly, J.E.; Maritorena, S.; Siegel, D.; O’Brien, M.C. Ocean color chlorophyll a algorithms for SeaWiFs, OC2, and OC4: Technical report. In SeaWiFS Postlaunch Calibration and Validation Analyses, Part 3; Postlaunch Technical Report Series; NASA Goddard Space Flight Centre: Greenbelt, MD, USA, 2000; Volume 11, pp. 9–23. [Google Scholar]
- Bouman, H.A.; Platt, T.; Doblin, M.; Figueiras, F.G.; Gudmudsson, K.; Gudfinnsson, H.G.; Huang, B.; Hickman, A.; Hiscock, M.; Jackson, T.; et al. Photosynthesis-irradiance parameters of marine phytoplankton: Synthesis of a global data set. Earth Syst. Sci. Data 2018, 10, 251–266. [Google Scholar] [CrossRef]
- Sosik, H.M. Bio-optical modeling of primary production: Consequences of variability in quantum yield and specific absorption. Mar. Ecol. Prog. Ser. 1996, 143, 225–238. [Google Scholar] [CrossRef]
- Uitz, J.; Huot, Y.; Bruyant, F.; Babin, M.; Claustre, H. Relating phytoplankton photophysiological properties to community structure on large scales. Limnol. Oceanogr. 2008, 53, 614–630. [Google Scholar]
- Kok, B. On the inhibition of photosynthesis by intense light. Biochim. Biophys. Acta 1956, 21, 234–244. [Google Scholar] [CrossRef]
- Miller, C.B.; Wheeler, P.A. Biological Oceanography; John Wiley & Sons: Hoboken, NJ, USA, 2012; 504p. [Google Scholar]
- Ryther, J.H.; Menzel, D.W. Light adaptation by marine phytoplankton. Limnol. Oceanogr. 1959, 4, 492–497. [Google Scholar] [CrossRef]
- Steele, J.H. Environmental control of photosynthesis in the sea. Limnol. Oceanogr. 1962, 7, 137–150. [Google Scholar] [CrossRef]
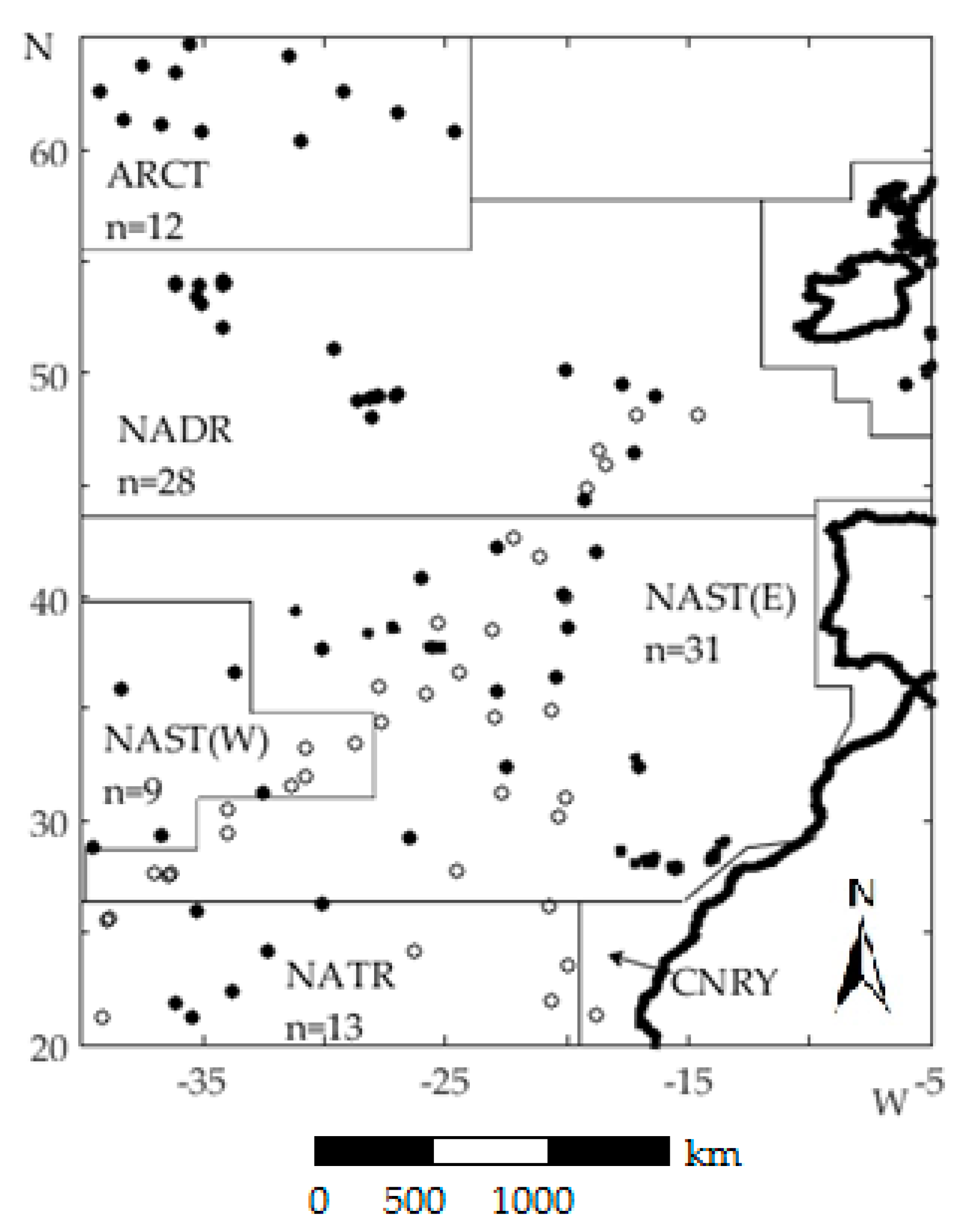
| Region | North East Atlantic (NEA): 20–65° N, 5–40° W |
|---|---|
| Period | 1998–2013 |
| Number of stations (n) | 95 |
| Seasons 1 | |
| summer, n = 56 | June-1998, July–August 2002, June-2003, May-2004, June-2005, July–August 2007, August-2009 |
| autumn, n = 38 | September-2003, September-2004, October-2008, September-2009, October-2011, October-2012, October-2013 |
| Provinces | ARCT 2—Atlantic Arctic Province (n = 12) |
| NADR—North Atlantic Drift (n = 28) | |
| NAST 3—North Atlantic Subtropical Gyre (East & West) (n = 40) | |
| NATR 4—North Atlantic Tropical Gyre (n = 14) |
| αB | PBm | φm | |
|---|---|---|---|
| N | 12 | 29 | 13 |
| mean | 0.049 | 3.316 | 0.032 |
| SD | 0.019 | 2.153 | 0.016 |
| min | 0.017 | 0.947 | 0.010 |
| max | 0.078 | 9.136 | 0.060 |
| Model | Mean | Min | Max |
|---|---|---|---|
| PPVGPM | −7 | −2 | −10 |
| PPPSM | −42 | −20 | −50 |
| PPAph | −11 | −4 | −15 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lobanova, P.; Tilstone, G.H.; Bashmachnikov, I.; Brotas, V. Accuracy Assessment of Primary Production Models with and without Photoinhibition Using Ocean-Colour Climate Change Initiative Data in the North East Atlantic Ocean. Remote Sens. 2018, 10, 1116. https://doi.org/10.3390/rs10071116
Lobanova P, Tilstone GH, Bashmachnikov I, Brotas V. Accuracy Assessment of Primary Production Models with and without Photoinhibition Using Ocean-Colour Climate Change Initiative Data in the North East Atlantic Ocean. Remote Sensing. 2018; 10(7):1116. https://doi.org/10.3390/rs10071116
Chicago/Turabian StyleLobanova, Polina, Gavin H. Tilstone, Igor Bashmachnikov, and Vanda Brotas. 2018. "Accuracy Assessment of Primary Production Models with and without Photoinhibition Using Ocean-Colour Climate Change Initiative Data in the North East Atlantic Ocean" Remote Sensing 10, no. 7: 1116. https://doi.org/10.3390/rs10071116
APA StyleLobanova, P., Tilstone, G. H., Bashmachnikov, I., & Brotas, V. (2018). Accuracy Assessment of Primary Production Models with and without Photoinhibition Using Ocean-Colour Climate Change Initiative Data in the North East Atlantic Ocean. Remote Sensing, 10(7), 1116. https://doi.org/10.3390/rs10071116







