1. Introduction
The retrieval of precipitation with radars and radiometers is important for a variety of environmental applications and human activities [
1]. They provide accurate precipitation estimates that are crucial for monitoring extreme climate events, such as droughts [
2,
3,
4], floods [
5,
6,
7], and hailstorms [
8,
9]. Due to its global coverage and direct measurement, radars have become an essential tool to estimate precipitation, especially in complex terrains [
10,
11,
12] and in sparsely populated areas affected by poor rain gauge coverage [
13,
14,
15].
However, regardless of how powerful radars and radiometers are, they are not immune to retrieval biases. One such bias is the effect of multiple scattering in high-frequency radars [
16,
17]. It has been proved that multiple scattering in the microwave frequencies has to be accounted for in precipitation retrieval algorithms [
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28].
Another important, but sometimes overlooked, problem is the effect of the random arrangements of particles in space. Indeed, a single rain drop size distribution (RDSD) corresponds with many actual 3D distributions of those raindrops. Each spatial configuration is equivalent to any other in terms of the RDSD function; however, they scatter radiation differently both near and far from field due to changes in the relative phases among the particles. This paper investigates the variability of such scattering at microwave frequencies due to the random spatial distribution of drops.
The T-matrix formalism [
29] provides a sound approach to calculate radiometric quantities from first principles [
30,
31,
32,
33,
34,
35,
36]. It permits analysis of the effects of scattering not only of individual particles but also of systems with many interacting scatters. The approach of this paper is to use measured RDSDs from disdrometers and build ensembles of randomly-located drops in a volume to check whether or not there is a difference in the scattering as calculated by the T-matrix method. The aim of the research is to gauge the extent of the variability in a theoretical, first-order setting: the actual scattering depends on the sensor (radar or radiometer), beamwidth, and frequency of operation.
2. Data
Laser disdrometers (
Figure 1) provide estimates of the RDSD of precipitation. The RDSD can be built over a 2D instantaneous estimate or over a 2D time sliced estimate, with the extra dimension corresponding to the accumulation time (10 min). The time-integrated slice is deemed as a suitable representation of precipitation within a large 3D box around the instrument under the assumption that the spatial correlation of precipitation decreases only moderately with distance.
The University of Castilla-La Mancha (UCLM) has been maintaining a network of disdrometers since 2009. The original setup of the instruments consists of a dual arrangement with a solar panel and two batteries so the setup can work autonomously (
Figure 1 Left). Data from the sensors were automatically sent to a server every minute and then filtered and processed to standard accumulation periods (1, 5, and 10 min). They have been compared and cross-calibrated (
Figure 1 Right). Latest refinement and filtering of the database resulted in the empirical basis for this paper. For reference, the product of the whole process is tagged as the “UCLM disdrometer database v4.0.” This 2018 product supersedes previous versions of UCLM’s disdrometer data.
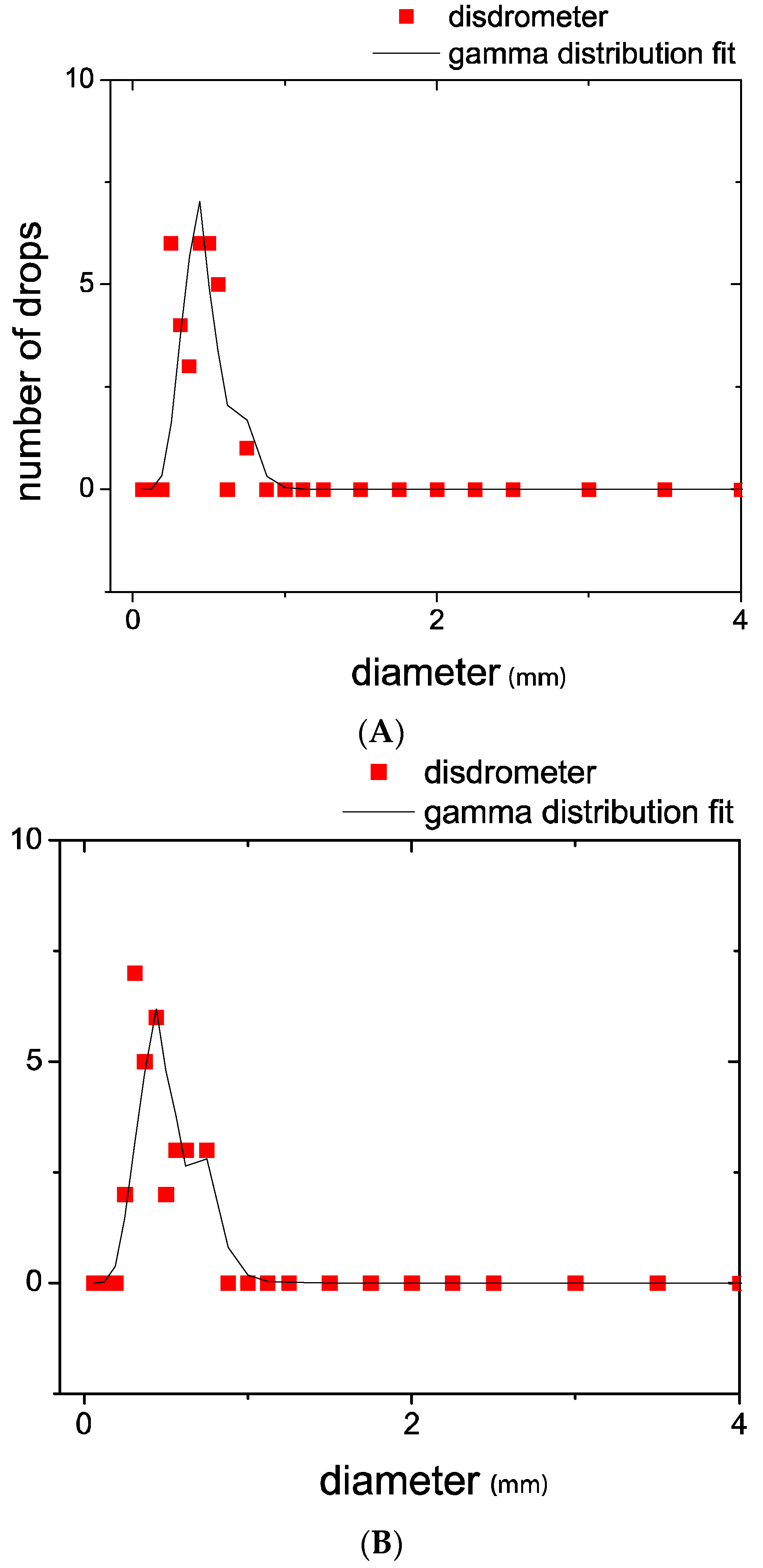
Two 10-min accumulated RDSDs were randomly selected from the database to calculate the radiometric quantities associated with several spatial configurations (
Figure 2). The small number of drops was chosen to alleviate the computational burden of the simulations since the burden of direct simulation of scattering escalates quickly with the number of scatters.
3. Methods
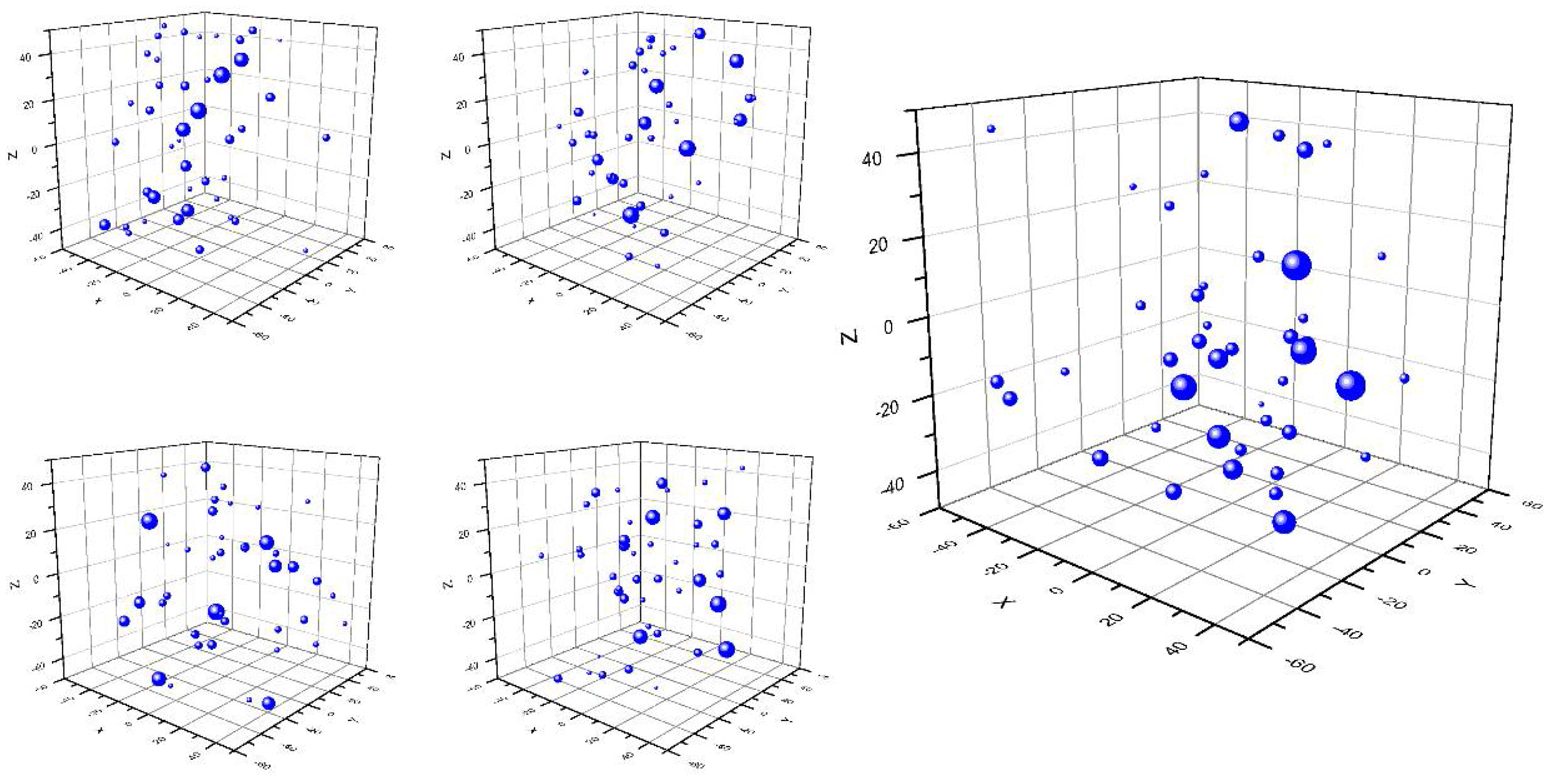
The 10-min data were used to derive an ensemble of 3D configurations. The measured RDSDs were used to derive the concentrations and size distributions in a 1 m3 cube. Such measurement was used as a starting point for which the positions were randomly perturbed. The algorithm used to locate the drops in space was a Monte Carlo generator, as follows. A Pseudo-Random Number Generator (PRNG) was used to generate the locations within the volume. At every iteration, raindrops were sequentially generated in decreasing size order. Collisions are identified and avoided using a relaxation technique.
Drops were assumed to be spherical for simplicity; more complex and realistic geometries will only reinforce the point made—that is, that there is measurable variability because of the actual spatial configuration of the RDSD.
Two tests for randomness were carried out on the PRNG: (i) uniformity test and (ii) independence test. The latter was evaluated through a χ
2 test and a Kolmogorov-Smirnov test. It is worth noting that a simpler algorithm would not satisfy the randomness requirement since the raindrops need to be randomly distributed in a cube and not in a sphere (with the extra condition of not intersecting one to another,
Figure 3).
The parameters of the Stokes scattering matrix
S were calculated using the T-Matrix formalism. The relationship between the incident (
i) and scattered (
s) field amplitudes in the far field zone for spheres is given in Mie’s theory by Van der Hulst and Bohren [
39,
40]:
where
and
are the parallel and perpendicular components of the electric field,
S1,2 are phase functions,
k is the free-space propagation constant, and
r the distance from the origin to the observation point (with exp(ikz) the incident plane wave). The phase functions are:
where
and
, with
the associated Legendre functions.
Since the drops are randomly located, averaging over all orientations results in a scattering matrix with only six independent significant elements (i.e., there is not preferential scattering direction in
xy when the incident wave comes from -
z). The Stokes parameters
I,
Q,
U and
V for the scattered wave (
S) are derived from the scattering matrix
Si,j and the parameters of the incident wave (
I) as follows:
with:
The equations used in the calculations of multiple spheres are those in Mackowski et al. [
32]. Spherical drops were assumed in order to generate a first-order analysis. Further work will be devoted to the analyses of the effects of other shapes, including solid precipitation.
The T-matrix v.3.0 code was used for all the members of the two ensembles and for X-band wavelength (3.197 cm = 9.375 GHz; length scale factor of 1.9653). Temperature was set to 5 °C. Refractive index was set according to frequency and temperature. The beamwidth of the incident wave was restricted to the domain. Processing time for each configuration varied (typically, about 72 h).
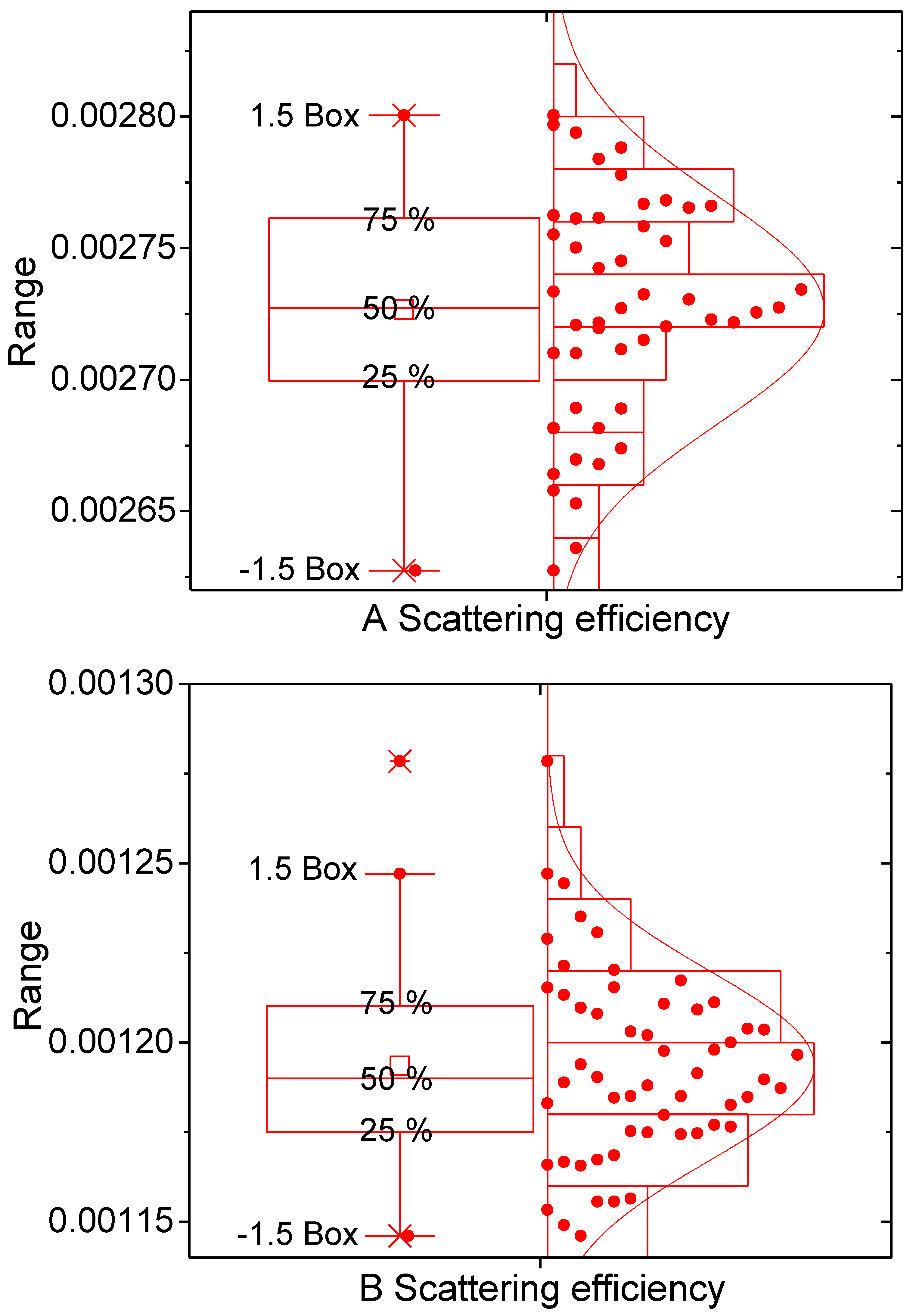
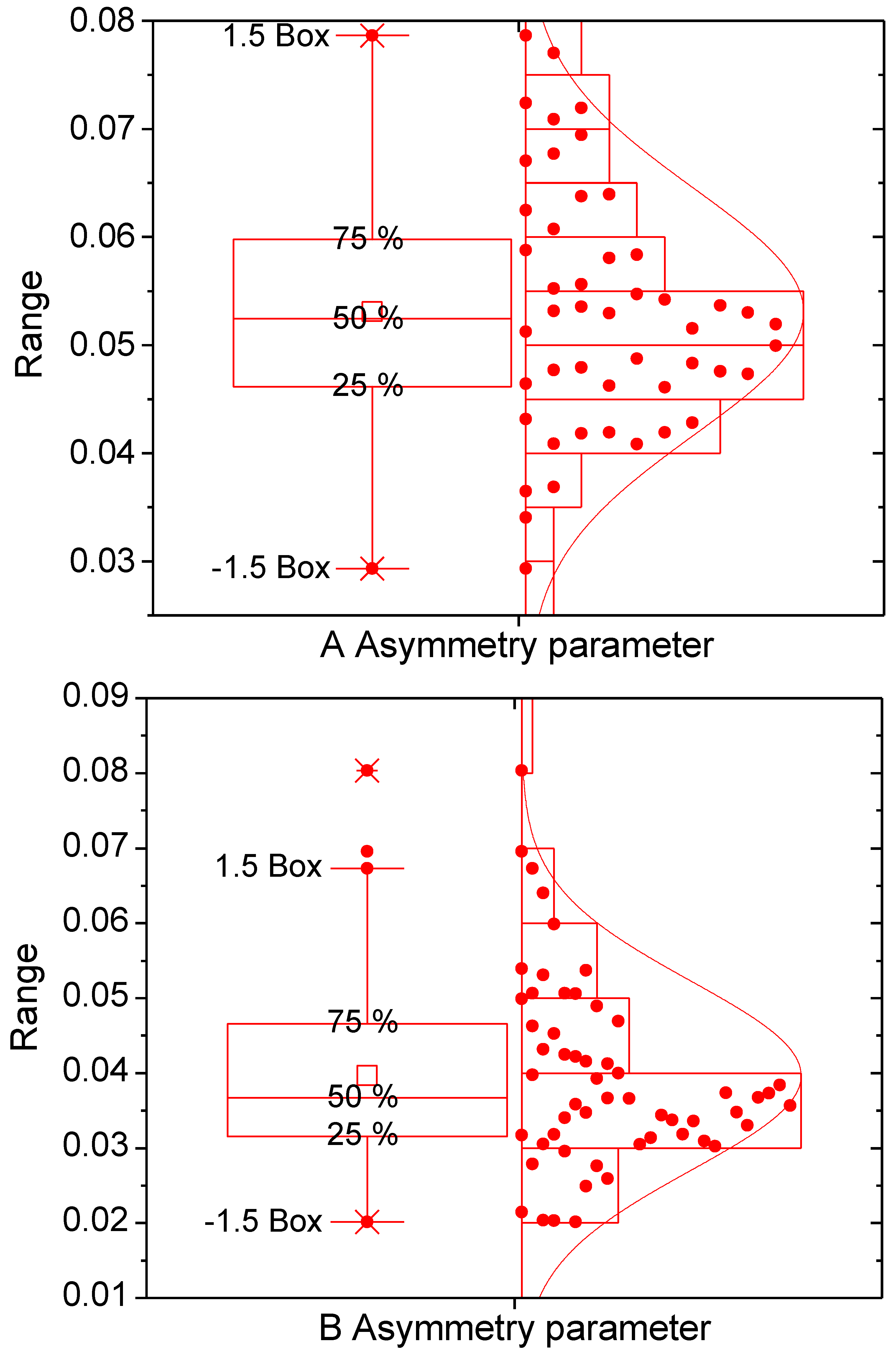
Once the whole ensemble was processed, the spread of the radiometric outputs was calculated, and the estimates for the two cases were cross-compared. The quantities of interest were total extinction, absorption, scattering efficiency, and asymmetry factor.
4. Results and Discussion
The randomness tests for the location of the drops were satisfied: the histogram of the uniformity test was flat, and the statistics for the independence test also proved that the drops were randomly located in space.
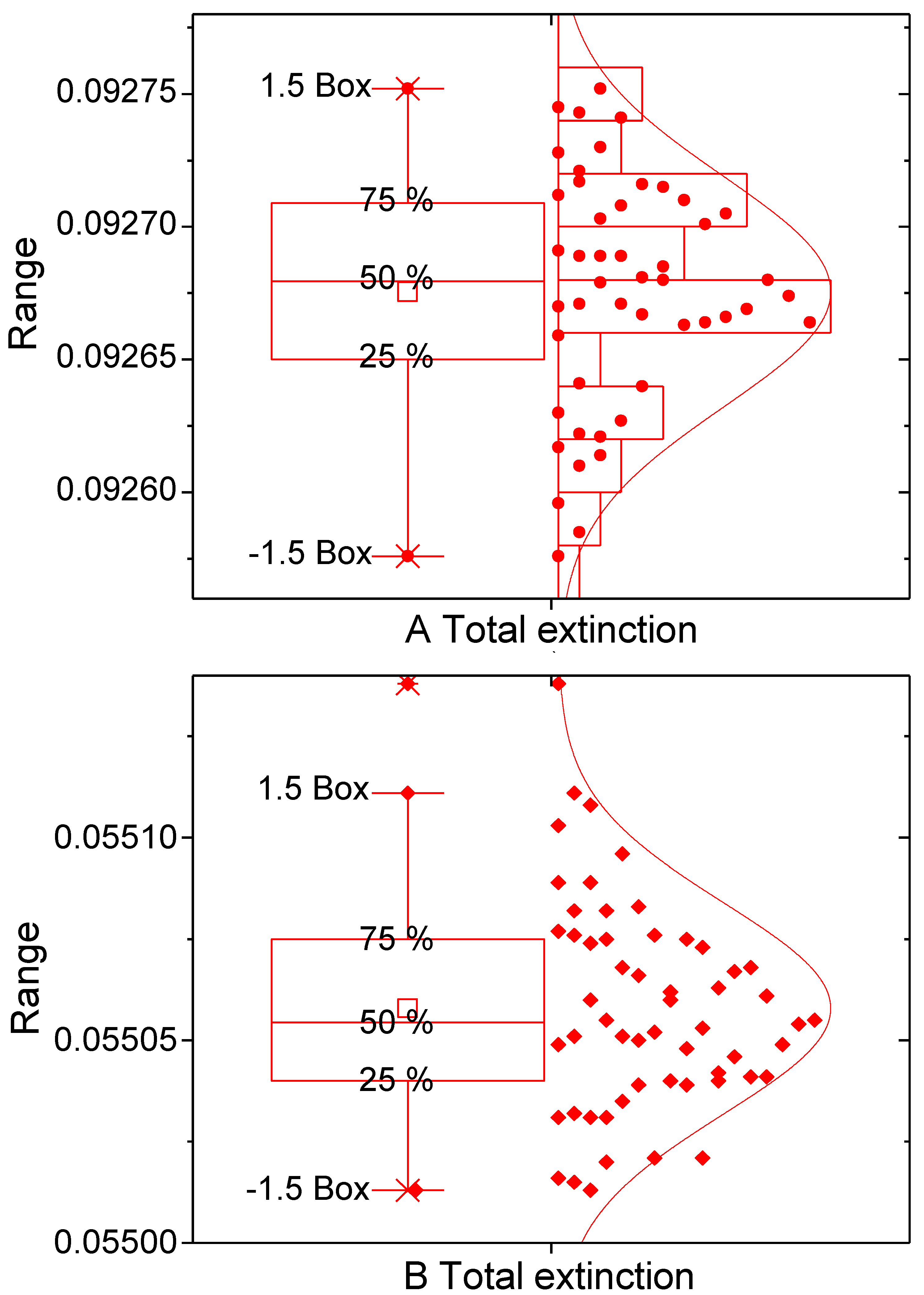
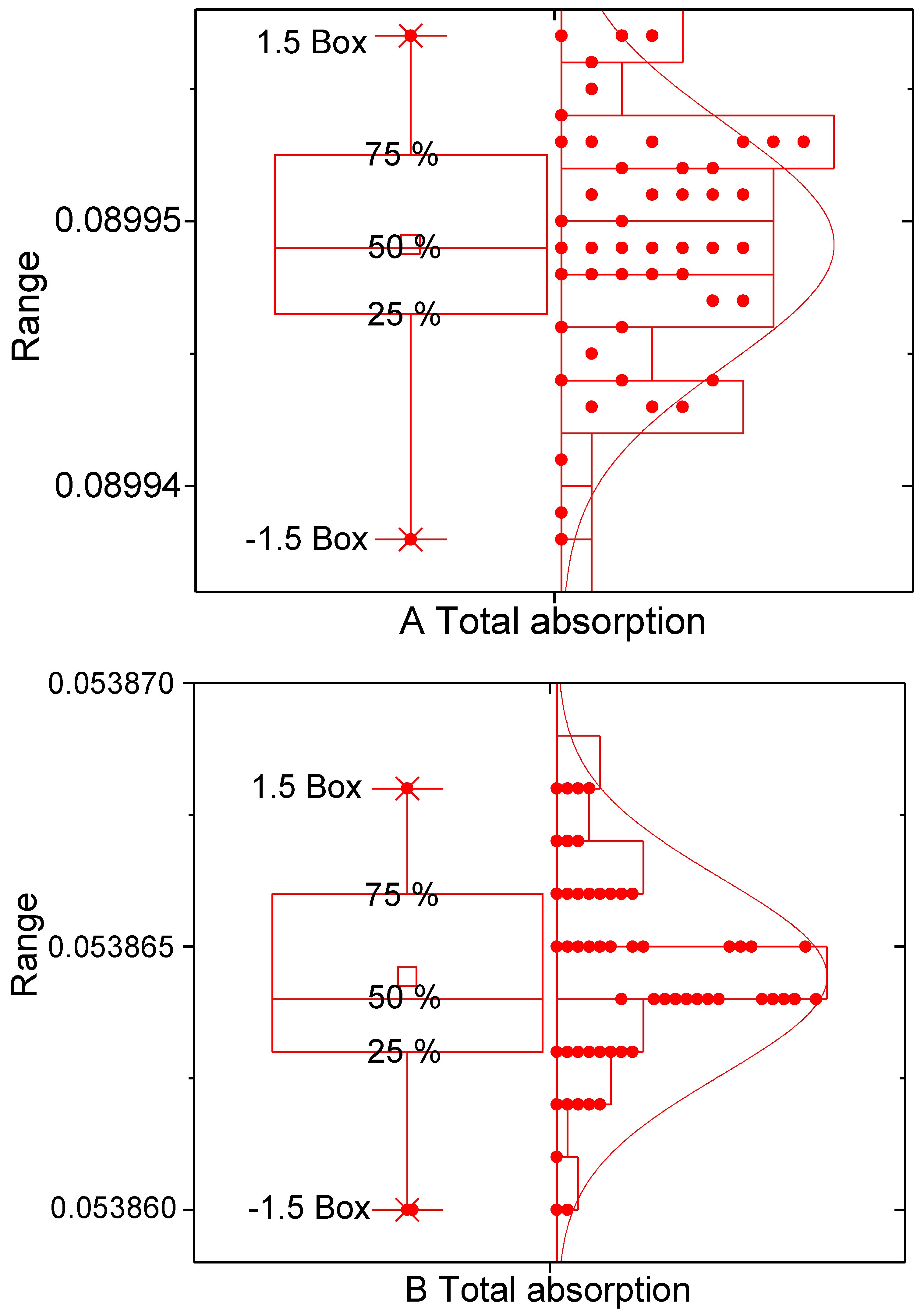
Figure 4,
Figure 5,
Figure 6 and
Figure 7 gathers the results of calculations of basic radiometric quantities of interest calculated for the two cases in
Figure 2. It is clear that the results are consistent and that the actual 3D distribution has an impact, as demonstrated by the existence of a distribution. In spite of the limited number of members in the ensembles, there is a clear shape around a central, more likely value. If there were no effect of different 3D arrangements in the scattering, no spread would appear. A purely random effect (“noise”) would generate a random distribution.
Most of the resulting distributions are normal and the skew is low. The tails are relatively large, however, revealing that some configurations produce quite different values. This seems to not be a problem for the retrieval of precipitation from radiometer or radar algorithms, however, as the central tendency is strong. The extent of the variability is low except for the asymmetry factor.
Such variations are consistent with changes in the relative phases among the particles, even under the single scattering hypothesis. In order to ascertain the effect of multiple scattering, different frequencies would need to explored (multiple scattering should increase with frequency). The results, however, show that there is a measurable effect due to the random arrangement of the scatters.
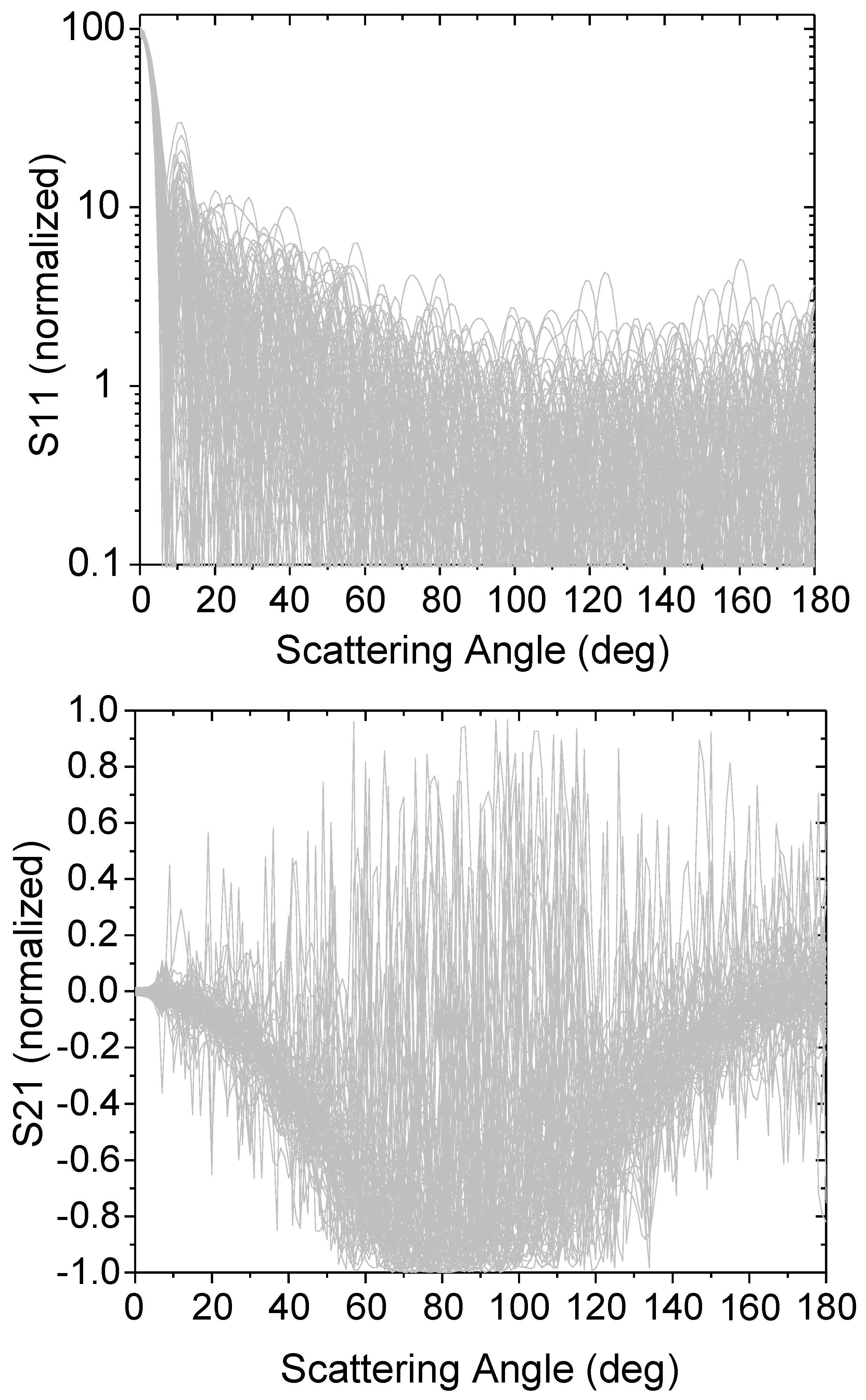
Figure 8 shows the effect of the scattering angle in the retrievals. Here, the
S11 and
S12 phase functions are depicted for one of the ensembles. Departures from the mean value appear, albeit the overall behavior is strong and consistent with theory.
Comparison between the two RDSD cases shows that there is a larger variability over time than within each case. The fact that the RDSDs are consecutive (10 min apart) allows examination of how different the scattered radiation is between the two distributions.
Figure 4,
Figure 5,
Figure 6 and
Figure 7 also show that there is a large difference in spite of the similarities between the two distributions (cf.
Figure 2).
Two ensembles, 10 min apart, for 50 different stochastically-derived 3D configurations from two measured RDSDs, with 30 and 31 drops, respectively, were used (
Figure 2). The RDSD are consecutive, and hence, aimed to derive conclusions on microphysical processes [
41]. The number of drops is small on purpose to alleviate the computational burden of the quite intensive calculations required. While the scattering matrix needs to be calculated just once for all of the beam orientations (as the matrix is defined by the properties and distribution of the particles), the many possible distributions require re-calculating a matrix for each configuration.
5. Conclusions and Further Work
Multiple scattering in the microwave frequencies has to be accounted for in precipitation retrieval algorithms [
42], but the effects of random arrangements of particles in space has seldom been investigated. Here, such effects have been described using modelled microwave scattering properties using the T-matrix formalism on the simplified case of spherical, non-intersecting raindrops.
The results of measured RDSDs reveal that the random distribution of particles in space have a measurable but small effect on the scattering because of changes in the relative phases among the particles. The effect is only apparent in the asymmetry factor.
Scattering calculations at the microwave frequencies using spherical raindrops are a simplification over the real situations where both ice and mixed-phase exist. The assumption in this research is that a small number of non-interacting spherical water drops are the most favorable possible case in the real atmosphere and thus a good baseline value for the extent of variability induced by random 3D configurations and other shapes and phases of water. By simplifying the water phase, geometry and number of drops, information about the randomness of the scattering quantities has been found, and a first estimate of the expected variability provided. The addition of further realism to the simulations in the form of oblate spheroids [
43], melting ice, mixed phase, or other more realistic setups can only increase the differences.
Further research will be devoted to expand the number of cases in order to derive systematic conclusions of the extent of the variability and its effects on the retrievals of precipitation. Indeed, in order to investigate the effects of multiple scattering in precipitation retrievals from radars, the Field of Vision (FOV) would need to be commensurate with the domain of observation of the sensor, and the effects of different frequencies and beamwidths would also need to be investigated. The present paper is only concerned with the first-order variability due to the many possible configurations of a given RDSD.
Author Contributions
F.J.T. lead the research and drafted the manuscript. R.M., E.A., D.C., A.J. and A.N. contributed to analysis, plotting, and literature research.
Acknowledgments
Funding from projects CGL2013-48367-P and CGL2016-80609-R (Ministerio de Economía y Competitividad, Ciencia e Innovación) is gratefully acknowledged. We are indebted to M. Mishchenko of NASA Goddard Institute for Space Studies in New York, NY, USA, for making his T-matrix code publicly available. Thanks are due to the referees for crucial input into the interpretation of the results, especially in that referring to multiple scattering, and to Nabhonil Kar (Princeton University) for editing the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| FOV | Field of Vision |
| PRNG | Pseudo-random Number Generator |
| RDSD | Rain Drop Size Distribution |
| UCLM | University of Castilla-La Mancha |
References
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Bayissa, Y.; Tadesse, T.; Demisse, G.; Shiferaw, A. Evaluation of satellite-based rainfall estimates and application to monitor meteorological drought for the Upper Blue Nile Basin, Ethiopia. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, J.; Sun, K.; Yin, J.; Chen, X. Estimation of soil moisture index using multi-temporal Sentinel-1 images over Poyang Lake ungauged zone. Remote Sens. 2018, 10, 12. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Sheffield, J.; Pan, M.; Wood, E.F. Evaluation of the Tropical Rainfall Measuring Mission Multi-Satellite Precipitation Analysis (TMPA) for assessment of large-scale meteorological drought. Remote Sens. Environ. 2015, 159, 181–193. [Google Scholar] [CrossRef]
- Ban, H.-J.; Kwon, Y.-J.; Shin, H.; Ryu, H.-S.; Hong, S. Flood Monitoring Using Satellite-Based RGB Composite Imagery and Refractive Index Retrieval in Visible and Near-Infrared Bands. Remote Sens. 2017, 9, 313. [Google Scholar] [CrossRef]
- Alahacoon, N.; Matheswaran, K.; Pani, P.; Amarnath, G. A decadal historical satellite data and rainfall trend analysis (2001-2016) for flood hazard mapping in Sri Lanka. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Yoshimot, S.; Amarnath, G. Applications of satellite-based rainfall estimates in flood inundation modeling-A case study in Mundeni Aru River Basin, Sri Lanka. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Marra, A.C.; Porcù, F.; Baldini, L.; Petracca, M.; Casella, D.; Dietrich, S.; Mugnai, A.; Sanò, P.; Vulpiani, G.; Panegrossi, G. Observational analysis of an exceptionally intense hailstorm over the Mediterranean area: Role of the GPM Core Observatory. Atmos. Res. 2017, 192, 72–90. [Google Scholar] [CrossRef]
- Cecil, D.J. Passive microwave brightness temperatures as proxies for hailstorms. J. Appl. Meteorol. Climatol. 2009, 48, 1281–1286. [Google Scholar] [CrossRef]
- Gabella, M.; Speirs, P.; Hamann, U.; Germann, U.; Berne, A. Measurement of precipitation in the alps using dual-polarization C-Band ground-based radars, the GPM Spaceborne Ku-Band Radar, and rain gauges. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Wah Win, K.W.; Ren, L.; Zhao, C.; Zhu, Y.; Jiang, S.; Liu, Y. Assessment of GPM and TRMM multi-satellite precipitation products in streamflow simulations in a data sparse mountainous watershed in Myanmar. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, B.; Yang, S.; Huang, Y.; Dong, G.; Bai, J.; Wang, Z. Systematical estimation of GPM-based global satellite mapping of precipitation products over China. Atmos. Res. 2018, 201, 206–217. [Google Scholar] [CrossRef]
- Arvor, D.; Funatsu, B.M.; Michot, V.; Dubreui, V. Monitoring rainfall patterns in the southern amazon with PERSIANN-CDR data: Long-term characteristics and trends. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Kimani, M.W.; Hoedjes, J.C.B.; Su, Z. An assessment of satellite-derived rainfall products relative to ground observations over East Africa. Remote Sens. 2017, 9. [Google Scholar] [CrossRef]
- Nogueira, S.M.C.; Moreira, M.A.; Volpato, M.M.L. Evaluating precipitation estimates from Eta, TRMM and CHRIPS data in the south-southeast region of Minas Gerais state-Brazil. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- Battaglia, A.; Ajewole, M.O.; Simmer, C. Multiple scattering effects due to hydrometeors on precipitation radar systems. Geophys. Res. Lett. 2005, 32, 1–5. [Google Scholar] [CrossRef]
- Battaglia, A.; Mroz, K.; Tanelli, S.; Tridon, F.; Kirstetter, P.-E. Multiple-scattering-induced “ghost echoes” in GPM DPR observations of a tornadic supercell. J. Appl. Meteorol. Climatol. 2016, 55, 1653–1666. [Google Scholar] [CrossRef]
- Battaglia, A.; Ajewole, M.O.; Simmer, C. Evaluation of radar multiple-scattering effects from a GPM perspective, Part II: Model results. J. Appl. Meteorol. Climatol. 2006, 45, 1648–1664. [Google Scholar] [CrossRef]
- Battaglia, A.; Ajewole, M.O.; Simmer, C. Evaluation of radar multiple scattering effects in Cloudsat configuration. Atmos. Chem. Phys. 2007, 7, 1719–1730. [Google Scholar] [CrossRef] [Green Version]
- Battaglia, A.; Tanelli, S.; Mroz, K.; Tridon, F. Multiple scattering in observations of the GPM dual-frequency precipitation radar: Evidence and impact on retrievals. J. Geophys. Res. 2015, 120, 4090–4101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ishimaru, A.; Cheung, R.L.-T. Multiple scattering effects on wave propagation due to rain. Ann. Des Télécommunications 1980, 35, 373–379. [Google Scholar] [CrossRef]
- Battaglia, A.; Ajewole, M.O.; Simmer, C. Evaluation of radar multiple-scattering effects from a GPM perspective. Part I: Model description and validation. J. Appl. Meteorol. Climatol. 2006, 45, 1634–1647. [Google Scholar] [CrossRef]
- Battaglia, A.; Tanelli, S.; Heymsfield, G.M.; Tian, L. The dual wavelength ratio Knee: A signature of multiple scattering in airborne Ku-Ka observations. J. Appl. Meteorol. Climatol. 2014, 53, 1790–1808. [Google Scholar] [CrossRef]
- Amrullah, F.F.; Setijadi, E.; Hendrantoro, G. Computation of rain attenuation in tropical region with multiple scattering and multiple absorption effects using exponential drop size distribution. In Proceedings of the 2011 XXXth URSI General Assembly and Scientific Symposium, Istanbul, Turkey, 13–20 August 2011. [Google Scholar]
- Ito, S.; Oguchi, T.; Iguchi, T.; Meneghini, R. Depolarization of Radar Signals due to Multiple Scattering in Rain. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1057–1062. [Google Scholar] [CrossRef]
- Korotkov, V.A.; Sukhonin, E.V. The radiometric millimeter wave sensing of atmospheric precipitation for measuring attenuation and precipitation parameters with account of the multiple scattering. Radiotekhnika i Elektron. 1998, 43, 266–270. [Google Scholar]
- Bebbington, D.H.O.; Chandra, M.; Watson, R.J. Multiple scattering effects in C-band polarimetric radar observations of intense precipitation. In Proceedings of the 29th International Conference on Radar Meteorology, Montreal, QC, Canada, 12–16 July 1999; pp. 908–909. [Google Scholar]
- Oguchi, T.; Ishida, N. Effect of Multiple Scattering on the Estimation of Rainfall Rates Using Dual-Wavelength Radar Techniques. IEEE Trans. Geosci. Remote Sens. 1994, 32, 943–946. [Google Scholar] [CrossRef]
- Waterman, P.C. Symmetry, unitarity, and geometry in electromagnetic scattering. Phys. Rev. D 1971, 3, 825–839. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Liu, L.; Mackowski, D.W. T-matrix modeling of linear depolarization by morphologically complex soot and soot-containing aerosols. J. Quant. Spectrosc. Radiat. Transf. 2013, 123, 135–144. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D. Capabilities and limitations of a current FORTRAN implementation of the T-matrix method for randomly oriented, rotationally symmetric scatterers. J. Quant. Spectrosc. Radiat. Transf. 1998, 60, 309–324. [Google Scholar] [CrossRef]
- Mackowski, D.W.; Mishchenko, M.I. A multiple sphere T-matrix Fortran code for use on parallel computer clusters. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2182–2192. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Mackowski, D.W. T-matrix computations of light scattering by nonspherical particles: A review. J. Quant. Spectrosc. Radiat. Transf. 1996, 55, 535–575. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Mackowski, D.W. T-matrix method and its applications to electromagnetic scattering by particles: A current perspective. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1700–1703. [Google Scholar] [CrossRef] [Green Version]
- Mishchenko, M.I.; Martin, P.A. Peter Waterman and T-matrix methods. J. Quant. Spectrosc. Radiat. Transf. 2013, 123, 2–7. [Google Scholar] [CrossRef]
- Bi, L.; Yang, P.; Kattawar, G.W.; Mishchenko, M.I. Efficient implementation of the invariant imbedding T-matrix method and the separation of variables method applied to large nonspherical inhomogeneous particles. J. Quant. Spectrosc. Radiat. Transf. 2013, 116, 169–183. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Checa, R.; De Castro, M. An experiment to measure the spatial variability of rain drop size distribution using sixteen laser disdrometers. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef] [Green Version]
- Tapiador, F.J.; Navarro, A.; Moreno, R.; Jiménez-Alcázar, A.; Marcos, C.; Tokay, A.; Durán, L.; Bodoque, J.M.; Martín, R.; Petersen, W.; et al. On the optimal measuring area for pointwise rainfall estimation: A dedicated experiment with 14 laser disdrometers. J. Hydrometeorol. 2017, 18, 753–760. [Google Scholar] [CrossRef]
- Van de Hulst, H.C. Light Scattering by Small Particles; Dover Publications: Mineola, NY, USA, 1981. [Google Scholar]
- Bohren, C.F. Absorption and Scattering of Light by Small Particles; John Wiley & Sons: Hoboken, NJ, USA, 1983. [Google Scholar]
- Tapiador, F.J.; Haddad, Z.S.; Turk, J. A probabilistic view on raindrop size distribution modeling: A physical interpretation of rain microphysics. J. Hydrometeorol. 2014, 15, 427–443. [Google Scholar] [CrossRef]
- Marzano, F.S.; Ferrauto, G.; Roberti, L.; Di Michele, S.; Mugnai, A.; Tassa, A. Numerical Simulation of Multiple Scattering Effects due to Convective Clouds on Satellite Radar Reflectivity at 14 and 35 GHz. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volume 2, pp. 881–883. [Google Scholar]
- Seow, Y.-L.; Li, L.-W.; Leong, M.-S.; Kooi, P.-S.; Yeo, T.-S. An efficient TCS formula for rainfall microwave attenuation: T-matrix approach and 3-D fitting for oblate spheroidal raindrops. IEEE Trans. Antennas Propag. 1998, 46, 1176–1181. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).