Assessment of Satellite and Radar Quantitative Precipitation Estimates for Real Time Monitoring of Meteorological Extremes Over the Southeast of the Iberian Peninsula
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Rainfall Events
2.3. Satellite-Based Quantitative Precipitation Estimates : PERSIANN-CCS
2.4. Ground-Based Quantitative Precipitation Estimates : Meteorological Radar
2.5. Rain Gauges
2.6. Assesssment of Quantitative Precipitation Estimates
3. Results
3.1. Statistics
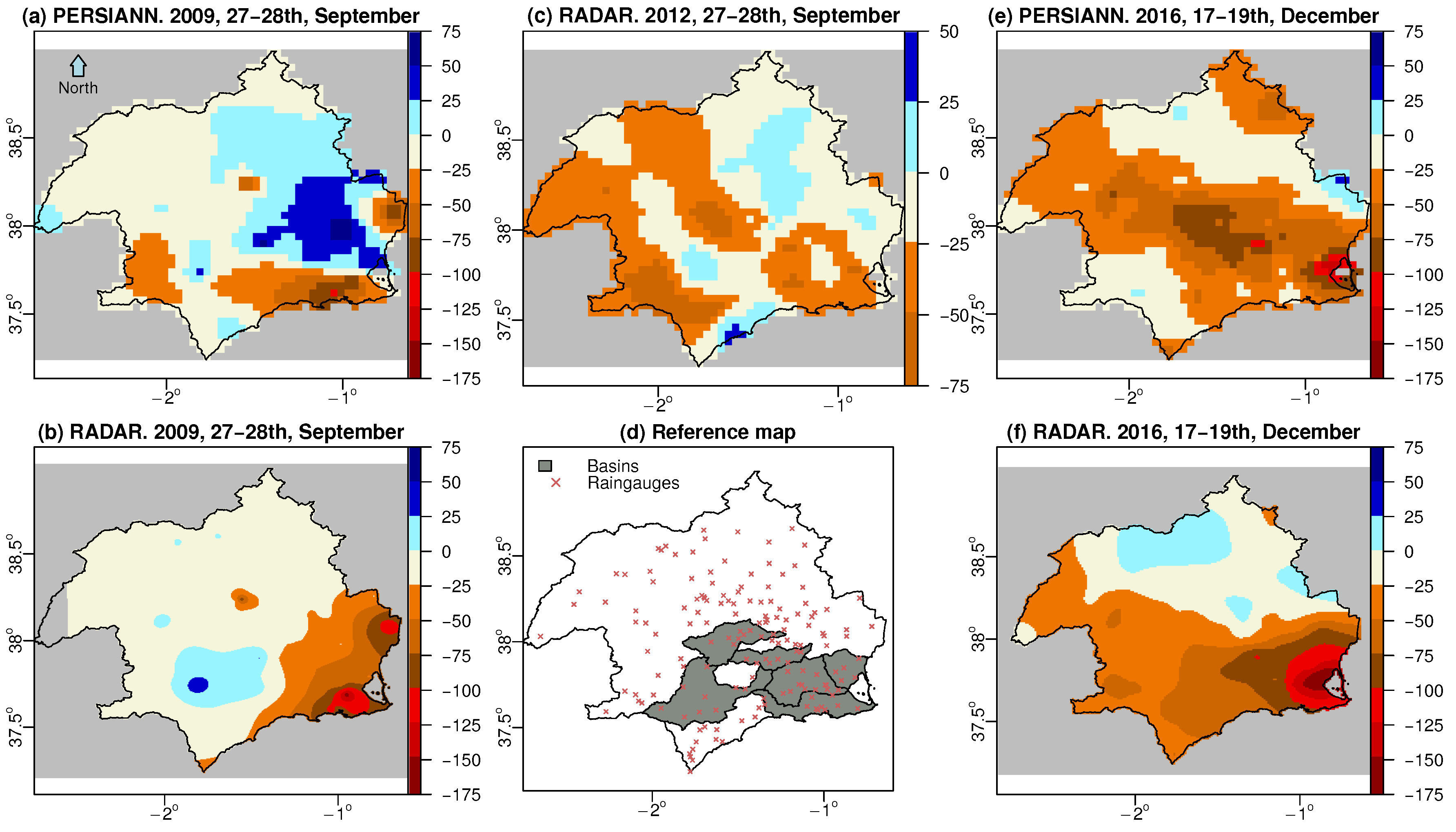
3.2. Hourly Monitoring of Differences
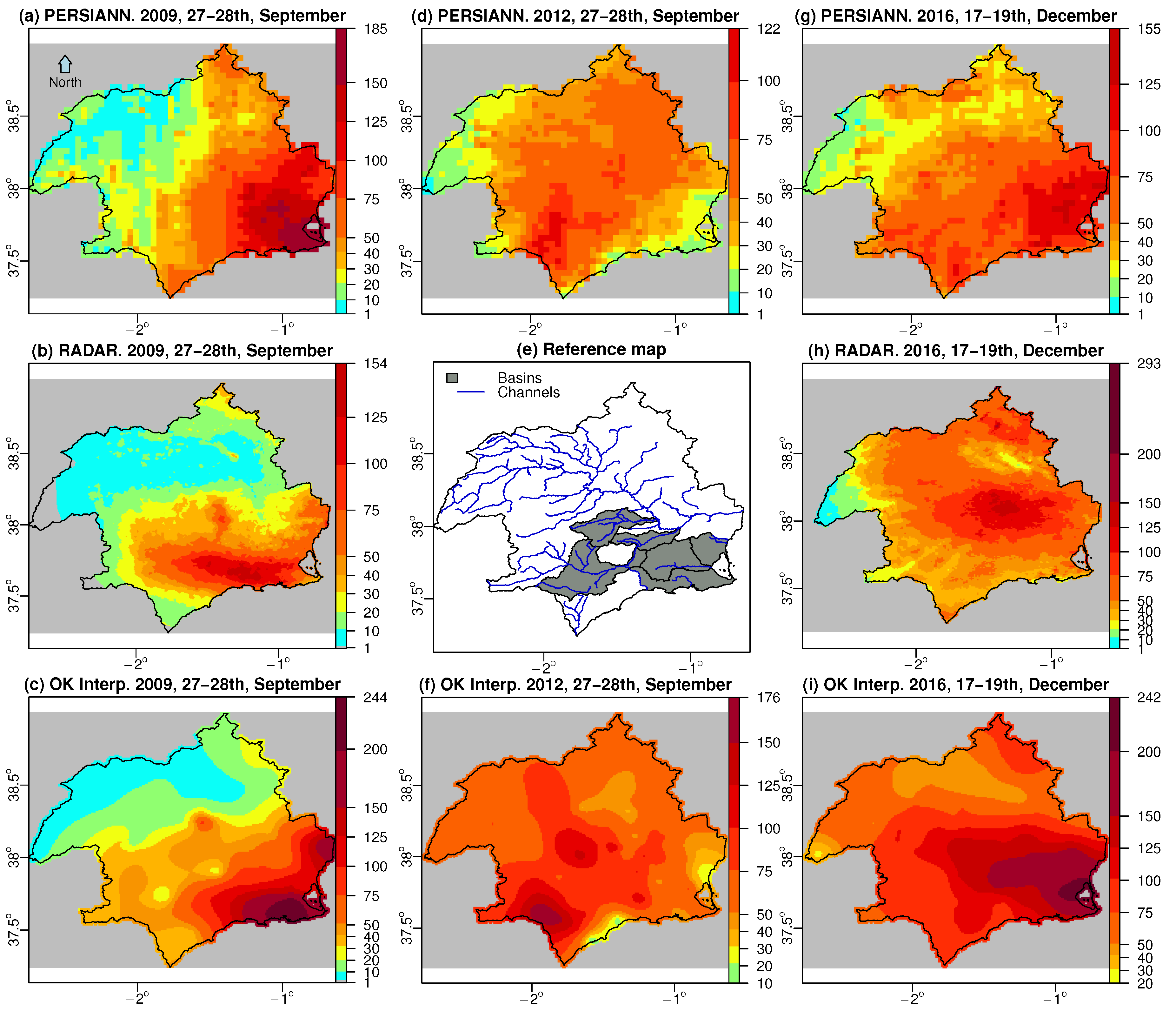
3.3. Side-By-Side Comparison of Accumulated Precipitation
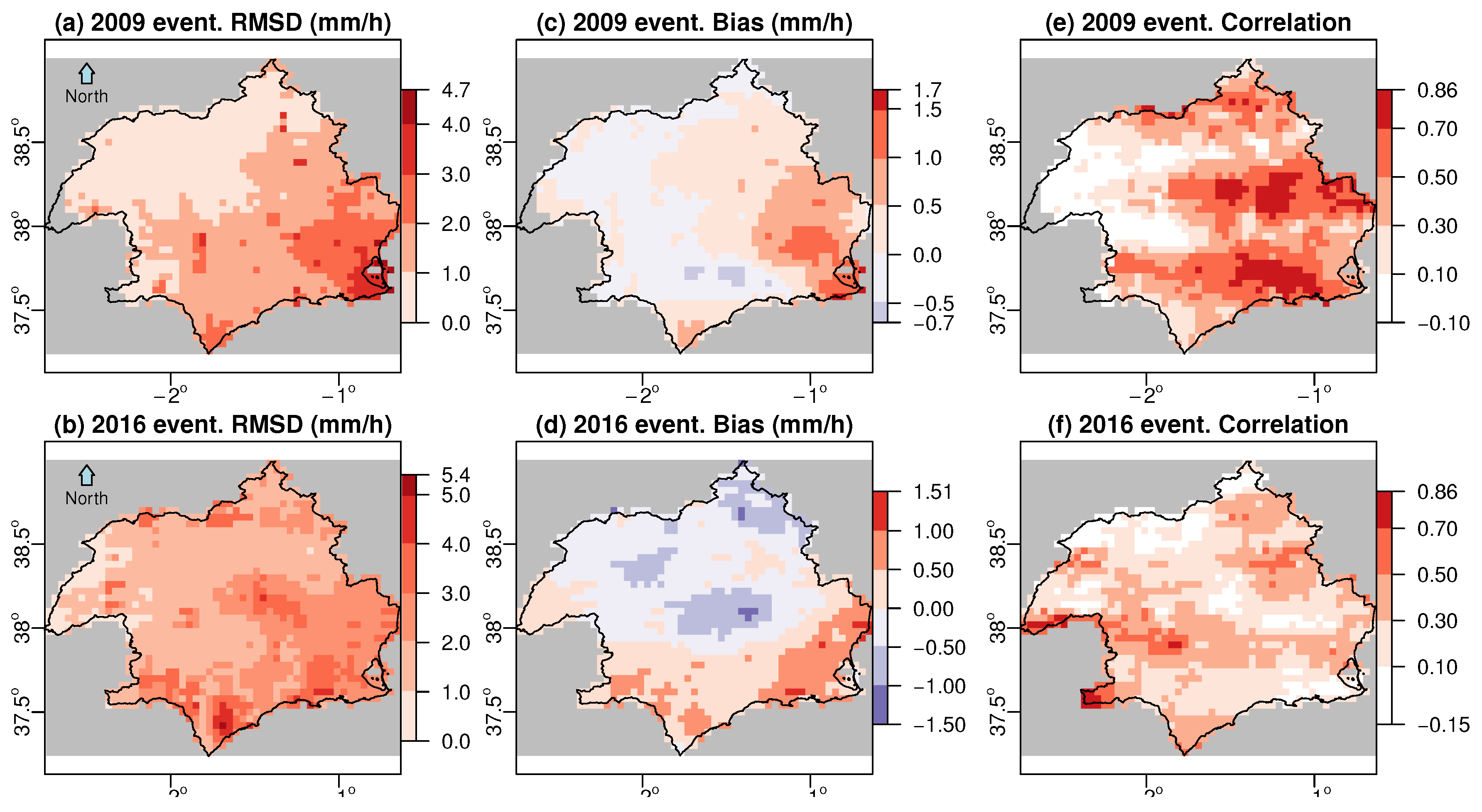
3.4. Spatial Statistics
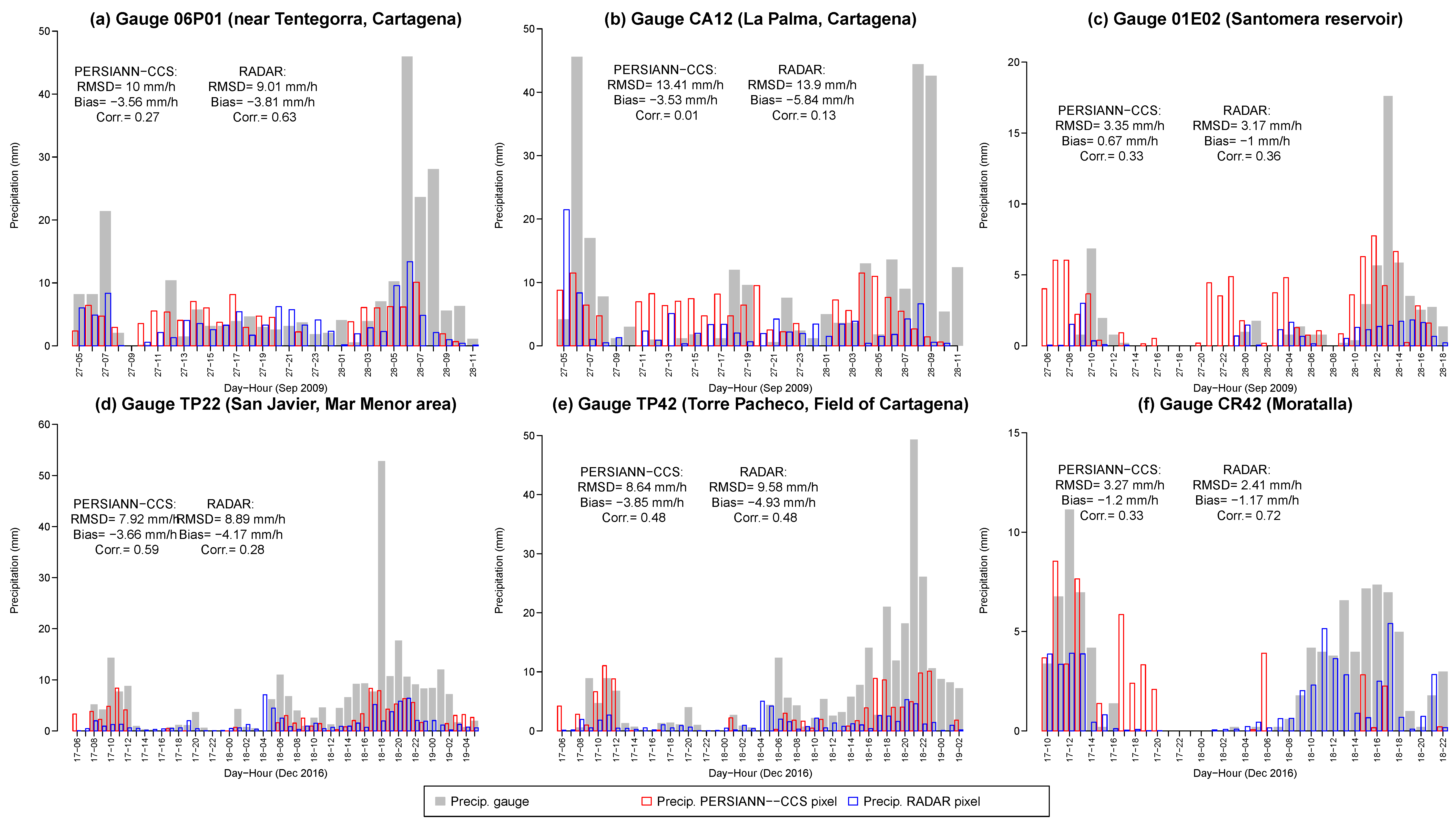
3.5. Hyetograpths
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hong, Y.; Hsu, K.L.; Sorooshian, S.; Gao, X. Precipitation Estimation from Remotely Sensed Imagery Using an Artificial Neural Network Cloud Classification System. J. Appl. Meteorol. 2004, 43, 1834–1852. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Sorooshian, S.; Hsu, K.L. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Sorooshian, S.; Nguyen, P.; Sellars, S.; Braithwaite, D.; AghaKouchak, A.; Hsu, K. Satellite-based remote sensing estimation of precipitation for early warning systems. In Extreme Natural Hazards, Disaster Risks and Societal Implications; Cambridge University Press: Cambridge, UK, 2014; pp. 99–112. [Google Scholar]
- Bendix, J.; Fries, A.; Zárate, J.; Trachte, K.; Rollenbeck, R.; Pucha-Cofrep, F.; Paladines, R.; Palacios, I.; Orellana, J.; Oñate Valdivieso, F.; et al. RadarNet-Sur First Weather Radar Network in Tropical High Mountains. Bull. Am. Meteorol. Soc. 2017, 98, 1235–1254. [Google Scholar] [CrossRef]
- Nikolopoulos, E.I.; Anagnostou, E.N.; Borga, M. Using High-Resolution Satellite Rainfall Products to Simulate a Major Flash Flood Event in Northern Italy. J. Hydrometeorol. 2013, 14, 171–185. [Google Scholar] [CrossRef]
- Miao, C.; Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Duan, Q. Evaluation of the PERSIANN-CDR Daily Rainfall Estimates in Capturing the Behavior of Extreme Precipitation Events over China. J. Hydrometeorol. 2015, 16, 1387–1396. [Google Scholar] [CrossRef]
- Schiemann, R.; Erdin, R.; Willi, M.; Frei, C.; Berenguer, M.; Sempere-Torres, D. Geostatistical radar- raingauge combination with nonparametric correlograms: methodological considerations and application in Switzerland. Hydrol. Earth Syst. Sci. 2011, 15, 1515–1536. [Google Scholar] [CrossRef]
- Ballari, D.; Castro, E.; Campozano, L. Validation of Satellite Precipitation (TRMM 3B43) in Ecuadorian Coastal Plains, Andean Higlands and Amazonian Rainforest. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; Copernicus GmbH: Prague, Czech Republic, 2016; Volume XLI-B8, pp. 305–311. [Google Scholar]
- Zambrano-Bigiarini, M.; Nauditt, A.; Birkel, C.; Verbist, K.; Ribbe, L. Temporal and spatial evaluation of satellite-based rainfall estimates across the complex topographical and climatic gradients of Chile. Hydrol. Earth Syst. Sci. 2017, 21, 1295–1320. [Google Scholar] [CrossRef]
- Barredo, J.I. Major flood disasters in Europe: 1950–2005. Nat. Hazards 2007, 42, 125–148. [Google Scholar] [CrossRef]
- López-Martínez, F.; Gil-Guirado, S.; Pérez-Morales, A. Who can you trust? Implications of institutional vulnerability in flood exposure along the Spanish Mediterranean coast. Environ. Sci. Policy 2017, 76, 29–39. [Google Scholar] [CrossRef]
- Serrano-Notivoli, R.; Martín-Vide, J.; Saz, M.A.; Longares, L.A.; Beguería, S.; Sarricolea, P.; Meseguer-Ruiz, O.; de Luis, M. Spatio-temporal variability of daily precipitation concentration in Spain based on a high- resolution gridded data set. Int. J. Climatol. 2017, 38, e518–e530. [Google Scholar] [CrossRef]
- López-Bermúdez, F.; Conesa-García, C.; Alonso-Sarría, F. Floods: Magnitude and Frequency in Ephemeral Streams of the Spanish Mediterranean Region. In Dryland Rivers: Hydrology and Geomorphology of Semi-Arid Channels; John Wiley & Sons: Hoboken, NJ, USA, 2002; pp. 329–350. [Google Scholar]
- AghaKouchak, A.; Behrangi, A.; Sorooshian, S.; Hsu, K.; Amitai, E. Evaluation of satellite-retrieved extreme precipitation rates across the central United States. J. Geophys. Res. 2015, 116. [Google Scholar] [CrossRef]
- Hong, Y.; Gochis, D.; Cheng, J.T.; Hsu, K.L.; Sorooshian, S. Evaluation of PERSIANN-CCS Rainfall Measurement Using the NAME Event Rain Gauge Network. J. Hydrometeorol. 2007, 8, 469–482. [Google Scholar] [CrossRef]
- Pellicer-Martínez, F.; Martínez-Paz, J.M. Probabilistic evaluation of the water footprint of a river basin: Accounting method and case study in the Segura River Basin, Spain. Sci. Total Environ. 2018, 627, 28–38. [Google Scholar] [CrossRef] [PubMed]
- Gomariz-Castillo, F.; Alonso-Sarría, F.; Cabezas-Calvo-Rubio, F. Calibration and spatial modelling of daily ET0 in semiarid areas using Hargreaves equation. In Earth Science Informatics; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Pellicer-Martínez, F.; Martínez-Paz, J.M. Grey water footprint assessment at the river basin level: Accounting method and case study in the Segura River Basin, Spain. Ecol. Indic. 2016, 60, 1173–1183. [Google Scholar] [CrossRef]
- Giordano, R.; Pagano, A.; Pluchinotta, I.; Olivo del Amo, R.; Hernandez, S.M.; Lafuente, E.S. Modelling the complexity of the network of interactions in flood emergency management: The Lorca flash flood case. Environ. Model. Softw. 2017, 95, 180–195. [Google Scholar] [CrossRef]
- García-Ayllón, S. GIS Assessment of Mass Tourism Anthropization in Sensitive Coastal Environments: Application to a Case Study in the Mar Menor Area. Sustainability 2018, 10, 1344. [Google Scholar] [CrossRef]
- Ministerio de Fomento. Dirección General de Carreteras. In Máximas Lluvias Diarias en la España Peninsular; Ministerio de Fomento: Madrid, Spain, 1999. [Google Scholar]
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Thorstensen, A.R. The PERSIANN Family of Global Satellite Precipitation Data: A Review and Evaluation of Products. Hydrol. Earth Syst. Sci. Discuss. 2018. in review. [Google Scholar] [CrossRef]
- Nguyen, P.; Sellars, S.; Thorstensen, A.; Tao, Y.; Ashouri, H.; Braithwaite, D.; Hsu, K.; Sorooshian, S. Satellites Track Precipitation of Super Typhoon Haiyan. Eos Trans. Am. Geophys. Union 2014, 95, 133–155. [Google Scholar] [CrossRef]
- Nguyen, P.; Thorstensen, A.; Sorooshian, S.; Hsu, K.; AghaKouchak, A. Flood Forecasting and Inundation Mapping Using HiResFlood-UCI and Near-Real-Time Satellite Precipitation Data: The 2008 Iowa Flood. J. Hydrometeorol. 2015, 16, 1171–1183. [Google Scholar] [CrossRef]
- Karbalaee, N.; Hsu, K.; Sorooshian, S.; Braithwaite, D. Bias adjustment of infrared-based rainfall estimation using Passive Microwave satellite rainfall data. J. Geophys. Res. Atmos. 2017, 122, 3859–3876. [Google Scholar] [CrossRef]
- Fukao, S.; Hamazu, K.; Doviak, R.J. Radar for Meteorological and Atmospheric Observations; Springer: Tokyo, Japan, 2014. [Google Scholar]
- Velasco-Forero, C.A.; Sempere-Torres, D.; Cassiraga, E.F.; Gómez-Hernández, J.J. A non-parametric automatic blending methodology to estimate rainfall fields from rain gauge and radar data. Adv. Water Resour. 2009, 32, 986–1002. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; Levizzani, V.; De Roo, A. Validation of Satellite-Based Precipitation Products over Sparsely Gauged African River Basins. J. Hydrometeorol. 2012, 13, 1760–1783. [Google Scholar] [CrossRef]
- Ulloa, J.; Ballari, D.; Campozano, L.; Samaniego, E. Two-Step Downscaling of Trmm 3b43 V7 Precipitation in Contrasting Climatic Regions With Sparse Monitoring: The Case of Ecuador in Tropical South America. Remote Sens. 2017, 9, 758. [Google Scholar] [CrossRef]
- Hill, D.J.; Baron, J. radar.IRIS: A free, open and transparent R library for processing Canada’s weather radar data. Can. Water Resour. J. 2015, 40, 409–422. [Google Scholar] [CrossRef]
- Zawadzki, I. On Radar-Raingage Comparision. J. Appl. Meteorol. 1975, 14, 1430–1436. [Google Scholar] [CrossRef]
- Freedman, D.; Pisani, R.; Purves, R. Statistics, 4 ed.; Viva Books: New Delhi, India, 2009. [Google Scholar]
- Germann, U.; Berenguer, M.; Sempere-Torres, D.; Zappa, M. REAL—Ensemble radar precipitation estimation for hydrology in a mountainous region. Q. J. R. Meteorol. Soc. 2009, 135, 445–456. [Google Scholar] [CrossRef]
- Speirs, P.; Gabella, M.; Berne, A. A Comparison between the GPM Dual-Frequency Precipitation Radar and Ground-Based Radar Precipitation Rate Estimates in the Swiss Alps and Plateau. J. Hydrometeorol. 2017, 18, 1247–1269. [Google Scholar] [CrossRef]
- Burcea, S.; Cheval, S.; Dumitrescu, A.; Antonescu, B.; Bell, A.; Breza, T. Comparision Between Radar Estimated and Rain Gauge Measured Precipitation in the Moldavian Plateau. Environ. Eng. Manag. J. 2012, 11, 723–731. [Google Scholar]
- Germann, U.; Galli, G.; Boscacci, M.; Bolliger, M. Radar precipitation measurement in a mountainous region. Q. J. R. Meteorol. Soc. 2006, 132, 1669–1692. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable geostatistics in S: the gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Hijmans, R.J. raster: Geographic Data Analysis and Modeling. 2016. Available online: https://cran.r-project.org/web/packages/raster/ (accessed on 10 May 2018).
- Yoon, S.-S.; Lee, B. Effects of Using High-Density Rain Gauge Networks and Weather Radar Data on Urban Hydrological Analyses. Water 2017, 9, 931. [Google Scholar] [CrossRef]
- Scheel, M.L.M.; Rohrer, M.; Huggel, C.; Santos Villar, D.; Silvestre, E.; Huffman, G.J. Evaluation of TRMM Multi-satellite Precipitation Analysis (TMPA) performance in the Central Andes region and its dependency on spatial and temporal resolution. Hydrol. Earth Syst. Sci. 2011, 15, 2649–2663. [Google Scholar] [CrossRef]
- Zhang, X.; Anagnostou, E.N.; Frediani, M. Using NWP Simulations in Satellite Rainfall Estimation of Heavy Precipitation Events over Mountainous Areas. J. Hydrometeorol. 2013, 14, 1844–1858. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Kirstetter, P.E.; Gourley, J.J.; Qi, Y.; Zhang, J.; Howard, K.; Hu, J.; Wang, J. Performance evaluation of radar and satellite rainfalls for Typhoon Morakot over Taiwan: Are remote-sensing products ready for gauge denial scenario of extreme events? J. Hydrol. 2013, 506, 4–13. [Google Scholar] [CrossRef]
- Xu, Y.; Knudby, A.; Ho, H.C. Estimating daily maximum air temperature from MODIS in British Columbia, Canada. Int. J. Remote Sens. 2014, 35, 8108–8121. [Google Scholar] [CrossRef]
- Jang, J.; Viau, A.; Anctil, F. Neural network estimation of air temperatures from AVHRR data. Int. J. Remote Sens. 2004, 25, 4541–4554. [Google Scholar] [CrossRef]

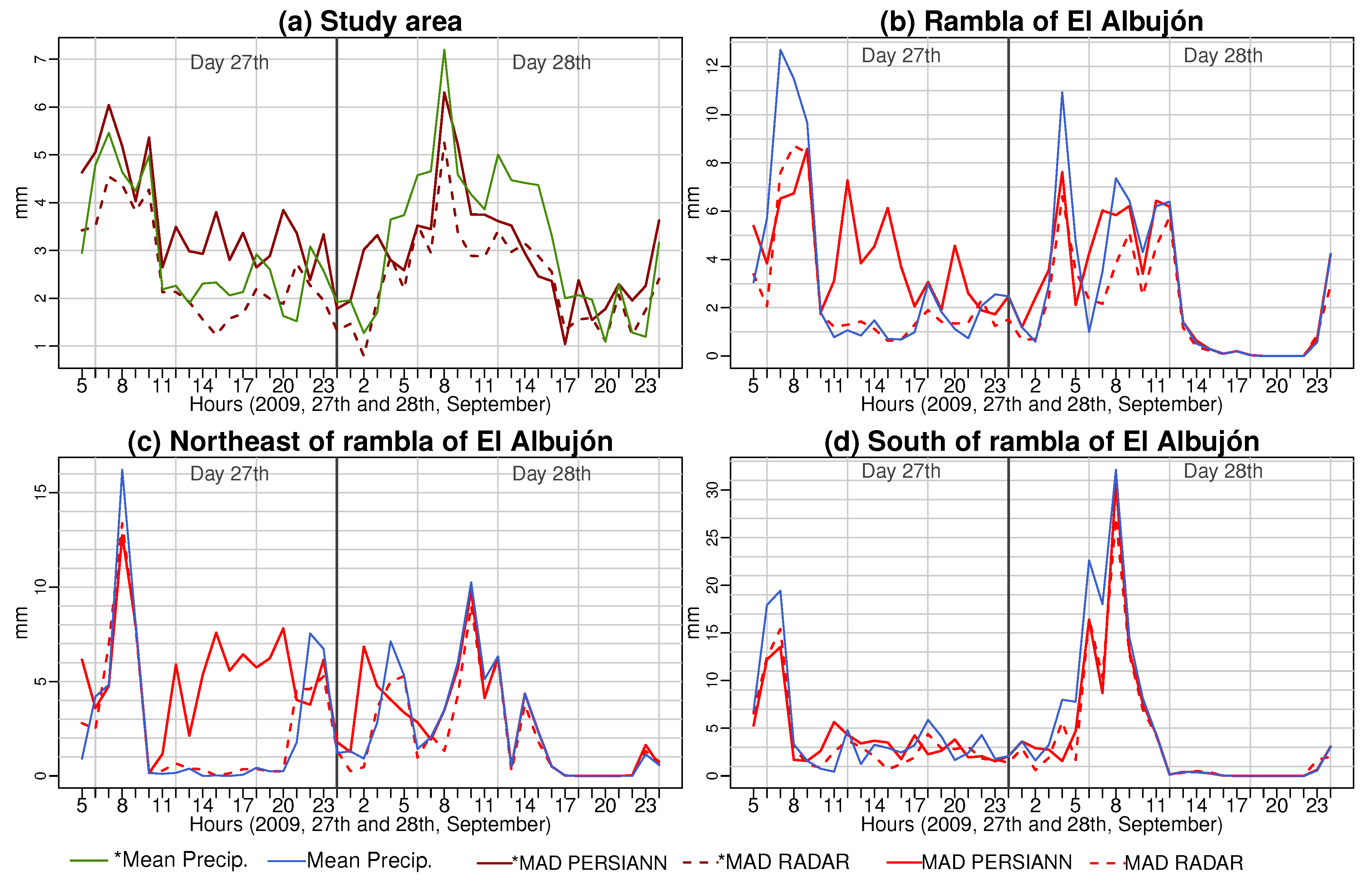
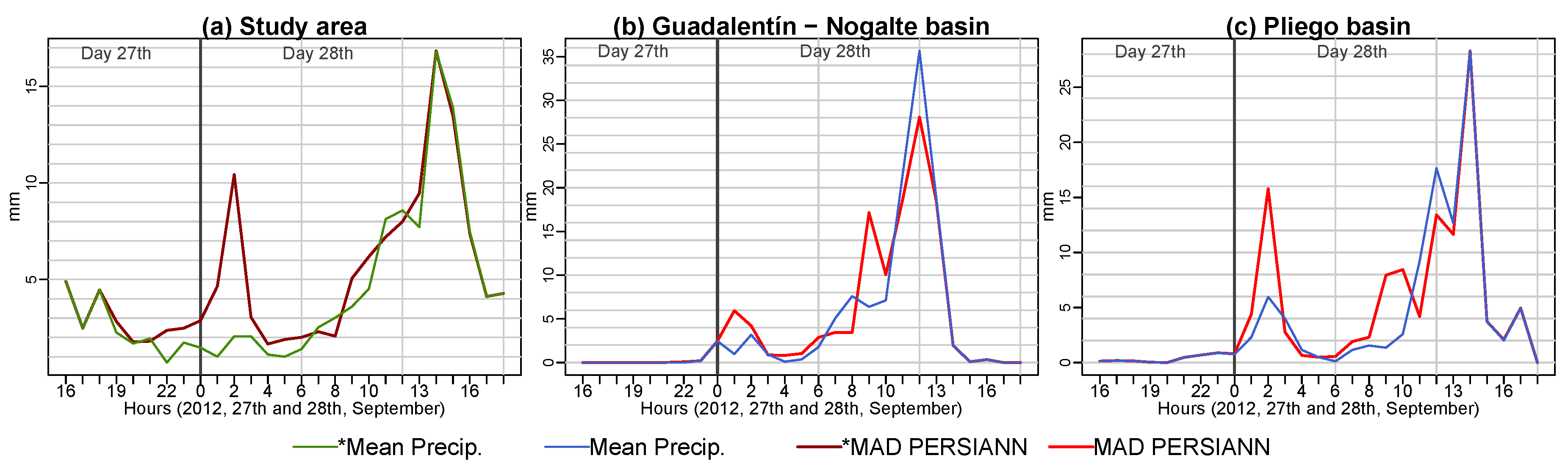
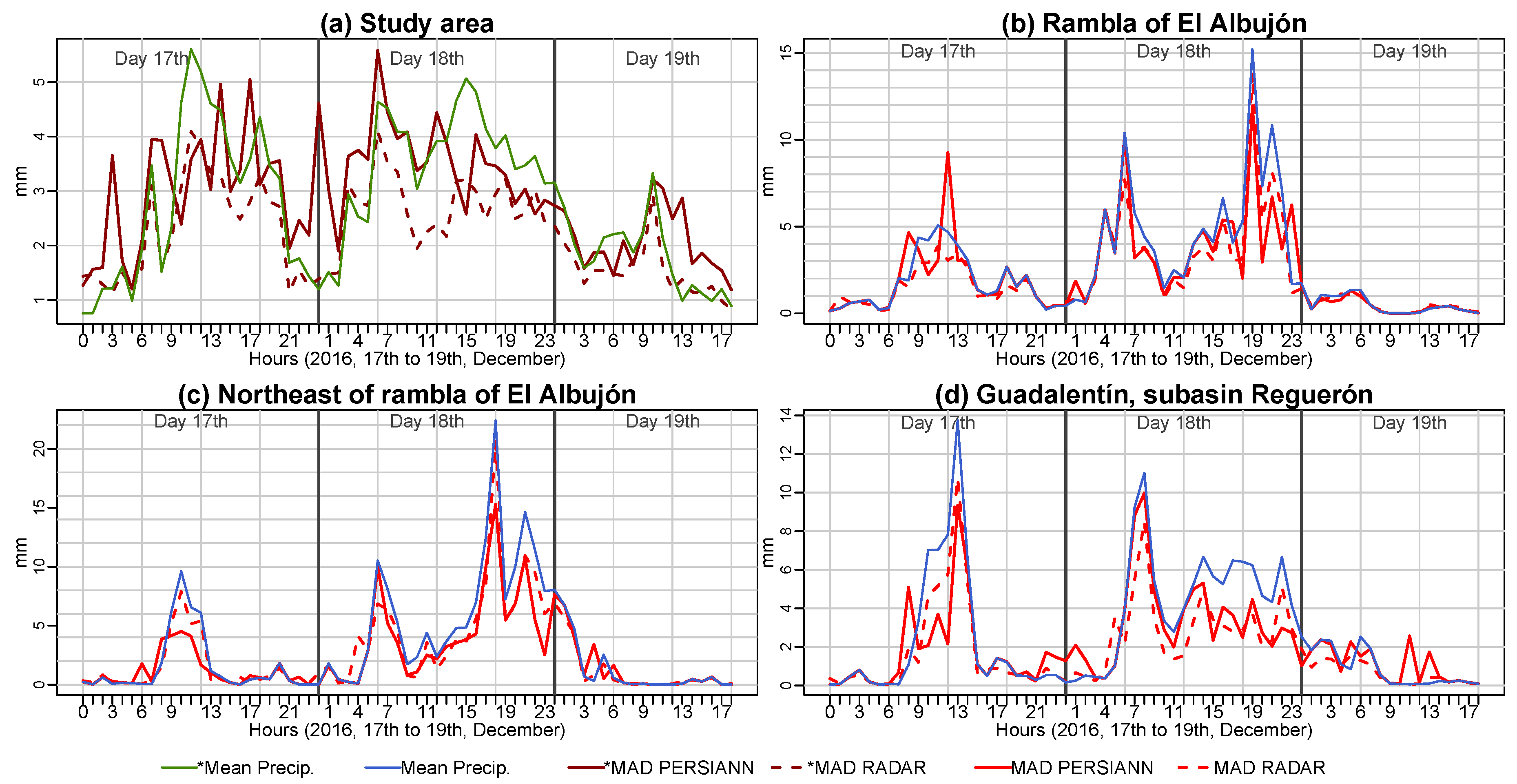

| (a) 27th and 28th September 2009 Event | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PERSIANN-CCS, Spatial Resolution ≈ | |||||||||||||||
| Name | No. pix | Obs. | *Obs. | * | * | RMSD | *RMSD | rRMSD | *rRMSD | Bias | *Bias | R | *R | ||
| S. Al | 5 | 220 | 158 | 2.9 | 4.0 | 5.0 | 6.9 | 8.2 | 9.6 | 1.6 | 1.4 | −2.1 | −2.9 | 0.34 | 0.18 |
| Al | 6 | 264 | 193 | 3.0 | 4.0 | 2.9 | 3.9 | 5.1 | 6.0 | 1.8 | 1.5 | 0.1 | 0.1 | 0.22 | 0.04 |
| NE. Al | 5 | 220 | 155 | 3.2 | 4.5 | 2.6 | 3.7 | 5.6 | 6.7 | 2.1 | 1.8 | 0.6 | 0.8 | 0.07 | −0.17 |
| Total | 106 | 4664 | 2060 | 1.4 | 3.0 | 1.4 | 2.9 | 3.5 | 5.2 | 2.6 | 1.8 | 0.0 | 0.1 | 0.31 | 0.08 |
| Radar, CAPPI Product in Short Range Mode, Spatial Resolution ≈ | |||||||||||||||
| Name | No. pix | Obs. | *Obs. | * | * | RMSD | *RMSD | rRMSD | *rRMSD | Bias | *Bias | R | *R | ||
| S. Al | 5 | 220 | 159 | 2.5 | 3.4 | 5.0 | 6.9 | 7.9 | 9.3 | 1.6 | 1.4 | −2.5 | −3.4 | 0.46 | 0.34 |
| Al | 6 | 264 | 168 | 1.8 | 2.8 | 2.9 | 4.5 | 4.2 | 5.2 | 1.4 | 1.2 | −1.1 | −1.7 | 0.49 | 0.31 |
| NE. Al | 5 | 220 | 110 | 1.2 | 2.3 | 2.6 | 5.1 | 4.6 | 6.5 | 1.8 | 1.3 | −1.4 | −2.9 | 0.29 | −0.06 |
| Total | 108 | 4752 | 1664 | 0.8 | 2.1 | 1.3 | 3.6 | 2.9 | 4.9 | 2.2 | 1.4 | −0.5 | −1.5 | 0.50 | 0.28 |
| (b) 27th and 28th Septemner 2012 Event | |||||||||||||||
| PERSIANN-CCS, Spatial Resolution ≈ | |||||||||||||||
| Name | No. pix | Obs. | *Obs. | * | * | RMSD | *RMSD | rRMSD | *rRMSD | Bias | *Bias | R | *R | ||
| G-No | 8 | 216 | 97 | 3.0 | 6.6 | 4.2 | 9.4 | 11.0 | 16.4 | 2.6 | 1.8 | −1.2 | −2.8 | 0.32 | 0.13 |
| R. Pli | 6 | 162 | 92 | 2.5 | 4.4 | 3.8 | 6.6 | 10.0 | 13.2 | 2.6 | 2.0 | −1.3 | −2.1 | 0.08 | −0.11 |
| Total | 107 | 2889 | 1379 | 2.0 | 4.1 | 2.7 | 5.6 | 7.7 | 11.1 | 2.8 | 2.0 | −0.7 | −1.5 | 0.18 | −0.02 |
| (c) 17–19 December 2016 Event | |||||||||||||||
| PERSIANN-CCS, Spatial Resolution ≈ | |||||||||||||||
| Name | No. pix | Obs. | *Obs. | * | * | RMSD | *RMSD | rRMSD | *rRMSD | Bias | *Bias | R | *R | ||
| Al | 9 | 603 | 330 | 1.5 | 2.8 | 2.5 | 4.4 | 4.4 | 5.9 | 1.7 | 1.3 | −1.0 | −1.7 | 0.32 | 0.12 |
| NE. Al | 5 | 335 | 181 | 1.6 | 3.0 | 3.1 | 5.7 | 5.2 | 7.1 | 1.7 | 1.3 | −1.5 | −2.7 | 0.51 | 0.33 |
| G-Re | 7 | 469 | 282 | 1.4 | 2.3 | 2.6 | 4.2 | 3.5 | 4.5 | 1.3 | 1.1 | −1.3 | −2.0 | 0.41 | 0.19 |
| Total | 140 | 9380 | 4425 | 1.0 | 2.1 | 1.7 | 3.3 | 3.1 | 4.5 | 1.9 | 1.4 | −0.6 | −1.2 | 0.34 | 0.13 |
| Radar, SRI Product in Long Range Mode, Spatial Resolution ≈ | |||||||||||||||
| Name | No. pix | Obs. | *Obs. | * | * | RMSD | *RMSD | rRMSD | *rRMSD | Bias | *Bias | R | *R | ||
| Al | 11 | 737 | 417 | 0.8 | 1.2 | 2.4 | 4.1 | 4.2 | 5.6 | 1.8 | 1.4 | −1.6 | −2.9 | 0.29 | 0.07 |
| NE. Al | 5 | 335 | 178 | 1.0 | 1.7 | 3.1 | 5.8 | 5.8 | 8.0 | 1.9 | 1.4 | −2.1 | −4.1 | 0.42 | 0.21 |
| G-Re | 7 | 469 | 276 | 1.3 | 2.0 | 2.6 | 4.3 | 3.2 | 4.1 | 1.2 | 1.0 | −1.3 | −2.3 | 0.58 | 0.31 |
| Total | 151 | 10117 | 4738 | 1.0 | 1.9 | 1.6 | 3.3 | 2.7 | 3.9 | 1.6 | 1.2 | −0.7 | −1.5 | 0.43 | 0.19 |
| Obs. | *Obs | Bias (dB) | Scatter (dB) | |
|---|---|---|---|---|
| 2009 event | ||||
| PERSIANN-CCS | 4664 | 1200 | −0.06 | 5.00 |
| Radar CAPPI | 4752 | 1563 | −2.38 | 3.37 |
| 2012 event | ||||
| PERSIANN-CCS | 2289 | 770 | −0.19 | 7.06 |
| 2016 Event | ||||
| PERSIANN-CCS | 9380 | 2375 | −0.60 | 5.36 |
| Radar SRI | 10,117 | 5118 | −2.41 | 3.25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cánovas-García, F.; García-Galiano, S.; Alonso-Sarría, F. Assessment of Satellite and Radar Quantitative Precipitation Estimates for Real Time Monitoring of Meteorological Extremes Over the Southeast of the Iberian Peninsula. Remote Sens. 2018, 10, 1023. https://doi.org/10.3390/rs10071023
Cánovas-García F, García-Galiano S, Alonso-Sarría F. Assessment of Satellite and Radar Quantitative Precipitation Estimates for Real Time Monitoring of Meteorological Extremes Over the Southeast of the Iberian Peninsula. Remote Sensing. 2018; 10(7):1023. https://doi.org/10.3390/rs10071023
Chicago/Turabian StyleCánovas-García, Fulgencio, Sandra García-Galiano, and Francisco Alonso-Sarría. 2018. "Assessment of Satellite and Radar Quantitative Precipitation Estimates for Real Time Monitoring of Meteorological Extremes Over the Southeast of the Iberian Peninsula" Remote Sensing 10, no. 7: 1023. https://doi.org/10.3390/rs10071023
APA StyleCánovas-García, F., García-Galiano, S., & Alonso-Sarría, F. (2018). Assessment of Satellite and Radar Quantitative Precipitation Estimates for Real Time Monitoring of Meteorological Extremes Over the Southeast of the Iberian Peninsula. Remote Sensing, 10(7), 1023. https://doi.org/10.3390/rs10071023







