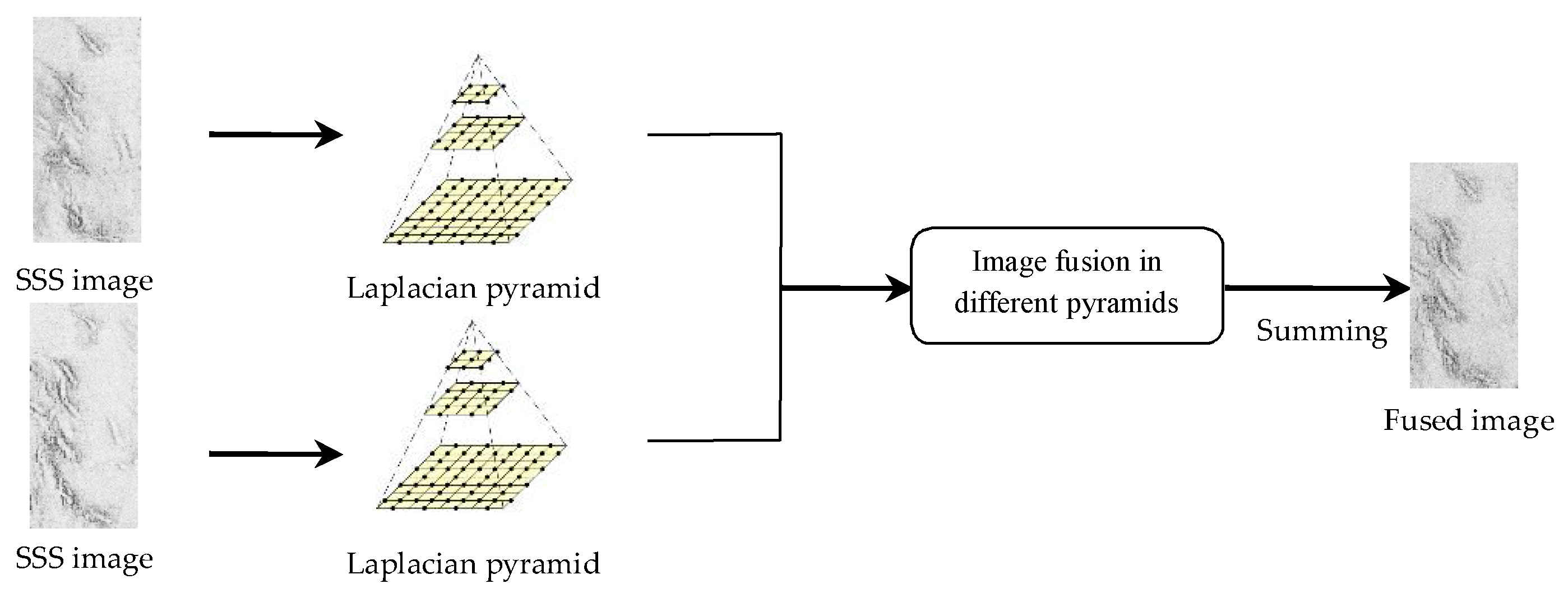
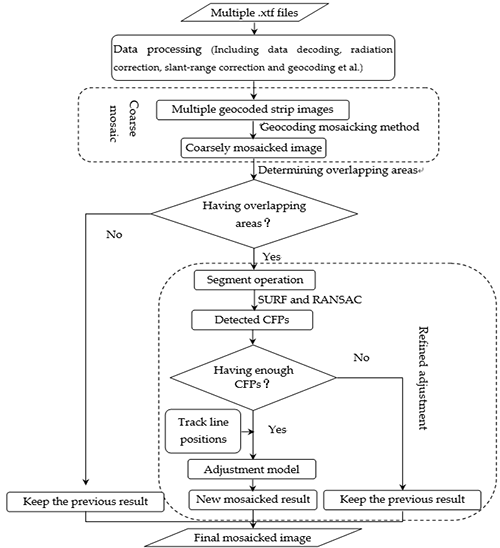
3.2. Mosaic Process Using Adjacent Strips
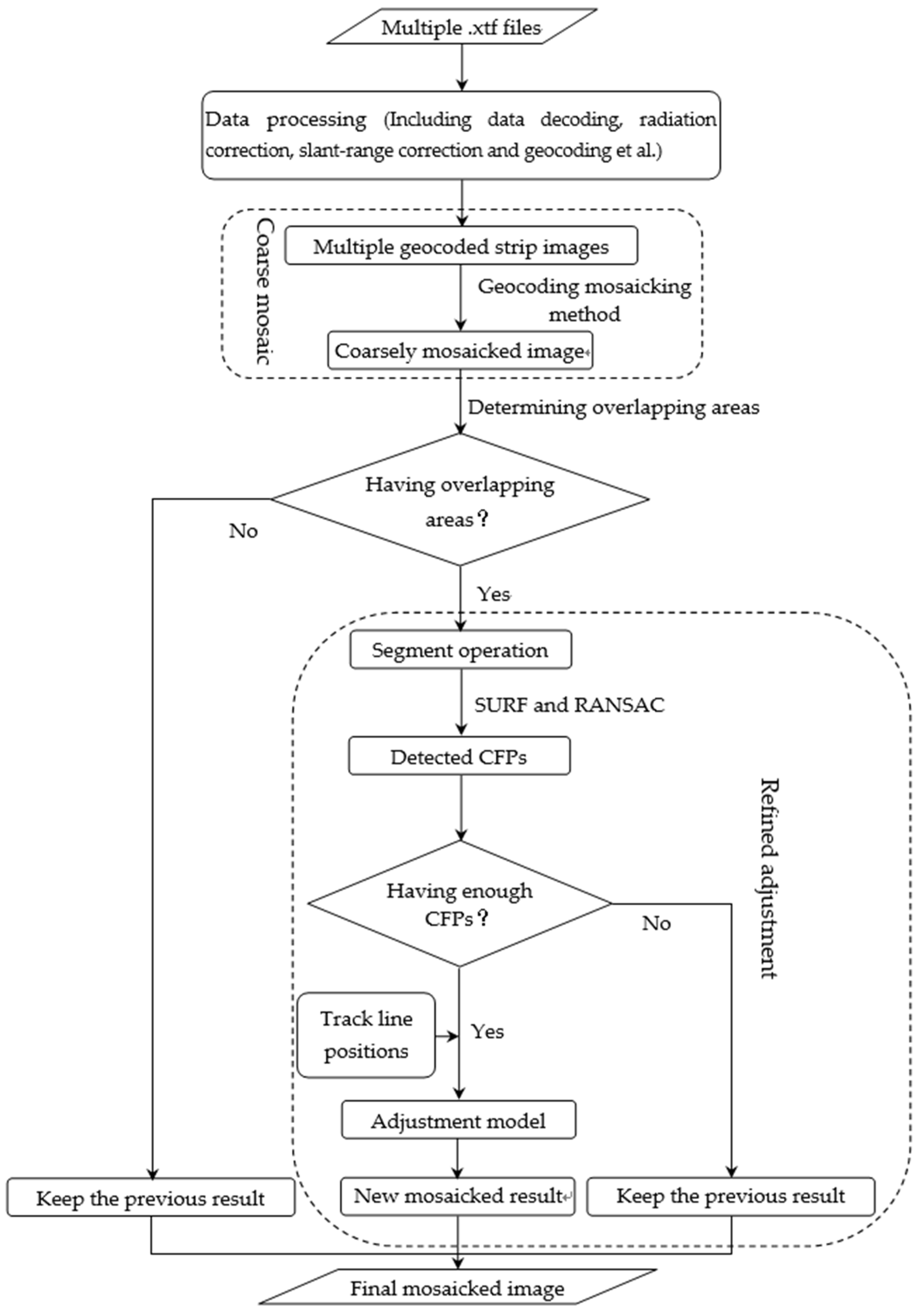
Strip I and Strip II are used as the examples to illustrate the mosaic method according to the flow diagram shown in
Figure 3 in detail.
(1) Geocoding mosaic. Use the SSS geocoded images to obtain the mosaicked one in the same geographic frame using the method described in
Section 2.1. The mosaicked image in
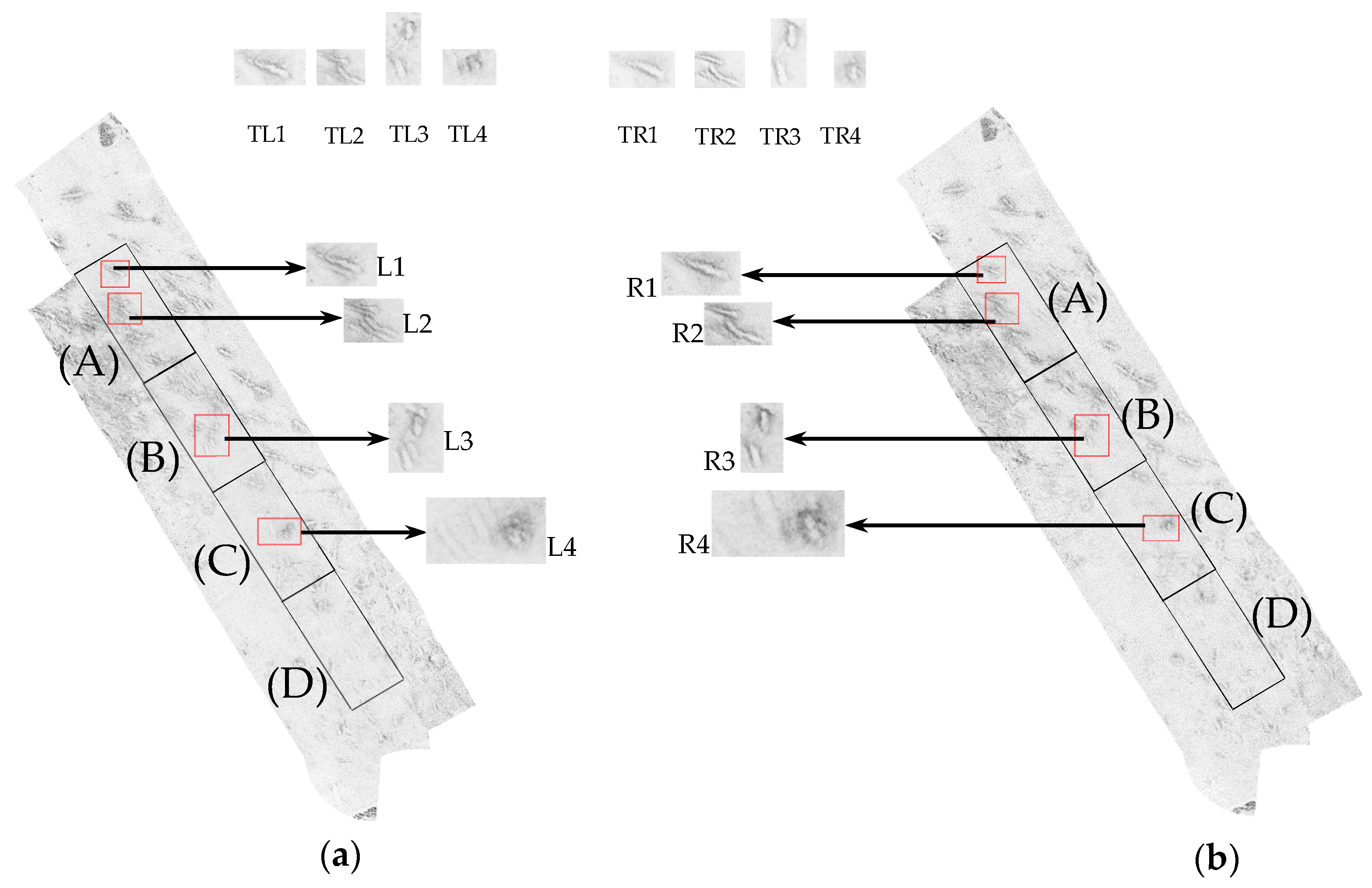
Figure 5a shows there exist target ghosting and dislocation which can be clearly seen as L1–L4. It can be found in
Figure 5 that common features exist in the overlapping areas of adjacent SSS images, which are named TL1–TL4 in one SSS image and TR1–TR4 in the other one. The mosaicked image is supposed to show the four corresponding features in the same positions. However, affected by the wave and currents, the vessel velocity, the cable length variation and the topography changes as mentioned and analyzed in
Section 1, the obtained SSS image feature coordinates may contain errors, which will result in the problem of target dislocation. As a result, the same feature may locate in more than one positions in the mosaicked image and the phenomenon is called target ghosting. In positions L1–L4 of
Figure 5a, ghosts accompany the four targets, which means that target ghosting and dislocation exist in these positions.
(2) Conducting the overlapping area determination and segment. Determine the overlapping areas according to the SSS image coordinates and segment these areas into several equal regions along the track line based on the target distribution and image textures. Considering that enough independent targets should be contained in each segmented part and split lines should lie on the edge of these distinct targets, this experiment separated the overlapping area along the track line into several parts with the length of 420 m, which are obviously shown as the black rectangles (A)–(D) in
Figure 5.
(3) Detecting CFPs. When two surveying lines are designed in the same area, the overlapping areas exist. Even measured along different surveying lines using SSS, the obtained SSS images could reflect the same seabed features after data preprocessing, such as the radiometric correction, slant range correction, geocoding, etc. The features and its neighborhoods in SSS images can be detected and described by the SURF algorithm, which will generate feature vectors, namely descriptors. By matching the descriptors of the features in different SSS images, similar features can be obtained. The matching is based on a distance between the feature vectors, e.g., the Euclidean distance [
26]. To eliminate the incorrect matched FPs, RANSAC algorithm is then adopted. After this step, the CFPs are finally paired. For the areas with no or few CFPs detected, no further processes are conducted. While for these with abundant CFPs, evenly distributed couple ones are selected for the subsequent image registration and mosaicking. The detected CFPs in the areas (A)–(C) of
Figure 5 are shown in
Figure 6. When the SURF and RANSAC algorithms are conducted for the adjacent SSS images in area (D), no distinctive CFPs are detected because no significant features exist. Thus, no image registration will be conducted in area (D).
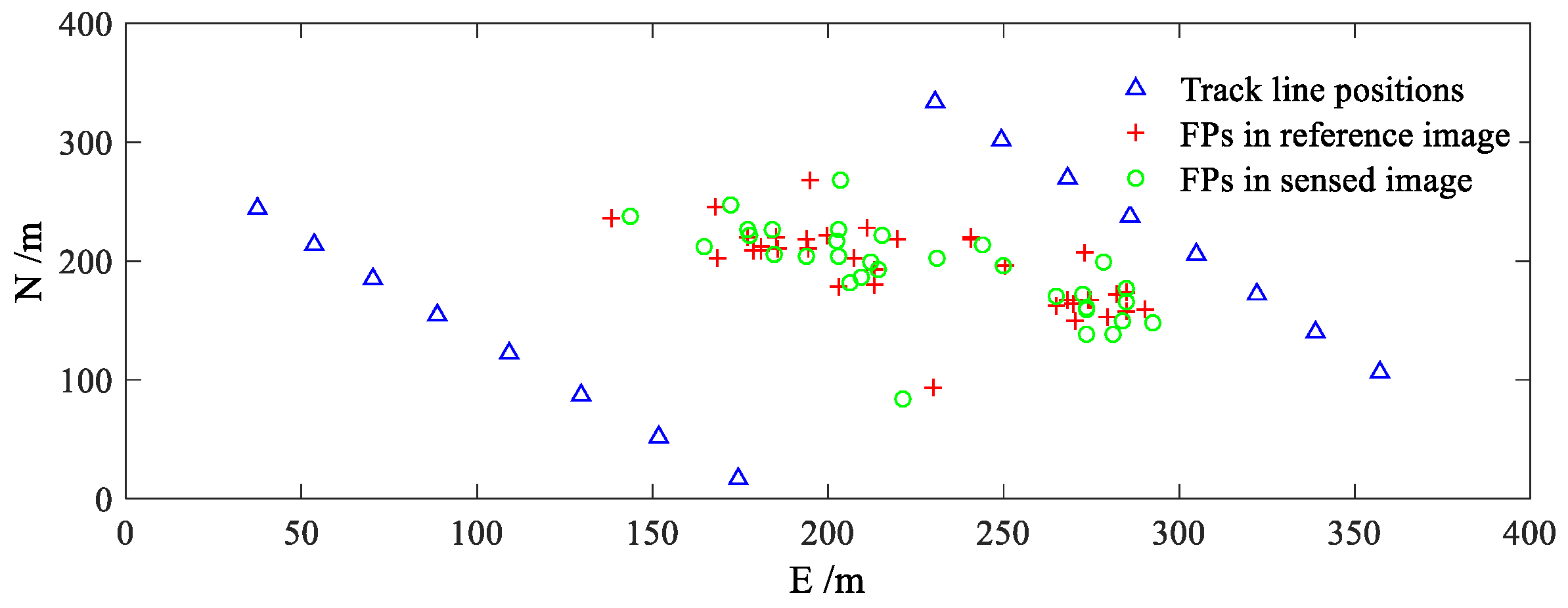
(4) The constraint of track line positions. For every segmented part, the corresponding track line positions are selected as the constraint to ensure the sensed image not deviate from the actual measurement region after geometric transformation. In this experiment, points with the interval of about 30 m in the track line are selected, which are shown in
Figure 7 and denoted by the “△” symbols. When establishing the geometric transformation model between the reference image and the sensed one, both the selected CFPs and the constraint of track line positions are used to accommodate the local distortions and global stability.
The relative positions of CFPs of both SSS images in area (a) are shown in
Figure 7, which are, respectively, denoted by “+” and “○” symbols. It can be seen that the coordinate deviation of CFPs is variational in different positions. In some positions, the FPs in reference image lie to the east of the ones in sensed image, while, in other positions, the situation becomes reversed. In the areas (b,c), a similar situation also exists and implies that the local distortions in the SSS geocoded image are diverse.
(5) Adjustment model. Some evenly distributed CFPs and track line positions are combined together to construct the adjustment model similar to Equation (2), which can accommodate local distortions to match the CFPs as well as be globally stable with the constraint of track line positions. For the separated overlapping areas (A)–(C) shown in
Figure 5, the adjustment models are respectively established. After the sensed image has been transformed by the adjustment model, a gap filling method, as displayed as Equation (4), should be conducted to obtain a completed image.
(6) Mosaicking images. Fusing the transformed sensed image and the reference one in the overlapping areas (A)–(C), a new mosaicked image can be obtained. Replacing the coarsely mosaicked image with these newly obtained ones, a better mosaicked image can be formed.
Through above processing, the finally mosaicked image is shown in
Figure 5b. The CFP coordinates in R1–R4 are more accordant with each other than these in L1–L4 as shown in
Figure 5a, which is more helpful for image interpretation and application. Because segment operation is conducted in the overlapping area in
Figure 5b, the CFPs can be detected and selected separately in these segmented parts as described in Step (3). In this experiment, topography changes exist in the measurement area and are reflected by the image intensities, which means that the positions with obvious image intensity gradients correspond to these with topography undulations. As SURF algorithm is adopted to generate feature vector to describe the intensity gradients, the CFPs detected in this measurement area are mainly located in the positions with distinctive topography changes.
3.5. Multi-Strip Image Mosaics and Analysis
Constructing four strip image mosaics together using the proposed method and the result is shown in
Figure 12. As no obviously common targets present in Strip III and IV, only geocoding method is used when mosaicking the two images. While there exist distinct objectives in both Strips I and II, and Strips II and III, the refined adjustment operation must be performed and the complete mosaic process must be conducted. The mosaicked image in
Figure 12 shows clear target distribution and ensures the coordinate consistency of CFPs in the overlapping areas.
In the mosaic process using the four strip images, only geocoding method is used in the nonoverlapping areas or overlapping areas with few CFPs. While for overlapping areas with abundant CFPs, the refined adjustment operation is subsequently performed. When conducting the adjustment operation, the port and starboard of SSS images are considered independent and the overlapping area is segmented. For every segmented part, the corresponding track line positions are jointed with the CFPs to serve as the constraint to construct an adjustment model to refine the mosaicked result. Using the obtained adjustment model, the position error can be disintegrated inside individual segmented areas and will not propagate over other regions. In such a situation, there only exist position errors resulted from the adjacent image mosaic operation even when multi-strip images are processed and the problem of positional accumulated errors is solved. Thus, the proposed method ensures the global stability of the sensed image even after the geometric transform and raw measurement information can be reserved and utilized to the maximum.
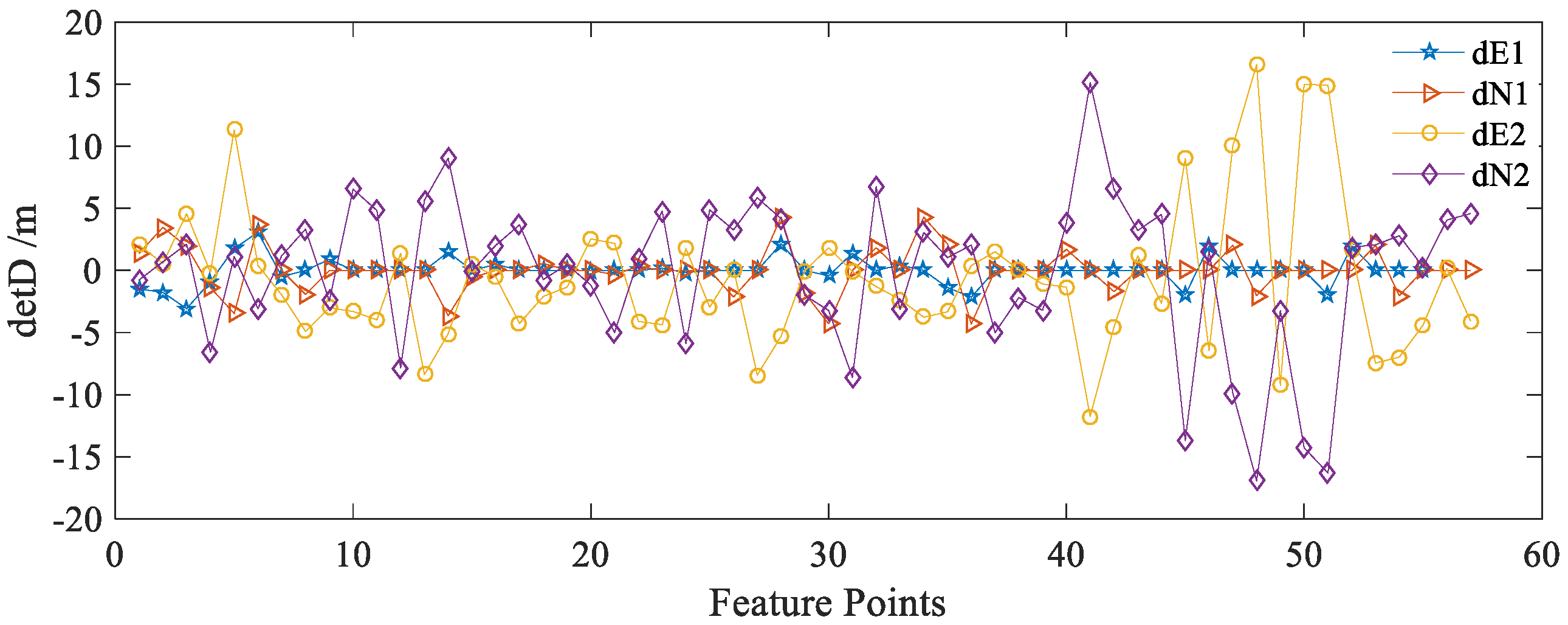
The last two SSS images (Strip II and Strip III) are used to evaluate the mosaic method when conducting multi-strip image mosaics. Strip II is used as the reference and consequently Strip III is used as the sensed one. The coordinate deviations of the CFPs between the reference and sensed image before and after the mosaicking process are analyzed. These coordinate deviations are shown in
Figure 13, where “☆” and “▷” symbols denote coordinate deviations in east–west and north–south directions between the reference image and transformed sensed image; “○”and “◇” symbols denote these between the reference image and raw sensed image. The corresponding statistical parameters of these coordinate deviations are shown in
Table 5. It can be seen in
Figure 13 and
Table 5 that the deviations after the refined adjustment become much smaller than the raw deviations and the maximum deviations in east–west and north–south directions are separately 3.90 m and 4.07 m. Meanwhile, compared to the standard deviations of raw coordinates in both directions (3.85 m and 4.67 m), the ones after adjustment become much smaller (1.48 m and 1.59 m). In the experiment, the pixel resolution is set as 0.6 m, the coordinate deviations presented in the refined mosaicked image would be less than 7 pixels after adjustment. These statistics prove that the adjustment model have rectified the local distortions around the CFPs and the coordinates of CFPs in the mosaicked image show good consistency.
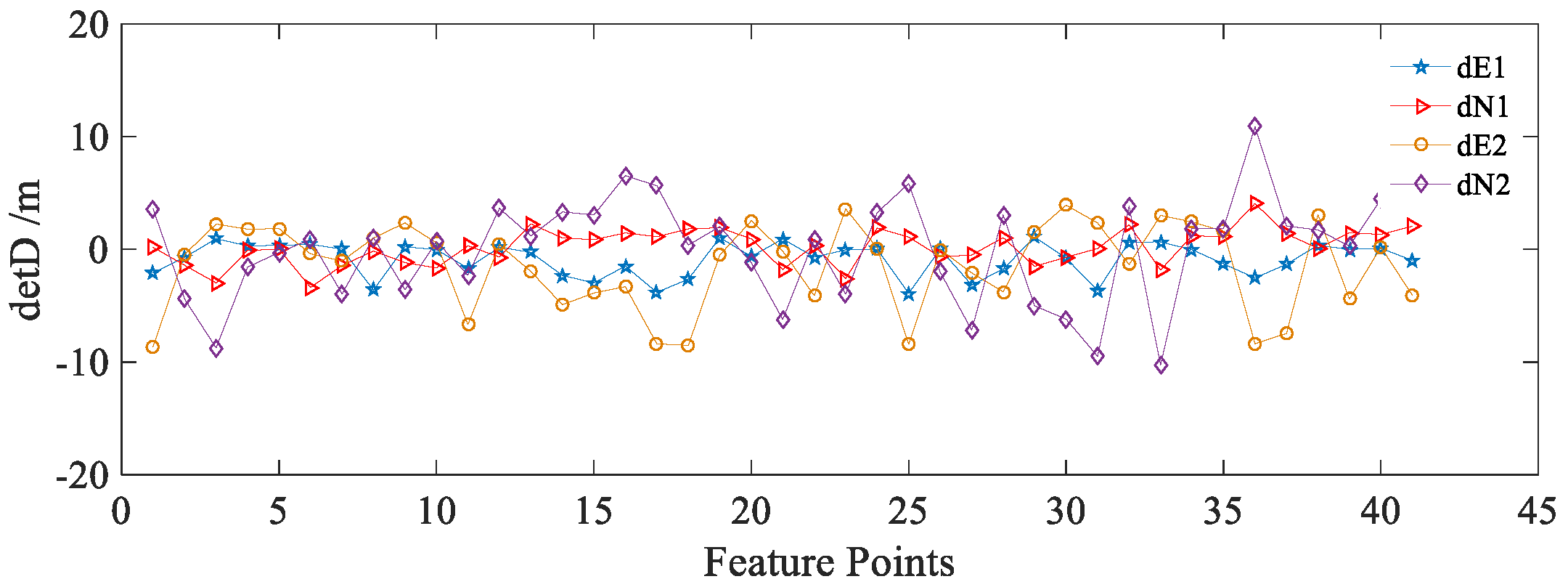
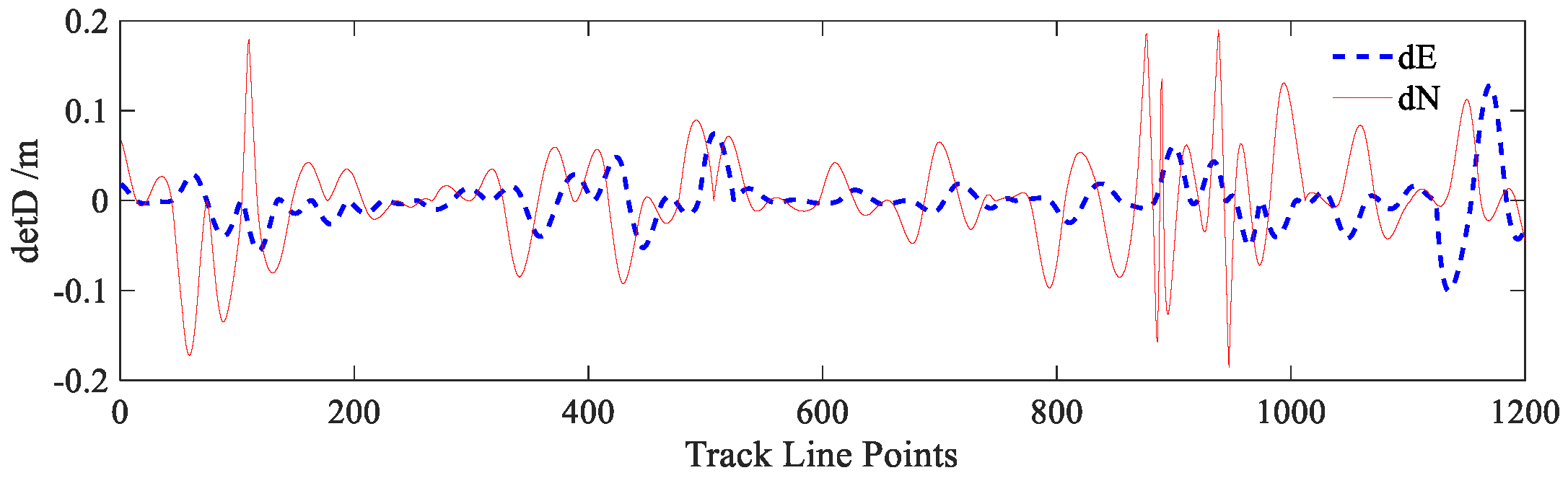
Besides, the track line positions in the mosaicked image are also analyzed. As Strip III and IV are mosaicked only by the geocoding information, the track line positions of Strip IV maintain unchanged, whereas Strips I, II and III are mosaicked using the complete process of the proposed method. Choosing the track line points of Strip III not used in establishing the adjustment model, their coordinate deviations before and after the mosaicking process are computed and shown in
Figure 14, where dotted and solid lines which can be seen as “----” and “—” symbols, respectively, denote the coordinate deviations in east–west and north–south directions. The corresponding statistical parameters of these coordinate deviations are shown in
Table 5.
Figure 14 and
Table 5 show that the maximum deviations in both the east–west and north–south directions are less than 0.2 m. Meanwhile, the deviations distributed evenly around the mean deviation of 0.0 m, whose standard deviations are respectively 0.02 m and 0.04 m. These statistics prove that the mosaicked result is not deviated from the original measurement range.
In
Figure 8,
Figure 9,
Figure 13 and
Figure 14 and
Table 1,
Table 2 and
Table 5, it can be seen that the coordinate deviations of CFPs and track line positions in the multi-strip image mosaics have the same order of magnitude with that in the adjacent image mosaics. These statistics and the above theoretical analysis prove that the proposed method can not only accommodate the local distortions of CFPs, but also ensure the mosaicked image in the valid measurement area.
Comparing the proposed method to others, the SSS image mosaic results, the computing time and the accuracy statistics are separately shown in
Figure 15 and
Table 6. The geocoding method performs faster of all, but obvious target ghosting can be seen in positions (A)–(E) in
Figure 15a. The other three mosaic results avoid the target ghosting problem even though more computing time is used. Considering the mosaic performance, computing time and the accuracy statistics, the image mosaic method using the CFPs with constraint of track line positions is recommended.