Investigation and Analysis of All-Day Atmospheric Water Vapor Content over Xi’an Using Raman Lidar and Sunphotometer Measurements
Abstract
1. Introduction
2. Configuration and Retrieval Method
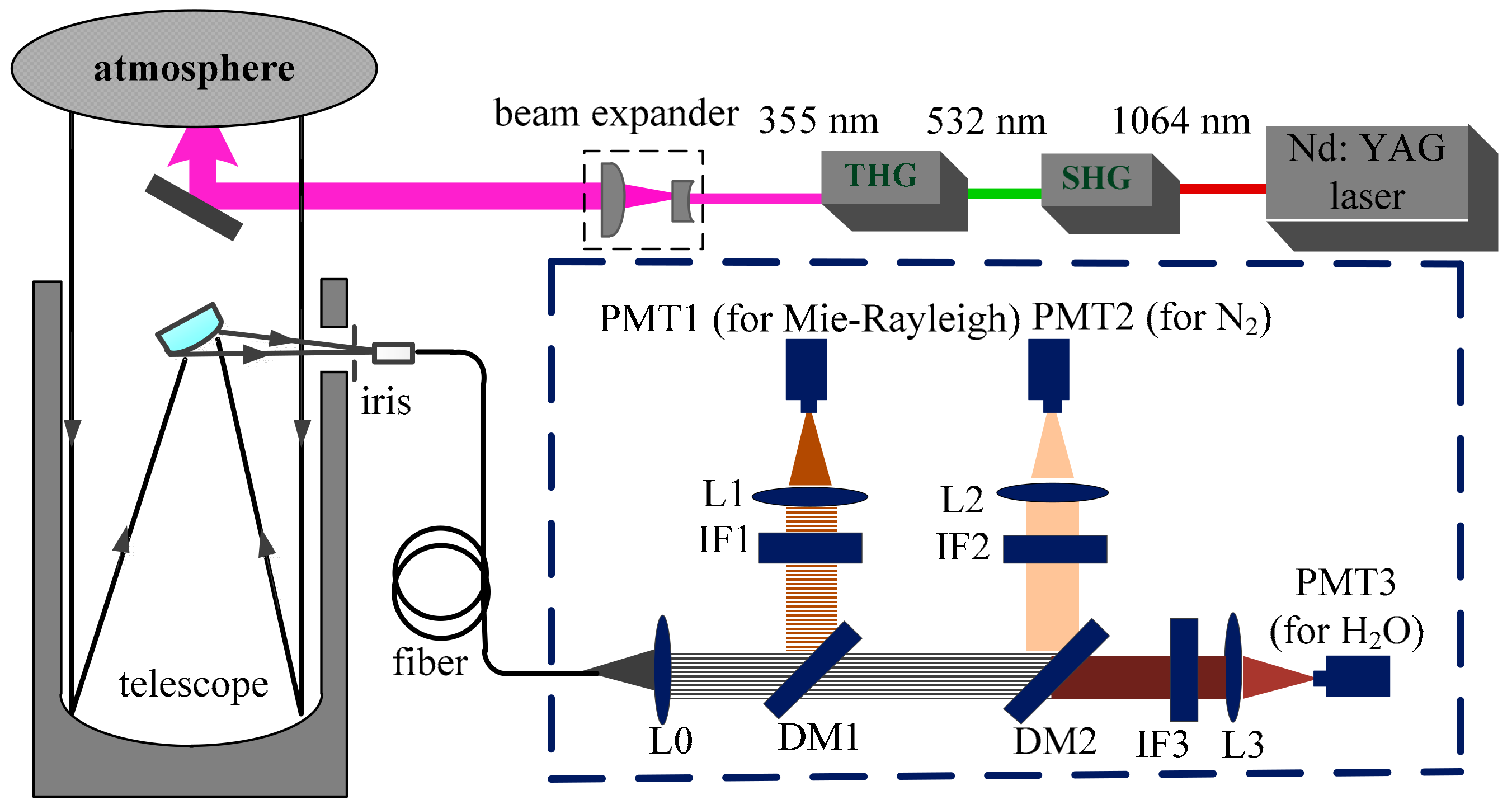
2.1. Raman Lidar and Retrieval Methods for Water Vapor
2.2. Sunphotometer and Retrieval Methods for Total Column Water Vapor Content
3. Daytime Performance of Raman Lidar
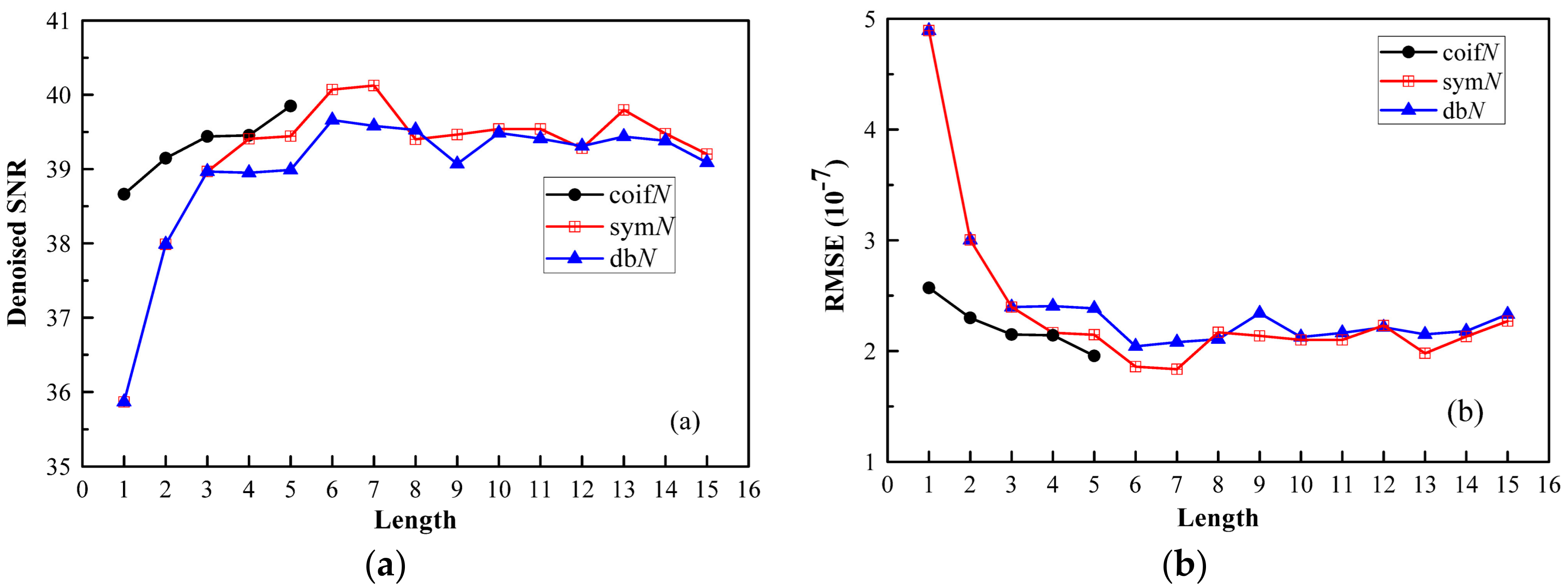
3.1. Wavelet De-Noising Method
- (1)
- First, it is necessary to select the appropriate wavelet base and decomposition level through the de-composition of the original lidar return signals;
- (2)
- Second, it is important to choose the appropriate threshold and threshold function to remove noise and background light from the detected signals;
- (3)
- Finally, it is necessary to reconstruct the signals according to the each level of wavelet decomposition for low-frequency coefficients and high-frequency coefficients.
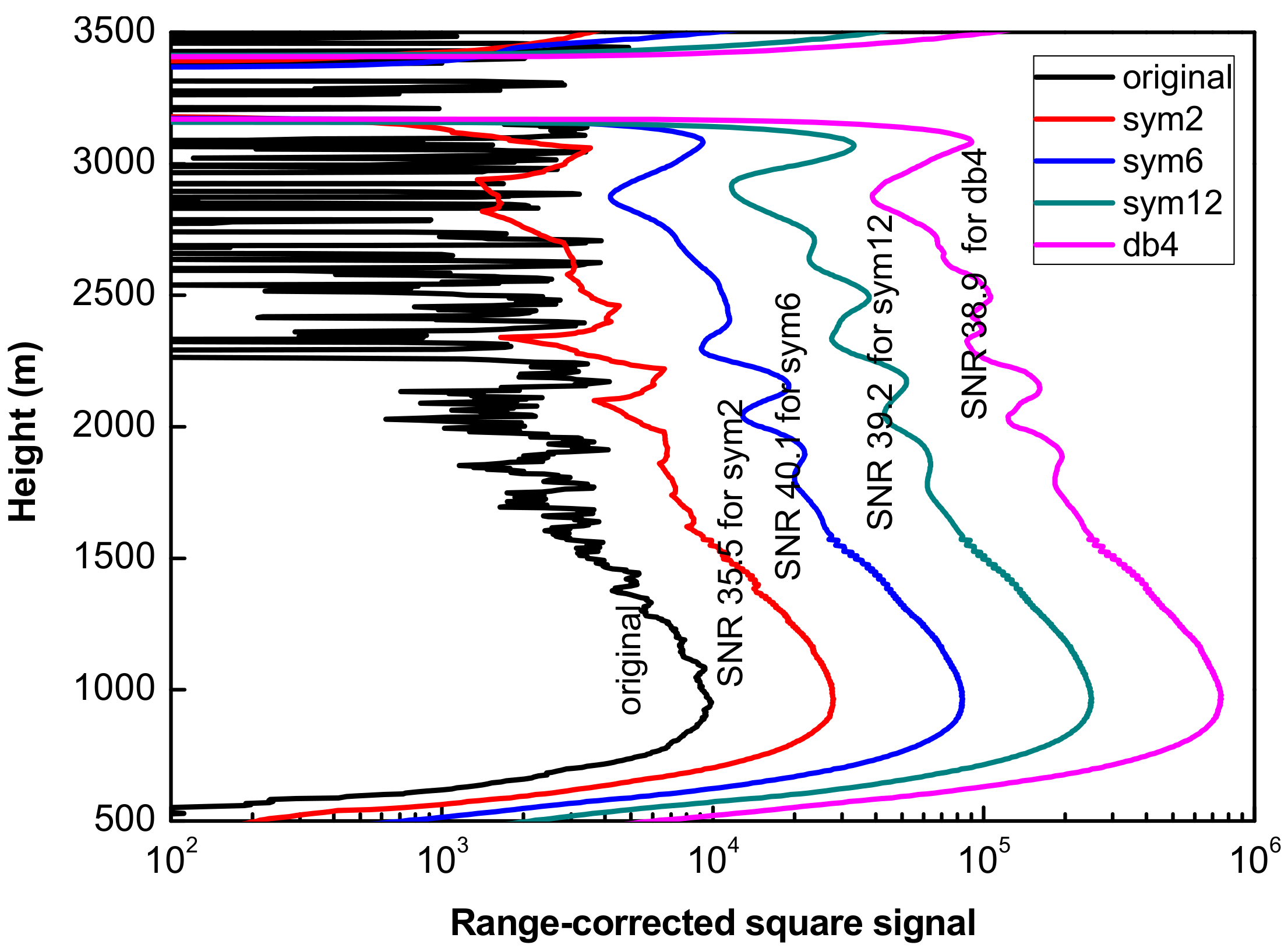
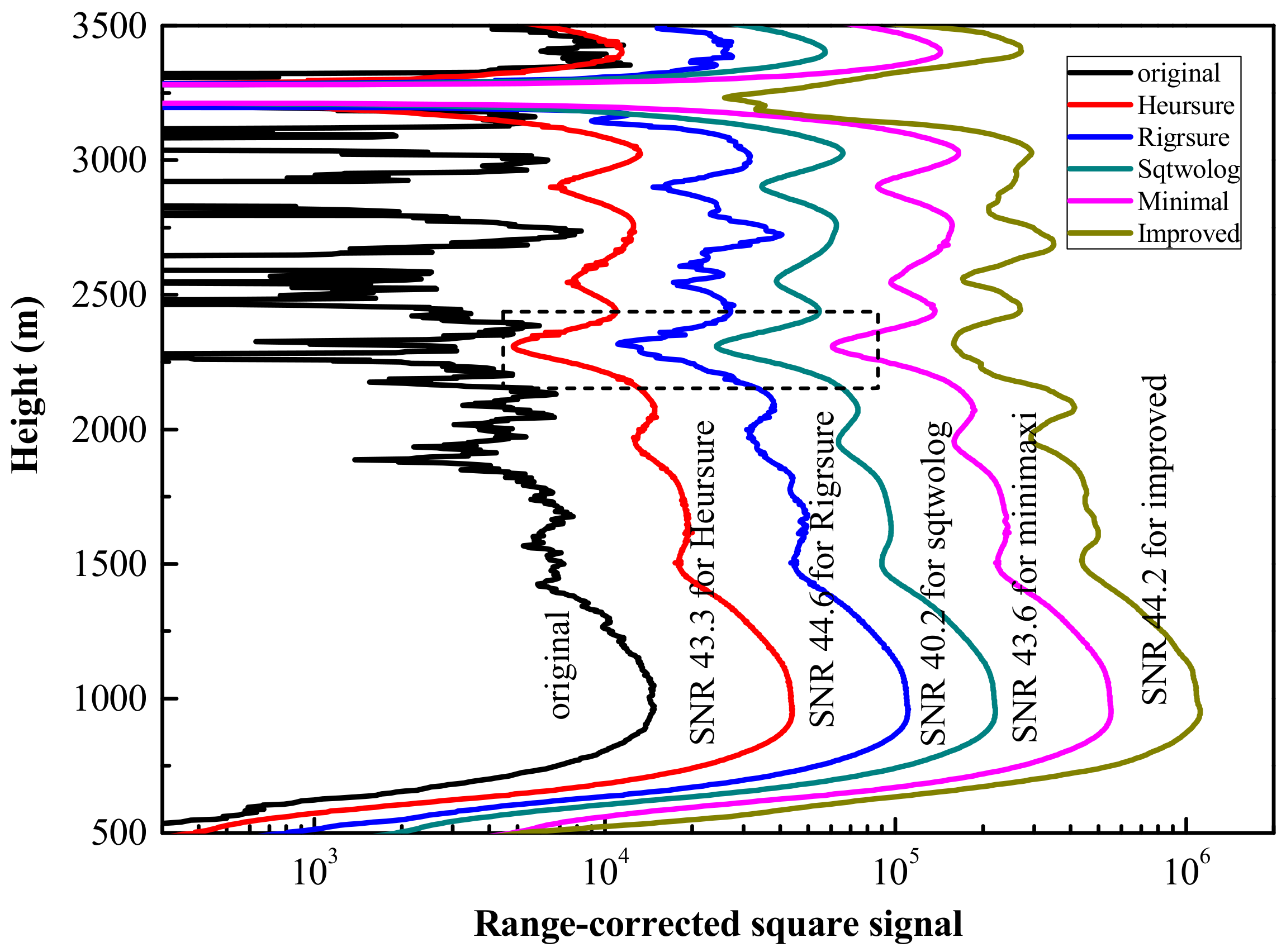
3.2. De-Noising Processing and Discussion
3.3. Validation of the Daytime Performance
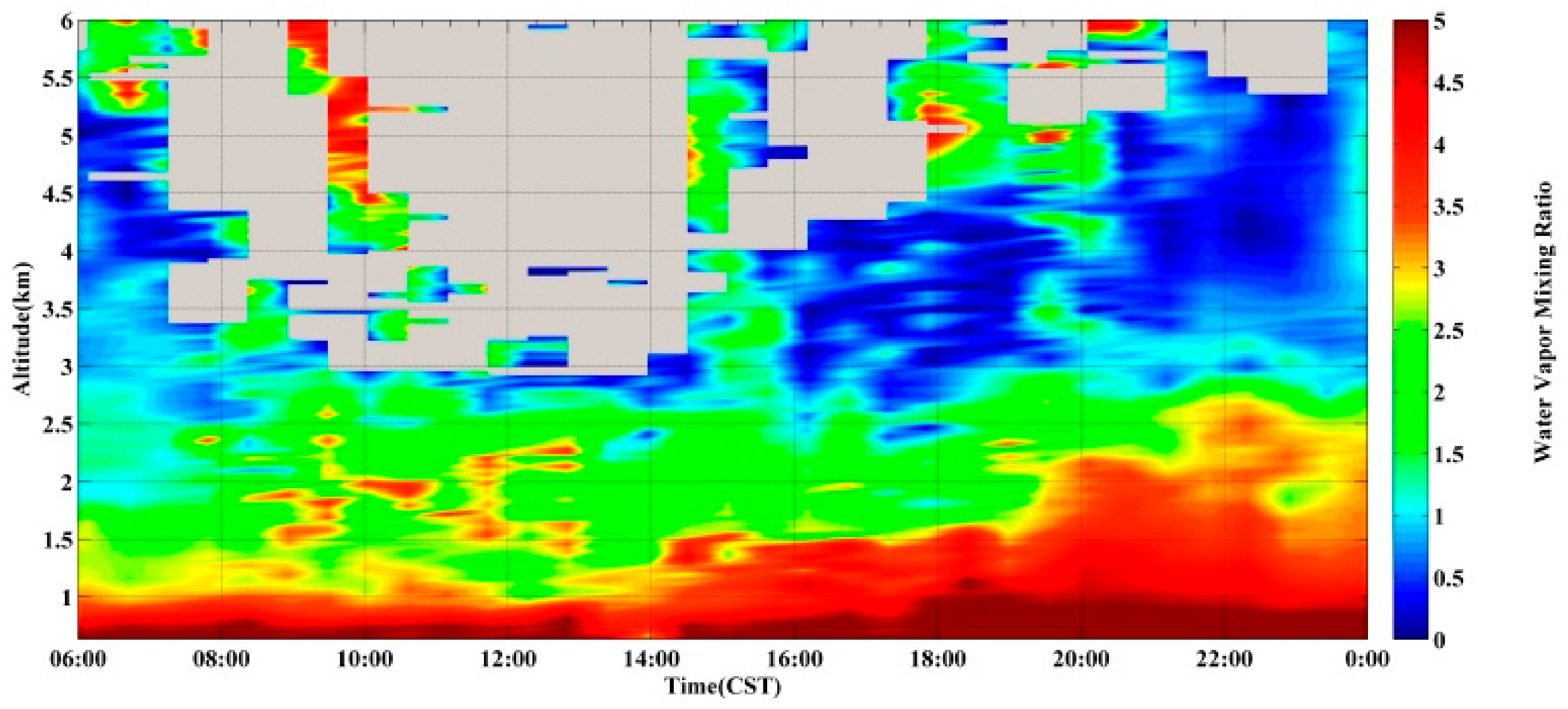
4. Investigation of the All-Day Water Vapor Variation
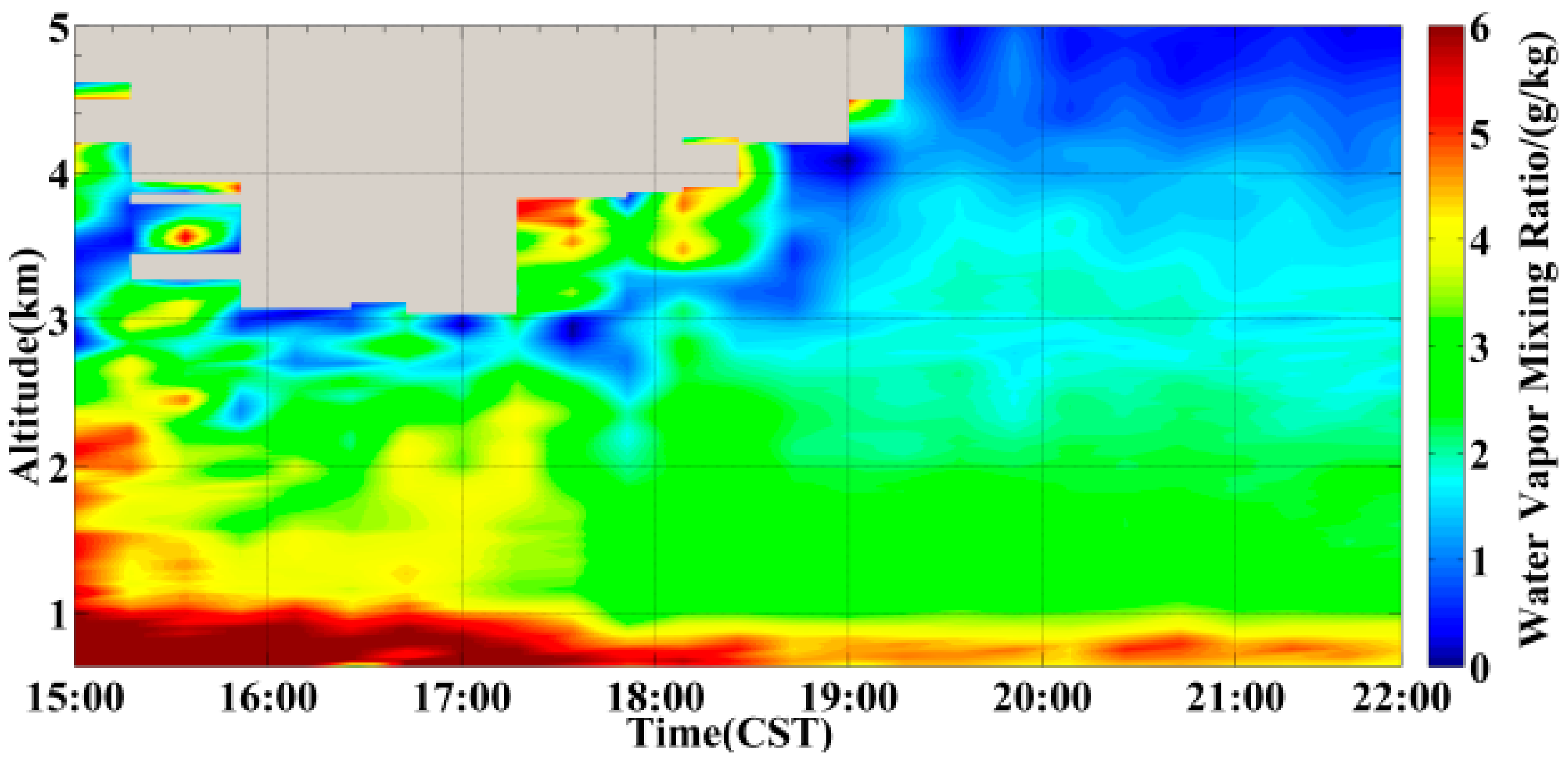
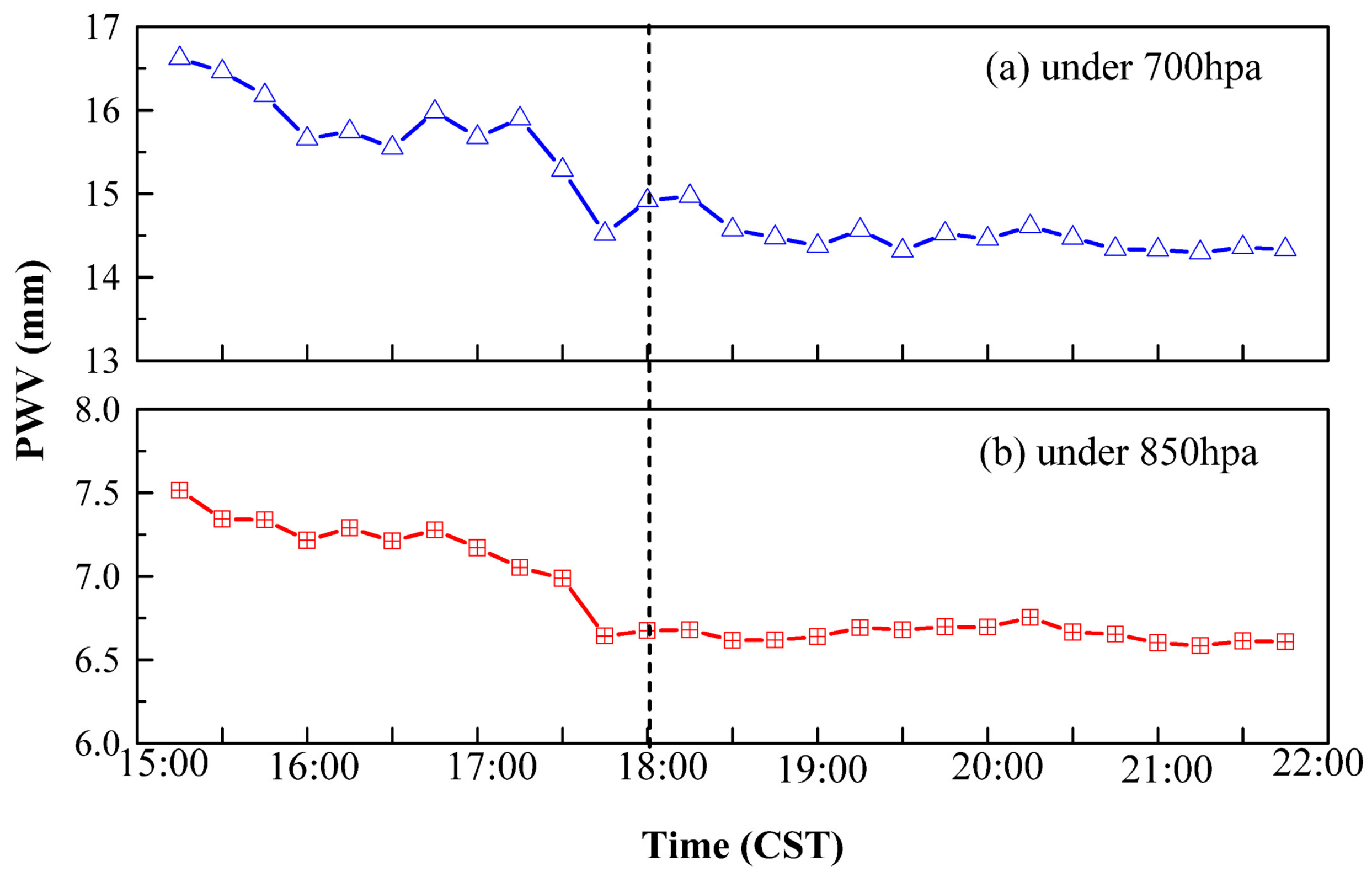
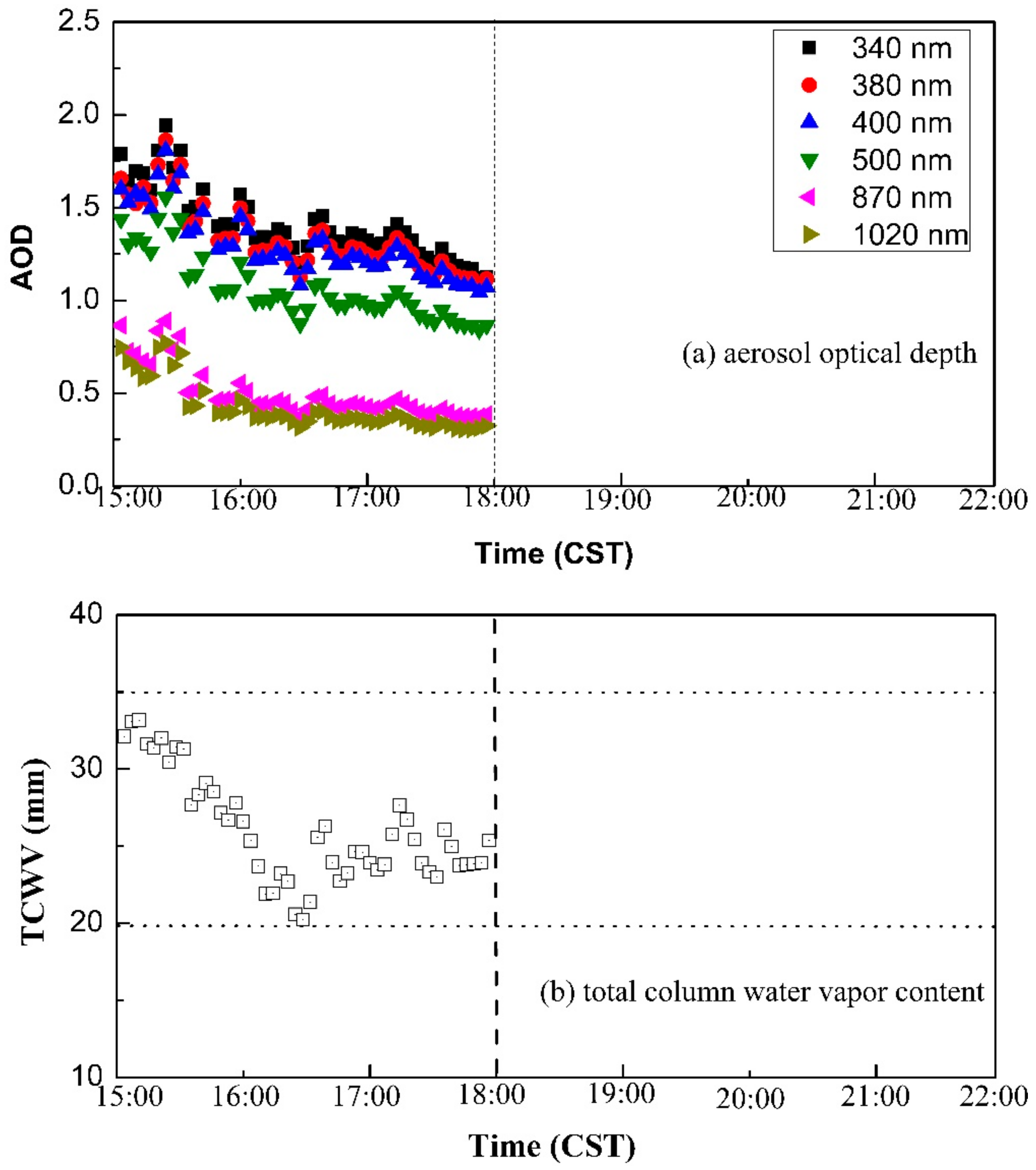
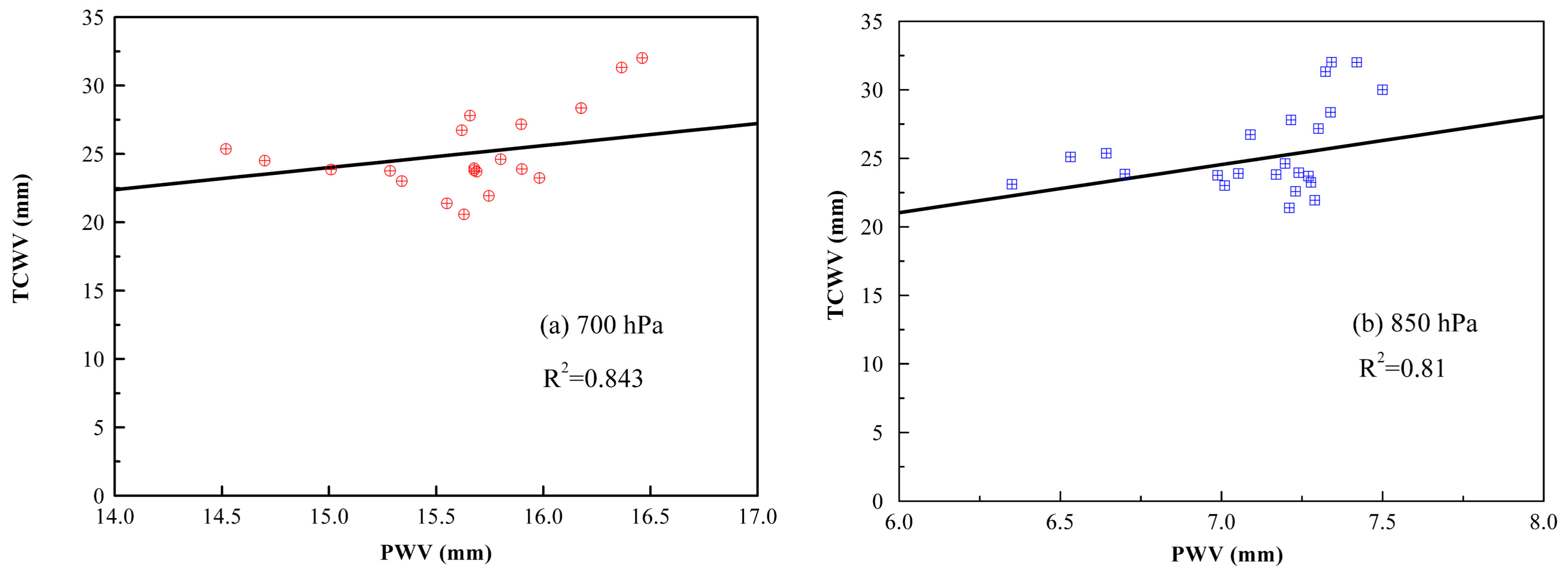
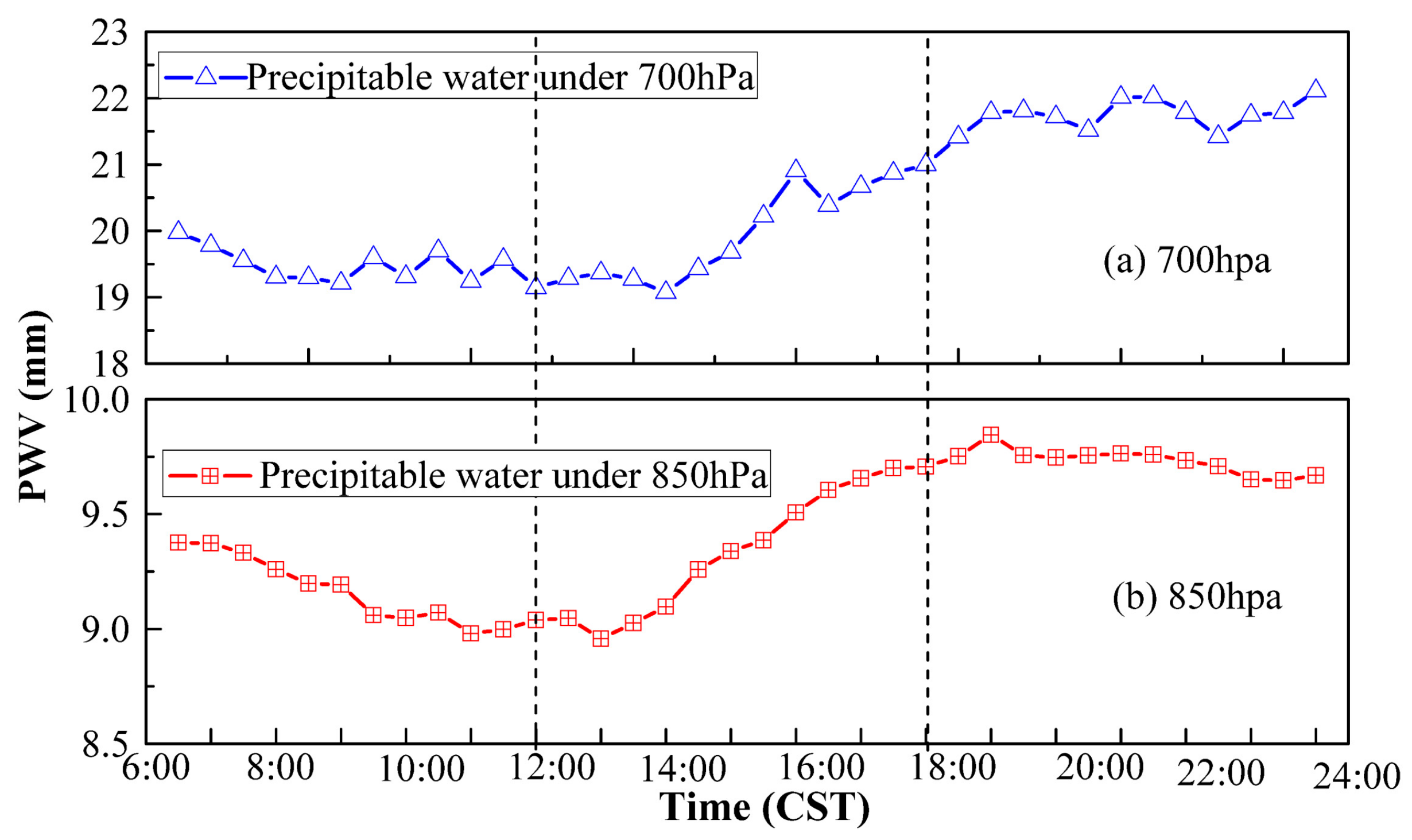
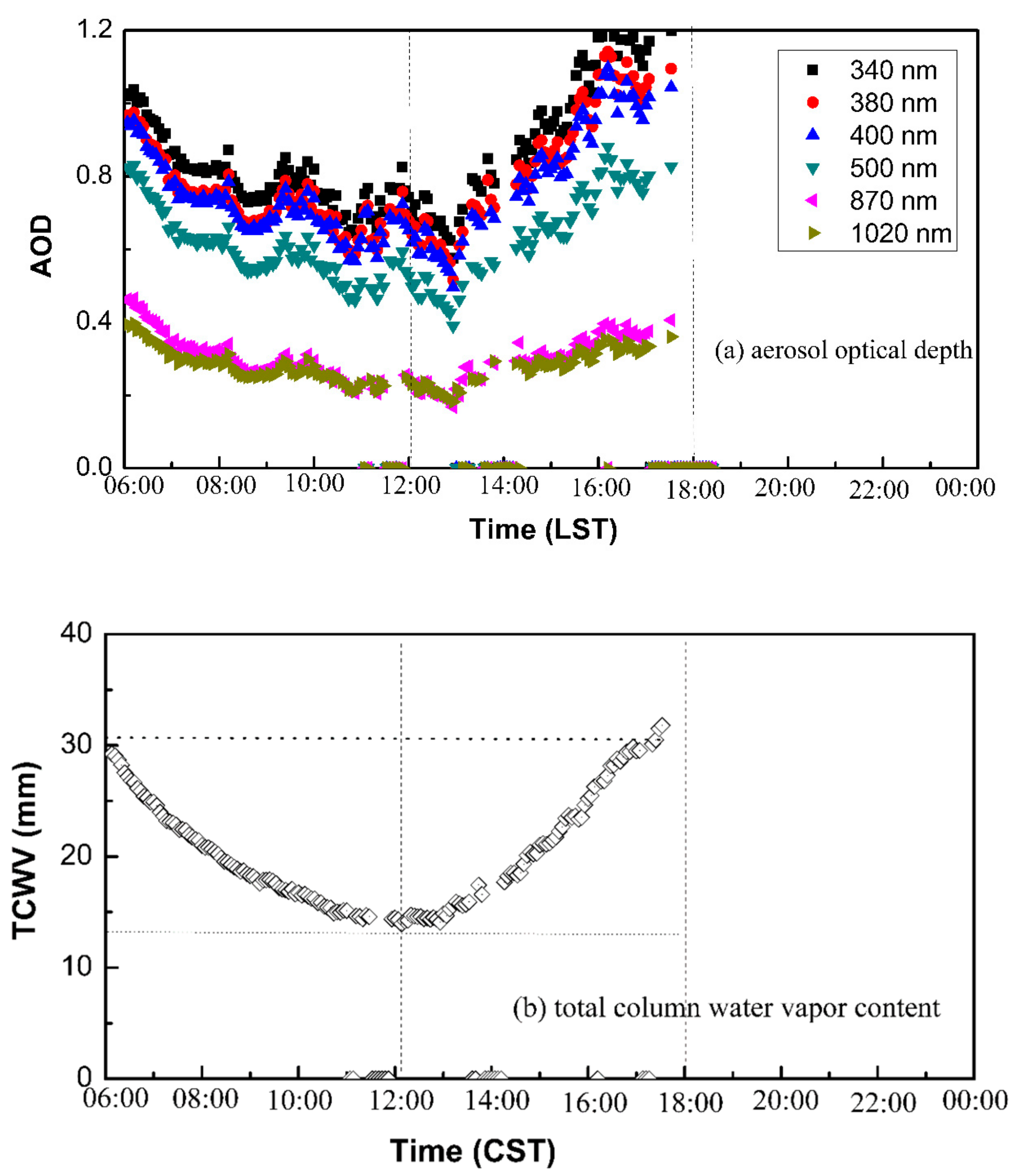
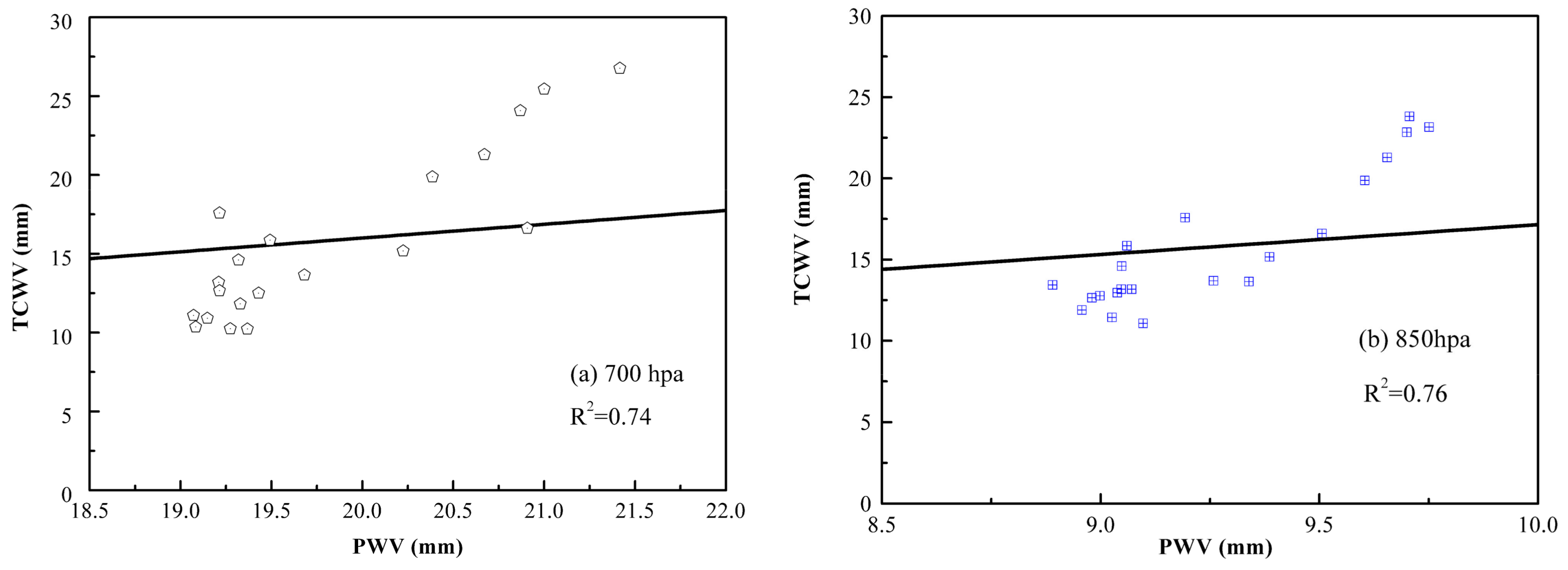
4.1. Case Study 1
4.2. Case Study 2
5. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Wang, C.X.; Gao, S.T.; Liang, L.; Deng, D.F.; Gong, H.N. Multi-scale characteristics of moisture transport during a rainstorm process in North China. Atmos. Res. 2014, 145, 189–204. [Google Scholar] [CrossRef]
- Ye, H.; Fetzer, E.J.; Wong, S.; Behrangi, A.; Yang, D.; Lambrigtson, B.H. Increasing atmospheric water vapor and higher daily precipitation intensity over northern Eurasia. Geophys. Res. Lett. 2016, 42, 9404–9410. [Google Scholar] [CrossRef]
- Raval, A.; Ramanathan, V. Observational determination of the greenhouse effect. Nature 1989, 342, 758–761. [Google Scholar] [CrossRef]
- Held, I.M.; Soden, B.J. Robust responses of the hydrological cycle to global warming. J. Clim. 2010, 19, 5686–5699. [Google Scholar] [CrossRef]
- Solomon, S.; Rosenlof, K.H.; Portmann, R.W.; Daniel, J.S.; Davis, S.M.; Sanford, T.J.; Plattner, G.-K. Contributions of stratospheric water vapor to decadal changes in the rate of global warming. Science 2010, 327, 1219–1223. [Google Scholar] [CrossRef] [PubMed]
- Tregoning, P.; Boers, R.; O’Brien, D.; Hendy, M. Accuracy of absolute precipitable water vapor estimates from GPS observations. J. Geophys. Res. Atmos. 1998, 103, 28701–28710. [Google Scholar] [CrossRef]
- Fetzer, E.J.; Lambrigtsen, B.H.; Eldering, A.; Aumann, H.H.; Chahine, M.T. Biases in total precipitable water vapor climatologies from atmospheric infrared sounder and advanced microwave scanning radiometer. J. Geophys. Res. Atmos. 2006. [Google Scholar] [CrossRef]
- Mattis, I.; Ansmann, A.; Althausen, D.; Jaenisch, V.; Wandinger, U.; Müller, D.; Arshinov, Y.F.; Bobrovnikov, S.M.; Serikov, I.B. Relative-humidity profiling in the troposphere with a Raman lidar. Appl. Opt. 2002, 41, 6451–6462. [Google Scholar] [CrossRef] [PubMed]
- Pandolfi, M.; Amodeo, A.; Mona, L.; Pappalardo, G. Lidar measurements of atmospheric aerosol, water vapour and clouds. Recent Res. Dev. Opt. 2003, 3, 543–562. [Google Scholar]
- De Tomasi, F.; Perrone, M.R. Lidar measurements of tropospheric water vapour and aerosol profiles over south-eastern Italy. J. Geophys. Res. 2003, 108, 9–12. [Google Scholar] [CrossRef]
- Navas-Guzmán, F.; Fernández-Gálvez, J.; Granados-Muñoz, M.J.; Guerrero-Rascado, J.L.; Bravo-Aranda, J.A.; Alados-Arboledas, L. Tropospheric water vapour and relative humidity profiles from lidar and microwave radiometry. Atmos. Meas. Tech. 2014, 7, 1201–1211. [Google Scholar] [CrossRef]
- Jia, J.; Yi, F. Atmospheric temperature measurements at altitudes of 5–30 km with double-grating-based pure rotational Raman lidar. Appl. Opt. 2014, 53, 5330–5343. [Google Scholar] [CrossRef] [PubMed]
- Behrendt, A.; Nakamura, T.; Onishi, M.; Baumgrat, R.; Tsuda, T. Combined Raman lidar for the measurement of atmospheric temperature, water vapor, particle extinction coefficient, and particle backscatter coefficient. Appl. Opt. 2002, 41, 7657–7666. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Fu, Q.; Zhao, M.; Gao, F.; Di, H.; Song, Y.; Hua, D. A UV multifunctional Raman lidar system for the observation and analysis of atmospheric temperature, humidity, aerosols and their conveying characteristics over Xi’an. J. Quant. Spectrosc. Radiat. Transf. 2018, 205, 114–126. [Google Scholar]
- Whiteman, D.N. Examination of the traditional Raman lidar technique. II. Evaluating the ratios for water vapor and aerosol. Appl. Opt. 2003, 42, 2593–2608. [Google Scholar] [CrossRef] [PubMed]
- Xie, C.; Zhou, J.; Yue, G.-M.; Fan, A.-Y. Mobile lidar system for measuring tropospheric aerosol and water vapor. Infrared Laser Eng. 2007, 36, 365–367. [Google Scholar]
- Bedoya-Velásquez, A.E.; Navas-Guzmán, F.; Granados-Muñoz, M.J.; Titos, G.; Román, R.; Andrés Casquero-Vera, J.; Ortiz-Amezcua, P.; Antonio Benavent-Oltra, J.; De Arruda Moreira, G.; Montilla-Rosero, E.; et al. Hygroscopic growth study in the framework of EARLINET during the SLOPE i campaign: Synergy of remote sensing and in situ instrumentation. Atmos. Chem. Phys. 2018, 18, 7001–7017. [Google Scholar] [CrossRef]
- Granados-Muñoz, M.J.; Navas-Guzmán, F.; Bravo-Aranda, J.A.; Guerrero-Rascado, J.L.; Lyamani, H.; Valenzuela, A.; Titos, G.; Fernández-Gálvez, J.; Alados-Arboledas, L. Hygroscopic growth of atmospheric aerosol particles based on active remote sensing and radiosounding measurements: Selected cases in southeastern Spain. Atmos. Meas. Tech. 2015, 8, 705–718. [Google Scholar] [CrossRef]
- Tsekeri, A.; Amiridis, V.; Marenco, F.; Nenes, A.; Marinou, E.; Solomos, S.; Rosenberg, P.; Trembath, J.; Nott, G.J.; Allan, J.; et al. Profiling aerosol optical, microphysical and hygroscopic properties in ambient conditions by combining in situ and remote sensing. Atmos. Meas. Tech. 2017, 10, 83–107. [Google Scholar] [CrossRef]
- Veselovskii, I.; Whiteman, D.N.; Kolgotin, A.; Andrews, E.; Korenskii, M. Demonstration of aerosol property profiling by multiwavelength lidar under varying relative humidity conditions. J. Atmos. Ocean. Tech. 2009, 26, 1543–1557. [Google Scholar] [CrossRef]
- Guerrero-Rascado, J.; Ruiz, B.; Chourdakis, G.; Georgoussis, G.; Alados-Arboledas, L. One year of water vapour Raman lidar measurements at the Andalusian Centre for Environmental Studies (CEAMA). Int. J. Remote Sens. 2008, 29, 5437–5453. [Google Scholar] [CrossRef]
- Froidevaux, M.; Higgins, C.W.; Simeonov, V.; Ristori, P.; Pardyjak, E.; Serikov, I.; Calhoun, R.; den Bergh, H.V.; Parlange, M.B. A Raman lidar to measure water vapor in the atmospheric boundary layer. Adv. Water Res. 2013, 51, 345–356. [Google Scholar] [CrossRef]
- Leblanc, T.; McDermid, I.S.; Walsh, T.D. Ground-based water vapor Raman lidar measurements up to the upper troposphere and lower stratosphere for long-term monitoring. Atmos. Meas. Tech. 2012, 5, 17–36. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, X.; He, T.; Gao, F.; Hua, D.; Zhao, M. Observation and analysis of the temperature inversion layer by Raman lidar up to the lower stratosphere. Appl. Opt. 2015, 54, 10079–10088. [Google Scholar] [CrossRef] [PubMed]
- Mazzola, M.; Stone, R.S.; Herber, A.; Tomasi, C.; Lupi, A.; Vitale, V.; Lanconelli, C.; Toledano, C.; Cachorro, V.E.; O’Neill, N.T.; et al. Evaluation of sun photometer capabilities for retrievals of aerosol optical depth at high latitudes: The POLAR-AOD intercomparison campaigns. Atmos. Environ. 2012, 52, 4–17. [Google Scholar] [CrossRef]
- Toledano, C.; Cachorro, V.E.; Gausa, M.; Stebel, K.; Aaltonen, V.; Berjón, A.; de Galisteo, J.P.O.; de Frutos, A.M.; Bennouna, Y.; Blindheim, S.; et al. Overview of sun photometer measurements of aerosol properties in Scandinavia and Svalbard. Atmos. Environ. 2012, 52, 18–28. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J.; King, M.D.; Tanré, D.; Slutsker, I. Variability of absorption and optical properties of key aerosol types observed in worldwide locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar] [CrossRef]
- Hu, X.; Liu, J.; Sun, L.; Rong, Z.; Li, Y.; Zhang, Y.; Zheng, Z.; Wu, R.; Zhang, L.; Gu, X. Characterization of CRCS Dunhuang test site and vicarious calibration utilization for Fengyun (FY) series sensors. Can. J. Remote Sens. 2010, 36, 566–582. [Google Scholar] [CrossRef]
- Schmid, B.; Wehrli, C. Comparison of Sun photometer calibration by use of the Langley technique and the standard lamp. Appl. Opt. 1995, 34, 4500–4512. [Google Scholar] [CrossRef] [PubMed]
- Michalsky, J.J.; Liljegren, J.C.; Harrison, L.C. A comparison of sun photometer derivations of total column water vapor and ozone to standard measures of same at the southern great plains atmospheric radiation measurement site. J. Geophys. Res. Atmos. 1995, 100, 25995–26003. [Google Scholar] [CrossRef]
- Halthore, R.N.; Eck, T.F.; Holben, B.N.; Markham, B.L. Sun photometric measurements of atmospheric water vapor. J. Geophys. Res. Atmos. 1997, 102, 4243–4352. [Google Scholar] [CrossRef]
- Ichoku, C.; Levy, R.; Kaufman, Y.J.; Remer, L.A.; Li, R.-R.; Martins, V.-J.; Holben, B.N.; Abuhassan, N.; Slutsker, I.; Eck, T.F. Analysis of the performance characteristics of the five-channel Microtops II Sun photometer for measuring aerosol optical thickness and precipitable water vapor. J. Geophys. Res. 2002, 107. [Google Scholar] [CrossRef]
- Wu, S.H.; Liu, Z.S.; Liu, B.Y. Enhancement of lidar back scatters signal to noise ratio using empirical mode decomposition method. Opt. Commun. 2006, 267, 137–144. [Google Scholar] [CrossRef]
- Tian, P.; Cao, X.; Liang, J.; Zhang, L. Improved empirical mode decomposition based denoising method for lidar signals. Opt. Commun. 2014, 325, 54–59. [Google Scholar] [CrossRef]
- Zhou, Z.; Hua, D.; Wang, Y.; Yan, Q.; Li, S.; Li, Y.; Wang, H. Improvement of the signal to noise ratio of Lidar echo signal based on wavelet de-noising technique. Opt. Lasers Eng. 2013, 51, 961–966. [Google Scholar] [CrossRef]
- Mix, D.F.; Olejniczak, K.J. Elements of wavelets for engineers and scientists. Phys. Today 2005, 58, 54. [Google Scholar]
- Thakur, K.V.; Ambhore, P.G.; Sapkal, A.M. Novel technique for performance improvement of the wavelet based denoising algorithms using rotated wavelet filters. Procedia Comput. Sci. 2016, 79, 499–508. [Google Scholar] [CrossRef]
- Mallat, S.; Hwang, M.L. Singularity detection and processing with wavelet. IEEE Trans. IT 1992, 38, 617–643. [Google Scholar] [CrossRef]
- Tzabazis, A.; Eisenried, A.; Yeomans, D.C.; Hyatt, M., IV. Wavelet analysis of heart rate variability: Impact of wavelet selection. Biomed. Signal Process. Control 2018, 40, 220–225. [Google Scholar] [CrossRef]
- Genovese, L.; Neelov, A.; Goedecker, S.; Deutsch, T.; Ghasemi, S.A.; Willand, A.; Caliste, D.; Zilberberg, O.; Rayson, M.; Bergman, A.; et al. Daubechies wavelets as a basis set for density functional pseudopotential calculations. J. Chem. Phys. 2008, 129. [Google Scholar] [CrossRef] [PubMed]
- Abdolmaleki, M.; Tabaei, M.; Fathianpour, N.; Gorte, B.G.H. Selecting optimum base wavelet for extracting spectral alteration features associated with porphyry copper mineralization using hyperspectral images. Int. J. Appl. Earth Obs. Geoinform. 2017, 58, 134–144. [Google Scholar] [CrossRef]
- Luo, W.; Chen, F. Improved wavelet-denoising method. Infrared Laser Eng. 2008, 37, 226–228. [Google Scholar]
- Krim, H.; Tucker, D.; Mallat, S.; Donoho, D. On denoising and best signal representation. IEEE Trans. Inf. Theory 1997, 45, 2225–2238. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Threshold selection for wavelet shrinkage of noisy data. In Proceedings of the 16th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Baltimore, MD, USA, 3–6 November 1994. [Google Scholar]
- Cui, H.; Zhao, R.; Hou, Y. Improved threshold denoising method based on wavelet transform. Phys. Procedia 2012, 33, 1354–1359. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Tang, L.; Gao, T.; Wang, Q.; Lu, C.; Song, Y.; Hua, D. Investigation and Analysis of All-Day Atmospheric Water Vapor Content over Xi’an Using Raman Lidar and Sunphotometer Measurements. Remote Sens. 2018, 10, 951. https://doi.org/10.3390/rs10060951
Wang Y, Tang L, Gao T, Wang Q, Lu C, Song Y, Hua D. Investigation and Analysis of All-Day Atmospheric Water Vapor Content over Xi’an Using Raman Lidar and Sunphotometer Measurements. Remote Sensing. 2018; 10(6):951. https://doi.org/10.3390/rs10060951
Chicago/Turabian StyleWang, Yufeng, Liu Tang, Tianle Gao, Qing Wang, Chuan Lu, Yuehui Song, and Dengxin Hua. 2018. "Investigation and Analysis of All-Day Atmospheric Water Vapor Content over Xi’an Using Raman Lidar and Sunphotometer Measurements" Remote Sensing 10, no. 6: 951. https://doi.org/10.3390/rs10060951
APA StyleWang, Y., Tang, L., Gao, T., Wang, Q., Lu, C., Song, Y., & Hua, D. (2018). Investigation and Analysis of All-Day Atmospheric Water Vapor Content over Xi’an Using Raman Lidar and Sunphotometer Measurements. Remote Sensing, 10(6), 951. https://doi.org/10.3390/rs10060951



