A Ship Detector Applying Principal Component Analysis to the Polarimetric Notch Filter
Abstract
1. Introduction
2. Theoretical Background
2.1. Theory of Polarimetric SAR Data
2.2. Geometrical Perturbation-Polarimetric Notch Filter (GP-PNF)
2.3. Principal Component Analysis (PCA)
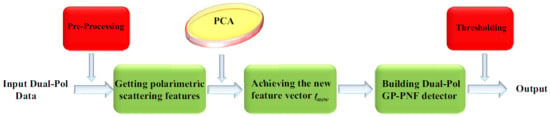
3. Methodology
3.1. Analysis of Polarimetric Features
3.2. Constructions of Scattering Vectors
- SV: It is the original feature vector of GP-PNF. We consider these features as they are the basic representations of the PolSAR data directly selected from the covariance matrix [C].
- SV: In this paper, we extend the 3D SV vector using three extra polarimetric features, i.e., SPAN, MTC and DoD. They have all been successfully used for ship detection and can effectively supplement the ship polarimetric information in the framework of GP-PNF.
- SV and SV: They are feature vectors derived by the first three axes of the basis resulting of PCA. SV has the same dimension as the original SV, but the basis used to represent it is different and it is shifted at the center of the data cluster. SV considers a reduction of dimension from 6 to 3 compared to the 6D SV vector.
3.3. The Proposed Ship Detection Method
| Algorithm 1 The proposed ship detection algorithm. |
| Input: The original SAR data D, , k, M, F, , , T. Output: The final result. Extracting the set of reliable negative and/or positive samples from with help of ; Converting D into covariance matrices for individual pixel; Set ; For to M; Get the six scattering features of the pixel based on D; Put these features into a vector F; Use PCA to transform F, and obtain a new vector ; Choose the first three columns of to form the final vector ; Adopt Equation (15) to calculate ; End For; Set a threshold T to output the final result. |
4. Results and Discussion
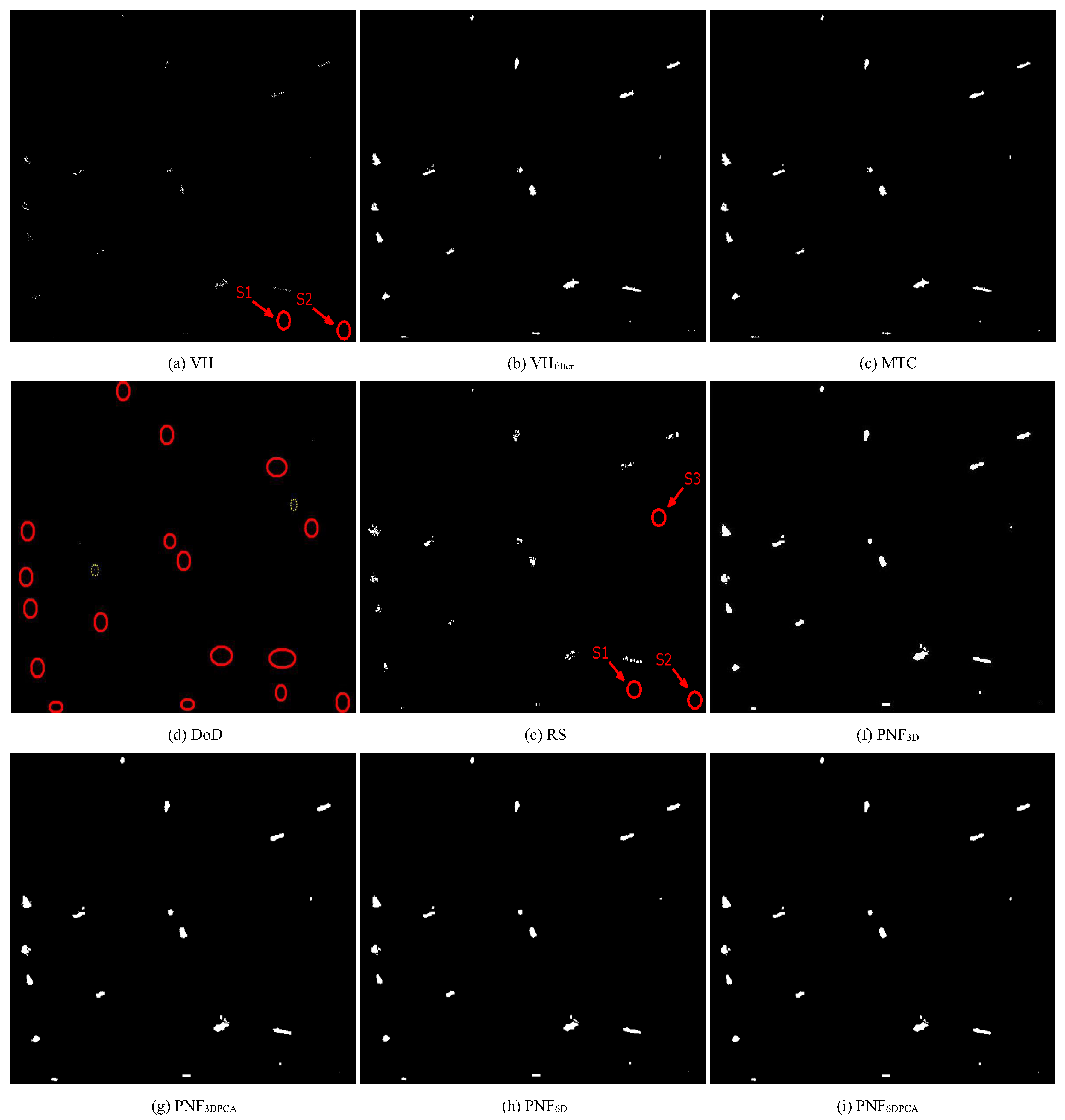
- VH : Amplitude of VH,
- MTC : Product of amplitudes VV and VH,
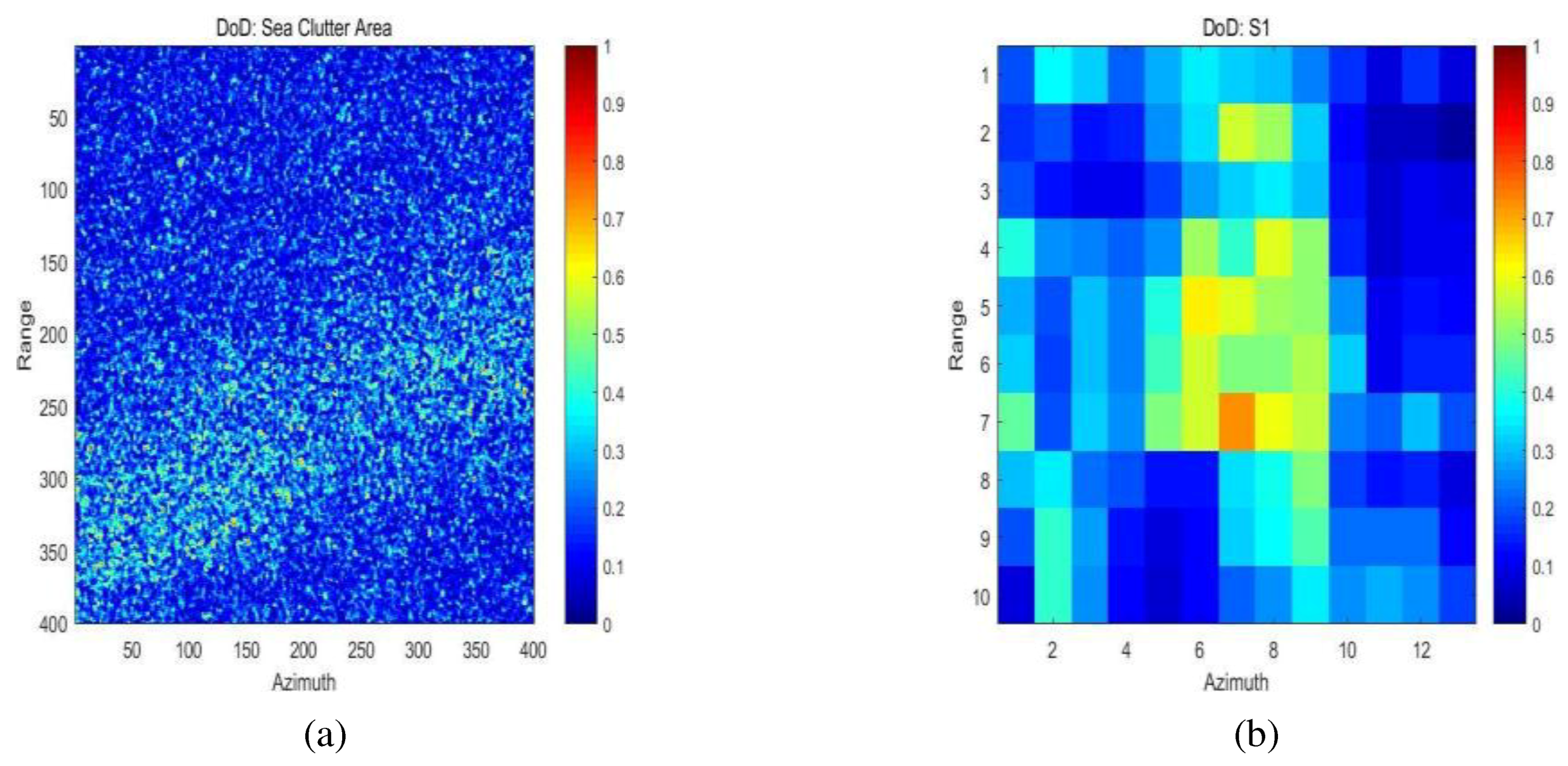
- DoD : Degree of depolarization,
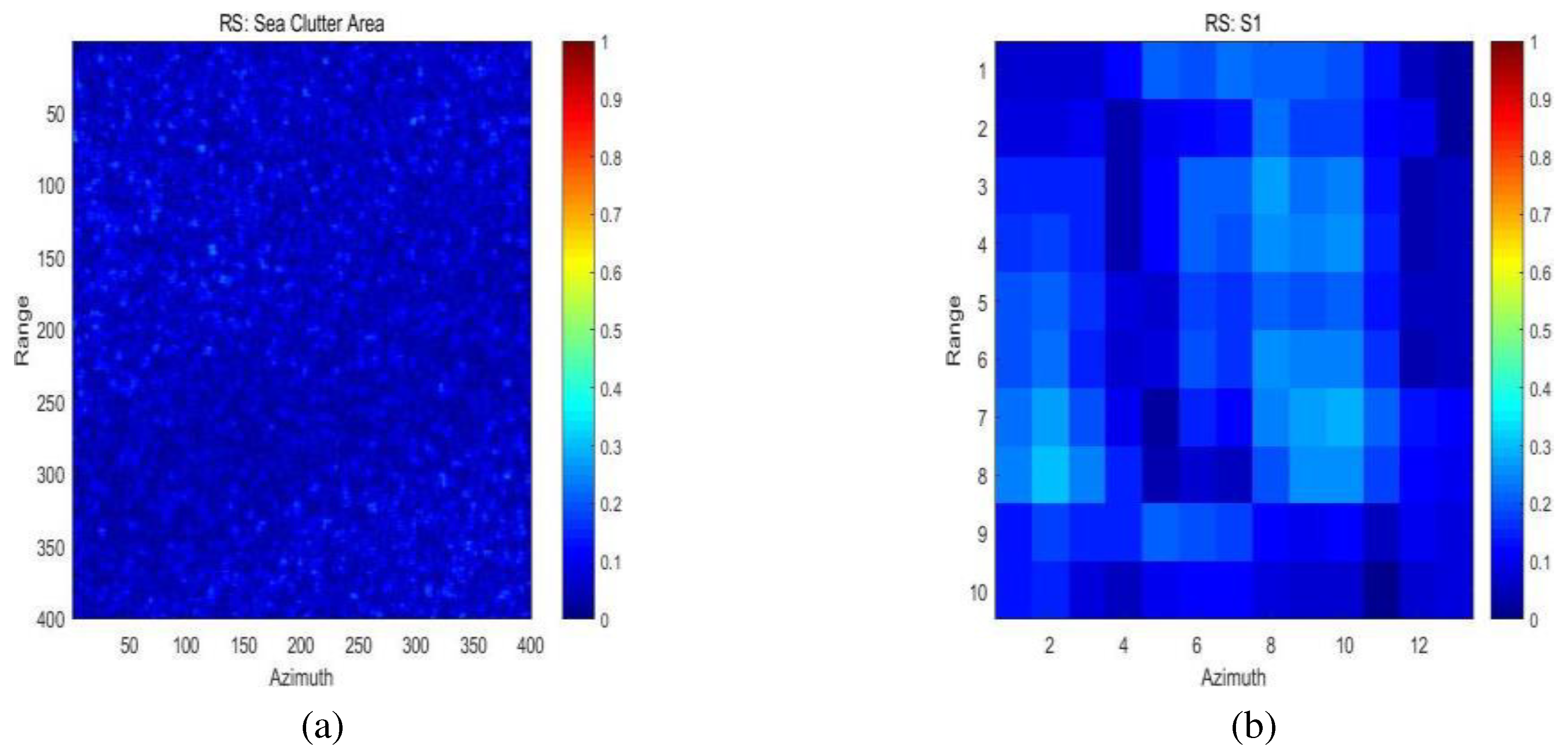
- RS : Reflection symmetry,
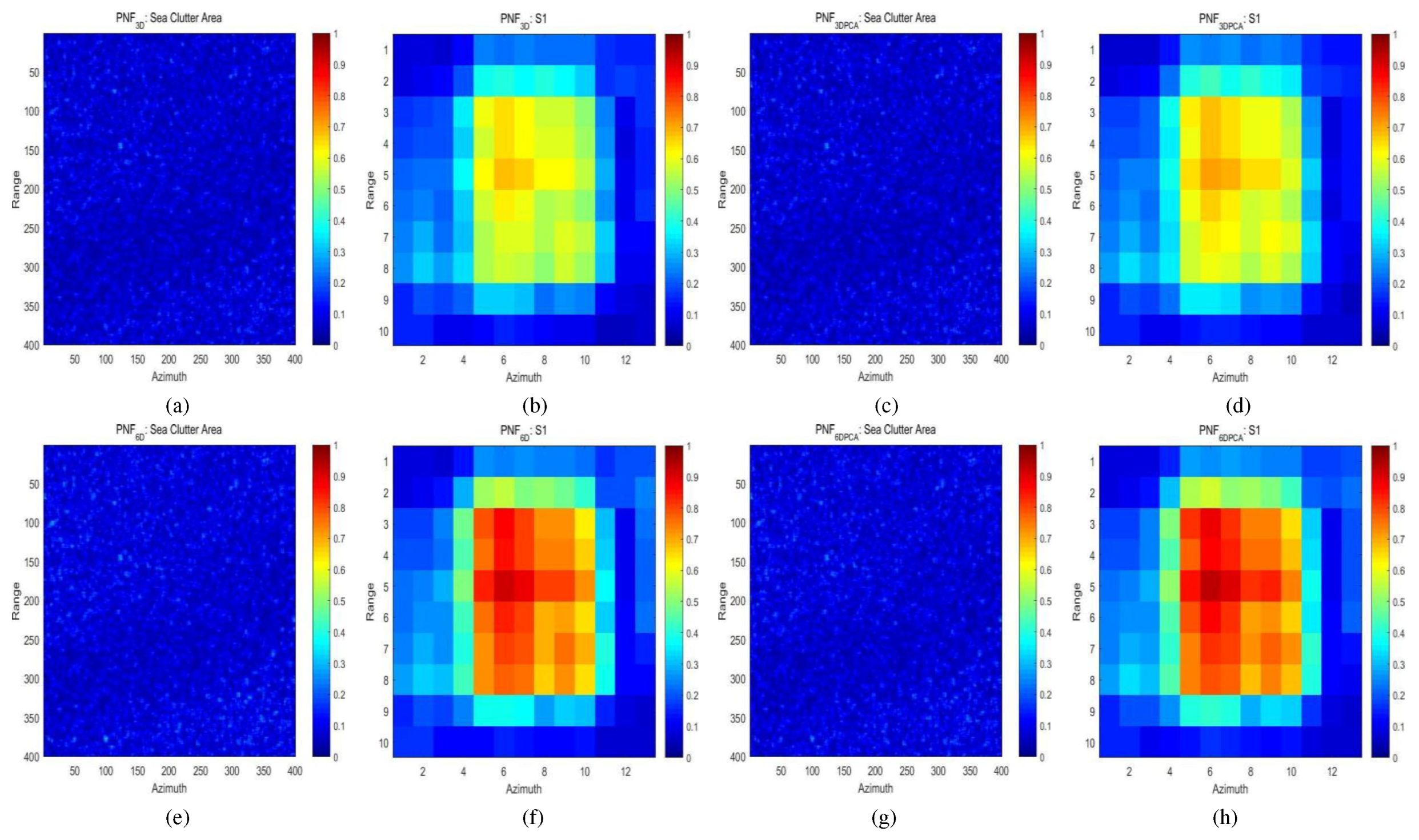
- PNF : Using the SV feature vector (Original),
- PNF : Using the SV feature vector (Proposed),
- PNF : Using the SV feature vector (Proposed),
- PNF : Using the SV feature vector (Proposed).
4.1. Datasets
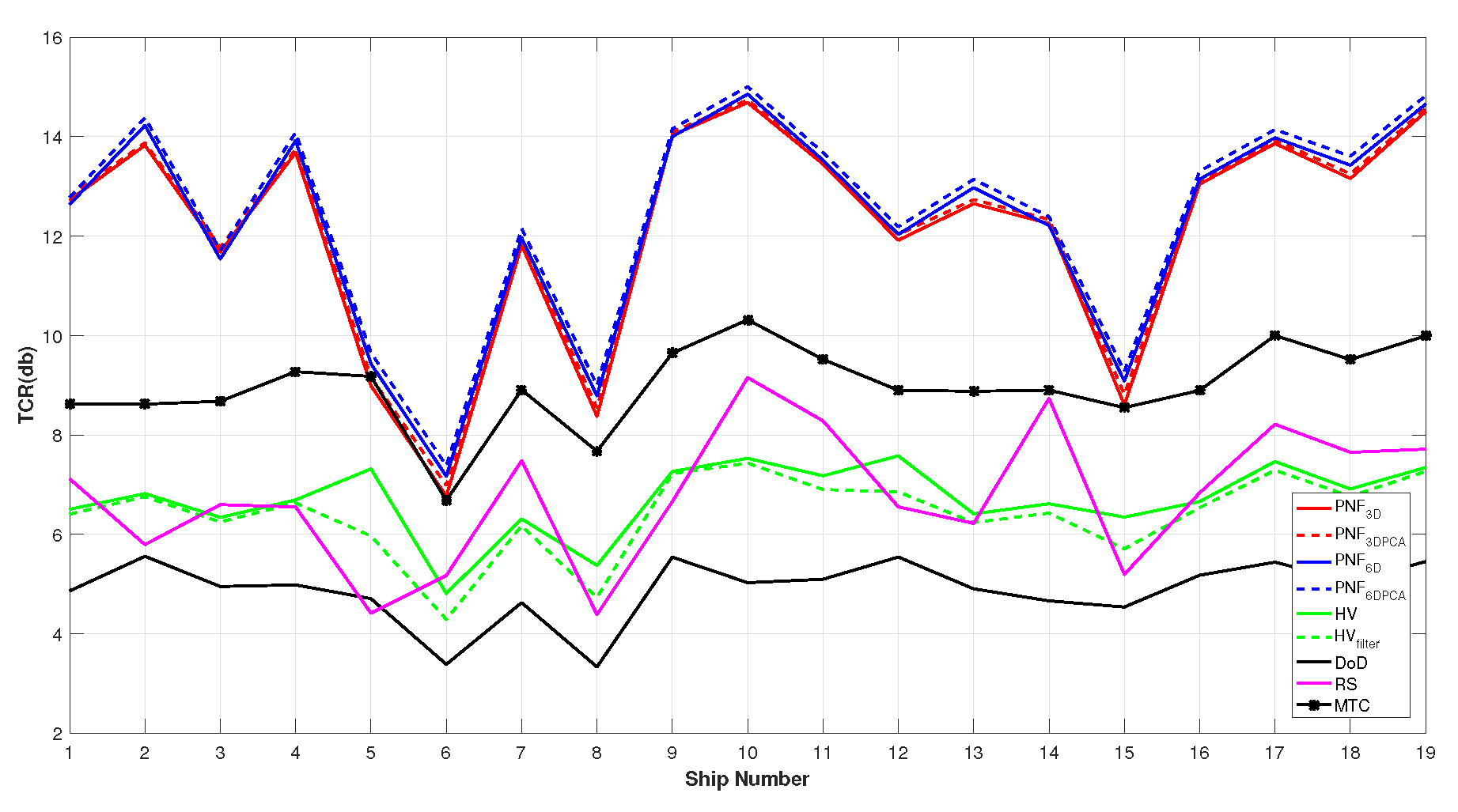
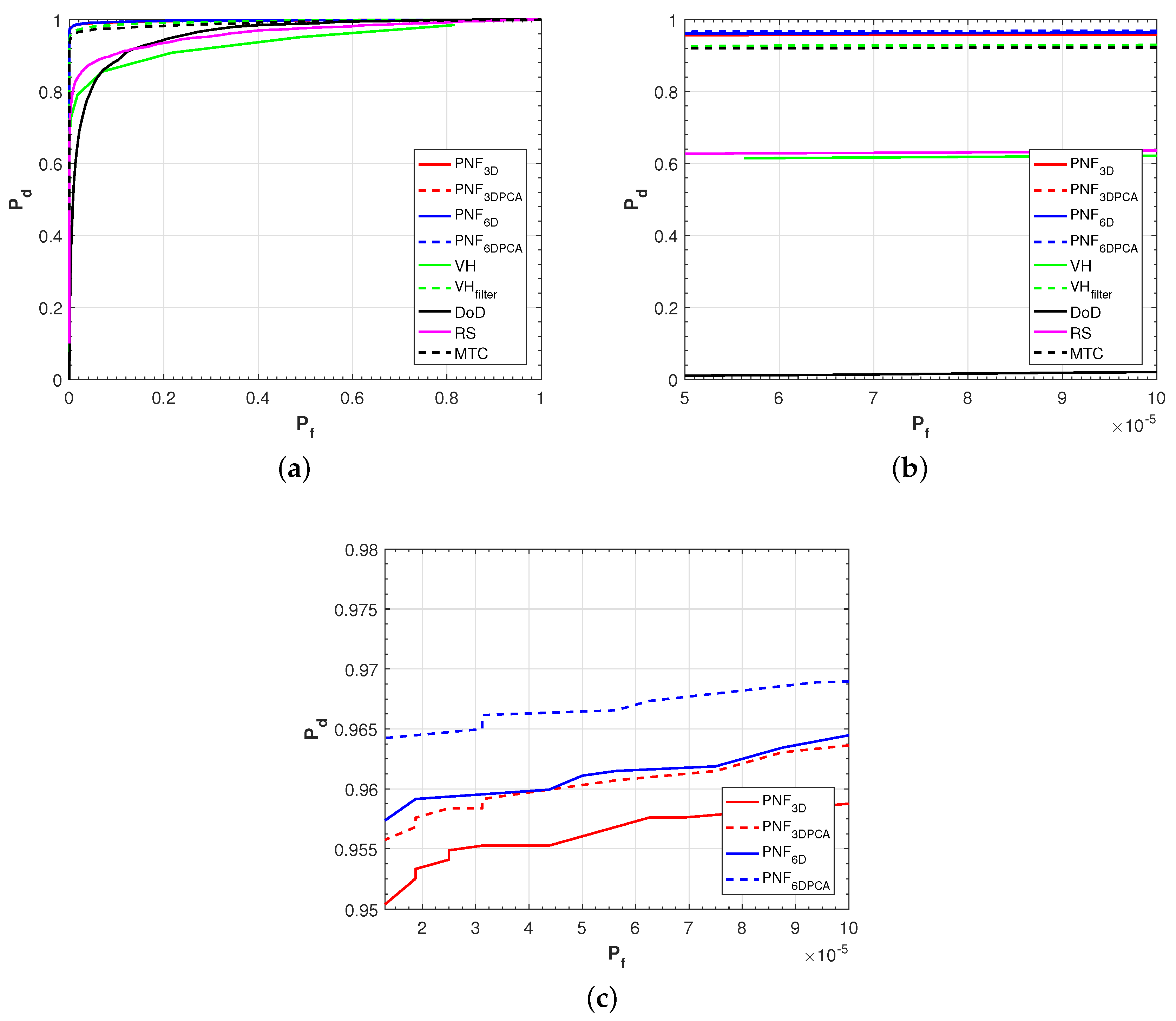
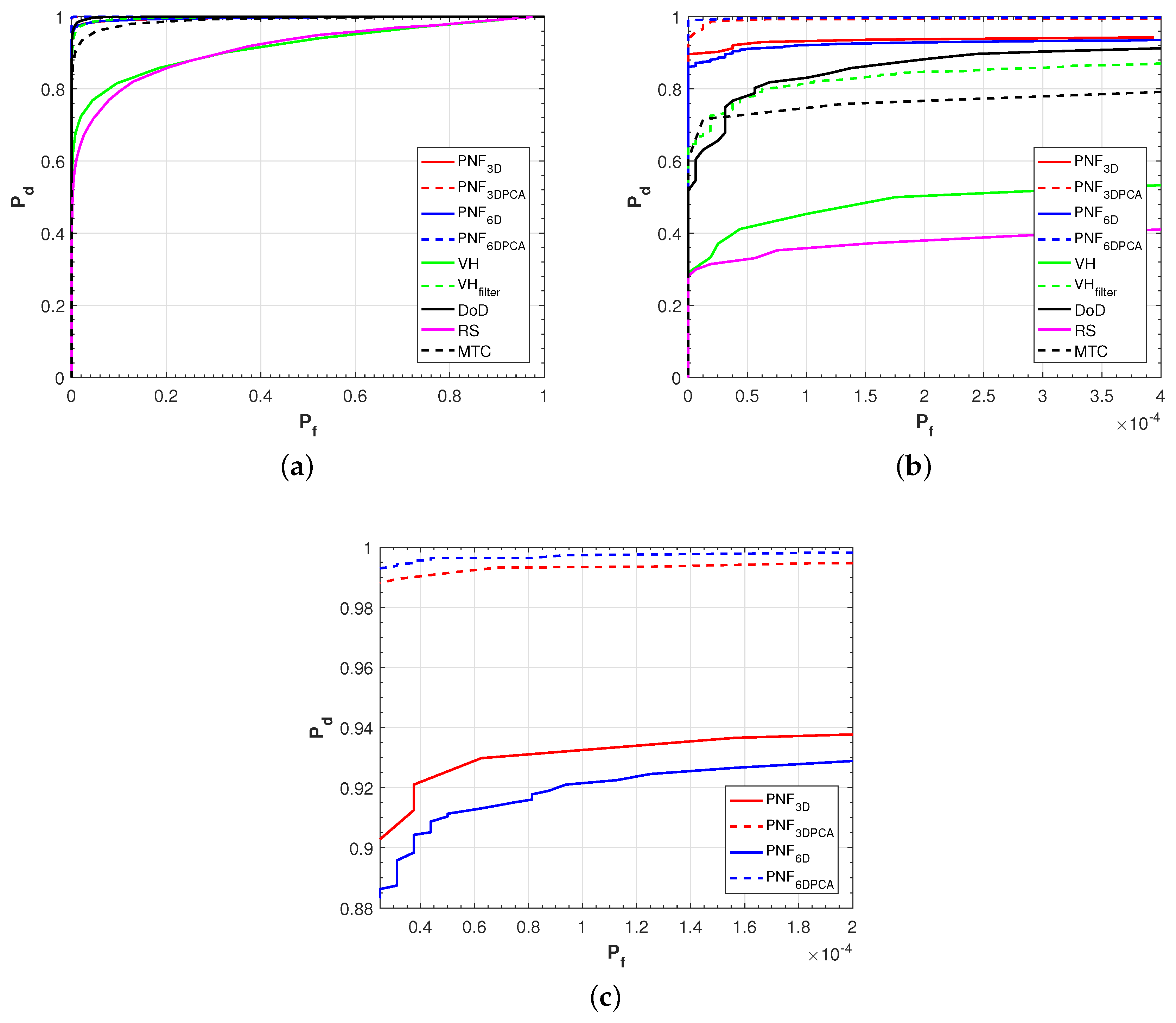
4.2. Evaluation Criteria
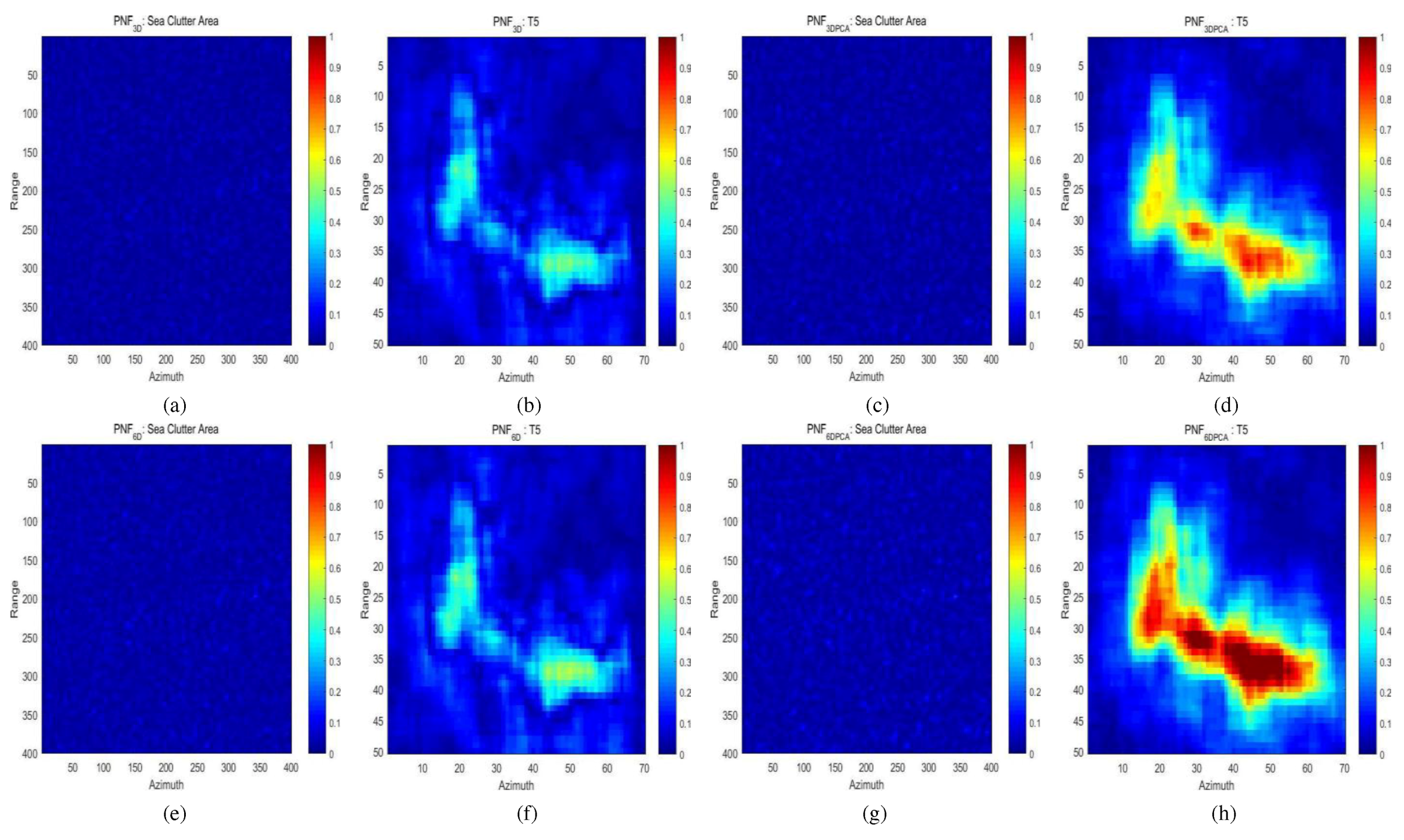
4.3. Results and Discussions on the First Sentinel-1 Dataset
4.4. Results and Discussions on the Second Sentinel-1 Dataset
4.5. Results and Discussions on the Third Sentinel-1 Dataset
4.6. Results and Discussions on the Fourth Sentinel-1 Dataset
5. Conclusions
- Adding more polarimetric features, which can more effectively reflect the difference between ships and clutter, in the original feature vector of the dual-pol GP-PNF method. Thus, the feature vector is extended from three to six dimensions.
- Based on the 6D vector, we use the PCA method to reduce again the space to three dimensions. The experiments tested on four real Sentinel-1 datasets confirm that the PCA operation is useful. In particular, the smaller ships can be more effectively detected after PCA when the ocean condition is higher. Meanwhile, we also demonstrate that only adding polarimetric features in the feature vector may be not effective when high sea condition appears.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lessing, P.; Bernard, L.; Tetreault, B.; Chaffin, J. Use of the automatic identification system (AIS) on autonomous weather buoys for maritime domain awareness applications. In Proceedings of the OCEANS 2006, Boston, MA, USA, 18–21 September 2006; pp. 1–6. [Google Scholar]
- Velotto, D.; Soccorsi, M.; Lehner, S. Azimuth ambiguities removal for ship detection using full polarimetric X-band SAR data. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 7621–7624. [Google Scholar]
- Lee, J.S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Copeland, A.C.; Ravichandran, G.; Trivedi, M.M. Localized Radon transform-based detection of ship wakes in SAR images. IEEE Trans. Geosci. Remote Sens. 1995, 33, 35–45. [Google Scholar] [CrossRef]
- Vachon, P.; Campbell, J.; Bjerkelund, C.; Dobson, F.; Rey, M. Ship detection by the RADARSAT SAR: Validation of detection model predictions. Can. J. Remote Sens. 1997, 23, 48–59. [Google Scholar] [CrossRef]
- Eldhuset, K. An automatic ship and ship wake detection system for spaceborne SAR images in coastal regions. IEEE Trans. Geosci. Remote Sens. 1996, 34, 1010–1019. [Google Scholar] [CrossRef]
- Leng, X.; Ji, K.; Yang, K.; Zou, H. A bilateral CFAR algorithm for ship detection in SAR images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1536–1540. [Google Scholar] [CrossRef]
- Tello, M.; López-Martínez, C.; Mallorqui, J.J. A novel algorithm for ship detection in SAR imagery based on the wavelet transform. IEEE Geosci. Remote Sens. Lett. 2005, 2, 201–205. [Google Scholar] [CrossRef]
- Chaney, R.; Burl, M.; Novak, L. On the performance of polarimetric target detection algorithms. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 7–10 May 1990; pp. 520–525. [Google Scholar]
- Goodman, N.R. Statistical analysis based on a certain multivariate complex Gaussian distribution (an introduction). Ann. Math. Stat. 1963, 34, 152–177. [Google Scholar] [CrossRef]
- Novak, L.M.; Burl, M.C.; Irving, W.; Owirka, G. Optimal polarimetric processing for enhanced target detection. In Proceedings of the National Telesystems Conference, Atlanta, GA, USA, 26–27 March 1991; pp. 69–75. [Google Scholar]
- Liu, T.; Lampropoulos, G. A new polarimetric CFAR ship detection system. In Proceedings of the Geoscience and Remote Sensing Symposium (IGARSS), Denver, CO, USA, 31 July–4 August 2006; pp. 137–140. [Google Scholar]
- Sugimoto, M.; Ouchi, K.; Nakamura, Y. On the novel use of model-based decomposition in SAR polarimetry for target detection on the sea. Remote Sens. Lett. 2013, 4, 843–852. [Google Scholar] [CrossRef]
- Wang, J.; Huang, W.; Yang, J.; Chen, P.; Zhang, H. Polarization scattering characteristics of some ships using polarimetric SAR images. In Proceedings of the International Society for Optics and Photonics SAR Image Analysis, Modeling, and Techniques XI, Prague, Czech Republic, 19–22 September 2011; Volume 8179, p. 81790W. [Google Scholar]
- Touzi, R.; Charbonneau, F. Characterization of target symmetric scattering using polarimetric SARs. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2507–2516. [Google Scholar] [CrossRef]
- Cameron, W.L.; Youssef, N.N.; Leung, L.K. Simulated polarimetric signatures of primitive geometrical shapes. IEEE Trans. Geosci. Remote Sens. 1996, 34, 793–803. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Nunziata, F.; Migliaccio, M.; Brown, C.E. Reflection symmetry for polarimetric observation of man-made metallic targets at sea. IEEE J. Ocean. Eng. 2012, 37, 384–394. [Google Scholar] [CrossRef]
- Yang, J.; Peng, Y.N.; Lin, S.M. Similarity between two scattering matrices. Electron. Lett. 2001, 37, 193–194. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, H.; Yamaguchi, Y. GOPCE-based approach to ship detection. IEEE Geosci. Remote Sens. Lett. 2012, 9, 1089–1093. [Google Scholar] [CrossRef]
- Marino, A.; Woodhouse, I.H. Selectable target detector using the polarization fork. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Cape Town, South Africa, 12–17 July 2009; Volume 3. [Google Scholar]
- Marino, A.; Cloude, S.R.; Woodhouse, I.H. Detecting depolarized targets using a new geometrical perturbation filter. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3787–3799. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H. PolSAR ship detection based on superpixel-level scattering mechanism distribution features. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1780–1784. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, Z.; Xiong, H.; Yu, W. Ship detection based on the power of the Radarsat-2 polarimetric data. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1254–1257. [Google Scholar]
- Zhang, T.; Yang, Z.; Xiong, H. PolSAR Ship Detection Based on the Polarimetric Covariance Difference Matrix. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3348–3359. [Google Scholar] [CrossRef]
- MacDonald, Dettwiler and Associates Ltd. Available online: https://mdacorporation.com/docs/default-source/technical-documents/geospatial-services/52-1238_rs2_product_description.pdf?sfvrsn=10 (accessed on 21 March 2016).
- Sentinel-1 Document Library. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-1-sar/document-library/-/asset_publisher/1dO7RF5fJMbd/content/sentinel-1-product-definition (accessed on 25 March 2016).
- Velotto, D.; Bentes, C.; Tings, B.; Lehner, S. First comparison of Sentinel-1 and TerraSAR-X data in the framework of maritime targets detection: South Italy case. IEEE J. Ocean. Eng. 2016, 41, 993–1006. [Google Scholar] [CrossRef]
- Vachon, P.W.; Wolfe, J.; Greidanus, H. Analysis of Sentinel-1 marine applications potential. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 1734–1737. [Google Scholar]
- Pelich, R.; Longépé, N.; Mercier, G.; Hajduch, G.; Garello, R. Performance evaluation of Sentinel-1 data in SAR ship detection. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 2103–2106. [Google Scholar]
- Jolliffe, I.T. Principal component analysis and factor analysis. In Principal Component Analysis; Springer: New York, NY, USA, 1986; pp. 115–128. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital image processing. Prentice Hall Int. 1977, 28, 484–486. [Google Scholar]
- Ready, P.; Wintz, P. Information extraction, SNR improvement, and data compression in multispectral imagery. IEEE Trans. Commun. 1973, 21, 1123–1131. [Google Scholar] [CrossRef]
- Eklundh, L.; Singh, A. A comparative analysis of standardised and unstandardised principal components analysis in remote sensing. Int. J. Remote Sens. 1993, 14, 1359–1370. [Google Scholar] [CrossRef]
- Lee, J.S.; Hoppel, K.W.; Mango, S.A.; Miller, A.R. Intensity and phase statistics of multilook polarimetric and interferometric SAR imagery. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1017–1028. [Google Scholar]
- Gao, G.; Luo, Y.; Ouyang, K.; Zhou, S. Statistical modeling of PMA detector for ship detection in high-resolution dual-polarization SAR images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4302–4313. [Google Scholar] [CrossRef]
- Marino, A. A New Target Detector Based on Geometrical Perturbation Filters for Polarimetric Synthetic Aperture Radar (POL-SAR); Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Marino, A.; Cloude, S.R.; Woodhouse, I.H. A polarimetric target detector using the Huynen fork. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2357–2366. [Google Scholar] [CrossRef]
- Marino, A.; Cloude, S.R.; Lopez-Sanchez, J.M. A new polarimetric change detector in radar imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2986–3000. [Google Scholar] [CrossRef]
- Marino, A. A notch filter for ship detection with polarimetric SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1219–1232. [Google Scholar] [CrossRef]
- Tipping, M.E.; Bishop, C.M. Probabilistic principal component analysis. J. R. Stat. Soc. Ser. B 1999, 61, 611–622. [Google Scholar] [CrossRef]
- Zhang, T.; Marino, A.; Xiong, H. A ship detection applying principal component analysis to the polarimetric notch filter. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1864–1867. [Google Scholar]
- Thomaz, C.E.; Giraldi, G.A. A new ranking method for principal components analysis and its application to face image analysis. Image Vis. Comput. 2010, 28, 902–913. [Google Scholar] [CrossRef]
- Hajnsek, I.; Pottier, E.; Cloude, S.R. Inversion of surface parameters from polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 2003, 41, 727–744. [Google Scholar] [CrossRef]
- Arnesen, T.N.; Olsen, R.B.; Weydahl, D.J. Ship detection signatures in AP mode data. In Proceedings of the 56th International Astronautical Congress, Fukuoka, Japan, 17–21 October 2005. [Google Scholar]
- Hannevik, T.N.A. Multi-channel and multi-polarisation ship detection. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 5149–5152. [Google Scholar]
- Hannevik, T.N. Polarisation and mode combinations for ship detection using radarsat-2. In Proceedings of the IEEE Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; pp. 3676–3679. [Google Scholar]
- Green, P. Radar measurements of target scattering properties. In Radar Astronomy; Evans, J.V., Hagfors, T., Eds.; McGraw–Hill: New York, NY, USA, 1968; pp. 1–78. [Google Scholar]
- Shirvany, R.; Chabert, M.; Tourneret, J.Y. Ship and oil-spill detection using the degree of polarization in linear and hybrid/compact dual-pol SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 885–892. [Google Scholar] [CrossRef]
- Touzi, R.; Hurley, J.; Vachon, P.W. Optimization of the degree of polarization for enhanced ship detection using polarimetric RADARSAT-2. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5403–5424. [Google Scholar] [CrossRef]
- UK Met Office. Available online: http://www.metoffice.gov.uk/public/weather (accessed on 10 May 2017).
- National Meteorological Center of CMA. Available online: http://eng.nmc.cn/ (accessed on 18 June 2017).




| Name | Vector Description | Dimension |
|---|---|---|
| SV | [,,] | 3 |
| SV(Improved) | The first three columns of PCA feature matrix using SV | 3 |
| SV(Improved) | [,,, | 6 |
| ,,] | ||
| SV(Improved) | The first three columns of PCA feature matrix using SV | 3 |
| Scene | Product | Polarization | Range Pixel | Azimuth Pixel | PRF | Azimuth | Range | Wind | Time | Data |
|---|---|---|---|---|---|---|---|---|---|---|
| Type | Space (m) | Space (m) | (Hz) | Looks | Looks | Level | Site | |||
| A | SLC | VV/VH | 2.3296 | 14.0117 | 1717.129 | 1 | 1 | 1–3 | 25 November 2015 23:31:23 | Panama City |
| B | SLC | VV/VH | 2.3296 | 13.9372 | 1717.129 | 1 | 1 | 3–5 | 13 June 2016 18:17:46 | Gibraltar |
| C | SLC | VV/VH | 2.3296 | 13.8990 | 1717.129 | 1 | 1 | 6–9 | 12 January 2017 17:56:51 | English Channel |
| D | SLC | VV/VH | 2.3296 | 13.9556 | 1717.129 | 1 | 1 | 6–7 | 12 December 2016 09:45:56 | East China Sea |
| Methods | VH | VH | MTC | DoD | RS | PNF | PNF | PNF | PNF | TCR | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ships | (None) | (3 × 3) | (3 × 3) | (3 × 3) | (7 × 7) | ||||||
| S1 (L:33 m, W:14 m) | |||||||||||
| S2 (L:72 m, W:24 m) | |||||||||||
| S3 (L:65 m, W:10 m) | |||||||||||
| S4 (L:125 m, W:20 m) | |||||||||||
| Methods | VH | VH | MTC | DoD | RS | PNF | PNF | PNF | PNF | TCR | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ships | (none) | (3 × 3) | (3 × 3) | (3 × 3) | (7 × 7) | ||||||
| T1 (L:166 m, W:54 m) | |||||||||||
| T2 (L:198 m, W:70 m) | |||||||||||
| T3 (L:174 m, W:63 m) | |||||||||||
| T4 (L:120 m, W:41 m) | |||||||||||
| T5 (L:160 m, W:50 m) | |||||||||||
| T6 (L:224 m, W:73 m) | |||||||||||
| T7 (L:204 m, W:58 m) | |||||||||||
| T8 (L:64 m, W:27 m) | |||||||||||
| T9 (L:108 m, W:40 m) | |||||||||||
| T10 (L:168 m, W:56 m) | |||||||||||
| T11 (L:130 m, W:46 m) | |||||||||||
| T12 (L:150 m, W:51 m) | |||||||||||
| T13 (L:147 m, W:49 m) | |||||||||||
| T14 (L:48 m, W:23 m) | |||||||||||
| T15 (L:285 m, W:48 m) | |||||||||||
| T16 (L:96 m, W:27 m) | |||||||||||
| T17 (L:138 m, W:30 m) | |||||||||||
| T18 (L:278 m, W:84 m) | |||||||||||
| T19 (L:54 m, W:24 m) | |||||||||||
| T20 (L:181 m, W:53 m) | |||||||||||
| T21 (L:126 m, W:33 m) | |||||||||||
| T22 (L:173 m, W:52 m) | |||||||||||
| T23 (L:133 m, W:31 m) | |||||||||||
| T24 (L:64 m, W:15 m) | |||||||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Marino, A.; Xiong, H.; Yu, W. A Ship Detector Applying Principal Component Analysis to the Polarimetric Notch Filter. Remote Sens. 2018, 10, 948. https://doi.org/10.3390/rs10060948
Zhang T, Marino A, Xiong H, Yu W. A Ship Detector Applying Principal Component Analysis to the Polarimetric Notch Filter. Remote Sensing. 2018; 10(6):948. https://doi.org/10.3390/rs10060948
Chicago/Turabian StyleZhang, Tao, Armando Marino, Huilin Xiong, and Wenxian Yu. 2018. "A Ship Detector Applying Principal Component Analysis to the Polarimetric Notch Filter" Remote Sensing 10, no. 6: 948. https://doi.org/10.3390/rs10060948
APA StyleZhang, T., Marino, A., Xiong, H., & Yu, W. (2018). A Ship Detector Applying Principal Component Analysis to the Polarimetric Notch Filter. Remote Sensing, 10(6), 948. https://doi.org/10.3390/rs10060948