Low-Frequency Sea Surface Radar Doppler Echo
Abstract
:1. Introduction
2. Methods
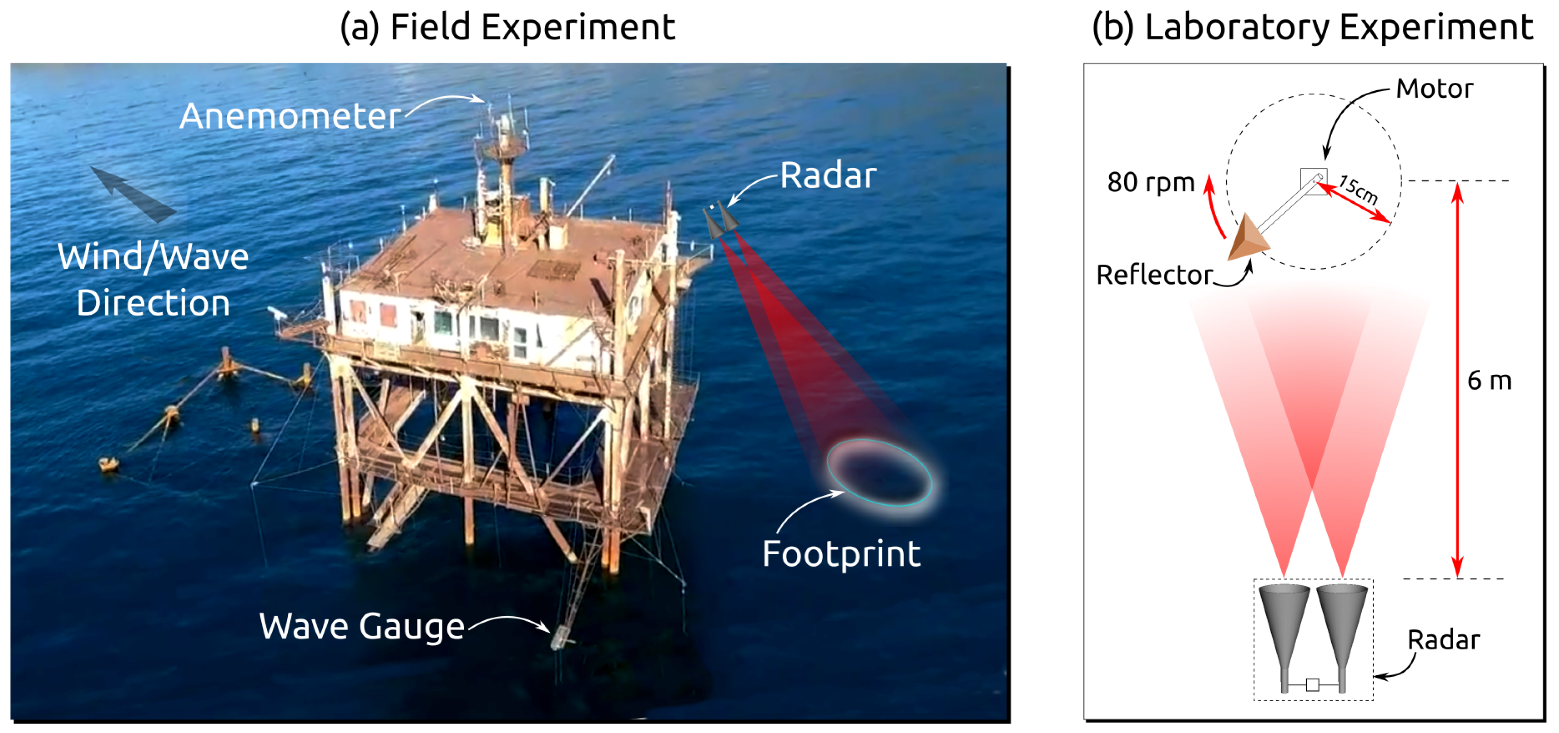
2.1. Field Experiment
2.2. Analyzed Parameters and Their Relations
2.3. System Noise Estimation
3. Results
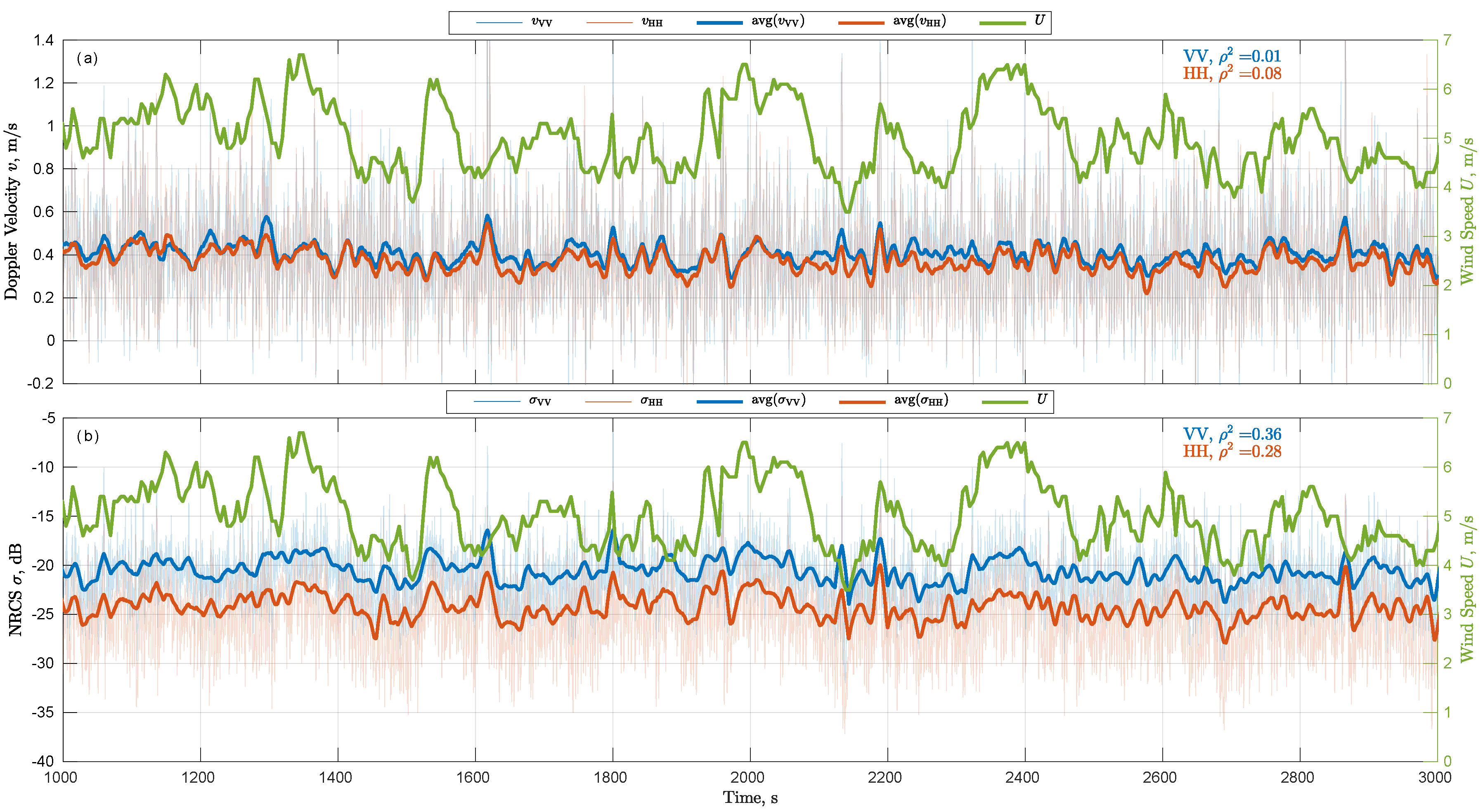
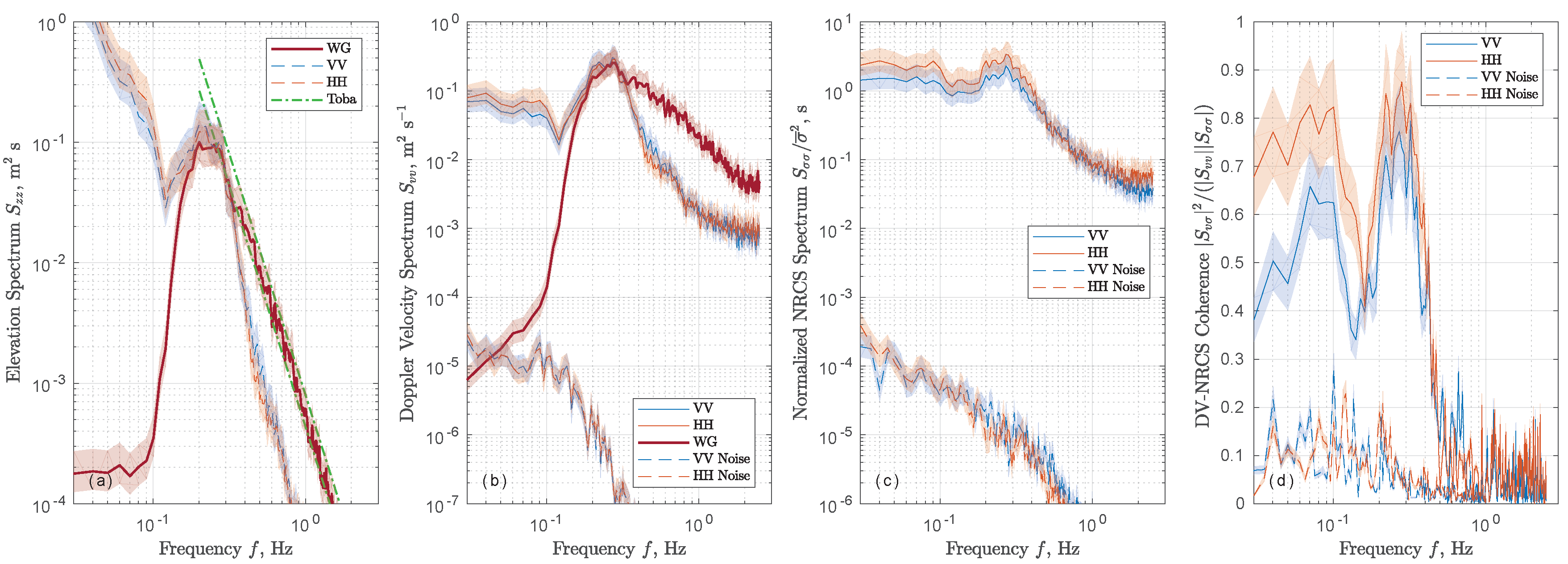
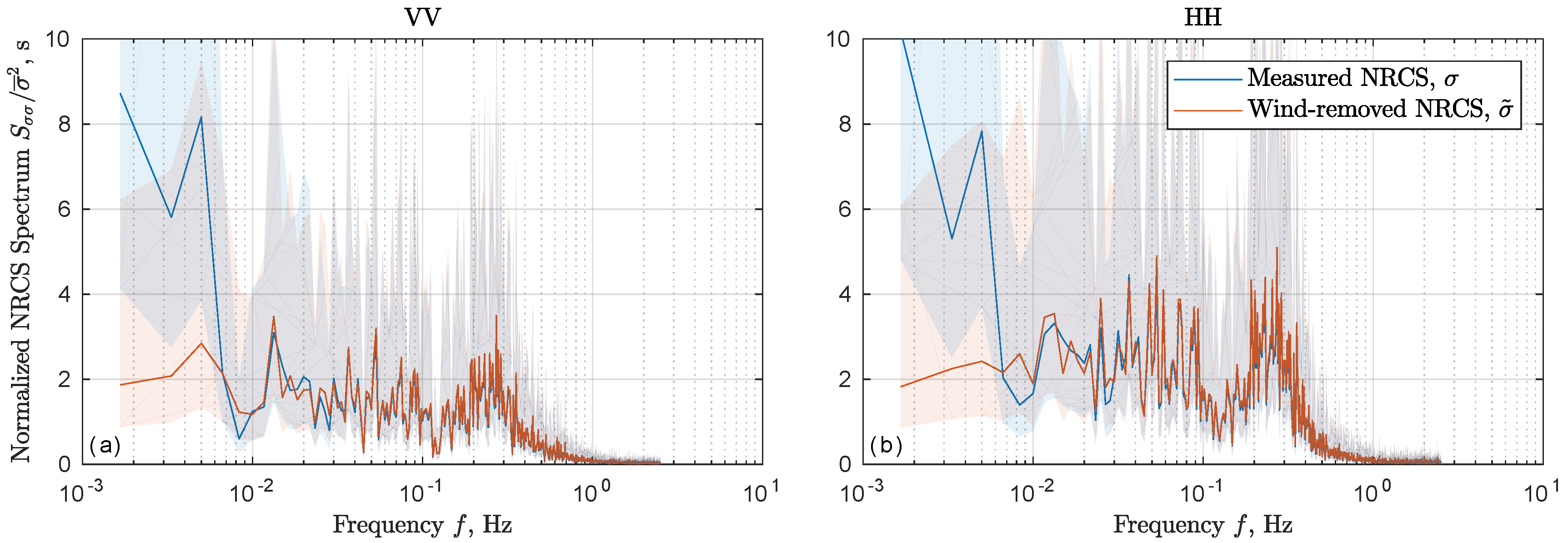
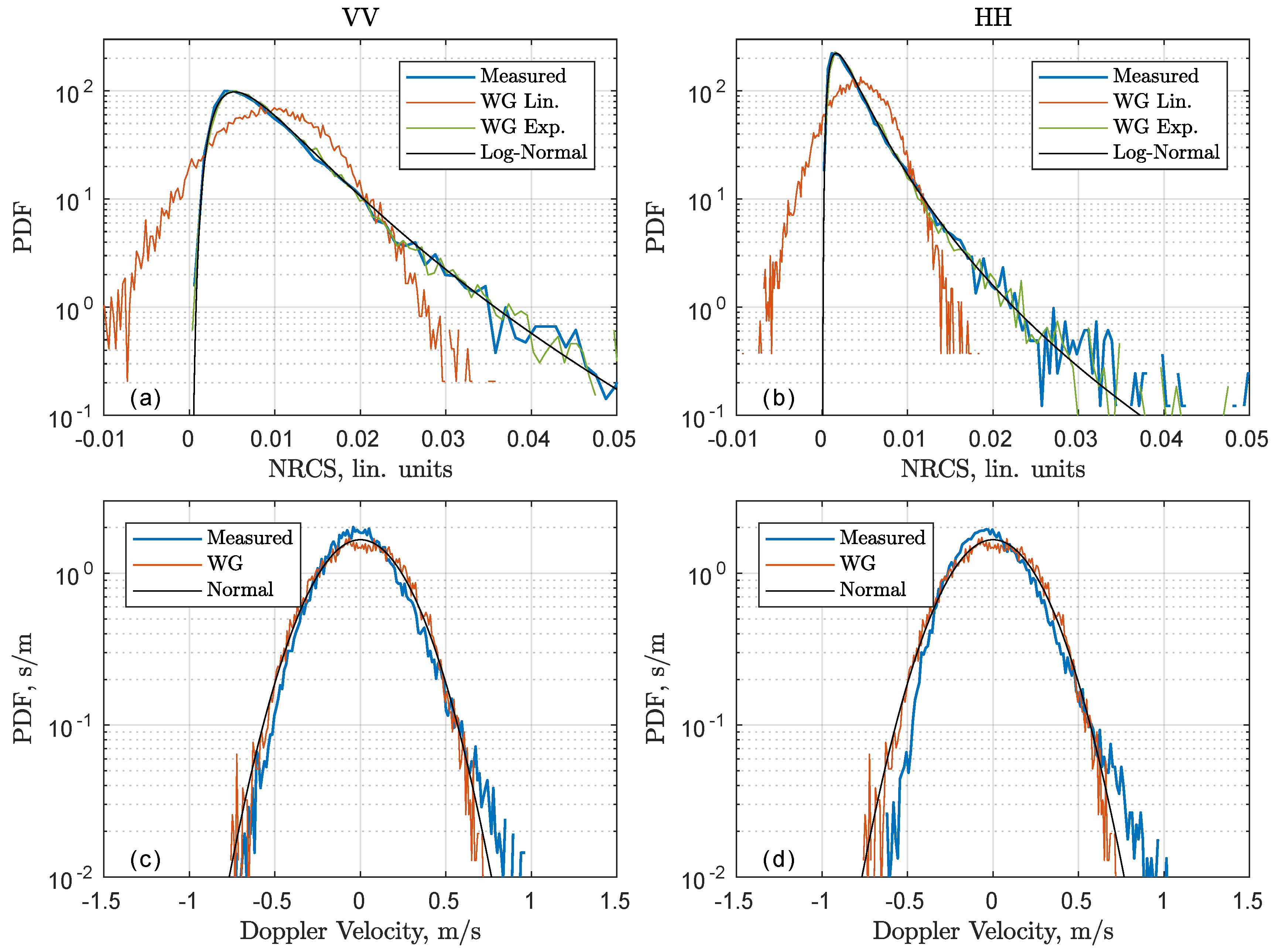
3.1. Observed Low-Frequency Signatures
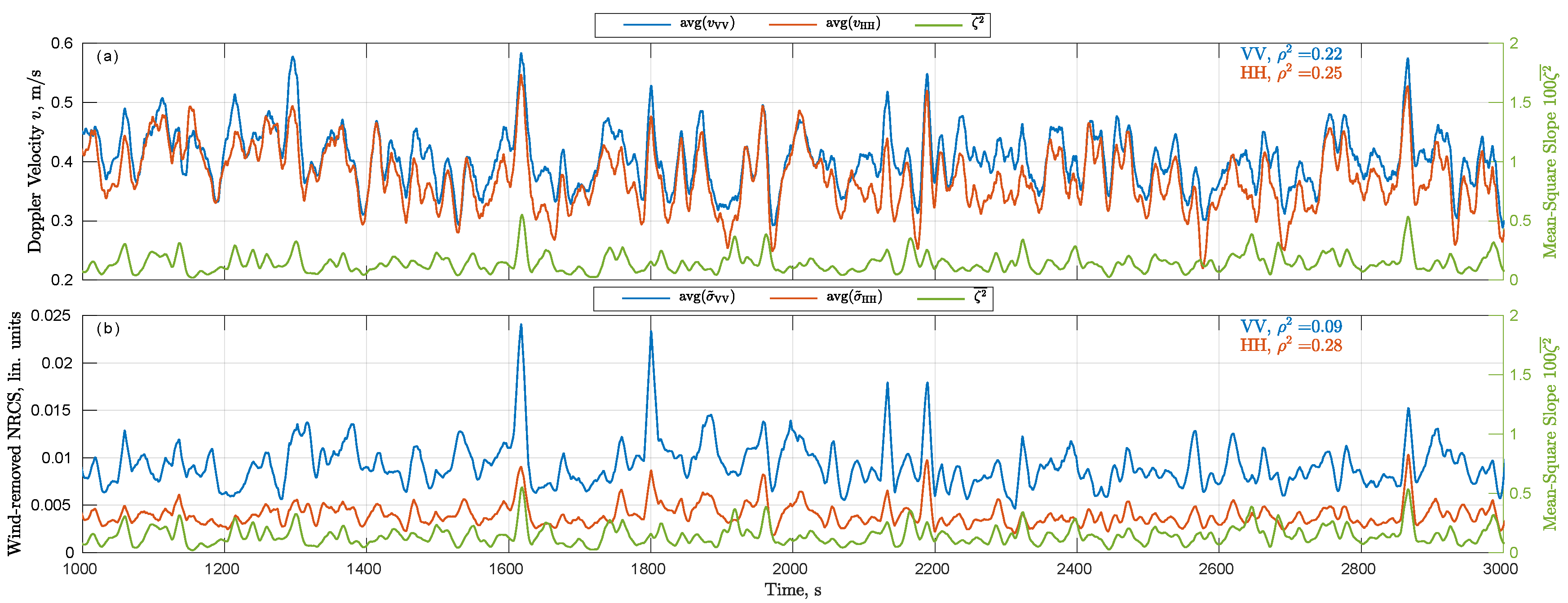
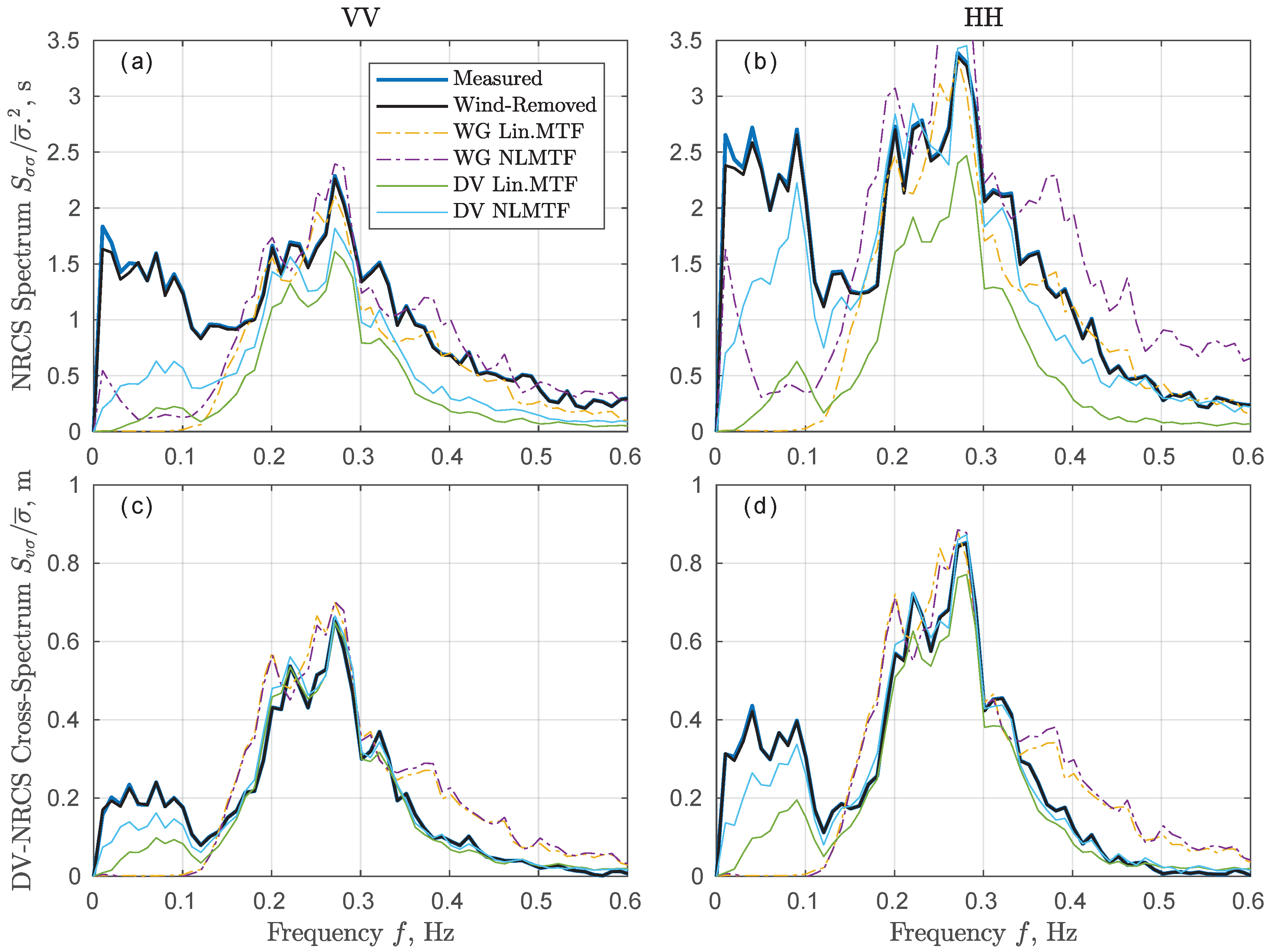
3.2. Non-Linear Transfer Function
4. Discussion
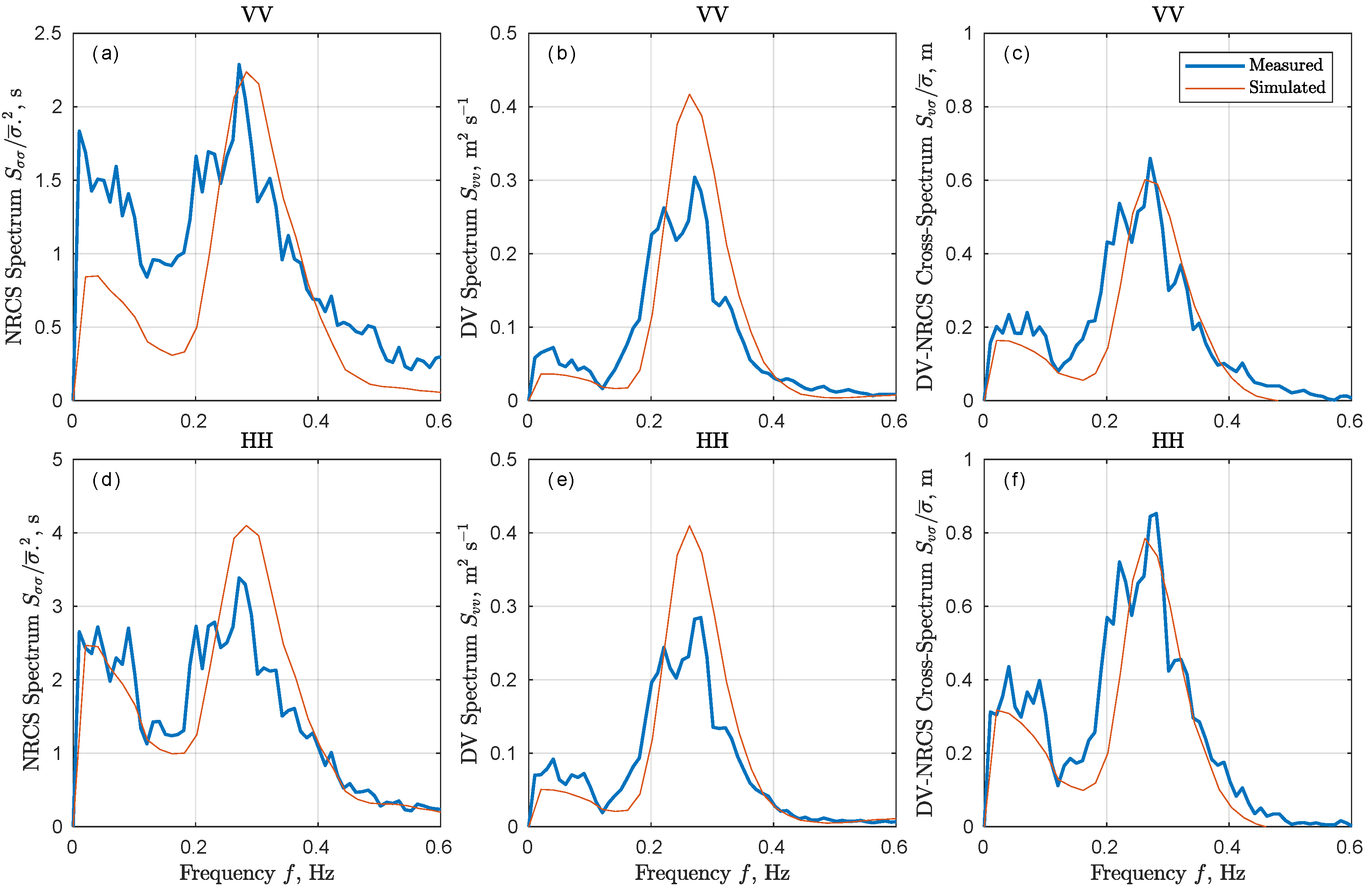
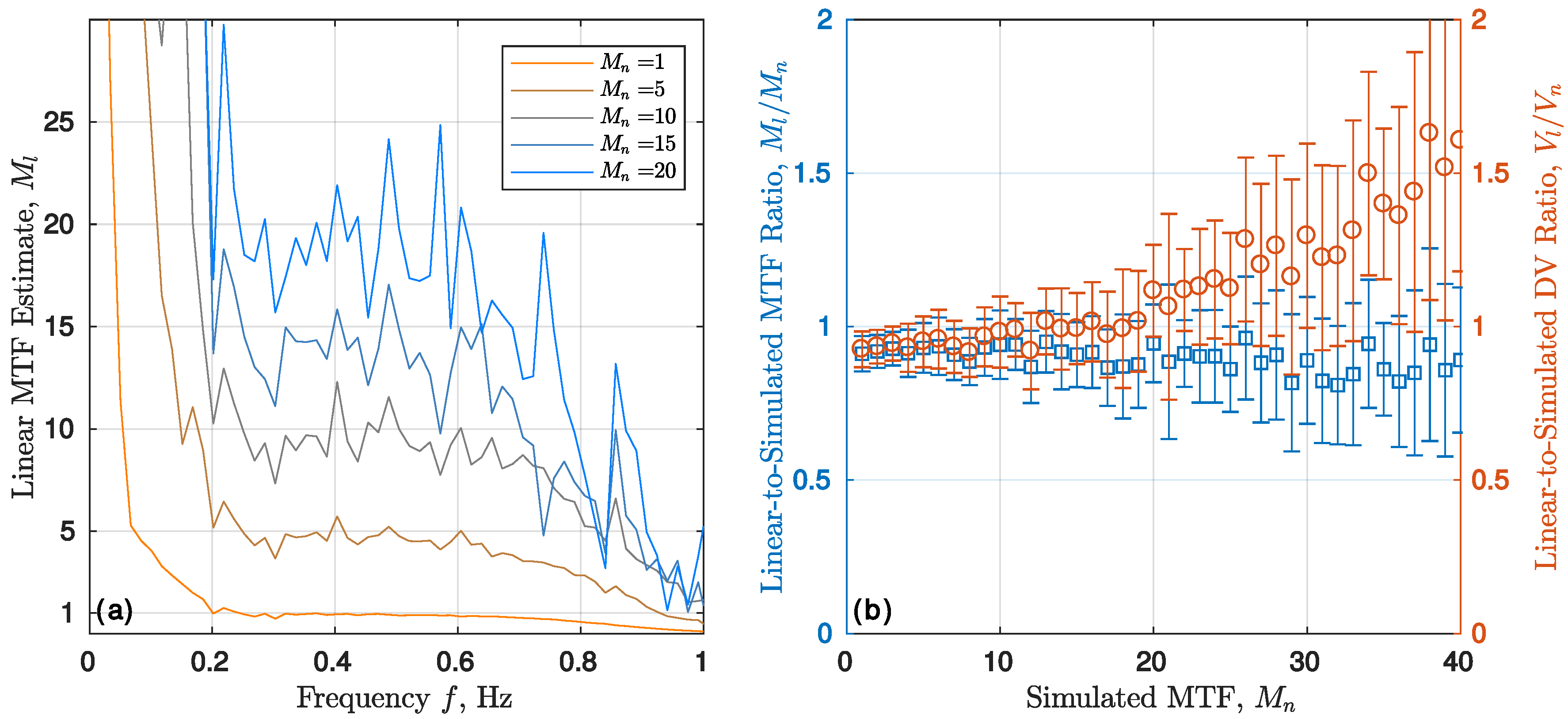
4.1. Numerical Simulation
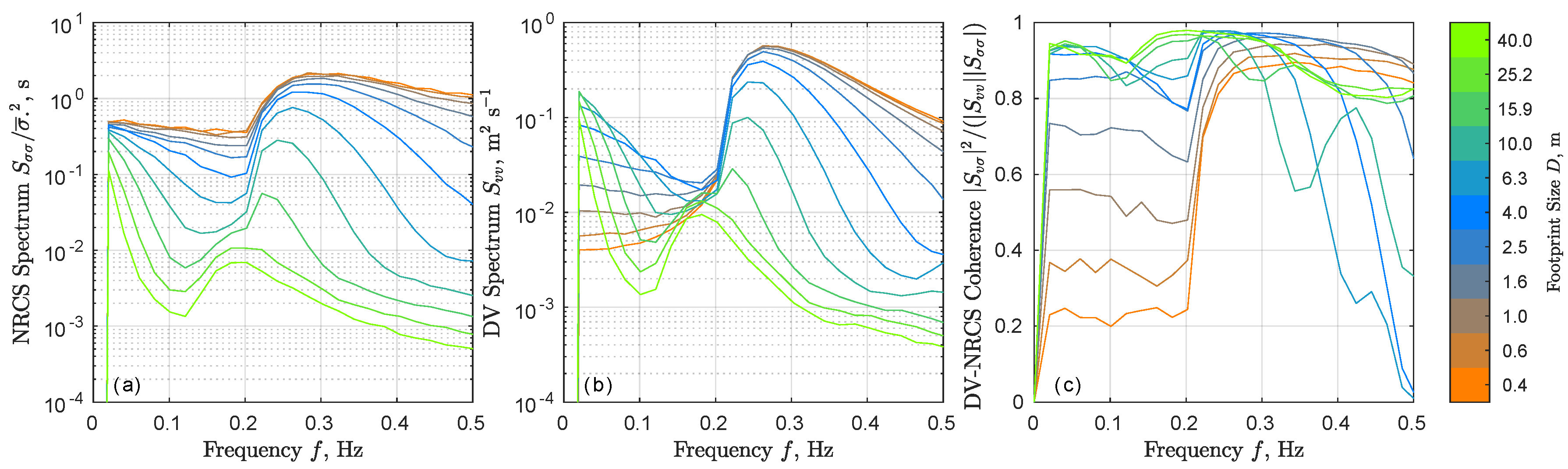
4.2. Footprint Effects
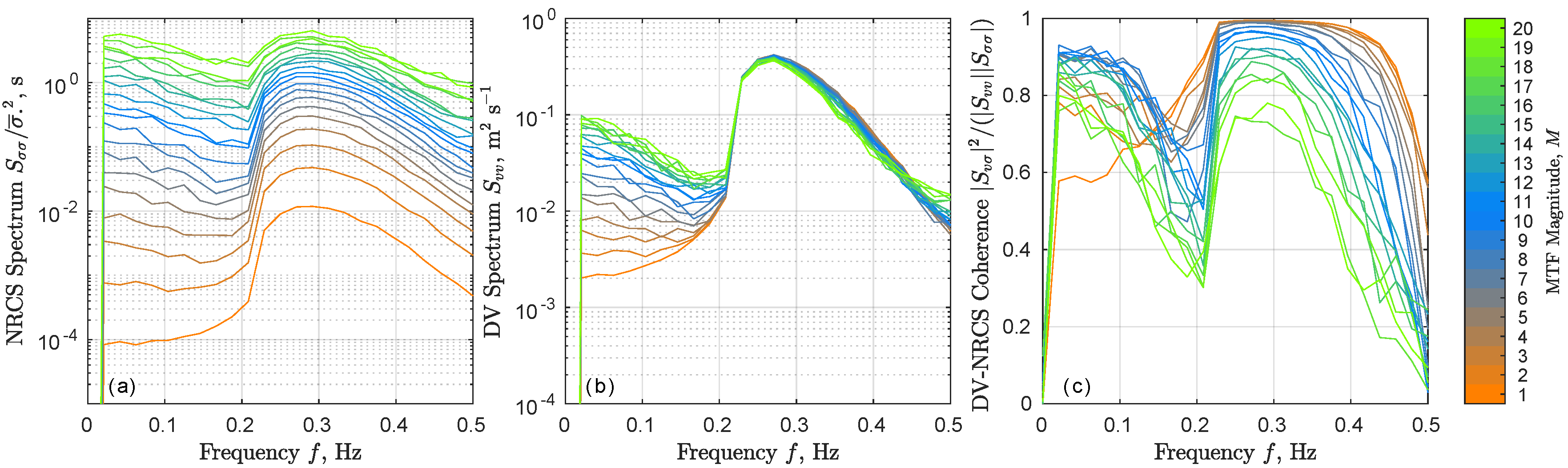
4.3. Non-Linearity Effects
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| DV | Doppler Velocity |
| FFT | Fast Fourier Transform |
| HH | Horizontal Transmit-Receive Polarization |
| LF | Low Frequency |
| MSS | Mean-Square Slope |
| MTF | Modulation Transfer Function |
| NLMTF | Non-Linear Modulation Transfer Function |
| NRCS | Normalized Radar Cross-Section |
| Probability Density Function | |
| VV | Vertical Transmit-Receive Polarization |
| UTC | Coordinated Universal Time |
| WG | Wave Gauge |
References
- Keller, W.C.; Wright, J.W. Microwave scattering and the straining of wind-generated waves. Radio Sci. 1975, 10, 139–147. [Google Scholar] [CrossRef]
- Schröter, J.; Feindt, F.; Alpers, W.; Keller, W.C. Measurement of the ocean wave-radar modulation transfer function at 4.3 GHz. J. Geophys. Res. (Oceans) 1986, 91, 923–932. [Google Scholar] [CrossRef]
- Plant, W.J. The Modulation Transfer Function: Concept and Applications. In Radar Scattering from Modulated Wind Waves; Springer: Berlin, Germany, 1989; pp. 155–172. [Google Scholar]
- Goldstein, R.M.; Zebker, H.A. Interferometric radar measurement of ocean surface currents. Nature 1987, 328, 707–709. [Google Scholar] [CrossRef]
- Romeiser, R.; Thompson, D.R. Numerical study on the along-track interferometric radar imaging mechanism of oceanic surface currents. IEEE Trans. Geosci. Remote Sens. 2000, 38, 446–458. [Google Scholar] [CrossRef]
- Martin, A.; Gommenginger, C. Towards wide-swath high-resolution mapping of total ocean surface current vectors from space: Airborne proof-of-concept and validation. Remote Sens. Environ. 2017, 197, 58–71. [Google Scholar] [CrossRef] [Green Version]
- Chapron, B.; Collard, F.; Ardhuin, F. Direct measurements of ocean surface velocity from space: Interpretation and validation. J. Geophys. Res. (Oceans) 2005, 110, 7008. [Google Scholar] [CrossRef]
- Johannessen, J.A.; Chapron, B.; Collard, F.; Kudryavtsev, V.; Mouche, A.; Akimov, D.; Dagestad, K.F. Direct ocean surface velocity measurements from space: Improved quantitative interpretation of Envisat ASAR observations. Geophys. Res. Lett. 2008, 35, 22608. [Google Scholar] [CrossRef]
- Mouche, A.A.; Collard, F.; Chapron, B.; Dagestad, K.F.; Guitton, G.; Johannessen, J.A.; Kerbaol, V.; Hansen, M.W. On the Use of Doppler Shift for Sea Surface Wind Retrieval From SAR. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2901–2909. [Google Scholar] [CrossRef]
- Bourassa, M.A.; Rodriguez, E.; Chelton, D. Winds and currents mission: Ability to observe mesoscale AIR/SEA coupling. Proc. Int. Geosci. Remote Sens. Symp. 2016, 7392–7395. [Google Scholar] [CrossRef]
- Ardhuin, F.; Aksenov, Y.; Benetazzo, A.; Bertino, L.; Brandt, P.; Caubet, E.; Chapron, B.; Collard, F.; Cravatte, S.; Dias, F.; et al. Measuring currents, ice drift, and waves from space: the Sea Surface KInematics Multiscale monitoring (SKIM) concept. Ocean Sci. Discuss. 2017, 2017, 1–26. [Google Scholar] [CrossRef]
- Bao, Q.; Lin, M.; Zhang, Y.; Dong, X.; Lang, S.; Gong, P. Ocean Surface Current Inversion Method for a Doppler Scatterometer. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6505–6516. [Google Scholar] [CrossRef]
- Rodriguez, E.; Wineteer, A.; Perkovic-Martin, D.; Gál, T.; Stiles, B.; Niamsuwan, N.; Rodriguez Monje, R. Estimating Ocean Vector Winds and Currents Using a Ka-Band Pencil-Beam Doppler Scatterometer. Remote Sens. 2018, 10, 576. [Google Scholar] [CrossRef]
- Nouguier, F.; Chapron, B.; Collard, F.; Mouche, A.; Rascle, N.; Ardhuin, F.; Wu, X. Sea Surface Kinematics From Near-Nadir Radar Measurement. IEEE Trans. Geosci. Remote Sens. 2018. accepted. [Google Scholar]
- Fois, F.; Hoogeboom, P.; Le Chevalier, F.; Stoffelen, A. An analytical model for the description of the full-polarimetric sea surface Doppler signature. J. Geophys. Res. (Oceans) 2015, 120, 988–1015. [Google Scholar] [CrossRef] [Green Version]
- Yurovsky, Y.Y.; Grodsky, S.A.; Kudryavtsev, V.N.; Chapron, B. Wave-induced Doppler shift of Ka-band radar signal backscattered from the sea surface. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium-Fall (PIERS-FALL), Singapore, 19–22 November 2017; pp. 2299–2306. [Google Scholar]
- Plant, W.J.; Keller, W.C.; Cross, A. Parametric dependence of ocean wave-radar modulation transfer functions. J. Geophys. Res. (Oceans) 1983, 88, 9747–9756. [Google Scholar] [CrossRef]
- Grodsky, S.A.; Kudryavtsev, V.N.; Bol’shakov, A.N.; Smolov, V.E. Experimental investigation of fluctuations of radar signals caused by surface waves. Phys. Ocean. 2001, 11, 333–352. [Google Scholar] [CrossRef]
- Plant, W.J. A model for microwave Doppler sea return at high incidence angles: Bragg scattering from bound, tilted waves. J. Geophys. Res. (Oceans) 1997, 102, 21131–21146. [Google Scholar] [CrossRef] [Green Version]
- Hwang, P.A.; Sletten, M.A.; Toporkov, J.V. A note on Doppler processing of coherent radar backscatter from the water surface: With application to ocean surface wave measurements. J. Geophys. Res. (Oceans) 2010, 115, C03026. [Google Scholar] [CrossRef]
- Donelan, M.; Longuet-Higgins, M.S.; Turner, J.S. Periodicity in whitecaps. Nature 1972, 239, 449–451. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Ka-Band Dual Copolarized Empirical Model for the Sea Surface Radar Cross Section. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1629–1647. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Chapron, B.; Grodsky, S.A. Modulation of Ka-band Doppler Radar Signals Backscattered from the Sea Surface. IEEE Trans. Geosci. Remote Sens. 2018, 1–19. [Google Scholar] [CrossRef]
- Toba, Y.; Koga, M. A parameter describing overall conditions of wave breaking, whitecapping, sea-spray production and wind stress. In Oceanic Whitecaps; Monahan, E.C., Niocaill, G.M., Eds.; Reidel Publishing Company: Boston, MA, USA, 1986; pp. 37–47. [Google Scholar]
- Jessup, A.T.; Melville, W.K.; Keller, W.C. Breaking waves affecting microwave backscatter 1. Detection and verification. J. Geophys. Res. (Oceans) 1991, 96, 20547–20559. [Google Scholar] [CrossRef]
- Thompson, D.R.; Jensen, J.R. Synthetic aperture radar interferometry applied to ship-generated internal waves in the 1989 Loch Linnhe experiment. J. Geophys. Res. (Oceans) 1993, 98, 10259–10270. [Google Scholar] [CrossRef]
- Klugmann, D.; Stephan, R. Calibration of portable FM-CW Doppler radar profilers with an artificial target. Proc. Int. Geosci. Remote Sens. Symp. 2004, 6, 3953–3955. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semiempirical model of the normalized radar cross-section of the sea surface 1. Background model. J. Geophys. Res. (Oceans) 2003, 108, C08054. [Google Scholar] [CrossRef]
- Hesany, V.; Moore, R.K.; Gogineni, S.P.; Holtzman, J.C. Slope-induced nonlinearities on imaging of ocean waves. IEEE J. Oceanic Eng. 1991, 16, 279–284. [Google Scholar] [CrossRef]
- Schmidt, A.; Bao, M. The modulation of radar backscatter by long ocean waves: A quadratically nonlinear process? J. Geophys. Res. (Oceans) 1998, 103, 5551–5562. [Google Scholar] [CrossRef] [Green Version]
- Trunk, G.V. Radar Properties of Non-Rayleigh Sea Clutter. IEEE Trans. Aerosp. Electron. Syst. 1972, AES-8, 196–204. [Google Scholar] [CrossRef]
- Gotwols, B.L.; Thompson, D.R. Ocean microwave backscatter distributions. J. Geophys. Res. (Oceans) 1994, 99, 9741–9750. [Google Scholar] [CrossRef]
- Thompson, D.R.; Gotwols, B.L. Comparisons of model predictions for radar backscatter amplitude probability density functions with measurements from SAXON. J. Geophys. Res. (Oceans) 1994, 99, 9725–9739. [Google Scholar] [CrossRef]
- Nouguier, F.; Guerin, C.A.; Chapron, B. Scattering From Nonlinear Gravity Waves: The “Choppy Wave” Model. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4184–4192. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Makin, V.K.; Chapron, B. Coupled sea surface-atmosphere model: 2. Spectrum of short wind waves. J. Geophys. Res. (Oceans) 1999, 104, 7625–7639. [Google Scholar] [CrossRef] [Green Version]
- Yurovskaya, M.V.; Dulov, V.A.; Chapron, B.; Kudryavtsev, V.N. Directional short wind wave spectra derived from the sea surface photography. J. Geophys. Res. (Oceans) 2013, 118, 4380–4394. [Google Scholar] [CrossRef] [Green Version]
- Alpers, W.; Ross, D.; Rufenach, C. On the detectability of ocean surface waves by real and synthetic aperture radar. J. Geophys. Res. (Oceans) 1981, 86, 6481–6498. [Google Scholar] [CrossRef]
- Feindt, F.; Schroeter, J.; Alpers, W. Measurement of the ocean wave-radar modulation transfer function at 35 GHz from a sea-based platform in the North Sea. J. Geophys. Res. (Oceans) 1986, 91, 9701–9708. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Low-Frequency Sea Surface Radar Doppler Echo. Remote Sens. 2018, 10, 870. https://doi.org/10.3390/rs10060870
Yurovsky YY, Kudryavtsev VN, Grodsky SA, Chapron B. Low-Frequency Sea Surface Radar Doppler Echo. Remote Sensing. 2018; 10(6):870. https://doi.org/10.3390/rs10060870
Chicago/Turabian StyleYurovsky, Yury Yu., Vladimir N. Kudryavtsev, Semyon A. Grodsky, and Bertrand Chapron. 2018. "Low-Frequency Sea Surface Radar Doppler Echo" Remote Sensing 10, no. 6: 870. https://doi.org/10.3390/rs10060870
APA StyleYurovsky, Y. Y., Kudryavtsev, V. N., Grodsky, S. A., & Chapron, B. (2018). Low-Frequency Sea Surface Radar Doppler Echo. Remote Sensing, 10(6), 870. https://doi.org/10.3390/rs10060870




