On the Desiccation of the South Aral Sea Observed from Spaceborne Missions
Abstract
:1. Introduction
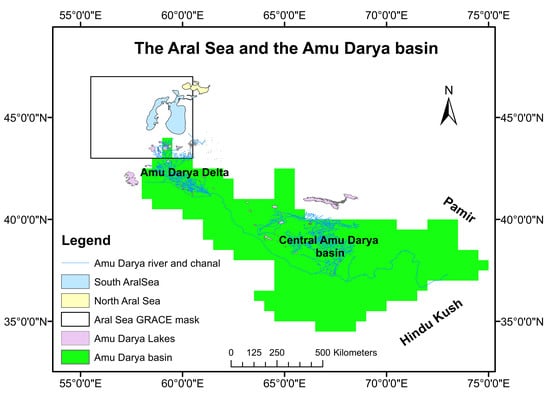
2. Study Area
3. Observation and Model Data
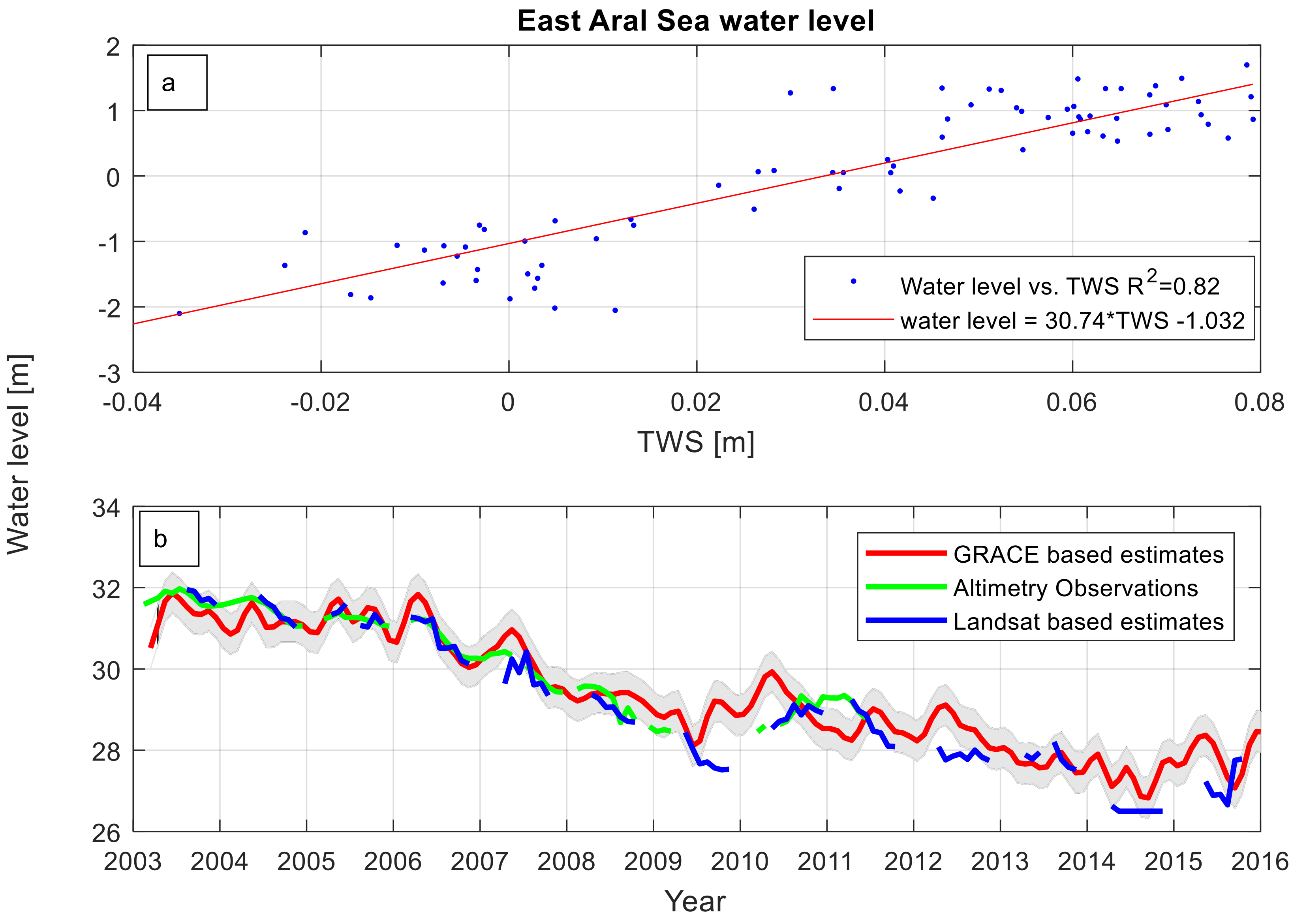
3.1. Lake Water Storage (LWS)
3.2. Terrestrial Water Storage (TWS)
3.3. Vegetation Index
3.4. Evapotranspiration (ET)
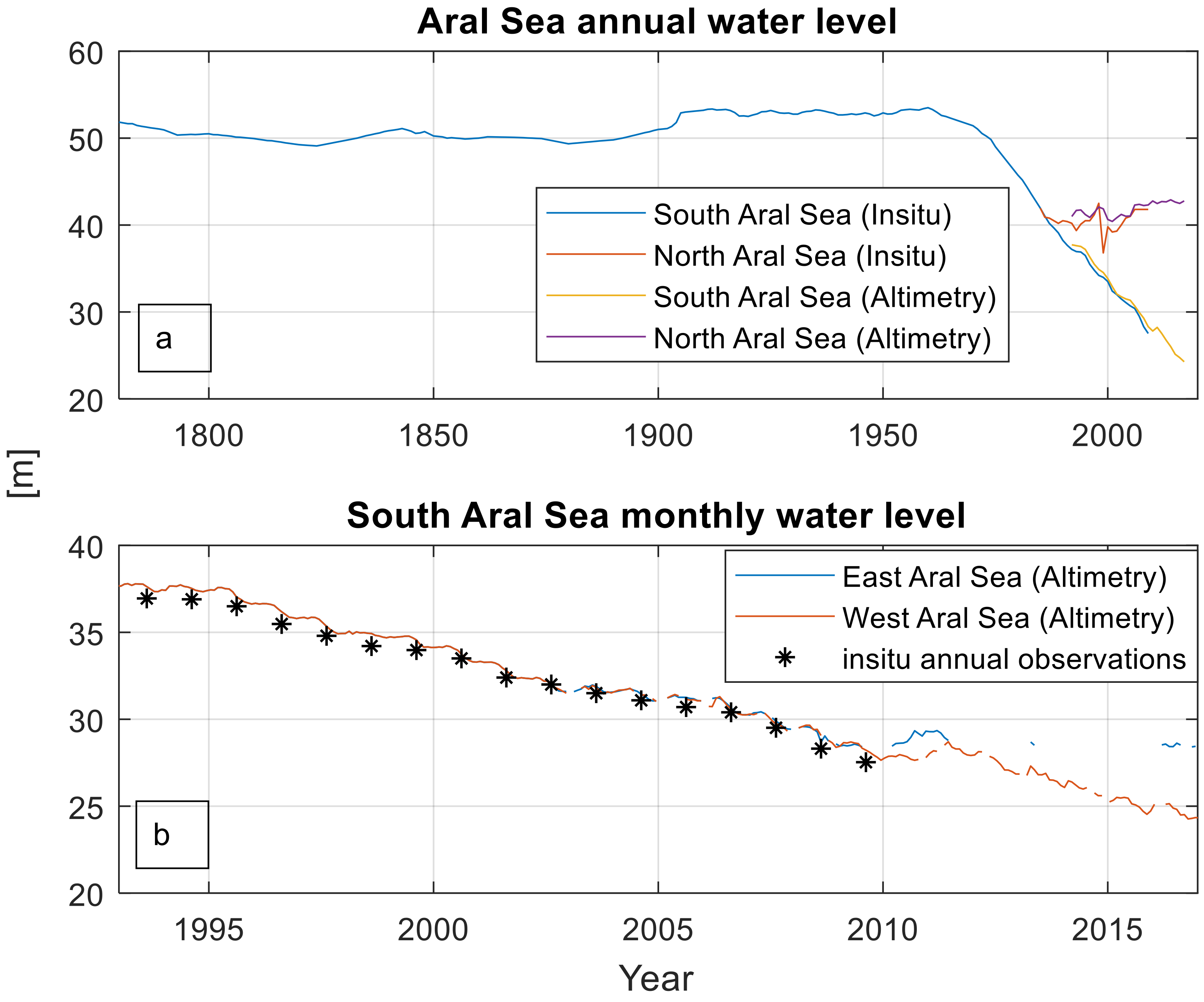
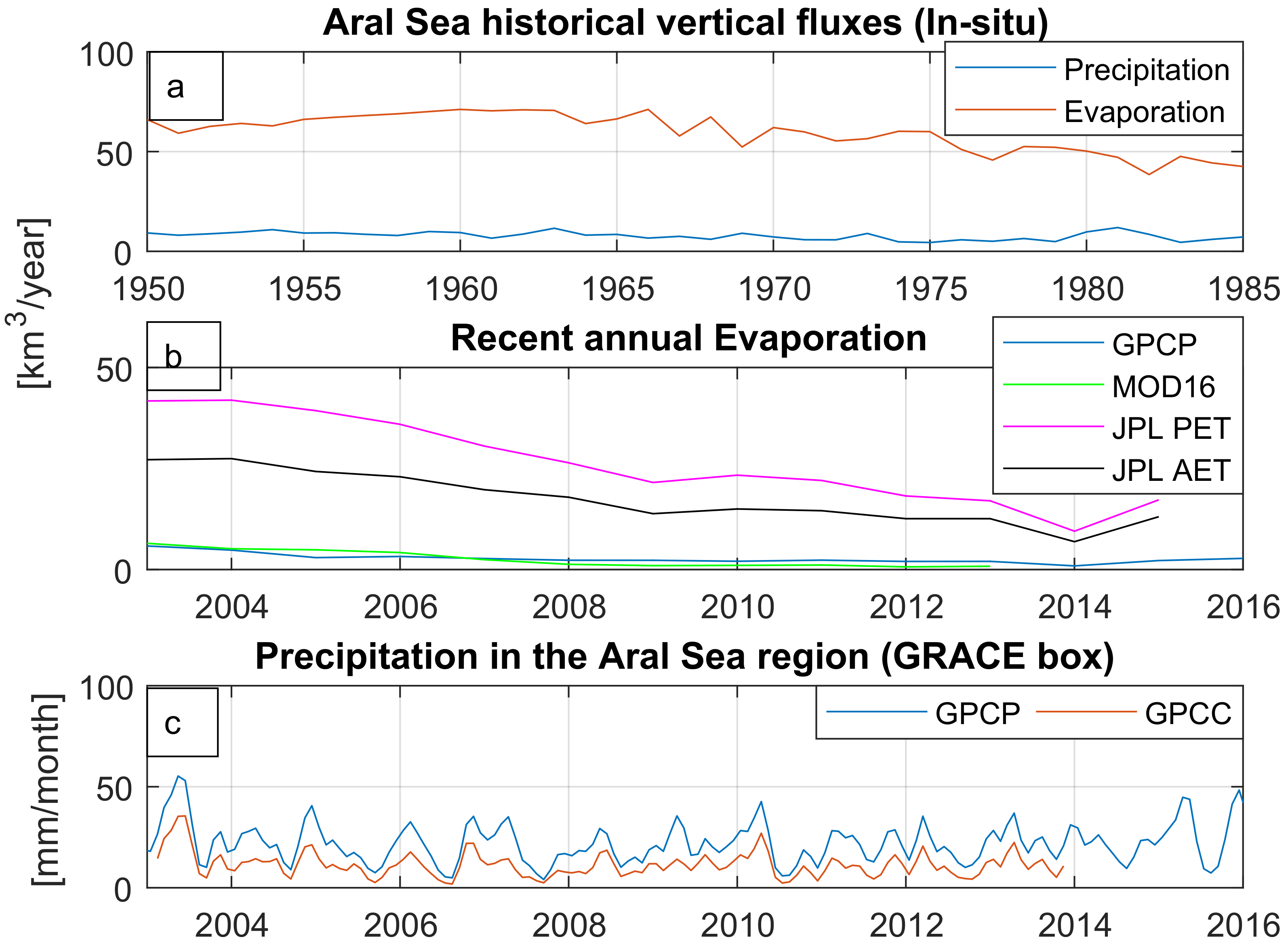
3.5. In Situ Data
3.6. Precipitation
4. Methods and Results
4.1. South Aral Sea Volume Dynamics
- = Volumetric variations with respect to the initial state (t0) at the nth month
- = Area of the water extent at month t
- = Area of the water extent at the previous month
- = Level of the water body at month t
- = Level of the water body at the previous month.
- n = Number of months.
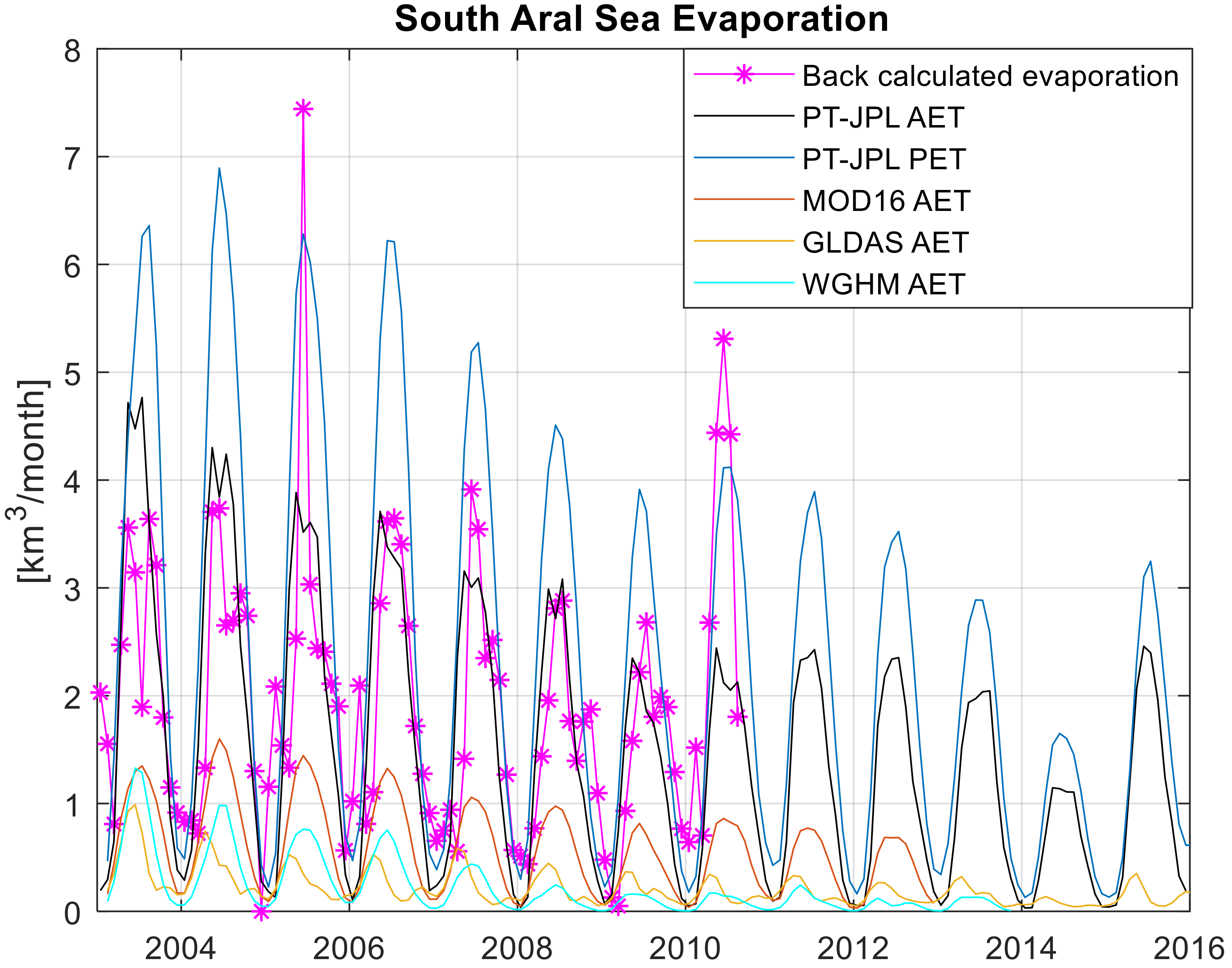
4.2. Evaporation from the South Aral Sea
- BCE = Back-calculated evaporation from the lake (magenta plot in Figure 6)
- = Diffrential of the lake volume (calculated by Equation (2)) with respect to its previous month
- R = Amu Darya streamflow into the South Aral Sea
- P = Precipitation
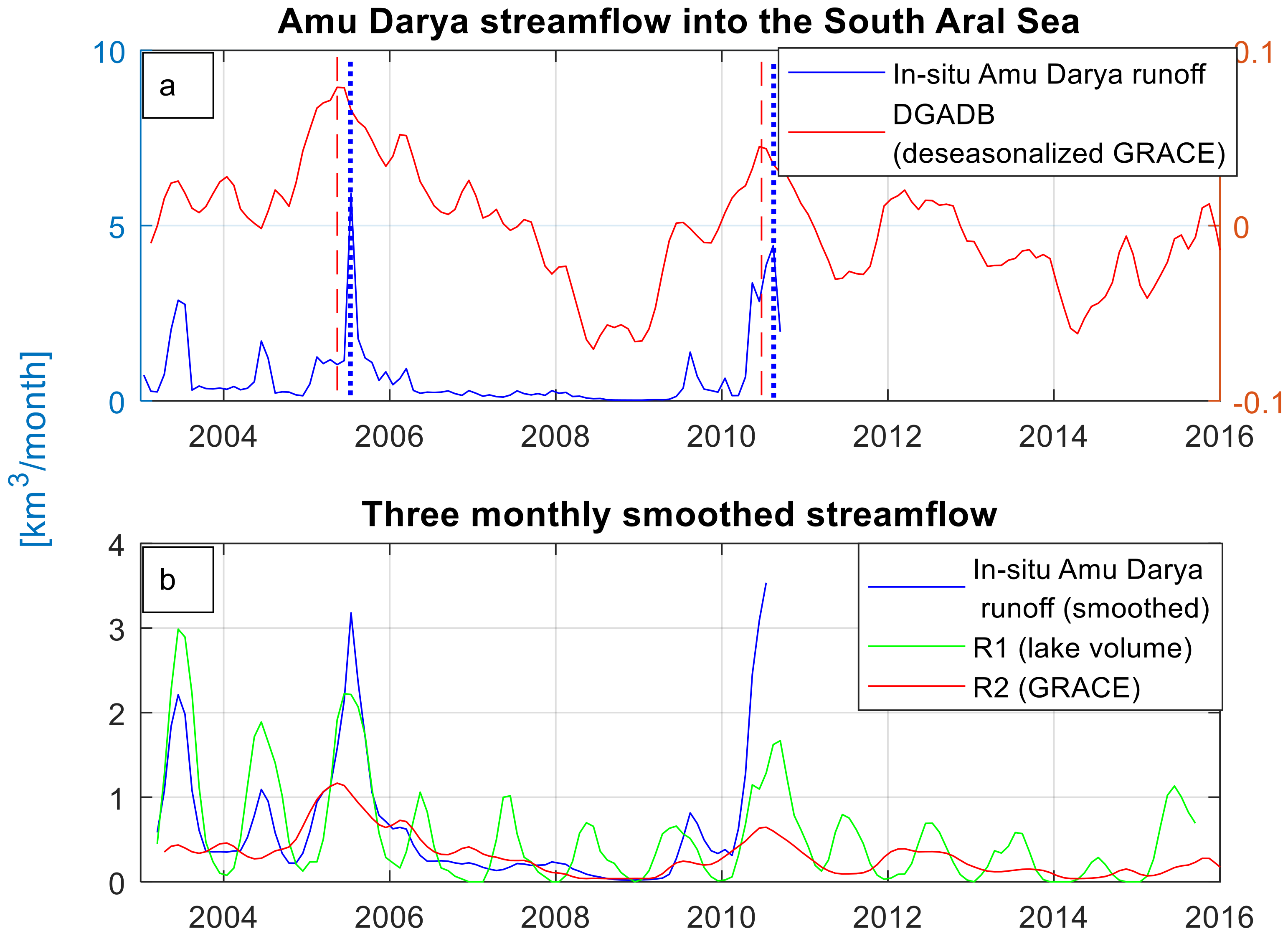
4.3. Amu Darya Streamflow into the Lake
- A water balance-based streamflow estimate (R1, Figure 7b, green plot) is generated by combining PT-JPL ET (assuming it as actual evaporation from the lake), GPCP and South Aral Sea volumetric variations (Equation (4)). The average annual Amu Darya streamflow into the lake (except 2005 and 2010 flow) ranges between 0–1 km3/month while the accumulated error from different datasets in Equation (4) is more than one km3/month. Consequently, accurate estimation of the streamflow is not possible with this method. Therefore, three-monthly weighted-average (3MWA) by 0.25, 0.5, 0.25 weights, is calculated to obtain a long-term trend of the streamflow into the lake. The derived estimate (R1, Figure 7b) showed 0.71 correlation with the in situ 3MWA streamflow.where,
- R1 = Streamflow estimated from lake water budget (green plot in Figure 7b)
- 3MWA = three-monthly weighted-average
- ET = Evaporation from the lake (PT-JPL ET) and P = Precipitation (GPCP)
- Second streamflow (R2, Figure 7b, red plot) is calculated from the deseasonalized GRACE signal obtained from the Amu Darya basin (DGADB) (Figure 1, green polygon). An empirical relation between 3MWA of the in-situ Amu Darya streamflow and 3MWA of the DGADB is used to generate GRACE-based streamflow (R2). The Least-absolute-residuals method based two-degree polynomial curve showed a good agreement (r2 = 0.94 and RMSE = 0.2 km3) between the two. The derived curve (R2, Figure 7b) showed 0.68 correlation with the in situ 3MWA streamflow.
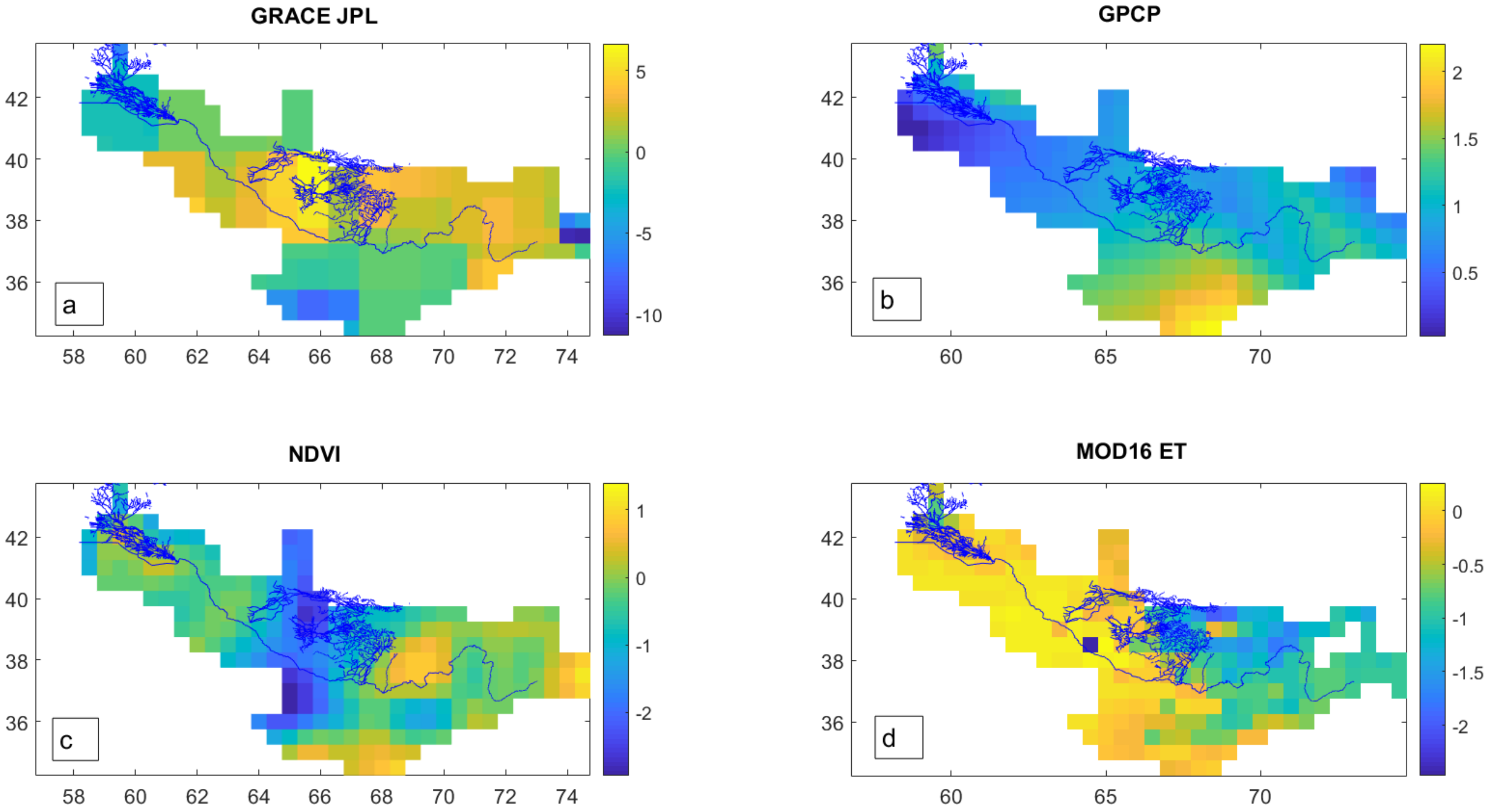
4.4. The Amu Darya Basin
5. Discussion
- Lake level estimate: this paper suggests methods for filling gaps in the altimetry observations. These data gaps may occur due to intermission time lag or loss of altimetry ground track due to changes in the shape of the water bodies. Landsat images together with bathymetry can provide an alternative water level estimate. However, sometimes, optical images have limitations during lousy weather. In that case, GRACE signals from lakes like the Aral Sea have a potential to estimate water level. The linear regression between the TWS and water level has been explored to generate the water level from GRACE.
- The rate of evaporation loss: most of the models/data products do not estimate evapotranspiration (ET) from inland waterbodies well, except for one. We have back-calculated the lake evaporation (BCE) by integrating altimetry-based lake volume variations, with the in situ runoff and GPCP precipitation. This study found the PT-JPL ET estimate to have the closest approximation to the BCE compared to the other existing ET products MODIS (MOD16) and hydrological models (WGHM and GLDAS). While PT-JPL has never been tested over open water bodies, our findings are consistent with multiple studies that have consistently found PT-JPL to be the top-performing ET remote-sensing algorithm over terrestrial vegetation [44,45,48,49,51,63].
- Estimating river streamflow to the lake: the study also suggests that the GRACE signal from the Amu Darya basin can provide a long-term trend of streamflow into the lake and may predict flood events one or two months in advance. Another streamflow is estimated based on the lake water budget, which showed a good long-term progression but has some false highs. The back-calculated streamflow (R1) indicated strikingly high seasonality, which demonstrates possible seasonal groundwater infiltration into the lake, assuming error in other datasets are not seasonally biased. Nevertheless, in the absence of any in-situ streamflow, these methods can be explored.
- Assessing the spatiotemporal variations in the water cycle of the Amu Darya basin: finally, we monitored the spatial changes of the Amu Darya basin to examine the cause of reducing streamflow. Various insights could be gained through analyzing the maps of a temporal trend in ET, TWS, NDVI, and Precipitation. The decrease in TWS in the Amu Darya delta region is mainly due to the increase in water mass in the central part of the Amu Darya basin, which is probably due to rising infiltration with the worsening of the canal system. This assumption cannot be validated due to lack of ground-based observations but is supported by the decrease in ET and NDVI in the region with the increase in TWS.
- Future of the Aral Sea: the low Amu Darya streamflow and huge evaporation loss from the vast open body have endangered the existence of the South Aral Sea. If the present trend continues, the remnant West Aral Sea will also disappear by nearly 2032 or reach the level of its base flow. One possible solution is to drain the Amu Darya streamflow directly into the West Aral Sea to avoid evaporation loss from the vast shallow East Aral Sea. Assuming 4 km3/year water flows into the West Aral Sea based on the current the annual Amu Darya streamflow (without any flood), the West Aral Sea will start increasing at a rate of more than 1 km3/year. Additionally, a dam is also required to be built between the East and West Aral Sea to stop flooding from the west when it reaches more than 28 m above MSL.
6. Concluding Remarks
- Higher spatial resolution GRACE signals can improve its application tremendously by reducing the impact of contributions from other hydrological compartments.
- Evaporation estimates from the waterbodies need to be better estimated. The lake’s volume variations and its salinity need to be incorporated in the models.
- With the recent operation of Global Precipitation Measurements (GPM) and Soil Moisture Active Passive (SMAP) missions, precipitation, soil moisture is expected to be monitored better than before. The role of new observations in studies like that presented here needs to be further investigated.
- The upcoming Surface Water and Ocean Topography (SWOT) mission is expected to provide volumetric variations of most of the inland water bodies because of its wide swath altimetry. This can potentially advance water balance studies such as that investigated in this work.
- By increasing confidence in the quality of surface/sub-surface estimates (surface water and soil moisture), the role of groundwater dynamics can be better explored from GRACE.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Gleick, P.H.; Pacific Institute for Studies in Development, Environment; Security, Stockholm Environment Institute. Water in Crisis: A Guide to the World’s Fresh Water Resources; Oxford University Press: New York, NY, USA, 1993; ISBN 978-0-19-507627-1. [Google Scholar]
- Nicholson, S.E. Historical Fluctuations of Lake Victoria and Other Lakes in the Northern Rift Valley of East Africa. In Environmental Change and Response in East African Lakes; Lehman, J.T., Ed.; Springer Netherlands: Dordrecht, The Netherlands, 1998; Volume 79, pp. 7–35. ISBN 978-90-481-5043-4. [Google Scholar]
- Bortnik, V.N.; Chistyaeva, S.P. Hydrometeorology and Hydrochemistry of the USSR Seas. Aral Sea Leningr. Gidrometeoizdat 1990, VII, 196. [Google Scholar]
- Zavialov, P.O. Physical Oceanography of the Dying Aral Sea; Springer Science & Business Media: Berlin, Germany, 2005; ISBN 978-3-540-22891-2. [Google Scholar]
- Dodson, J.; Betts, A.V.G.; Amirov, S.S.; Yagodin, V.N. The nature of fluctuating lakes in the southern Amu-dar’ya delta. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2015, 437, 63–73. [Google Scholar] [CrossRef]
- Micklin, P.P. The Water Management Crisis in Soviet Central Asia. Carl Beck Pap. Russ. East Eur. Stud. 1991, 131. [Google Scholar] [CrossRef]
- Asokan, S.M.; Rogberg, P.; Bring, A.; Jarsjö, J.; Destouni, G. Climate model performance and change projection for freshwater fluxes: Comparison for irrigated areas in Central and South Asia. J. Hydrol. Reg. Stud. 2016, 5, 48–65. [Google Scholar] [CrossRef]
- Bosch, K.; Erdinger, L.; Ingel, F.; Khussainova, S.; Utegenova, E.; Bresgen, N.; Eckl, P.M. Evaluation of the toxicological properties of ground- and surface-water samples from the Aral Sea Basin. Sci. Total Environ. 2007, 374, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Micklin, P. Introduction to the Aral Sea and Its Region. In The Aral Sea; Springer Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2014; pp. 15–40. ISBN 978-3-642-02355-2. [Google Scholar]
- Roget, E.; Khimchenko, E.; Forcat, F.; Zavialov, P. The internal seiche field in the changing South Aral Sea (2006–2013). Hydrol. Earth Syst. Sci. 2017, 21, 1093–1105. [Google Scholar] [CrossRef]
- Singh, A.; Seitz, F.; Eicker, A.; Güntner, A. Water Budget Analysis within the Surrounding of Prominent Lakes and Reservoirs from Multi-Sensor Earth Observation Data and Hydrological Models: Case Studies of the Aral Sea and Lake Mead. Remote Sens. 2016, 8, 953. [Google Scholar] [CrossRef]
- Vörösmarty, C.J.; Fekete, B.M.; Meybeck, M.; Lammers, R.B. Geomorphometric attributes of the global system of rivers at 30-minute spatial resolution. J. Hydrol. 2000, 237, 17–39. [Google Scholar] [CrossRef]
- Fekete, B.M.; Vörösmarty, C.J.; Lammers, R.B. Scaling gridded river networks for macroscale hydrology: Development, analysis, and control of error. Water Resour. Res. 2001, 37, 1955–1967. [Google Scholar] [CrossRef]
- Singh, A.; Seitz, F.; Schwatke, C. Application of Multi-Sensor Satellite Data to Observe Water Storage Variations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1502–1508. [Google Scholar] [CrossRef]
- Birkett, C.; Murtugudde, R.; Allan, T. Indian Ocean Climate event brings floods to East Africa’s lakes and the Sudd Marsh. Geophys. Res. Lett. 1999, 26, 1031–1034. [Google Scholar] [CrossRef]
- Crétaux, J.-F.; Biancamaria, S.; Arsen, A.; Bergé-Nguyen, M.; Becker, M. Global surveys of reservoirs and lakes from satellites and regional application to the Syrdarya river basin. Environ. Res. Lett. 2015, 10, 15002. [Google Scholar] [CrossRef]
- Kleinherenbrink, M.; Ditmar, P.G.; Lindenbergh, R.C. Retracking Cryosat data in the SARIn mode and robust lake level extraction. Remote Sens. Environ. 2014, 152, 38–50. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, U.; Seitz, F. Remote Sensing of Storage Fluctuations of Poorly Gauged Reservoirs and State Space Model (SSM)-Based Estimation. Remote Sens. 2015, 7, 17113–17134. [Google Scholar] [CrossRef]
- Medina, C.E.; Gomez-Enri, J.; Alonso, J.J.; Villares, P. Water level fluctuations derived from ENVISAT Radar Altimeter (RA-2) and in-situ measurements in a subtropical waterbody: Lake Izabal (Guatemala). Remote Sens. Environ. 2008, 112, 3604–3617. [Google Scholar] [CrossRef]
- Crétaux, J.-F.; Abarca-del-Río, R.; Bergé-Nguyen, M.; Arsen, A.; Drolon, V.; Clos, G.; Maisongrande, P. Lake Volume Monitoring from Space. Surv. Geophys. 2016, 37, 269–305. [Google Scholar] [CrossRef]
- Schwatke, C.; Dettmering, D.; Bosch, W.; Seitz, F. DAHITI—An innovative approach for estimating water level time series over inland waters using multi-mission satellite altimetry. Hydrol. Earth Syst. Sci. 2015, 19, 4345–4364. [Google Scholar] [CrossRef]
- Wahr, J.; Swenson, S.; Zlotnicki, V.; Velicogna, I. Time-variable gravity from GRACE: First results. Geophys. Res. Lett. 2004, 31, L11501. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Chen, J.; Seneviratne, S.I.; Viterbo, P.; Holl, S.; Wilson, C.R. Basin scale estimates of evapotranspiration using GRACE and other observations. Geophys. Res. Lett. 2004, 31, L20504. [Google Scholar] [CrossRef]
- Richey, A.S.; Thomas, B.F.; Lo, M.-H.; Reager, J.T.; Famiglietti, J.S.; Voss, K.; Swenson, S.; Rodell, M. Quantifying renewable groundwater stress with GRACE. Water Resour. Res. 2015, 51, 5217–5238. [Google Scholar] [CrossRef] [PubMed]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Wiese, D.N.; Landerer, F.W.; Watkins, M.M. Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution. Water Resour. Res. 2016, 52, 7490–7502. [Google Scholar] [CrossRef]
- Wiese, D.N.; Yuan, D.-N.; Boening, C.; Landerer, F.W.; Watkins, M.M. JPL GRACE Mascon Ocean, Ice, and Hydrology Equivalent Water Height RL05M.1 CRI Filtered Version 2, PO.DAAC. 2016. [CrossRef]
- Didan, K. MYD13C2 MODIS/Aqua Vegetation Indices Monthly L3 Global 0.05Deg CMG V006; NASA: Washington, DC, USA, 2015. [Google Scholar]
- Running, S.W.; Kimball, J.S. Satellite-Based Analysis of Ecological Controls for Land-Surface Evaporation Resistance. In Encyclopedia of Hydrological Sciences; Anderson, M.G., McDonnell, J.J., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; ISBN 978-0-470-84894-4. [Google Scholar] [CrossRef]
- Mu, Q.; Heinsch, F.; Zhao, M.; Running, S. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Rodell, M. GLDAS CLM Land Surface Model L4 Monthly 1.0 × 1.0 degree, Version 1; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA. [CrossRef]
- Derber, J.C.; Parrish, D.F.; Lord, S.J. The New Global Operational Analysis System at the National Meteorological Center. Weather Forecast. 1991, 6, 538–547. [Google Scholar] [CrossRef]
- Benduhn, F.; Renard, P. A dynamic model of the Aral Sea water and salt balance. J. Mar. Syst. 2004, 47, 35–50. [Google Scholar] [CrossRef]
- Singh, A.; Seitz, F. Updated bathymetric chart of the East Aral Sea, supplement to: Singh, Alka; Kumar, Ujjwal; Seitz, Florian (2015): Remote sensing of storage fluctuations of poorly gauged reservoirs and State Space Model (SSM)-based estimation. Remote Sens. 2015, 7, 17113–17134. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Ziese, M. GPCC Full Data Reanalysis Version 7.0 at 0.5°: Monthly Land-Surface Precipitation from Rain-Gauges built on GTS-based and Historic Data; NCAR: Boulder, CO, USA, 2015. [Google Scholar] [CrossRef]
- Adler, R.F.; Sapiano, M.; Huffman, G.J.; Bolvin, D.; Wang, J.-J.; Nelkin, E.; Xie, P.; Chiu, L.; Ferraro, R.; Schneider, U.; et al. New Global Precipitation Climatology Project monthly analysis product corrects satellite data drifts. GEWEX News 2016, 26, 7–9. [Google Scholar]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.-P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The Version-2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979–Present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Arsen, A.; Crétaux, J.-F.; Berge-Nguyen, M.; del Rio, R. Remote Sensing-Derived Bathymetry of Lake Poopó. Remote Sens. 2013, 6, 407–420. [Google Scholar] [CrossRef]
- Gao, H.; Birkett, C.; Lettenmaier, D.P. Global monitoring of large reservoir storage from satellite remote sensing: Global monitoring of large reservoir storage from space. Water Resour. Res. 2012, 48, W09504. [Google Scholar] [CrossRef]
- The Aral Sea Crisis. Available online: http://www.columbia.edu/~tmt2120/introduction.htm (accessed on 10 November 2017).
- Issanova, G.; Abuduwaili, J.; Galayeva, O.; Semenov, O.; Bazarbayeva, T. Aeolian transportation of sand and dust in the Aral Sea region. Int. J. Environ. Sci. Technol. 2015, 12, 3213–3224. [Google Scholar] [CrossRef]
- Chen, Y.; Xia, J.; Liang, S.; Feng, J.; Fisher, J.B.; Li, X.; Li, X.; Liu, S.; Ma, Z.; Miyata, A.; et al. Comparison of satellite-based evapotranspiration models over terrestrial ecosystems in China. Remote Sens. Environ. 2014, 140, 279–293. [Google Scholar] [CrossRef]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Chaney, N.W.; Wood, E.F. Multi-site evaluation of terrestrial evaporation models using FLUXNET data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The future of evapotranspiration: Global requirements for ecosystem functioning, carbon and climate feedbacks, agricultural management, and water resources: The future of evapotranspiration. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Fisher, J.B.; Malhi, Y.; Bonal, D.; Da Rocha, H.R.; De AraãšJo, A.C.; Gamo, M.; Goulden, M.L.; Hirano, T.; Huete, A.R.; Kondo, H.; et al. The land–atmosphere water flux in the tropics. Glob. Chang. Biol. 2009, 15, 2694–2714. [Google Scholar] [CrossRef]
- McCabe, M.F.; Ershadi, A.; Jimenez, C.; Miralles, D.G.; Michel, D.; Wood, E.F. The GEWEX LandFlux project: Evaluation of model evaporation using tower-based and globally gridded forcing data. Geosci. Model Dev. 2016, 9, 283–305. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; Jiménez, C.; Jung, M.; Michel, D.; Ershadi, A.; McCabe, M.F.; Hirschi, M.; Martens, B.; Dolman, A.J.; Fisher, J.B.; et al. The WACMOS-ET project – Part 2: Evaluation of global terrestrial evaporation data sets. Hydrol. Earth Syst. Sci. 2016, 20, 823–842. [Google Scholar] [CrossRef] [Green Version]
- Polhamus, A.; Fisher, J.B.; Tu, K.P. What controls the error structure in evapotranspiration models? Agric. For. Meteorol. 2013, 169, 12–24. [Google Scholar] [CrossRef]
- Vinukollu, R.K.; Wood, E.F.; Ferguson, C.R.; Fisher, J.B. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches. Remote Sens. Environ. 2011, 115, 801–823. [Google Scholar] [CrossRef]
- Reager, J.T.; Thomas, B.F.; Famiglietti, J.S. River basin flood potential inferred using GRACE gravity observations at several months lead time. Nat. Geosci. 2014, 7, 588–592. [Google Scholar] [CrossRef]
- Forkutsa, I.; Sommer, R.; Shirokova, Y.I.; Lamers, J.P.A.; Kienzler, K.; Tischbein, B.; Martius, C.; Vlek, P.L.G. Modeling irrigated cotton with shallow groundwater in the Aral Sea Basin of Uzbekistan: I. Water dynamics. Irrig. Sci. 2009, 27, 331–346. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Zarghami, M.; Hassanzadeh, Y. Determining the Main Factors in Declining the Urmia Lake Level by Using System Dynamics Modeling. Water Resour. Manag. 2012, 26, 129–145. [Google Scholar] [CrossRef]
- Jeihouni, M.; Toomanian, A.; Alavipanah, S.K.; Hamzeh, S. Quantitative assessment of Urmia Lake water using spaceborne multisensor data and 3D modeling. Environ. Monit. Assess. 2017, 189, 572. [Google Scholar] [CrossRef] [PubMed]
- Lemoalle, J.; Bader, J.-C.; Leblanc, M.; Sedick, A. Recent changes in Lake Chad: Observations, simulations and management options (1973–2011). Glob. Planet. Chang. 2012, 80, 247–254. [Google Scholar] [CrossRef]
- Okpara, U.T.; Stringer, L.C.; Dougill, A.J. Lake drying and livelihood dynamics in Lake Chad: Unravelling the mechanisms, contexts and responses. Ambio 2016, 45, 781–795. [Google Scholar] [CrossRef] [PubMed]
- Ali, W. Environment and Water Resources in the Jordan Valley and Its Impact on the Dead Sea Situation. In Water Security in the Mediterranean Region; Scozzari, A., El Mansouri, B., Eds.; Springer Netherlands: Dordrecht, The Netherlands, 2011; pp. 229–238. ISBN 978-94-007-1622-3. [Google Scholar]
- Rawashdeh, S.A.; Ruzouq, R.; Al-Fugara, A.; Pradhan, B.; Ziad, S.H.A.-H.; Ghayda, A.R. Monitoring of Dead Sea water surface variation using multi-temporal satellite data and GIS. Arab. J. Geosci. 2013, 6, 3241–3248. [Google Scholar] [CrossRef] [Green Version]
- Shafir, H.; Alpert, P. Regional and local climatic effects on the Dead-Sea evaporation. Clim. Chang. 2011, 105, 455–468. [Google Scholar] [CrossRef]
- Satgé, F.; Espinoza, R.; Zolá, R.P.; Roig, H.; Timouk, F.; Molina, J.; Garnier, J.; Calmant, S.; Seyler, F.; Bonnet, M.-P. Role of Climate Variability and Human Activity on Poopó Lake Droughts between 1990 and 2015 Assessed Using Remote Sensing Data. Remote Sens. 2017, 9, 218. [Google Scholar] [CrossRef]
- Zola, R.P.; Bengtsson, L. Long-term and extreme water level variations of the shallow Lake Poopó, Bolivia. Hydrol. Sci. J. 2006, 51, 98–114. [Google Scholar] [CrossRef]
- Michel, D.; Jiménez, C.; Miralles, D.G.; Jung, M.; Hirschi, M.; Ershadi, A.; Martens, B.; McCabe, M.F.; Fisher, J.B.; Mu, Q.; et al. The WACMOS-ET project – Part 1: Tower-scale evaluation of four remote-sensing-based evapotranspiration algorithms. Hydrol. Earth Syst. Sci. 2016, 20, 803–822. [Google Scholar] [CrossRef] [Green Version]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, A.; Behrangi, A.; Fisher, J.B.; Reager, J.T. On the Desiccation of the South Aral Sea Observed from Spaceborne Missions. Remote Sens. 2018, 10, 793. https://doi.org/10.3390/rs10050793
Singh A, Behrangi A, Fisher JB, Reager JT. On the Desiccation of the South Aral Sea Observed from Spaceborne Missions. Remote Sensing. 2018; 10(5):793. https://doi.org/10.3390/rs10050793
Chicago/Turabian StyleSingh, Alka, Ali Behrangi, Joshua B. Fisher, and John T. Reager. 2018. "On the Desiccation of the South Aral Sea Observed from Spaceborne Missions" Remote Sensing 10, no. 5: 793. https://doi.org/10.3390/rs10050793
APA StyleSingh, A., Behrangi, A., Fisher, J. B., & Reager, J. T. (2018). On the Desiccation of the South Aral Sea Observed from Spaceborne Missions. Remote Sensing, 10(5), 793. https://doi.org/10.3390/rs10050793