Abstract
Combining persistent scatterers (PS) and distributed scatterers (DS) is important for effective displacement monitoring using time-series of SAR data. However, for large stacks of synthetic aperture radar (SAR) data, the DS analysis using existing algorithms becomes a time-consuming process. Moreover, the whole procedure of DS selection should be repeated as soon as a new SAR acquisition is made, which is challenging considering the short repeat-observation of missions such as Sentinel-1. SqueeSAR is an approach for extracting signals from DS, which first applies a spatiotemporal filter on images and optimizes DS, then incorporates information from both optimized DS and PS points into interferometric SAR (InSAR) time-series analysis. In this study, we followed SqueeSAR and implemented a new approach for DS analysis using two-sample t-test to efficiently identify neighboring pixels with similar behaviour. We evaluated the performance of our approach on 50 Sentinel-1 images acquired over Trondheim in Norway between January 2015 and December 2016. A cross check on the number of the identified neighboring pixels using the Kolmogorov–Smirnov (KS) test, which is employed in the SqueeSAR approach, and the t-test shows that their results are strongly correlated. However, in comparison to KS-test, the t-test is less computationally intensive (98% faster). Moreover, the results obtained by applying the tests under different SAR stack sizes from 40 to 10 show that the t-test is less sensitive to the number of images.
1. Introduction
Efficient space-based techniques are a key tool to assess changes and deformation related to natural hazards such as earthquakes [1,2,3,4], volcanoes [5,6], and landslides [7,8] and anthropogenic hazards such as subsidence/uplift due to fluid withdrawal/injection [9,10,11]. The techniques could be used to manage natural and man-made disasters and plan prevention measures for the infrastructures at risk [12,13,14,15].
Space-born synthetic aperture radar (SAR) with spatial-resolution of 1–20 m, temporal-resolution of 6–45 days, and broad spatial coverage has proven powerful capabilities for precise displacement monitoring (mm scale) using differential interferometric SAR (DInSAR) and advanced multi-temporal InSAR (MTI) techniques such as persistent scatterer (PS) [16,17,18,19,20]. The data acquired by very high resolution (spatial resolution up to 25 cm) SAR sensors such as TerraSAR-X and CosmoSky-Med further enhance the applicability of these techniques for mapping instability related to individual infrastructure [21,22,23,24].
Sentinel-1A/B images, with high temporal resolution (6–12 days) and moderate spatial resolution (5 m × 20 m), can provide ground deformation maps with enough density of PS points in urban areas [25,26]. For non-urban regions, they also have potential to provide maps with enough density of distributed scatterers (DS), defined as pixels whose neighboring pixels share similar statistical behavior [27]. The sampling density of measurements points in both urban and agricultural regions can be further increased either by incorporating information from polarimetric observations [28] or by integrating DS and PS pixels [29] in single-polarimetry time-series analysis. These not only lead to more effective filtering of the atmospheric signals affecting InSAR measurements, but also result in more accurate phase unwrapping.
Coherence, defined as cross-correlation coefficient between two SAR images, can be used as one criterion to select DS pixels over the whole time period of observation [30]. However, since the changes in the scattering properties with time result in temporal decorrelation [31], there are DS pixels, which may contain coherent information only for a specific period and not necessarily for the whole observation period covered by SAR data. Such DSs are disregarded from InSAR time-series analysis if coherence thresholding is applied for the whole SAR data-stack. To overcome this problem in DS analysis of Small BAseline Subset (SBAS) method [30], temporal coherency criterion has been proposed [18], which is a measure of the phase stability of the pixel over the whole time period of observation (explained in Section 2.3). The method has been implemented in StaMPS/MTI software, which also provides the option to combine DS with PS points. However, for large stacks of images, DS selection and phase unwrapping of the resulting small baseline subsampled interferograms becomes very time-consuming. Moreover, the whole procedure should be repeated as soon as a new SAR acquisition is made, which is challenging considering the short repeat-observation of missions such as Sentinel-1.
SqueeSAR [32] is another approach to extract the signal from DS. It identifies a high spatial density of measurement points in both natural targets and smooth surfaces in urban [33] and non-urban areas [34,35,36]. The technique uses a spatially adaptive filtering procedure over statistically homogeneous pixels (SHP) to enhance the signal-to-noise ratio (SNR) over distributed targets, while preserving information associated with PS targets. Therefore, the phase values of the identified points are filtered before the unwrapping, which leads to more accurate phase unwrapping. Different statistical methods have already been proposed to identify the SHP families. These include using two-sample Kolmogorov–Smirnov (KS) test [32], the mean amplitude and the mean amplitude difference [37], exploiting polarimetry information [38], confidence interval according to the central limit theorem [39], one-sample test [40], similarity test of the covariance matrix [41], geometric distance and target features [42], various amplitude statistics [43], and non-local filters [44,45]. In this study, we followed the approach proposed by [32] in SqueeSAR technique and implemented a new method using the two-sample t-test for DS selection. Compared to the one-sample test implemented in [40], which assumes that the samples are dependent, the two-sample t-test does not consider dependency assumption between the samples. We analyzed the efficiency of the t-test in terms of processing speed, sensitivity to the number of images and reliability of the results using 50 Sentinel-1 SAR images acquired over Trondheim in Norway. A cross check of the displacement derived by PS and our new method was carried out. We implemented our method in the StaMPS/MTI processing chain, which benefits from existing algorithms for PS extraction and 3D phase unwrapping for displacement analysis.
2. Methodology
The key steps of the algorithm developed in this research for the time-series analysis of Sentinel-1 data are shown in Figure 1, and summarized in the following subsections. All of the processing was implemented on full-resolution data.
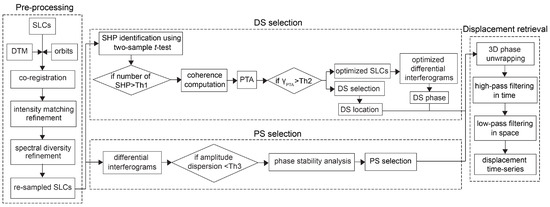
Figure 1.
Flow diagram of the implemented method in this study.
2.1. Pre-Processing
One scene is selected to provide the reference geometry and the remaining images are co-registered and re-sampled to the master reference geometry using intensity matching and spectral diversity methods [46], implemented in GAMMA software [47].
2.2. DS Selection
For the DS analysis, we developed a new algorithm, which relies on the t-test to identify the SHPs. This includes two steps, which are discussed below.
2.2.1. DS Candidate Selection
To detect DS candidates, the first step is the identification of the SHP families. To this end, we used the two-sample t-test. According to the test, two pixels are defined as statistically homogeneous if the null hypothesis that their averaged amplitudes are the same cannot be disproved for a certain level of significance. The two-sample t-test is defined as:
where and are the averaged amplitudes of the populations. The corresponding test statistic for the same sample sizes is as follows:
where N is the sample size, and are the sample means, and and are the sample variances.
To select the homogeneous statistical population, for each pixel, an estimation window centered on the pixel is defined. Then, the test is applied between the amplitude vector of the central pixel and that of all pixels within the window for a predefined significance level (0.95 in this study).
After identifying the initial set of SHPs for each pixel, to increase the probability that all selected pixels share the same reflectively values, the direct connectivity between the central pixel and the identified neighbors within the window is investigated. For this purpose, we first labeled all eight connected neighbors within the window, then discarded those pixels with labels that differed from the label of the central pixel (see Figure 2). Afterwards, to select DS candidates, a threshold was defined (Section 3) and discarded those pixels for which the number of SHPs is less than the threshold. Finally, after applying the threshold, the central pixel (DS candidate point), and its directly connected SHPs were considered for further analysis.
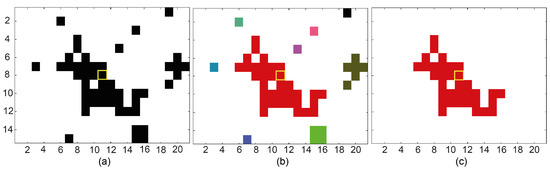
Figure 2.
One example for SHPs selection, showing: (a) all neighbors selected by applying the t-test; (b) labeling the eight connected pixels, which are shown with different colors; and (c) discarding those pixels with labels different from the label of the central pixel. The outline of the central pixel is shown with yellow.
2.2.2. Final DS Selection
After identification of SHPs for each DS candidate pixel, we estimated the coherence matrix from the ensemble coherence of the set of SHPs. The principal diagonal of the covariance matrix for each pixel contained despeckled intensity values for each image, and the phase values of the off-diagonal terms corresponded to spatially filtered interferometric phase between different SAR image pairs [32]. Due to the spatial filtering process, for a DS candidate, the interferometric phase values were not redundant, as is the case of PS. Therefore, following the SqueeSAR algorithm, the next step was to implement Phase Triangulation Algorithm (PTA) by estimating optimized phases () from the interferometric phase values in the coherence matrix () for each DS candidate, as follows [32]:
where , indicates Hermitian conjugation, and ∘ represents the entry-wise product. The Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm [48], which is a quasi-Newton method for non-constrained nonlinear optimization, was used to optimize the phase values. It is worth noting that, after performing this procedure, the phase values of DS pixels were filtered, which results in more reliable phase unwrapping.
Once the optimal solution was obtained, the final set of DS pixels were selected based on their quality; i.e., the PTA temporal coherence (), defined as follows [32]:
where N is the number of images, is the spatially filtered interferometric phase (off-diagonal elements of ), and is the optimal phase (the elements of ). The initial set of DS candidate pixels that have PTA temporal coherence greater than a predefined threshold (0.5 in this study) were selected as the final set of DS pixels. Afterwards, the phase values of the DS pixels in the SLCs were replaced with the optimized ones, while the phase values of the other pixels were preserved. Optimized single-master interferograms were generated using the optimized SLCs and repeat-pass technique, implemented in Delft object-oriented radar interferometric software (DORIS) [49]. Initial topographic phase components were subtracted from the interferograms using a digital terrain model (DTM) at 40-m resolution provided by the Norwegian Mapping Authority. The optimized differential interferograms were geocoded using the same DTM.
2.3. PS Selection
PS analysis was carried out using the standard PS processing algorithm in StaMPS/MTI [18,50]. Differential single-master interferograms were generated using the original SLCs and with the same repeat-pass method explained in Section 2.2.2. PS candidates were picked based on amplitude dispersion and a phase stability analysis was performed for each PS candidate by computing temporal coherence () defined as follows:
where N is the number of interferograms. is the differential interferometric phase of the pixel x in the interferogram i. is the estimated spatially correlated terms, including deformation, atmospheric signal, orbital inaccuracies, and spatially correlated part of the topographic phase due to DTM errors. The terms were estimated iteratively using a combination of low pass and adaptive phase filters. is the estimated spatially uncorrelated part of the topographic phase, which is correlated with perpendicular baseline. The term was estimated by least squares inversion. The temporal coherence was then calculated iteratively from residuals. Finally, pixels were selected as PS points, considering their amplitude dispersion, as well as their temporal coherence.
2.4. Displacement Retrieval
Once the DS and PS selection was complete and their differential interferometric phases were retrieved, we combined the selected PS and DS pixels, implemented a three-dimensional phase unwrapping [51], and estimated the atmospheric and orbital errors by applying high-pass filtering in time followed by a low-pass filtering in space. Subtracting the atmospheric and orbital terms from the adjusted unwrapped phase of each points left the surface displacement estimate.
3. Experimental Results
We applied our technique for a dataset composed of 50 SLC Sentinel-1 images acquired between January 2015 and December 2016 over Trondheim central Norway. The images were acquired in the interferometric wide swath (IW) mode, from an ascending track number 73, with a mean incidence angle of 33 degrees and “VV” polarization. The azimuth and slant range resolutions are approximately 22 and 2.65 m, with pixel-spacing of approximately 13.90 and 4.24 m in azimuth and ground range directions, respectively. We applied the processing over a pixel portion of the first swath of the images. The outline of the processed section superimposed over the Sentinel-2 image is shown in Figure 3.
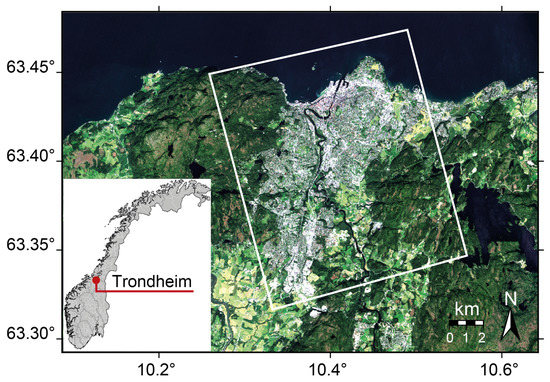
Figure 3.
Sentinel-2 satellite image of the Trondheim study area. The white rectangle shows the outline of the Sentinel-1 data processed in this study.
We generated single-master interferograms using the scene acquired on 25 July 2015 for the reference geometry. We used all 50 images for the SHP identification, but only 48 scenes (snow-free scenes) were suitable for the multi-interferometric analysis. To identify the PS candidates using StaMPS/MTI, we considered a threshold of 0.4 for the amplitude dispersion index criterion. To identify DS candidates, we considered an estimation window of pixels and performed the two-sample t-test at the 95% significance level. Since 94% of the selected PS points have less than 20 SHPs, we considered 20 SHPs as the threshold for DS candidate selection [32]. Afterwards, we implemented the PTA (described in Section 2.2.2) for the DS candidates. Figure 4 shows the PTA temporal coherence of the initially selected pixels. As shown in the figure, the DS pixels over the urban areas, which is our focus, can be well distinguished from the rest of the pixels by only thresholding their coherence. In this study, we set the coherence threshold to 0.5, and selected DS candidates with PTA temporal coherence greater than 0.5 as final DS pixels.

Figure 4.
The PTA temporal coherence corresponding to the SHP map obtained by using the two-sample t-test
Figure 5 shows the average line-of-sight (LOS) displacement maps at PS points only (Figure 5a) and both PS and DS pixels using either the t-test for SHP identification (Figure 5b), or the KS-test (Figure 5c). All the maps are relative to the reference area (marked in the Figure 5 as a triangle). The standard deviation of the maps, estimated by bootstrap resampling assuming a linear rate of motion, ranges from 0.1 to 3.6 mm/year. We used 1.5 mm/year standard deviation as a threshold; i.e., the points with a standard deviation above 1.5 mm/year were discarded from the results (1.5% and 2.3% of the points derived using the t-test and the KS-test were discarded, respectively). It is worth noting that the performance estimated with bootstrap refers to the local noise, clutter, etc., and does not consider the systematic contributions that arise from mathematical model (i.e., non-linear rate of motion) [52,53].
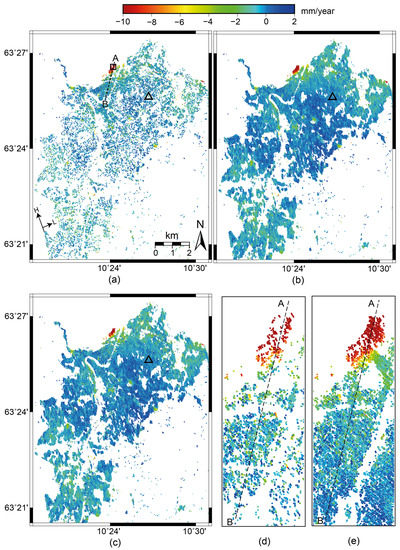
Figure 5.
Mean line-of-sight velocity maps considering: (a) only PS points; (b) PS and DS pixels derived by our new method using the two-sample t-test; and (c) PS and DS pixels identified by the two-sample KS-test. The triangles show the selected reference area. The vectors H and L represent the satellite heading and look angle. Negative implies away from satellite. For the point labeled A, the displacement time-series is shown in Figure 9a.BA indicates the location of the profile analyzed in Figure 9b. A zoomed in area around section BA from: (d) the PS result; and (e) the PS and DS pixels derived by the t-test.
By comparing the LOS velocities illustrated in Figure 5, we observe a common pattern in all of the results. However, the contribution of the DS pixels leads to a higher density of measurements (increased by four times), which allows the identification of some deformation features that are difficult to detect with PS points only.
The maps show that the ground is generally stable within the processing area except for some localized moving areas, most of them located along the coastline. The highest displacement rate of −15 mm/year occurs in the east and west coastlines.
4. Discussion
In this section, we quantify the reliability of our results in terms of SHP maps, despeckled intensity, time-series and velocity of displacement, computational time, and sensitivity to the number of images. We also compare the performance of the tests with the one obtained using one-sample test implemented in [40].
4.1. SHP Maps
Figure 6 shows the number of SHP identified at each pixel using both the two sample t-test and the KS-test. The figure indicates that, using large stack size (50 images), the performances of both tests are similar. The SHP maps derived by these tests have a correlation of 0.96. As shown in the figure, both tests are capable of distinguishing targets of different scattering characteristics and delineating the borders.
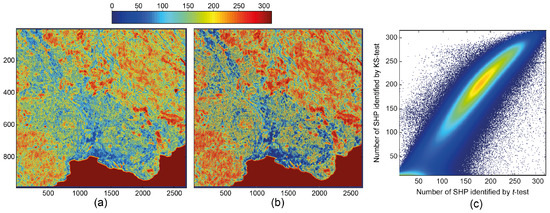
Figure 6.
The number of SHP identified considering a estimation window and performing the two-sample (a) t-test and (b) KS-test, both at 95% significance level, and (c) the scatter plot of the number identified by the t-test versus the KS-test, color-coded by the smoothed density of pixels.
4.2. Despeckled Intensity
As an alternative way to compare the results using the t-test to those using the KS-test, we show in Figure 7 one portion of the amplitude image of the SLC on 25 July 2015 and the despeckled versions using both tests. The figures show that both filtering methods have similar results. The non-urban areas have been denoised, while the PS points and their side-lobes have been preserved well.

Figure 7.
(a) Amplitude image of the SLC on date 25 July 2015; and the filtered version using two-sample: (b) t-test; and (c) KS-test.
4.3. Consistency Assessment of the Displacements
To investigate the effect of the statistical tests on the final velocity maps, we plotted in Figure 8a the displacement velocity derived using the KS-test versus the t-test for the common points. The plot has been color-coded by the smoothed density of the points [54], in which the blue points have the minimum and the red points have the maximum density. The correlation between these results is approximately 0.93. Figure 8b shows the histogram of the differences between these velocities. The root-mean-square error (RMSE) level of a difference is 0.47 mm/year. It shows that the performance of the KS and t-test for the majority of pixels are similar, with a difference that is within the 95% bounds of the estimated accuracy (see Figure 8c).
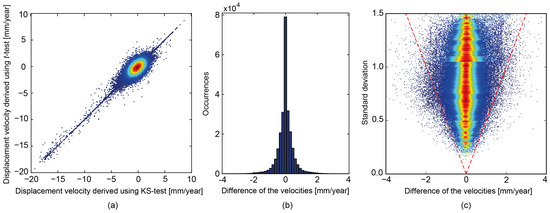
Figure 8.
(a) The line-of-sight displacement velocity derived using KS-test versus t-test, color-coded by the smoothed density of pixels; (b) the histogram of the difference between the velocities; and (c) the difference of the velocities versus the standard deviation, color-coded by the normalized smoothed density of pixels for each standard deviation bin with the width of 0.05. Dashed lines show region where absolute of the difference is less than twice the standard deviation.
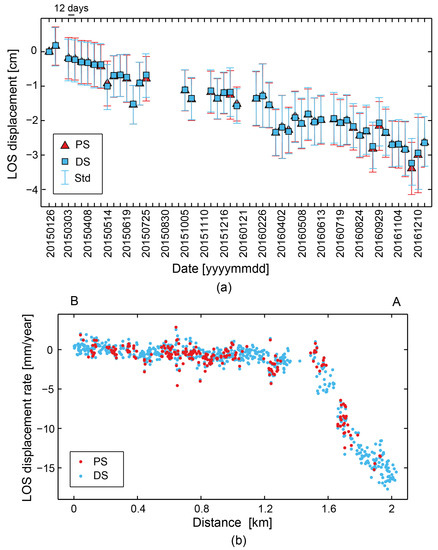
We also plot in Figure 9a the averaged displacement time-series of the point A labeled in Figure 5a, derived from PS and from DS using the t-test. As shown in the figure, the time-series derived by PS and DS is almost identical. We also extracted a 2-km profile along the line BA (marked in Figure 5a, and plotted in Figure 9b). As shown in the figure, the profiles are in good agreement with each other.
4.4. Computational Time
The processing time for SHP identification is around 43 hours using the KS-test. Using the same window size (15 × 21) and SAR stack size (50 images) for the common portion of images (990 × 2700), the processing takes only around 1 h using the t-test. A computer with a Core i7 processor and 16 GB of RAM memory was used during the processing runs. Therefore, replacing the KS-test with the t-test results in a reduction in processing time of 98%.
4.5. Different SAR Stack-Sizes
As mentioned earlier in this section, there is a high correlation between the SHP map derived using the t-test and that derived using the KS-test. We also checked the robustness of the tests to fewer images. We achieved this by calculating the correlation between the number of identified SHPs for each pixel for the full 50 images and that obtained using fewer images (Figure 10). The results show that the t-test is less sensitive to the number of images than the KS-test with, for example, a correlation of 0.95 for 30 images, compared to 0.75 using the KS-test.
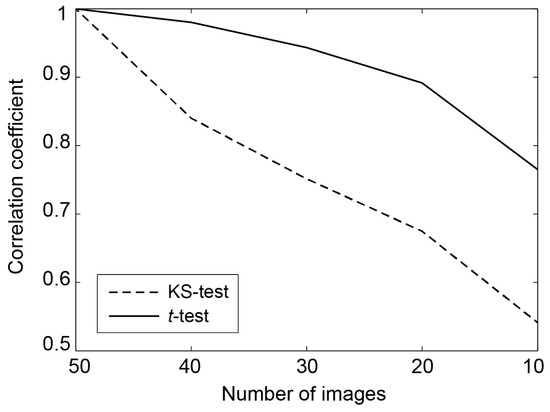
Figure 10.
Correlation coefficient between the number of SHPs found for all pixels, for the full 50 images and for fewer images.
We also implemented the one-sample test proposed in [40], and compared the SHPs identified by the test with the two-sample KS and T tests under different stack sizes. Figure 11 shows the SHPs for one point. It can be observed that, for the large stack size, the performances of the tests are almost the same. Comparing the SHPs for different number of images shows that the two-sample t-test has the most robust performance between the tests. For fewer images, it acts more homogeneously compared to the one-sample t and KS tests.
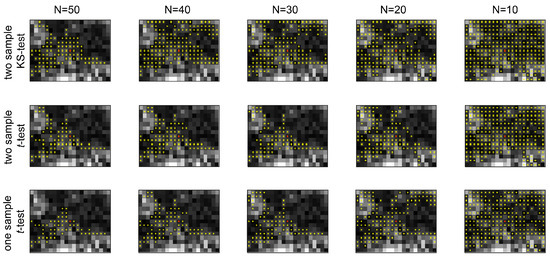
Figure 11.
An example of the SHPs (yellow points) identified by performing the two-sample KS-test, the two-sample t-test, and the one-sample t-test for the full 50 images and for fewer images. The central pixel is shown with red.
5. Conclusions
By replacing the KS-test with the t-test, we have made the SqueeSAR SHP selection algorithm 98% more efficient and more robust in the case of few images. We implemented this approach in the StaMPS/MTI processing chain to deliver a time-series of combined PS and DS more efficiently than the existing StaMPS/MTI combined algorithm. By applying the technique over 50 Sentinel-1 SAR images acquired over Trondheim in Norway and comparing the displacement velocities derived by the combined method using both tests, we derived a correlation of 0.93 between the results. The root-mean-square error (RMSE) level of the difference between the velocities for the t-test and KS-test is less than 0.5 mm/year and, within the 95% confidence limits for 98.7% of pixels, this validating the t-test as an effective, and more efficient replacement for the KS-test.
Author Contributions
R.S. designed the study, did the InSAR analysis and wrote the manuscript. H.N., M.M. and A.H. contributed to the analysis, discussion and writing. All authors discussed the results and commented on the manuscript.
Acknowledgments
This work was supported by the Norwegian University of Science and Technology (NTNU). The digital terrain model was provided by the Norwegian Mapping Authority. The Gamma scripts for pre-processing step are provided by Mahmud Haghshenas Haghighi.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vigny, C.; Socquet, A.; Peyrat, S.; Ruegg, J.C.; Métois, M.; Madariaga, R.; Morvan, S.; Lancieri, M.; Lacassin, R.; Campos, J.; et al. The 2010 Mw 8.8 Maule megathrust earthquake of central Chile, monitored by GPS. Science 2011, 332, 1417–1421. [Google Scholar] [CrossRef] [PubMed]
- Motagh, M.; Klotz, J.; Tavakoli, F.; Djamour, Y.; Arabi, S.; Wetzel, H.U.; Zschau, J. Combination of precise leveling and InSAR data to constrain source parameters of the Mw = 6.5, 26 December 2003 Bam earthquake. Pure Appl. Geophys. 2006, 163, 1–18. [Google Scholar] [CrossRef]
- Moreno, M.; Li, S.; Melnick, D.; Bedford, J.R.; Baez, J.C.; Motagh, M.; Metzger, S.; Vajedian, S.; Sippl, C.; Gutknecht, B.D.; et al. Chilean megathrust earthquake recurrence linked to frictional contrast at depth. Nature Geosci. 2018, 11, 285–290. [Google Scholar] [CrossRef]
- Chen, J.; Wilson, C.; Tapley, B.; Grand, S. GRACE detects coseismic and postseismic deformation from the Sumatra-Andaman earthquake. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Vajedian, S.; Motagh, M.; Nilfouroushan, F. StaMPS improvement for deformation analysis in mountainous regions: Implications for the Damavand volcano and Mosha fault in Alborz. Remote Sens. 2015, 7, 8323–8347. [Google Scholar] [CrossRef]
- Larson, K.M.; Poland, M.; Miklius, A. Volcano monitoring using GPS: Developing data analysis strategies based on the June 2007 Kīlauea Volcano intrusion and eruption. J. Geophys. Res. Solid Earth 2010, 115. [Google Scholar] [CrossRef]
- Haghshenas Haghighi, M.; Motagh, M. Assessment of ground surface displacement in Taihape landslide, New Zealand, with C-and X-band SAR interferometry. N. Z. J. Geol. Geophys. 2016, 59, 136–146. [Google Scholar] [CrossRef]
- Benoit, L.; Briole, P.; Martin, O.; Thom, C.; Malet, J.P.; Ulrich, P. Monitoring landslide displacements with the Geocube wireless network of low-cost GPS. Eng. Geol. 2015, 195, 111–121. [Google Scholar] [CrossRef]
- Teatini, P.; Tosi, L.; Strozzi, T.; Carbognin, L.; Wegmüller, U.; Rizzetto, F. Mapping regional land displacements in the Venice coastland by an integrated monitoring system. Remote Sens. Environ. 2005, 98, 403–413. [Google Scholar] [CrossRef]
- Joodaki, G.; Wahr, J.; Swenson, S. Estimating the human contribution to groundwater depletion in the Middle East, from GRACE data, land surface models, and well observations. Water Resour. Res. 2014, 50, 2679–2692. [Google Scholar] [CrossRef]
- Motagh, M.; Walter, T.R.; Sharifi, M.A.; Fielding, E.; Schenk, A.; Anderssohn, J.; Zschau, J. Land subsidence in Iran caused by widespread water reservoir overexploitation. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Gu, M. Recent research and applications of GPS-based monitoring technology for high-rise structures. Struct. Control Health Monit. 2013, 20, 649–670. [Google Scholar] [CrossRef]
- Lazecky, M.; Hlavacova, I.; Bakon, M.; Sousa, J.J.; Perissin, D.; Patricio, G. Bridge displacements monitoring using space-borne X-band SAR Interferometry. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 205–210. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.X.; Zeisl, B.; Pollefeys, M. Fusing meter-resolution 4-D InSAR point clouds and optical images for semantic urban infrastructure monitoring. IEEE Trans. Geosci. Remote Sens. 2017, 55, 14–26. [Google Scholar] [CrossRef]
- Montazeri, S.; Zhu, X.X.; Eineder, M.; Bamler, R. Three-dimensional deformation monitoring of urban infrastructure by tomographic SAR using multitrack TerraSAR-X data stacks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6868–6878. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Colesanti, C.; Ferretti, A.; Novali, F.; Prati, C.; Rocca, F. SAR monitoring of progressive and seasonal ground deformation using the permanent scatterers technique. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1685–1701. [Google Scholar] [CrossRef]
- Kampes, B.M.; Hanssen, R.F. Ambiguity resolution for permanent scatterer interferometry. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2446–2453. [Google Scholar] [CrossRef]
- Emadali, L.; Motagh, M.; Haghshenas Haghighi, M. Characterizing post-construction settlement of the Masjed-Soleyman embankment dam, Southwest Iran, using TerraSAR-X SpotLight radar imagery. Eng. Struct. 2017, 143, 261–273. [Google Scholar] [CrossRef]
- Shamshiri, R.; Motagh, M.; Baes, M.; Sharifi, M.A. Deformation analysis of the Lake Urmia causeway (LUC) embankments in northwest Iran: Insights from multi-sensor interferometry synthetic aperture radar (InSAR) data and finite element modeling (FEM). J. Geodesy 2014, 88, 1171–1185. [Google Scholar] [CrossRef]
- Lan, H.; Li, L.; Liu, H.; Yang, Z. Complex urban infrastructure deformation monitoring using high resolution PSI. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2012, 5, 643–651. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.B.; Allievi, J. Damage to buildings in large slope rock instabilities monitored with the PSInSARTM technique. Remote Sens. 2013, 5, 4753–4773. [Google Scholar] [CrossRef]
- Haghshenas Haghighi, M.; Motagh, M. Sentinel-1 InSAR over Germany: Large-Scale Interferometry, Atmospheric Effects, and Ground Deformation Mapping. ZFV-Zeitschrift fur Geodasie, Geoinformation und Landmanagement 2017. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent scatterer interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Motagh, M.; Shamshiri, R.; Haghshenas Haghighi, M.; Wetzel, H.U.; Akbari, B.; Nahavandchi, H.; Roessner, S.; Arabi, S. Quantifying groundwater exploitation induced subsidence in the Rafsanjan plain, southeastern Iran, using InSAR time-series and in situ measurements. Eng. Geol. 2017, 218, 134–151. [Google Scholar] [CrossRef]
- Esmaeili, M.; Motagh, M.; Hooper, A. Application of Dual-Polarimetry SAR Images in Multitemporal InSAR Processing. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1489–1493. [Google Scholar] [CrossRef]
- Paradella, W.R.; Ferretti, A.; Mura, J.C.; Colombo, D.; Gama, F.F.; Tamburini, A.; Santos, A.R.; Novali, F.; Galo, M.; Camargo, P.O.; et al. Mapping surface deformation in open pit iron mines of Carajás Province (Amazon Region) using an integrated SAR analysis. Eng. Geol. 2015, 193, 61–78. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.X.; Bamler, R. Retrieval of phase history parameters from distributed scatterers in urban areas using very high resolution SAR data. ISPRS J. Photogramm. Remote Sens. 2012, 73, 89–99. [Google Scholar] [CrossRef]
- Mirzaee, S.; Motagh, M.; Akbari, B.; Wetzel, H.; Roessner, S. Evaluating three InSAR time-series methods to assess creep motion, case study: Masouleh landslide in north Iran. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 223. [Google Scholar] [CrossRef]
- Raspini, F.; Moretti, S.; Casagli, N. Landslide mapping using SqueeSAR data: Giampilieri (Italy) case study. In Landslide Science and Practice; Springer: Berlin/Heidelberg, Germany, 2013; pp. 147–154. [Google Scholar]
- Falorni, G.; Morgan, J.; Eneva, M. Advanced InSAR techniques for geothermal exploration and production. Geotherm. Resour. Council Trans. 2011, 35, 1661–1666. [Google Scholar]
- Spaans, K.; Hooper, A. InSAR processing for volcano monitoring and other near-real time applications. J. Geophys. Res. Solid Earth 2016, 121, 2947–2960. [Google Scholar] [CrossRef]
- Vasile, G.; Trouvé, E.; Lee, J.S.; Buzuloiu, V. Intensity-driven adaptive-neighborhood technique for polarimetric and interferometric SAR parameters estimation. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1609–1621. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.; Hanssen, R.F.; Malhotra, R.; Chang, L. Fast statistically homogeneous pixel selection for covariance matrix estimation for multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1213–1224. [Google Scholar] [CrossRef]
- Lin, K.F.; Perissin, D. Identification of Statistically Homogeneous Pixels Based on One-Sample Test. Remote Sens. 2017, 9, 37. [Google Scholar] [CrossRef]
- Song, H.; Sun, Y.; Wang, R.; Zhang, B.; Li, N.; Wang, Y.; Fei, W. Statistically homogeneous pixel selection for small SAR data sets based on the similarity test of the covariance matrix. Remote Sens. Lett. 2017, 8, 927–936. [Google Scholar] [CrossRef]
- Wang, Y.; Deng, Y.; Fei, W.; Wang, R.; Song, H.; Wang, J.; Li, N. Modified statistically homogeneous pixels selection with multitemporal SAR images. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1930–1934. [Google Scholar] [CrossRef]
- Parizzi, A.; Brcic, R. Adaptive InSAR stack multilooking exploiting amplitude statistics: A comparison between different techniques and practical results. IEEE Geosci. Remote Sens. Lett. 2011, 8, 441–445. [Google Scholar] [CrossRef]
- Deledalle, C.A.; Tupin, F.; Denis, L. A non-local approach for SAR and interferometric SAR denoising. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 714–717. [Google Scholar]
- Sica, F.; Reale, D.; Poggi, G.; Verdoliva, L.; Fornaro, G. Nonlocal adaptive multilooking in SAR multipass differential interferometry. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 1727–1742. [Google Scholar] [CrossRef]
- Scheiber, R.; Moreira, A. Coregistration of interferometric SAR images using spectral diversity. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2179–2191. [Google Scholar] [CrossRef]
- Wegmüller, U.; Werner, C. Gamma SAR processor and interferometry software. In Proceedings of the 3rd ERS Symposium ’Space at the Service of our Environment’, Florence, Italy, 14–21 March 1997; pp. 1687–1692. [Google Scholar]
- Battiti, R.; Masulli, F. BFGS optimization for faster and automated supervised learning. In Proceedings of the International Neural Network Conference, Paris, France, 9–13 July 1990; Springer: Dordrecht, The Netherlands, 1990; pp. 757–760. [Google Scholar]
- Kampes, B.M.; Hanssen, R.F.; Perski, Z. Radar interferometry with public domain tools. In Proceedings of the FRINGE 2003 Workshop, Frascati, Italy, 1–5 December 2003; Volume 3. [Google Scholar]
- Hooper, A.; Segall, P.; Zebker, H. Persistent scatterer interferometric synthetic aperture radar for crustal deformation analysis, with application to Volcán Alcedo, Galápagos. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Hooper, A. A statistical-cost approach to unwrapping the phase of InSAR time series. In Proceedings of the International Workshop on ERS SAR Interferometry, Frascati, Italy, 30 November–4 December 2009; pp. 1–6. [Google Scholar]
- Motagh, M.; Hoffmann, J.; Kampes, B.; Baes, M.; Zschau, J. Strain accumulation across the Gazikoy–Saros segment of the North Anatolian Fault inferred from Persistent Scatterer Interferometry and GPS measurements. Earth Planet. Sci. Lett. 2007, 255, 432–444. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for spatial data. Terra Nova 1992, 4, 613–617. [Google Scholar] [CrossRef]
- Eilers, P.H.; Goeman, J.J. Enhancing scatterplots with smoothed densities. Bioinformatics 2004, 20, 623–628. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).