Modeling Solar Radiation in the Forest Using Remote Sensing Data: A Review of Approaches and Opportunities
Abstract
1. Introduction
2. Overview of Concepts
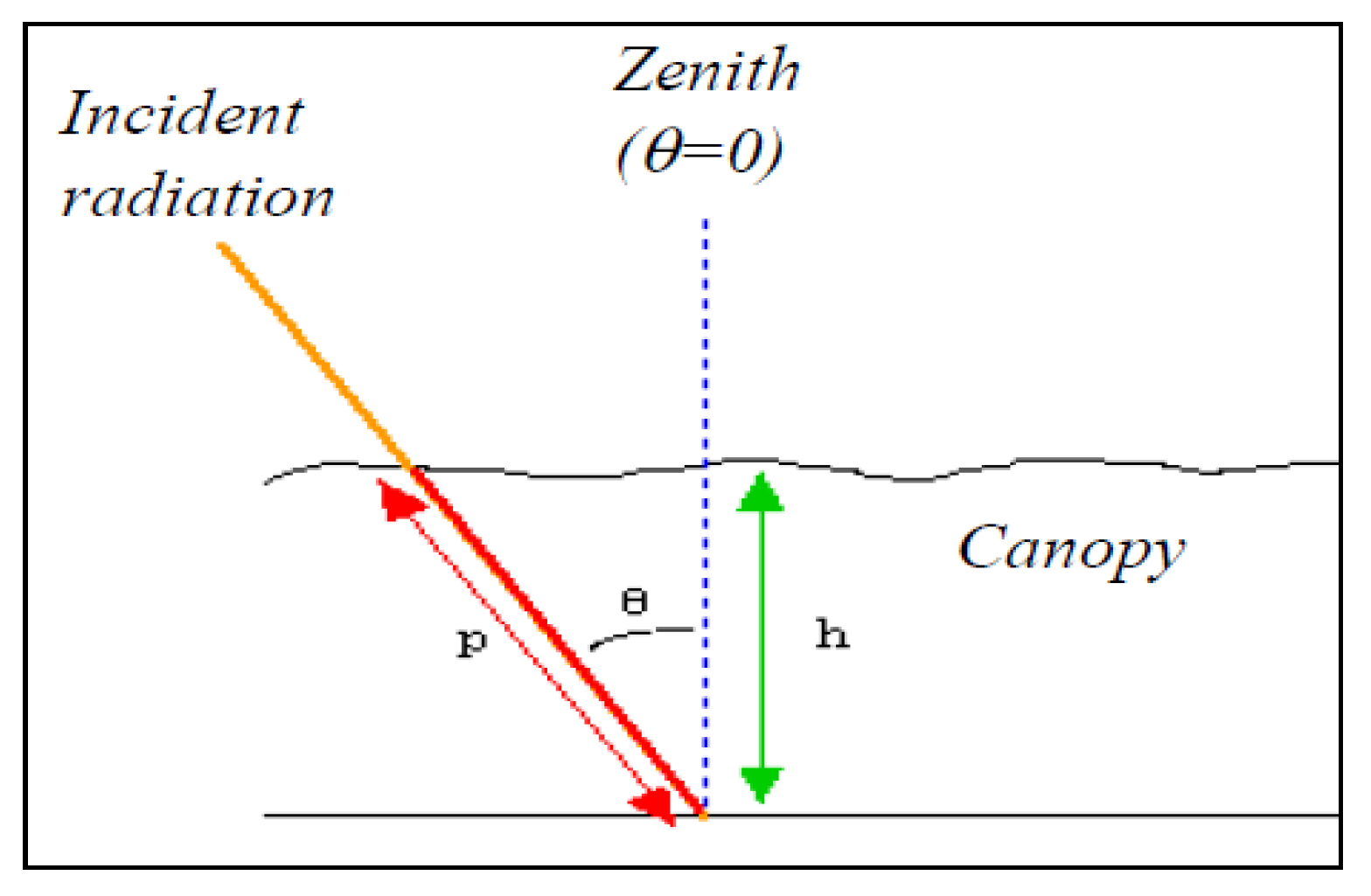
- = incident radiation at the canopy top
- k = extinction coefficient
- L = leaf area index (LAI)
3. Modelling Approaches Using RS Technology
3.1. Physical Models and Techniques
3.2. Summary of the Studies
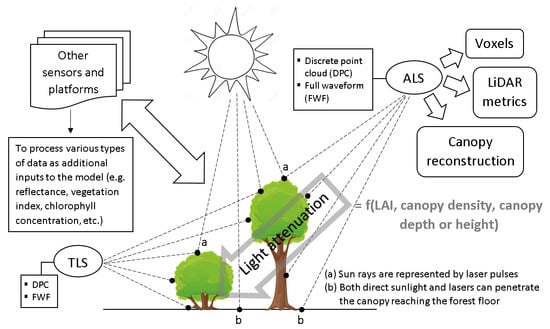
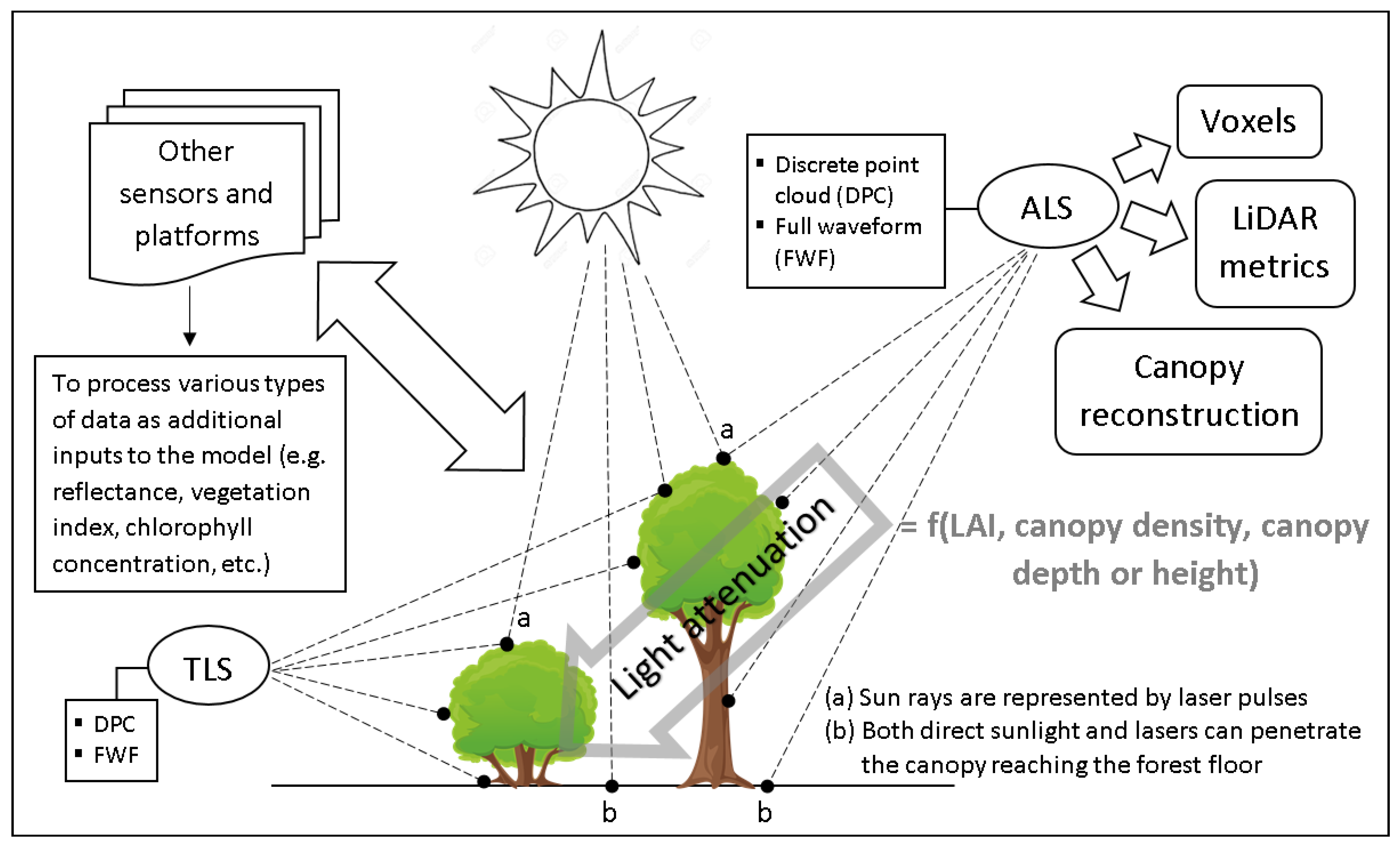
4. Integration of RS Data and Models
5. Critical Issues for Future Research Perspective
5.1. The Diffuse Component of Radiation
5.2. Dataset Fusion
5.3. Light along Vertical Gradients
5.4. Limited Representation in Terms of Biomes
5.5. Cost and Time Consideration
6. Summary
7. Conclusions
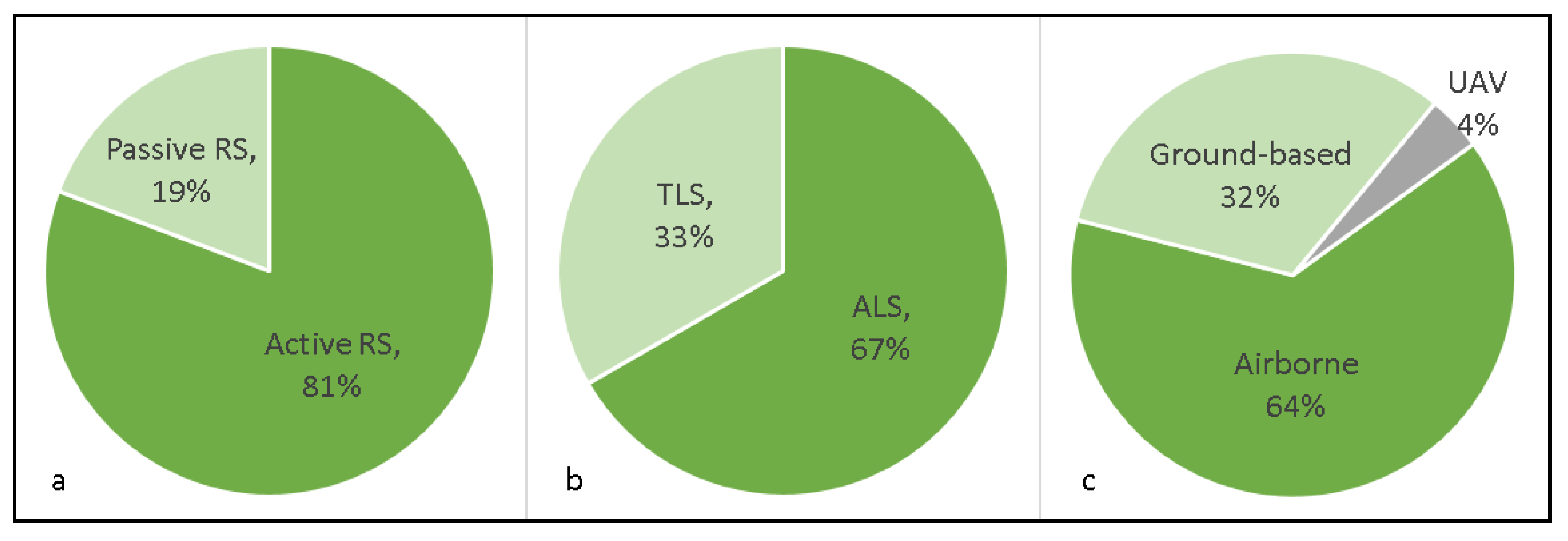
- As far the type of sensors is concerned, the active domain, particularly laser technology, rules the choice in analyzing light conditions below or within the forest canopy.
- Not a single set of data derived from a passive sensor inferring spatial solar radiation was used in the reviewed studies.
- Aside from high 3D spatial resolution, airborne laser scanner’s ability to penetrate the canopy through the gap openings is also an advantage, as it takes account of the forest floor. Those studies that utilized laser scanning mostly applied voxel models or the laser penetration index (LPI).
- The latter may exhibit varying performance and accuracy, depending on the forest type and consequently, the canopy structure.
- The use of UAVs for future research is also an interesting prospect, as it gives flexibility in terms of the coverage, and can address the gaps by both ALS and TLS.
- Lastly, as evident in the market where LiDAR technology is getting less expensive and more countries are opening their databases for public access, various entities are encouraged to take advantage and the initiative to expand their research efforts for a more science-based monitoring and management of our resources.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Graham, C.P. The Water Cycle: Feature Articles. Available online: https://earthobservatory.nasa.gov/Features/Water/page2.php (accessed on 2 October 2017).
- Martens, S.N.; Breshears, D.D.; Meyer, C.W. Spatial distributions of understory light along the grassland/forest continuum: Effects of cover, height, and spatial pattern of tree canopies. Ecol. Model. 2000, 126, 79–93. [Google Scholar] [CrossRef]
- Van der Zande, D.; Stuckens, J.; Verstraeten, W.W.; Mereu, S.; Muys, B.; Coppin, P. 3D modeling of light interception in heterogeneous forest canopies using ground-based LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 792–800. [Google Scholar] [CrossRef]
- Riebeek, H. Water Watchers: Feature Articles. Available online: https://earthobservatory.nasa.gov/Features/WaterWatchers/printall.php (accessed on 22 November 2017).
- Leuchner, M.; Hertel, C.; Rötzer, T.; Seifert, T.; Weigt, R.; Werner, H.; Menzel, A. Solar Radiation as a Driver for Growth and Competition in Forest Stands; Springer: Berlin/Heidelberg, Germany, 2012; pp. 175–191. [Google Scholar]
- Peng, S.; Zhao, C.; Xu, Z. Modeling spatiotemporal patterns of understory light intensity using airborne laser scanner (LiDAR). ISPRS J. Photogramm. Remote Sens. 2014, 97, 195–203. [Google Scholar] [CrossRef]
- Oliver, C.; Larson, B. Forest Stand Dynamics, update ed; John Wiley and Sons Inc.: New York, NY, USA; ISBN 0-471-13833-9.
- Grant, R. Partitioning of biologically active radiation in plant canopies. Int. J. Biometeorol. 1997, 40, 26–40. [Google Scholar] [CrossRef]
- Englund, S.R.; O’brien, J.J.; Clark, D.B. Evaluation of digital and film hemispherical photography and spherical densiometry for measuring forest light environments. Can. J. Forest Res. 2000, 30, 1999–2005. [Google Scholar] [CrossRef]
- Zavitkovski, J. Ground vegetation biomass, production, and efficiency of energy utilization in some northern Wisconsin forest ecosystems. Ecology 1976, 57, 694–706. [Google Scholar] [CrossRef]
- Anderson, M.; Denhead, O. Shortwave radiation on inclined surfaces in model plant communities. Agron. J. 1969, 61, 867–872. [Google Scholar] [CrossRef]
- Van der Zande, D.; Stuckens, J.; Verstraeten, W.W.; Muys, B.; Coppin, P. Assessment of Light Environment Variability in Broadleaved Forest Canopies Using Terrestrial Laser Scanning. Remote Sens. 2010, 2, 1564–1574. [Google Scholar] [CrossRef]
- Mücke, W.; Hollaus, M. Modelling light conditions in forests using airborne laser scanning data. In Proceedings of the SilviLaser 2011, 11th International Conference on LiDAR Applications for Assessing Forest Ecosystems, University of Tasmania, Hobart, TAS, Australia, 16–20 October 2011; Volume 2011. [Google Scholar]
- Sakai, T.; Akiyama, T. Quantifying the spatio-temporal variability of net primary production of the understory species, Sasa senanensis, using multipoint measuring techniques. Agric. Forest Meteorol. 2005, 134, 60–69. [Google Scholar] [CrossRef]
- von Arx, G.; Dobbertin, M.; Rebetez, M. Spatio-temporal effects of forest canopy on understory microclimate in a long-term experiment in Switzerland. Agric. Forest Meteorol. 2012, 166–167, 144–155. [Google Scholar] [CrossRef]
- Musselman, K.N.; Margulis, S.A.; Molotch, N.P. Estimation of solar direct beam transmittance of conifer canopies from airborne LiDAR. Remote Sens. Environ. 2013, 136, 402–415. [Google Scholar] [CrossRef]
- Théry, M. Forest light and its influence on habitat selection. In Tropical Forest Canopies: Ecology and Management; Springer: Berlin/Heidelberg, Germany, 2001; pp. 251–261. [Google Scholar]
- Battisti, A.; Marini, L.; Pitacco, A.; Larsson, S. Solar radiation directly affects larval performance of a forest insect: Effects of solar radiation on larval performance. Ecol. Entomol. 2013, 38, 553–559. [Google Scholar] [CrossRef]
- Jennings, S.B.; Brown, A.G.; Sheil, D. Assessing forest canopies and understorey illumination: Canopy closure, canopy cover and other measures. Forestry 1999, 72, 59–74. [Google Scholar] [CrossRef]
- Anderson, M. Studies of the woodland light climate I. The photographic computation of light conditions. J. Ecol. 1964, 52, 27–41. [Google Scholar] [CrossRef]
- Alexander, C.; Moeslund, J.E.; Bøcher, P.K.; Arge, L.; Svenning, J.-C. Airborne laser scanner (LiDAR) proxies for understory light conditions. Remote Sens. Environ. 2013, 134, 152–161. [Google Scholar] [CrossRef]
- Bode, C.A.; Limm, M.P.; Power, M.E.; Finlay, J.C. Subcanopy Solar Radiation model: Predicting solar radiation across a heavily vegetated landscape using LiDAR and GIS solar radiation models. Remote Sens. Environ. 2014, 154, 387–397. [Google Scholar] [CrossRef]
- Jones, H.G.; Archer, N.; Rotenberg, E.; Casa, R. Radiation measurement for plant ecophysiology. J. Exp. Bot. 2003, 54, 879–889. [Google Scholar] [CrossRef] [PubMed]
- Álvarez, J.; Mitasova, H.; Allen, H.L. Estimating monthly solar radiation in South-Central Chile. Chil. J. Agric. Res. 2011, 71, 601–609. [Google Scholar] [CrossRef]
- Widlowski, J.-L.; Côté, J.-F.; Béland, M. Abstract tree crowns in 3D radiative transfer models: Impact on simulated open-canopy reflectances. Remote Sens. Environ. 2014, 142, 155–175. [Google Scholar] [CrossRef]
- Welles, J.M.; Cohen, S. Canopy structure measurement by gap fraction analysis using commercial instrumentation. J. Exp. Bot. 1996, 47, 1335–1342. [Google Scholar] [CrossRef]
- Angelini, A.; Corona, P.; Chianucci, F.; Portoghesi, L. Structural attributes of stand overstory and light under the canopy. CRA J. 2015, 39, 23–31. [Google Scholar]
- Lieffers, V.J.; Messier, C.; Stadt, K.J.; Gendron, F.; Comeau, P.G. Predicting and managing light in the understory of boreal forests. Can. J. Forest Res. 1999, 29, 796–811. [Google Scholar] [CrossRef]
- Moeser, D.; Roubinek, J.; Schleppi, P.; Morsdorf, F.; Jonas, T. Canopy closure, LAI and radiation transfer from airborne LiDAR synthetic images. Agric. Forest Meteorol. 2014, 197, 158–168. [Google Scholar] [CrossRef]
- Stereńczak, K.; Ciesielski, M.; Balazy, R.; Zawiła-Niedźwiecki, T. Comparison of various algorithms for DTM interpolation from LIDAR data in dense mountain forests. Eur. J. Remote Sens. 2016, 49, 599–621. [Google Scholar] [CrossRef]
- Sterenczak, K.; Zasada, M.; Brach, M. The accuracy assessment of DTM generated from LIDAR data for forest area—A case study for scots pine stands in Poland. Balt. For. 2013, 19, 252–262. [Google Scholar]
- Parker, G.G.; Lefsky, M.A.; Harding, D.J. PAR Transmittance in Forest Canopies Determined Using Airborne Laser Altimetry and In-Canopy Quantum Measurements; SERC: London, UK, 2001. [Google Scholar]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar Remote Sensing for Ecosystem Studies. BioScience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- van Leeuwen, M.; Coops, N.C.; Hilker, T.; Wulder, M.A.; Newnham, G.J.; Culvenor, D.S. Automated reconstruction of tree and canopy structure for modeling the internal canopy radiation regime. Remote Sens. Environ. 2013, 136, 286–300. [Google Scholar] [CrossRef]
- Comeau, P. Measuring Light in the Forest; Technical Report; Ministry of Forests: Victoria, BC, Canada, 2000. [CrossRef]
- Promis, Á. Measuring and estimating the below-canopy light environment in a forest: A Review. In Revista Chapingo Serie Ciencias Forestales y del Ambiente; Universidad Autónoma Chapingo: Chapingo, Mexico, 2013; Volume XIX, pp. 139–146. [Google Scholar] [CrossRef]
- Kumar, L. Reliability of GIS-based solar radiation models and their utilisation in agro-meteorological research. In Proceedings of the 34th International Symposium on Remote Sensing of Environment—The GEOSS Era: Towards Operational Environmental Monitoring, Sydney, Australia, 10–15 April 2011. [Google Scholar]
- Moskal, L.M.; Erdody, T.; Kato, A.; Richardson, J.; Zheng, G.; Briggs, D. Lidar applications in precision forestry. In Proceedings of the SilviLaser 2009, College Station, TX, USA, 14–16 October 2009; pp. 154–163. [Google Scholar]
- Seidel, D.; Fleck, S.; Leuschner, C. Analyzing forest canopies with ground-based laser scanning: A comparison with hemispherical photography. Agric. Forest Meteorol. 2012, 154–155, 1–8. [Google Scholar] [CrossRef]
- Magney, T.S.; Eitel, J.U.H.; Griffin, K.L.; Boelman, N.T.; Greaves, H.E.; Prager, C.M.; Logan, B.A.; Zheng, G.; Ma, L.; Fortin, E.A.; et al. LiDAR canopy radiation model reveals patterns of photosynthetic partitioning in an Arctic shrub. Agric. Forest Meteorol. 2016, 221, 78–93. [Google Scholar] [CrossRef]
- Zheng, G.; Moskal, L.M. Retrieving Leaf Area Index (LAI) Using Remote Sensing: Theories, Methods and Sensors. Sensors 2009, 9, 2719–2745. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Sammis, T.W.; Gutschick, V.P.; Gebremichael, M.; Dennis, S.O.; Harrison, R.E. Review of Satellite Remote Sensing Use in Forest Health Studies. Open Geogr. J. 2010, 3, 28–42. [Google Scholar] [CrossRef]
- Brewer, C.; Monty, J.; Johnson, A.; Evans, D.; Fisk, H. Forest Carbon Monitoring: A Review of Selected Remote Sensing and Carbon Measurement Tools for REDD+; RSAC-10018-RPT1; Department of Agriculture, Forest Service, Remote Sensing Applications Center: Salt Lake City, UT, USA, 2011; p. 35. [Google Scholar]
- Toth, C.; Jóźków, G. Remote sensing platforms and sensors: A survey. ISPRS J. Photogramm. Remote Sens. 2016, 115, 22–36. [Google Scholar] [CrossRef]
- John Weier, R.C. Solar Radiation and Climate Experiment (SORCE) Fact Sheet: Feature Articles. Available online: https://earthobservatory.nasa.gov/Features/SORCE/sorce.php (accessed on 15 April 2018).
- Lindsey, R. Climate and Earth’s Energy Budget: Feature Articles. Available online: https://earthobservatory.nasa.gov/Features/EnergyBalance/ (accessed on 22 November 2017).
- Gibson, J. UVB Radiation, Definitions and Characteristics. Available online: http://uvb.nrel.colostate.edu/UVB/publications/uvb_primer.pdf (accessed on 10 September 2017).
- Canada Center for Remote Sensing Fundamentals of Remote Sensing: A Tutorial. Available online: https://www.nrcan.gc.ca/sites/www.nrcan.gc.ca/files/earthsciences/pdf/resource/tutor/fundam/pdf/fundamentals_e.pdf (accessed on 20 March 2018).
- Brown, R.D.; Gillespie, T.J. Microclimatic Landscape Design; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Shahidan, M.F.; Shariff, M.K.M.; Jones, P.; Salleh, E.; Abdullah, A.M. A comparison of Mesua ferrea L. and Hura crepitans L. for shade creation and radiation modification in improving thermal comfort. Landsc. Urban Plan. 2010, 97, 168–181. [Google Scholar] [CrossRef]
- Schleppi, P.; Paquette, A. Solar Radiation in Forests: Theory for Hemispherical Photography. In Hemispherical Photography in Forest Science: Theory, Methods, Applications; Fournier, R.A., Hall, R.J., Eds.; Springer: Dordrecht, The Netherlands, 2017; Volume 28, pp. 15–52. ISBN 978-94-024-1096-9. [Google Scholar]
- Chazdon, R. Sunflecks and Their Importance to Forest Understorey Plants. Adv. Ecol. Res. 1998, 18, 1–63. [Google Scholar]
- Chazdon, R.L.; Pearcy, R.W. The Importance of Sunflecks for Forest Understory Plants. BioScience 1991, 41, 760–766. [Google Scholar] [CrossRef]
- Promis, A.; Schindler, D.; Reif, A.; Cruz, G. Solar radiation transmission in and around canopy gaps in an uneven-aged Nothofagus betuloides forest. Int. J. Biometeorol. 2009, 53, 355–367. [Google Scholar] [CrossRef] [PubMed]
- Nyman, P.; Metzen, D.; Hawthorne, S.N.D.; Duff, T.J.; Inbar, A.; Lane, P.N.J.; Sheridan, G.J. Evaluating models of shortwave radiation below Eucalyptus canopies in SE Australia. Agric. Forest Meteorol. 2017, 246, 51–63. [Google Scholar] [CrossRef]
- Monsi, M.; Saeki, T. On the Factor Light in Plant Communities and its Importance for Matter Production. Ann. Bot. 2005, 95, 549–567. [Google Scholar] [CrossRef] [PubMed]
- Breda, N.J.J. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Macfarlane, C.; Hoffman, M.; Eamus, D.; Kerp, N.; Higginson, S.; McMurtrie, R.; Adams, M. Estimation of leaf area index in eucalypt forest using digital photography. Agric. Forest Meteorol. 2007, 143, 176–188. [Google Scholar] [CrossRef]
- Solberg, S.; Brunner, A.; Hanssen, K.H.; Lange, H.; Næsset, E.; Rautiainen, M.; Stenberg, P. Mapping LAI in a Norway spruce forest using airborne laser scanning. Remote Sens. Environ. 2009, 113, 2317–2327. [Google Scholar] [CrossRef]
- Cowling, S.A.; Field, C.B. Environmental control of leaf area production: Implications for vegetation and land-surface modeling: Environmental controls of leaf area production. Glob. Biogeochem. Cycles 2003, 17. [Google Scholar] [CrossRef]
- Waring, R.H.; Running, S.W. CHAPTER 2—Water Cycle. In Forest Ecosystems, 3rd ed.; Academic Press: San Diego, CA, USA, 2007; pp. 19–57. ISBN 978-0-12-370605-8. [Google Scholar]
- Seyednasrollah, B.; Kumar, M. Effects of tree morphometry on net snow cover radiation on forest floor for varying vegetation densities: Tree morphometry effects on radiation. J. Geophys. Res. Atmos. 2013, 118, 12508–12521. [Google Scholar] [CrossRef]
- Regent Instrument Canada. WinSCANOPY Technical Manual for Canopy Analysis; Regent Instrument Canada: Quebec City, QC, Canada, 2014. [Google Scholar]
- Skye Instrument Ltd Light Guidance Notes. Available online: http://www.skyeinstruments.com/wp-content/uploads/LightGuidanceNotes.pdf (accessed on 30 January 2018).
- Rich, P.M. A Manual for Analysis of Hemispherical Canopy Photography; Los Alamos National Laboratory, New Mexico: Los Alamos, NM, USA, 1989; Volume 92.
- Alados, I.; Foyo-Moreno, I.; Alados-Arboledas, L. Photosynthetically active radiation: Measurements and modelling. Agric. Forest Meteorol. 1996, 78, 121–131. [Google Scholar] [CrossRef]
- Bittner, S.; Gayler, S.; Biernath, C.; Winkler, J.B.; Seifert, S.; Pretzsch, H.; Priesack, E. Evaluation of a ray-tracing canopy light model based on terrestrial laser scans. Can. J. Remote Sens. 2012, 38, 619–628. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Martin, E.; Gascon, F. DART: A 3D model for simulating satellite images and studying surface radiation budget. Int. J. Remote Sens. 2004, 25, 73–96. [Google Scholar] [CrossRef]
- Seidel, D.; Beyer, F.; Hertel, D.; Fleck, S.; Leuschner, C. 3D-laser scanning: A non-destructive method for studying above- ground biomass and growth of juvenile trees. Agric. Forest Meteorol. 2011, 151, 1305–1311. [Google Scholar] [CrossRef]
- Omasa, K.; Hosoi, F.; Uenishi, T.M.; Shimizu, Y.; Akiyama, Y. Three-Dimensional Modeling of an Urban Park and Trees by Combined Airborne and Portable On-Ground Scanning LIDAR Remote Sensing. Environ. Model. Assess. 2008, 13, 473–481. [Google Scholar] [CrossRef]
- Yang, X.; Strahler, A.H.; Schaaf, C.B.; Jupp, D.L.B.; Yao, T.; Zhao, F.; Wang, Z.; Culvenor, D.S.; Newnham, G.J.; Lovell, J.L.; et al. Three-dimensional forest reconstruction and structural parameter retrievals using a terrestrial full-waveform lidar instrument (Echidna®). Remote Sens. Environ. 2013, 135, 36–51. [Google Scholar] [CrossRef]
- Jupp, D.L.B.; Culvenor, D.S.; Lovell, J.L.; Newnham, G.J.; Strahler, A.H.; Woodcock, C.E. Estimating forest LAI profiles and structural parameters using a ground-based laser called ’Echidna(R). Tree Physiol. 2008, 29, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Strahler, A.; Jupp, D.; Woodcock, C.; Schaaf, C.; Yao, T.; Zhao, F.; Yang, X.; Lovell, J.; Culvenor, D.; Newnham, G.; et al. Retrieval of forest structural parameters using a ground-based LiDAR instrument (Echidna †). Can. J. Remote Sens. 2014, 34. [Google Scholar] [CrossRef]
- Armston, J.; Disney, M.; Lewis, P.; Scarth, P.; Phinn, S.; Lucas, R.; Bunting, P.; Goodwin, N. Direct retrieval of canopy gap probability using airborne waveform Lidar. Remote Sens. Environ. 2013, 134, 24–38. [Google Scholar] [CrossRef]
- Yang, W.; Ni-Meister, W.; Kiang, N.Y.; Moorcroft, P.R.; Strahler, A.H.; Oliphant, A. A clumped-foliage canopy radiative transfer model for a Global Dynamic Terrestrial Ecosystem Model II: Comparison to measurements. Agric. Forest Meteorol. 2010, 150, 895–907. [Google Scholar] [CrossRef]
- Comeau, P.; Macdonald, R.; Bryce, R.; Groves, B. Lite: A Model for Estimating Light Interception and Transmission Through Forest Canopies, User’s Manual and Program Documentation; Working Paper 35/1998; Research Branch, Ministry of Forests: Victoria, BC, Canada, 1998.
- Comeau, P. Modeling Light Using SLIM & LITE. Available online: https://sites.ualberta.ca/~pcomeau/Light_Modeling/lightusingSLIM_and_LITE.htm (accessed on 20 July 2017).
- Gastellu-Etchegorry, J.-P.; Grau, E.; Lauret, N. DART: A 3D model for remote sensing images and radiative budget of earth surfaces. In Modeling and Simulation in Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 978-953-307-959-2. [Google Scholar]
- Estimating Light Beneath Forest Canopies with LITE and SLIM—Ministry of Forests and Range—Research Branch. Available online: https://www.for.gov.bc.ca/hre/StandDevMod/LiteSlim/ (accessed on 24 April 2018).
- Malenovskỳ, Z.; Martin, E.; Homolová, L.; Gastellu-Etchegorry, J.-P.; Zurita-Milla, R.; Schaepman, M.E.; Pokornỳ, R.; Clevers, J.G.; Cudlín, P. Influence of woody elements of a Norway spruce canopy on nadir reflectance simulated by the DART model at very high spatial resolution. Remote Sens. Environ. 2008, 112, 1–18. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Mattar, C.; Gastellu-Etchegorry, J.P.; Jimenez-Munoz, J.C.; Grau, E. Evaluation of the DART 3D model in the thermal domain using satellite/airborne imagery and ground-based measurements. Int. J. Remote Sens. 2011, 1–25. [Google Scholar] [CrossRef]
- Guillevic, P.; Gastellu-Etchegorry, J.-P. Modeling BRF and Radiation Regime of Boreal and Tropical Forest. Remote Sens. Environ. 1999, 68, 281–316. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.-P.; Yin, T.; Lauret, N.; Cajgfinger, T.; Gregoire, T.; Grau, E.; Feret, J.-B.; Lopes, M.; Guilleux, J.; Dedieu, G. Discrete Anisotropic Radiative Transfer (DART 5) for modeling airborne and satellite spectroradiometer and LIDAR acquisitions of natural and urban landscapes. Remote Sens. 2015, 7, 1667–1701. [Google Scholar] [CrossRef]
- Yamamoto, K.; Murase, Y.; Etou, C.; Shibuya, K. Estimation of relative illuminance within forests using small-footprint airborne LiDAR. J. Forest Res. 2015, 20, 321–327. [Google Scholar] [CrossRef]
- Essery, R.; Bunting, P.; Rowlands, A.; Rutter, N.; Hardy, J.; Melloh, R.; Link, T.; Marks, D.; Pomeroy, J. Radiative Transfer Modeling of a Coniferous Canopy Characterized by Airborne Remote Sensing. J. Hydrometeorol. 2008, 9, 228–241. [Google Scholar] [CrossRef]
- Thomas, V.; Finch, D.A.; McCaughey, J.H.; Noland, T.; Rich, L.; Treitz, P. Spatial modelling of the fraction of photosynthetically active radiation absorbed by a boreal mixed wood forest using a lidar–hyperspectral approach. Agric. Forest Meteorol. 2006, 140, 287–307. [Google Scholar] [CrossRef]
- Mallet, C.; Bretar, F. Full-waveform topographic lidar: State-of-the-art. ISPRS J. Photogramm. Remote Sens. 2009, 64, 1–16. [Google Scholar] [CrossRef]
- Beland, M.; Parker, G.; Harding, D.; Hopkinson, C.; Chasmer, L.; Antonarakis, A. White Paper–On the Use of LiDAR Data at AmeriFlux Sites; Ameriflux Network, Berkeley Lab: Berkeley, CA, USA, 2015.
- Flood, M. Laser altimetry: From science to commercial lidar mapping. Photogramm. Eng. Remote Sens. 2001, 67, 1209–1217. [Google Scholar]
- Barilotti, A.; Turco, S.; Alberti, G. LAI determination in forestry ecosystem by LiDAR data analysis. In Proceedings of the Workshop 3D Remote Sensing in Forestry, Vienna, Austria, 14–15 February 2006; Volume 1415. [Google Scholar]
- Kwak, D.-A.; Lee, W.-K.; Cho, H.-K. Estimation of LAI Using Lidar Remote Sensing in Forest. In Proceedings of the ISPRS Workshop on Laser Scanning and SilviLaser, Espoo, Finland, 12–14 September 2007; Volume 6. [Google Scholar]
- Yamamoto, K.; Takahashi, T.; Miyachi, Y.; Kondo, N.; Morita, S.; Nakao, M.; Shibayama, T.; Takaichi, Y.; Tsuzuku, M.; Murate, N. Estimation of mean tree height using small-footprint airborne LiDAR without a digital terrain model. J. Forest Res. 2011, 16, 425–431. [Google Scholar] [CrossRef]
- Takahashi, T.; Yamamoto, K.; Senda, Y.; Tsuzuku, M. Predicting individual stem volumes of sugi (Cryptomeria japonica) plantations in mountainous areas using small-footprint airborne LiDAR. J. Forest Res. 2005, 10, 305–312. [Google Scholar] [CrossRef]
- Ellenberg, H. Vegetation Ecology of Central Europe, 4th ed.; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Tymen, B.; Vincent, G.; Courtois, E.A.; Heurtebize, J.; Dauzat, J.; Marechaux, I.; Chave, J. Quantifying micro-environmental variation in tropical rainforest understory at landscape scale by combining airborne LiDAR scanning and a sensor network. Ann. Forest Sci. 2017, 74. [Google Scholar] [CrossRef]
- Dozier, J.; Frew, J. Rapid calculation of terrain parameters for radiation modeling from digital elevation data. IEEE Trans. Geosci. Remote Sens. 1990, 28, 963–969. [Google Scholar] [CrossRef]
- Fu, P.; Rich, P.M. Design and implementation of the Solar Analyst: An ArcView extension for modeling solar radiation at landscape scales. In Proceedings of the Nineteenth Annual ESRI User Conference, San Diego, CA, USA, 1999; Volume 1, pp. 1–31. [Google Scholar]
- Hofierka, J.; Suri, M.; Šúri, M. The solar radiation model for Open source GIS: Implementation and applications. In Proceedings of the Open source GIS—GRASS Users Conference, Trento, Italy, 11–13 September 2002; pp. 1–19. [Google Scholar]
- Cifuentes, R.; Van der Zande, D.; Salas, C.; Tits, L.; Farifteh, J.; Coppin, P. Modeling 3D Canopy Structure and Transmitted PAR Using Terrestrial LiDAR. Can. J. Remote Sens. 2017, 43, 124–139. [Google Scholar] [CrossRef]
- Guillen-Climent, M.L.; Zarco-Tejada, P.J.; Berni, J.A.J.; North, P.R.J.; Villalobos, F.J. Mapping radiation interception in row-structured orchards using 3D simulation and high-resolution airborne imagery acquired from a UAV. Precis. Agric. 2012, 13, 473–500. [Google Scholar] [CrossRef]
- Kobayashi, H.; Baldocchi, D.D.; Ryu, Y.; Chen, Q.; Ma, S.; Osuna, J.L.; Ustin, S.L. Modeling energy and carbon fluxes in a heterogeneous oak woodland: A three-dimensional approach. Agric. Forest Meteorol. 2012, 152, 83–100. [Google Scholar] [CrossRef]
- Lee, H.; Slatton, K.C.; Roth, B.E.; Cropper, W.P. Prediction of forest canopy light interception using three-dimensional airborne LiDAR data. Int. J. Remote Sens. 2009, 30, 189–207. [Google Scholar] [CrossRef]
- Todd, K.W.; Csillag, F.; Atkinson, P.M. Three-dimensional mapping of light transmittance and foliage distribution using lidar. Can. J. Remote Sens. 2003, 29, 544–555. [Google Scholar] [CrossRef]
- Kucharik, C.J.; Norman, J.M.; Gower, S.T. Measurements of leaf orientation, light distribution and sunlit leaf area in a boreal aspen forest. Agric. Forest Meteorol. 1998, 91, 127–148. [Google Scholar] [CrossRef]
- Lillesand, T.M.; Kieffer, R.W. Remote Sensing and Image Interpretation, 2nd ed.; John Wiley and Sons, Inc.: Toronto, ON, Canada, 1987. [Google Scholar]
- Brunner, A. A light model for spatially explicit forest stand models. Forest Ecol. Manag. 1998, 107, 19–46. [Google Scholar] [CrossRef]
- Baltsavias, E.P. Airborne laser scanning: Existing systems and firms and other resources. ISPRS J. Photogramm. Remote Sens. 1999, 54, 164–198. [Google Scholar] [CrossRef]
- Gu, L.; Baldocchi, D.; Verma, S.B.; Black, T.A.; Vesala, T.; Falge, E.M.; Dowty, P.R. Advantages of diffuse radiation for terrestrial ecosystem productivity. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef]
- Cavazzoni, J.; Volk, T.; Tubiello, F.; Monje, O. Modelling the effect of diffuse light on canopy photosynthesis in controlled environments. Acta Hortic. 2002, 593, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Heuvelink, E.; Dueck, T.A.; Janse, J.; Gort, G.; Marcelis, L.F.M. Enhancement of crop photosynthesis by diffuse light: Quantifying the contributing factors. Ann. Bot. 2014, 114, 145–156. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Yang, Q. Advantages of diffuse light for horticultural production and perspectives for further research. Front. Plant Sci. 2015, 6. [Google Scholar] [CrossRef] [PubMed]
- Chasmer, L.; Hopkinson, C.; Treitz, P. Assessing the three-dimensional frequency distribution of airborne and ground-based lidar data for red pine and mixed deciduous forest plots. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36, W2. [Google Scholar]
- Hopkinson, C.; Lovell, J.; Chasmer, L.; Jupp, D.; Kljun, N.; van Gorsel, E. Integrating terrestrial and airborne lidar to calibrate a 3D canopy model of effective leaf area index. Remote Sens. Environ. 2013, 136, 301–314. [Google Scholar] [CrossRef]
- GlobALS: Global ALS Data Providers Database. Interactive Map. Available online: https://www.google.com/maps/d/viewer?mid=1-K-a1MvbjFRE19i8YzOvgkAfEwQ2SGBU&ll=38.48478719903015%2C53.557913999999926&z=3 (accessed on 26 February 2018).
- McGaughey, R.J.; Andersen, H.-E.; Reutebuch, S.E. Considerations for planning, acquiring, and processing LiDAR data for forestry applications. In Proceedings of the 11th Biennial USDA Forest Service Remote Sensing Applications Conference, Salt Lake City, Utah, USA, 24–28 April 2006. [Google Scholar]
- Hummel, S.; Hudak, A.T.; Uebler, E.H.; Falkowski, M.J.; Megown, K.A. A comparison of accuracy and cost of LiDAR versus stand exam data for landscape management on the Malheur National Forest. J. For. 2011, 109, 267–273. [Google Scholar]
- Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; Gonzalez de Tanago, J.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for Terrestrial Laser Scanning of forest plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
- Widlowski, J.-L.; Pinty, B.; Clerici, M.; Dai, Y.; De Kauwe, M.; de Ridder, K.; Kallel, A.; Kobayashi, H.; Lavergne, T.; Ni-Meister, W.; et al. RAMI4PILPS: An intercomparison of formulations for the partitioning of solar radiation in land surface models. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef]
- Pinty, B.; Gobron, N.; Widlowski, J.-L.; Gerstl, S.A.; Verstraete, M.M.; Antunes, M.; Bacour, C.; Gascon, F.; Gastellu, J.-P.; Goel, N. Radiation transfer model intercomparison (RAMI) exercise. J. Geophys. Res. Atmos. 2001, 106, 11937–11956. [Google Scholar] [CrossRef]
- Saremi, H.; Kumar, L.; Turner, R.; Stone, C.; Melville, G. DBH and height show significant correlation with incoming solar radiation: A case study of a radiata pine (Pinus radiata D. Don) plantation in New South Wales, Australia. GISci. Remote Sens. 2014, 51, 427–444. [Google Scholar] [CrossRef]
- Szymanowski, M.; Kryza, M.; Miga, K.; Sobolewski, P.; Kolondra, L. Modelowanie. Modelling and validation of the potential solar radiation for the hornsund region—Application of the r.sun model. Rocz. Geomatyki Ann. Geomat. 2008, 6, 107–112. [Google Scholar]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 2015, 8, 1991–2007. [Google Scholar] [CrossRef]


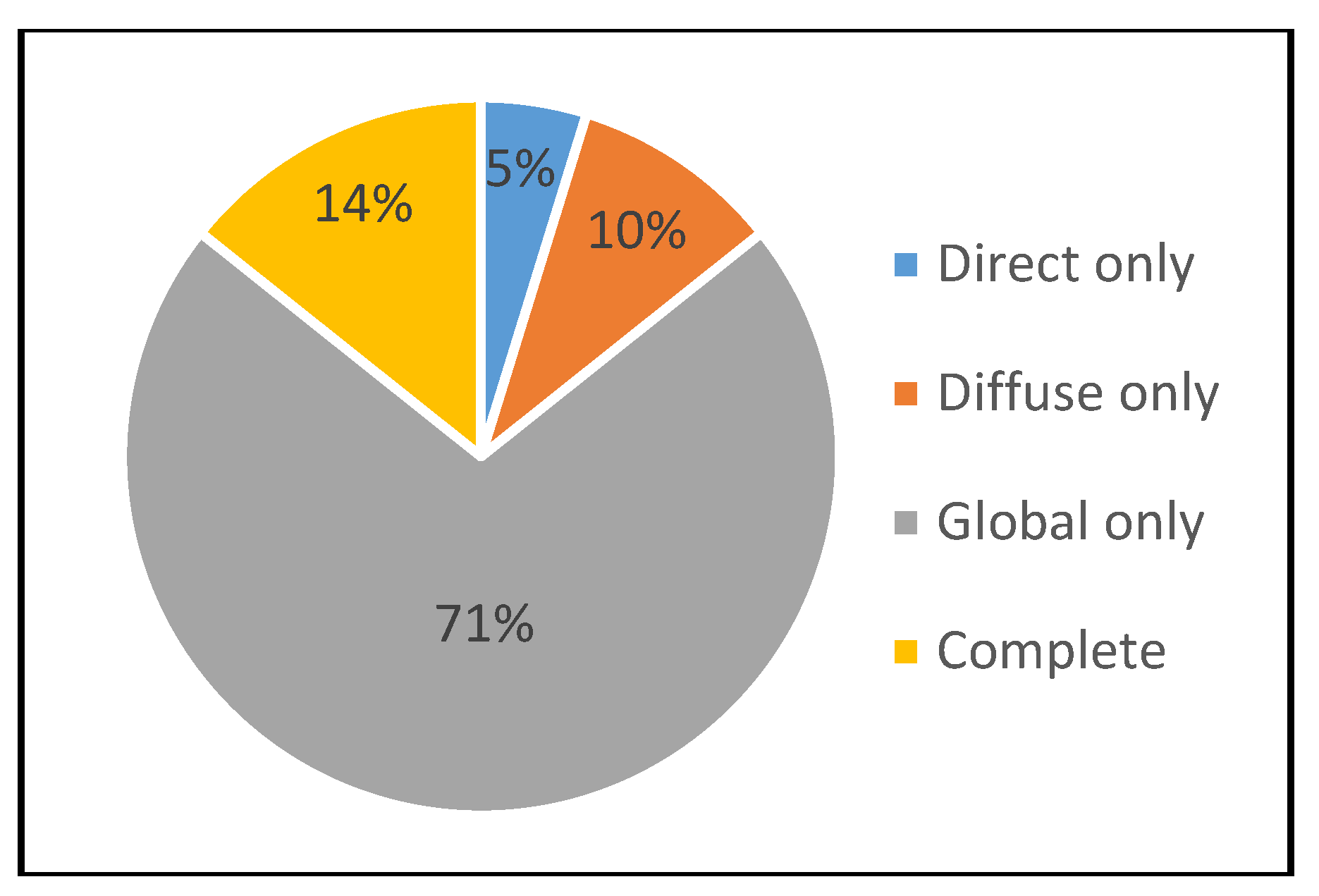
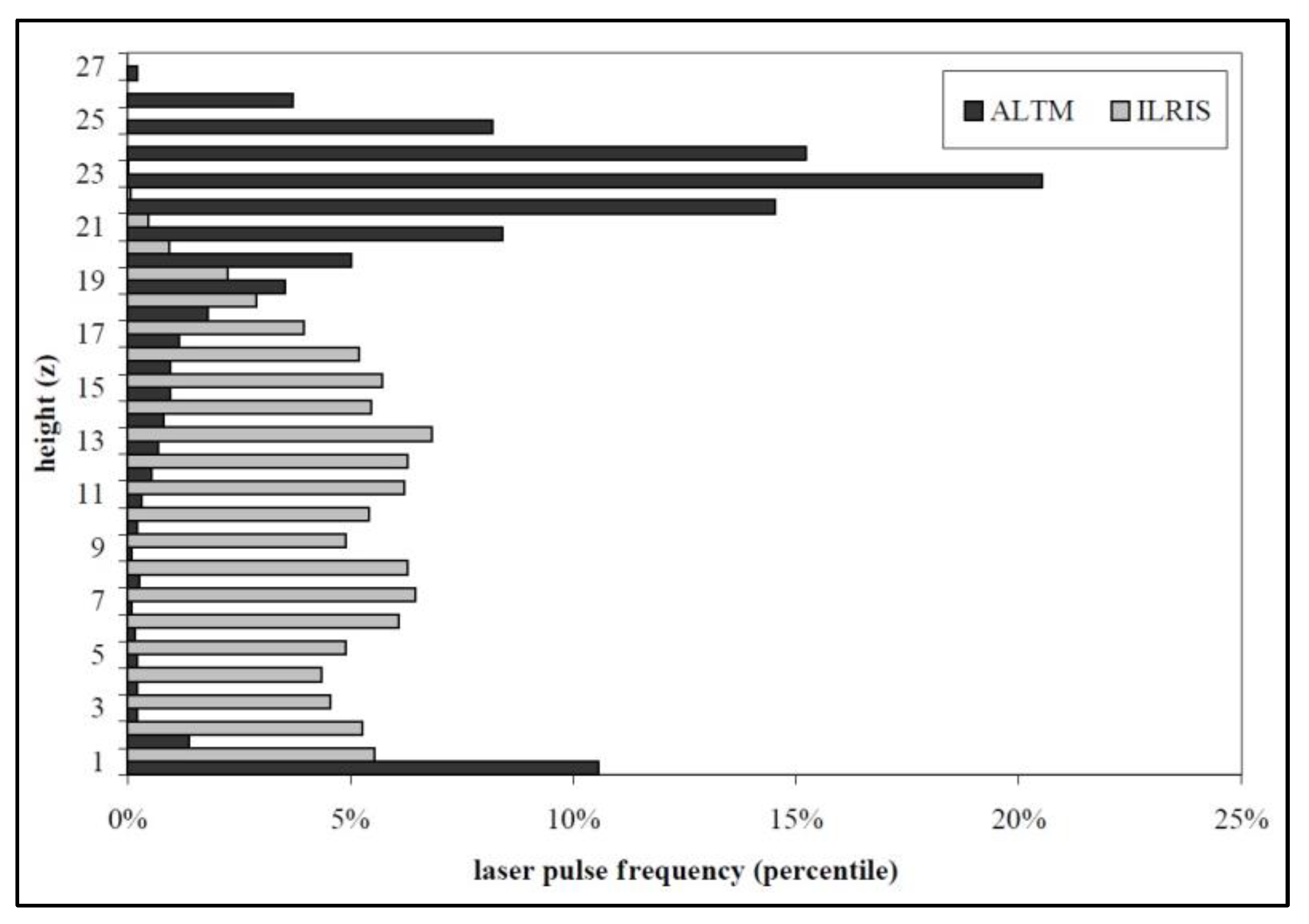
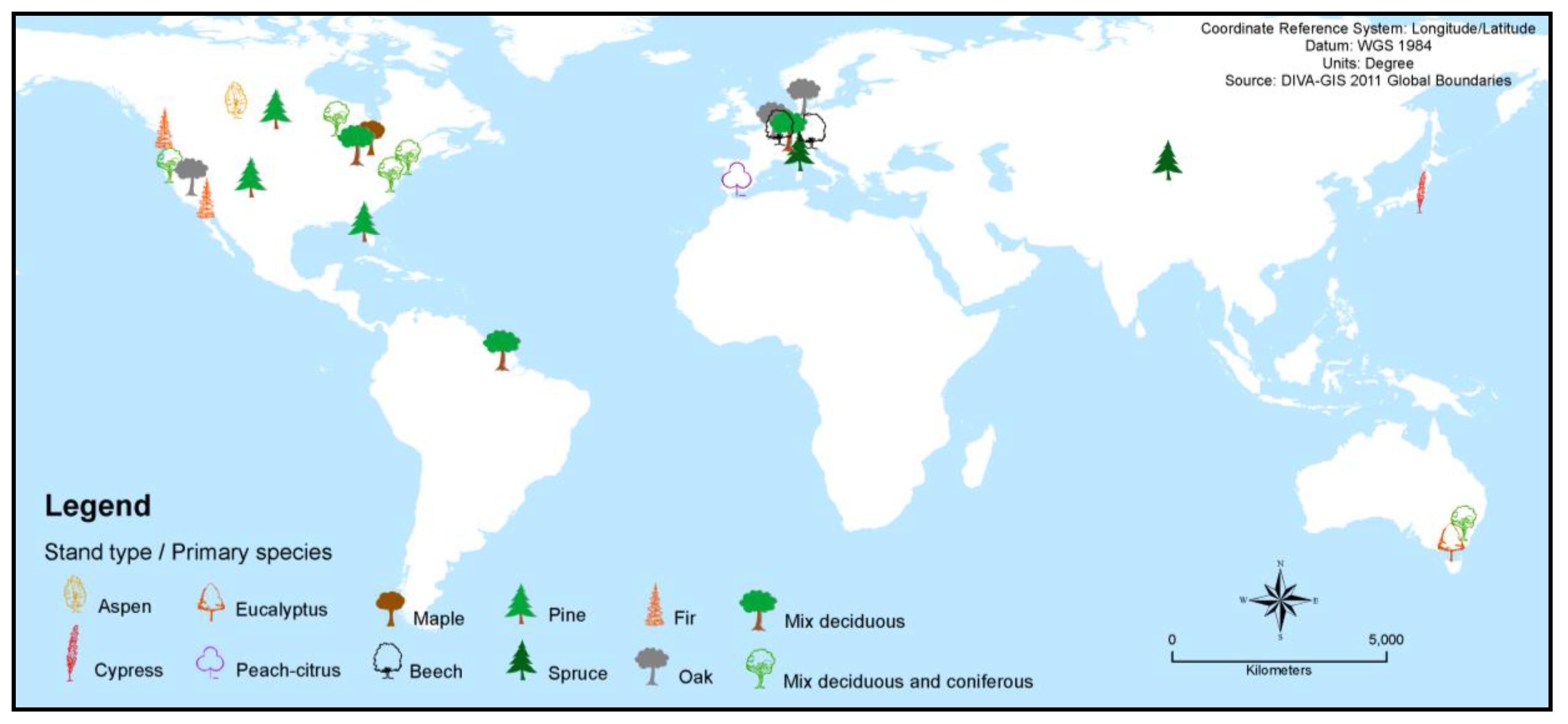
| References | Salient Methodology Features |
|---|---|
| Nyman et al., 2017 [55] | ▪ Compared various transmission models including a light penetration index (LPI) with a weighing factor to account for the path length |
| Tymen et al., 2017 [95] | ▪ Developed light transmission model using voxels generated from point clouds ▪ Used LPI |
| Cifuentes et al., 2017 [99] | ▪ Voxel-based canopy modeling generated from terrestrial laser system (TLS) ▪ Classified point clouds into leaves and non-leaves, then assigned properties before conducting light simulation |
| Yamamoto et al., 2015 [84] | ▪ Utilized owned version of LPI then correlated with relative illuminance |
| Bode et al., 2014 [22] | ▪ Used LPI and solar radiation module of GRASS software (r.sun) |
| Peng et al., 2014 [6] | ▪ Generated 3D canopy structure from point clouds ▪ Implemented Beer’s Law through voxel models with ray trace method |
| Moeser et al., 2014 [29] | ▪ Improvised synthetic hemispherical photos generated from point clouds |
| Widlowski et al., 2014 [25] | ▪ Voxel-based canopy reconstruction from TLS ▪ Bidirectonal reflectance factor (BRF) simulation in virtual environment |
| van Leeuwen et al., 2013 [34] | ▪ Used ground-based laser scanner Echidna Validation Instrument (EVI) to ▪ reconstruct geometric explicit models of canopy ▪ characterize radiation transmission properties from LiDAR full waveform |
| Musellman et al., 2013 [16] | ▪ Used Beer’s-type transmittance model based on LiDAR-derived LAI ▪ Developed solar raytrace model applied to 3D canopy derived from multiple LiDAR flights |
| Alexander et al., 2013 [21] | ▪ Estimated canopy cover by producing Thiessen polygons from point clouds ▪ Calculated canopy closure by transforming point clouds from Cartesian to spherical coordinates |
| Bittner et al., 2012 [67] | ▪ 3D voxel representation of the canopy architecture derived from TLS ▪ Different attributes of light assigned to voxels of stem, leaf or air |
| Guillen-Climent et al., 2012 [100] | ▪ Used a 3D radiative transfer model called forest light interaction model (FLIGHT) ▪ Mapped with high-resolution imagery from unmanned aerial vehicle (UAV) with multispectral camera |
| Kobayashi et al., 2011 [101] | ▪ Generated canopy height model, tree and crown segmentation from point clouds as inputs to CANOAK-FLiES (forest light environmental simulator) ▪ Derived canopy reflectance from airborne airborne visible/infrared imaging spectroradiometer (AVIRIS) |
| Van der Zande et al., 2011 [3] | ▪ Voxel-based representation of trees derived from TLS ▪ Light simulation using voxel-based light interception model (VLIM) |
| Van der Zande et al., 2010 [12] | ▪ Generate 3D representations of the forest stands, enabling structure feature extraction and light interception modeling, using the voxel-based light interception model (VLIM) |
| Yang et al., 2010 [75] | ▪ Estimated canopy gap probability from ground-based LiDAR (EVI) |
| Lee et al., 2009 [102] | ▪ Defined a conical field-of-view (scope) function between observer points just above the forest floor and the sun, which relates PAR to the LiDAR data |
| Essery et al., 2008 [85] | ▪ Colored orthophotograph and laser scanning were used to map out tree locations, heights, and crown diameter as inputs to mathematical radiation modeling and simulation |
| Thomas et al., 2006 [86] | ▪ LiDAR metrics generated from airborne laser system (ALS) to determine spatial variability of canopy structure ▪ Canopy chlorophyll concentration was derived from airborne hyperspectral imagery |
| Todd et al., 2003 [103] | ▪ Analyzed foliage distribution from LiDAR observation |
| Parker et al., 2001 [32] | ▪ Estimated canopy transmittance using the scanning LiDAR imager of canopies by echo recovery (SLICER), a waveform-sampling laser altimeter |
| Kucharik et al., 1998 [104] | ▪ Captured visible and NIR images of canopies from 16-bit charge-coupled device (CCD) multiband camera from the ground looking vertically upward to estimate sunlit and shaded foliage |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olpenda, A.S.; Stereńczak, K.; Będkowski, K. Modeling Solar Radiation in the Forest Using Remote Sensing Data: A Review of Approaches and Opportunities. Remote Sens. 2018, 10, 694. https://doi.org/10.3390/rs10050694
Olpenda AS, Stereńczak K, Będkowski K. Modeling Solar Radiation in the Forest Using Remote Sensing Data: A Review of Approaches and Opportunities. Remote Sensing. 2018; 10(5):694. https://doi.org/10.3390/rs10050694
Chicago/Turabian StyleOlpenda, Alex S., Krzysztof Stereńczak, and Krzysztof Będkowski. 2018. "Modeling Solar Radiation in the Forest Using Remote Sensing Data: A Review of Approaches and Opportunities" Remote Sensing 10, no. 5: 694. https://doi.org/10.3390/rs10050694
APA StyleOlpenda, A. S., Stereńczak, K., & Będkowski, K. (2018). Modeling Solar Radiation in the Forest Using Remote Sensing Data: A Review of Approaches and Opportunities. Remote Sensing, 10(5), 694. https://doi.org/10.3390/rs10050694