A Method of Retrieving BRDF from Surface-Reflected Radiance Using Decoupling of Atmospheric Radiative Transfer and Surface Reflection
Abstract
:1. Introduction
2. Methodology
2.1. Equation for Surface-Reflected Radiance
2.2. Iterative Fitting Algorithm to Derive BRDF from the Surface-Reflected Radiance
2.3. Numerical Consideration
3. Results of BRDF Retrievals
4. Discussion
5. Conclusions
References
- Meister, G.; Wiemker, R.; Bienlein, J. In Situ BRDF Measurements of Selected Surface Materials to Improve Analysis of Remotely Sensed Multispectral Imagery. ISPRS Arch. 1996, 31 Pt B7, 493–498. [Google Scholar]
- Deering, D.W.; Eck, T.F.; Grier, T. Shinnery Oak Bidirectional Reflectance Properties and Canopy Model Inversion. IEEE Trans. Geosci. Remote Sens. 1992, 30, 339–348. [Google Scholar] [CrossRef]
- Leroux, C.; Deuzé, J.-L.; Goloub, P.; Sergent, C.; Fily, M. Ground measurements of the polarized bidirectional reflectance of snow in the near-infrared spectral domain: Comparison with model results. J. Geophys. Res. 1998, 103, 19721–19731. [Google Scholar] [CrossRef]
- Hudson, S.R.; Warren, S.G.; Brandt, R.E.; Grenfell, T.C.; Six, D. Spectral bidirectional reflectance of Antarctic snow: Measurements and parameterization. J. Geophys. Res. 2006, 111, D18106. [Google Scholar] [CrossRef]
- Huang, X.; Jiao, Z.; Dong, Y.; Zhang, H.; Li, X. Analysis of BRDF and Albedo Retrieved by Kernel-Driven Models Using Field Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 149–161. [Google Scholar] [CrossRef]
- Chopping, M.J. Testing a LiSK BRDF Model with in Situ Bidirectional Reflectance Factor Measurements over Semiarid Grasslands. Remote Sens. Environ. 2000, 74, 287–312. [Google Scholar] [CrossRef]
- Walthall, C.; Roujean, J.-L.; Morisette, J. Field and landscape BRDF optical wavelength measurements: Experience, techniques and the future. Remote Sens. Rev. 2000, 18, 503–531. [Google Scholar] [CrossRef]
- Bruegge, C.; Helmlinger, M.; Conel, J.; Gaitley, B.; Abdou, W. PARABOLA III—A sphere-scanning radiometer for field determination of surface anisotropic reflectance functions. Remote Sens. Rev. 2000, 19, 75–94. [Google Scholar] [CrossRef]
- Martonchik, J.V. Retrieval of surface directional reflectance properties using ground level multiangle measurements. Remote Sens. Environ. 1994, 50, 303–316. [Google Scholar] [CrossRef]
- Lyapustin, A.I.; Privette, J.L. A new method of retrieving surface bidirectional reflectance from ground measurements: Atmospheric sensitivity study. J. Geophys Res. 1999, 104, 6257–6268. [Google Scholar] [CrossRef]
- Lyapustin, A.I.; Knyazikhin, Y. Green’s function method for the radiative transfer problem. I. Homogeneous non-Lambertian surface. Appl. Opt. 2001, 40, 3495–3501. [Google Scholar] [CrossRef] [PubMed]
- Lyapustin, A.; Martonchik, J.; Wang, Y.; Laszlo, I.; Korkin, S. Multi-Angle Implementation of Atmospheric Correction (MAIAC): Part 1. Radiative Transfer Basis and Look-Up Tables. J. Geophys. Res. 2011, 116, D03210. [Google Scholar] [CrossRef]
- Radkevich, A. A new look at decoupling of atmospheric radiative transfer and anisotropic surface reflection. JQSRT 2013, 127, 140–148. [Google Scholar] [CrossRef]
- Radkevich, A. Iterative discrete ordinates solution of the equation for surface-reflected radiance. JQSRT 2017, 202, 114–125. [Google Scholar] [CrossRef]
- Roujean, J.-L.; Leroy, M.; Deschamps, P.Y. A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. J. Geophys. Res. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Lewis, P. The utility of kernel-driven BRDF models in global BRDF and albedo studies. In Proceedings of the Geoscience and Remote Sensing Symposium, Firenze, Italy, 10–14 July 1995. [Google Scholar] [CrossRef]
- Lucht, W.; Schaaf, C.B.; Strahler, A.H. An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote Sens. 2000, 38, 977–998. [Google Scholar] [CrossRef]
- Pokrovsky, O.; Roujean, J.-L. Land surface albedo retrieval via kernel-based BRDF modeling: I. Statistical inversion method and model comparison. Remote Sens. Environ. 2002, 84, 100–119. [Google Scholar] [CrossRef]
- Gao, F.; Schaaf, C.B.; Strahler, A.H.; Jin, Y.; Li, X. Detecting vegetation structure using a kernel-based BRDF model. Remote Sens. Environ. 2003, 86, 198–205. [Google Scholar] [CrossRef]
- Román, M.O.; Gatebe, C.K.; Schaaf, C.B.; Poudyal, R.; Wang, Z.; King, M.D. Variability in surface BRDF at different spatial scales (30 m–500 m) over a mixed agricultural landscape as retrieved from airborne and satellite spectral measurements. Remote Sens. Environ. 2011, 115, 2184–2203. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Q.; Liu, Q.; Wen, J.; Li, X. The Angular and Spectral Kernel Model for BRDF and Albedo Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 242–256. [Google Scholar] [CrossRef]
- Roujean, J.-L. Inversion of Lumped Parameters Using BRDF Kernels. Compre Remote Sens. 2018, 3, 23–34. [Google Scholar] [CrossRef]
- Gatebe, C.K.; King, M.D.; Lyapustin, A.I.; Arnold, G.T.; Redemann, J. Airborne Spectral Measurements of Ocean Directional Reflectance. J. Atmos. Sci. 2005, 62, 1072–1092. [Google Scholar] [CrossRef]
- Lyapustin, A.I.; Wang, Y.; Laszlo, I.; Hilker, T.; Hall, F.G.; Sellers, P.J.; Tucker, C.J.; Korkin, S.V. Multi-angle implementation of atmospheric correction for MODIS (MAIAC): 3. Atmospheric correction. Remote Sens. Environ. 2012, 127, 385–393. [Google Scholar] [CrossRef]
- Hess, M.; Koepke, P.; Schult, I. Optical Properties of Aerosols and Clouds: The Software Package OPAC. BAMS 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Lacis, A.A. Scattering, Absorption, and Emission of Light by Small Particles; Cambridge University Press: Cambridge, UK, 2002; 448p, ISBN 9780521782524. [Google Scholar]
- Nilson, T.; Kuusk, A. A reflectance model for the homogeneous plant canopy and its inversion. Remote Sens. Environ. 1989, 27, 157–167. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P.; et al. First Operational BRDF, Albedo and Nadir Reflectance Products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Pokrovsky, O.; Roujean, J.-L. Land surface albedo retrieval via kernel-based BRDF modeling: II. An optimal design scheme for the angular sampling. Remote Sens. Environ. 2002, 84, 120–142. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanre, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
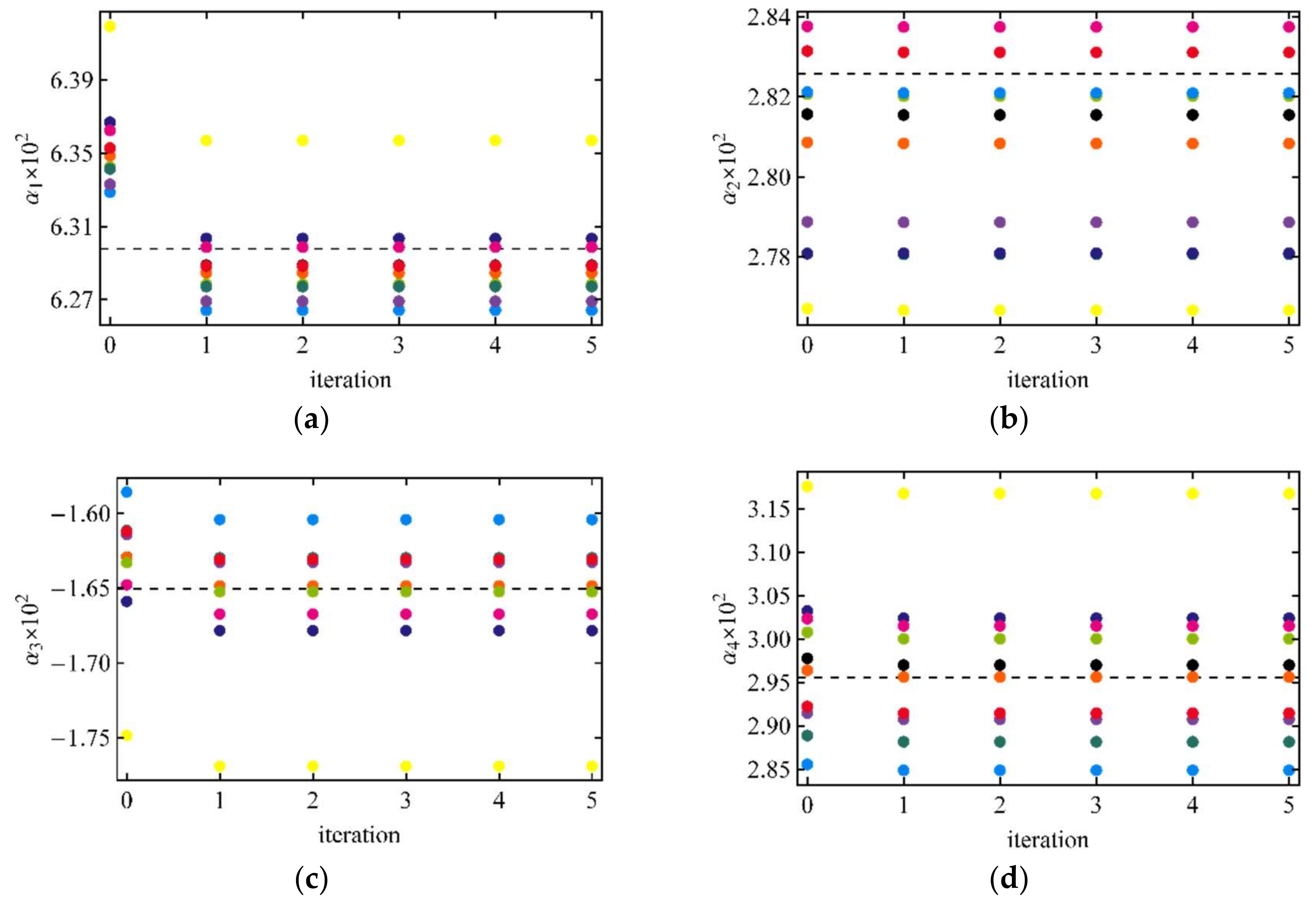
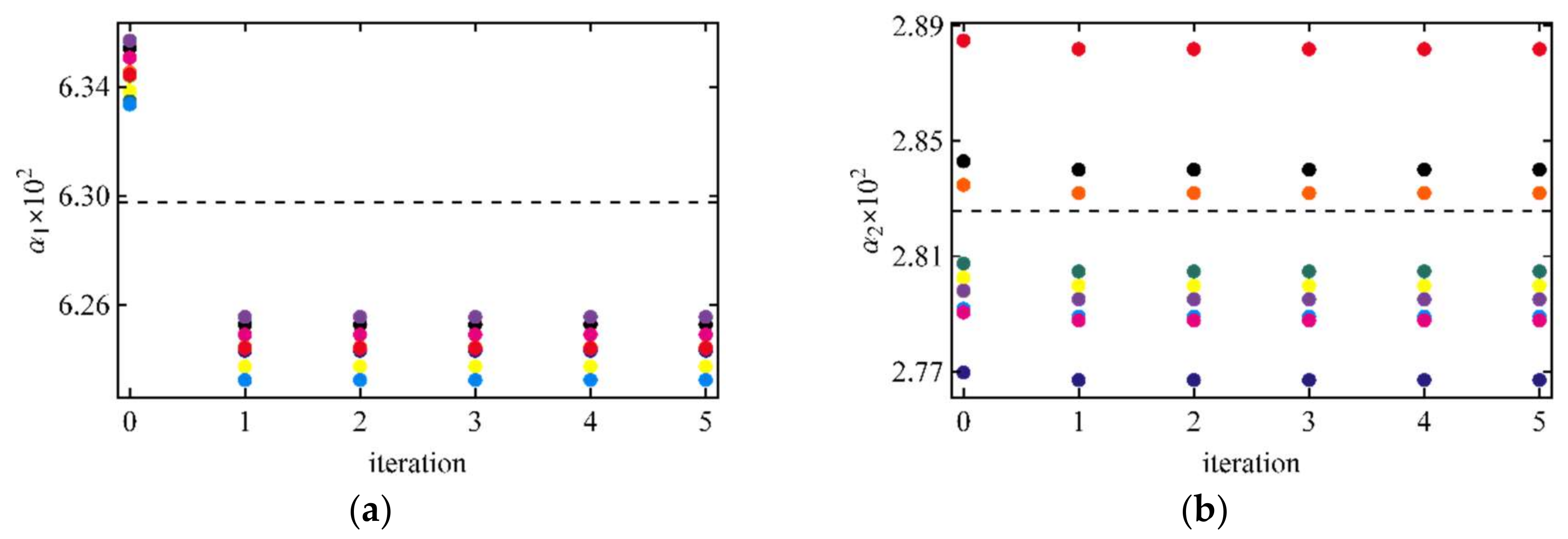
| τt = 0.2: τR = 0.1, τA = 0.1 | τt = 0.6: τR = 0.1, τA = 0.5 | τt = 1.1: τR = 0.1, τA = 1.0 | |||||
|---|---|---|---|---|---|---|---|
| Parameter | Theoretical Value | Mean Value | Standard Deviation | Mean Value | Standard Deviation | Mean Value | Standard Deviation |
| (a) | |||||||
| α1 | 6.298 | 6.286 | 0.004 | 6.260 | 0.015 | 6.243 | 0.008 |
| α2 | 2.826 | 2.815 | 0.008 | 2.793 | 0.027 | 2.809 | 0.033 |
| α3 | −1.650 | −1.646 | 0.004 | −1.645 | 0.019 | −1.637 | 0.017 |
| α4 | 2.956 | 2.948 | 0.013 | 2.964 | 0.055 | 2.953 | 0.061 |
| (b) | |||||||
| α1 | 6.298 | 6.291 | 0.026 | 6.256 | 0.109 | 6.193 | 0.325 |
| α2 | 2.826 | 2.805 | 0.024 | 2.866 | 0.141 | 2.770 | 0.160 |
| α3 | −1.650 | −1.656 | 0.045 | −1.622 | 0.195 | −1.564 | 0.314 |
| α4 | 2.956 | 2.968 | 0.091 | 2.933 | 0.297 | 2.860 | 0.323 |
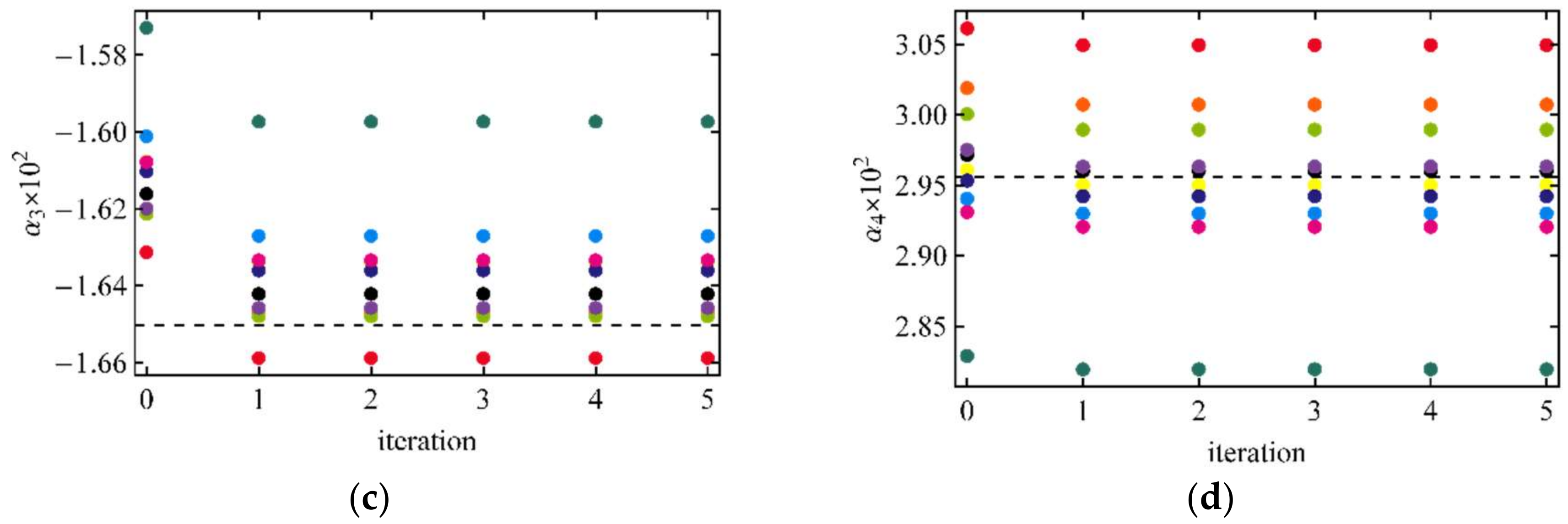
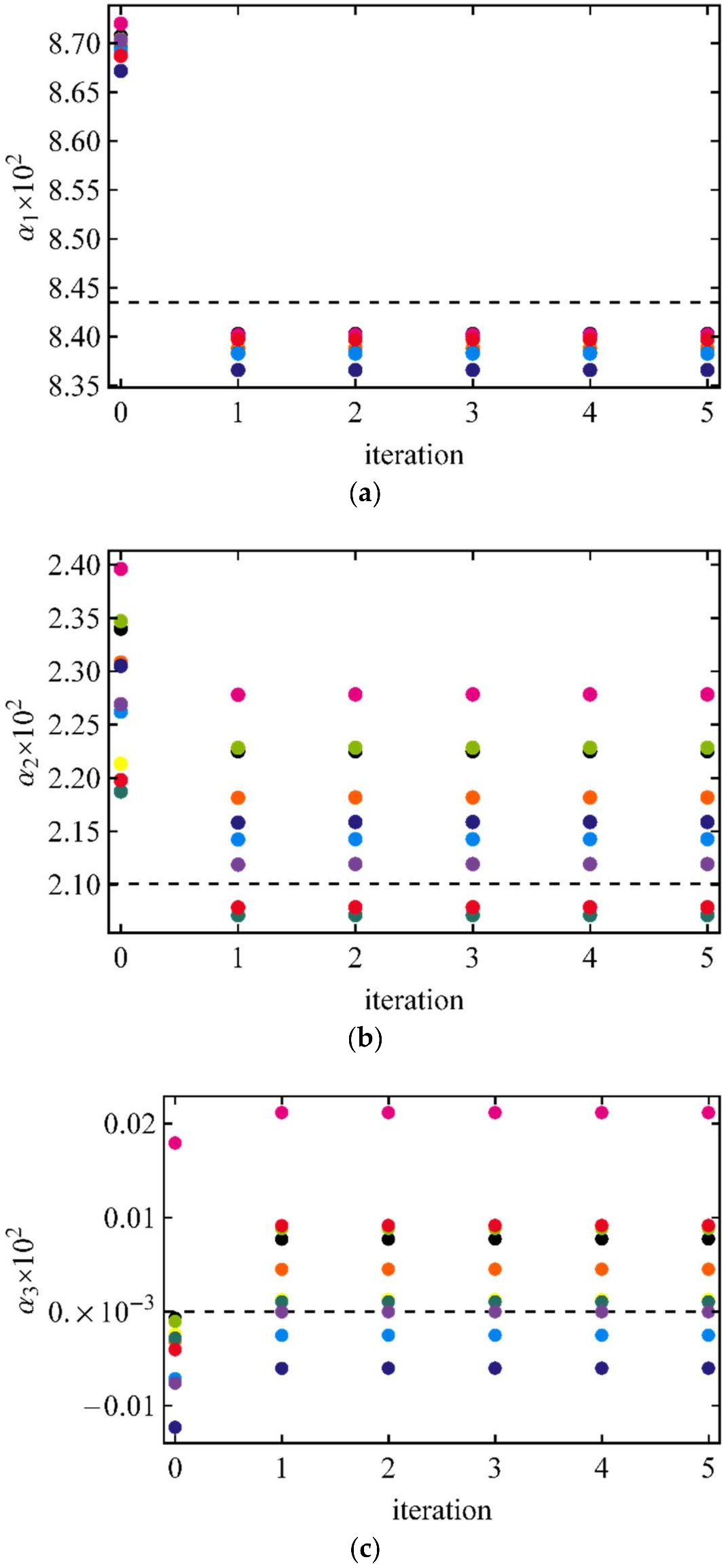
| τt = 0.6: τR = 0.1, τA = 0.5 | τt = 1.1: τR = 0.1, τA = 1.0 | ||||
|---|---|---|---|---|---|
| Parameter | Theoretical Value | Mean Value | Standard Deviation | Mean Value | Standard Deviation |
| (a) | |||||
| α1 | 8.435 | 8.392 | 0.012 | 8.373 | 0.016 |
| α2 | 2.101 | 2.156 | 0.072 | 2.099 | 0.058 |
| α3 | 0. | 0.005 | 0.008 | −0.001 | 0.005 |
| (b) | |||||
| α1 | 8.435 | 8.348 | 0.079 | 8.404 | 0.086 |
| α2 | 2.101 | 2.163 | 0.171 | 2.187 | 0.146 |
| α3 | 0. | −0.026 | 0.060 | 0.012 | 0.043 |
| τt = 0.2: τR = 0.1, τA = 0.1 | τt = 0.6: τR = 0.1, τA = 0.5 | τt = 1.1: τR = 0.1, τA = 1.0 | ||||
|---|---|---|---|---|---|---|
| (a) | ||||||
| α1 | −0.25 | −0.13 | −0.84 | −0.37 | −1.00 | −0.75 |
| α2 | −0.67 | −0.11 | −2.12 | −0.21 | −1.77 | 0.57 |
| α3 | −0.48 | 0.00 | −1.45 | 0.85 | −1.82 | 0.24 |
| α4 | −0.71 | 0.17 | −1.59 | 2.13 | −2.17 | 1.96 |
| (b) | ||||||
| α1 | −0.52 | 0.30 | −2.40 | 1.06 | −6.83 | 3.49 |
| α2 | −1.59 | 0.11 | −3.57 | 6.40 | −7.64 | 3.68 |
| α3 | −2.36 | 3.09 | −13.52 | 10.12 | −24.24 | 13.82 |
| α4 | −2.67 | 3.48 | −10.83 | 9.27 | −14.17 | 7.68 |
| τt = 0.6: τR = 0.1, τA = 0.5 | τt = 1.1: τR = 0.1, τA = 1.0 | |||
|---|---|---|---|---|
| (a) | ||||
| α1 | −0.65 | −0.37 | −0.92 | −0.55 |
| α2 | −0.81 | 6.04 | −2.86 | 2.67 |
| (b) | ||||
| α1 | −1.97 | −0.09 | −1.39 | 0.65 |
| α2 | −5.19 | 11.09 | −2.86 | 11.04 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radkevich, A. A Method of Retrieving BRDF from Surface-Reflected Radiance Using Decoupling of Atmospheric Radiative Transfer and Surface Reflection. Remote Sens. 2018, 10, 591. https://doi.org/10.3390/rs10040591
Radkevich A. A Method of Retrieving BRDF from Surface-Reflected Radiance Using Decoupling of Atmospheric Radiative Transfer and Surface Reflection. Remote Sensing. 2018; 10(4):591. https://doi.org/10.3390/rs10040591
Chicago/Turabian StyleRadkevich, Alexander. 2018. "A Method of Retrieving BRDF from Surface-Reflected Radiance Using Decoupling of Atmospheric Radiative Transfer and Surface Reflection" Remote Sensing 10, no. 4: 591. https://doi.org/10.3390/rs10040591
APA StyleRadkevich, A. (2018). A Method of Retrieving BRDF from Surface-Reflected Radiance Using Decoupling of Atmospheric Radiative Transfer and Surface Reflection. Remote Sensing, 10(4), 591. https://doi.org/10.3390/rs10040591





