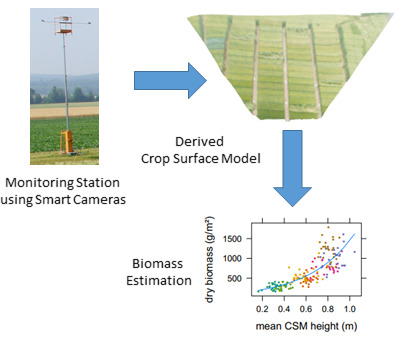
Estimating Barley Biomass with Crop Surface Models from Oblique RGB Imagery
Abstract
:1. Introduction
2. Materials and Methods
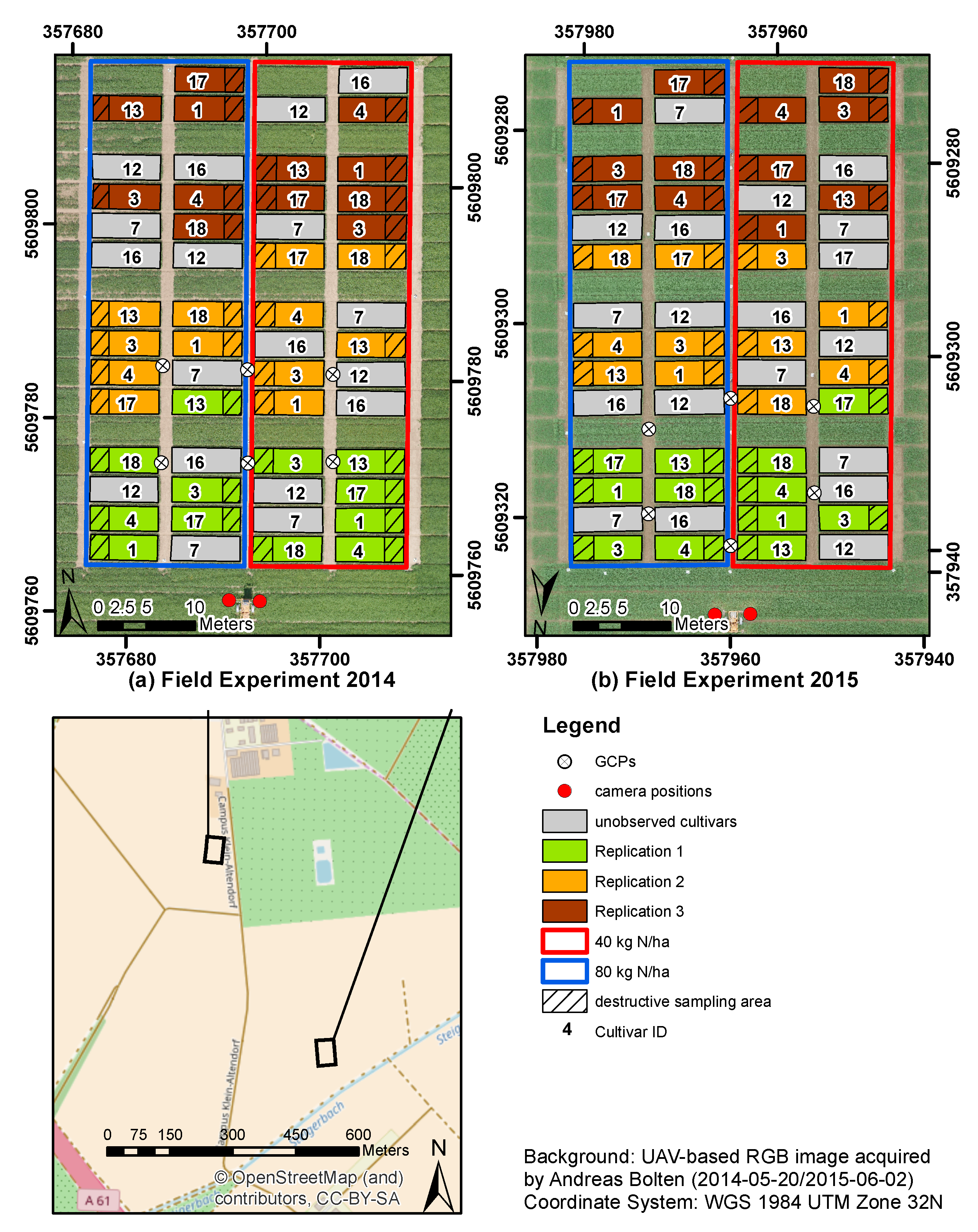
2.1. Study Site
2.2. Plant Height and Biomass Measurements
2.3. Crop Surface Models Derived Using Structure-from-Motion
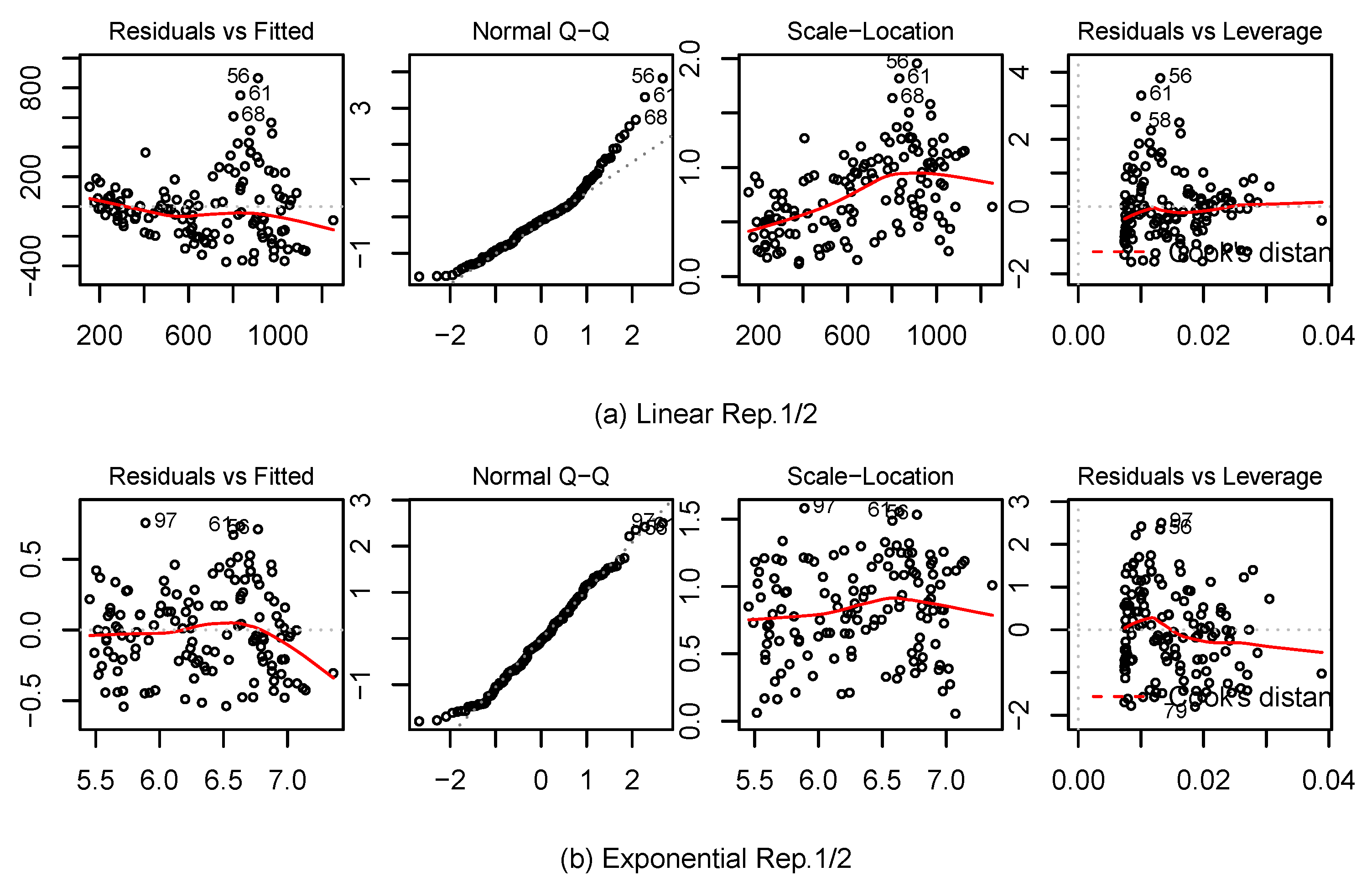
2.4. Statistical Analysis
- using two replications for calibration and one for validation;
- using one year for calibration and the other for validation; and
- randomly splitting the dataset 70%/30% and using the 70% part for calibration and the 30% part for validation 10,000 times and averaging the results.
3. Results
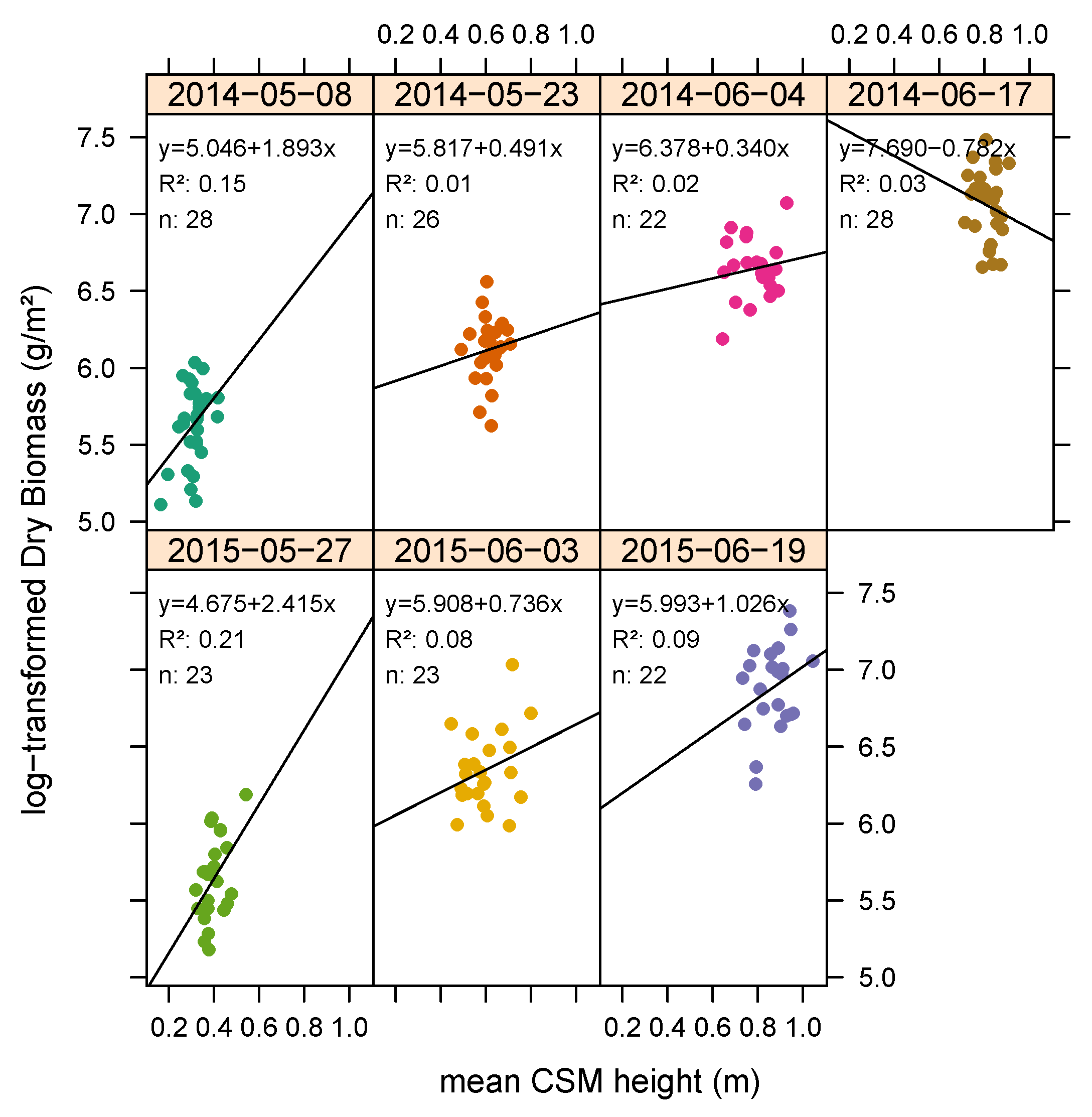
3.1. Plant Height Measurements
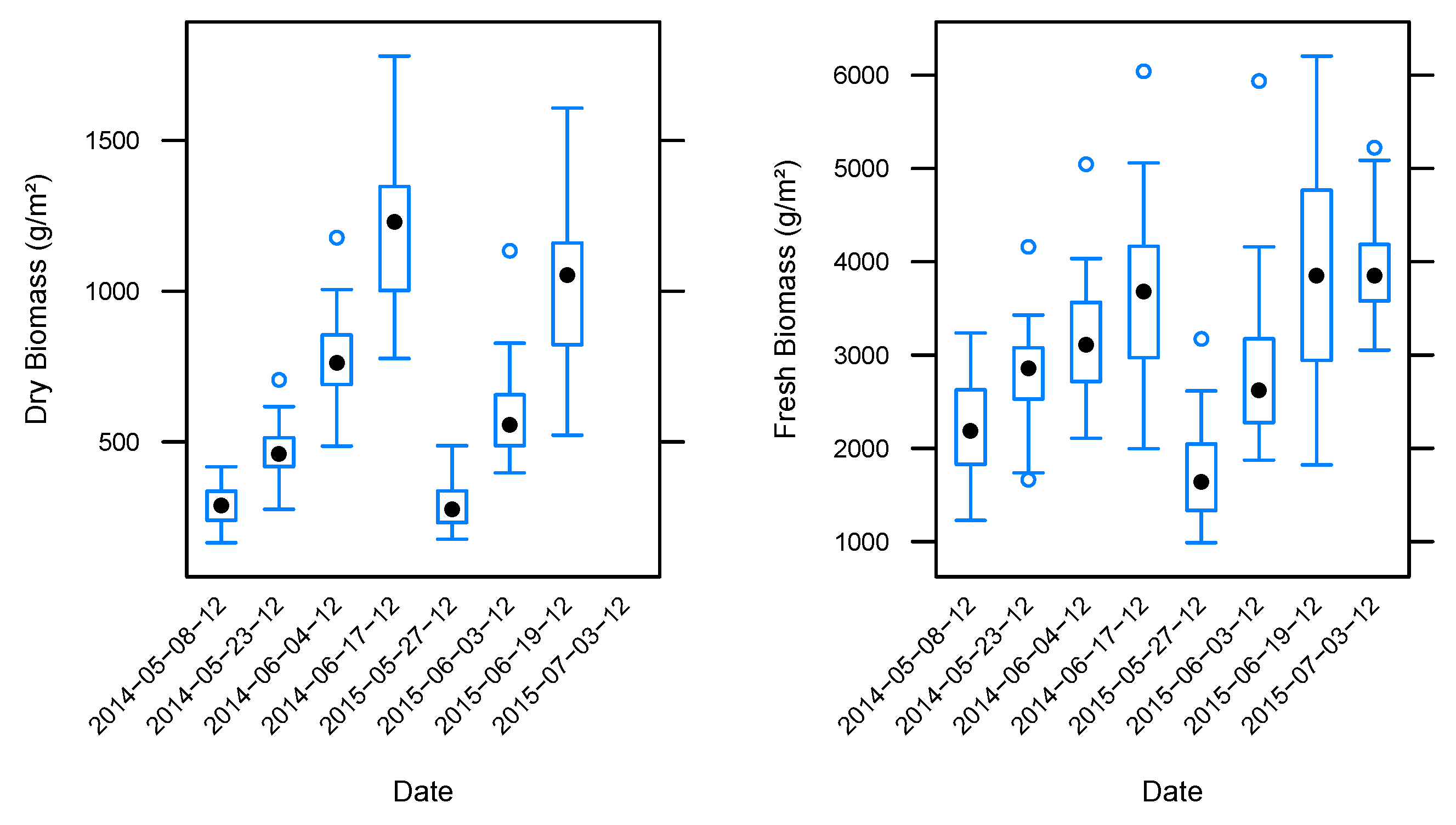
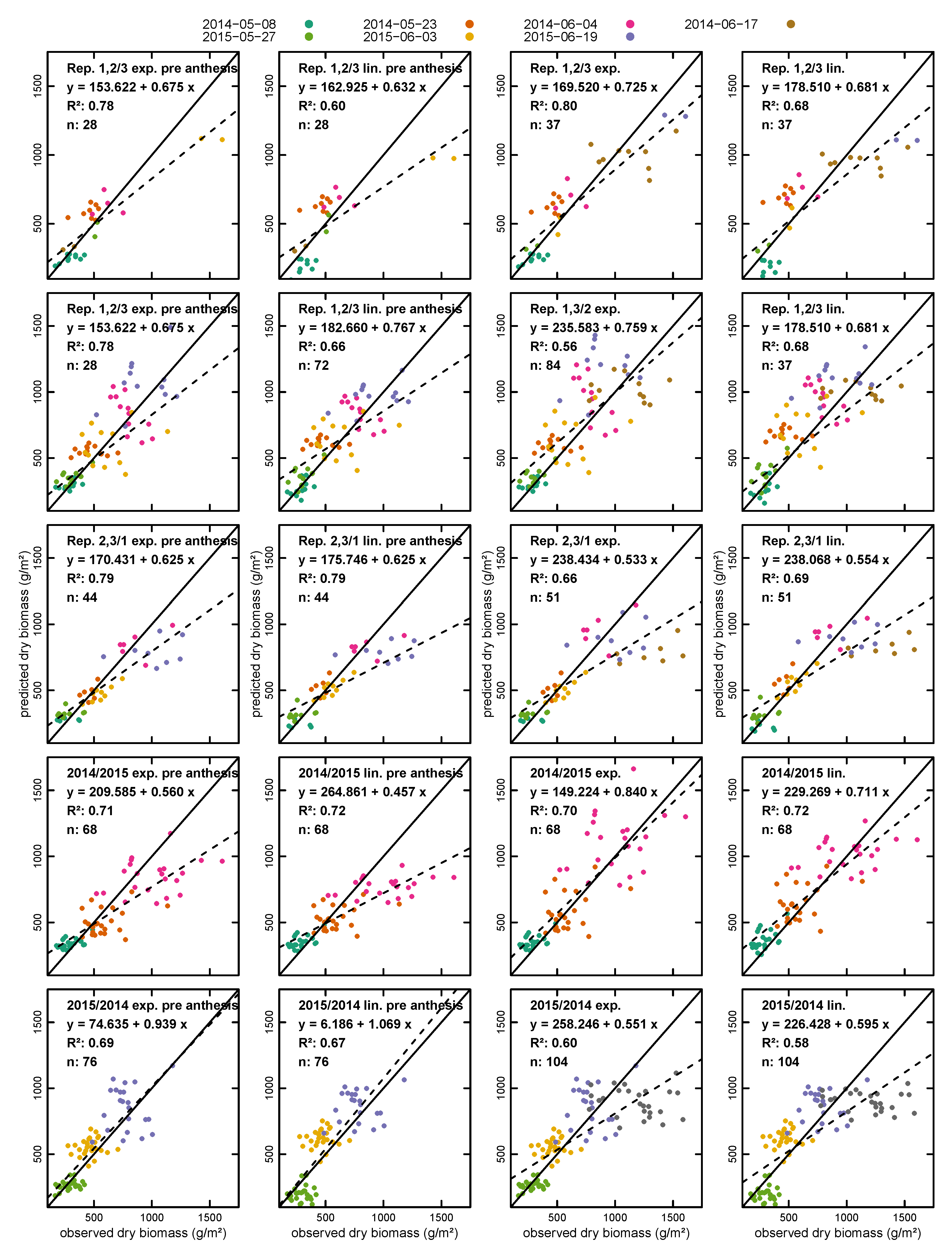
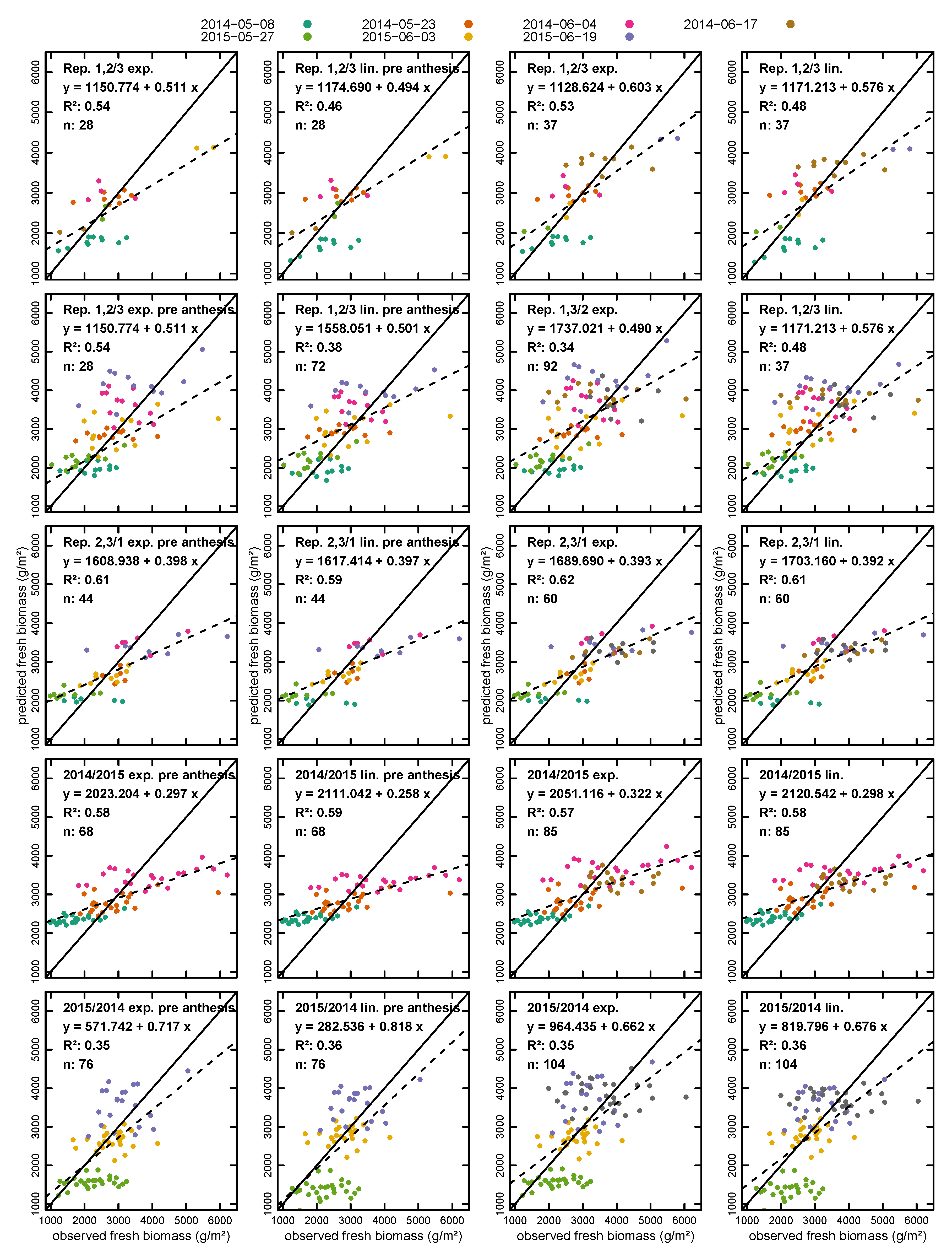
3.2. Biomass Estimation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Bouman, B.A.M.; Goudriaan, J. Estimation of crop growth from optical and microwave soil cover. Int. J. Remote Sens. 1989, 10, 1843–1855. [Google Scholar] [CrossRef]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Jay, S.; Gorretta, N.; Morel, J.; Maupas, F.; Bendoula, R.; Rabatel, G.; Dutartre, D.; Comar, A.; Baret, F. Estimating leaf chlorophyll content in sugar beet canopies using millimeter- to centimeter-scale reflectance imagery. Remote Sens. Environ. 2017, 198, 173–186. [Google Scholar] [CrossRef]
- Jin, X.; Liu, S.; Baret, F.; Hemerlé, M.; Comar, A. Estimates of plant density of wheat crops at emergence from very low altitude UAV imagery. Remote Sens. Environ. 2017, 198, 105–114. [Google Scholar] [CrossRef]
- Yang, G.; Liu, J.; Zhao, C.; Li, Z.; Huang, Y.; Yu, H.; Xu, B.; Yang, X.; Zhu, D.; Zhang, X.; et al. Unmanned Aerial Vehicle Remote Sensing for Field-Based Crop Phenotyping: Current Status and Perspectives. Front. Plant Sci. 2017, 8, 1111. [Google Scholar] [CrossRef] [PubMed]
- Hoffmeister, D.; Bolten, A.; Curdt, C.; Waldhoff, G.; Bareth, G. High-resolution Crop Surface Models (CSM) and Crop Volume Models (CVM) on field level by terrestrial laser scanning. Proc. SPIE 2010. [Google Scholar] [CrossRef]
- Aasen, H.; Burkart, A.; Bolten, A.; Bareth, G. Generating 3D hyperspectral information with lightweight UAV snapshot cameras for vegetation monitoring: From camera calibration to quality assurance. ISPRS J. Photogramm. Remote Sens. 2015, 108, 245–259. [Google Scholar] [CrossRef]
- Tilly, N.; Aasen, H.; Bareth, G. Fusion of Plant Height and Vegetation Indices for the Estimation of Barley Biomass. Remote Sens. 2015, 7, 11449–11480. [Google Scholar] [CrossRef]
- Lucieer, A.; Turner, D.; King, D.H.; Robinson, S.A. International Journal of Applied Earth Observation and Geoinformation Using an Unmanned Aerial Vehicle ( UAV ) to capture micro-topography of Antarctic moss beds. Int. J. Appl. Earth Obs. Geoinf. 2014, 27, 53–62. [Google Scholar] [CrossRef]
- Bendig, J.; Bolten, A.; Bareth, G. UAV-based Imaging for Multi-Temporal, very high Resolution Crop Surface Models to monitor Crop Growth Variability. Photogramm. Fernerkund. Geoinf. 2013, 6, 551–562. [Google Scholar] [CrossRef]
- Friedli, M.; Kirchgessner, N.; Grieder, C.; Liebisch, F.; Mannale, M.; Walter, A. Terrestrial 3D laser scanning to track the increase in canopy height of both monocot and dicot crop species under field conditions. Plant Methods 2016, 12, 9. [Google Scholar] [CrossRef] [PubMed]
- Bareth, G.; Bendig, J.; Tilly, N.; Hoffmeister, D.; Aasen, H.; Bolten, A. A Comparison of UAV- and TLS-derived Plant Height for Crop Monitoring: Using Polygon Grids for the Analysis of Crop Surface Models (CSMs). Photogramm. Fernerkund. Geoinf. 2016, 2016, 85–94. [Google Scholar] [CrossRef]
- Geipel, J.; Link, J.; Claupein, W. Combined Spectral and Spatial Modeling of Corn Yield Based on Aerial Images and Crop Surface Models Acquired with an Unmanned Aircraft System. Remote Sens. 2014, 11, 10335–10355. [Google Scholar] [CrossRef]
- Andrade-Sanchez, P.; Gore, M.A.; Heun, J.T.; Thorp, K.R.; Carmo-Silva, E.; French, A.N.; Salvucci, M.E.; White, J.W. Development and evaluation of a field-based high-throughput phenotyping platform. Funct. Plant Biol. 2014, 41, 68–79. [Google Scholar] [CrossRef]
- Großkinsky, D.K.; Pieruschka, R.; Svensgaard, J.; Rascher, U.; Christensen, S.; Schurr, U.; Roitsch, T. Phenotyping in the fields: Dissecting the genetics of quantitative traits and digital farming. New Phytol. 2015, 207, 950–952. [Google Scholar] [CrossRef] [PubMed]
- Brocks, S.; Bendig, J.; Bareth, G. Toward an automated low-cost three-dimensional crop surface monitoring system using oblique stereo imagery from consumer-grade smart cameras. J. Appl. Remote Sens. 2016, 10, 046021. [Google Scholar] [CrossRef]
- Madec, S.; Baret, F.; de Solan, B.; Thomas, S.; Dutartre, D.; Jezequel, S.; Hemmerlé, M.; Colombeau, G.; Comar, A. High-Throughput Phenotyping of Plant Height: Comparing Unmanned Aerial Vehicles and Ground LiDAR Estimates. Front. Plant Sci. 2017, 8, 2002. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, F.; Lucieer, A.; Barry, K.; Wells, R. Poppy Crop Height and Capsule Volume Estimation from a Single UAS Flight. Remote Sens. 2017, 9, 647. [Google Scholar] [CrossRef]
- Tilly, N.; Hoffmeister, D.; Cao, Q.; Huang, S.; Lenz-Wiedemann, V.; Miao, Y.; Bareth, G. Multitemporal crop surface models: Accurate plant height measurement and biomass estimation with terrestrial laser scanning in paddy rice. J. Appl. Remote Sens. 2014, 8, 083671. [Google Scholar] [CrossRef]
- Marshall, M.; Thenkabail, P. Developing in situ non-destructive estimates of crop biomass to address issues of scale in remote sensing. Remote Sens. 2015, 7, 808–835. [Google Scholar] [CrossRef]
- Lancashire, P.D.; Bleiholder, H.; Van Den Boom, T.; Langelüddeke, P.; Stauss, R.; Weber, E.; Witzenberger, A. A uniform decimal code for growth stages of crops and weeds. Ann. Appl. Biol. 1991, 119, 561–601. [Google Scholar] [CrossRef]
- Ullman, S. The Interpretation of Structure from Motion. Proc. R. Soc. Lond. Ser. B 1979, 203, 405–426. [Google Scholar] [CrossRef]
- Seitz, S.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006; Volume 1, pp. 519–528. [Google Scholar]
- Topcon Positioning Systems Inc. HiPer Pro Operator’s Manual. 2006. Available online: https://www.servicestopni.com/resources/top-survey/downloads/HiPerPro_om.pdf (accessed on 8 February 2018).
- Newman, M.C. Regression analysis of log-transformed data: Statistical bias and its correction. Environ. Toxicol. Chem. 1993, 12, 1129–1133. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M.; Matsuura, K. A refined index of model performance. Int. J. Climatol. 2012, 32, 2088–2094. [Google Scholar] [CrossRef]
- Hoffmeister, D.; Waldhoff, G.; Korres, W.; Curdt, C.; Bareth, G. Crop height variability detection in a single field by multi-temporal terrestrial laser scanning. Precis. Agric. 2016, 17, 296–312. [Google Scholar] [CrossRef]
- Moeckel, T.; Safari, H.; Reddersen, B.; Fricke, T.; Wachendorf, M. Fusion of ultrasonic and spectral sensor data for improving the estimation of biomass in grasslands with heterogeneous sward structure. Remote Sens. 2017, 9, 98. [Google Scholar] [CrossRef]
- Hämmerle, M.; Höfle, B. Direct derivation of maize plant and crop height from low-cost time-of-flight camera measurements. Plant Methods 2016, 12, 50. [Google Scholar] [CrossRef] [PubMed]
- Holman, F.H.; Riche, A.B.; Michalski, A.; Castle, M.; Wooster, M.J.; Hawkesford, M.J. High throughput field phenotyping of wheat plant height and growth rate in field plot trials using UAV based remote sensing. Remote Sens. 2016, 8, 1031. [Google Scholar] [CrossRef]
- Watanabe, K.; Guo, W.; Arai, K.; Takanashi, H.; Kajiya-Kanegae, H.; Kobayashi, M.; Yano, K.; Tokunaga, T.; Fujiwara, T.; Tsutsumi, N.; et al. High-Throughput Phenotyping of Sorghum Plant Height Using an Unmanned Aerial Vehicle and Its Application to Genomic Prediction Modeling. Front. Plant Sci. 2017, 8, 421. [Google Scholar] [CrossRef] [PubMed]
- Bendig, J.; Bolten, A.; Bennertz, S.; Broscheit, J.; Eichfuss, S.; Bareth, G. Estimating Biomass of Barley Using Crop Surface Models (CSMs) Derived from UAV-Based RGB Imaging. Remote Sens. 2014, 6, 10395–10412. [Google Scholar] [CrossRef]
- Naito, H.; Ogawa, S.; Valencia, M.O.; Mohri, H.; Urano, Y.; Hosoi, F.; Shimizu, Y.; Chavez, A.L.; Ishitani, M.; Selvaraj, M.G.; et al. Estimating rice yield related traits and quantitative trait loci analysis under different nitrogen treatments using a simple tower-based field phenotyping system with modified single-lens reflex cameras. ISPRS J. Photogramm. Remote Sens. 2017, 125, 50–62. [Google Scholar] [CrossRef]
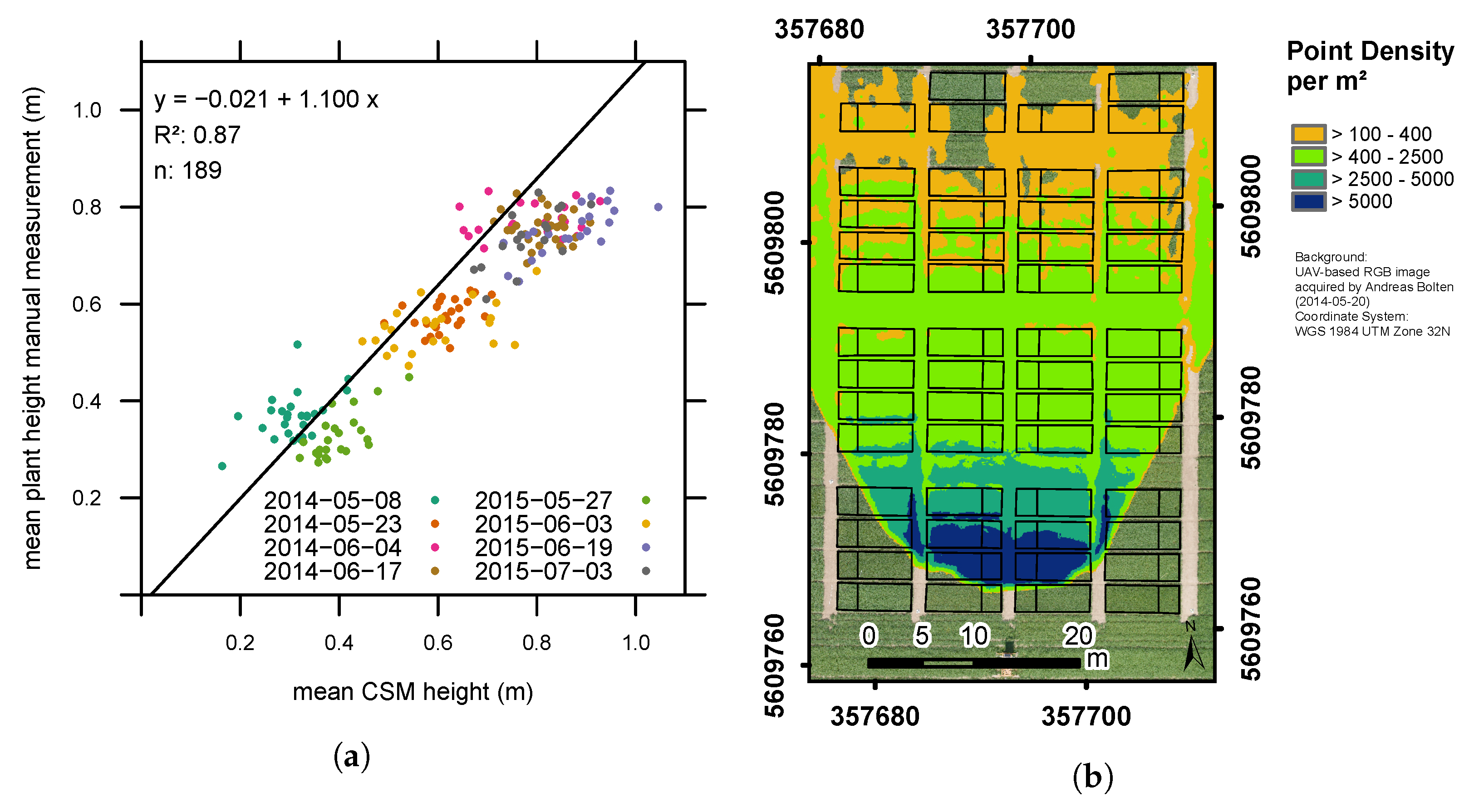
| Date | Number of Plots with Point Density > 150/m2 (Average Point Density/m2 per Plot) | BBCH | ||
|---|---|---|---|---|
| Morning | Noon | Evening | ||
| 7 May 2014 (55 DAS) | * | n = 23 (991) | n = 25 (1412) | tillering–stem elongation (24–32) |
| 8 May 2014 (56 DAS) | n = 29 (1297) | n = 28 (1324) | n = 30 (1399) | |
| 9 May 2014 (57 DAS) | n = 29 (1271) | n = 17 (1064) | n = 28 (1029) | |
| 26 May 2015 (60 DAS) | * | * | n = 24 (2106) | tillering (21–27) |
| 27 May 2015 (61 DAS) | n = 24 (2077) | n = 23 (2271) | n = 23 (2461) | |
| 1 June 2015 (66 DAS) | n = 20 (1848) | n = 22 (2122) | n = 22 (2146) | booting (41–47) |
| 2 June 2015 (67 DAS) | n = 6 (509) | n = 22 (2143) | n = 10 (509) | |
| 3 June 2015 (68 DAS) | n = 23 (2743) | n = 23 (2451) | n = 22 (2319) | |
| 21 May 2014 (69 DAS) | n = 25 (1185) | n = 23 (1356) | n = 25 (1224) | booting (47–49) |
| 22 May 2014 (70 DAS) | n = 22 (1222) | n = 20 (1443) | n = 17 (1785) | |
| 23 May 2014 (71 DAS) | n = 20 (1368) | n = 26 (1222) | n = 24 (1244) | |
| 17 June 2015 (82 DAS) | n = 22 (2298) | n = 17 (1377) | n = 23 (1608) | inflorescence emergence, heading (51–59) |
| 18 June 2015 (83 DAS) | n = 17 (1415) | n = 21 (1593) | n = 18 (1214) | |
| 19 June 2015 (84 DAS) | n = 16 (944) | n = 22 (1683) | n = 23 (2004) | |
| 4 June 2014 (83 DAS) | n = 26 (1145) | n = 22 (1297) | n = 11 (1136) | inflorescence emergence, heading (52–59) |
| 5 June 2014 (84 DAS) | * | n = 12 (1186) | n = 20 (1267) | |
| 16 June 2014 (95 DAS) | n = 28 (1462) | n = 23 (1404) | n = 27 (1277) | development of fruit (71–75) |
| 17 June 2014 (96 DAS) | n = 27 (1351) | n = 28 (1397) | n = 27 (1407) | |
| 18 June 2014 (97 DAS) | n = 28 (1299) | n = 24 (1061) | n = 27 (1269) | |
| 1 July 2015 (96 DAS) | * | n = 17 (2727) | n = 17 (3108) | development of fruit (73–75) |
| 2 July 2015 (97 DAS) | n = 17 (2159) | n = 17 (1810) | n = 18 (1824) | |
| 3 July 2015 (98 DAS) | n = 17 (3337) | n = 17 (3350) | n = 18 (2016) | |
| Acquisition Time | RMSE (m) | ||
|---|---|---|---|
| morning (n = 194) | 0.81 | 0.09 | 0.77 |
| noon (n = 189) | 0.87 | 0.08 | 0.77 |
| evening (n = 189) | 0.81 | 0.09 | 0.75 |
| Calibration Dataset | ncal | Expon. | Lin. | |||
|---|---|---|---|---|---|---|
| RMSE | RMSE | |||||
| Dry Biomass | ||||||
| Pre Anthesis | Rep. 1, 2 | 116 | 0.74 | 0.27 | 0.70 | 158.6 |
| Rep. 1, 3 | 72 | 0.78 | 0.25 | 0.71 | 169.2 | |
| Rep. 2, 3 | 100 | 0.72 | 0.27 | 0.64 | 173.3 | |
| 2014 | 76 | 0.74 | 0.24 | 0.67 | 129.3 | |
| 2015 | 68 | 0.75 | 0.28 | 0.72 | 181.3 | |
| 70% * | 101 | 0.74 | 0.27 | 0.68 | 166.9 | |
| (std. dev.) | ±0.02 | ±0.01 | ±0.02 | ±8.3 | ||
| Whole Period | Rep. 1, 2 | 135 | 0.73 | 0.30 | 0.62 | 226.3 |
| Rep. 1, 3 | 88 | 0.79 | 0.29 | 0.68 | 225.2 | |
| Rep. 2, 3 | 121 | 0.74 | 0.29 | 0.62 | 224.9 | |
| 2014 | 104 | 0.74 | 0.30 | 0.58 | 250.8 | |
| 2015 | 68 | 0.75 | 0.28 | 0.72 | 181.3 | |
| 70% * | 120 | 0.75 | 0.30 | 0.63 | 227.2 | |
| (std. dev.) | ±0.02 | ±0.01 | ±0.02 | ±10.2 | ||
| Fresh Biomass | ||||||
| Pre Anthesis | Rep. 1, 2 | 116 | 0.47 | 0.27 | 0.46 | 736.1 |
| Rep. 1, 3 | 72 | 0.51 | 0.27 | 0.53 | 723.7 | |
| Rep. 2, 3 | 100 | 0.42 | 0.26 | 0.40 | 736.7 | |
| 2014 | 76 | 0.37 | 0.22 | 0.36 | 563.4 | |
| 2015 | 68 | 0.62 | 0.27 | 0.59 | 799.1 | |
| 70% * | 101 | 0.46 | 0.27 | 0.45 | 734.4 | |
| (std. dev.) | ±0.04 | ±0.01 | ±0.04 | ±36.3 | ||
| Whole Period | Rep. 1, 2 | 152 | 0.48 | 0.27 | 0.44 | 797.0 |
| Rep. 1, 3 | 97 | 0.56 | 0.26 | 0.55 | 744.4 | |
| Rep. 2, 3 | 129 | 0.43 | 0.26 | 0.39 | 790.4 | |
| 2014 | 104 | 0.40 | 0.23 | 0.36 | 700.7 | |
| 2015 | 85 | 0.63 | 0.27 | 0.59 | 799.4 | |
| 70% * | 132 | 0.48 | 0.27 | 0.45 | 784.7 | |
| (std. dev.) | ±0.03 | ±0.01 | ±0.03 | ±29.9 | ||
| Calibration/Validation | nval | Exponential | Linear | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Split | RMSE (g/m²) | RE (%) | RMSE (g/m²) | RE (%) | ||||||
| Dry Biomass | ||||||||||
| Pre Anthesis | Rep. 1, 2/Rep. 3 | 28 | 0.77 | 112.57 | 0.72 | 21.88 | 0.58 | 163.32 | 0.60 | 34.08 |
| Rep. 1, 3/Rep. 2 | 72 | 0.63 | 174.77 | 0.70 | 26.40 | 0.65 | 152.31 | 0.71 | 27.42 | |
| Rep. 2, 3/Rep. 1 | 44 | 0.79 | 99.95 | 0.77 | 23.00 | 0.79 | 99.89 | 0.77 | 21.17 | |
| 2014/2015 | 68 | 0.70 | 124.01 | 0.74 | 24.80 | 0.72 | 97.33 | 0.73 | 25.27 | |
| 2015/2014 | 76 | 0.69 | 141.98 | 0.68 | 24.69 | 0.67 | 168.32 | 0.59 | 34.84 | |
| 70%/30% * | 43 | 0.70 | 135.45 | 0.73 | 23.76 | 0.68 | 135.14 | 0.72 | 25.81 | |
| (std. dev.) | ±0.06 | ±16.42 | ±0.03 | ±2.50 | ±0.05 | ±12.62 | ±0.03 | ±2.82 | ||
| Whole Period | Rep. 1, 2/Rep. 3 | 37 | 0.79 | 146.79 | 0.79 | 23.49 | 0.67 | 189.54 | 0.71 | 36.84 |
| Rep. 1, 3/Rep. 2 | 84 | 0.55 | 234.16 | 0.66 | 31.34 | 0.59 | 198.86 | 0.67 | 33.04 | |
| Rep. 2, 3/Rep. 1 | 51 | 0.66 | 149.32 | 0.75 | 25.19 | 0.68 | 146.01 | 0.76 | 23.48 | |
| 2014/2015 | 68 | 0.69 | 190.49 | 0.74 | 27.36 | 0.72 | 151.46 | 0.75 | 27.97 | |
| 2015/2014 | 104 | 0.60 | 173.39 | 0.73 | 25.06 | 0.58 | 195.29 | 0.70 | 32.23 | |
| 70%/30% * | 52 | 0.63 | 184.93 | 0.73 | 26.60 | 0.63 | 177.29 | 0.71 | 29.71 | |
| (std. dev.) | ±0.06 | ±21.37 | ±0.03 | ±2.63 | ±0.05 | ±15.22 | ±0.03 | ±3.05 | ||
| Fresh Biomass | ||||||||||
| Pre Anthesis | Rep. 1, 2/Rep. 3 | 28 | 0.52 | 468.85 | 0.60 | 21.02 | 0.44 | 530.80 | 0.58 | 21.76 |
| Rep. 1, 3/Rep. 2 | 72 | 0.37 | 641.12 | 0.56 | 24.84 | 0.37 | 594.62 | 0.56 | 24.73 | |
| Rep. 2, 3/Rep. 1 | 44 | 0.60 | 352.40 | 0.66 | 26.02 | 0.58 | 360.10 | 0.66 | 25.54 | |
| 2014/2015 | 68 | 0.58 | 312.38 | 0.63 | 31.87 | 0.58 | 268.69 | 0.62 | 32.47 | |
| 2015/2014 | 76 | 0.34 | 689.01 | 0.45 | 22.34 | 0.35 | 769.92 | 0.39 | 25.63 | |
| 70%/30% *,a | 43 | 0.47 | 491.29 | 0.60 | 23.82 | 0.46 | 488.90 | 0.60 | 23.76 | |
| (std. dev.) | ±0.09 | ±74.27 | ±0.05 | ±2.78 | ±0.09 | ±71.65 | ±0.05 | ±2.85 | ||
| Whole Period | Rep. 1, 2/Rep. 3 | 37 | 0.52 | 575.74 | 0.64 | 20.74 | 0.46 | 610.82 | 0.61 | 21.54 |
| Rep. 1, 3/Rep. 2 | 92 | 0.34 | 683.30 | 0.57 | 25.87 | 0.35 | 621.47 | 0.58 | 25.46 | |
| Rep. 2, 3/Rep. 1 | 60 | 0.61 | 355.41 | 0.64 | 24.37 | 0.61 | 358.75 | 0.64 | 23.99 | |
| 2014/2015 | 85 | 0.57 | 348.26 | 0.64 | 29.46 | 0.58 | 313.45 | 0.64 | 29.82 | |
| 2015/2014 | 104 | 0.35 | 784.93 | 0.49 | 23.80 | 0.35 | 790.85 | 0.48 | 25.14 | |
| 70%/30% *,b | 57 | 0.45 | 536.64 | 0.61 | 23.63 | 0.45 | 521.90 | 0.61 | 23.53 | |
| (std. dev.) | ±0.08 | ±64.09 | ±0.04 | ±2.43 | ±0.07 | ±61.89 | ±0.03 | ±2.42 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brocks, S.; Bareth, G. Estimating Barley Biomass with Crop Surface Models from Oblique RGB Imagery. Remote Sens. 2018, 10, 268. https://doi.org/10.3390/rs10020268
Brocks S, Bareth G. Estimating Barley Biomass with Crop Surface Models from Oblique RGB Imagery. Remote Sensing. 2018; 10(2):268. https://doi.org/10.3390/rs10020268
Chicago/Turabian StyleBrocks, Sebastian, and Georg Bareth. 2018. "Estimating Barley Biomass with Crop Surface Models from Oblique RGB Imagery" Remote Sensing 10, no. 2: 268. https://doi.org/10.3390/rs10020268
APA StyleBrocks, S., & Bareth, G. (2018). Estimating Barley Biomass with Crop Surface Models from Oblique RGB Imagery. Remote Sensing, 10(2), 268. https://doi.org/10.3390/rs10020268