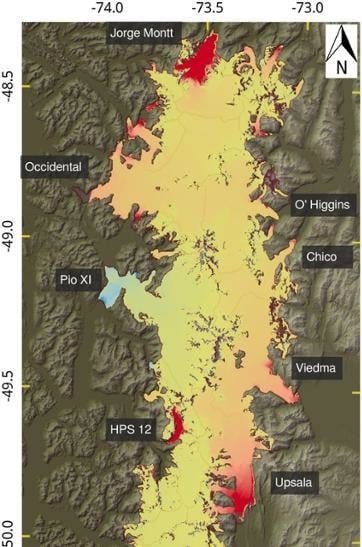
Elevation and Mass Changes of the Southern Patagonia Icefield Derived from TanDEM-X and SRTM Data
Abstract
1. Introduction
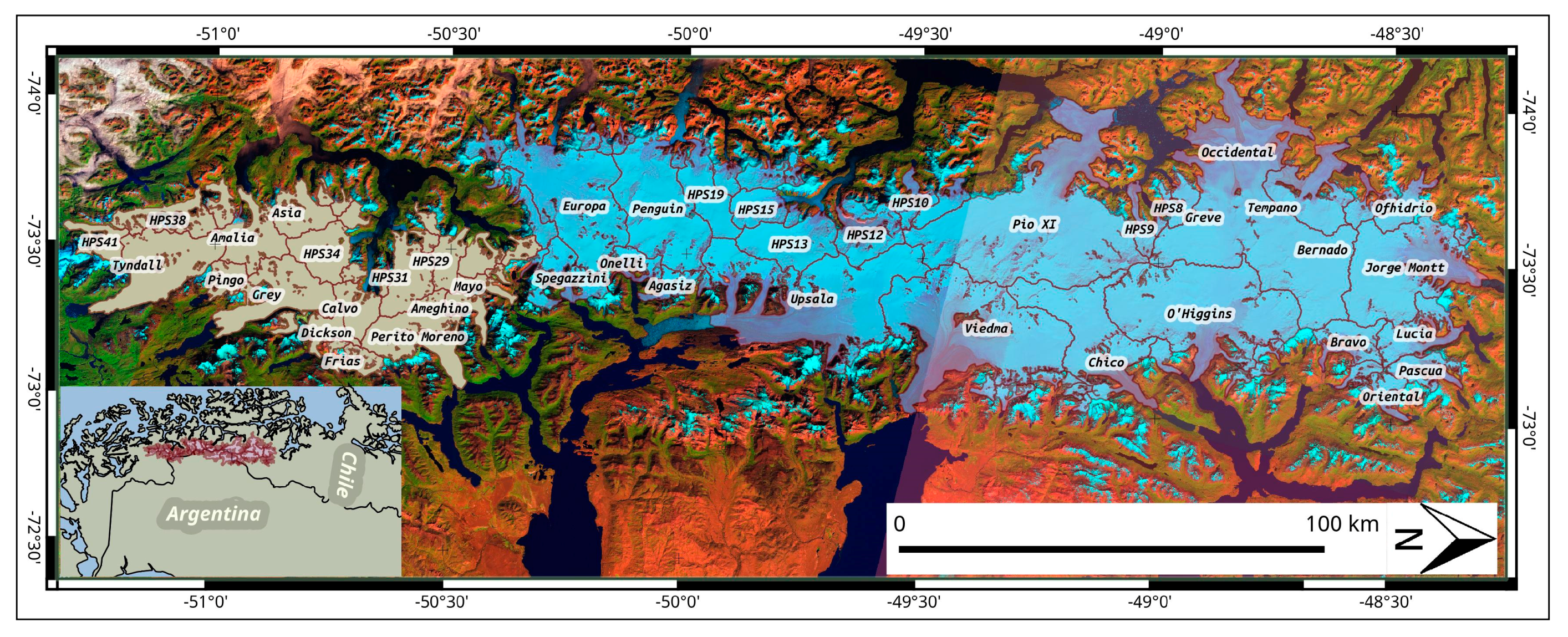
Study Site
2. Materials and Methods
2.1. Data
2.2. Dataprocessing for DEM Production
2.2.1. Interferometric Processing
2.2.2. Postprocessing and Mosaicking
2.3. Elevation and Volume Changes Rates and Mass Balance
2.4. Glacier Outline Mapping
2.5. Accuracy Assessment
3. Results
3.1. Elevation Changes: SPI 2000–2015/16
3.2. Geodetic Mass Balance Entire SPI 2000-2015/16
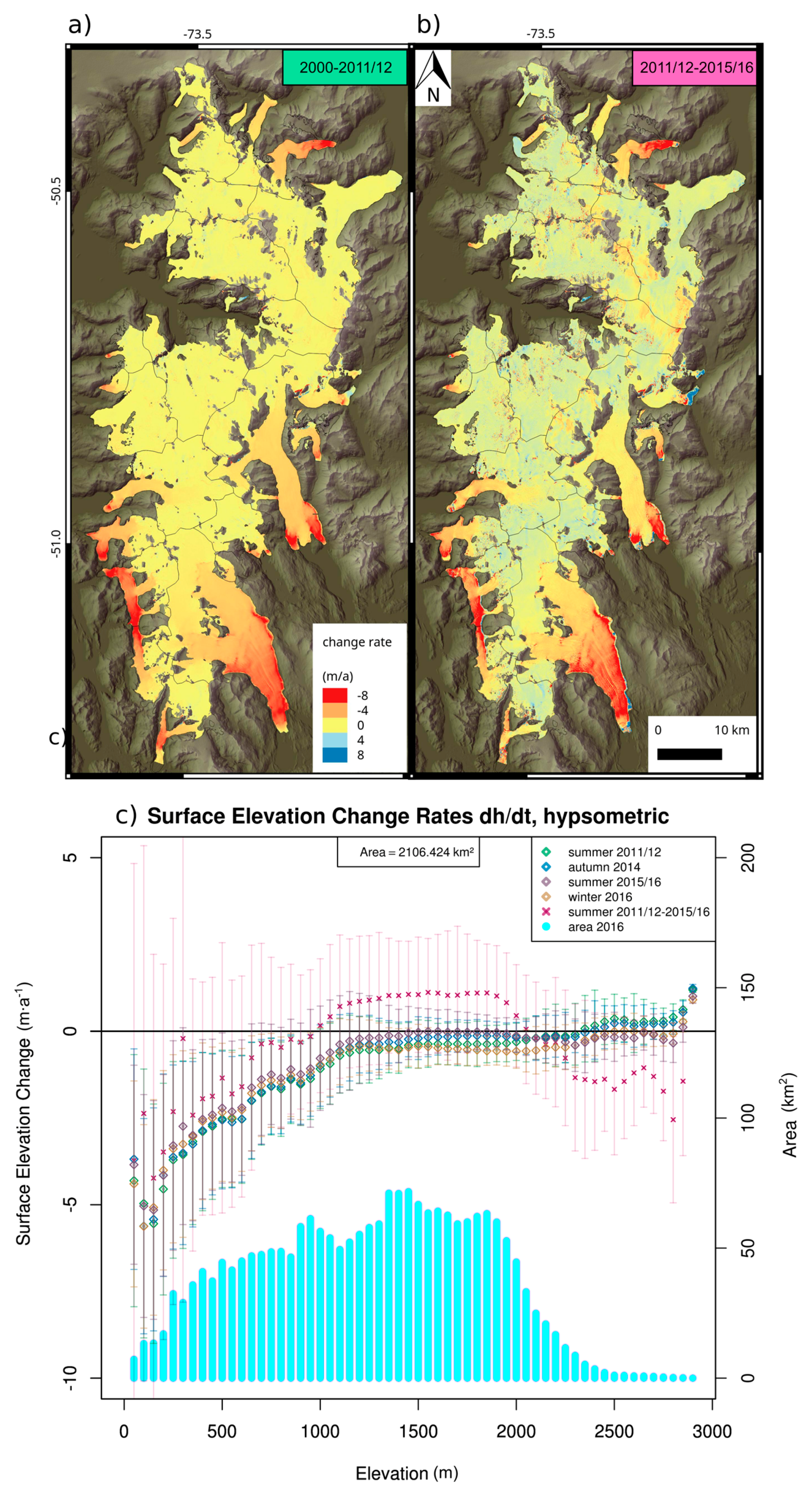
3.3. Elevation Changes: Southern SPI on Multiple Timesteps
4. Discussion
4.1. Elevation and Mass Changes of the Entire SPI
4.2. Elevation Changes: Southern SPI on Multiple Timesteps
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Garreaud, R.; Lopez, P.; Minvielle, M.; Rojas, M. Large-Scale Control on the Patagonian Climate. J. Clim. 2013, 26, 215–230. [Google Scholar] [CrossRef]
- Lliboutry, L. Nieves y glaciares de Chile: Fundamentos de glaciologia; Ediciones de la Universidad de Chile; Universidad de Chile: Santiago, RM, Chile, 1956. [Google Scholar]
- Naruse, R.; Aniya, M. Outline of Glacier Research Project in Patagonia, 1990. Bull. Glacier Res. 1992, 10, 31–38. [Google Scholar]
- Aniya, M.; Sato, H.; Naruse, R.; Skvarca, P.; Casassa, G. The use of satellite and airborne imagery to inventory outlet glaciers of the Southern Patagonia Icefield, South America. Photogramm. Eng. Remote Sens. 1996, 62, 1361–1369. [Google Scholar]
- Casassa, G.; Rodríguez, J.L.; Loriaux, T. A New Glacier Inventory for the Southern Patagonia Icefield and Areal Changes 1986–2000. In Global Land Ice Measurements from Space; Kargel, J.S.S., Leonard, G.J.J., Bishop, M.P.P., Kääb, A., Raup, B.H.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 639–660. ISBN 978-3-540-79818-7. [Google Scholar]
- Aniya, M. Recent Glacier Variations of the Hielos Patagónicos, South America, and Their Contribution to Sea-Level Change. Arct. Antarct. Alp. Res. 1999, 31, 165–173. [Google Scholar] [CrossRef]
- Willis, M.J.; Melkonian, A.K.; Pritchard, M.E.; Rivera, A. Ice loss from the Southern Patagonian Ice Field, South America, between 2000 and 2012. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Rignot, E.; Rivera, A.; Casassa, G. Contribution of the Patagonia Icefields of South America to sea level rise. Science 2003, 302, 434–437. [Google Scholar] [CrossRef] [PubMed]
- Davies, B.J.; Glasser, N.F. Accelerating shrinkage of Patagonian glaciers from the Little Ice Age (∼AD 1870) to 2011. J. Glaciol. 2012, 58, 1063–1084. [Google Scholar] [CrossRef]
- Rivera, A.; Casassa, G.; Bamber, J.; Kääb, A. Ice-elevation changes of Glaciar Chico, southern Patagonia, using ASTER DEMs, aerial photographs and GPS data. J. Glaciol. 2005, 51, 105–112. [Google Scholar] [CrossRef]
- Raymond, C.; Neumann, T.A.; Rignot, E.; Echelmeyer, K.; Rivera, A.; Casassa, G. Retreat of Glaciar Tyndall, Patagonia, over the last half-century. J. Glaciol. 2005, 51, 239–247. [Google Scholar] [CrossRef]
- Casassa, G.; Rivera, A.; Schwikowski, M. Glacier Mass-Balance Data For Southern South America (30°S-56°S). In Glacier Science and Environmental Change; Knight, P.G.G., Ed.; Blackwell Publishing: Malden, MA, USA, 2006; pp. 239–241. ISBN 978-0-470-75063-6. [Google Scholar]
- Schaefer, M.; Machguth, H.; Falvey, M.; Casassa, G.; Rignot, E. Quantifying mass balance processes on the Southern Patagonia Icefield. Cryosphere 2015, 9, 25–35. [Google Scholar] [CrossRef]
- Mernild, S.H.; Liston, G.E.; Hiemstra, C.; Wilson, R. The Andes Cordillera. Part III: Glacier surface mass balance and contribution to sea level rise (1979–2014): Glacier Surface Mass Balance and Contribution to Sea Level Rise. Int. J. Climatol. 2017, 37, 3154–3174. [Google Scholar] [CrossRef]
- Richter, A.; Ivins, E.; Lange, H.; Mendoza, L.; Schröder, L.; Hormaechea, J.L.; Casassa, G.; Marderwald, E.; Fritsche, M.; Perdomo, R.; et al. Crustal deformation across the Southern Patagonian Icefield observed by GNSS. Earth Planet. Sci. Lett. 2016, 452, 206–215. [Google Scholar] [CrossRef]
- Dietrich, R.; Ivins, E.R.; Casassa, G.; Lange, H.; Wendt, J.; Fritsche, M. Rapid crustal uplift in Patagonia due to enhanced ice loss. Earth Planet. Sci. Lett. 2010, 289, 22–29. [Google Scholar] [CrossRef]
- De Angelis, H. Hypsometry and sensitivity of the mass balance to changes in equilibrium-line altitude: The case of the Southern Patagonia Icefield. J. Glaciol. 2014, 60, 14–28. [Google Scholar] [CrossRef]
- Hoffmann, J.; Walter, D. How complementary are SRTM-X and-C band digital elevation models? Photogramm. Eng. Remote Sens. 2006, 72, 261–268. [Google Scholar] [CrossRef]
- Zink, M.; Bartusch, M.; Miller, D. TanDEM-X mission status. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 2290–2293. [Google Scholar]
- Pfeffer, W.T.; Arendt, A.A.; Bliss, A.; Bolch, T.; Cogley, J.G.; Gardner, A.S.; Hagen, J.-O.; Hock, R.; Kaser, G.; Kienholz, C.; et al. The Randolph Glacier Inventory: A globally complete inventory of glaciers. J. Glaciol. 2014, 60, 537–552. [Google Scholar] [CrossRef]
- Vijay, S.; Braun, M. Elevation Change Rates of Glaciers in the Lahaul-Spiti (Western Himalaya, India) during 2000–2012 and 2012–2013. Remote Sens. 2016, 8, 1038. [Google Scholar] [CrossRef]
- Rankl, M.; Braun, M. Glacier elevation and mass changes over the central Karakoram region estimated from TanDEM-X and SRTM/X-SAR digital elevation models. Ann. Glaciol. 2016, 57, 273–281. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hiramatsu, A.; Hiramatsu, A. Two-Dimensional Phase Unwrapping fo SAR Interferograms by Charge Connection Through Neutral Trees; Caltech/ JPL: Pasadena, CA, USA, 1994. Available online: https://trs.jpl.nasa.gov/handle/2014/36655 (accessed on 20 January 2018).
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef]
- Huss, M. Density assumptions for converting geodetic glacier volume change to mass change. Cryosphere 2013, 7, 877–887. [Google Scholar] [CrossRef]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Winsvold, S.H.; Andreassen, L.M.; Kienholz, C. Glacier area and length changes in Norway from repeat inventories. Cryosphere 2014, 8, 1885–1903. [Google Scholar] [CrossRef]
- Andreassen, L.M.; Paul, F.; Kääb, A.; Hausberg, J.E. Landsat-derived glacier inventory for Jotunheimen, Norway, and deduced glacier changes since the 1930s. Cryosphere 2008, 2, 131–145. [Google Scholar] [CrossRef]
- Falaschi, D.; Bravo, C.; Masiokas, M.; Villalba, R.; Rivera, A. First Glacier Inventory and Recent Changes in Glacier Area in the Monte San Lorenzo Region (47°S), Southern Patagonian Andes, South America. Arct. Antarct. Alp. Res. 2013, 45, 19–28. [Google Scholar] [CrossRef]
- Paul, F.; Andreassen, L.M. A new glacier inventory for the Svartisen region, Norway, from Landsat ETM+ data: Challenges and change assessment. J. Glaciol. 2009, 55, 607–618. [Google Scholar] [CrossRef]
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef] [PubMed]
- Gardelle, J.; Berthier, E.; Arnaud, Y. Impact of resolution and radar penetration on glacier elevation changes computed from DEM differencing. J. Glaciol. 2012, 58, 419–422. [Google Scholar] [CrossRef]
- Paul, F.; Barrand, N.E.; Baumann, S.; Berthier, E.; Bolch, T.; Casey, K.; Frey, H.; Joshi, S.P.; Konovalov, V.; Bris, R.L.; et al. On the accuracy of glacier outlines derived from remote-sensing data. Ann. Glaciol. 2013, 54, 171–182. [Google Scholar] [CrossRef]
- Muto, M.; Furuya, M. Surface velocities and ice-front positions of eight major glaciers in the Southern Patagonian Ice Field, South America, from 2002 to 2011. Remote Sens. Environ. 2013, 139, 50–59. [Google Scholar] [CrossRef]
- Masiokas, M.H.; Rivera, A.; Espizua, L.E.; Villalba, R.; Delgado, S.; Aravena, J.C. Glacier fluctuations in extratropical South America during the past 1000 years. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 242–268. [Google Scholar] [CrossRef]
- Harrison, S.; Winchester, V.; Glasser, N. The timing and nature of recession of outlet glaciers of Hielo Patagónico Norte, Chile, from their Neoglacial IV (Little Ice Age) maximum positions. Glob. Planet. Chang. 2007, 59, 67–78. [Google Scholar] [CrossRef]
- Glasser, N.F.; Harrison, S.; Jansson, K.N.; Anderson, K.; Cowley, A. Global sea-level contribution from the Patagonian Icefields since the Little Ice Age maximum. Nat. Geosci. 2011, 4, 303–307. [Google Scholar] [CrossRef]
- Abdel Jaber, W. Derivation of Mass Balance and Surface Velocity of Glaciers by Means of High Resolution Synthetic Aperture Radar: Application to the Patagonian Icefields and Antarctica. DLR-Forschungsbericht: ISBN 1434-8454. Available online: http://elib.dlr.de/109075/1/Thesis_AbdelJaber_final.pdf (accessed on 1 November 2017).
- Jaber, W.A.; Floricioiu, D.; Rott, H.; Eineder, M. Surface elevation changes of glaciers derived from SRTM and TanDEM-X DEM differences. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, VIC, Australia, 21–26 July 2013; pp. 1893–1896. [Google Scholar]
- Lange, H.; Casassa, G.; Ivins, E.R.; Schröder, L.; Fritsche, M.; Richter, A.; Groh, A.; Dietrich, R. Observed crustal uplift near the Southern Patagonian Icefield constrains improved viscoelastic Earth models. Geophys. Res. Lett. 2014, 41, 805–812. [Google Scholar] [CrossRef]
- Mouginot, J.; Rignot, E. Ice motion of the Patagonian Icefields of South America: 1984–2014. Geophys. Res. Lett. 2015, 42, 2014GL062661. [Google Scholar] [CrossRef]
- Sakakibara, D.; Sugiyama, S.; Sawagaki, T.; Marinsek, S.; Skvarca, P. Rapid retreat, acceleration and thinning of Glaciar Upsala, Southern Patagonia Icefield, initiated in 2008. Ann. Glaciol. 2013, 54, 131–138. [Google Scholar] [CrossRef]
- Sakakibara, D.; Sugiyama, S. Ice-front variations and speed changes of calving glaciers in the Southern Patagonia Icefield from 1984 to 2011: Calving glaciers in southern Patagonia. J. Geophys. Res. Earth Surf. 2014, 119, 2541–2554. [Google Scholar] [CrossRef]
- Floricioiu, D.; Eineder, M.; Rott, H.; Yague-Martinez, N.; Nagler, T. Surface Velocity and Variations of Outlet Glaciers of the Patagonia Icerfields by Means of TerraSAR-X. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Jaber, W.A.; Floricioiu, D.; Rott, H.; Eineder, M. Dynamics of fast glaciers in the Patagonia Icefields derived from TerraSAR-X and TanDEM-X data. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 3226–3229. [Google Scholar]
- Skvarca, P.; De Angelis, H.; Naruse, R.; Warren, C.R.; Aniy, M. Calving rates in fresh water: New data from southern Patagonia. Ann. Glaciol. 2002, 34, 379–384. [Google Scholar] [CrossRef]
- Skvarca, P.; Raup, B.; De Angelis, H. Recent behaviour of Glaciar Upsala, a fast-flowing calving glacier in Lago Argentino, southern Patagonia. Ann. Glaciol. 2003, 36, 186–188. [Google Scholar] [CrossRef]
- Sugiyama, S.; Minowa, M.; Sakakibara, D.; Skvarca, P.; Sawagaki, T.; Ohashi, Y.; Naito, N.; Chikita, K. Thermal structure of proglacial lakes in Patagonia. J. Geophys. Res. Earth Surf. 2016, 121, 2270–2286. [Google Scholar] [CrossRef]
- Rivera, A.; Casassa, G. Ice Elevation, Areal, and Frontal Changes of Glaciers from National Park Torres del Paine, Southern Patagonia Icefield. Arct. Antarct. Alp. Res. 2004, 36, 379–389. [Google Scholar] [CrossRef]
- Naruse, R.; Aniya, M.; Skvarca, P. Gino Casassa Recent variations of calving glaciers in Patagonia, South America, revealed by ground surveys, satellite-data analyses and numerical experiments. Ann. Glaciol. 1995, 21, 297–303. [Google Scholar] [CrossRef]
- Rott, H.; Stuefer, M.; Siegel, A.; Skvarca, P.; Eckstaller, A. Mass fluxes and dynamics of Moreno Glacier, Southern Patagonia Icefield. Geophys. Res. Lett. 1998, 25, 1407–1410. [Google Scholar] [CrossRef]
- Stuefer, M.; Rott, H.; Skvarca, P. Glaciar Perito Moreno, Patagonia: Climate sensitivities and glacier characteristics preceding the 2003/04 and 2005/06 damming events. J. Glaciol. 2007, 53, 3–16. [Google Scholar] [CrossRef]
- Aniya, M.; Skvarca, P. Characteristics and variations of Upsala and Moreno glaciers, southern Patagonia. Bull. Glacier Res. 1992, 10, 39–53. [Google Scholar]
- Minowa, M.; Sugiyama, S.; Sakakibara, D.; Sawagaki, T. Contrasting glacier variations of Glaciar Perito Moreno and Glaciar Ameghino, Southern Patagonia Icefield. Ann. Glaciol. 2015, 56, 26–32. [Google Scholar] [CrossRef]
- Minowa, M.; Sugiyama, S.; Sakakibara, D.; Skvarca, P. Seasonal Variations in Ice-Front Position Controlled by Frontal Ablation at Glaciar Perito Moreno, the Southern Patagonia Icefield. Front. Earth Sci. 2017, 5, 1–15. [Google Scholar] [CrossRef]
- Warren, C.R.; Rivera, A.; Post, A. Greatest Holocene advance of Glaciar PIO XI, Chilean Patagonia: Possible causes. Ann. Glaciol. 1997, 24, 11–15. [Google Scholar] [CrossRef]
- Rivera, A.; Casassa, G. Volume changes on Pio XI glacier, Patagonia: 1975–1995. Glob. Planet. Chang. 1999, 22, 233–244. [Google Scholar] [CrossRef]
- Motoki, A.; Orihashi, Y.; Naranjo, J.A.; Hirata, D.; Skvarca, P.; Anma, R. Geologic reconnaissance of Lautaro Volcano, Chilean Patagonia. Rev. Geol. Chile 2006, 33, 177–187. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef] [PubMed]
- Vaughan, D.G.; Comiso, J.C.; Allison, I.; Carrasco, J.; Kaser, G.; Kwok, R.; Mote, P.; Murray, T.; Paul, F.; Ren, J.; et al. Observations: Cryosphere. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M.B., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A Reconciled Estimate of Glacier Contributions to Sea Level Rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef] [PubMed]
- Ivins, E.R.; Watkins, M.M.; Yuan, D.N.; Dietrich, R.; Casassa, G.; Rulke, A. On-land ice loss and glacial isostatic adjustment at the Drake Passage: 2003–2009. J. Geophys. Res.-Solid Earth 2011, 116, 1–24. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Blankenship, D.D.; Ivins, E.R. Patagonia icefield melting observed by gravity recovery and climate experiment (GRACE). Geophys. Res. Lett. 2007, 34, 1–6. [Google Scholar] [CrossRef]
- Willis, M.J.; Melkonian, A.K.; Pritchard, M.E.; Ramage, J.M. Ice loss rates at the Northern Patagonian Icefield derived using a decade of satellite remote sensing. Remote Sens. Environ. 2012, 117, 184–198. [Google Scholar] [CrossRef]
- Melkonian, A.K.; Willis, M.J.; Pritchard, M.E.; Rivera, A.; Bown, F.; Bernstein, S.A. Satellite-derived volume loss rates and glacier speeds for the Cordillera Darwin Icefield, Chile. Cryosphere 2013, 7, 823–839. [Google Scholar] [CrossRef]
- Mätzler, C.; Schanda, E. Snow mapping with active microwave sensors. Int. J. Remote Sens. 1984, 5, 409–422. [Google Scholar] [CrossRef]
| ID | Mosaic | Date | Start Time | Scenes | Pass Dir. | Beff (m) | HoA (m) | Inc Angle (degree) | PU Mode |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Summer 2011/12 | 31 January 2012 | 09:54:19–09:54:26 | 2 | D | 69.03 | −94.04 | 37.17 | mcf |
| 2 | 15 March 2012 | 09:54:19–09:54:26 | 2 | D | 68.97 | −98.42 | 40.61 | mcf | |
| 3 | Autumn 2014 | 16 May 2014 | 09:54:32–09:54:39 | 2 | D | 159.71 | 40.20 | 38.41 | mcf |
| 4 | 27 May 2014 | 09:54:33–09:54:40 | 2 | D | 162.34 | 42.39 | 41.95 | mcf | |
| 5 | Summer 2015/16 | 3 December 2015 | 10:02:40–10:02:51 | 3 | D | 114.68 | 49.91 | 35.35 | mcf |
| 6 | 3 December 2015 | 10:03:12–10:03:26 | 3 | D | 106.48 | 38.28 | 24.81 | mcf | |
| 7 | 9 December 2015 | 09:54:10–09:54:28 | 4 | D | 119.71 | −65.39 | 44.54 | mcf | |
| 8 | 9 December 2015 | 09:54:42–09:54:56 | 3 | D | 115.25 | −53.47 | 36.03 | mcf | |
| 9 | 20 December 2016 | 09.54:19–09:54:35 | 5 | D | 117.79 | −62.93 | 42.92 | bc | |
| 10 | 31 December 2015 | 09:54:25–09:54:48 | 5 | D | 117.64 | −59.31 | 41.09 | mcf | |
| 11 | Winter 2016 | 20 September 2016 | 09:54:50–09:55:04 | 3 | D | 105.43 | −61.22 | 38.52 | mcf |
| 12 | 1 October 2016 | 09:54:45–09:54:57 | 2 | D | 105.63 | −65.10 | 40.65 | mcf |
| Scenarios | dh/dt (m·a−1) | dV/dt (km3·a−1) | dM/dt (Gt·a−1) |
|---|---|---|---|
| Scenario 1 | −1.06 ± 0.21 | −11.5 ± 2.3 | −10.34 ± 2.2 |
| Scenario 2 | −9.77 ± 2.1 | ||
| Scenario 3 | −7.97 ± 1.7 | ||
| Scenario 1, (extrapolated) | −1.05 ± 0.28 | −13.2 ± 3.6 | −11.84 ± 3.3 |
| Area (km²) | Volume (km3·a−1) | Mass (Gt·a−1) | Spec. Mass Balance (m w.e.a−1) | Region | Period | Method/Data | Reference |
|---|---|---|---|---|---|---|---|
| −1.39 ± 0.28 | SPI | 1650–2000 | dh/dt reconstruction | [39] | |||
| 13.000 | −13.5 ± 0.8 | −15.2 ± 0.72 | −0.934 | SPI | 1968/75–2000 | dh/dt, maps-SRTM | [61] |
| 13.000 | −38.7 ± 4.4 | −2.679 | SPI | 1995–2000 | dh/dt maps SRTM | [8] | |
| 12.118 | −22.2 ± 1.3 | −20.0 ± 1.2 | −1.476 | SPI | 2000–2011 | dh/dt ASTER-SRTM | [7] |
| 12.880 | −14.59 ± 0.37 | −13.14 ± 0.42 | −1.019 | SPI | 2000–2011/12 | dh/dt TDX-SRTM | [40] |
| 10.772 | −11.5 ± 2.3 | −10.39 ± 2.2 | −0.954 | SPI | 2000–2015/16 | dh/dt TDX-SRTM | this study |
| 12.573 | −13.2 ± 3.6 | −11.84 ± 2.2 | −0.9.41 | SPI | 2000–2015/16 | dh/dt TDX-SRTM | this study |
| --- | −29 ± 10 | Southern Andes | 2003–2009 | Gravimetry/GRACE | [62,63] | ||
| --- | −23.0 ± 3.0 | Fuego-Patagonia | 2003–2011 | Gravimetry/GRACE | |||
| --- | −26.6 ± 6.0 | Fuego-Patagonia | 2003–2009 | Gravimetry/GRACE | [64] | ||
| −27.9 ± 11 | −1.6 | Patagonia | 04/2002–12/2006 | Gravimetry/GRACE | [65] | ||
| −0.79 ± 0.16 | −0.65 | NPI | 1870–2000 | dh/dt reconstruction | [39] | ||
| −3.2 ± 0.4 | NPI | 1968/75–2000 | dh/dt, maps-SRTM | [8] | |||
| −4.06 ± 0.11 | −3.96 ± 0.14 | NPI | 2000–2011 | dh/dt ASTER-SRTM | [66] | ||
| −4.4 ± 0.13 | −3.96 ± 0.14 | NPI | 2000–2014 | dh/dt TDX-SRTM | [40] | ||
| −4.06 ± 0.11 | −3.4 ± 0.07 | Cordillera Darwin | 2000–2011 | dh/dt ASTER-SRTM | [67] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malz, P.; Meier, W.; Casassa, G.; Jaña, R.; Skvarca, P.; Braun, M.H. Elevation and Mass Changes of the Southern Patagonia Icefield Derived from TanDEM-X and SRTM Data. Remote Sens. 2018, 10, 188. https://doi.org/10.3390/rs10020188
Malz P, Meier W, Casassa G, Jaña R, Skvarca P, Braun MH. Elevation and Mass Changes of the Southern Patagonia Icefield Derived from TanDEM-X and SRTM Data. Remote Sensing. 2018; 10(2):188. https://doi.org/10.3390/rs10020188
Chicago/Turabian StyleMalz, Philipp, Wolfgang Meier, Gino Casassa, Ricardo Jaña, Pedro Skvarca, and Matthias H. Braun. 2018. "Elevation and Mass Changes of the Southern Patagonia Icefield Derived from TanDEM-X and SRTM Data" Remote Sensing 10, no. 2: 188. https://doi.org/10.3390/rs10020188
APA StyleMalz, P., Meier, W., Casassa, G., Jaña, R., Skvarca, P., & Braun, M. H. (2018). Elevation and Mass Changes of the Southern Patagonia Icefield Derived from TanDEM-X and SRTM Data. Remote Sensing, 10(2), 188. https://doi.org/10.3390/rs10020188