Abstract
The contribution to sea level rise from Patagonian icefields is one of the largest mass losses outside the large ice sheets of Antarctica and Greenland. However, only a few studies have provided large-scale assessments in a spatially detailed way to address the reaction of individual glaciers in Patagonia and hence to better understand and explain the underlying processes. In this work, we use repeat radar interferometric measurements of the German TerraSAR-X-Add-on for Digital Elevation Measurements (TanDEM-X) satellite constellation between 2011/12 and 2016 together with the digital elevation model from the Shuttle Radar Topography Mission (SRTM) in 2000 in order to derive surface elevation and mass changes of the Southern Patagonia Icefield (SPI). Our results reveal a mass loss rate of −11.84 ± 3.3 Gt·a−1 (corresponding to 0.033 ± 0.009 mm·a−1 sea level rise) for an area of 12573 km2 in the period 2000–2015/16. This equals a specific glacier mass balance of −0.941 ± 0.19 m w.e.·a−1 for the whole SPI. These values are comparable with previous estimates since the 1970s, but a magnitude larger than mass change rates reported since the Little Ice Age. The spatial pattern reveals that not all glaciers respond similarly to changes and that various factors need to be considered in order to explain the observed changes. Our multi-temporal coverage of the southern part of the SPI (south of 50.3° S) shows that the mean elevation change rates do not vary significantly over time below the equilibrium line. However, we see indications for more positive mass balances due to possible precipitation increase in 2014 and 2015. We conclude that bi-static radar interferometry is a suitable tool to accurately measure glacier volume and mass changes in frequently cloudy regions. We recommend regular repeat TanDEM-X acquisitions to be scheduled for the maximum summer melt extent in order to minimize the effects of radar signal penetration and to increase product quality.
1. Introduction
The Andes in Patagonia form a major obstacle for the southern hemisphere westerlies. Moist air masses from the Pacific Ocean nourish the glaciers and icefields of the Patagonian Andes [1]. The largest of these ice bodies is the Southern Patagonia Icefield (SPI) covering ~13,500 km2 in 1944/1945 [2], measured to a reduced ~13,000 km2 in a 1986 Landsat TM mosaic [3], used for the first glacier inventory (1992) [4,5]. Several studies have reported a continuous retreat and thinning of its outlet glaciers causing one of the largest contributions to sea level rise outside the large ice sheets [6,7,8]. Davies and Glasser [9] showed that mass loss rates of Patagonian glaciers in the 21st century are about a magnitude larger when compared to those of the period since the Little Ice Age to today. Still, there are considerable uncertainties about the absolute mass change rates, the processes driving those changes and how they vary over time. Additionally, there is only limited knowledge about the regional climate conditions and their changes. Only very few surface mass balance measurements exist (e.g., [10,11,12]) and modeling attempts are also very limited (e.g., [13,14]).
Modern remote sensing technologies offer the potential to cover large areas and to provide glacier mass balance estimates for entire regions. Time series from the Gravity Recovery and Climate Experiment satellite (GRACE) revealed mass changes between 23 and 29 Gt·a−1 for the southern Andes. However, the measured gravity signal is also strongly influenced by the mass changes due to glacio-isostatic adjustments. For Patagonia, rates of up to 41 mm·a−1 have been reported close to the SPI [15,16]. Moreover, the integrated GRACE signal cannot resolve individual glacier catchments. Satellite radar and laser altimetry techniques are not optimal for Patagonia due to the large footprint (radar) or frequent cloud coverage (laser). Similar difficulties exist for optical satellite imagery and photogrammetric approaches. Synthetic aperture radar (SAR) imagery is not affected by clouds and interferometric techniques allow the repeated derivation of surface elevation. In February 2000, the SRTM acquired a global baseline digital elevation model (DEM) by bi-static SAR interferometry between 56° S and 60° N, to which subsequent measurements can be compared.
In this study, we aim at (1) measuring elevation and mass changes of the entire SPI between 2000 and 2015/16 using DEMs from the TanDEM-X and SRTM missions and (2) investigating possible seasonal or annual changes of the elevation for the southern tip of the SPI using repeat TanDEM-X acquisitions between 2012 and 2016.
Study Site
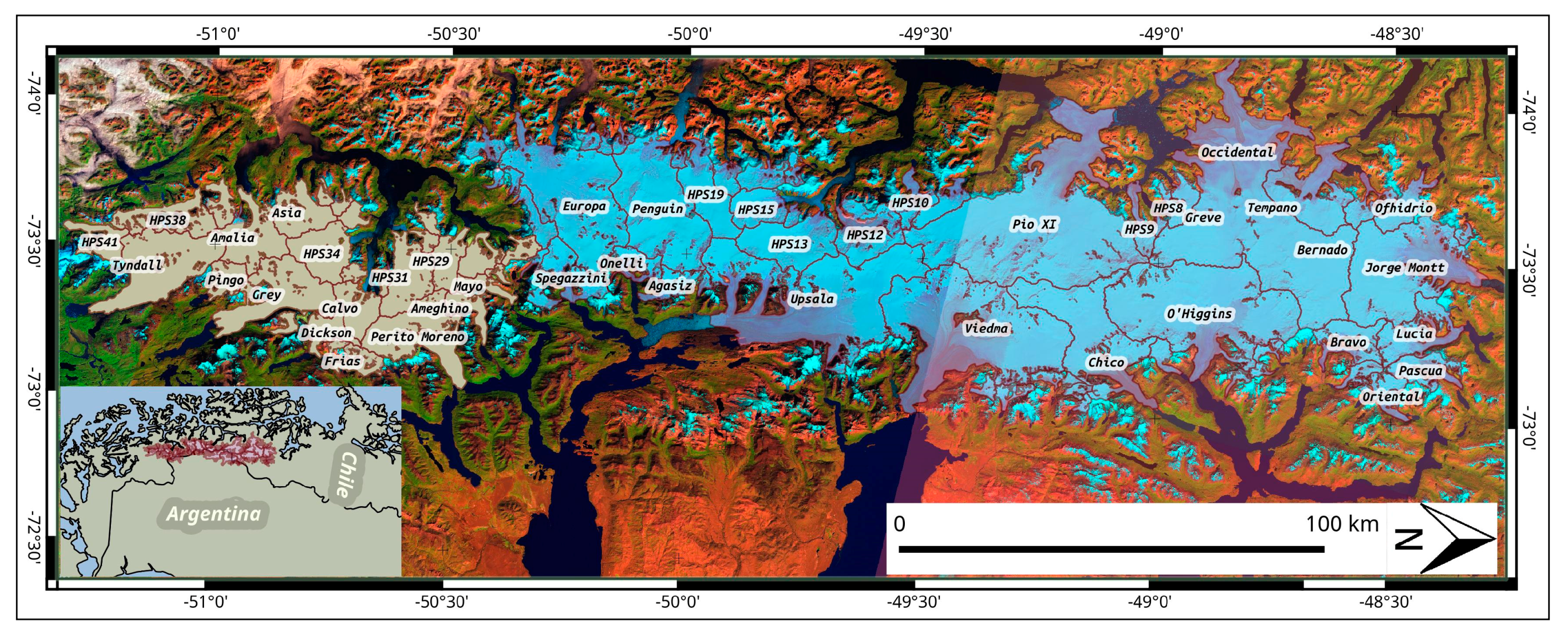
The Southern Patagonian Icefield stretches from 49.5° to 51.5° S along the 73.5° W meridian (Figure 1). The accumulation zone of the icefield is reported for elevations ranging between 670 m to 3540 m a.s.l. [17] and comprises 48 major outlet glaciers [4], with a total of 139 outlet glaciers draining either into the sea (west coast) or into freshwater lakes (east side).
Figure 1.
Overview of the Southern Patagonian Icefield, location map in southern South America and glacier names referred to in the text. The grey glacier outlines indicate the southern tip of the SPI which was repeatedly covered by TanDEM-X data (cf. Section 3.3). Background image: Landsat mosaic from Landsat 5 and 8©USGS, 2015.
2. Materials and Methods
2.1. Data
From 11–22 February 2000, the Shuttle Radar Topography Mission of the National Aeronautics and Space Administration (NASA) acquired a near global data coverage outside the polar regions with a bi-static C-band SAR interferometer [18]. We used the void-filled LP DAAC NASA Version 3 SRTM DEM with a ground resolution of 1 arcsecond, resampled to the local UTM zone 18S as reference dataset. DEMs of subsequent dates were derived from data of the satellite constellation of the ongoing TerraSAR-X and TanDEM-X (further referred to as TDX) missions. The two satellites, operated jointly by the German Aerospace Center (DLR) and ASTRIUM Defense and Space GmbH, fly in a close helix orbit formation. As such, they form a bi-static or pursuit monostatic SAR interferometer with both satellites acquiring data. The system has a swath width of 30 km and enables a ground resolution of 0.4 arcsecond. The TDX constellation is acquiring data since 2010 [19]. The datasets are provided as a pair of Single Look Complex scenes of an average scan-time of seven seconds in along-track direction. To cover our study area, multiple scenes along track and across orbits had to be mosaicked (see Supplementary Materials Figure S1). Table 1 summarizes the major characteristics of the TDX data sets used. For the total coverage of the SPI in the austral summer 2015/16 we used 23 scenes. For the southern tip of SPI a repeat coverage was available, consisting of 4/4–5 scenes from two relative orbits (summer 2011/12, autumn 2014, winter 2016) and seven scenes from three relative orbits (summer 2015/16) (see Supplementary Materials Figure S1). All data was acquired in descending path direction and with similar incident angles facilitating comparable viewing geometries.

Table 1.
Summary of the TanDEM-X data takes used for DEM generation. Beff: effective baseline; HoA: height of ambiguity; Inc. angle: incident angle; PU: phase unwrapping method used for the specific data set.
We used optical satellite data to derive raster masks for the DEM post-processing and to refine the glacier catchments of the Randolph Glacier Inventory Version 5.0 [20]. The respective Landsat-5 and Landsat-8 data is listed in supplemental Table S1. Data was chosen as a trade-off between most adequate acquisition date and minimum cloud cover.
2.2. Dataprocessing for DEM Production
2.2.1. Interferometric Processing
We used a differential SAR interferometric approach to generate DEMs out of bi-static TDX image pairs [21,22]. In a first step all scenes along one track and of one date were concatenated. A simulated topographic phase was created from the reference DEM (SRTM) using the geometric parameters of the TDX satellite acquisition and subtracted from the TanDEM-X interferogram. The resulting differential phase was filtered to reduce the noise using a Goldstein filter [23]. Subsequently, the differential phase was unwrapped. We chose to execute this step in parallel with two algorithms: the branch cut (BC) [24] and the minimum cost flow (MCF) [25] method. Phase unwrapping was guided by a coherence mask using a threshold of 0.2 to discard areas of low signal-to-noise ratios. The product was finally recombined with the reference phase after a phase-to-height conversion to get the absolute terrain heights. In a final step we geocoded the resulting DEMs. Since the unwrapping methods are sensitive to errors in the interpretation we visually checked each scene and chose the results of the algorithm with less apparent faulty areas. We additionally excluded any unreliable parts of images that contained artifacts of obvious phase jumps by masking those out manually digitizing a polygon-shapefile mask. The output is considered a raw DEM product with need for refined horizontal and vertical adjustments on the reference SRTM DEM.
2.2.2. Postprocessing and Mosaicking
Due to the concatenation of scenes along-track a consistent raw DEM was generated for each track. However, across orbits, the raw DEM strips needed to be mosaicked to a continuous DEM. For this step, we introduced an automatic sequence to adjust the raw DEM strips using stable points off-glacier. Stable ground was identified as pixels below a 10° slope threshold in the TDX DEM, after applying masks for vegetation and water bodies derived from optical data. The bias obtained from the stable points was removed by fitting a bilinear plane with a least squares approach. After this vertical offset correction, we introduced a horizontal co-registration of the TDX DEMs with the reference SRTM DEM. Following Nuth and Kääb [26], an iterative process was used to minimize shifts between both DEMs in x and y direction. Stable ground pixels were examined for direction and amplitude of elevation deviations with respect to the aspect of the DEM. We extracted the shift parameters as polar coordinates from sinusoidal least squares fitted modeling of the function describing the dh/tan(slope) to aspect dependencies found in the sample of assumed stable points (Supplementary Materials Figure S2). The sum of the consecutively derived shift parameters was applied as a global transformation of the DEM to the new origin with subsequent resampling to the reference SRTM raster parameters. An additional loop of bilinear vertical adjustment was run to correct for residual vertical offsets after horizontal co-registration. These improved TDX DEM tiles were then mosaicked to the final DEM-product. We applied a simple merge where only values of one raster dataset were considered in overlapping areas. Without any averaging, these values were referenced to one exact acquisition date for further calculations.
2.3. Elevation and Volume Changes Rates and Mass Balance
The area-wide DEMs for each timestep were differenced on the glaciated areas from the reference SRTM DEM and annual change rates were computed accounting for the exact timespan between both acquisitions. Glaciers were outlined by an updated Randolph Glacier Inventory Version 5 to the reference year 2000 (cf. Section 2.4). Outliers in the DEMs close to nunataks, icefalls or processing artifacts were removed by a moving window function (Supplementary Materials Figure S3). For each pixel the median was calculated and differenced from the actual value for a 5 × 5, 7 × 7 and a 9 × 9 Kernel. If the mean of those differences exceeded 33 m the center pixel was removed as an outlier.
For the total SPI coverage (summer 2015/16) we calculated the pixel-based elevation change rates to volume by multiplying with the pixel area (30 × 30 m2) and volume to mass changes using different density scenarios (cf. Table 2). For Scenario 1 we used a constant density value of 900 kg·m−3. Scenario 2 was calculated for 850 kg·m−3 [27], while for Scenario 3 the density was not constant. We applied a density of 900 kg·m−3 below the Equilibrium Line Altitude (ELA) and 600 kg·m−3 for areas above this elevation [21,22,28]. To derive the ELA we used the average ELA of the glaciers we studied from De Angelis [17] and divided the areas according to the hypsometric distribution we found to find an area weighted average ELA of 1050 m. The error for this latter scenario was estimated with a mean density of 750 kg·m−3.

Table 2.
Volume and mass change computations for the SPI (10.772 km2 of measured area corresponding to 85.7% of the SPI area) using different density scenarios for volume-to-mass conversion. last row: as Scenario 1 but including extrapolation for the missing 14.3 percent.
To provide a mean dh/dt on glacier catchment basis, we excluded glaciers <10 km2 in the analysis due to a predominance of faulty or missing values. The area of valid TDX to SRTM elevation differences (surveyed area) amounted to 10,772 km2 corresponding to 85.7% of the glaciated area (12,569 km2). We extrapolated the missing 14.3% using to the mean elevation change of the respective altitudinal bin of SRTM elevation. Our study does not account for mass changes of calving glaciers below lake or sea level. As a consequence, our estimates of mass changes are a lower bound.
2.4. Glacier Outline Mapping
Different techniques for an automated glacier mapping with optical satellite imagery have been successfully applied in various glaciated regions [29,30,31]. Since optical sensors are restricted by cloud-cover and glacier mapping requires a low coverage of seasonal snow, the choice of suitable satellite scenes at the end of the ablation period is limited. Hence, several Landsat-5 TM satellite scenes from the period 1 March 2000–7 May 2001 served as basis for a semi-automatic mapping covering the entire SPI (see Supplementary Materials Table S1). Each scene was checked for its orthorectification quality. Ratio images were calculated for bands TM3/TM5 dividing the raw digital numbers (DN) and were converted to a binary mask using different threshold values. Subsequently, the resulting raster was vectorized to generate glacier polygons. To obtain the most suitable threshold value, we compared the glacier polygons to a false color composite of channels 5-4-3 (mid-infrared, near infrared, red). Rationing the red and mid-infrared channel provided the advantage that glaciers situated in cast shadows could be better delineated than by using a ratio of near-infrared and mid-infrared (TM4/TM5) [32]. Waterbodies that were mistakenly classified as glacier and snow were excluded superimposing water bodies from the HydroLAKES database [33] that precludes lakes >0.1 km2. A DEM derived mask was used to exclude the sea surface in fjords, discarding glaciers <0.25 km2. In the next step, some manual correction was still required, especially regarding the separation between seasonal or perennial snow and small glaciers. We used a temporal consistency test to identify and erase annual snowfields. For this we reviewed all available Landsat scenes since the beginning of the Landsat missions (acquisition date summer and autumn) and compared them to the inventory. The arrangement of scenes with different acquisition dates permitted the manual correction for debris-covered glaciers, as some glaciological structures i.e., flow patterns, novel water discharge structures, expanding melting ponds and collapse structures were visible. As a final step, the glacier outlines were subdivided into glacier catchments by extracting the ridgelines and glacier basins using the gap-filled SRTM-DEM. In order to maintain compatibility to the Randolph Glacier Inventory Version 5 [17] a spatial join with its attribute was performed to preserve names and index numbers according to the inventory (cf. Figure 2, titles of plots c-h).
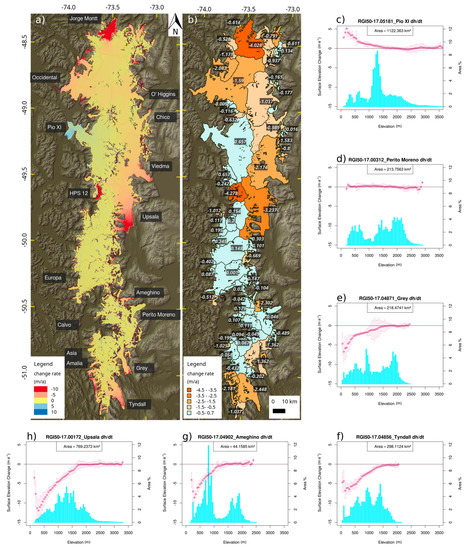
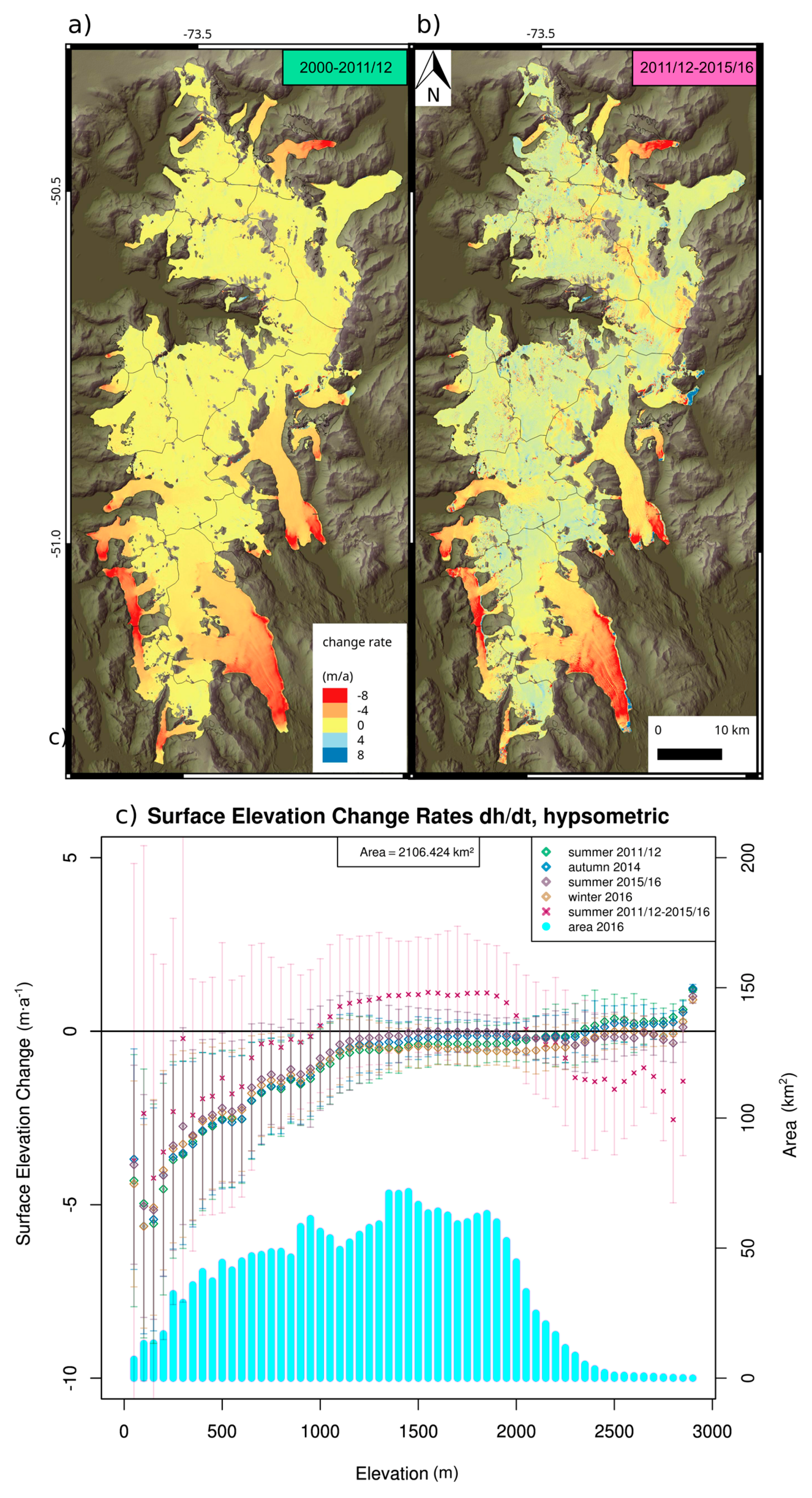
Figure 2.
Elevation change maps of the SPI; names denote the major outlet glaciers. (a) pixel-based assessment 2000–2015/16; (b) averaged on catchment basis; (c–h) hypsometry (cyan) and elevation changes (red) plotted for 50 m elevation bins for different glaciers. Pio XI glacier is known for its anomalous development at its two termini. As a singular exceptional case over the whole icefield it is attributed a neutral to slightly positive surface change rate on the plateau-like higher altitudes but experiencing lifted surface at the tongue, with rates increasing downstream to a maximum of 8 m·a−1 at its southern terminus. All graphs only refer to surveyed area which amounted for a total of 10772 km2 for (a) and (b).
2.5. Accuracy Assessment
The mass balance inaccuracy measures result from the following term for error propagation
where δ identifies the uncertainty of the respective variable of elevation change rate (dh/dttot), area (A) and volume to mass conversion (ρ).
In the following we describe these error terms with their composition and determination in more detail. The error of the elevation change rate (δdh/dt tot) comprises the error of the relative vertical accuracy of the two DEMs (δdh/dt vert), the radar penetration into snow and ice (δdh/dt radar) and an error contribution resulting from the extrapolation during gap filling (δdh/dt extrpl). This error term can hence be written as
We assessed the relative vertical accuracy of our TDX DEMs to SRTM on land (off glaciers, fjords, lakes) for every examined time step. For each mosaic, we provide a map to judge the spatial distribution of the error and a plot displaying the median elevation change between the respective DEMs (cf. Supplementary Materials Figure S1). This error estimation method uses a conservative approach, including more pixels than assumed to be stable in the DEM adjustment (c.f. Section 2.3). Vegetation effects, landscape changes or outliers due to inaccuracies of the signal are not eliminated a priori. Nevertheless, elevation changes exceeding 15 m were not taken into account for the calculation, as we assume this a threshold for a remaining non-stable target. Since the deviation is known to be dependent on the slope of the examined area [21,34], we provide the median calculated for each bin of 5° slope (c.f. Supplementary Materials Figure S4,). The increase in the median absolute deviation (MAD) between the compared elevation values with increasing slope remains in a range of 6 m for all mosaics for slopes ≤ 45° with the median ranging within ±1.2 m.
Equation (3) shows the calculation for each area weighted MAD (MADAw), where the area proportion of each slope bin of 5° (A slp i) is considered (with A being the entire measured area and MADslp i the respective MAD of the slope bin) This resulted in an MADAW of 3.14 for our 2000–2015 elevation change measurements corresponding to a δdh/dt vert of ±0.198 m·a−1 when divided by the mean time span of 15.86 years. In order to account for differences radar signal penetration of C- and X-band in the snow and glacier surface, we add the term of δdh/dt radar. We assume no penetration on melting surfaces up to the average ELA (1050 m cf. Section 2.3) for both frequency bands and a linear increase of up to 5 m in the highest areas. This results in an uncertainty of ±0.081 m·a−1 after area weighting.
For the error contribution of gap filling (δdh/dt extpl) using hypsometry (cf. Supplementary Materials Figure S5b) the uncertainty is given by the standard deviation in each bin. Performing again area weighting we reach a value of ±0.191 m·a−1.
Using Equation (2) the dh/dt uncertainty computes then to ±0.287 m·a−1 for the entire SPI including the interpolated areas. For the actually measured area (without interpolation) the error is ±0.214 m·a−1. For the uncertainty resulting from the glacier area determination (δA) we take a mean value of 0.6%. This value is justified since previous detailed analysis by Paul and others [35] revealed an error of 3% for alpine catchments. However, their area to perimeter ratio is much larger (5.03) than in our case (0.99) corresponding to the dominating effects of a scattered glacier coverage and long valley glaciers in contrast to a more compact icefield with outlet glaciers in our case. As a consequence, the outline error contributes much less to the overall error in our case.
Regarding volume-to-mass conversion, we adopt the density uncertainty of ±60 kg·m−3 given by Huss [27]. We apply this for each of the density scenarios.
3. Results
3.1. Elevation Changes: SPI 2000–2015/16
Figure 2 shows the elevation change rates (dh/dt) between SRTM (2000) and the mosaicked TDX acquisitions from austral summer 2015/16. The spatial pattern of changes is quite heterogeneous. The accumulation areas of most glaciers show no to slightly positive changes in elevation uniformly over the whole icefield from about 49.77° S to the southern end of the SPI. However, some glacier catchments such as Upsala, Viedma, Chico, O’Higgins, Occidental and Jorge Montt show thinning rates of up to 2 m·a−1 also in the accumulation areas. There is no marked difference between the east and west side of the icefield in this northern part of SPI. Only Pío XI Glacier shows overall balanced to slightly positive elevation changes. This catchment is also particular since the glacier is known to have advanced [36] and the positive elevation changes at the tongue (up to 8 m a−1 within the period 2000–2015/16) document this dynamic behavior. The hypsometry of Pío XI Glacier shows the largest proportion of its catchment area to be above 1000 m (Figure 2c). South of 49.7° S, almost balanced conditions exist for many glaciers including Perito Moreno and Asia glacier. These glaciers have considerable areas above 1000 m surface elevation. Perito Moreno Glacier shows a marked hypsometric minimum around 1000 m (Figure 2d). The adjacent Ameghino Glacier contrasts this pattern with considerable elevation decrease with up to −10 m·a−1. As Perito Moreno Glacier, it exhibits a bi-modal distribution of its surface elevation, but with more area below 1000 m and a second maximum around 1900 m. Glaciers at the southern end of SPI, i.e., Amalia, Tyndall and Grey glaciers, show overall negative elevation changes. While the elevation changes at the tongues of e.g., Grey, Amalia and Chico glaciers reach up to −6 to −8 m·a−1 at maximum, Tyndall and Viedma glaciers show smaller maximum lowering rates with values up to −4 m·a−1. Still, the mean elevation changes for the entire glaciers are among the most negative ones (Figure 2b and Supplementary Materials Table S2). All those glaciers have a large proportion of their catchment areas below 1000 m. Highest lowering rates are observed on glaciers HPS12, Upsala and Jorge Montt with mean elevation changes ranging from −4.3 to −3.2 m·a−1 and peak losses reaching −51, −19 and −27 m·a−1 for the mentioned glaciers, respectively. These three glaciers cover 95.4% of the area that experienced more than −10 m of elevation change per year (157.11 km2 in total). Whereas Jorge Mont Glacier does not show the most extreme minimum value, it is the glacier with the largest extent of decrease below −10 m·a−1 (94.87 km2). Those glaciers show a hypsometric distribution that hardly reaches 2000 m, with the major part below the snow line altitude.
3.2. Geodetic Mass Balance Entire SPI 2000-2015/16
Results of the geodetic glacier mass balance calculations are given in Table 2. Averaged over the entire SPI the volume loss dominates over the 16-year period. With a negative mean elevation change, the total SPI shows also a negative mass balance for all the scenarios calculated. With lower densities assumed for the accumulation area (Scenario 3), the balance becomes significantly less negative, since the area above the assumed Equilibrium Line Altitude of 1050 m is large (7258 km2) compared to the ablation area (3514 km2).
3.3. Elevation Changes: Southern SPI on Multiple Timesteps
In Figure 3 we compare different time periods for a subset of the southernmost SPI. The maps (a) and (b) reveal that the interval 2011/12–2015/16 shows positive dh/dt values in particular at higher elevations, but also on some of the glacier tongues such as at Perito Moreno. On the other hand, glacier tongues having shown negative elevation changes in 2000–2011/12 also exhibit a similar negative pattern in the 2011/12–2015/16 period. For the altitude range between 1000–2000 m the surface increased at maximum rates of 1.11 m·a−1 (2011/12–2015/16). As the area at this level is notably large it causes the overall mean elevation change of the studied southern part of the SPI to turn out positive for this period, with 0.128 ± 1.1 m·a−1. The vertical and lateral co-registration accuracy is comparable for both time intervals. It has to be noted that the image differencing 2011/12–2015/16 is based, for both years, on summer acquisitions.
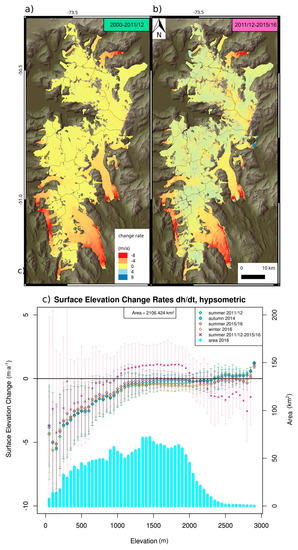
Figure 3.
Elevation changes of the southern SPI for different time periods. The maps (a,b) show the spatial pattern 2000–2011/12 and winter 2011/12–2015/16 respectively; The graph (c) illustrates the dh/dt measured by the mosaics of the different time steps 2011/12 summer, 2014 autumn, 2015/16 summer and 2016 winter with reference to SRTM (2000). The hypsometry is given as cyan bars for 50 m elevation bins while the elevation changes are plotted as mean and standard deviation of the respective time interval.
The mean elevation changes of the TDX mosaics of 2011/12 to 2015/16 in reference to SRTM (2000) and 2011/12–2015/16 (TDX-TDX) are shown as hypsometric plots in Figure 3c. The range of values for each elevation bin of 50 m is indicated by the standard deviation (sd). As described in Section 3.1 the large variability at levels below 1300 m is caused by the heterogeneous change rates at the glacier tongues (cf. sd bars). At higher altitudes theses ranges get narrower, varying at ±1 m·a−1. The change rates for the lower elevation (≤1300 m) vary less over time than higher up. Especially the areas at heights between 1300 and 2000 m show a big variance in the mean elevation change values. That is remarkable, as it represents 52% of the total glaciated area. The values for summer 2015/16 and winter 2016 delineate the upper and lower bound of the mean change rates in this elevation band. These values show seasonal differences with only about nine months temporal baseline. The two dates also reflect different surface conditions in winter and summer and hence not only elevation change, but also different signal penetration into the snow and fern cover.
4. Discussion
4.1. Elevation and Mass Changes of the Entire SPI
The proportion of 10% of total sea level rise related to mountain glaciers being associated with the South American glaciers [8] emphasizes the importance of a comprehensive discussion of glacier variations beyond our studied area and time period. Since last peak extents during Little Ice Age (LIA), glaciers of South America are reported to show a pattern of overall recession, synchronous along latitudes and with slight local fluctuations [37,38]. The depletion pattern we found all over the SPI with highest change rates at the glacier tongues reflects these findings Harrison and others [38] attributed to climate forcing for the recent study period. Nevertheless, the magnitudes differ remarkably comparing the period between the LIA to date to the last two decades: Table 3 displays results of several studies on mass balance in the region that have been carried out by different teams with different methods. The volume loss estimated by Glasser and others [39] since the LIA peak extents which we downscaled to annual rates is a magnitude lower than other listed studies. The overview accentuates the increase in volume/mass loss rates accompanying the accelerated retreat of over 90% of the glaciers over the last century [9] as well as it stresses the dominant role of the SPI in the region, reacting to recent forcing. To improve the comparability of the various studies, we have generated specific mass balances (where possible), by dividing the mass change rates by the investigated area. Our results compare well with previous studies covering a similar time interval as e.g., [7,8,40]. We cannot confirm the magnitude of the acceleration of mass change estimates for the 5-year period 1995–2000 as compared to the period 1975–2000. This acceleration was stated by Rignot and others [8] and estimated on a small subset of glaciers only. Nonetheless, it has to be considered, that those computations were done only on a comparable small sub-sample and extrapolated to the entire icefield. Our results differ from the study by Willis and others [7] since we use no penetration depth correction for the SRTM C-band data. In contrast to those authors and in line with Abdel Jaber [40,41] we consider surface melt conditions for almost the entire SPI during SRTM acquisition and hence no signal penetration. Our TDX data from the austral summer 2015/16 show similar surface conditions as the careful inspection of the SAR intensity imagery revealed. In contrast to Abdel Jaber [41] our analysis of entire SPI covers a larger time span and uses the SRTM C-Band 30 m dataset as reference in contrast to the 90 m product used in those earlier studies. We used a different processing approach as the operational TanDEM-X DEM processor of the German Aerospace Center. This, together with slight differences in glacier outlines and upscaling in unmeasured areas, explains the differences between these two studies.

Table 3.
Overview of elevation and mass change estimates for the SPI compiled from different studies. Grey background indicates values of this study. The 10.772 km2 refer to actually measured area while 12.573 km2 correspond to the value extrapolated to data gaps as described in method section.
We want to stress that our estimate is a lower bound since we did not consider mass loss due to subaqueous calving, which is larger than indicated above the sea/lake level, since calving glaciers often occupy over deepened valleys. However, only very limited information is available on the ice thickness and bathymetry in front of the glaciers. Nevertheless, this may explain partly the differences to the data retrieved from gravimetric time series of the Gravity and Climate Experiment (GRACE). Those measurements are additionally influenced by uncertainties in the estimation of the glacio-isostatic uplift (GIA) for which rates are known to be one of the highest in Patagonia in a global comparison. Recent studies report maximum uplift rates of up to 41 mm a−1 at the margin of the icefield [15,16,42]. Moreover, the GRACE measurements cover both icefield plus ice bodies to the north and south of the NPI and SPI.
The observed spatial pattern in our results is comparable to the work of Willis and others [7], although our dh/dt map is smoother. This is caused by the interferometric approach of our study while in the optical ASTER datasets cloudy pixels or correlation mismatches remain in bright areas of the accumulation areas, which might not have been filtered out sufficiently by the time series analysis. The most pronounced surface lowering rates of Jorge Montt and Upsala as well as HPS12 Glacier have been noted by previous studies as well [7,41]. Those are most likely caused by dynamic adjustments to the fast retreat of their glacier fronts. The retreat and acceleration had been reported by various authors [43,44,45,46,47]. For Upsala glacier the retreat has accelerated between 2008 and 2011 remaining stable since then [46,48,49,50]. Those glaciers show also the largest dh/dt rates despite accumulation area ratios (AAR) ranging from 0.65 to 0.7 (Supplementary Materials Table S2). Negative elevation changes are also measured on Occidental, Chico, O’Higgins, Viedma and Ameghino glaciers as well as in the very south of SPI. Occidental Glacier is also considered most sensitive to Equilibrium Line Altitude (ELA) changes by de Angelis [17], since the bulk area is located below the ELA—addressed as class C in his study. This is supported by our measured mean dh/dt rates of more than 1.5 m a−1 and an AAR of about 0.26. Our observed negative mass balance for the catchment of Chico Glacier is slightly higher than previous observations finding −0.29 ± 0.097 w.e. a−1 between 1975 and 2001 [10], which was attributed to increasing temperatures and reduced precipitation. Grey Glacier has also lost major parts of its northern and southern frontal lobe causing largest lowering rates to occur in those areas. For the main branch lowering rates are comparable to adjacent Tyndall Glacier or the low glacier tongues on the west coast e.g., Amalia Glacier. Our surface lowering rates at the tongue of Tyndall Glacier are higher than the thinning rates of 1.7 m·a−1 (1975–1985), 3.3 m·a−1 (1985–1993) and 3.6 m·a−1 (1993–2002) obtained by markers at the central part of the glaciers reported by Raymond and others [11]. Another study by Rivera and others [51] reported a similar magnitude of elevation changes, but also states maximum rates of up to 7.6 m·a−1 surface lowering at Dickson Glacier. Those patterns can most likely be explained by the hypsometry of the glaciers. First mentioned by Naruse and others [52], de Angelis [17] showed by mass balance computations, that for many of the Patagonian glaciers the Accumulation Area Ratio (AAR) and hypsometry can explain many of the observed glacier changes of SPI despite dynamic adjustments. Several studies [53,54,55] also attributed the stability of Perito Moreno Glacier partly to this, since the equilibrium line is located in a steep area and hence a shift does not affect large areas as e.g., on flat areas or glaciers with a primarily low elevation distribution such as Upsala [55]. De Angelis referred to this as the location of the bulge in the hypsometric profile [17]. For most of the intermediate sensitive glaciers to changes in ELA he observed a bi- or multi-modal hypsometric distribution with the ELA between peaks (class E) or uni-modal distribution with the bulge at the ELA (class D). This also explains the considerable larger surface lowering rates at Ameghino Glacier in close vicinity to Perito Moreno Glacier, since its hypsometry shows a considerably larger proportion below the ELA in addition to differences in the calving and basal melt [56,57]. A large proportion of the SPI glaciers show almost balanced or slightly positive elevation changes. Pio XI glacier has the second largest positive geodetic mass balances. This is in accordance with de Angelis, who contested for this class of glacier having the bulk area above the ELA (class B) and low sensitivity towards ELA changes [17]. The advance of Pío XI Glacier has been described in previous studies and attributed to a surge or possibly triggered by geothermal activity [58,59]. However, our results do not show a clear source area from where the mass would have been transported down-glacier in a surge causing the advance and thickening of the tongue. Such a pattern was observed at many other surging glaciers e.g., in the Karakoram or western Himalaya [21,22]. In contrast, the potential source area in the accumulation zone shows positive elevation change rates as do many other glaciers on the west coast of the SPI. Minowa and others [56] already proposed that the geometry and pinning points of the glacier tongue may also be relevant to explain the observed advance. This agrees with the interpretation by de Angelis stating that his class B glaciers have long and narrow tongues that are nourished by a large high elevation accumulation area [17]. It may hence be speculated that continuous positive surface mass balances together with the particular glacier geometry may be responsible for the observed dh/dt pattern of Pío XI rather than surging or geothermal activity in the accumulation area (e.g., reported by [60]).
4.2. Elevation Changes: Southern SPI on Multiple Timesteps
Glaciers of the southernmost end of the SPI show a positive elevation change rate for the years 2011/12–2015/16. In Section 3.3 we emphasized the role of the accumulation area, with its overly proportional size and a positive change rate. The positive change rates of <1 m·a−1 relate to ~4 m of actual surface rise over the 3 years. Already the dh/dt measurements of autumn 2014 indicate more positive accumulation rates. We assume that heavy snowfall events in winters 2014 and 2015 have caused this increase. We cannot confirm such anomalous high precipitation events by observations, since there are no measurements available. However, it is known that the westerlies have become more intense in southern Patagonia in recent years, resulting in enhanced precipitation, driven by the orographic effect across the Andes [1]. This is a possible explanation of the measured positive elevation changes up to about 2000 m. Another aspect to explain the differences in the accumulation area (>2000 m) is differences in radar signal penetration. Mätzler and Schanda [68] showed that the signal penetration into snow/fern covers depends on the grain size and surface wetness. Liquid water limits the signal penetration to the first centimeters. The depth of the scattering phase centers of a radar wave in a frozen, stratified fern cover formed during wet snow metamorphosis on the SPI may differ from season to season. Hence, the pronounced drop of the 2011/12–2015/16 mean dh/dt line (Figure 3c) in regions >2000 m might also be partially attributed to this influence. The winter 2016 data also shows higher negative elevation changes rates in elevations >1500 m, which can also be attributed to stronger signal penetration during winter conditions. The effect and visibility are partly reduced since the differencing was done over a 16-year period. This clearly shows the relevance to consider appropriate image acquisitions for radar elevation change measurements. In the case of SPI, summer conditions prove most suitable since wet snow conditions probably prevailed over most of the glaciated area.
5. Conclusions
Our results confirm the large mass loss from the Southern Patagonian Icefield. Our estimates are slightly smaller than given in several previous studies. This might be attributed to the fact that in recent years the orographically-driven precipitation due to enhanced westerly flow has also increased [1]. We cannot observe an increase in mass loss rates compared to earlier studies since the 1970s, however we confirm the increase by one magnitude of mass loss since the Little Ice Age. We provide a lower bound estimate, since we did not consider volume and mass changes resulting from the subaqueous loss of retreating tidewater and freshwater calving glaciers. Due to the lack of respective information on ice thickness in those areas estimates would be hardly reliable. We also provide computations for different density scenarios for volume-mass conversion in order to enable direct comparison with previous studies.
The spatially detailed analysis shows a very heterogeneous pattern of glacier elevation changes. While some glaciers such as Jorge Montt, Upsala or HPS12 show very high lowering rates mainly driven by dynamic adjustment to the new glacier front position after fast retreat, other major glaciers such as Perito Moreno or Europa have remained roughly balanced. Our analysis is in line with a previous study considering hypsometry as a major factor to explain the sensitivity of SPI glaciers to change in equilibrium line altitude. Pío XI still shows a positive mass balance with a thickening of the glacier tongue by several meters per year on average. Our observations do not reveal indications for a surge-type behavior of this glacier, but rather support an explanation of continuous mass gain in conjunction with the specific glacier geometry. This illustrates that various factors have to be taken into account to explain the impact and reaction of glaciers of the SPI.
Our multi-temporal analysis reveals that bi-static TanDEM-X synthetic aperture radar imagery is highly suitable to study glacier volume changes over large regions, in a semi-operational way and in frequently cloudy regions such as Fuego-Patagonia. Even shorter time periods of 2–3 years can be used for balancing if image pairs with favorable acquisition conditions are available. Uncertainties and limitations (in particular for short temporal baselines) arise from the unknown radar penetration in frozen fern and snow. It is, therefore, recommended that regular acquisitions be carried out over fast changing regions such as glaciers and that the timing of acquisitions is coordinated according to previously available data or reference data sets, preferentially to the peak of summer melting conditions. More specifically dedicated research on radar signal penetration under different surface conditions and fern/snow structures are required in order to further reduce these uncertainties.
Supplementary Materials
The following are available online at http://www.mdpi.com/2072-4292/10/2/188/s1, Figure S1: Distribution of elevation changes on off-glacier areas for the different mosaics. The panels show the absolute changes for the timesteps of (a) summer 2015/16 (b) summer 2012 (c) autumn 2014 and (d) winter 2015/16, Figure S2: Every Scene as shown in Figure S1 is horizontally co-registered following Nuth and Kääb [24]. (a) Curve fit of scene 3 (summer 2012) for the first of 6 iterative steps to horizontally align the respective TDX to the reference SRTM dataset. Colored lines visualize the fitted function parameters (formula at plots bottom): beige vertical is angular offset, blue horizontal: amplitude, green horizontal: oscillation center. (b) Histogram showing the improvement of dh offset on non-glaciated ground during the coregistration steps, Figure S3: Scene on Tyndall glacier showing dataset before (left) and after filtering (right). The filter cuts out disproportionately high (low) values in relation to its surrounding, Figure S4: Off-ice elevation changes for different slope bins. Grey bars indicate the area covered while the blue diamonds refer to the median elevation change off ice. Median absolute deviations of elevation changes are given as blue bars. Area weighted mean absolute deviations: (a) 2.85 m (b) 2.80 m (c) 3.14 m (d) 3.22 m, Figure S5: (a) Cyan showing coverage of SRTM and TDX data for dh/dt differencing and data gaps to extrapolate for in the inventory. (b) hypsometric area distribution; colors similar to a, diamonds and bars draw mean dh/dt and respective sd for each altitudinal bin, Table S1: List of Landsat scenes used for semiautomatic outline mapping, Table S2: Mean glacier elevation change 2000–2015/16 for various SPI glaciers. ELA, AAR and type are taken from DeAngelis [1], as is Area except for 1: Upsala was summed up with tributaries Cono and Bertachi (not listed).Unnamed glaciers in [1] where named with corresponding RGI-ID through spatial join with our RGI-based inventory.
Acknowledgments
This study was financially supported by the German Ministry of Science and Education (BMBF) under contract 01 DN 15020 as well as the German Research Foundation (DFG) in the Priority Program 1889 “Regional Sea Level Change and Society in the project SATELLITE (BR 2105/14-1). Methodological developments and coding for TanDEM-X data processing have been done under DLR/BMWi project TanDEM-ICE (50 EE 1414) and the HGF-EDA Alliance Remote Sensing and Earth System Dynamics. The authors would like to thank the German Aerospace Center for providing TanDEM-X data free of charge under AO XTI_GLAC0264. Landsat data was kindly provided via USGS Earth Explorer.
Author Contributions
Philipp Malz processed all TanDEM-X data, performed the subsequent analysis and wrote the manuscript. Wolfgang Meier provided outline changes derived from Landsat data. Matthias Braun initiated and supervised the study and wrote jointly with Philipp Malz the manuscript. Ricardo Jaña., Gino Casassa and Pedro Skvarca support field studies. All authors contributed to the discussion of results and revised the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Garreaud, R.; Lopez, P.; Minvielle, M.; Rojas, M. Large-Scale Control on the Patagonian Climate. J. Clim. 2013, 26, 215–230. [Google Scholar] [CrossRef]
- Lliboutry, L. Nieves y glaciares de Chile: Fundamentos de glaciologia; Ediciones de la Universidad de Chile; Universidad de Chile: Santiago, RM, Chile, 1956. [Google Scholar]
- Naruse, R.; Aniya, M. Outline of Glacier Research Project in Patagonia, 1990. Bull. Glacier Res. 1992, 10, 31–38. [Google Scholar]
- Aniya, M.; Sato, H.; Naruse, R.; Skvarca, P.; Casassa, G. The use of satellite and airborne imagery to inventory outlet glaciers of the Southern Patagonia Icefield, South America. Photogramm. Eng. Remote Sens. 1996, 62, 1361–1369. [Google Scholar]
- Casassa, G.; Rodríguez, J.L.; Loriaux, T. A New Glacier Inventory for the Southern Patagonia Icefield and Areal Changes 1986–2000. In Global Land Ice Measurements from Space; Kargel, J.S.S., Leonard, G.J.J., Bishop, M.P.P., Kääb, A., Raup, B.H.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 639–660. ISBN 978-3-540-79818-7. [Google Scholar]
- Aniya, M. Recent Glacier Variations of the Hielos Patagónicos, South America, and Their Contribution to Sea-Level Change. Arct. Antarct. Alp. Res. 1999, 31, 165–173. [Google Scholar] [CrossRef]
- Willis, M.J.; Melkonian, A.K.; Pritchard, M.E.; Rivera, A. Ice loss from the Southern Patagonian Ice Field, South America, between 2000 and 2012. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Rignot, E.; Rivera, A.; Casassa, G. Contribution of the Patagonia Icefields of South America to sea level rise. Science 2003, 302, 434–437. [Google Scholar] [CrossRef] [PubMed]
- Davies, B.J.; Glasser, N.F. Accelerating shrinkage of Patagonian glaciers from the Little Ice Age (∼AD 1870) to 2011. J. Glaciol. 2012, 58, 1063–1084. [Google Scholar] [CrossRef]
- Rivera, A.; Casassa, G.; Bamber, J.; Kääb, A. Ice-elevation changes of Glaciar Chico, southern Patagonia, using ASTER DEMs, aerial photographs and GPS data. J. Glaciol. 2005, 51, 105–112. [Google Scholar] [CrossRef]
- Raymond, C.; Neumann, T.A.; Rignot, E.; Echelmeyer, K.; Rivera, A.; Casassa, G. Retreat of Glaciar Tyndall, Patagonia, over the last half-century. J. Glaciol. 2005, 51, 239–247. [Google Scholar] [CrossRef]
- Casassa, G.; Rivera, A.; Schwikowski, M. Glacier Mass-Balance Data For Southern South America (30°S-56°S). In Glacier Science and Environmental Change; Knight, P.G.G., Ed.; Blackwell Publishing: Malden, MA, USA, 2006; pp. 239–241. ISBN 978-0-470-75063-6. [Google Scholar]
- Schaefer, M.; Machguth, H.; Falvey, M.; Casassa, G.; Rignot, E. Quantifying mass balance processes on the Southern Patagonia Icefield. Cryosphere 2015, 9, 25–35. [Google Scholar] [CrossRef]
- Mernild, S.H.; Liston, G.E.; Hiemstra, C.; Wilson, R. The Andes Cordillera. Part III: Glacier surface mass balance and contribution to sea level rise (1979–2014): Glacier Surface Mass Balance and Contribution to Sea Level Rise. Int. J. Climatol. 2017, 37, 3154–3174. [Google Scholar] [CrossRef]
- Richter, A.; Ivins, E.; Lange, H.; Mendoza, L.; Schröder, L.; Hormaechea, J.L.; Casassa, G.; Marderwald, E.; Fritsche, M.; Perdomo, R.; et al. Crustal deformation across the Southern Patagonian Icefield observed by GNSS. Earth Planet. Sci. Lett. 2016, 452, 206–215. [Google Scholar] [CrossRef]
- Dietrich, R.; Ivins, E.R.; Casassa, G.; Lange, H.; Wendt, J.; Fritsche, M. Rapid crustal uplift in Patagonia due to enhanced ice loss. Earth Planet. Sci. Lett. 2010, 289, 22–29. [Google Scholar] [CrossRef]
- De Angelis, H. Hypsometry and sensitivity of the mass balance to changes in equilibrium-line altitude: The case of the Southern Patagonia Icefield. J. Glaciol. 2014, 60, 14–28. [Google Scholar] [CrossRef]
- Hoffmann, J.; Walter, D. How complementary are SRTM-X and-C band digital elevation models? Photogramm. Eng. Remote Sens. 2006, 72, 261–268. [Google Scholar] [CrossRef]
- Zink, M.; Bartusch, M.; Miller, D. TanDEM-X mission status. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24–29 July 2011; pp. 2290–2293. [Google Scholar]
- Pfeffer, W.T.; Arendt, A.A.; Bliss, A.; Bolch, T.; Cogley, J.G.; Gardner, A.S.; Hagen, J.-O.; Hock, R.; Kaser, G.; Kienholz, C.; et al. The Randolph Glacier Inventory: A globally complete inventory of glaciers. J. Glaciol. 2014, 60, 537–552. [Google Scholar] [CrossRef]
- Vijay, S.; Braun, M. Elevation Change Rates of Glaciers in the Lahaul-Spiti (Western Himalaya, India) during 2000–2012 and 2012–2013. Remote Sens. 2016, 8, 1038. [Google Scholar] [CrossRef]
- Rankl, M.; Braun, M. Glacier elevation and mass changes over the central Karakoram region estimated from TanDEM-X and SRTM/X-SAR digital elevation models. Ann. Glaciol. 2016, 57, 273–281. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Werner, C.L. Radar interferogram filtering for geophysical applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hiramatsu, A.; Hiramatsu, A. Two-Dimensional Phase Unwrapping fo SAR Interferograms by Charge Connection Through Neutral Trees; Caltech/ JPL: Pasadena, CA, USA, 1994. Available online: https://trs.jpl.nasa.gov/handle/2014/36655 (accessed on 20 January 2018).
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Nuth, C.; Kääb, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef]
- Huss, M. Density assumptions for converting geodetic glacier volume change to mass change. Cryosphere 2013, 7, 877–887. [Google Scholar] [CrossRef]
- Kääb, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Winsvold, S.H.; Andreassen, L.M.; Kienholz, C. Glacier area and length changes in Norway from repeat inventories. Cryosphere 2014, 8, 1885–1903. [Google Scholar] [CrossRef]
- Andreassen, L.M.; Paul, F.; Kääb, A.; Hausberg, J.E. Landsat-derived glacier inventory for Jotunheimen, Norway, and deduced glacier changes since the 1930s. Cryosphere 2008, 2, 131–145. [Google Scholar] [CrossRef]
- Falaschi, D.; Bravo, C.; Masiokas, M.; Villalba, R.; Rivera, A. First Glacier Inventory and Recent Changes in Glacier Area in the Monte San Lorenzo Region (47°S), Southern Patagonian Andes, South America. Arct. Antarct. Alp. Res. 2013, 45, 19–28. [Google Scholar] [CrossRef]
- Paul, F.; Andreassen, L.M. A new glacier inventory for the Svartisen region, Norway, from Landsat ETM+ data: Challenges and change assessment. J. Glaciol. 2009, 55, 607–618. [Google Scholar] [CrossRef]
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef] [PubMed]
- Gardelle, J.; Berthier, E.; Arnaud, Y. Impact of resolution and radar penetration on glacier elevation changes computed from DEM differencing. J. Glaciol. 2012, 58, 419–422. [Google Scholar] [CrossRef]
- Paul, F.; Barrand, N.E.; Baumann, S.; Berthier, E.; Bolch, T.; Casey, K.; Frey, H.; Joshi, S.P.; Konovalov, V.; Bris, R.L.; et al. On the accuracy of glacier outlines derived from remote-sensing data. Ann. Glaciol. 2013, 54, 171–182. [Google Scholar] [CrossRef]
- Muto, M.; Furuya, M. Surface velocities and ice-front positions of eight major glaciers in the Southern Patagonian Ice Field, South America, from 2002 to 2011. Remote Sens. Environ. 2013, 139, 50–59. [Google Scholar] [CrossRef]
- Masiokas, M.H.; Rivera, A.; Espizua, L.E.; Villalba, R.; Delgado, S.; Aravena, J.C. Glacier fluctuations in extratropical South America during the past 1000 years. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2009, 281, 242–268. [Google Scholar] [CrossRef]
- Harrison, S.; Winchester, V.; Glasser, N. The timing and nature of recession of outlet glaciers of Hielo Patagónico Norte, Chile, from their Neoglacial IV (Little Ice Age) maximum positions. Glob. Planet. Chang. 2007, 59, 67–78. [Google Scholar] [CrossRef]
- Glasser, N.F.; Harrison, S.; Jansson, K.N.; Anderson, K.; Cowley, A. Global sea-level contribution from the Patagonian Icefields since the Little Ice Age maximum. Nat. Geosci. 2011, 4, 303–307. [Google Scholar] [CrossRef]
- Abdel Jaber, W. Derivation of Mass Balance and Surface Velocity of Glaciers by Means of High Resolution Synthetic Aperture Radar: Application to the Patagonian Icefields and Antarctica. DLR-Forschungsbericht: ISBN 1434-8454. Available online: http://elib.dlr.de/109075/1/Thesis_AbdelJaber_final.pdf (accessed on 1 November 2017).
- Jaber, W.A.; Floricioiu, D.; Rott, H.; Eineder, M. Surface elevation changes of glaciers derived from SRTM and TanDEM-X DEM differences. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, VIC, Australia, 21–26 July 2013; pp. 1893–1896. [Google Scholar]
- Lange, H.; Casassa, G.; Ivins, E.R.; Schröder, L.; Fritsche, M.; Richter, A.; Groh, A.; Dietrich, R. Observed crustal uplift near the Southern Patagonian Icefield constrains improved viscoelastic Earth models. Geophys. Res. Lett. 2014, 41, 805–812. [Google Scholar] [CrossRef]
- Mouginot, J.; Rignot, E. Ice motion of the Patagonian Icefields of South America: 1984–2014. Geophys. Res. Lett. 2015, 42, 2014GL062661. [Google Scholar] [CrossRef]
- Sakakibara, D.; Sugiyama, S.; Sawagaki, T.; Marinsek, S.; Skvarca, P. Rapid retreat, acceleration and thinning of Glaciar Upsala, Southern Patagonia Icefield, initiated in 2008. Ann. Glaciol. 2013, 54, 131–138. [Google Scholar] [CrossRef]
- Sakakibara, D.; Sugiyama, S. Ice-front variations and speed changes of calving glaciers in the Southern Patagonia Icefield from 1984 to 2011: Calving glaciers in southern Patagonia. J. Geophys. Res. Earth Surf. 2014, 119, 2541–2554. [Google Scholar] [CrossRef]
- Floricioiu, D.; Eineder, M.; Rott, H.; Yague-Martinez, N.; Nagler, T. Surface Velocity and Variations of Outlet Glaciers of the Patagonia Icerfields by Means of TerraSAR-X. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Jaber, W.A.; Floricioiu, D.; Rott, H.; Eineder, M. Dynamics of fast glaciers in the Patagonia Icefields derived from TerraSAR-X and TanDEM-X data. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 3226–3229. [Google Scholar]
- Skvarca, P.; De Angelis, H.; Naruse, R.; Warren, C.R.; Aniy, M. Calving rates in fresh water: New data from southern Patagonia. Ann. Glaciol. 2002, 34, 379–384. [Google Scholar] [CrossRef]
- Skvarca, P.; Raup, B.; De Angelis, H. Recent behaviour of Glaciar Upsala, a fast-flowing calving glacier in Lago Argentino, southern Patagonia. Ann. Glaciol. 2003, 36, 186–188. [Google Scholar] [CrossRef]
- Sugiyama, S.; Minowa, M.; Sakakibara, D.; Skvarca, P.; Sawagaki, T.; Ohashi, Y.; Naito, N.; Chikita, K. Thermal structure of proglacial lakes in Patagonia. J. Geophys. Res. Earth Surf. 2016, 121, 2270–2286. [Google Scholar] [CrossRef]
- Rivera, A.; Casassa, G. Ice Elevation, Areal, and Frontal Changes of Glaciers from National Park Torres del Paine, Southern Patagonia Icefield. Arct. Antarct. Alp. Res. 2004, 36, 379–389. [Google Scholar] [CrossRef]
- Naruse, R.; Aniya, M.; Skvarca, P. Gino Casassa Recent variations of calving glaciers in Patagonia, South America, revealed by ground surveys, satellite-data analyses and numerical experiments. Ann. Glaciol. 1995, 21, 297–303. [Google Scholar] [CrossRef]
- Rott, H.; Stuefer, M.; Siegel, A.; Skvarca, P.; Eckstaller, A. Mass fluxes and dynamics of Moreno Glacier, Southern Patagonia Icefield. Geophys. Res. Lett. 1998, 25, 1407–1410. [Google Scholar] [CrossRef]
- Stuefer, M.; Rott, H.; Skvarca, P. Glaciar Perito Moreno, Patagonia: Climate sensitivities and glacier characteristics preceding the 2003/04 and 2005/06 damming events. J. Glaciol. 2007, 53, 3–16. [Google Scholar] [CrossRef]
- Aniya, M.; Skvarca, P. Characteristics and variations of Upsala and Moreno glaciers, southern Patagonia. Bull. Glacier Res. 1992, 10, 39–53. [Google Scholar]
- Minowa, M.; Sugiyama, S.; Sakakibara, D.; Sawagaki, T. Contrasting glacier variations of Glaciar Perito Moreno and Glaciar Ameghino, Southern Patagonia Icefield. Ann. Glaciol. 2015, 56, 26–32. [Google Scholar] [CrossRef]
- Minowa, M.; Sugiyama, S.; Sakakibara, D.; Skvarca, P. Seasonal Variations in Ice-Front Position Controlled by Frontal Ablation at Glaciar Perito Moreno, the Southern Patagonia Icefield. Front. Earth Sci. 2017, 5, 1–15. [Google Scholar] [CrossRef]
- Warren, C.R.; Rivera, A.; Post, A. Greatest Holocene advance of Glaciar PIO XI, Chilean Patagonia: Possible causes. Ann. Glaciol. 1997, 24, 11–15. [Google Scholar] [CrossRef]
- Rivera, A.; Casassa, G. Volume changes on Pio XI glacier, Patagonia: 1975–1995. Glob. Planet. Chang. 1999, 22, 233–244. [Google Scholar] [CrossRef]
- Motoki, A.; Orihashi, Y.; Naranjo, J.A.; Hirata, D.; Skvarca, P.; Anma, R. Geologic reconnaissance of Lautaro Volcano, Chilean Patagonia. Rev. Geol. Chile 2006, 33, 177–187. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.; Pfeffer, W.T.; Swenson, S. Recent contributions of glaciers and ice caps to sea level rise. Nature 2012, 482, 514–518. [Google Scholar] [CrossRef] [PubMed]
- Vaughan, D.G.; Comiso, J.C.; Allison, I.; Carrasco, J.; Kaser, G.; Kwok, R.; Mote, P.; Murray, T.; Paul, F.; Ren, J.; et al. Observations: Cryosphere. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M.B., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A Reconciled Estimate of Glacier Contributions to Sea Level Rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef] [PubMed]
- Ivins, E.R.; Watkins, M.M.; Yuan, D.N.; Dietrich, R.; Casassa, G.; Rulke, A. On-land ice loss and glacial isostatic adjustment at the Drake Passage: 2003–2009. J. Geophys. Res.-Solid Earth 2011, 116, 1–24. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D.; Blankenship, D.D.; Ivins, E.R. Patagonia icefield melting observed by gravity recovery and climate experiment (GRACE). Geophys. Res. Lett. 2007, 34, 1–6. [Google Scholar] [CrossRef]
- Willis, M.J.; Melkonian, A.K.; Pritchard, M.E.; Ramage, J.M. Ice loss rates at the Northern Patagonian Icefield derived using a decade of satellite remote sensing. Remote Sens. Environ. 2012, 117, 184–198. [Google Scholar] [CrossRef]
- Melkonian, A.K.; Willis, M.J.; Pritchard, M.E.; Rivera, A.; Bown, F.; Bernstein, S.A. Satellite-derived volume loss rates and glacier speeds for the Cordillera Darwin Icefield, Chile. Cryosphere 2013, 7, 823–839. [Google Scholar] [CrossRef]
- Mätzler, C.; Schanda, E. Snow mapping with active microwave sensors. Int. J. Remote Sens. 1984, 5, 409–422. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).