Monitoring Crop Evapotranspiration and Crop Coefficients over an Almond and Pistachio Orchard Throughout Remote Sensing
Abstract
1. Introduction
2. Materials and Methods
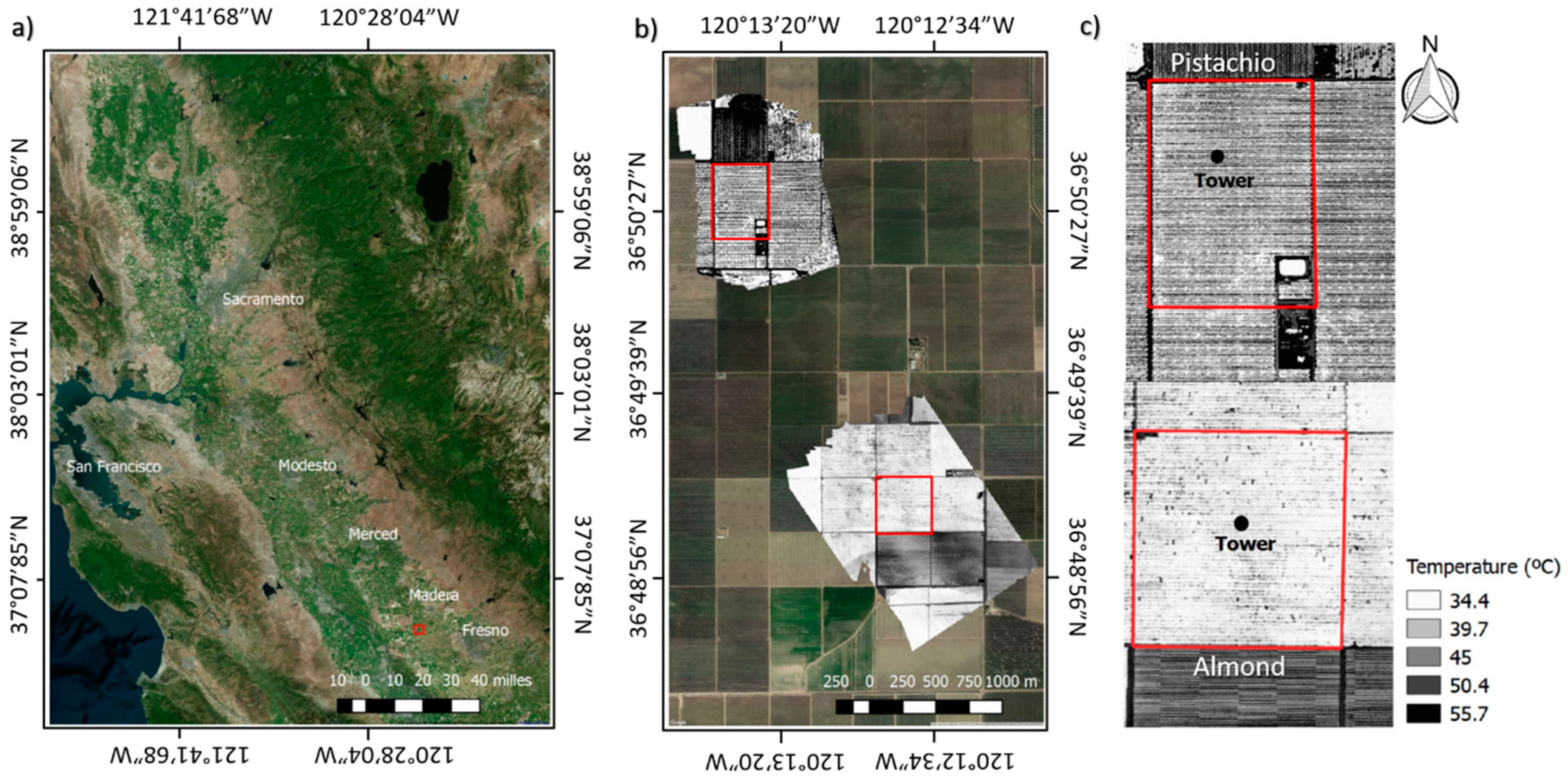
2.1. Study Site
2.2. Field Data
2.3. Remote Sensing Data
2.4. Evapotranspiration Measurements
2.5. Estimates of Actual Crop Evapotranspiration (ETa) and Coefficients
3. Results and Discussion
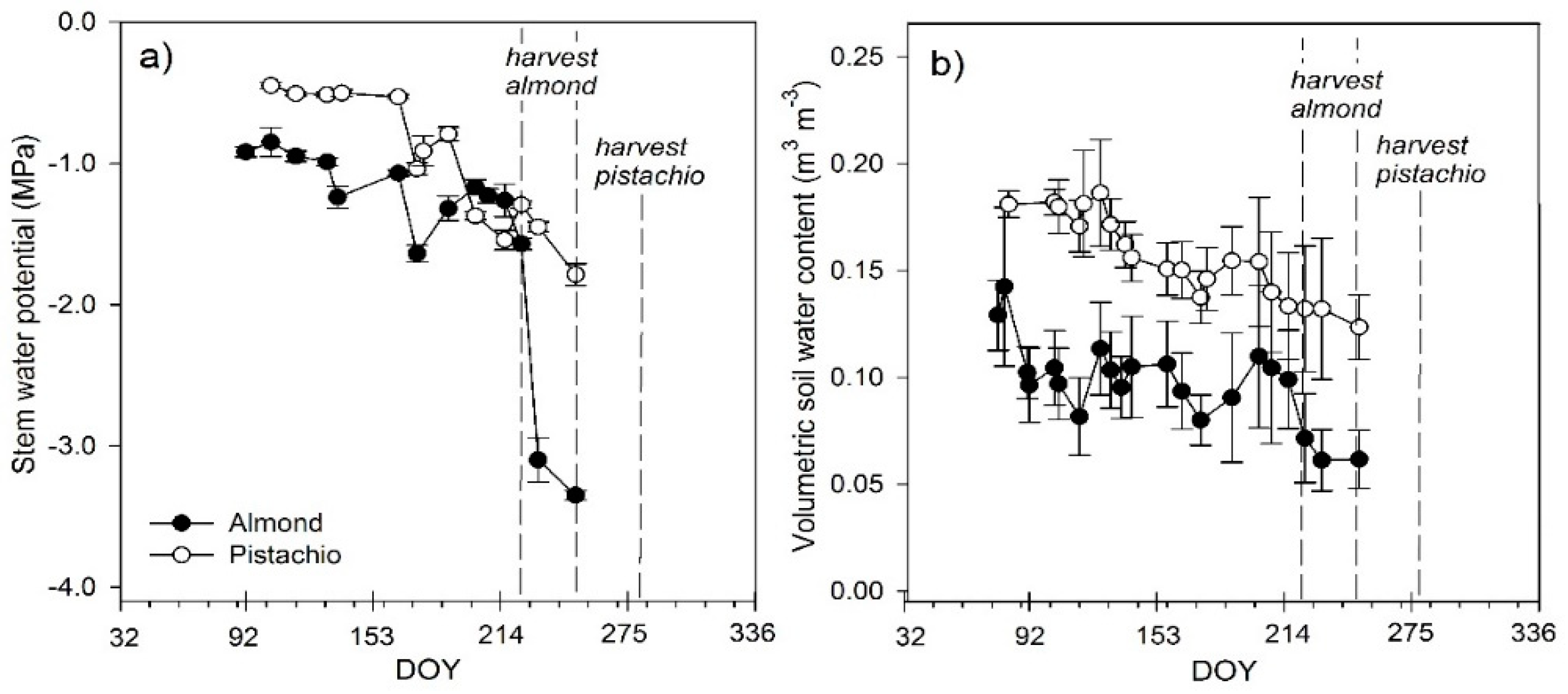
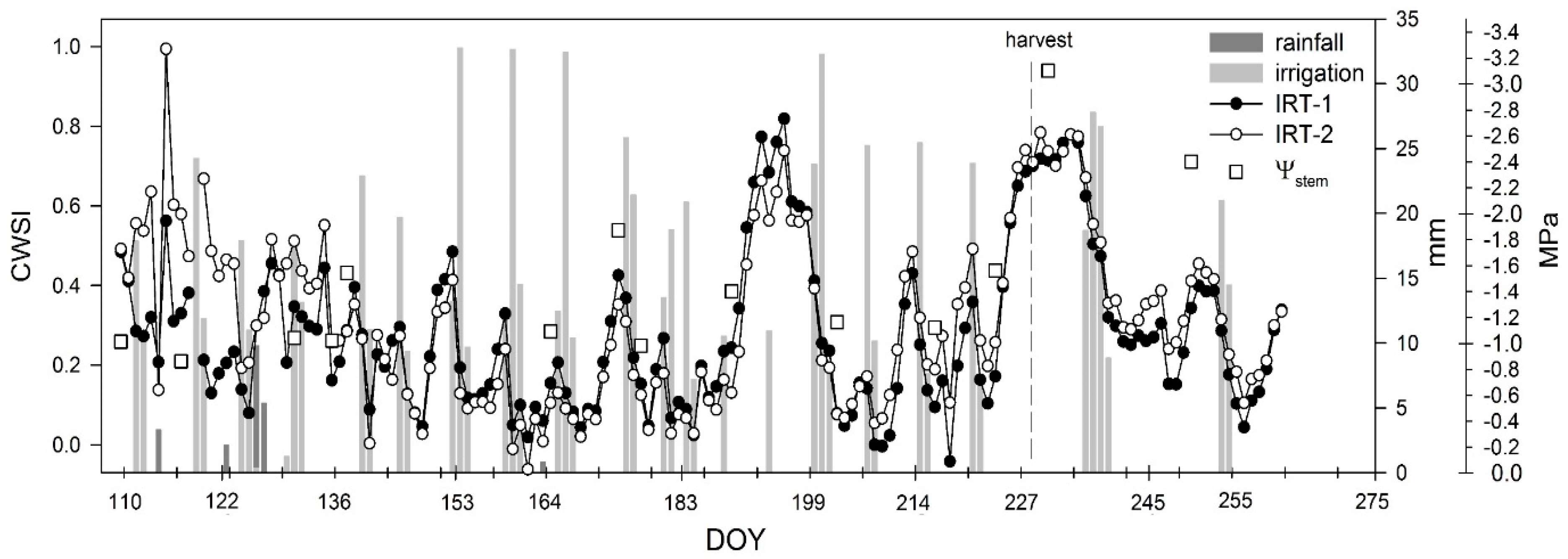
3.1. Stem Water Potential and Volumetric Soil Water Content
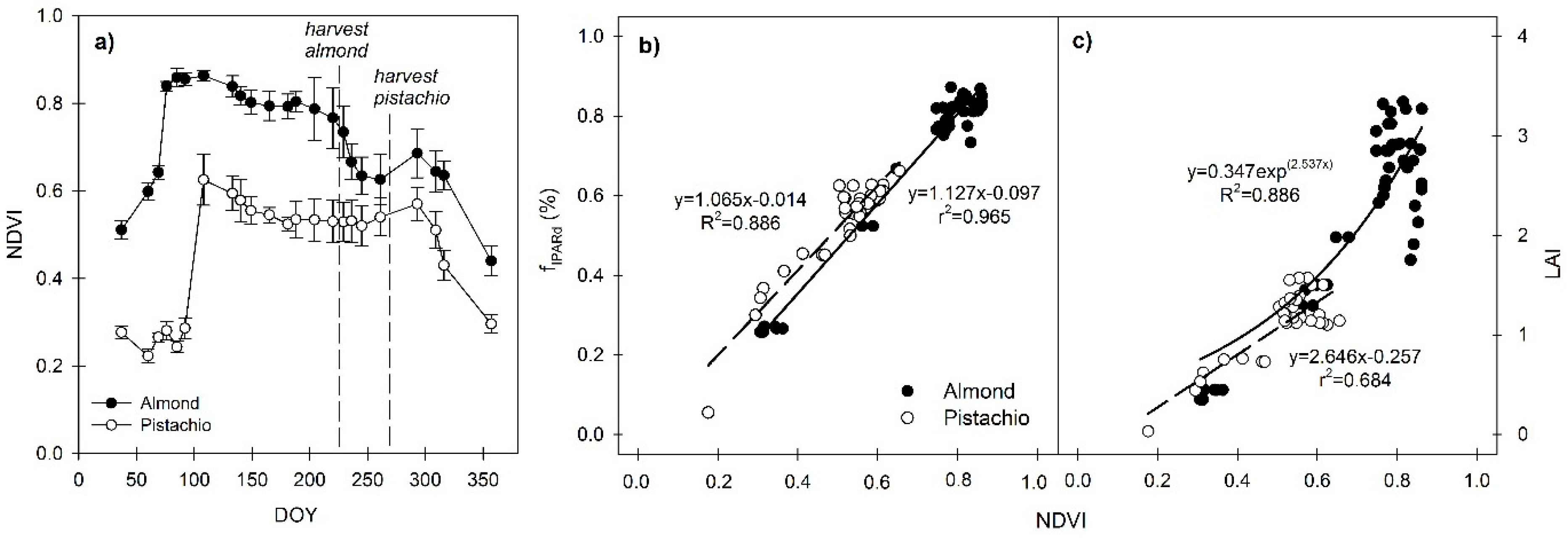
3.2. Seasonal Trends of NDVI
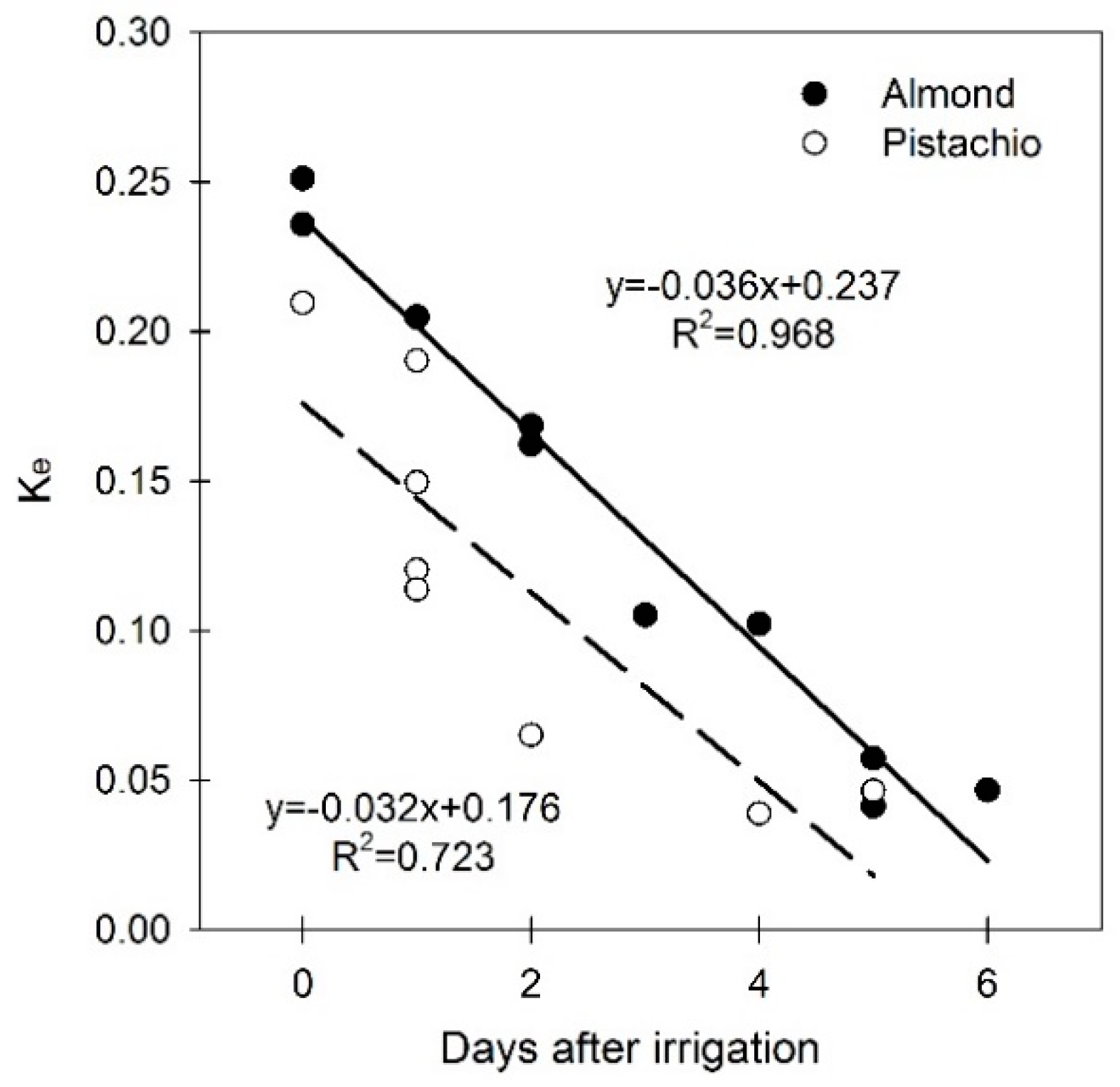
3.3. Soil Water Evaporation Coefficient (Ke)
3.4. Crop Water Stress Index (CWSI)
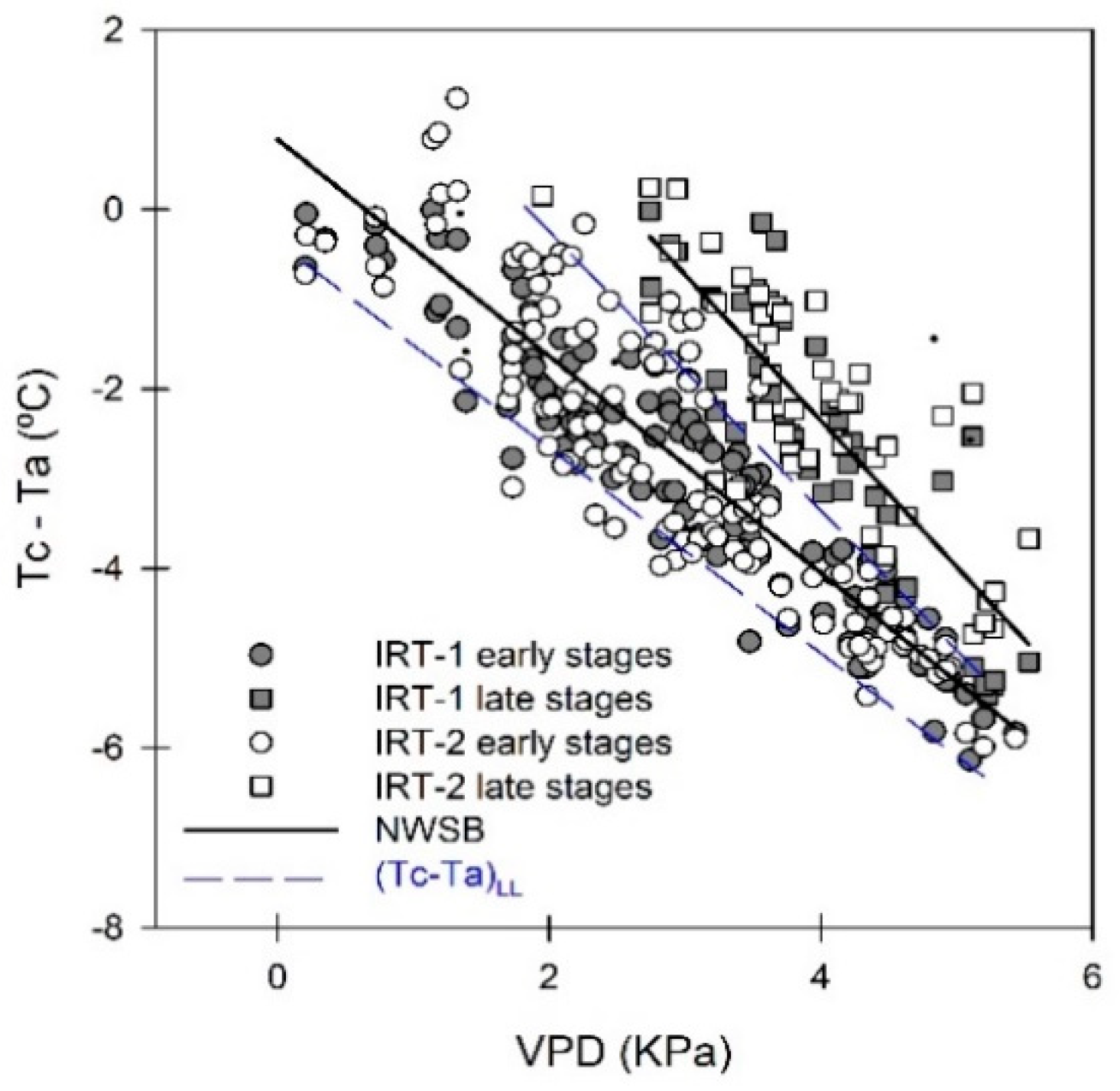
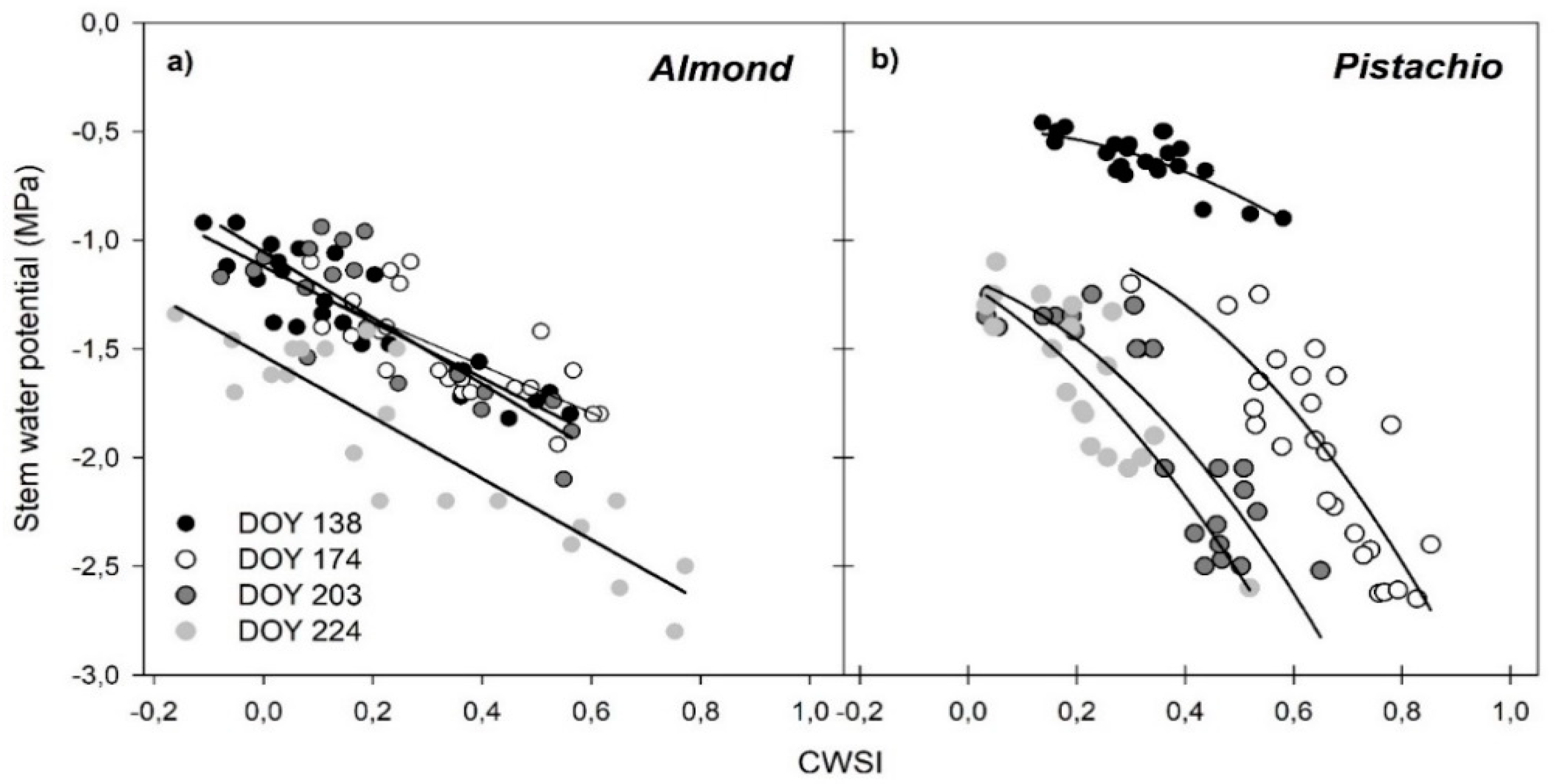
3.5. Regressions of Remotely Sensed CWSI with Stem Water Potential (Ψstem)
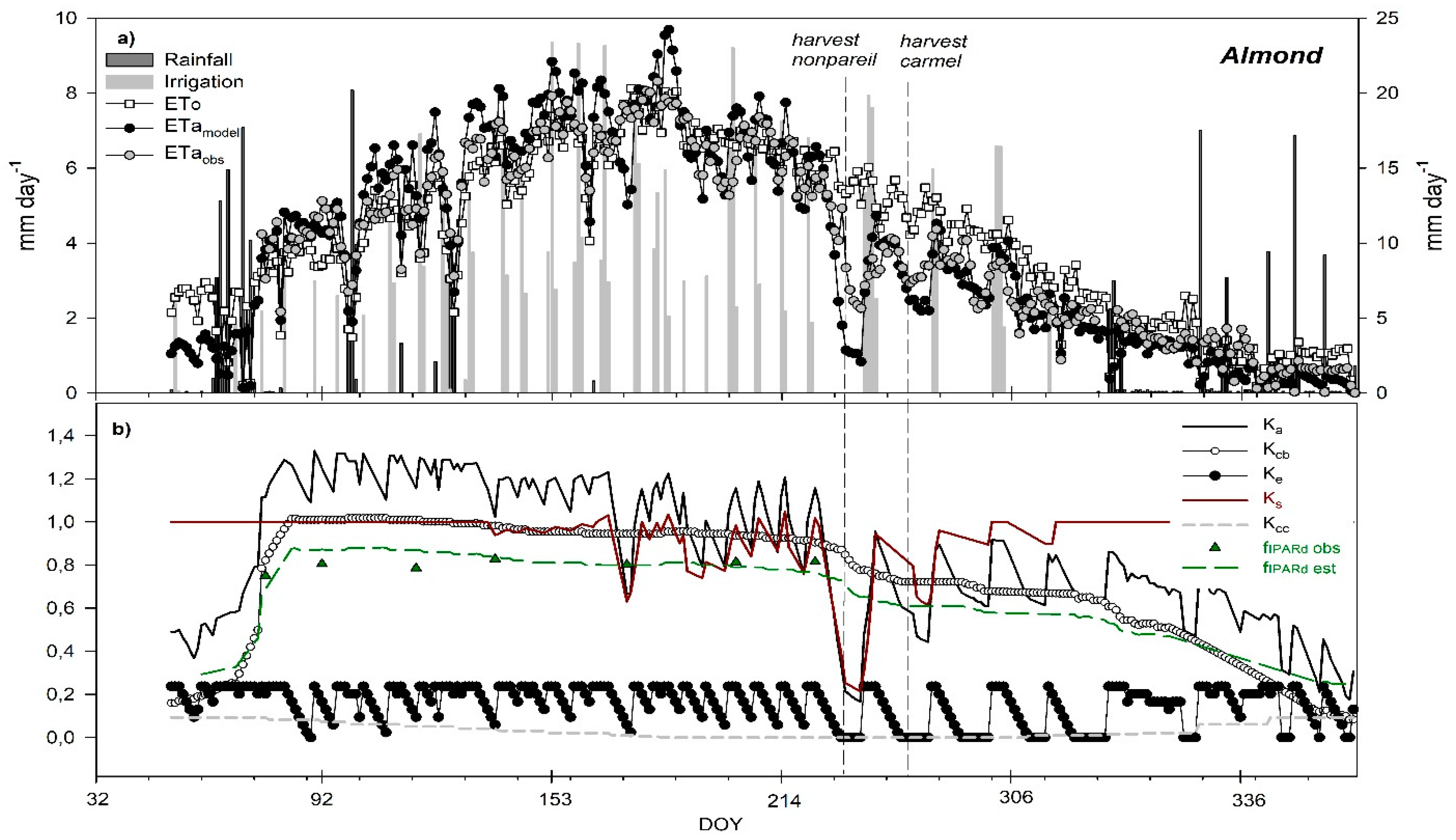
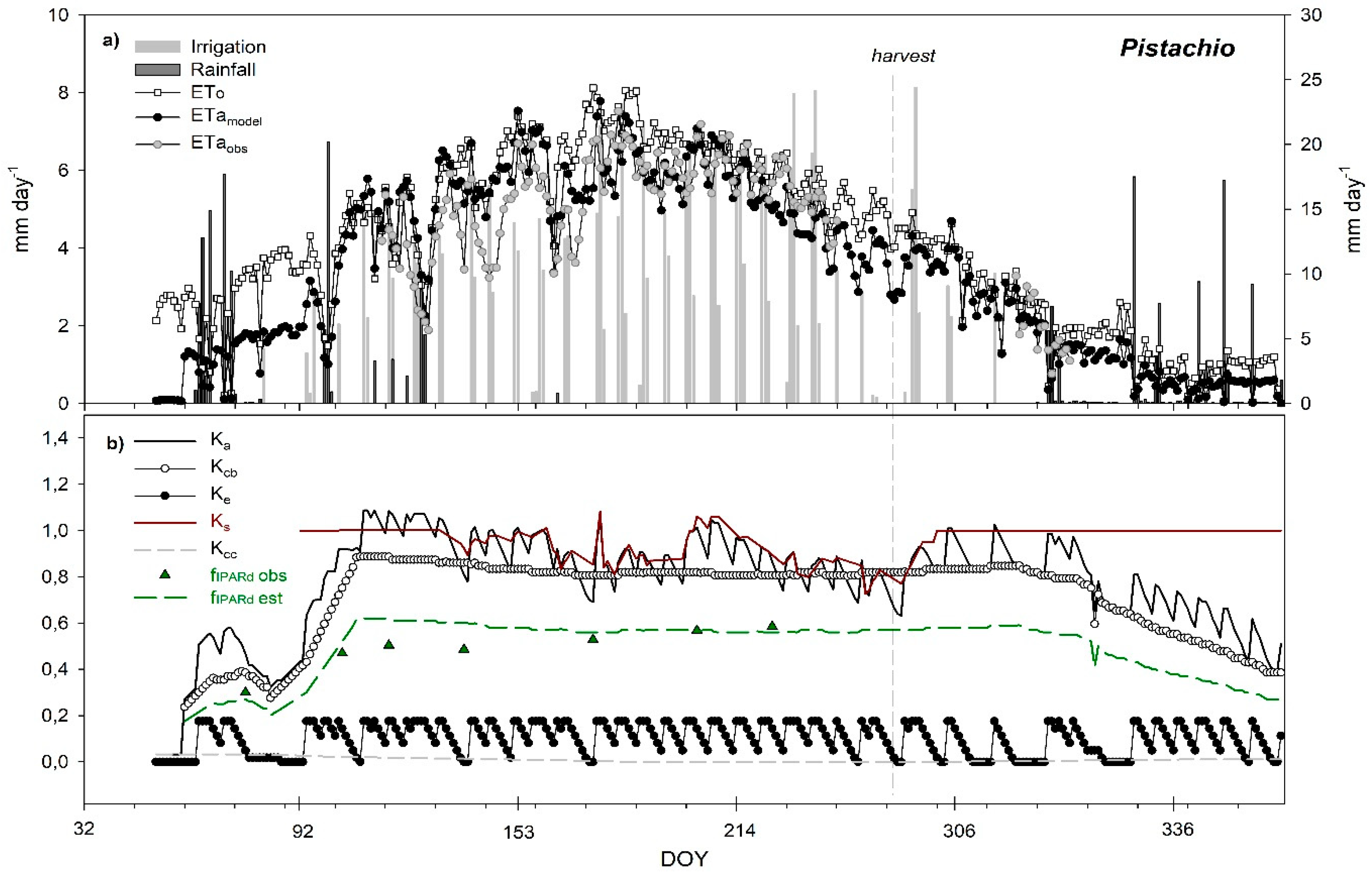
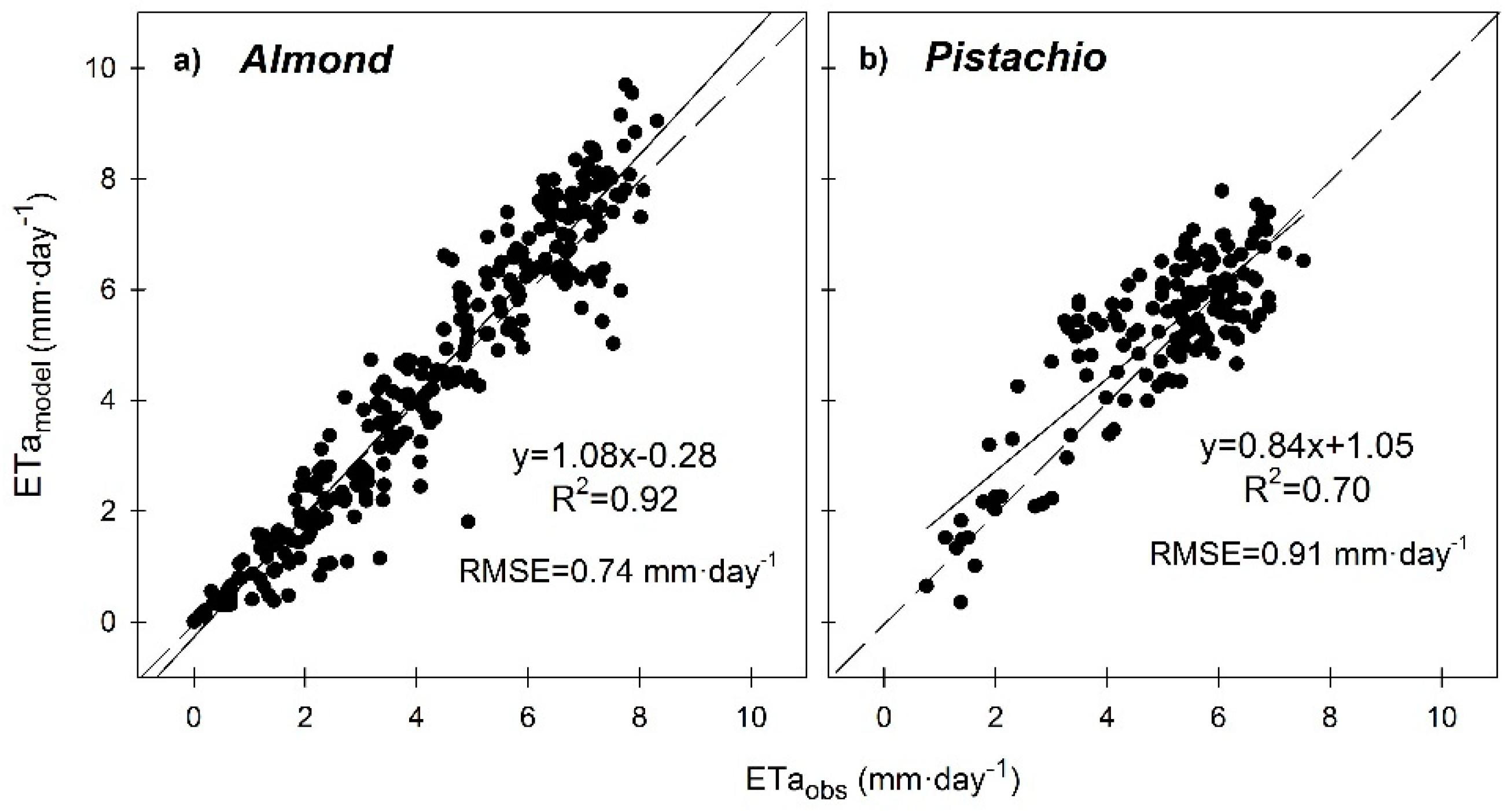
3.6. Seasonal Trend of Crop Evapotranspiration
4. Conclusions and Perspective
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- California Department of Food and Agriculture (CDFA). California Agricultural Statistics Review 2016–2017. 2017. Available online: https://www.cdfa.ca.gov/Statistics/PDFs/2016-17AgReport.pdf (accessed on 12 July 2018).
- California Legislative Information. Assembly Bill No. 1067. 2017; Chapter 49. Available online: https://leginfo.legislature.ca.gov/faces/billTextClient.xhtml?bill_id=201720180AB1067 (accessed on 12 July 2018).
- Goldhamer, D.A.; Kjelgren, R.; Williams, R.; Beede, R. Water use requirements of pistachio trees and response to water stress. In Proceedings of the National conference on advances in evapotranspiration, Chicago, IL, USA, 16–17 December 1985; pp. 216–273. [Google Scholar]
- Fereres, E.; Goldhamer, D.A. Irrigation of deciduous fruit and nut trees. In Irrigation of Agricultural Crops; Stewart, B.A., Nielsen, D.R., Eds.; Agronomy Monograph 30; American Society of Agronomy: Madison, WI, USA, 1990; pp. 987–1017. [Google Scholar]
- Goldhamer, D.A.; Viveros, M.; Salinas, M. Regulated deficit irrigation in almonds: Effects of variations in applied water and stress timing on yield and yield components. Irrig. Sci. 2006, 24, 101–114. [Google Scholar] [CrossRef]
- Goldhamer, D.A.; Fereres, E. Establishing an almond water production function for California using long-term yield response to variable irrigation. Irrig. Sci. 2017, 35, 169–179. [Google Scholar] [CrossRef]
- Goldhamer, D.A. Irrigation Scheduling. In Almond Production Manual; Micke, W.C., Ed.; Division of Agriculture and Natural Resources, University of California: Davis, CA, USA, 1996; pp. 171–178. [Google Scholar]
- Goldhamer, D.A.; Beede, R. Regulated deficit irrigation effects on yield, nut quality and water-use efficiency of mature pistachio trees. J. Hortic. Sci. Biotechnol. 2004, 79, 538–545. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Cheng, L.; Mazdiyasni, O.; Farahmand, A. Global warming and changes in risk of concurrent climate extremes: Insights from the 2014 California drought. Geophys. Res. Lett. 2014, 41, 8847–8852. [Google Scholar] [CrossRef]
- Ferreira, M.I. Stress coefficients for soil water balance combined with water stress indicators for irrigation scheduling of woody crops. Horticulturae 2017, 3, 38. [Google Scholar] [CrossRef]
- Calera, A.; Campos, I.; Osann, A.; D’Urso, G.; Menenti, M. Remote sensing for crop water management: From ET modelling to services for the end users. Sensors 2017, 17, 1104. [Google Scholar] [CrossRef]
- Johnson, L.F.; Trout, T.J. Satellite NDVI assisted monitoring of vegetable crop evapotranspiration in California’s San Joaquin Valley. Remote Sens. 2012, 4, 439–455. [Google Scholar] [CrossRef]
- Nieto, N.; Sandholt, I.; Olander, R.; Guzinski, R.; Bellvert, J.; Boye, L.; Blüthgen, J.; Bondo, T. Review of Remote Sensing for Evapotranspiration Models; Sentinels for Evapotranspiration project (4000121772/17/I-NB). 2018. Available online: http://esa-sen4et.org/outputs/methodology-review/ (accessed on 11 February 2018).
- Bastiaanssen, W.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL): 1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Allen, R.G.; Irmak, A.; Trezza, R.; Hendrickx, J.M.H.; Bastiaanssen, W.; Kjaersgaard, J. Satellite-based ET estimation in agriculture using SEBAL and METRIC. Hydrol. Process. 2011, 25, 4011–4027. [Google Scholar] [CrossRef]
- Allen, R.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)-Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Senay, G.B.; Budde, M.; Verdin, J.P.; Melesse, A.M. A coupled remote sensing and simplified surface energy balance approach to estimate actual evapotranspiration from irrigated fields. Sensors 2007, 7, 979–1000. [Google Scholar] [CrossRef]
- López, G.; Echevarria, G.; Bellvert, J.; Mata, M.; Behboudian, M.H.; Girona, J.; Marsal, J. Water stress for a short period before harvest in nectarine: Yield, fruit composition, sensory quality, and consumer acceptance of fruit. Sci. Hortic. 2016, 211, 1–7. [Google Scholar] [CrossRef]
- Moriana, A.; Orgaz, F.; Pastor, M.; Fereres, E. Yield responses of mature olive orchard to water deficits. J. Am. Soc. Hortic. Sci. 2003, 123, 425–431. [Google Scholar]
- Galindo, A.; Collado-González, J.; Griñán, I.; Centeno, A.; Martín-Palomo, M.J.; Girón, I.F.; Rodríguez, P.; Cruz, Z.N.; Hemmi, H.; Carbonell-Barrachina, A.A.; et al. Deficit irrigation and emergint fruit crops as strategy to save water in Mediterranean semiarid agrosystems. Agric. Water Manag. 2018, 202, 311–324. [Google Scholar] [CrossRef]
- Blanco, V.; Domingo, R.; Pérez-Pastor, A.; Blaya-Ros, P.J.; Torres-Sánchez, R. Soil and plant water indicators for deficit irrigation management of field-grown sweet cherry trees. Agric. Water Manag. 2018, 208, 83–94. [Google Scholar] [CrossRef]
- Spinelli, G.M.; Snyder, R.L.; Sanden, B.L.; Shackel, K.A. Water stress causes stomatal closure but does not reduce canopy evapotranspiration in almond. Agric. Water Manag. 2016, 168, 11–22. [Google Scholar] [CrossRef]
- McCutchan, H.; Schackel, K.A. Stem-water potential as a sensitivity of water stress (Prunus domestica L.). J. Am. Soc. Hortic. Sci. 1992, 117, 607–611. [Google Scholar]
- Garnier, E.; Berger, A. Testing water potential in peach trees as an indicator of water stress. J. Hortic. Sci. 1985, 60, 47–56. [Google Scholar] [CrossRef]
- Choné, X.; Cornelis, V.L.; Dubourdieu, D.; Gaudillères, J.P. Stem water potential is a sensitive indicator of grapevine water status. Ann. Bot. 2001, 87, 477–483. [Google Scholar] [CrossRef]
- González-Dugo, V.; Zarco-Tejada, P.; Nicolas, E.; Nortes, P.A.; Alarcon, J.J.; Intrigliolo, D.S.; Fereres, E. Using high resolution UAV thermal imagery to assess the variability in the water status of five fruit tree species within a commercial orchard. Precis. Agric. 2013, 14, 660–678. [Google Scholar] [CrossRef]
- Bellvert, J.; Marsal, J.; Girona, J.; Zarco-Tejada, P.J. Seasonal evolution of crop water stress index in grapevine varieties determined with high-resolution remote sensing thermal imagery. Irrig. Sci. 2015, 33, 81–93. [Google Scholar] [CrossRef]
- Bellvert, J.; Marsal, J.; Girona, J.; González-Dugo, V.; Fereres, E.; Ustin, S.; Zarco-Tejada, P.J. Airborne thermal imagery to detect the seasonal evolution of plant water status in peach, nectarine and Saturn peach orchards. Special issue: Remote Sensing in Precision Agriculture. Remote Sens. 2016, 8, 39. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D.; Pinter, P.J.; Reginato, R.J.; Hatfield, J.L. Normalizing the stress-degree day parameter for environmental variability. Agric. Meteorol. 1981, 24, 45–55. [Google Scholar] [CrossRef]
- Jackson, R.D.; Idso, S.B.; Reginato, R.J.; Pinter, P.J. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar] [CrossRef]
- SoilWeb—Interactive map of USDA-NCSS soil survey data for locations throughout most of the U.S. Calif. Soil Resour. Lab UC Davis UC-ANR Collab. with USDA Nat. Resour. Conserv. Serv. 2015. Available online: https://casoilresource.lawr.ucdavis.edu/soilweb-apps/ (accessed on 12 July 2018).
- Baram, S.; Couvreur, V.; Harter, T.; Brown, P.H.; Hopmans, J.W.; Smart, D.R. Assessment of orchard N losses to groundwater with vadose zone monitoring network. Agric. Water Manag. 2016, 172, 83–95. [Google Scholar] [CrossRef]
- McCutchan, H.; Shackel, K.A. Stem water potential as a sensitive indicator of water stress in prune trees (Prunus domestica L. cv French). J. Am. Soc. Hortic. Sci. 1992, 117, 607–611. [Google Scholar]
- Oyarzun, R.A.; Stöckle, C.O.; Whiting, M.D. A simple approach to modeling radiation interception by fruit-tree orchards. Agric. For. Meteorol. 2007, 142, 12–24. [Google Scholar] [CrossRef]
- Norman, J.M.; Campbell, G.S. Canopy structure. In Plant Physiological Ecology: Field Methods and Instrumentation; Pearcy, R.W., Mooney, H.A., Ehleringer, J.R., Rundel, P.W., Eds.; Chapman and Hall: New York, NY, USA, 1989; pp. 301–325. [Google Scholar]
- Paw, U.; Qiu, K.T.J.; Su, H.B.; Watanabe, T.; Brunet, Y. Surface renewal analysis: A new method to obtain scalar fluxes without velocity data. Agric. Meteorol. 1995, 74, 119–137. [Google Scholar]
- Castellví, F.; Snyder, R.L. Sensible heat flux estimates using surface renewal analysis: A study case over a peach orchard. Agric. Meteorol. 2009, 149, 1397–1402. [Google Scholar] [CrossRef]
- Shapland, T.M.; Snyder, R.L.; Paw, U.K.T.; McElrone, A.J. Thermocouple frequency response compensation leads to convergence of the surface renewal alpha calibration. Agric. Meteorol. 2014, 189–190, 36–47. [Google Scholar] [CrossRef]
- Spinelli, G.M.; Snyder, R.L.; Sanden, B.L.; Gilbert, M.; Shackel, K.A. Low and variable atmospheric coupling in irrigated almond (Prunus dulcis) canopies indicates a limited influence of stomata on orchard evapotranspiration. Agric. Water Manag. 2018, 196, 57–65. [Google Scholar] [CrossRef]
- California irrigation management information system (CIMIS). Available online: https://cimis.water.ca.gov/ (accessed on 12 July 2018).
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998; p. 297. [Google Scholar]
- Picón-Toro, J.; González-Dugo, V.; Uriarte, D.; Mancha, L.A.; Testi, L. Effects of canopy size and water stress over the crop coefficient of a “Tempranillo” vineyard in south-western Spain. Irrig. Sci. 2012, 30, 419–432. [Google Scholar] [CrossRef]
- Marsal, J.; Johnson, S.; Casadesús, J.; Lopez, G.; Girona, J.; Stöckle, C. Fraction of canopy intercepted radiation related differently with crop coefficient depending on the season and the fruit tree species. Agric. Meteorol. 2014, 184, 1–11. [Google Scholar] [CrossRef]
- Goldhamer, D.A. Tree water requirements & regulated deficit irrigation. In Pistachio Production Manual, 4th ed.; Beede, R.H., Freeman, M.W., Haviland, D.R., Holtz, B.A., Kallsen, C.E., Eds.; University of California: Davis, CA, USA, 2005; Available online: http://fruitsandnuts.ucdavis.edu/dsadditions/Pistachio_Manual_2005/ (accessed on 12 July 2018).
- Fereres, E.; Martinich, D.A.; Aldrich, T.M.; Castel, J.R.; Holzapfel, E.; Schulbach, H. Drip irrigation saves money in young almond orchards. Calif. Agric. 1982, 36, 12–13. [Google Scholar]
- Testi, L.; Goldhamer, D.A.; Iniesta, F.; Salinas, M. Crop water stress index is a sensitive water stress indicator in pistachio trees. Irrig. Sci. 2008, 26, 395–405. [Google Scholar] [CrossRef]
- Saxton, K.E.; Rawls, W.J.; Romberger, J.S.; Papendick, R.I. Estimating generalized soil water characteristics from texture. Trans. ASAE 1986, 50, 1031–1035. [Google Scholar] [CrossRef]
- Rocha, J.; Perdiao, A.; Melo, R.; Henriques, C. Remote Sensing Based Crop Coefficients for Water Management in Agriculture. In Sustainable Development—Authoritative and Leading Edge Content for Environmental Management; Curkovic, S., Ed.; IntechOpen Limited: London, UK, 2012; Chapter 8; pp. 167–191. [Google Scholar] [CrossRef]
- Zarate-Valdez, J.L.; Whiting, M.L.; Lampinen, B.D.; Metcalf, S.; Ustin, S.; Brown, P.H. Prediction of leaf area index in almonds by vegetation indexes. Comp. Electr. Agric. 2012, 85, 24–32. [Google Scholar] [CrossRef]
- Guillén-Climent, M.L.; Zarco-Tejada, P.J.; Villalobos, F.J. Estimating radiation interception in an olive orchard using physical models and multispectral airborne imagery. Isr. J. Plant Sci. 2012, 60, 107–121. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.U.; Calera, A.; Balbontin, C.; González-Piqueras, J. Assessing satellite-based basal crop coefficients for irrigated grapes (Vitis vinifera L.). Agric. Water Manag. 2010, 98, 45–54. [Google Scholar] [CrossRef]
- Odi-Lara, M.; Campos, I.; Neale, C.M.U.; Ortega-Farias, S.; Poblete-Echeverria, C.; Balbontin, C.; Calera, A. Estimating Evapotranspiration of an Apple Orchard Using a Remote Sensing–Based Soil Water Balance. Remote Sens. 2016, 8, 253. [Google Scholar] [CrossRef]
- López-López, M.; Espadafor, M.; Testi, L.; Lorite, I.J.; Orgaz, F.; Fereres, E. Yield response of almond trees to transpiration deficits. Irrig. Sci. 2018, 36, 111–120. [Google Scholar] [CrossRef]
- Iniesta, F.; Testi, L.; Goldhamer, D.A.; Fereres, E. Quantifying reductions in consumptive water use under regulated dèficit irrigation in pistachio (Pistacia vera L.). Agric. Water Manag. 2008, 95, 877–886. [Google Scholar] [CrossRef]
- Bonachela, S.; Orgaz, F.; Villalobos, F.J.; Fereres, E. Measurement and simulation of evaporation from soil in olive orchards. Irrig. Sci. 1999, 18, 205–211. [Google Scholar] [CrossRef]
- Jackson, R.D. Canopy temperature and crop water stress. In Advances in Irrigation; Hillel, D., Ed.; Academic Press: New York, NY, USA, 1982; pp. 43–85. [Google Scholar]
- Klein, I.; Esparza, G.; Weinbaum, S.A.; DeJong, T.M. Effects of irrigation deprivation during the harvest period on leaf persistence and function in mature almond trees. Tree Physiol. 2001, 21, 1063–1072. [Google Scholar] [CrossRef]
- Espadafor, M.; Orgaz, F.; Testi, L.; Lorite, I.J.; Villalobos, F.J. Transpiration of young almond trees in relation to intercepted radiation. Irrig. Sci. 2015, 33. [Google Scholar] [CrossRef]
- Hernández-Santana, V.; Rodríguez-Dominguez, C.M.; Fernández, J.E.; Diaz-Espejo, A. Role of leaf hydraulic conductance in the regulation of stomatal conductance in almond and olive in response to water stress. Tree Physiol. 2016, 36, 725–735. [Google Scholar] [CrossRef]
- Rahimi-Eichi, V. Water use efficiency in almonds (Prunus dulcis (Mill.) D.A. Webb. Master’s Thesis, School of Agriculture, Food and Wine, Faculty of Science, University of Adelaide, Adelaide, Australia, July 2013. Available online: https://digital.library.adelaide.edu.au/dspace/bitstream/2440/87112/8/02whole.pdf (accessed on 12 July 2018).
- Memmi, H.; Couceiro, J.F.; Gijón, C.; Pérez-López, D. Impacts of water stress, environment and rootstocks on the diurnal behavior of stem water potential and leaf conductance in pistachio (Pistachio vera L.). Span. J. Agric. Res. 2016, 14, 2. [Google Scholar] [CrossRef]
- Castel, J.R.; Fereres, E. Responses of young almond trees to two drought periods in the field. J. Hortic. Sci. 1982, 57, 175–187. [Google Scholar] [CrossRef]
- Torrecillas, A.; Ruiz-Sanchez, M.C.; Leon, A.; Garcia, A.L. Stomatal response to leaf water potential in almond trees under drip irrigated and non irrigated conditions. Plant and Soil 1988, 112, 151–153. [Google Scholar] [CrossRef]
- González-Dugo, V.; Goldhamer, D.; Zarco-Tejada, P.J.; Fereres, F. Improving the precision of irrigation in a pistachio farm using an unmanned airborne thermal system. Irrig. Sci. 2014, 33, 43–52. [Google Scholar] [CrossRef]
- Camino, C.; Zarco-Tejada, P.J.; González-Dugo, V. Effects of Heterogeneity within Tree Crowns on Airborne-Quantified SIF and the CWSI as Indicators of Water Stress in the Context of Precision Agriculture. Remote Sens. 2018, 10, 604. [Google Scholar] [CrossRef]
- Hsiao, T.G. Plant responses to water stress. A. Rev. Plant Physiol. 1973, 24, 519–570. [Google Scholar] [CrossRef]
- Turner, N.C. Stomatal behavior and water status of maize, sorghum, and tobacco under field conditions. II. At low soil water potential. Plant Physiol. 1974, 53, 360–365. [Google Scholar] [CrossRef] [PubMed]
- Begg, J.E.; Tonnet, M.L. Osmotic adjustment of sorghum and sunflower crops in response to water deficits and its influence on the water potential at which stomata close. Aust. J. PL Physiol. 1978, 5, 597–608. [Google Scholar]
- Hinckley, T.M.; Duhme, F.; Hinckey, A.R.; Richter, H. Water relations of drought-hardy shrubs: osmotic potential and stomatal reactivity. Pl. Cell. Environ. 1980, 3, 131–140. [Google Scholar]
- Behboudian, M.H.; Walker, R.R.; Törökfalvy, E. Effects of water stress and salinity on photosynthesis of pistachio. Sci. Hort. 1986, 29, 251–261. [Google Scholar] [CrossRef]
- Germana, C. The response of pistachio trees to water stress as affected by two different rootstocks. Acta Hort. 1997, 449, 513–519. [Google Scholar] [CrossRef]
- Gijón, M.C.; Gimenez, C.; Perez-López, D.; Guerrero, J.; Couceiro, J.F.; Moriana, A. Water relations of pistachio (Pistacia vera L.) as affected by phenological stages and water regimes. Sci. Hortic. 2011, 128, 415–422. [Google Scholar]
- Jarvis, P. Coupling of transpiration to the atmosphere in horticultural crops: the omega factor. In ISHS Acta Horticulturae 171, Proceedings of the I International Symposium on Water Relations in Fruit Crops, Pisa, Italy, 3–5 September 1984; ISHS; University of Wisconsin: Madison, WI, USA, 1985. [Google Scholar]
- Stevens, R.M.; Ewenz, C.M.; Grigson, G.; Conner, S.M. Water use by an irrigated almond orchard. Irrig. Sci. 2012, 30, 189–200. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S. Estimating crop coefficients from fraction of ground cover and height. Irrig. Sci. 2009, 28, 17–34. [Google Scholar] [CrossRef]
- García-Tejero, I.F.; Hernández, A.; Rodríguez, V.M.; Ponce, J.R.; Ramos, V.; Muriel, J.L.; Durán-Zuazo, V.H. Estimating almond crop coefficients and physiological response to water stress in semiarid environments (SW Spain). J. Agr. Sci. Tech. 2015, 1, 1255–1266. [Google Scholar]
- Stöckle, C.O.; Donatelli, M.; Nelson, R. CropSyst, a cropping systems simulation model. Eur. J. Agron. 2003, 18, 289–307. [Google Scholar] [CrossRef]
- Kanber, R.; Yazar, A.; Ónder, S.; Köksal, H. Irrigation response of pistachio (Pistacia vera L.). Irrig. Sci. 1993, 14, 7–14. [Google Scholar] [CrossRef]

| Feb | Mar | Apr | May | June | July | Aug | Sep | Oct | Nov | |
|---|---|---|---|---|---|---|---|---|---|---|
| α+ | 0.881 | 0.801 | 0.677 | 0.677 | 0.677 | 0.650 | 0.670 | 0.849 | 0.833 | 0.878 |
| α- | 0.316 | 0.201 | 0.206 | 0.206 | 0.206 | 0.200 | 0.220 | 0.226 | 0.183 | 0.153 |
| Almond | Pistachio | |
|---|---|---|
| ETo (mm) | 1242 | |
| Rainfall (mm) | 156.2 | |
| Irrigation (mm) | 898.0 | 762.5 |
| ETamodel (mm) | 1194.9 | 1021.5 |
| Tmodel (mm) | 975.7 | 878.9 |
| Esoil (mm) | 192.9 | 134.0 |
| CC (mm) | 26.3 | 8.6 |
| Water loss in Esoil (%) | 16.1 | 13.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellvert, J.; Adeline, K.; Baram, S.; Pierce, L.; Sanden, B.L.; Smart, D.R. Monitoring Crop Evapotranspiration and Crop Coefficients over an Almond and Pistachio Orchard Throughout Remote Sensing. Remote Sens. 2018, 10, 2001. https://doi.org/10.3390/rs10122001
Bellvert J, Adeline K, Baram S, Pierce L, Sanden BL, Smart DR. Monitoring Crop Evapotranspiration and Crop Coefficients over an Almond and Pistachio Orchard Throughout Remote Sensing. Remote Sensing. 2018; 10(12):2001. https://doi.org/10.3390/rs10122001
Chicago/Turabian StyleBellvert, Joaquim, Karine Adeline, Shahar Baram, Lars Pierce, Blake L. Sanden, and David R. Smart. 2018. "Monitoring Crop Evapotranspiration and Crop Coefficients over an Almond and Pistachio Orchard Throughout Remote Sensing" Remote Sensing 10, no. 12: 2001. https://doi.org/10.3390/rs10122001
APA StyleBellvert, J., Adeline, K., Baram, S., Pierce, L., Sanden, B. L., & Smart, D. R. (2018). Monitoring Crop Evapotranspiration and Crop Coefficients over an Almond and Pistachio Orchard Throughout Remote Sensing. Remote Sensing, 10(12), 2001. https://doi.org/10.3390/rs10122001





