Ground Deformation and Source Geometry of the 30 October 2016 Mw 6.5 Norcia Earthquake (Central Italy) Investigated Through Seismological Data, DInSAR Measurements, and Numerical Modelling
Abstract
1. Introduction
2. Collected Data
2.1. Seismological Data
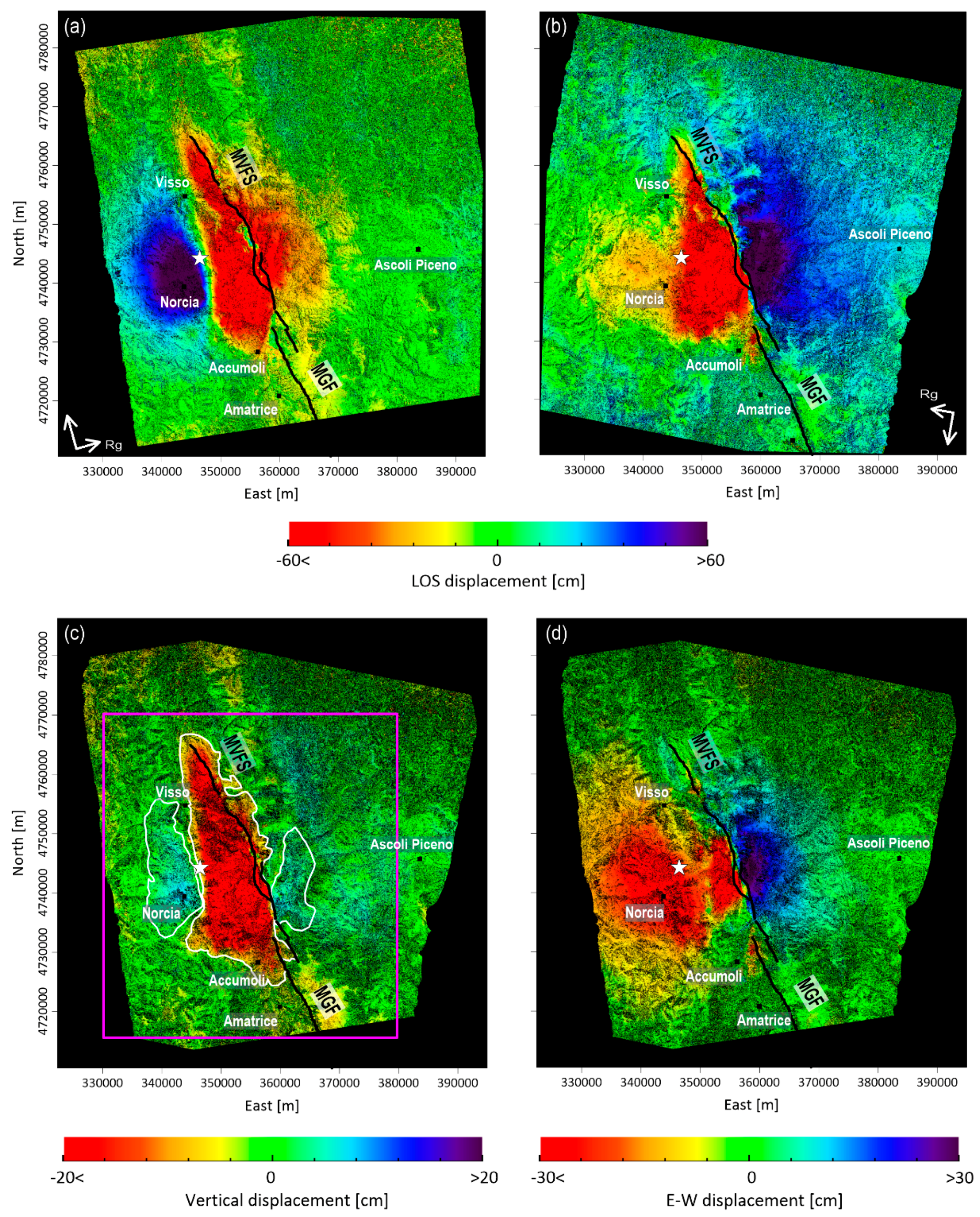
2.2. DInSAR Measurements
3. Rock Volumes Computation
3.1. Topographic Method (3D Cavalieri–Simpson Modified Method)
3.2. Numerical Approach Method
- the Extended Trapezoidal Rule, represented by the following formula:where ∆y is the grid row spacing and A is the area.
- the Extended Simpson’s Rule, represented by the following formula:where ∆y is the grid row spacing and A is the area.
- the Extended Simpson’s 3/8 Rule, represented by the following formula:where ∆y is the grid row spacing and A is the area.
3.3. Surfacing Method
3.4. Results
4. Numerical Modelling
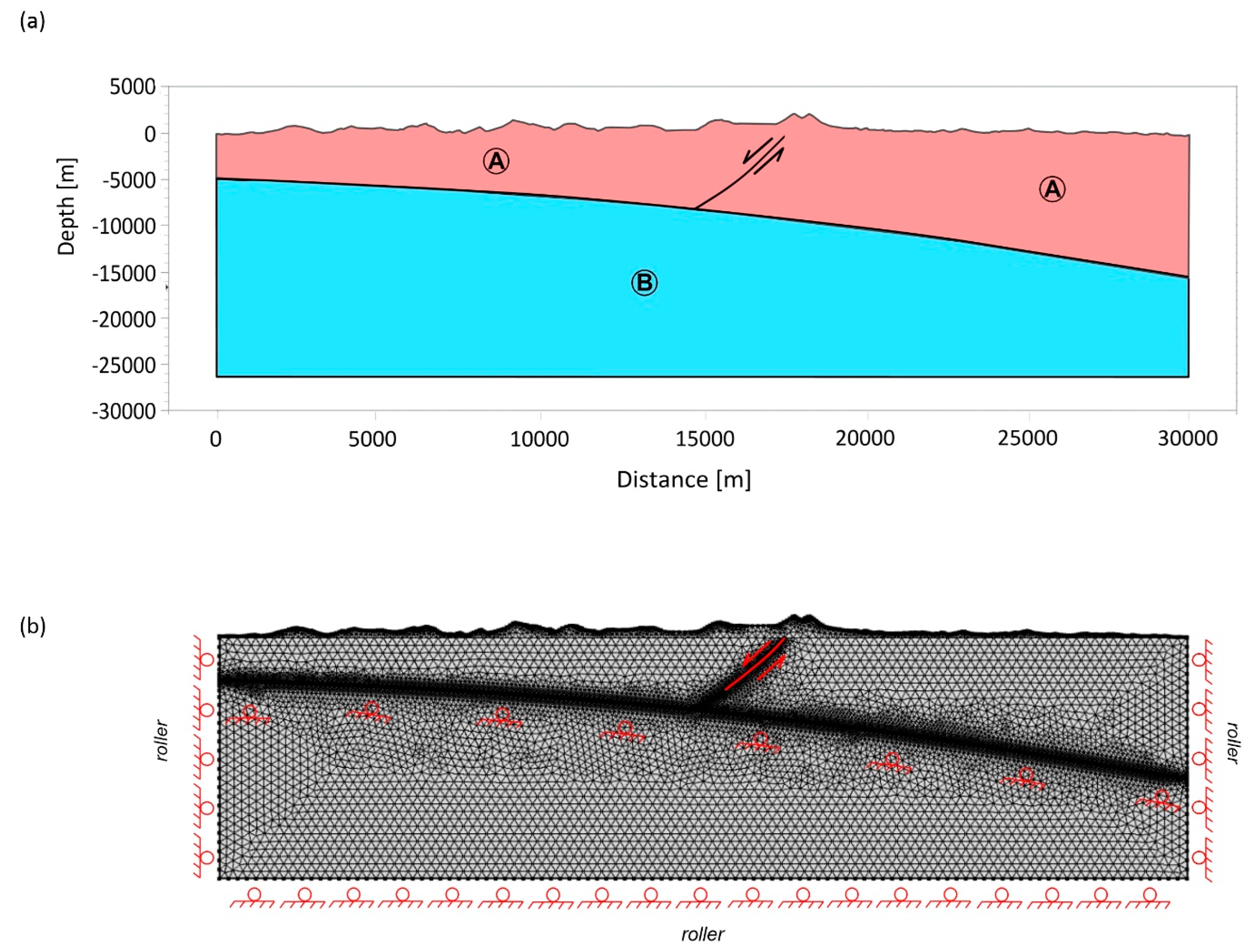
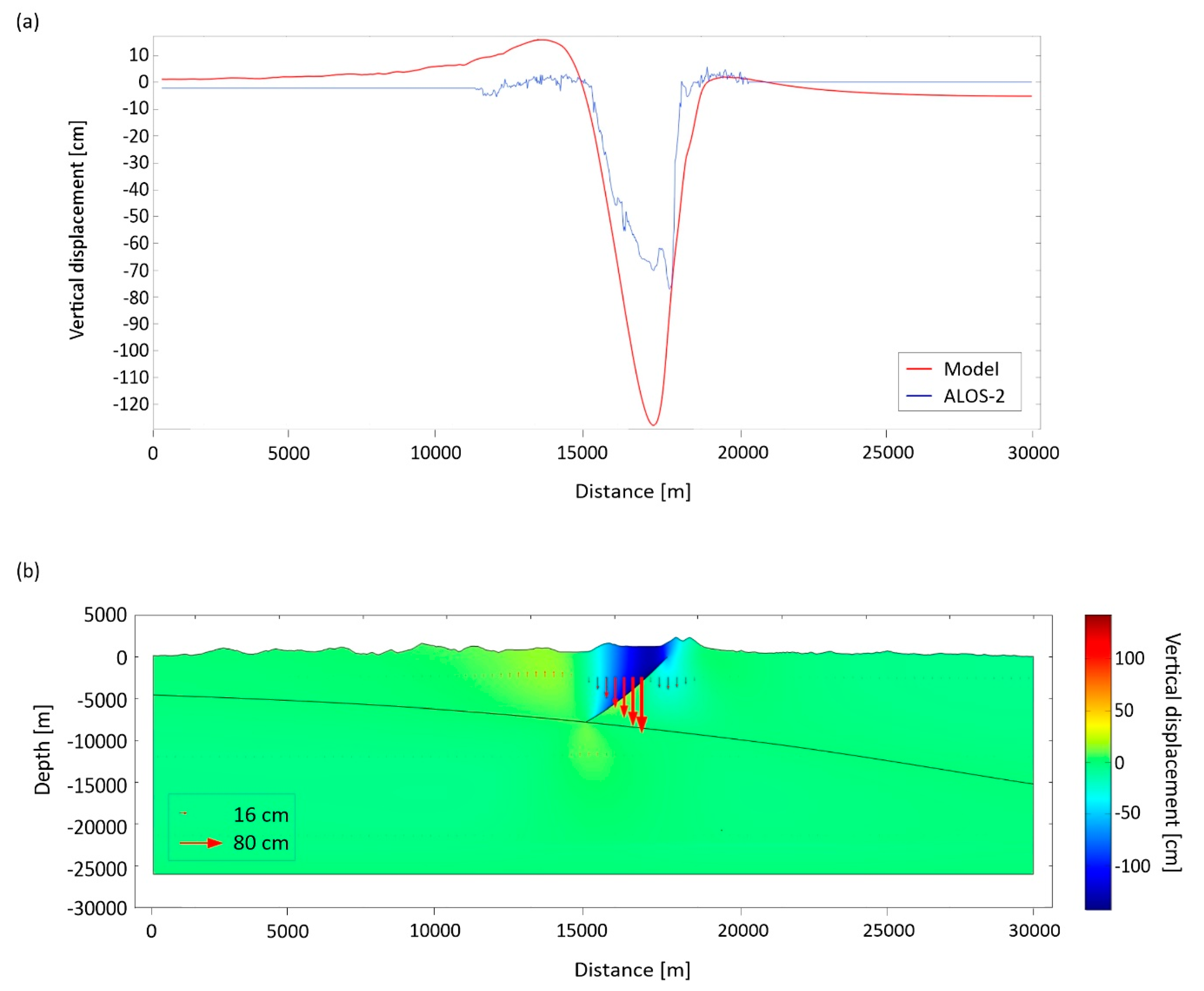
4.1. Single Fault
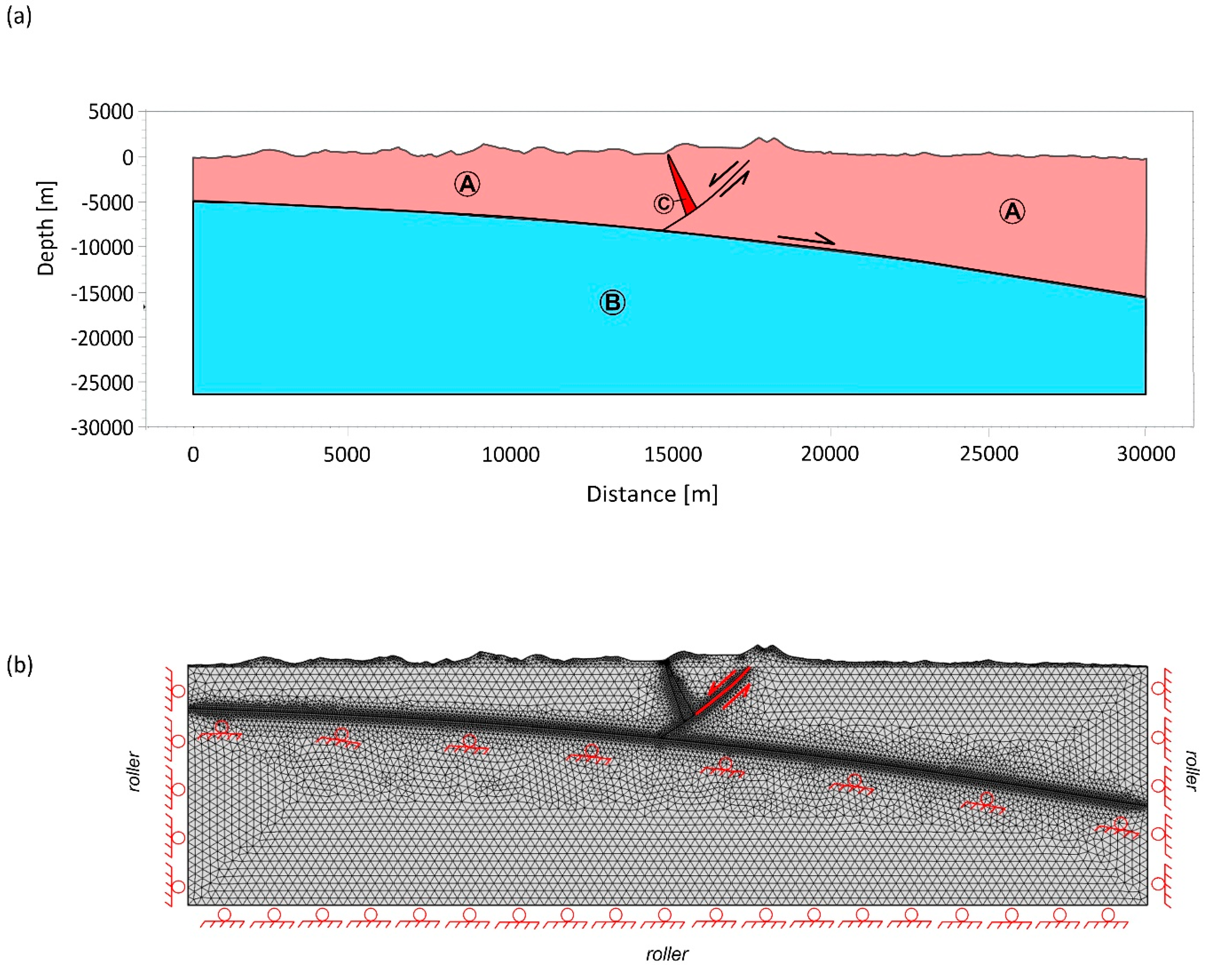
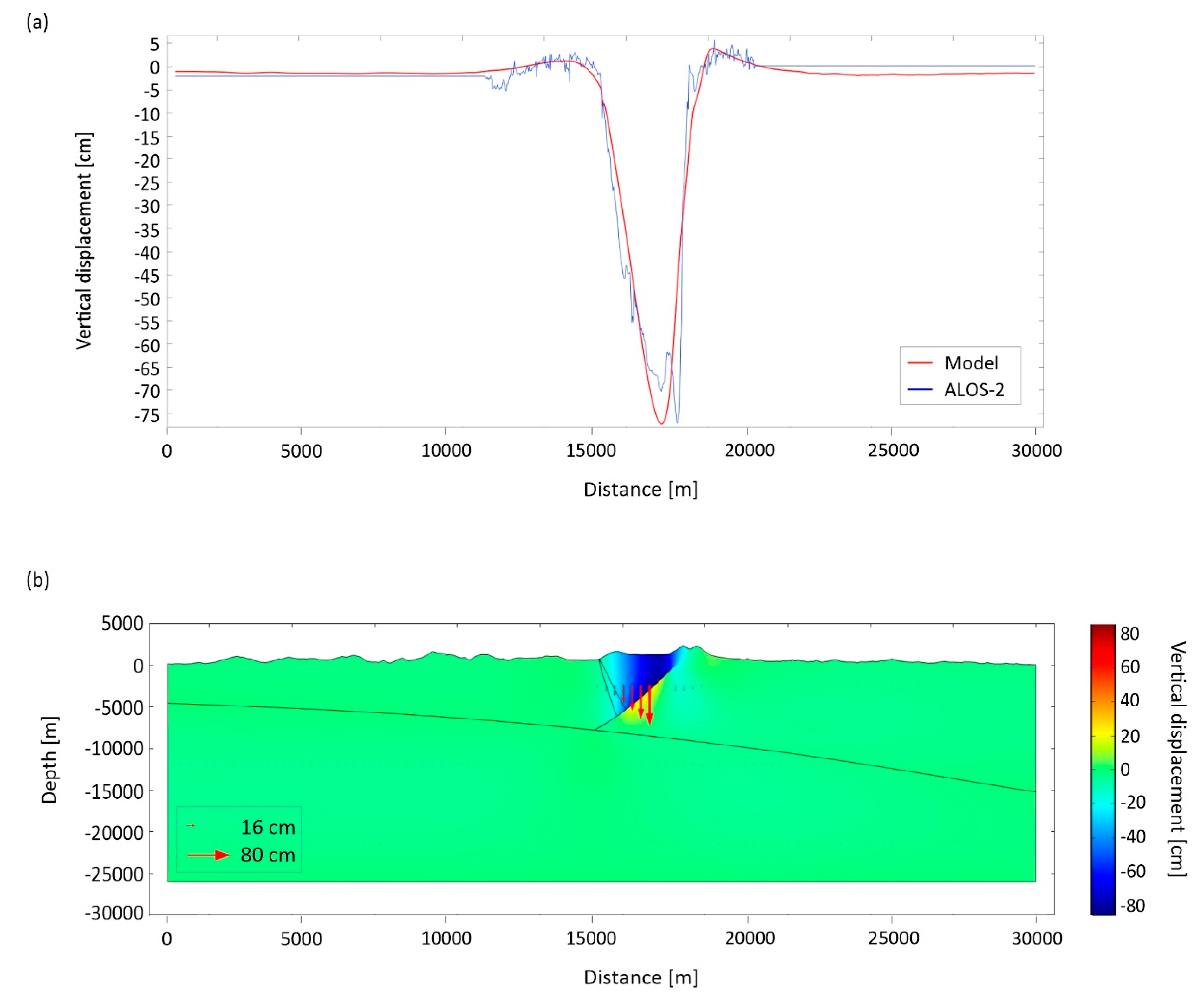
4.2. Antithetic Zone
5. Discussion
6. Conclusions
- the analysis of the relocated hypocenters allows us to highlight three main structures: (i) a SW-dipping alignment parallel to the main fault system; (ii) an E-dipping low-angle normal fault cutting through the upper crust; and (iii) ENE-dipping structures that are antithetic to the main fault;
- the DInSAR measurements show that the considered seismogenic area was interested by significant coseismic ground deformations. The vertical displacement map shows three main deformation patterns: (i) a major subsidence that reaches a maximum value of about 98 cm near the epicentral zones, nearby the town of Norcia; (ii) two smaller uplift lobes that affect both the hangingwall (reaching maximum values of about 14 cm) and the footwall blocks (reaching maximum values of about 10 cm);
- the coseismic uplift in the hangingwall block is about 1/14 of subsidence, suggesting an unbalance between the subsided and the uplifted volumes within the seismogenic crust;
- the results of our 2D modelling highlight that the presence of an antithetic zone is necessary to reach the best fit between measured and simulated coseismic surface deformations (RMS = 3.48 cm). This result allows us to interpret the subsidence and uplift phenomena caused by the Mw 6.5 Norcia earthquake as the result of the gravitational sliding of the hangingwall along the main fault plane and the frictional force acting in the opposite direction, consistently with the double couple fault plane mechanism.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chiarabba, C.; Jovane, L.; Di Stefano, R. A new view of Italian seismicity using 20 years of instrumental recordings. Tectonophysics 2005, 395, 251–268. [Google Scholar] [CrossRef]
- Petricca, P.; Barba, S.; Carminati, E.; Doglioni, C.; Riguzzi, F. Graviquakes in Italy. Tectonophysics 2015, 656, 202–214. [Google Scholar] [CrossRef]
- Lavecchia, G.; Castaldo, R.; de Nardis, R.; De Novellis, V.; Ferrarini, F.; Pepe, S.; Brozzetti, F.; Solaro, G.; Cirillo, D.; Bonano, M.; et al. Ground deformation and source geometry of the 24 August 2016 Amatrice earthquake (Central Italy) investigated through analytical and numerical modeling of DInSAR measurements and structural-geological data. Geophys. Res. Lett. 2016, 43. [Google Scholar] [CrossRef]
- Cheloni, D.; De Novellis, V.; Antonioli, A.; Anzidei, M.; Atzori, S.; Avallone, A.; Bignami, C.; Bonano, M.; Calcaterra, S.; Castaldo, R.; et al. Geodetic model of the 2016 Central Italy earthquake sequence inferred from InSAR and GPS data. Geophys. Res. Lett. 2017, 44, 6778–6787. [Google Scholar] [CrossRef]
- Thompson, G.A.; Parsons, T. From coseismic offsets to fault-block mountains. Proc. Nat. Acad. Sci. USA 2017, 114, 9820–9825. [Google Scholar] [CrossRef] [PubMed]
- Galli, P.; Galadini, F.; Pantosti, D. Twenty years of paleoseismology in Italy. Earth Sci. Rev. 2008, 88, 89–117. [Google Scholar] [CrossRef]
- Doglioni, C. A proposal for the kinematic modelling of W-dipping subductions-possible applications to the Tyrrhenian-Apennines system. Terra Nova 1991, 3, 423–434. [Google Scholar] [CrossRef]
- Carminati, E.; Lustrino, M.; Doglioni, C. Geodynamic evolution of the central and western Mediterranean: Tectonics vs. igneous petrology constraints. Tectonophysics 2012, 579, 173–192. [Google Scholar] [CrossRef]
- Chiaraluce, L. Unravelling the complexity of Apenninic extensional fault systems: A review of the 2009 L’Aquila earthquake (Central Apennines, Italy). J. Struct. Geol. 2012, 42, 2–18. [Google Scholar] [CrossRef]
- Avallone, A.; Latorre, D.; Serpelloni, E.; Cavaliere, A.; Herrero, A.; Cecere, G.; D’Agostino, N.; D’Ambrosio, C.; Devoti, R.; Giuliani, R.; et al. Coseismic displacement waveforms for the 2016 August 24 Mw 6.0 Amatrice earthquake (central Italy) carried out from High-Rate GPS data. Ann. Geophys. 2016, 59. [Google Scholar] [CrossRef]
- Wedmore, L.N.J.; Faure Walker, J.P.; Roberts, G.P.; Sammonds, P.R.; McCaffrey, K.J.W.; Cowie, P.A. A 667 year record of coseismic and interseismic Coulomb stress changes in central Italy reveals the role of fault interaction in controlling irregular earthquake recurrence intervals. J. Geophys. Res. Solid Earth 2017, 122, 5691–5711. [Google Scholar] [CrossRef]
- Chiaraluce, L.; Amato, A.; Cocco, M.; Chiarabba, C.; Selvaggi, G.; Di Bona, M.; Piccinini, D.; Deschamps, A.; Margheriti, L.; Courboulex, F.; et al. Complex normal faulting in the Apennines thrust-and-fold belt: The 1997 seismic sequence in central Italy. Bull. Seism. Soc. Am. 2004, 94, 99–116. [Google Scholar] [CrossRef]
- Chiaraluce, L.; Valoroso, L.; Piccinini, D.; Di Stefano, R.; De Gori, P. The anatomy of the 2009 L’Aquila norma fault system (central Italy) imaged by high resolution foreshock and aftershock locations. J. Geophys. Res. 2011, 116, B12311. [Google Scholar] [CrossRef]
- Valoroso, L.; Chiaraluce, L.; Piccinini, D.; Di Stefano, R.; Schaff, D.; Waldhauser, F. Radiography of a normal fault system by 64,000 high-precision earthquake locations: The 2009 L’Aquila (central Italy) case study. J. Geophys. Res. Solid Earth 2013, 118, 1156–1176. [Google Scholar] [CrossRef]
- Chiaraluce, L.; Di Stefano, R.; Tinti, E.; Scognamiglio, L.; Michele, M.; Casarotti, E.; Cattaneo, M.; De Gori, P.; Chiarabba, C.; Monachesi, G.; et al. The 2016 Central Italy seismic sequence: A first look at the mainshocks, aftershocks and source models. Seism. Res. Lett. 2017, 88, 757–771. [Google Scholar] [CrossRef]
- Smeraglia, L.; Billi, A.; Carminati, E.; Cavallo, A.; Doglioni, C. Field-to nano-scale evidence for weakening mechanisms along the fault of the 2016 Amatrice and Norcia earthquakes, Italy. Tectonophysics 2017, 712–713, 156–169. [Google Scholar] [CrossRef]
- Liu, C.; Zheng, Y.; Xie, Z.; Xiong, X. Rupture features of the 2016 Mw 6.2 Norcia earthquake and its possible relationship with strong seismic hazards. Geophys. Res. Lett. 2017, 44, 1320–1328. [Google Scholar] [CrossRef]
- Pizzi, A.; Di Domenica, A.; Gallovič, F.; Luzi, L.; Puglia, R. Fault segmentation as constraint to the occurrence of the main shocks of the 2016 Central Italy seismic sequence. Tectonics 2017, 36, 2370–2387. [Google Scholar] [CrossRef]
- Xu, G.; Xu, C.; Wen, Y.; Jiang, G. Source Parameters of the 2016–2017 Central Italy Earthquake Sequence from the Sentinel-1, ALOS-2 and GPS Data. Remote Sens. 2017, 9, 1182. [Google Scholar] [CrossRef]
- Scognamiglio, L.; Tinti, E.; Casarotti, E.; Pucci, S.; Villani, F.; Cocco, M.; Magnoni, F.; Michelini, A.; Dreger, D. Complex fault geometry and rupture dynamics of the Mw 6.5, 2016, October 30th central Italy earthquake. J. Geophys. Res. Solid Earth 2018. [Google Scholar] [CrossRef]
- Barchi, M.R.; Alvarez, W.; Shimabukuro, D.H. The Umbria-Marche Apennines as a Double Orogen: Observations and hypotheses. Ital. J. Geosci. 2012, 131, 258–271. [Google Scholar] [CrossRef]
- Boncio, P.; Lavecchia, G.; Milana, G.; Rozzi, B. Seismogenesis in Central Apennines, Italy: An integrated analysis of minor earthquake sequences and structural data in the Amatrice-Campotosto area. Ann. Geophys. 2004, 47, 1723–1742. [Google Scholar]
- Galadini, F.; Galli, P. Paleoseismology of silent faults in the Central Apennines (Italy): The Mt. Vettore and Laga Mts. Faults. Ann. Geophys. 2003, 46, 815–836. [Google Scholar]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Manzo, M.; Ricciardi, G.P.; Casu, F.; Ventura, G.; Zeni, G.; Borgström, S.; Berardino, P.; Del Gaudio, C.; Lanari, R. Surface deformation analysis in the Ischia Island (Italy) based on spaceborne radar interferometry. J. Volcanol. Geoth. Res. 2006, 151, 399–416. [Google Scholar] [CrossRef]
- Velleman, D.J. The generalized Simpson’s rule. Am. Math. Mon. 2005, 112, 342–350. [Google Scholar] [CrossRef]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in C; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Smith, W.H.F.; Wessel, P. Gridding with continuous curvature splines in tension. Geophysics 1990, 55, 293–305. [Google Scholar] [CrossRef]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.F.; Wobbe, F. Generic Mapping Tools: Improved version released. EOS Trans. AGU 2013, 94, 409–410. [Google Scholar] [CrossRef]
- Tizzani, P.; Castaldo, R.; Solaro, G.; Pepe, S.; Bonano, M.; Casu, F.; Manunta, M.; Manzo, M.; Pepe, A.; Samsonov, S.; et al. New insights into the 2012 Emilia (Italy) seismic sequence through advanced numerical modeling of ground deformation InSAR measurements. Geophys. Res. Lett. 2013, 40, 1971–1977. [Google Scholar] [CrossRef]
- Castaldo, R.; de Nardis, R.; DeNovellis, V.; Ferrarini, F.; Lanari, R.; Lavecchia, G.; Pepe, S.; Solaro, G.; Tizzani, P. Coseismic Stress and Strain Field Changes Investigation Through 3-D Finite Element Modeling of DInSAR and GPS Measurements and Geological/Seismological Data: The L’Aquila (Italy) 2009 Earthquake Case Study. J. Geophys. Res. Solid Earth 2018, 123, 4193–4222. [Google Scholar] [CrossRef]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005; ISBN 0-89871-572-5. [Google Scholar]
- Schön, J.H. Physical Properties of Rocks: Fundamentals and Principles of Petrophysics; Elsevier: Amsterdam, The Netherlands, 2015; Volume 65. [Google Scholar]
- Fagan, M.J. Finite Elements Analysis: Theory and Practice; Prentice Hall: Upper Saddle River, NJ, USA, 1992; pp. 1–311. [Google Scholar]
- Porreca, M.; Minelli, G.; Ercoli, M.; Brobia, A.; Mancinelli, P.; Cruciani, F.; Giorgetti, C.; Carbomi, F.; Mirabella, F.; Cavinato, G.; et al. Seismic Reflection Profiles and Subsurface Geology of the Area Interested by the 2016–2017 Earthquake Sequence (Central Italy). Tectonics 2018, 37, 1116–1137. [Google Scholar] [CrossRef]
- Gratier, J.P.; Thouvenot, F.; Jenatton, L.; Tourette, A.; Doan, M.L.; Renard, F. Geological control of the partitioning between seismic and aseismic sliding behaviours in active faults: Evidence from the Western Alps, France. Tectonophysics 2013, 600, 226–242. [Google Scholar] [CrossRef]
- Tesei, T.; Collettini, C.; Barchi, M.R.; Carpenter, B.M.; Di Stefano, G. Heterogeneous strength and fault zone complexity of carbonate-bearing thrusts with possible implications for seismicity. Earth Plan. Sci. Lett. 2014, 408, 307–318. [Google Scholar] [CrossRef]
- Doglioni, C.; Carminati, E.; Petricca, P.; Riguzzi, F. Normal fault earthquakes or graviquakes. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Barberio, M.D.; Barbieri, M.; Billi, A.; Doglioni, C.; Petitta, M. Hydrogeochemical changes before and during the 2016 Amatrice-Norcia seismic sequence (central Italy). Sci. Rep. 2017, 7. [Google Scholar] [CrossRef] [PubMed]
- Quattrocchi, F.; Pik, R.; Pizzino, L.; Guerra, M.; Scarlato, P.; Angelone, M.; Barbieri, M.; Conti, A.; Marty, B.; Sacchi, E. Geochemical changes at the Bagni di Triponzo thermal spring during the Umbria-Marche 1997–1998 seismic sequence. J. Seism. 2000, 4, 567–587. [Google Scholar] [CrossRef]
- Carro, M.; De Amicis, M.; Luzi, L. Hydrogeological changes related to the Umbria–Marche earthquake of 26 September 1997 (Central Italy). Nat. Hazards 2005, 34, 315–339. [Google Scholar] [CrossRef]
- Di Luccio, F.; Ventura, G.; Di Giovambattista, R.; Piscini, A.; Cinti, F.R. Normal faults and thrusts re-activated by deep fluids: The 6 April 2009 Mw 6.3 L’Aquila earthquake, central Italy. J. Geophys. Res. 2010, 115, B06315. [Google Scholar] [CrossRef]
- Terakawa, T.; Zoporowski, A.; Galvan, B.; Miller, S.A. High-pressure fluid at hypocentral depths in the L’Aquila region inferred from earthquake focal mechanisms. Geology 2010, 38, 995–998. [Google Scholar] [CrossRef]
- Doglioni, C.; Barba, S.; Carminati, E.; Riguzzi, F. Fault on–off versus coseismic fluids reaction. Geosci. Front. 2014, 5, 767–780. [Google Scholar] [CrossRef]
- Sugan, M.; Kato, A.; Miyake, H.; Nakagawa, S.; Vuan, A. The preparatory phase of the 2009 Mw 6.3 L’Aquila earthquake by improving the detection capability of low-magnitude foreshocks. Geophys. Res. Lett. 2014, 41, 6137–6144. [Google Scholar] [CrossRef]
| Sensor | InSAR Pair | Orbit | Wavelenght (cm) | Perpendicular Baseline (m) | Track | Look Angle (deg) |
|---|---|---|---|---|---|---|
| ALOS-2 | 24082016–02112016 | ASC | 24.2 | 99 | 197 | 36.6 |
| ALOS-2 | 31082016–09112016 | DESC | 24.2 | 59 | 92 | 32.8 |
| ALOS-2 | 24082016–06092017 | ASC | 24.2 | 99 | 197 | 36.6 |
| ALOS-2 | 31082016–24052017 | DESC | 24.2 | 59 | 92 | 32.8 |
| Deformed Volume [km3] | Topographic Method | Numerical Approach Method | Surfacing Method |
|---|---|---|---|
| Subsidence | 0.100 | 0.101 | 0.101 |
| Uplift | 0.0070 | 0.0074 | 0.0075 |
| Unbalance | 0.0930 | 0.0936 | 0.0935 |
| Parameters | Unit A | Unit B | Unit C |
|---|---|---|---|
| Density | 2600 | 2700 | 2300 |
| Young’s Modulus | 30 | 30 | 9 |
| Poisson’s Ratio | 0.33 | 0.32 | 0.27 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valerio, E.; Tizzani, P.; Carminati, E.; Doglioni, C.; Pepe, S.; Petricca, P.; De Luca, C.; Bignami, C.; Solaro, G.; Castaldo, R.; et al. Ground Deformation and Source Geometry of the 30 October 2016 Mw 6.5 Norcia Earthquake (Central Italy) Investigated Through Seismological Data, DInSAR Measurements, and Numerical Modelling. Remote Sens. 2018, 10, 1901. https://doi.org/10.3390/rs10121901
Valerio E, Tizzani P, Carminati E, Doglioni C, Pepe S, Petricca P, De Luca C, Bignami C, Solaro G, Castaldo R, et al. Ground Deformation and Source Geometry of the 30 October 2016 Mw 6.5 Norcia Earthquake (Central Italy) Investigated Through Seismological Data, DInSAR Measurements, and Numerical Modelling. Remote Sensing. 2018; 10(12):1901. https://doi.org/10.3390/rs10121901
Chicago/Turabian StyleValerio, Emanuela, Pietro Tizzani, Eugenio Carminati, Carlo Doglioni, Susi Pepe, Patrizio Petricca, Claudio De Luca, Christian Bignami, Giuseppe Solaro, Raffaele Castaldo, and et al. 2018. "Ground Deformation and Source Geometry of the 30 October 2016 Mw 6.5 Norcia Earthquake (Central Italy) Investigated Through Seismological Data, DInSAR Measurements, and Numerical Modelling" Remote Sensing 10, no. 12: 1901. https://doi.org/10.3390/rs10121901
APA StyleValerio, E., Tizzani, P., Carminati, E., Doglioni, C., Pepe, S., Petricca, P., De Luca, C., Bignami, C., Solaro, G., Castaldo, R., De Novellis, V., & Lanari, R. (2018). Ground Deformation and Source Geometry of the 30 October 2016 Mw 6.5 Norcia Earthquake (Central Italy) Investigated Through Seismological Data, DInSAR Measurements, and Numerical Modelling. Remote Sensing, 10(12), 1901. https://doi.org/10.3390/rs10121901









