Capability of Remotely Sensed Drought Indices for Representing the Spatio–Temporal Variations of the Meteorological Droughts in the Yellow River Basin
Abstract
1. Introduction
2. Materials and Methods
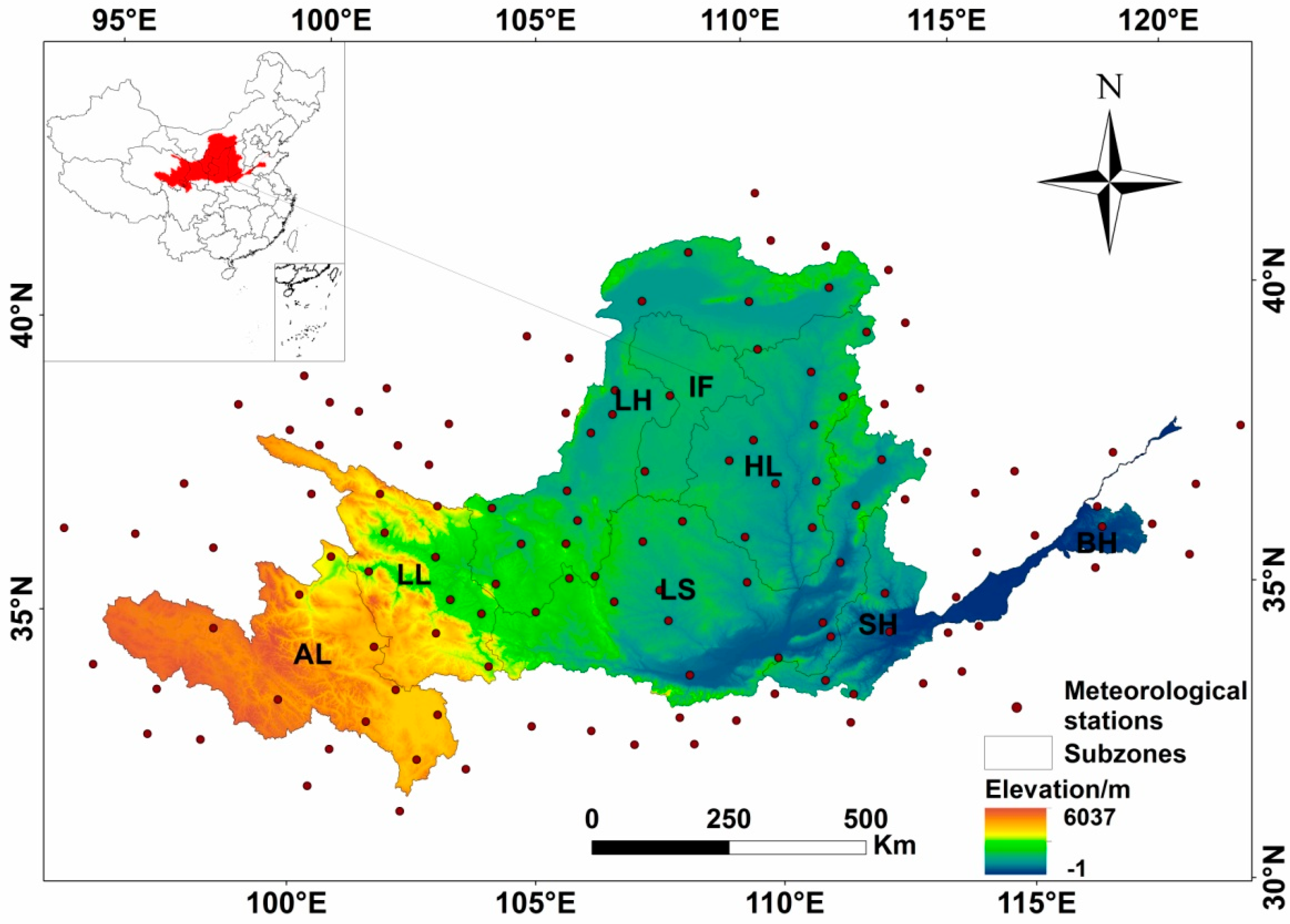
2.1. Study area
2.2. Drought indices
2.2.1. Remotely sensed drought indices (RSDIs)
2.2.2. Meteorological station-based drought index
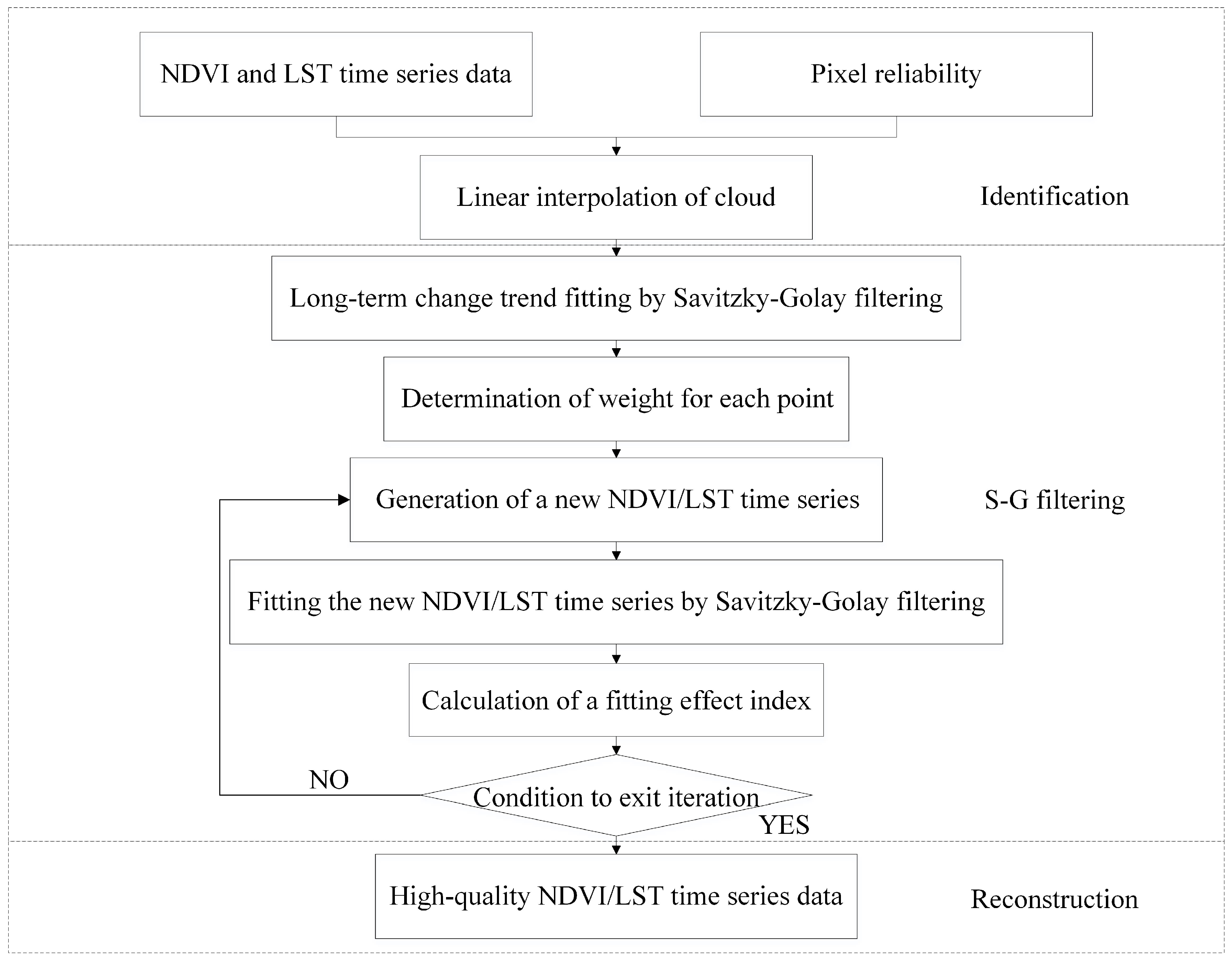
2.3. Savitzky–Golay (S-G) Filtering
2.4. Data Processing
2.5. Statistical methods
2.5.1. Extreme-Point Symmetric Mode Decomposition (ESMD)
2.5.2. The Modified Mann–Kendall (MMK) trend test method
2.5.3. Skill Score (SS)
3. Results
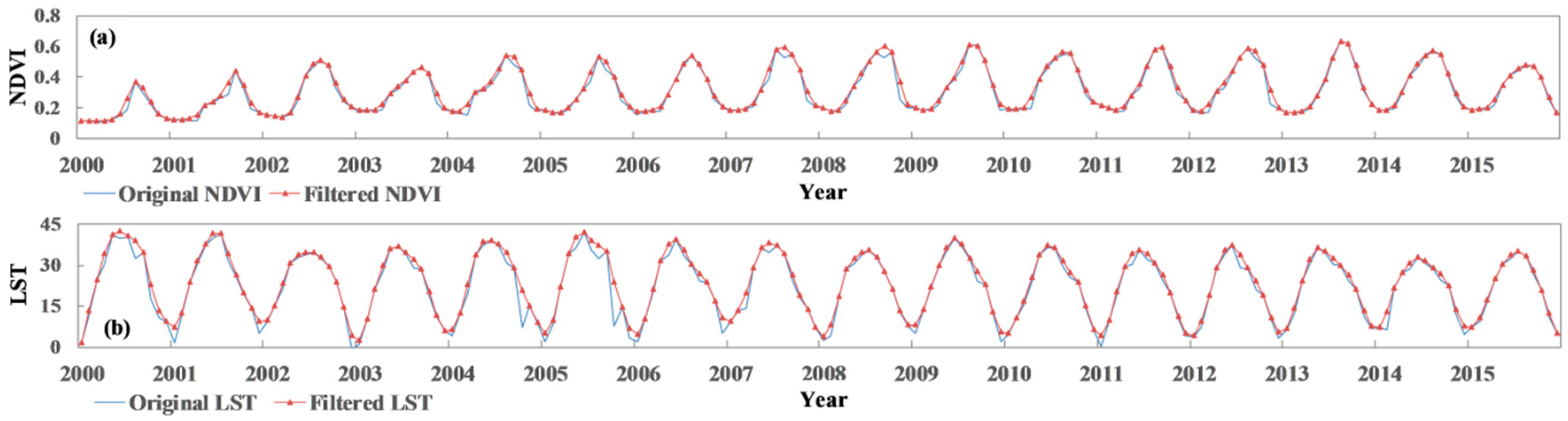
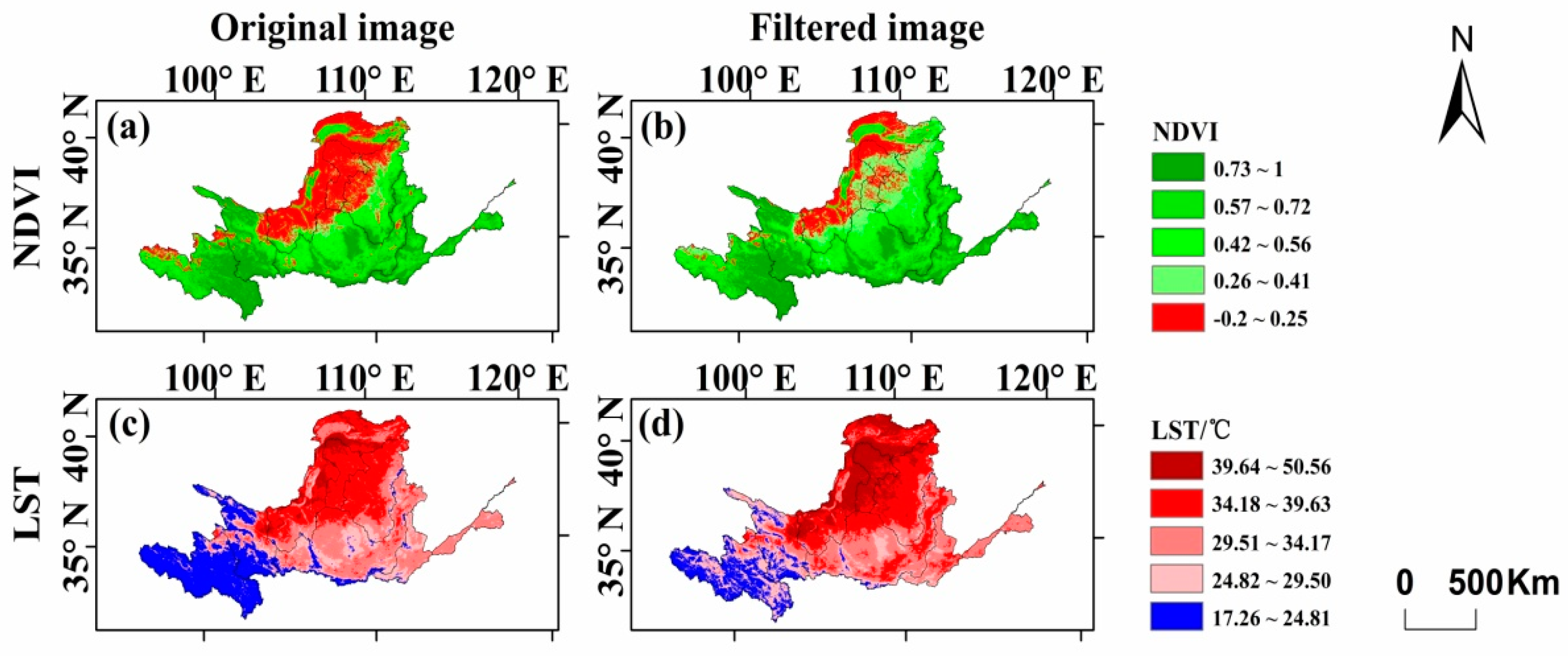
3.1. Reconstruction of NDVI and LST time series data
3.2. Temporal and spatial characteristics of drought
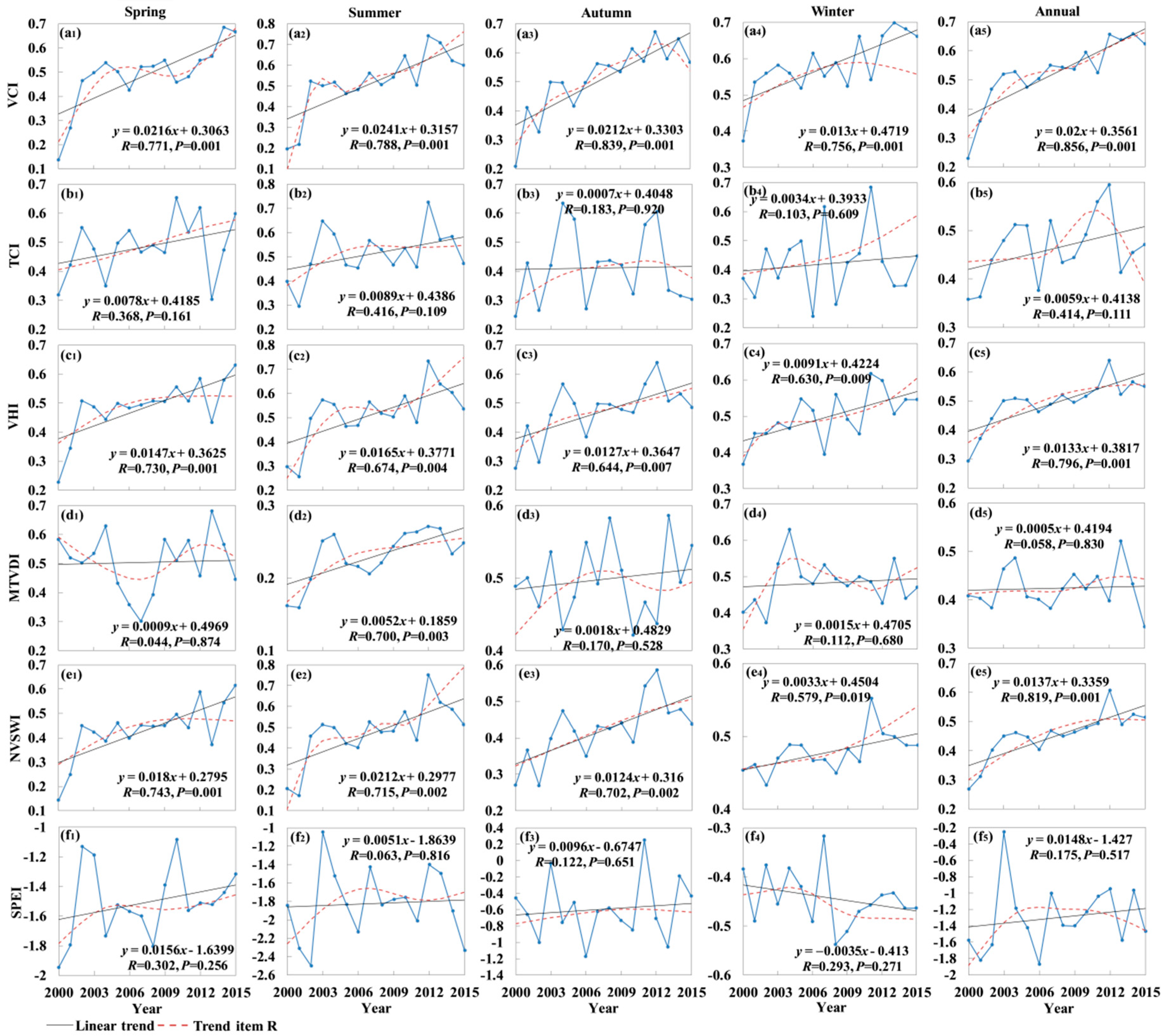
3.2.1. Temporal characteristics
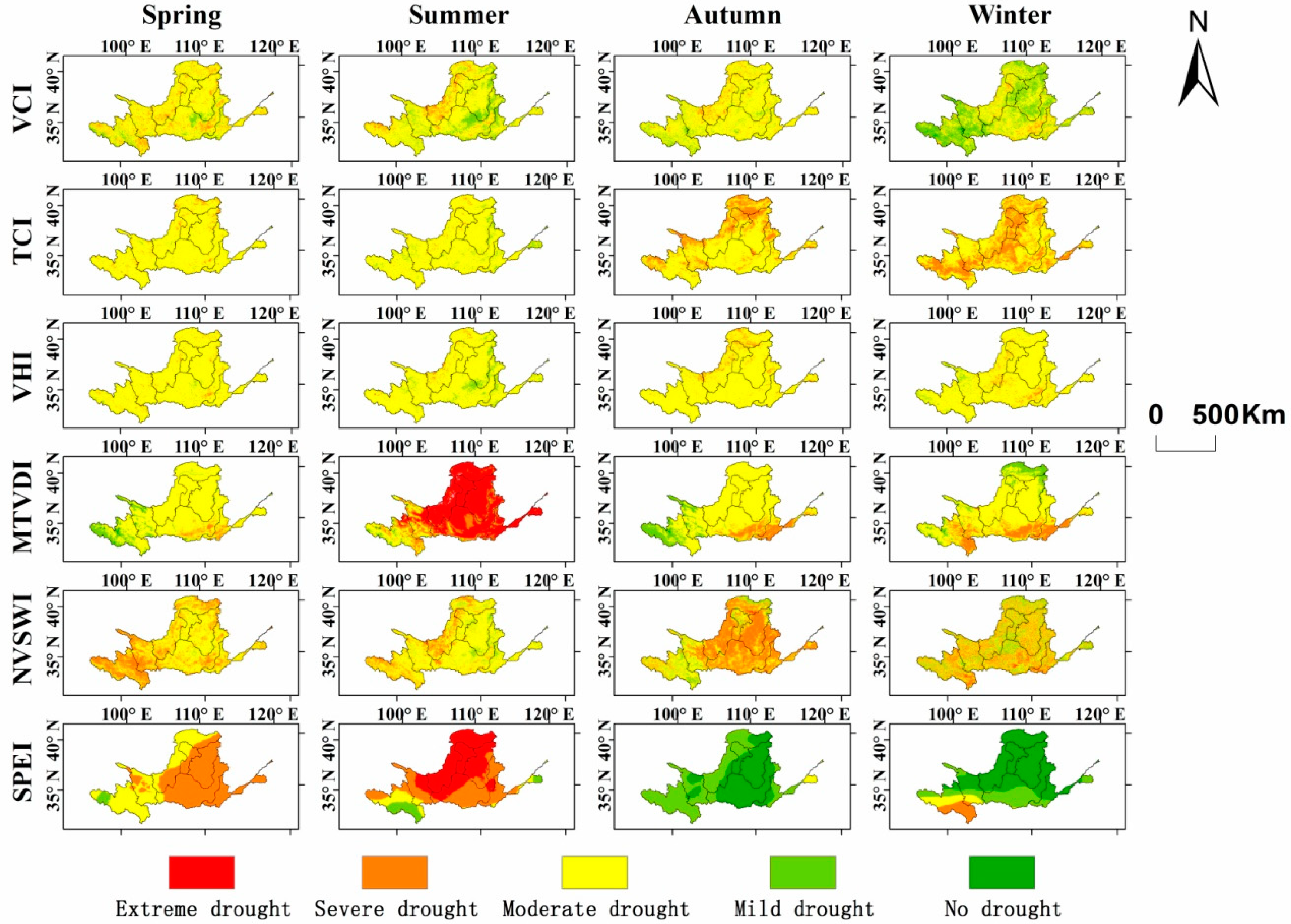
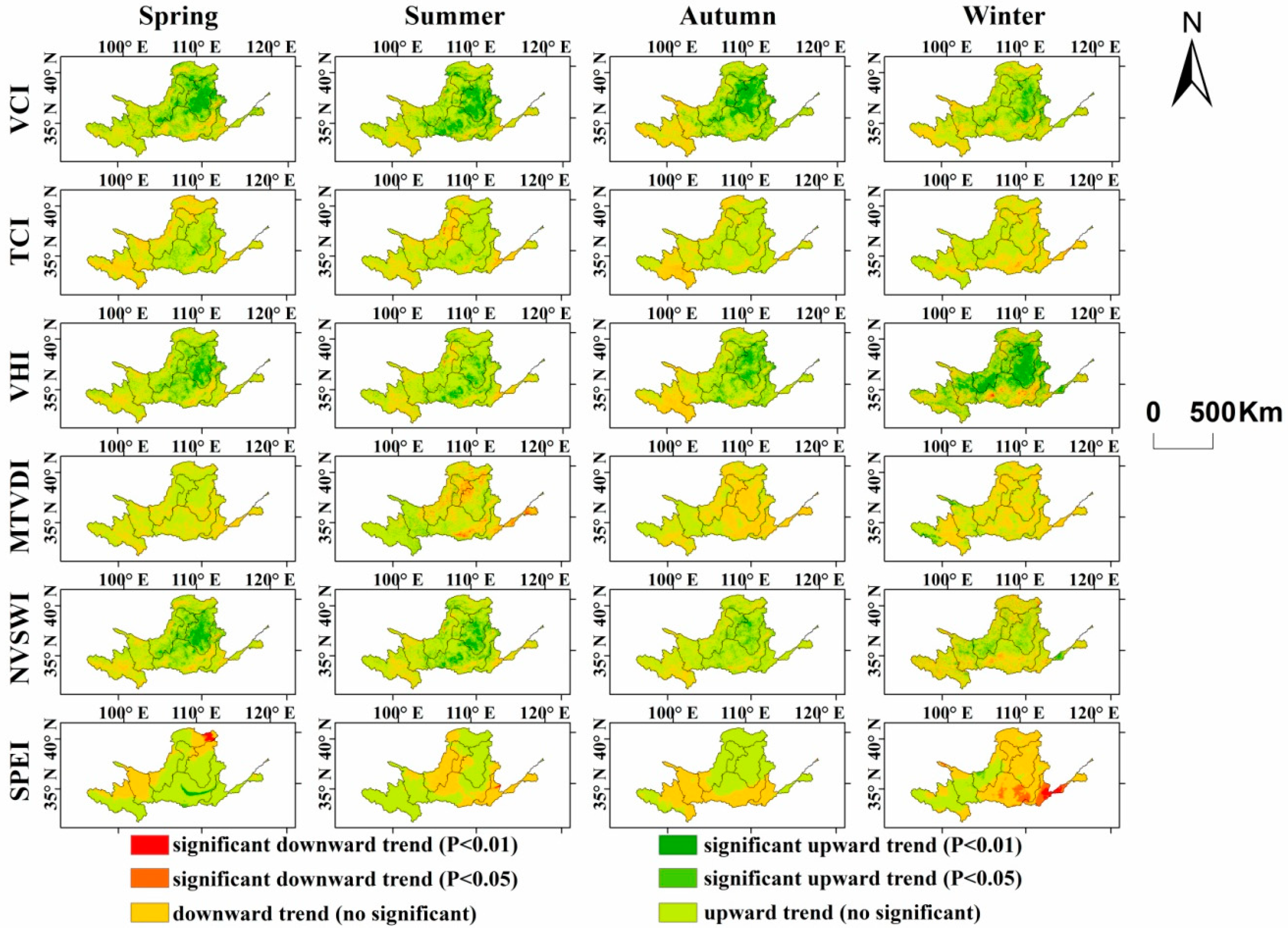
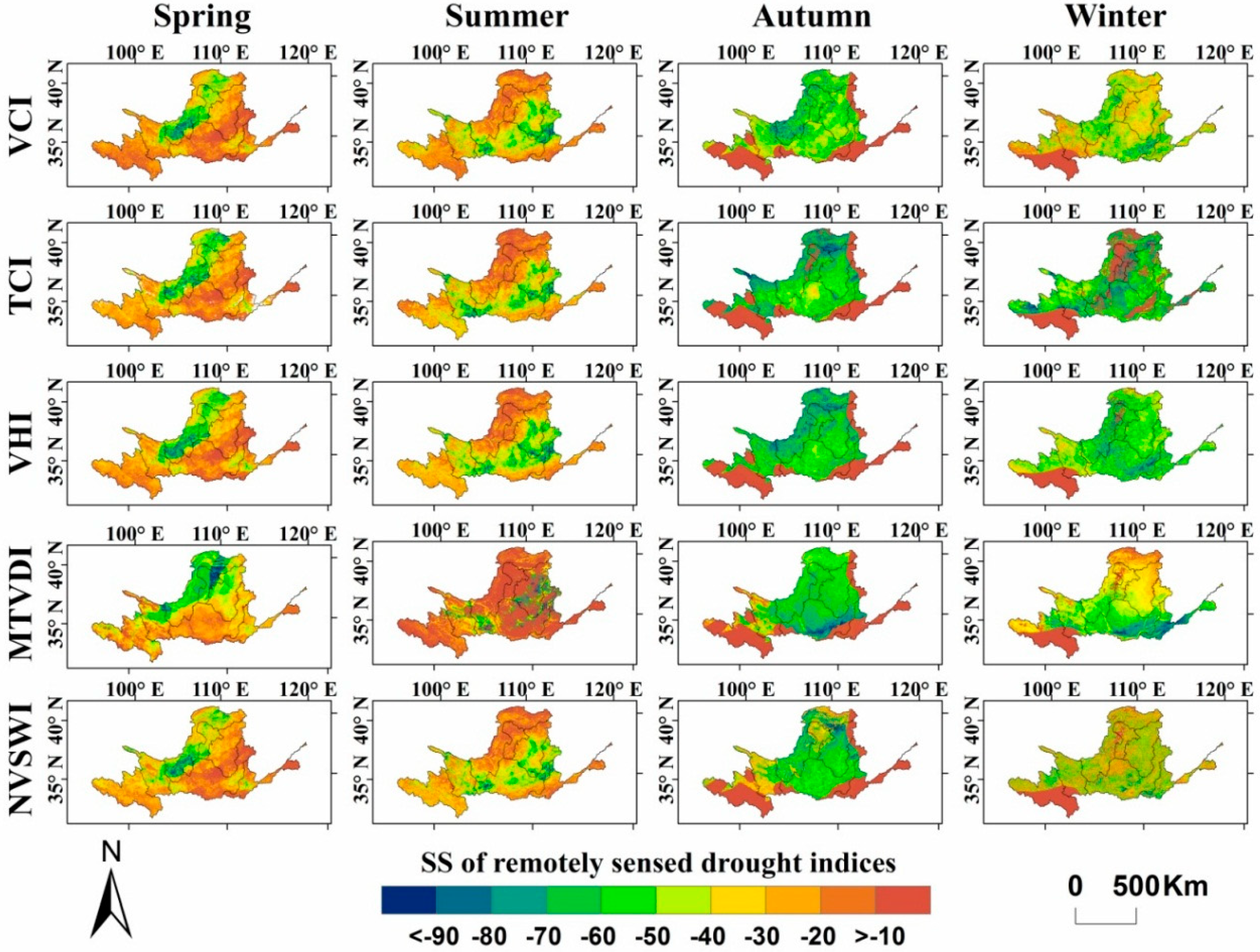
3.2.2. Spatial distribution
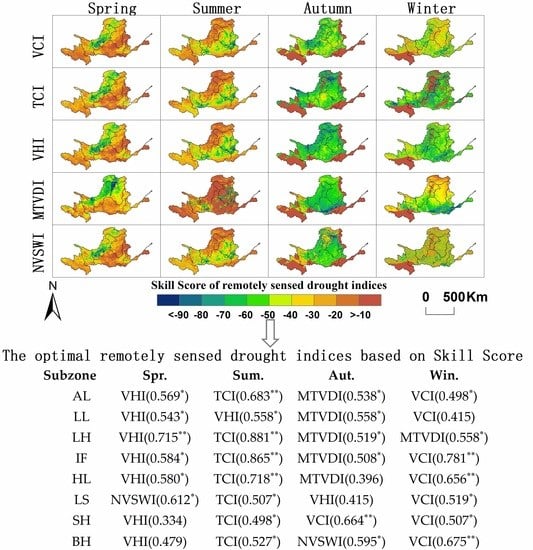
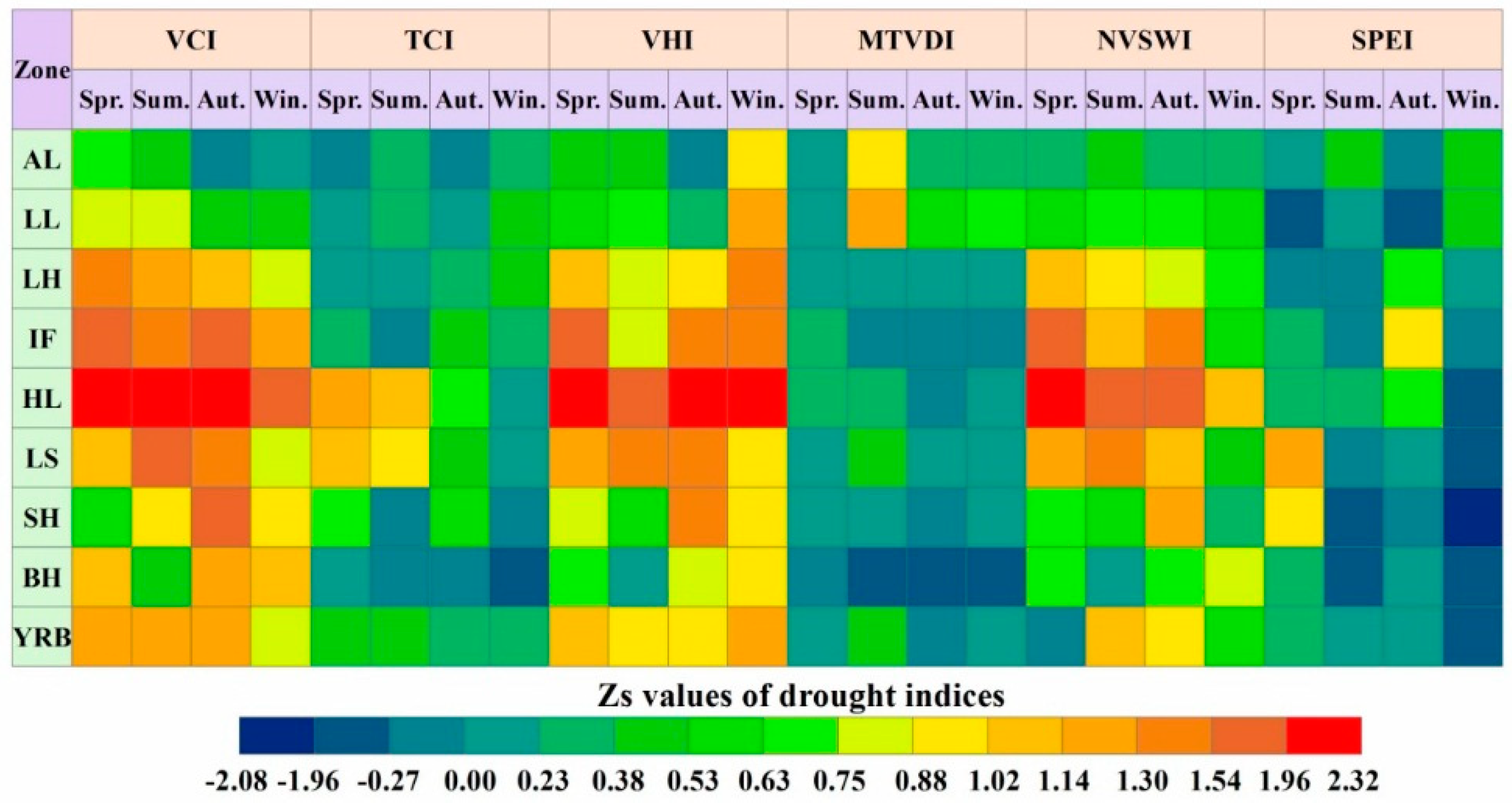
3.3. Capability of remotely sensed drought indices
4. Discussion
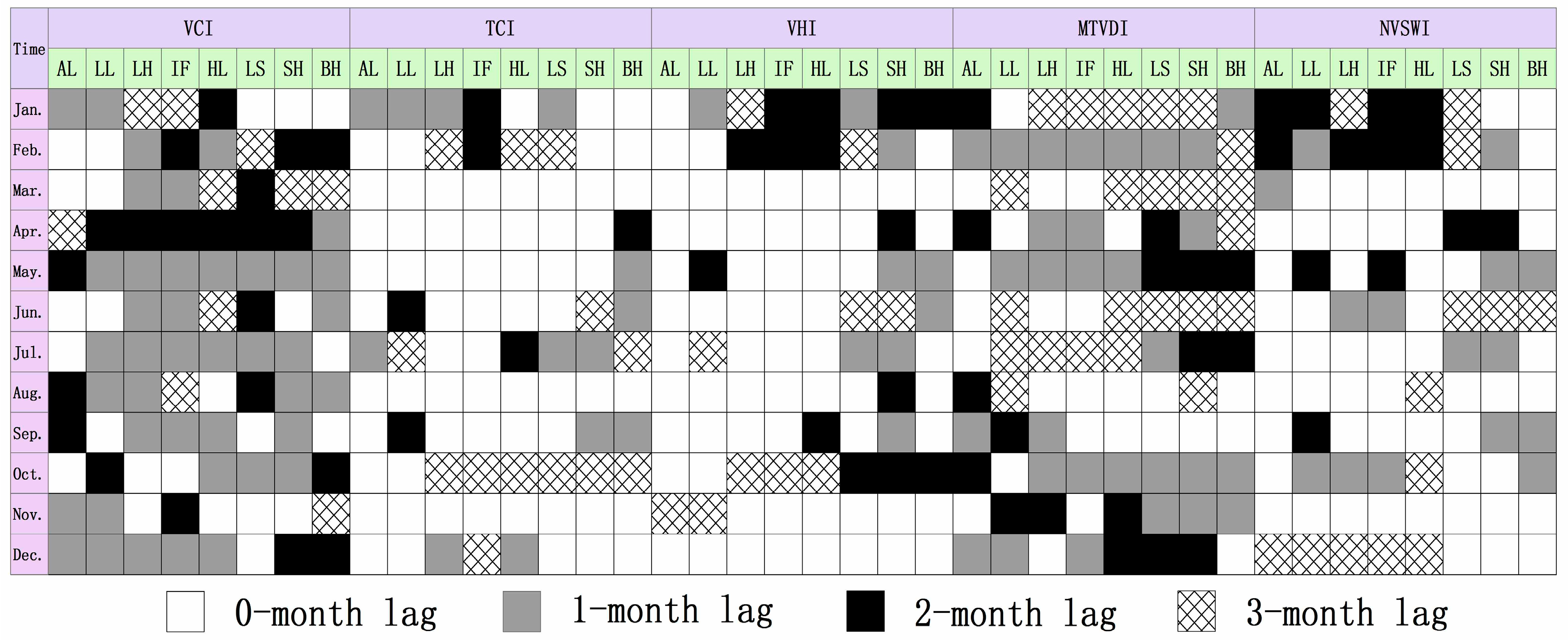
4.1. Hysteresis analysis
4.2. Drought evolution in the YRB
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, S.Z.; Chang, J.X.; Leng, G.Y.; Huang, Q. Integrated index for drought assessment based on variable fuzzy set theory: A case study in the Yellow River Basin, China. J. Hydrol. 2015, 527, 608–618. [Google Scholar] [CrossRef]
- Yao, J.Q.; Zhao, Y.; Chen, Y.N.; Yu, X.J.; Zhang, R.B. Multi-scale assessments of droughts: A case study in Xinjiang, China. Sci. Total Environ. 2018, 630, 444–452. [Google Scholar] [CrossRef] [PubMed]
- Yao, N.; Li, Y.; Lei, T.J.; Peng, L.L. Drought evolution, severity and trends in mainland China over 1961–2013. Sci. Total Environ. 2017, 616, 73–89. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Xia, J.; Zhang, Y.Y.; Zhan, C.S.; Qiao, Y.F. Comprehensive assessment of drought risk in the arid region of Northwest China based on the global palmer drought severity index gridded data. Sci. Total Environ. 2018, 627, 951–962. [Google Scholar] [CrossRef] [PubMed]
- Xia, L.; Zhao, F.; Mao, K.B.; Yuan, Z.J.; Zuo, Z.Y.; Xu, T.R. SPI-based analyses of drought changes over the past 60 years in China’s major crop-growing areas. Remote Sens. 2018, 10, 171. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought Research Paper 45; US Weather Bureau: Washington, DC, USA, 1965.
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. Am. Meteorol. Soc. 1993, 58, 174–184. [Google Scholar]
- Lopez-Moreno, J.I.; Vicente-Serrano, S.M.; Zabalzaa, J.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Hydrological response to climate variability at different time scales: A study in the Ebro basin. J. Hydrol. 2013, 477, 175–188. [Google Scholar] [CrossRef]
- Dorjsuren, M.; Liou, Y.A.; Cheng, C.H. Time series MODIS and in situ data analysis for Mongolia drought. Remote Sens. 2016, 8, 509. [Google Scholar] [CrossRef]
- Islam, M.M.; Shamsuddoha, M. Coastal and marine conservation strategy for Bangladesh in the context of achieving blue growth and sustainable development goals (SDGs). Environ. Sci. Policy. 2018, 87, 45–54. [Google Scholar] [CrossRef]
- Salvia, A.L.; Filho, W.L.; Brandli, L.L.; Griebeler, J.S. Assessing research trends related to Sustainable Development Goals: local and global issues. J. Clean. Prod. 2019, 208, 841–849. [Google Scholar] [CrossRef]
- Winkler, K.; Gessner, U.; Hochschild, V. Identifying droughts affecting agriculture in Africa based on remote sensing time series between 2000–2016: rainfall anomalies and vegetation condition in the context of ENSO. Remote Sens. 2017, 9, 831. [Google Scholar] [CrossRef]
- Wu, D.; Qu, J.J.; Hao, X.J. Agricultural drought monitoring using MODIS-based drought indices over the USA Corn Belt. Int. J. Remote Sens. 2015, 36, 5403–5425. [Google Scholar] [CrossRef]
- Cong, D.M.; Zhao, S.H.; Chen, C.; Duan, Z. Characterization of droughts during 2001-2014 based on remote sensing: A case study of Northeast China. Ecol. Inform. 2017, 39, 56–67. [Google Scholar] [CrossRef]
- Kogan, F.N. Droughts of the late 1980s in the United States as derived from NOAA polar-orbiting satellite data. B. Am. Meteorol. Soc. 1995, 76, 655–668. [Google Scholar] [CrossRef]
- Zambrano, F.; Lillo-Saavedra, M.; Verbist, K.; Lagos, O. Sixteen years of agricultural drought assessment of the BioBío region in Chile using a 250 m resolution Vegetation Condition Index (VCI). Remote Sens. 2016, 8, 530. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Chang, S.; Wu, B.F.; Yan, N.; Davdai, B.; Nasanbat, E. Suitability assessment of satellite-derived drought indices for Mongolian Grassland. Remote Sens. 2017, 9, 650. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Wang, P.X.; Gong, J.Y.; Li, X.W. Vegetation-Temperature condition index and its application for drought monitoring. Geomat. Inform. Sci. Wuhan Univ. 2001, 26, 412–418. (In Chinese) [Google Scholar]
- Abbas, S.; Nichol, J.E.; Qamer, F.M.; Xu, J.C. Characterization of drought development through Remote Sensing: A case study in Central Yunnan, China. Remote Sens. 2014, 6, 4998–5018. [Google Scholar] [CrossRef]
- Nichol, J.E.; Abbas, S. Integration of remote sensing datasets for local scale assessment and prediction of drought. Sci. Total Environ. 2015, 505, 503–507. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.W.; Liu, M.; Liu, L. Responses of MODIS spectral indices to typical drought events from 2000 to 2012 in southwest China. J. Remote Sens. 2014, 18, 432–452. [Google Scholar]
- Klisch, A.; Atzberger, C. Operational drought monitoring in Kenya using MODIS NDVI time series. Remote Sens. 2016, 8, 267. [Google Scholar] [CrossRef]
- Zhang, L.F.; Jiao, W.Z.; Zhang, H.M.; Huang, C.P.; Tong, Q.X. Studying drought phenomena in the Continental United States in 2011 and 2012 using various drought indices. Remote Sens. Environ. 2017, 190, 96–106. [Google Scholar] [CrossRef]
- Hao, C.; Zhang, J.H.; Yao, F.M. Combination of multi-sensor remote sensing data for drought monitoring over Southwest China. Int J Appl Earth Obs. 2015, 35, 270–283. [Google Scholar] [CrossRef]
- Du, L.T.; Tian, Q.J.; Yu, T.; Meng, Q.Y.; Jancso, T.; Udvardy, P.; Huang, Y. A comprehensive drought monitoring method integrating MODIS and TRMM data. Int J Appl Earth Obs. 2013, 23, 245–253. [Google Scholar] [CrossRef]
- Zhang, J.; Mu, Q.Z.; Huang, J.X. Assessing the remotely sensed drought severity index for agricultural drought monitoring and impact analysis in North China. Ecol. Indic. 2016, 63, 296–309. [Google Scholar] [CrossRef]
- Zhang, X.; Wei, C.H.; Obringer, R.; Li, D.; Chen, N.C.; Niyogi, D. Gauging the severity of the 2012 Midwestern U.S. drought for agriculture. Remote Sens. 2017, 9, 767. [Google Scholar] [CrossRef]
- Pierce, D.W.; Barnett, T.P.; Santer, B.D.; Gleckler, P.J. Selecting global climate models for regional climate change studies. Proc. Natl. Acad. Sci. 2009, 106, 8441–8446. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wu, Y.Z.; Feng, Z.Z.; Huang, X.R.Z.; Wang, D.G. Evaluation of a variety of satellite retrieved precipitation products based on extreme rainfall in China. Trop. Geogr. 2017, 37, 417–433. (In Chinese) [Google Scholar]
- Chen, W.L.; Jiang, Z.H.; Li, L. Probabilistic projections of climate change over China under the SRES A1B scenario using 28 AOGCMs. J. Climate. 2011, 24, 4741–4756. [Google Scholar] [CrossRef]
- Zhang, B.Q.; He, C.S.; Morey, B.; Zhang, L.H. Evaluating the coupling effects of climate aridity and vegetation restoration on soil erosion over the Loess Plateau in China. Sci. Total Environ. 2016, 539, 436–449. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.H.; Zhou, M.; Ren, L.L.; Cheng, X.R.; Zhang, P.J. Evaluation of latest TMPA and CMORPH satellite precipitation products over Yellow River Basin. Water Sci. Eng. 2016, 9, 87–96. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Gao, G.; An, W.; Zou, X.K.; Li, H.T.; Hou, M.T. Timescale differences between SC-PDSI and SPEI for drought monitoring in China. Phys. Chem. Earth. 2015, 10, 1–11. [Google Scholar] [CrossRef]
- Zhang, B.Q.; Zhao, X.N.; Jin, J.M.; Wu, P. Development and evaluation of a physically based multiscalar drought index: The Standardized Moisture Anomaly Index. J. Geophys. Res. 2015, 120, 11575–11588. [Google Scholar] [CrossRef]
- Beck, P.S.A.; Atzberger, C.; Høgda, K.A.; Johansen, B.; Skidmore, A.K. Improved monitoring of vegetation dynamics at very high latitudes: A new method using MODIS NDVI. Remote Sens. Environ. 2005, 100, 321–334. [Google Scholar] [CrossRef]
- Vuolo, F.; Ng, W.T.; Atzberger, C. Smoothing and gap-filling of high resolution multi-spectral time series: Example of Landsat data. Int J Appl Earth Obs. 2017, 57, 202–213. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.H.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series dataset based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Wang, J.L.; Li, Z.J. The ESMD method for climate data analysis. Clim. Change Res. Lett. 2014, 3, 1–5. [Google Scholar] [CrossRef]
- Li, H.F.; Wang, J.L.; Li, Z.J. Application of ESMD method to air-sea flux investigation. Int. J. Geos. 2013, 4, 8–11. [Google Scholar] [CrossRef]
- Huang, S.Z.; Chang, J.X.; Huang, Q.; Chen, Y.T. Spatio-temporal changes and frequency analysis of drought in the Wei River basin, China. Water Resour. Manag. 2014, 28, 3095–3110. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H.; Nadoushani, S.S.M.; Willems, P.; Marchetto, A. A survey of temperature and precipitation based aridity indices in Iran. Quatern. Int. 2014, 345, 158–166. [Google Scholar] [CrossRef]
- Huang, S.Z.; Huang, Q.; Zhang, H.B.; Chen, Y.T.; Leng, G.Y. Spatio-temporal changes in precipitation, temperature and their possibly changing relationship: a case study in the Wei River Basin, China. Int. J. Climatol. 2016, 36, 1160–1169. [Google Scholar] [CrossRef]
- Jiang, Z.H.; Lu, Y.; Ding, Y.G. Analysis of the high-resolution merged precipitation products over China based on the temporal and spatial structure score indices. Acta. Meteorol. Sin. 2013, 71, 891–900. [Google Scholar]
- Potopová, V.; Štěpánek, P.; Možný, M.; Türkott, L.; Soukup, J. Performance of the standardised precipitation evapotranspiration index at various lags for agricultural drought risk assessment in the Czech Republic. Agr. Forest Entomol. 2015, 202, 26–38. [Google Scholar] [CrossRef]
- Caccamo, G.; Chisholm, L.A.; Bradstock, R.A.; Puotinen, M.L. Assessing the sensitivity of MODIS to monitor drought in high biomass ecosystems. Remote Sens. Environ. 2011, 115, 2626–2639. [Google Scholar] [CrossRef]
- Wang, H.S.; Lin, H.; Liu, D.S. Remotely sensed drought Index and its responses to meteorological drought in Southwest China. Remote Sens. Lett. 2014, 5, 413–422. [Google Scholar] [CrossRef]
- Ji, L.; Peters, A.J. Assessing vegetation response to drought in the northern Great Plains using vegetation and drought indices. Remote Sens Environ. 2003, 87, 85–98. [Google Scholar] [CrossRef]
- Yuan, L.H.; Jiang, W.G.; Shen, W.M.; Liu, Y.H.; Wang, W.J.; Tao, L.L.; Zheng, H.; Liu, X.F. The spatial-temporal variations of vegetation cover in the Yellow River Basin from 2000 to 2010. Acta. Ecol. Sin. 2013, 33, 7798–7806. (In Chinese) [Google Scholar]
- Zhao, Q.; Chen, Q.Y.; Jiao, M.Y.; Wu, P.T.; Gao, X.R.; Ma, M.H.; Hong, Y. The temporal-spatial characteristics of drought in the Loess Plateau using the remote-sensed TRMM precipitation data from 1998 to 2014. Remote Sens. 2018, 10, 838. [Google Scholar] [CrossRef]
- Tang, Y.; Sun, R. Drought characteristics in Henan province with meteorological and remote sensing data. J. Nat. Resour. 2013, 28, 646–655. (In Chinese) [Google Scholar]
- Pablos, M.; Martínez-Fernández, J.; Sánchez, N.; González-Zamora, Á. Temporal and spatial comparison of agricultural drought indices from moderate resolution satellite soil moisture data over Northwest Spain. Remote Sens. 2017, 9, 1168. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Su, H.M.; Zhang, X.Y. The spatial-temporal changes of vegetation restoration in the Yellow River Basin from 1998 to 2012. J. Desert Res. 2014, 34, 597–602. (In Chinese) [Google Scholar]
- Jiang, W.G.; Yuan, L.H.; Wang, W.J.; Cao, R.; Zhang, Y.F.; Shen, W.M. Spatio-temporal analysis of vegetation variation in the Yellow River Basin. Ecol. Indic. 2015, 51, 117–126. [Google Scholar] [CrossRef]
- Gao, X.R.; Sun, M.; Zhao, Q.; Wu, P.T.; Zhao, X.N.; Pan, W.X.; Wang, Y.B. Actual ET modelling based on the Budyko framework and the sustainability of vegetation water use in the loess plateau. Sci. Total Environ. 2017, 579, 1550–1559. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.Z.; Huang, Q.; Chang, J.X.; Zhu, Y.L.; Leng, G.Y.; Xing, L. Drought structure based on a nonparametric multivariate standardized drought index across the Yellow River basin, China. J. Hydrol. 2015, 530, 127–136. [Google Scholar] [CrossRef]
- Liu, Q.; Yan, C.R.; He, W.Q. Drought variation and its sensitivity coefficients to climatic factors in the Yellow River Basin. Chin. J. Agrometeorol. 2016, 37, 623–632. (In Chinese) [Google Scholar]
| Index | Range | Formula | Parameter | Source |
|---|---|---|---|---|
| VCI | [0,1] | NDVIi is the NDVI value of a certain period, and NDVImax and NDVImin are the maximum and minimum NDVI values in multi-year dataset. | [13] | |
| TCI | [0,1] | LSTi is the LST value of a certain period, and LSTmax and LSTmin are the maximum and minimum LST values in multi-year dataset. | [15] | |
| VHI | [0,1] | a and b are used to show the contributions of VCI and TCI to VHI. Here we assume that the contributions are equal (a = b = 0.5). | [15] | |
| MTVDI | [0,1] | LSTs is the land surface temperature of an arbitrary pixel, and LSTsmin and LSTsmax are LST values on wet edge and dry edge. LSTsmin and LSTsmax are calculated by groups of points at the lower and upper limits of the scatterplots, where LSTsmin is the minimum LST for a given NDVI (wet edge), and LSTsmax is the maximum LST for a given NDVI (dry edge). | [18] | |
| NVSWI | [0,1] | VSWIi is the VSWI value of a certain period, VSWImax and VSWImin are the maximum and minimum VSWI values in multi-year dataset. | [19] |
| Grade | Classification | VCI | TCI | VHI | MTVDI | NVSWI | SPEI |
|---|---|---|---|---|---|---|---|
| 1 | No drought | [0.8,1] | [0.8,1] | [0.8,1] | [0.8,1] | [0.8,1] | (−0.5,+∞) |
| 2 | Mild drought | [0.6,0.8) | [0.6,0.8) | [0.6,0.8) | [0.6,0.8) | [0.6,0.8) | (−1, −0.5] |
| 3 | Moderate drought | [0.4,0.6) | [0.4,0.6) | [0.4,0.6) | [0.4,0.6) | [0.4,0.6) | (−1.5, −1] |
| 4 | Severe drought | [0.2,0.4) | [0.2,0.4) | [0.2,0.4) | [0.2,0.4) | [0.2,0.4) | (−2,−1.5] |
| 5 | Extreme drought | [0,0.2) | [0,0.2) | [0,0.2) | [0,0.2) | [0,0.2) | (−∞, −2] |
| Interpolation methods | MRE | RMSE | R | |
|---|---|---|---|---|
| Inverse Distance Weighting | IDW | 1.11 | 1.05 | 0.91 |
| Polynomial Interpolation | Global PI | 2.60 | 1.75 | 0.71 |
| Local PI | 1.49 | 1.09 | 0.90 | |
| Radial Basis Function | Completely Regularized Spline | 0.03 | 0.19 | 0.99 |
| Spline With Tension | 0.03 | 0.19 | 0.99 | |
| Multiquadric Spline | 0.04 | 0.21 | 0.99 | |
| Inverse Multiquadric Spline | 0.03 | 0.19 | 0.99 | |
| Thin Plate Spline | 0.03 | 0.19 | 0.99 | |
| Kriging Interpolation | Ordinary Kriging | 0.01 | 0.18 | 0.99 |
| Universal Kriging | 1.87 | 1.35 | 0.84 | |
| Subzone | Spr. | Sum. | Aut. | Win. |
|---|---|---|---|---|
| AL | VHI(0.569∗) | TCI(0.683∗∗) | MTVDI(0.538∗) | VCI(0.498∗) |
| LL | VHI(0.543∗) | VHI(0.558∗) | MTVDI(0.558∗) | VCI(0.415) |
| LH | VHI(0.715∗∗) | TCI(0.881∗∗) | MTVDI(0.519∗) | MTVDI(0.558∗) |
| IF | VHI(0.584∗) | TCI(0.865∗∗) | MTVDI(0.508∗) | VCI(0.781∗∗) |
| HL | VHI(0.580∗) | TCI(0.718∗∗) | MTVDI(0.396) | VCI(0.656∗∗) |
| LS | NVSWI(0.612∗) | TCI(0.507∗) | VHI(0.415) | VCI(0.519∗) |
| SH | VHI(0.334) | TCI(0.498∗) | VCI(0.664∗∗) | VCI(0.507∗) |
| BH | VHI(0.479) | TCI(0.527∗) | NVSWI(0.595∗) | VCI(0.675∗∗) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Wang, Z.; Yang, H.; Zhao, Y.; Li, Z.; Wu, J. Capability of Remotely Sensed Drought Indices for Representing the Spatio–Temporal Variations of the Meteorological Droughts in the Yellow River Basin. Remote Sens. 2018, 10, 1834. https://doi.org/10.3390/rs10111834
Wang F, Wang Z, Yang H, Zhao Y, Li Z, Wu J. Capability of Remotely Sensed Drought Indices for Representing the Spatio–Temporal Variations of the Meteorological Droughts in the Yellow River Basin. Remote Sensing. 2018; 10(11):1834. https://doi.org/10.3390/rs10111834
Chicago/Turabian StyleWang, Fei, Zongmin Wang, Haibo Yang, Yong Zhao, Zhenhong Li, and Jiapeng Wu. 2018. "Capability of Remotely Sensed Drought Indices for Representing the Spatio–Temporal Variations of the Meteorological Droughts in the Yellow River Basin" Remote Sensing 10, no. 11: 1834. https://doi.org/10.3390/rs10111834
APA StyleWang, F., Wang, Z., Yang, H., Zhao, Y., Li, Z., & Wu, J. (2018). Capability of Remotely Sensed Drought Indices for Representing the Spatio–Temporal Variations of the Meteorological Droughts in the Yellow River Basin. Remote Sensing, 10(11), 1834. https://doi.org/10.3390/rs10111834