Sentinel-1 and Ground-Based Sensors for Continuous Monitoring of the Corvara Landslide (South Tyrol, Italy)
Abstract
1. Introduction
2. Material
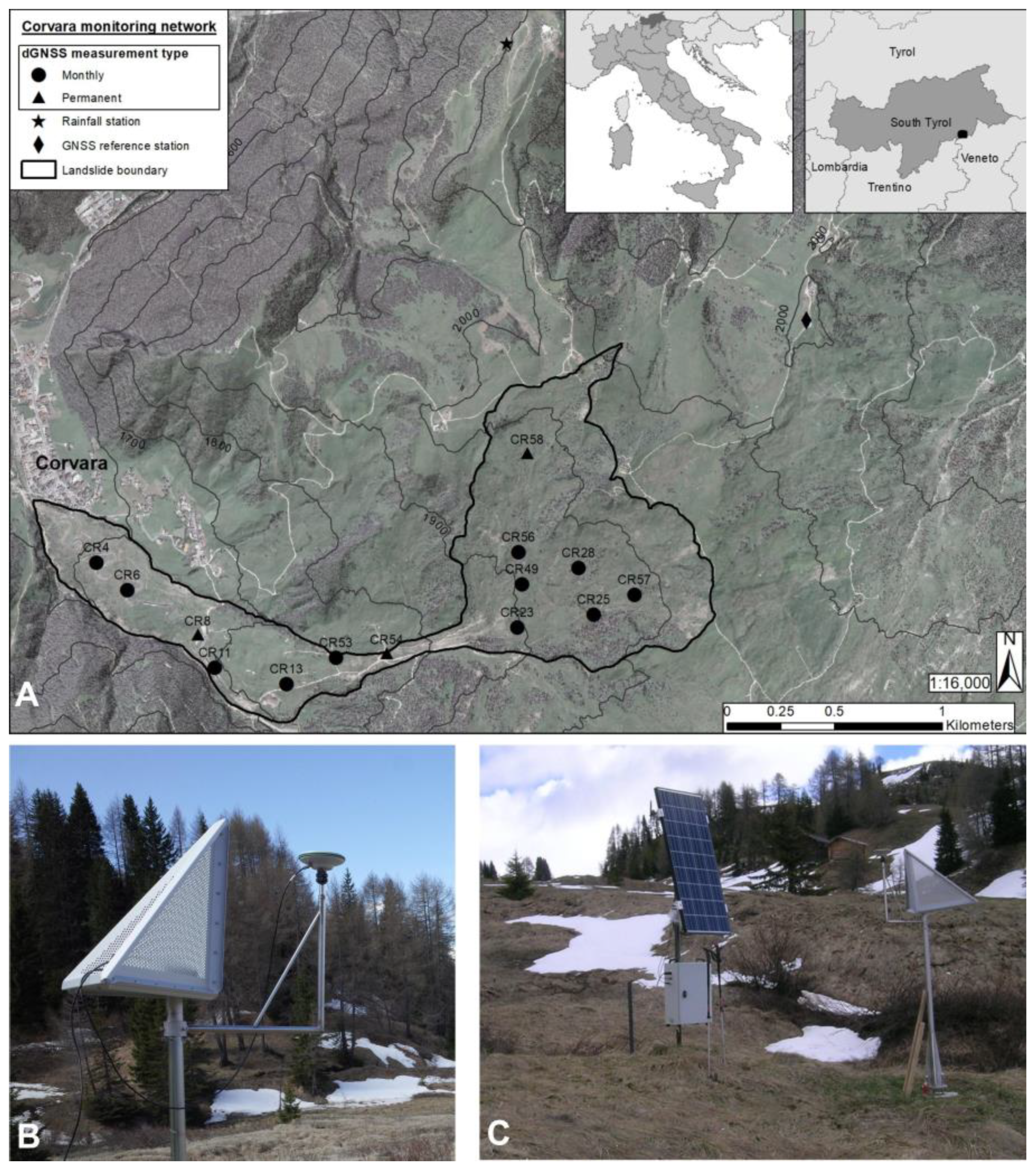
2.1. Study Site
2.2. Data
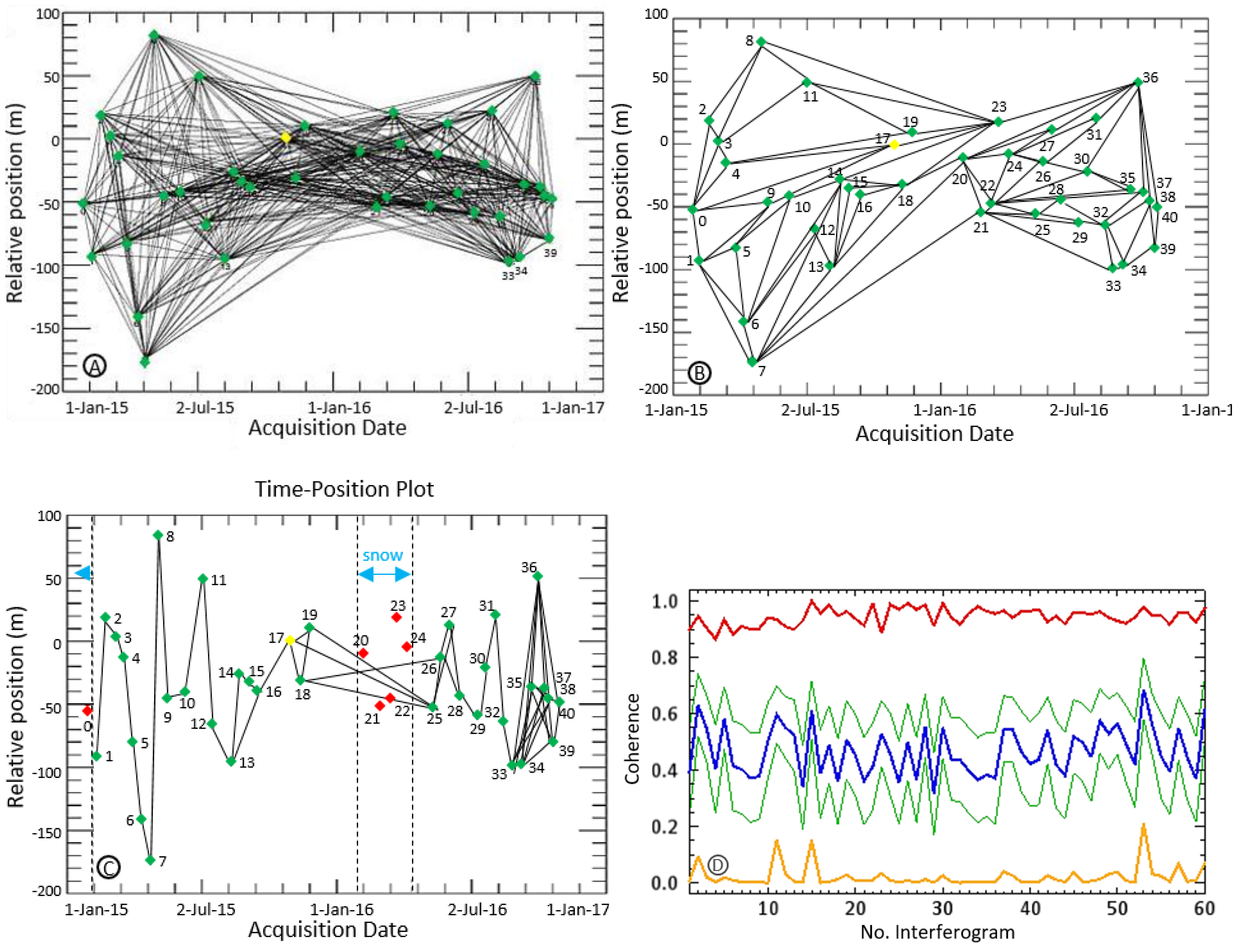
3. Methods
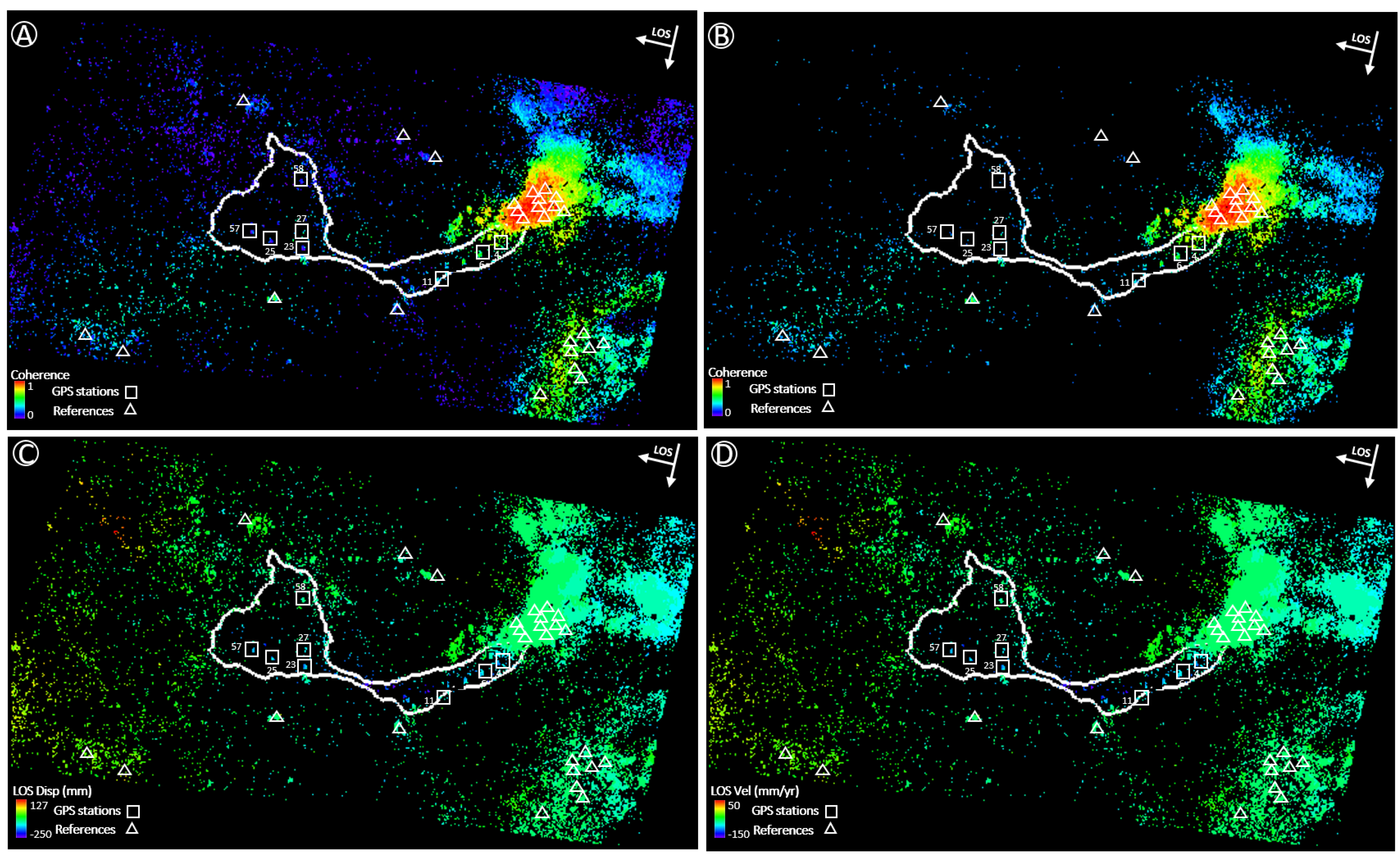
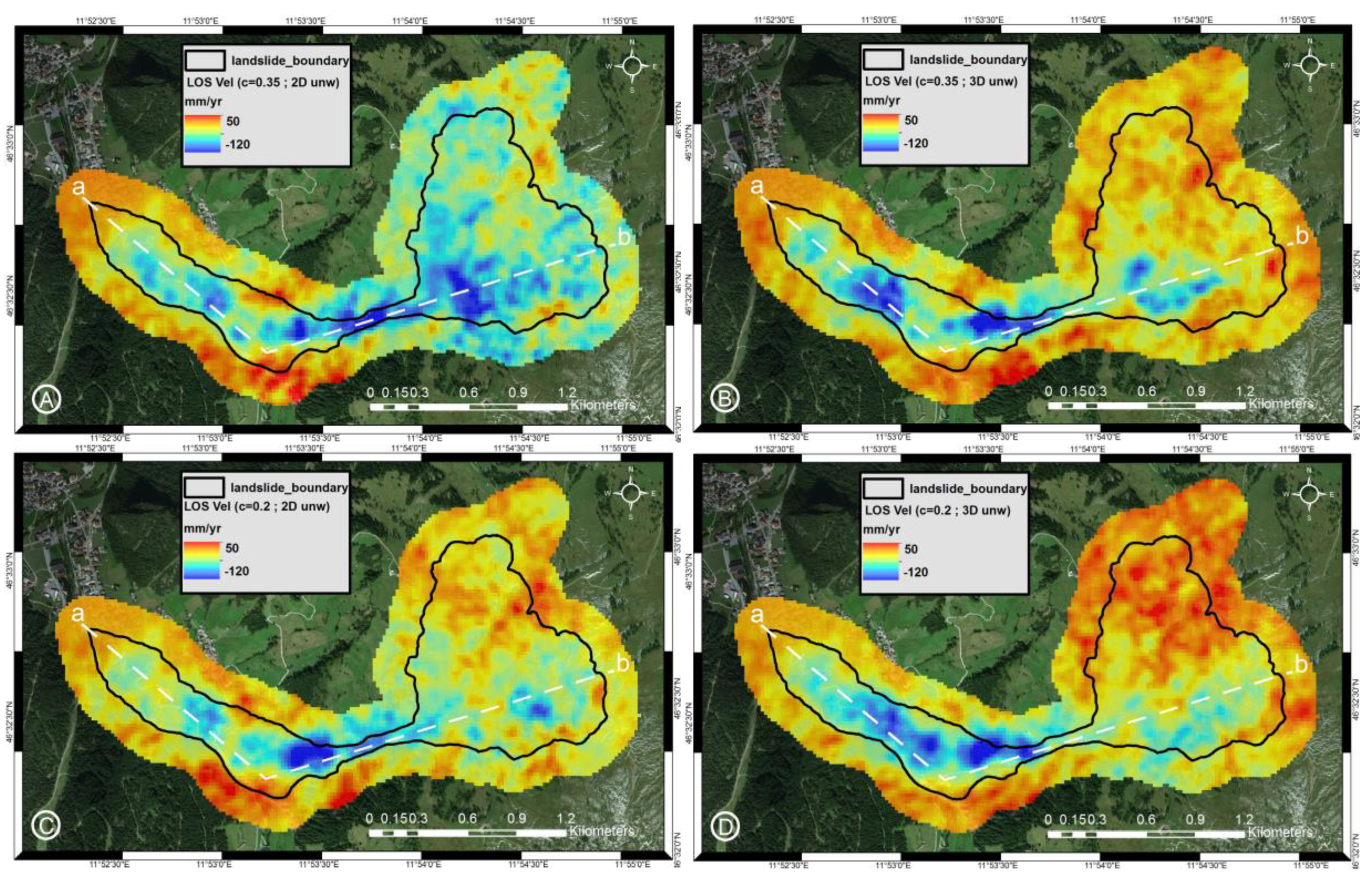
4. Results
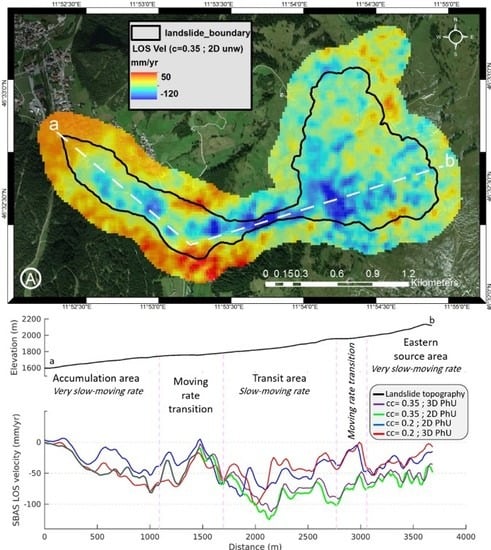
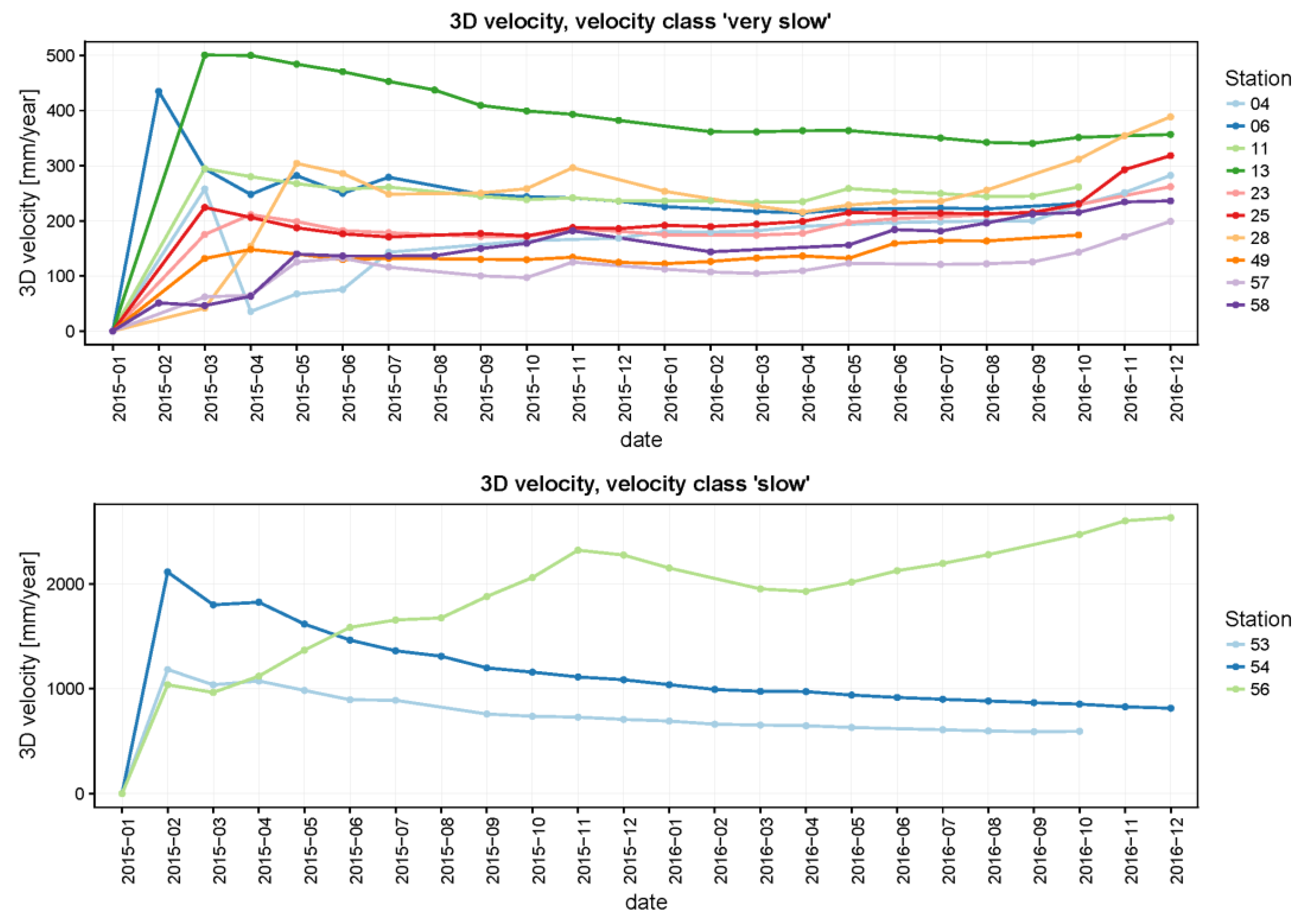
4.1. Sentinel-1 DInSAR Analysis
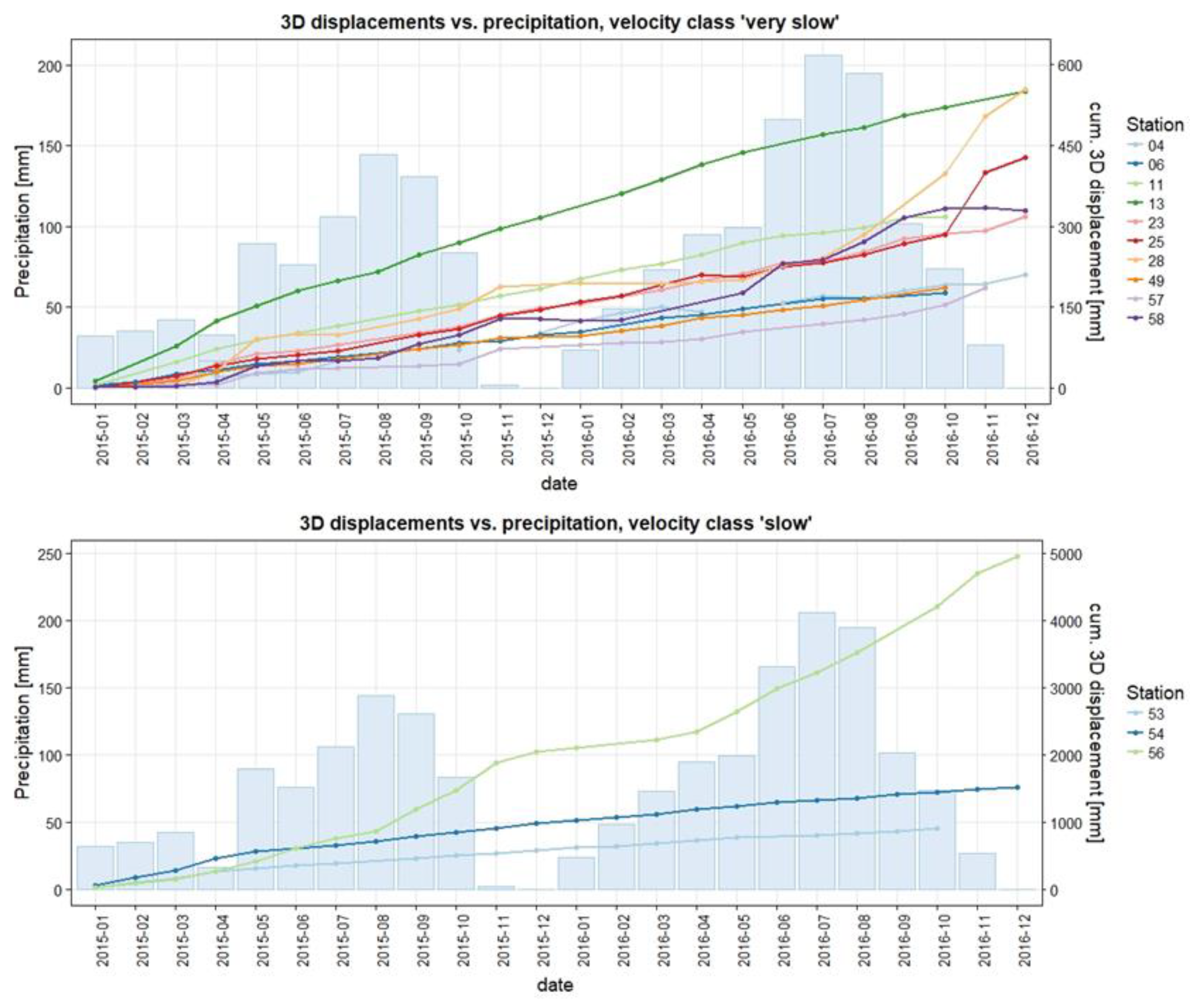
4.2. DGNSS Monitoring Results
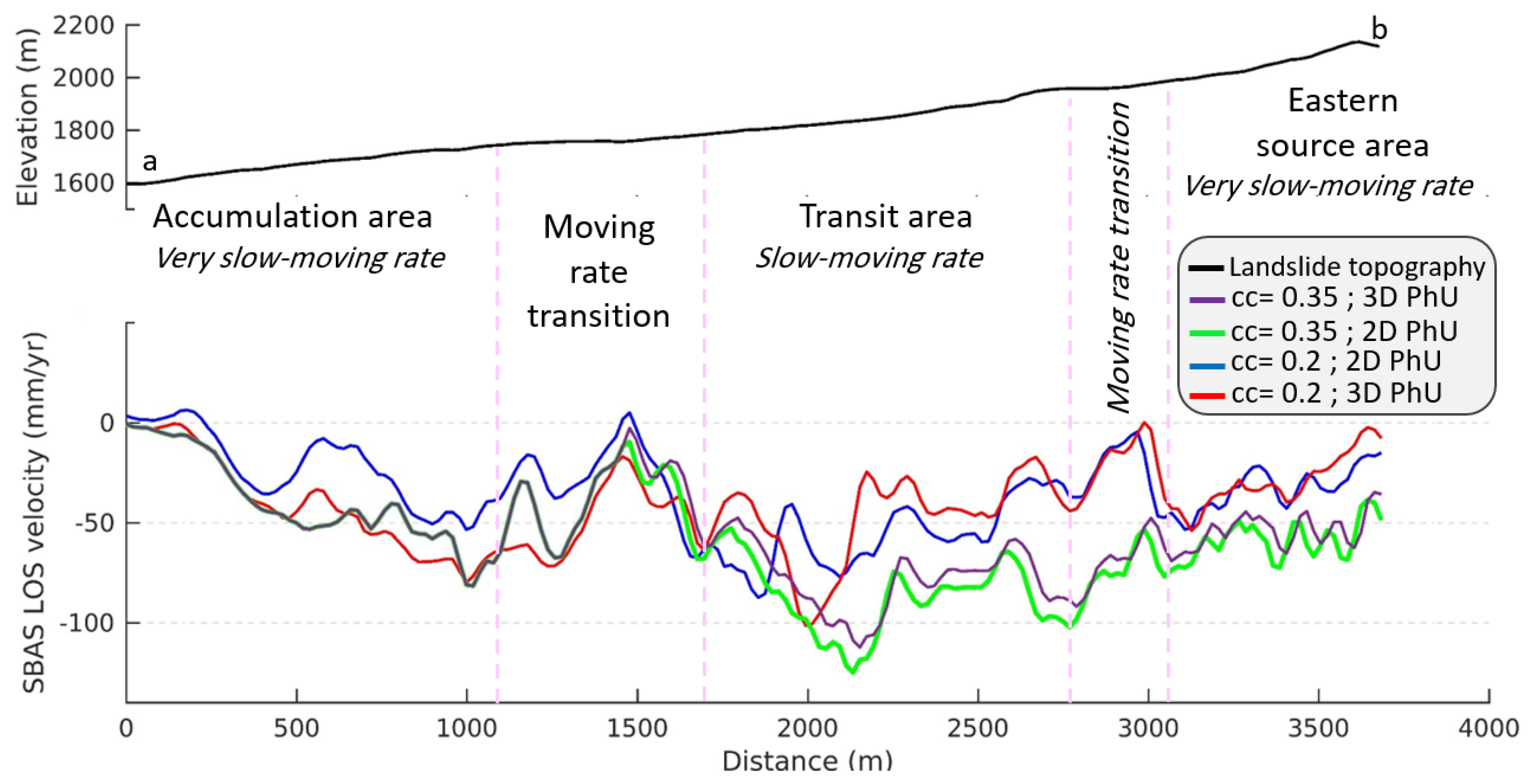
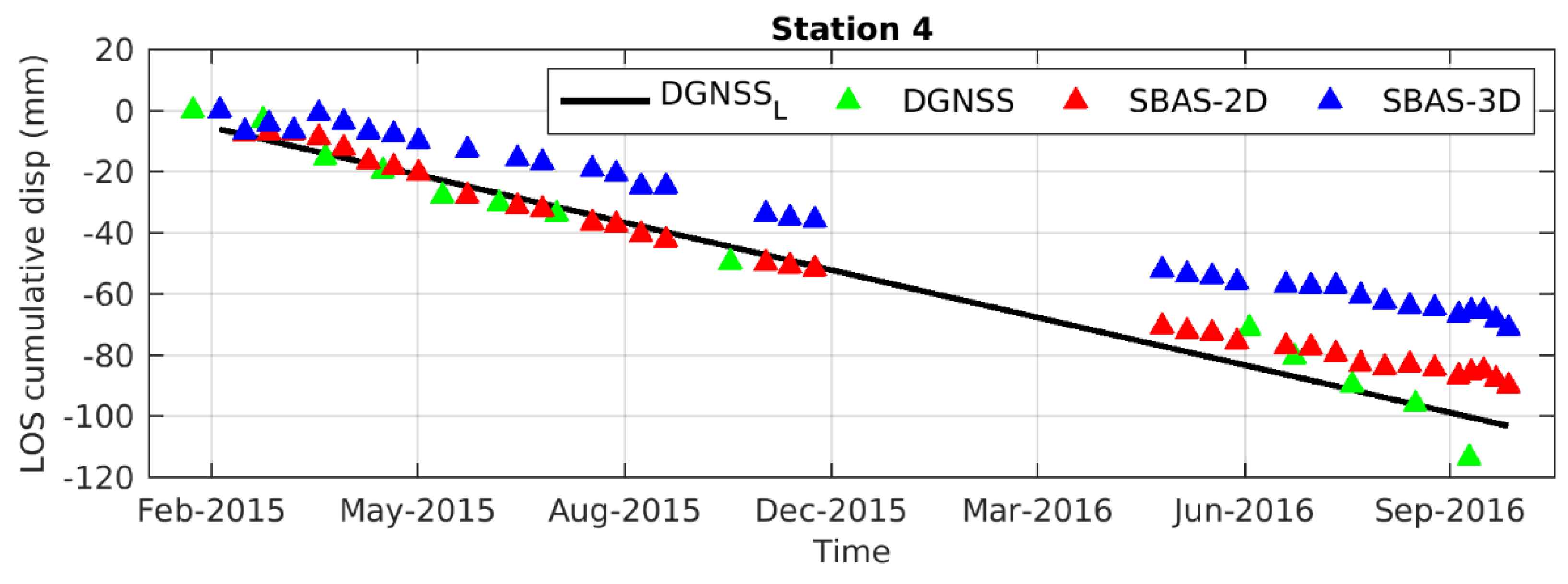
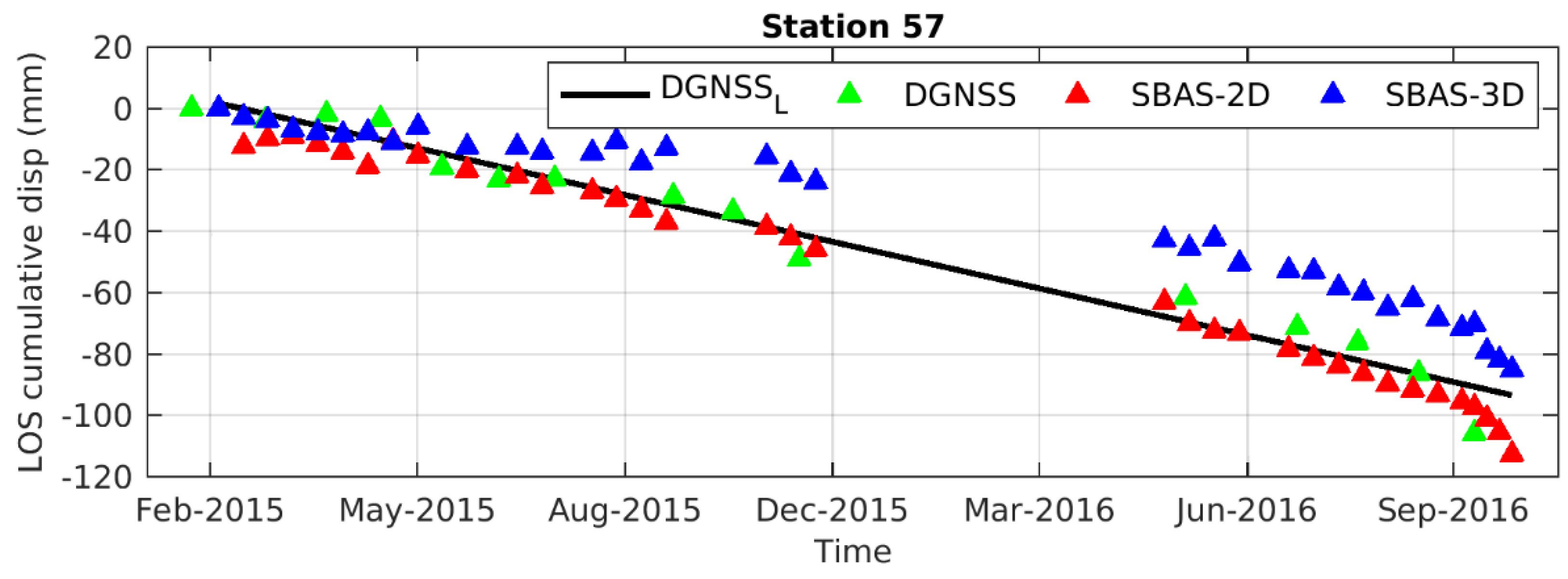
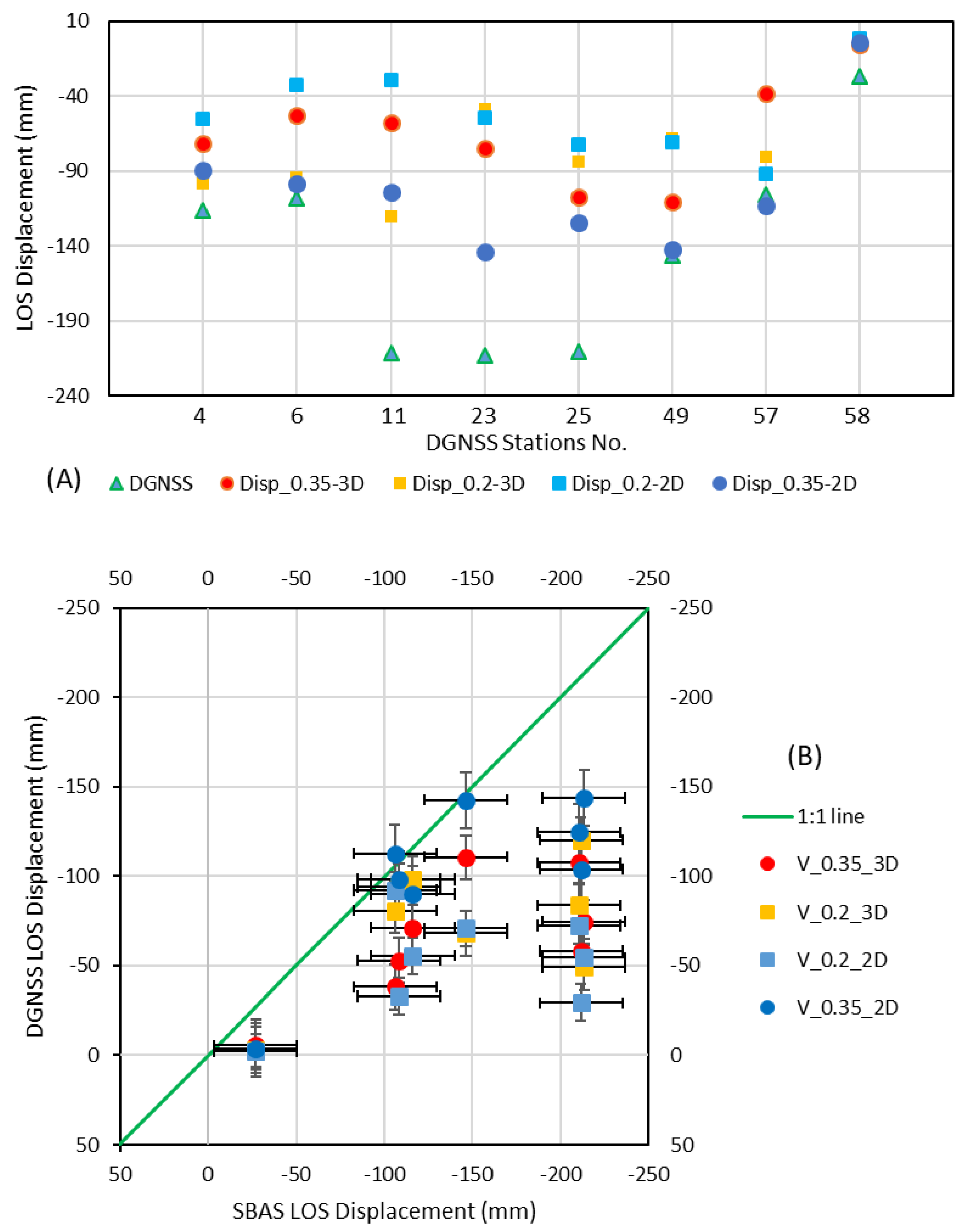
4.3. DInSAR and DGNSS Results Comparison
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Petley, D. Global patterns of loss of life from landslides. Geology 2012, 40, 927–930. [Google Scholar] [CrossRef]
- Guzzetti, F. Landslide Hazard and Risk Assessment. Ph.D. Thesis, University of Bonn, Bonn, Germany, 2006. [Google Scholar]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.-T. Landslide inventory maps: {New} tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Van Westen, C.J.; van Asch, T.W.J.; Soeters, R. Landslide hazard and risk zonation—Why is it still so difficult? Bull. Eng. Geol. Environ. 2006, 65, 167–184. [Google Scholar] [CrossRef]
- De Novellis, V.; Castaldo, R.; Lollino, P.; Manunta, M.; Tizzani, P. Advanced three-dimensional finite element modeling of a slow landslide through the exploitation of DInSAR measurements and in situ surveys. Remote Sens. 2016, 8. [Google Scholar] [CrossRef]
- Calò, F.; Ardizzone, F.; Castaldo, R.; Lollino, P.; Tizzani, P.; Guzzetti, F.; Lanari, R.; Angeli, M.G.; Pontoni, F.; Manunta, M. Enhanced landslide investigations through advanced DInSAR techniques: The Ivancich case study, Assisi, Italy. Remote Sens. Environ. 2014, 142, 69–82. [Google Scholar] [CrossRef]
- Tolomei, C.; Taramelli, A.; Moro, M.; Saroli, M.; Aringoli, D.; Salvi, S. Analysis of the deep-seated gravitational slope deformations over Mt. Frascare (Central Italy) with geomorphological assessment and DInSAR approaches. Geomorphology 2013, 201, 281–292. [Google Scholar] [CrossRef]
- Rodríguez, C.E.; Bommer, J.J.; Chandler, R.J. Earthquake-induced landslides: 1980–1997. Soil Dyn. Earthq. Eng. 1999, 18, 325–346. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Rucci, A.; Ferretti, A.; Monti-Guarnieri, A.; Rocca, F. Sentinel 1 SAR interferometry applications: The outlook for sub millimeter measurements. Remote Sens. Environ. 2012, 120, 156–163. [Google Scholar] [CrossRef]
- Dai, K.; Li, Z.; Tomás, R.; Liu, G.; Yu, B.; Wang, X.; Cheng, H.; Chen, J.; Stockamp, J. Monitoring activity at the Daguangbao mega-landslide (China) using Sentinel-1 TOPS time series interferometry. Remote Sens. Environ. 2016, 186, 501–513. [Google Scholar] [CrossRef]
- De Luca, C.; Bonano, M.; Casu, F.; Fusco, A.; Lanari, R.; Manunta, M.; Manzo, M.; Pepe, A.; Zinno, I. Automatic and systematic Sentinel-1 SBAS-DInSAR processing chain for deformation time-series generation. Procedia Comput. Sci. 2016, 100, 1176–1180. [Google Scholar] [CrossRef]
- Manunta, M.; Bonano, M.; Buonanno, S.; Casu, F.; De Luca, C.; Fusco, A.; Lanari, R.; Manzo, M.; Ojha, C.; Pepe, A.; et al. Unsupervised parallel SBAS-DInSAR chain for massive and systematic Sentinel-1 data processing. Int. Geosci. Remote Sens. Symp. 2016, 2016, 3890–3893. [Google Scholar] [CrossRef]
- Tomás, R.; Romero, R.; Mulas, J.; Marturià, J.J.; Mallorquí, J.J.; Lopez-Sanchez, J.M.; Herrera, G.; Gutiérrez, F.; González, P.J.; Fernández, J.; et al. Radar interferometry techniques for the study of ground subsidence phenomena: A review of practical issues through cases in Spain. Environ. Earth Sci. 2014, 71. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Prati, C.; Ferretti, A.; Perissin, D. Recent advances on surface ground deformation measurement by means of repeated space-borne SAR observations. J. Geodyn. 2010, 49, 161–170. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, L16302. [Google Scholar] [CrossRef]
- Wasowski, J.; Bovenga, F. Investigating landslides and unstable slopes with satellite Multi Temporal Interferometry: Current issues and future perspectives. Eng. Geol. 2014, 174, 103–138. [Google Scholar] [CrossRef]
- Colesanti, C.; Wasowski, J. Investigating landslides with space-borne Synthetic Aperture Radar (SAR) interferometry. Eng. Geol. 2006, 88, 173–199. [Google Scholar] [CrossRef]
- Pepe, A.; Euillades, L.D.; Manunta, M.; Lanari, R. New advances of the extended minimum cost flow phase unwrapping algorithm for SBAS-DInSAR analysis at full spatial resolution. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4062–4079. [Google Scholar] [CrossRef]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Two-dimensional phase unwrapping with use of statistical models for cost functions in nonlinear optimization. J. Opt. Soc. Am. A 2001, 18, 338–351. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Romero, L.A. Direct phase estimation from phase differences using fast elliptic partial differential equation solvers. Opt. Lett. 1989, 14, 1107–1109. [Google Scholar] [CrossRef] [PubMed]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Zebker, H.; Rosen, P.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- González, P.J.; Fernandez, J.; Camacho, A.G. Coseismic three-dimensional displacements determined using SAR data: Theory and an application test. Pure Appl. Geophys. 2009, 166, 1403–1424. [Google Scholar] [CrossRef]
- Guglielmino, F.; Nunnari, G.; Puglisi, G.; Spata, A. Simultaneous and integrated strain tensor estimation from geodetic and satellite deformation measurements to obtain three-dimensional displacement maps. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1815–1826. [Google Scholar] [CrossRef]
- Samsonov, S.; Tiampo, K. Analytical optimization of a DInSAR and GPS dataset for derivation of three-dimensional surface motion. IEEE Geosci. Remote Sens. Lett. 2006, 3, 107–111. [Google Scholar] [CrossRef]
- Samsonov, S.; Tiampo, K.; Rundle, J.; Li, Z.H. Application of DInSAR-GPS optimization for derivation of fine-scale surface motion maps of southern California. IEEE Trans. Geosci. Remote Sens. 2007, 45, 512–521. [Google Scholar] [CrossRef]
- David, F.W. A Guide to the Analysis and Display of Spatial Data 1992; Pergamon: Oxford, UK, 1992. [Google Scholar]
- Cressie, N. Statistics for Spatial Data; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Moritz, H. Advanced Physical Geodesy; Wichmann: Karlsruhe, Germany, 1980. [Google Scholar]
- Komac, M.; Holley, R.; Mahapatra, P.; van der Marel, H.; Bavec, M. Coupling of GPS/GNSS and radar interferometric data for a 3D surface displacement monitoring of landslides. Landslides 2015, 12, 241–257. [Google Scholar] [CrossRef]
- Lollino, G.; Giordan, D.; Thuro, K.; Carranza-Torres, C.; Wu, F.; Marinos, P.; Delgado, C. Engineering Geology for Society and Territory—Volume 6: Applied Geology for Major Engineering Projects; Springer: Berlin, Germany, 2015; ISBN 9783319090603. [Google Scholar]
- Xu, C.; Wang, H.; Ge, L.; Yonezawa, C.; Cheng, P. InSAR tropospheric delay mitigation by GPS observations: A case study in Tokyo area. J. Atmos. Sol. Terr. Phys. 2006, 68, 629–638. [Google Scholar] [CrossRef]
- Schlögel, R.; Thiebes, B.; Mulas, M.; Cuozzo, G.; Notarnicola, C.; Schneiderbauer, S.; Crespi, M.; Mazzoni, A.; Mair, V.; Corsini, A. Multi-temporal X-Band radar interferometry using corner reflectors: Application and validation at the Corvara Landslide (Dolomites, Italy). Remote Sens. 2017, 9, 739. [Google Scholar] [CrossRef]
- Soldati, M.; Corsini, A.; Pasuto, A. Landslides and climate change in the Italian Dolomites since the Late glacial. CATENA 2004, 55, 141–161. [Google Scholar] [CrossRef]
- Corsini, A.; Marchetti, M.; Soldati, M. Holocene slope dynamics in the area of Corvara in Badia (Dolomites, Italy): Chronology and paleoclimatic significance of some landslides. Geogr. Fis. Din. Quat. 2001, 24, 127–139. [Google Scholar]
- Borgatti, L.; Ravazzi, C.; Donegana, M.; Corsini, A.; Marchetti, M.; Soldati, M. A lacustrine record of early Holocene watershed events and vegetation history, Corvara in Badia, Dolomites (Italy). J. Quat. Sci. 2007, 22, 173–189. [Google Scholar] [CrossRef]
- Corsini, A.; Pasuto, A.; Soldati, M.; Zannoni, A. Field monitoring of the Corvara landslide (Dolomites, Italy) and its relevance for hazard assessment. Geomorphology 2005, 66, 149–165. [Google Scholar] [CrossRef]
- Cruden, D.M.; Varnes, D.J.; Turner, A.K.; Schuster, R.L. Landslides Investigation and Mitigation, Special Report 247; Transportation Research Board: Washington, DC, USA, 1996. [Google Scholar]
- Mulas, M.; Petitta, M.; Corsini, A.; Schneiderbauer, S.; Mair, F.V.; Iasio, C. Long-term monitoring of a deep-seated, slow-moving landslide by mean of C-Band and X-Band advanced interferometric products: The Corvara in Badia case study (Dolomites, Italy). Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2015, XL-7/W3, 827–829. [Google Scholar] [CrossRef]
- Darvishi, M.; Schlögel, R.; Bruzzone, L.; Cuozzo, G. Integration of PSI, MAI, and intensity-based sub-pixel offset tracking results for landslide monitoring with X-band corner reflectors-Italian Alps (Corvara). Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
- SARMAP. SARScape: Technical Description; SARMAP: Purasca, Switzerland, 2012. [Google Scholar]
- Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Pepe, A.; Lanari, R. On the extension of the minimum cost flow algorithm for phase unwrapping of multitemporal differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2374–2383. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin, Germany, 2001. [Google Scholar]
- Hooper, A.; Zebker, H.A. Phase unwrapping in three dimensions with application to InSAR time series. J. Opt. Soc. Am. 2007, 24, 2737–2747. [Google Scholar] [CrossRef]


| Product Type | Mode | Pass | Pol. | Inc/Az Angle | Rtime | Rg × Az Spacing | W.L |
|---|---|---|---|---|---|---|---|
| S1-A/B | IW | Descending | VV | 42°/−165° | 12/6 day | 3.8 m × 13.8 m | 5.6 cm |
| CR No. | DGNSS | DSBAS (0.35; 3D) | DSBAS (0.2; 3D) | DSBAS (0.2; 2D) | DSBAS (0.35; 2D) |
|---|---|---|---|---|---|
| 4M | −116.1 | −71.24 | −98.25 | −55.52 | −89.88 |
| 6H | −108.3 | −52.87 | −94.09 | −32.79 | −98.18 |
| 11H | −211.5 | −57.92 | −120.14 | −29.3 | −103.75 |
| 23 | −213.4 | −74.49 | −49.08 | −54.44 | −143.7 |
| 25 | −210.3 | −107.44 | −83.58 | −72.22 | −124.35 |
| 49H | −146.2 | −110.57 | −68.13 | −70.65 | −142.5 |
| 57M | −105.9 | −38.04 | −80.71 | −92.02 | −112.74 |
| 58H | −27.1 | −5.45 | 30.5 | 22.28 | −49.17 |
| RMSE | 7.9 | 7.8 | 9.0 | 6.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Darvishi, M.; Schlögel, R.; Kofler, C.; Cuozzo, G.; Rutzinger, M.; Zieher, T.; Toschi, I.; Remondino, F.; Mejia-Aguilar, A.; Thiebes, B.; et al. Sentinel-1 and Ground-Based Sensors for Continuous Monitoring of the Corvara Landslide (South Tyrol, Italy). Remote Sens. 2018, 10, 1781. https://doi.org/10.3390/rs10111781
Darvishi M, Schlögel R, Kofler C, Cuozzo G, Rutzinger M, Zieher T, Toschi I, Remondino F, Mejia-Aguilar A, Thiebes B, et al. Sentinel-1 and Ground-Based Sensors for Continuous Monitoring of the Corvara Landslide (South Tyrol, Italy). Remote Sensing. 2018; 10(11):1781. https://doi.org/10.3390/rs10111781
Chicago/Turabian StyleDarvishi, Mehdi, Romy Schlögel, Christian Kofler, Giovanni Cuozzo, Martin Rutzinger, Thomas Zieher, Isabella Toschi, Fabio Remondino, Abraham Mejia-Aguilar, Benni Thiebes, and et al. 2018. "Sentinel-1 and Ground-Based Sensors for Continuous Monitoring of the Corvara Landslide (South Tyrol, Italy)" Remote Sensing 10, no. 11: 1781. https://doi.org/10.3390/rs10111781
APA StyleDarvishi, M., Schlögel, R., Kofler, C., Cuozzo, G., Rutzinger, M., Zieher, T., Toschi, I., Remondino, F., Mejia-Aguilar, A., Thiebes, B., & Bruzzone, L. (2018). Sentinel-1 and Ground-Based Sensors for Continuous Monitoring of the Corvara Landslide (South Tyrol, Italy). Remote Sensing, 10(11), 1781. https://doi.org/10.3390/rs10111781