Fast Atmospheric Correction Method for Hyperspectral Data
Abstract
1. Introduction
2. Atmospheric Model
- molecular (Rayleigh) scattering,
- aerosol absorption and scattering,
- absorption by water vapor, oxygen and ozone.
- measurement geometry,
- the spectral land surface reflectance,
- vertical optical thickness of molecular scattering,
- aerosol optical thickness,
- scattering phase function parameter (average cosine of scattering angle),
- single scattering albedo,
- integrated content of water vapor (in the column of the atmosphere), oxygen, and ozone.
- (1)
- Vertical optical thickness of the atmosphere at the wavelength (excluding optical thickness for gaseous absorption) is defined aswhere is optical thickness of molecular (Rayleigh) scattering; is optical thickness of aerosol scattering; is optical thickness of aerosol absorption.
- (2)
- Single scattering albedo (quantum survival probability) is calculated as follows:
- (3)
- The vertical molecular optical thickness is determined by the atmospheric model (season and location) [14]Constants in Equation (3) are the following: the pressure and the temperature at the Earth’s surface are taken in the selected atmospheric model (for example, Midlatitude Summer); and are real values of pressure and temperature, accordingly, at the Earth’s surface at the measurement time; constants B, C, D are independent on atmospheric models. We have used six types of atmospheric models, values of the coefficients for which are given in Table 1.The spectral dependence of the aerosol optical thicknesses introduced in the atmospheric model is approximated by the power law function:where is the corresponding optical thickness at the reference wavelength , is Ångstroem exponent. The value of is supposed to be not dependent on the wavelength (it is usually small as compared to ).
- (4)
- The spectral reflectance of the underlying surface is considered to be Lambertian (isotropic).
- (5)
- The total scattering phase function is given as the weighted-average function of the Rayleigh and the aerosol scattering phase functions as follows:where aerosol scattering phase function is approximated by Henyey-Greenstein function. In particular, it follows:with an average cosine of scattering angle, , which is assumed to be independent on the wavelength. However, by means of Equation (5), the spectral dependence of the total scattering phase function on the wavelength is introduced. In Equation (6), is cosine of the scattering angle, the Sun zenith angle , is cosine of the zenith angle of observation , is azimuth angle of radiation propagation direction with respect to the solar vertical plane. The scattering angle (and ) is used later only in the term for atmospheric haze radiation. According to [10], the choice of the scattering phase function is not important in determining the surface reflectance, because the equation includes the product of aerosol optical thickness and the phase function, each of which may be incorrectly defined, but the product and the value of the surface reflectance is correctly determined.
- standard surface temperature 293 K;
- standard surface pressure kPa;
- standard total integrated precipitable water: g/cm;
- standard integrated ozone amount atm · cm.
- The fixed oxygen content is assumed, so the parameters depend only on the air mass.
- In contrast, due to considerable variability, the transmission function of water vapor depends on the unknown concentration. The parameter is adjustable, including both the concentration of water vapor and the effective path of radiation (effective air mass).
- Although variations in the ozone concentration are usually minor, the public datasets of the European Center for Medium-Range Weather Forecasts (ECMWF) were used to estimate the actual ozone concentration in the selected area.
3. Approximate Analytical Equation for Spectral Radiance at TOA
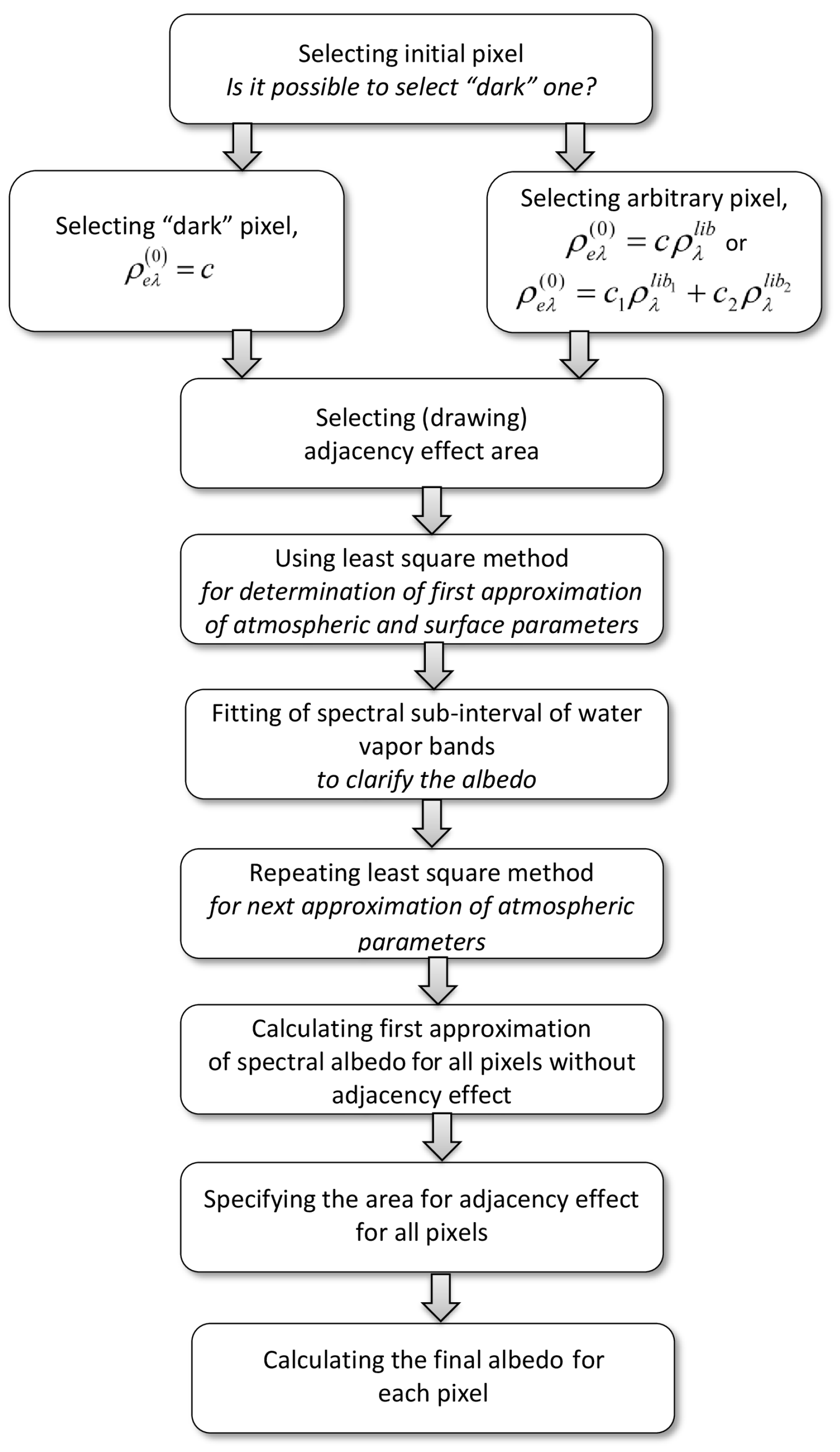
4. Atmospheric Correction of Hyperspectral Imagery
- The selection of original pixel and area in the image under study for which the atmospheric parameters are determined.
- (a)
- We choose a “dark” pixel, if possible, on the hyperspectral image (low reflectance value, it is important to note that it is “dark” in the “blue-green” part of the spectrum, where there is the largest contribution of atmospheric haze). The user has the option of selecting a “dark pixel” either interactively or automatically based on a high correlation of a hyperspectral pixel with the library of various objects such as water, dark soil, asphalt, coniferous forest, etc.
- (b)
- In the case of absent suitable “dark pixel” in the image, a pixel with an approximately identifiable underlying surface (for example: vegetation, water, soil, sand, etc., or a mixture thereof) is selected, which is determined visually from RGB image.
- Setup of the initial (zero) algorithm’s iteration for the reflectance of the selected pixel.
- (a)
- In case of a dark pixel surface (step 1a), we usein Equation (17). Since in this case the contribution of atmospheric haze to the detected signal exceeds the contribution of the reflected radiation from the surface (low reflectance value), then the spectral dependence of can be neglected. Therefore, the reflectance can be assumed constant over the spectrum.
- (b)
- In the case of a homogeneous pixel (step 1b) (“pure”—vegetation, water, soil, sand, etc), we assume that the spectral surface reflectance function of the selected pixel can be presented in the formwhere c is the unknown weighted positive parameter, is the spectral surface reflectance library function of the identified surface type of the selected pixel.If the selected surface for the pixel is an inhomogeneous (consisting of a mixture of several types of surfaces) one, then the reflectance is assumed to be a linear combination of two dominant surface types with unknown parameter c (which here can vary in the range [0, 1]):where is the spectral surface reflectance library. By selecting a pixel over land, it is recommended to choose a linear combination of typical surface reflectance of vegetation and bare soil ([10]).
- The choice of the neighborhood around the selected pixel (as an arbitrary polygon).The neighborhood should be (if possible) of the same type (with close reflectance values to the selected source pixel) as the selected pixel itself. The given zero-th order surface reflectance functions for the original pixel are considered as such for the whole selected neighborhood, i.e., are given by one of the formulas (18)–(20).The neighborhood area selected here is used to account for an adjacency effect in a non-traditional way: firstly, the initial iteration for atmospheric parameters is made with the average reflection signal via selected area around original (central) pixel, and then the new atmospheric parameters and reflectance of the original (central) pixel are found.
- Finding the first iteration of the optical atmospheric parameters and average reflectance of the neighborhood area.We consider for this case in (17), where in accordance with the choice of the original pixel, is determined by one of the formulas (18)–(20), and one can write (17) in the formHere is the average spectral reflectance of the hyperspectral image around the original pixel in the user-selected area (neighborhood, step 2). The next step is non-linear fit of the average spectral reflectance of selected area by given analytical formula (right-hand side of Equation (21)) with the non-linear least squares Levenberg–Marquardt (LM) algorithm finding a set of unknown optical parameters of the atmosphere (see 16) and average surface reflectance: . In (16), the water vapor exponent is replaced by two ones, and , in accordance with (17), and instead of the weighted parameter c stands here for the mean reflectance of the chosen neighborhood (from (18) or (20)).
- Additional smoothing of the spectral curve of the current pixel in the water absorption spectral bands by re-fitting, where we vary just and , corresponding to the water vapor.
- Refinement (next iteration).The atmospheric parameters and reflectance of the original (central) pixel , which may differ from the neighborhood reflectance and which are determined by one of Equations (18)–(20) with a new unknown value of the parameter are found. In this case, reflectance of the neighborhood pixels remains the same as in the previous iteration (step 4).
- Application of smoothing filter to the current pixel by re-fitting using exponents and .
- Calculation of the first approximation for the surface reflectance .The surface reflectance is found for all other pixels of the hyperspectral image without the adjacency effect from the following quadratic equation (it is obtained by solving the Equation (17) for the variable with putting there and taking into account the expressions (12,13) for ). Atmospheric parameters, which found in step 6 are substituted into Equation (17) (the atmosphere is assumed horizontally homogeneous, identical over all pixels). Then it follows:whereHere is the spectral reflectance of the processed pixel. Atmospheric parameters found above are substituted into Equations (24)–(27).
- The adjacency effect area specification by pixel-wise.At this step we specify a fixed neighborhood of each pixel and calculate the average reflectance to account for the adjacency effect. In this case, the spectral surface reflectance of pixels from the previous stage is used. The contribution to the total spectral surface reflectance from neighboring pixels is accounted for with an exponentially decay weight function depending on distance from the central (current) pixel:where are pixel numbers in the neighborhood, d is the half-width of the specified window in pixels, are the distribution parameters, N is the number of neighboring pixels (d is selected using iterations).
- The estimation of final reflectance value.The surface reflectance is found from the following formula, which follows from Equation (17) with :where one needs to substitute the following values: the spectral reflectance of the processed (current) pixel , the average spectral surface reflectance estimated for each current pixel using Equation (28) (calculated based on step 8) and atmospheric parameters found in step 6.
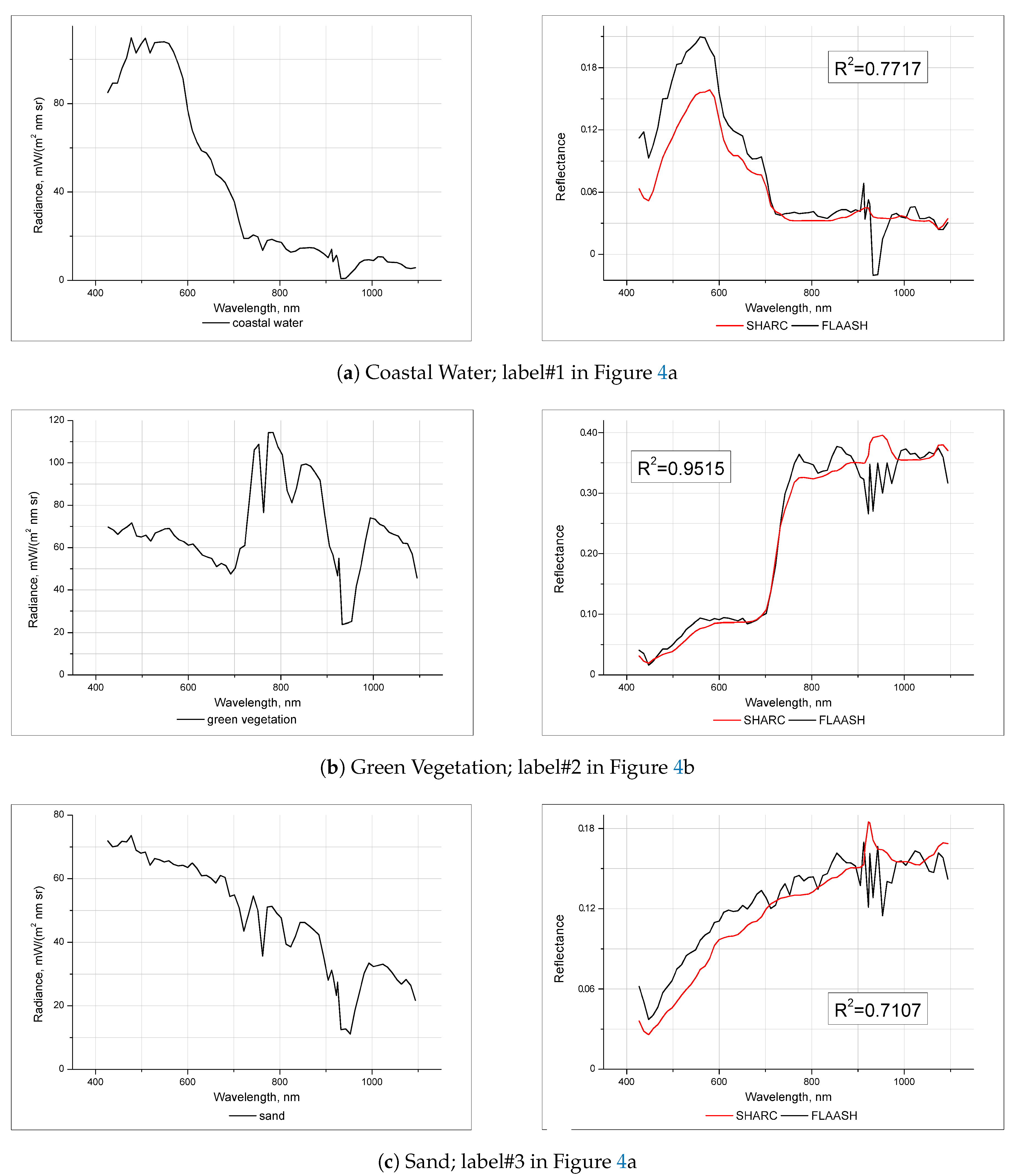
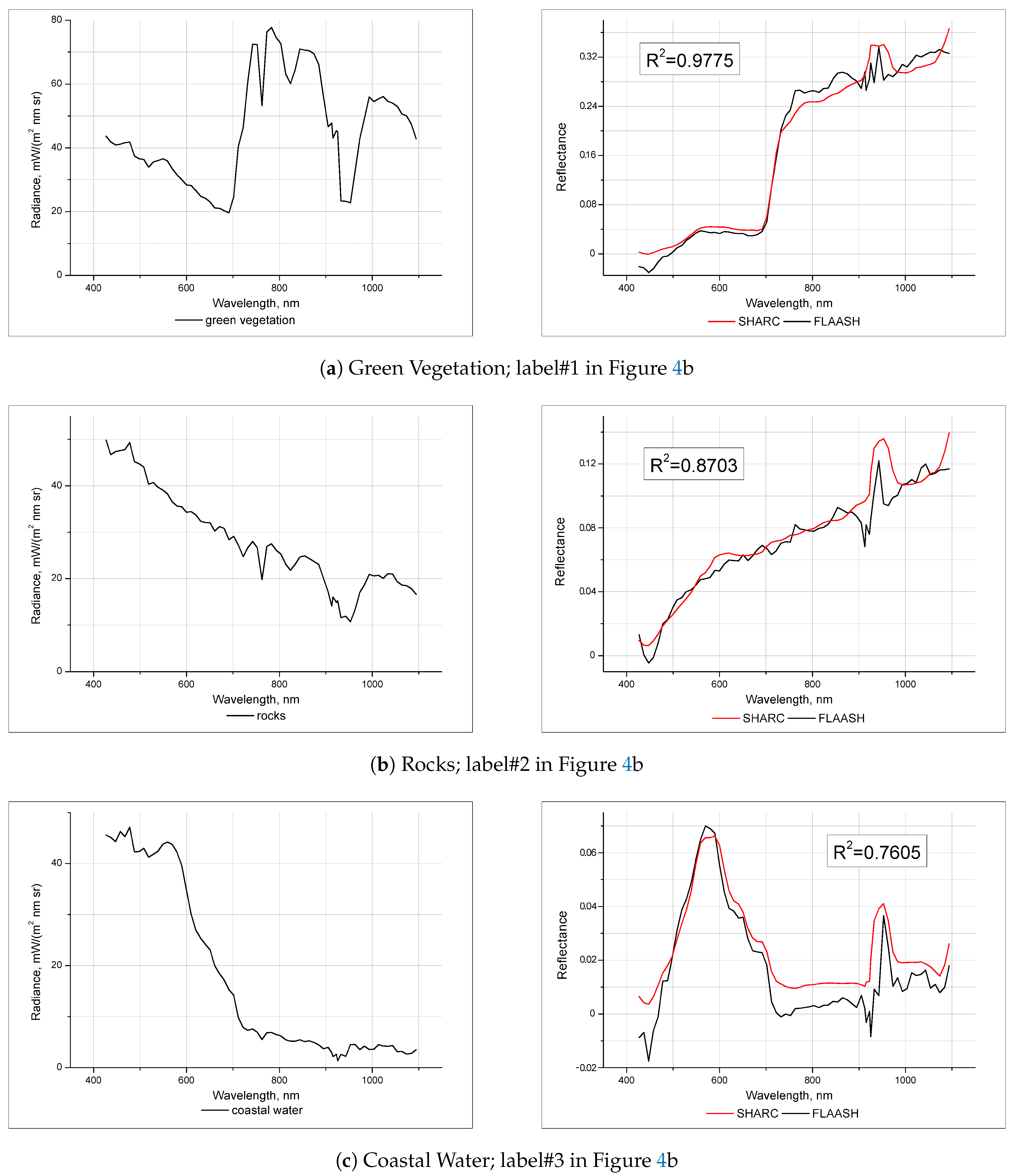
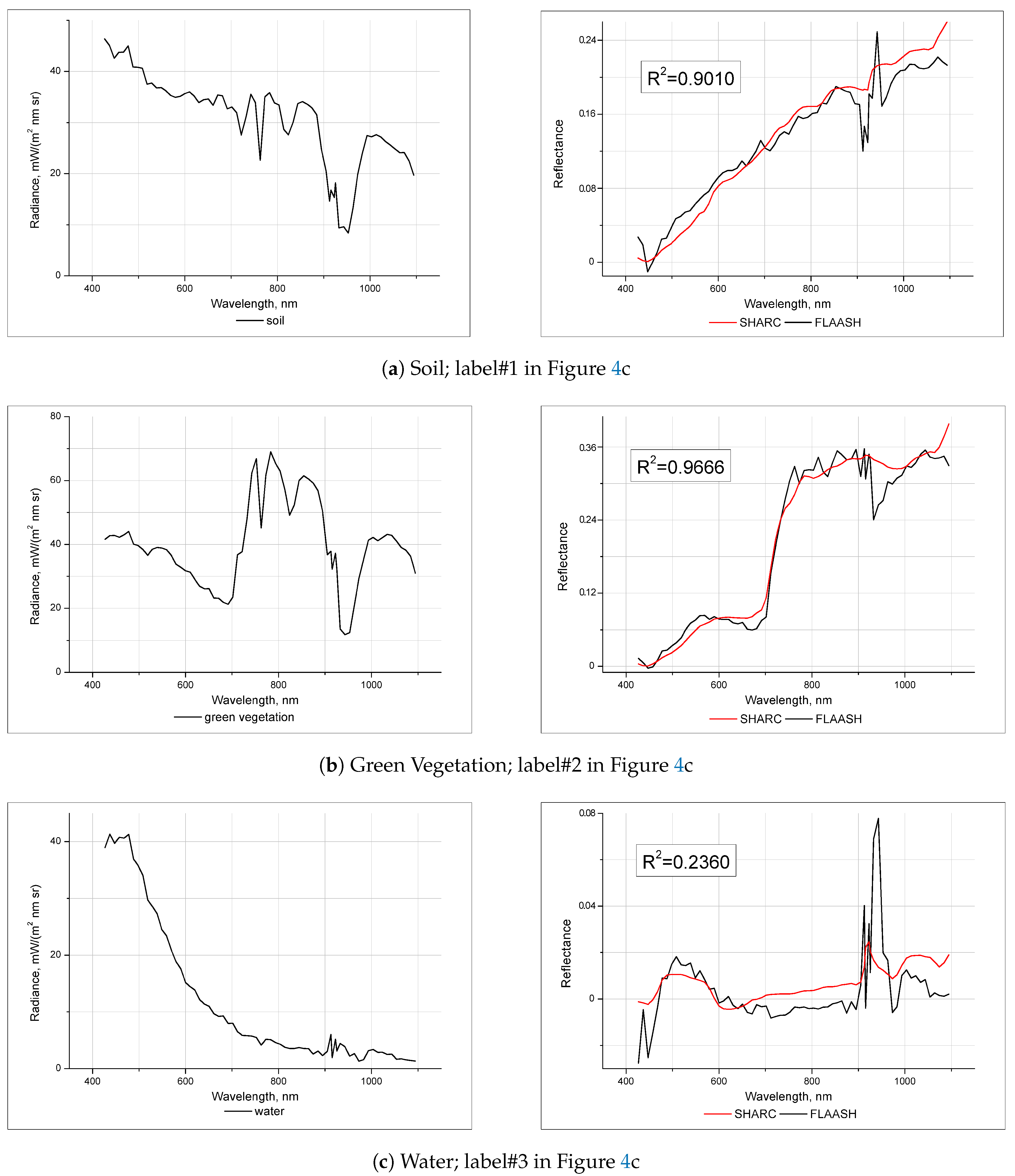
5. Validation
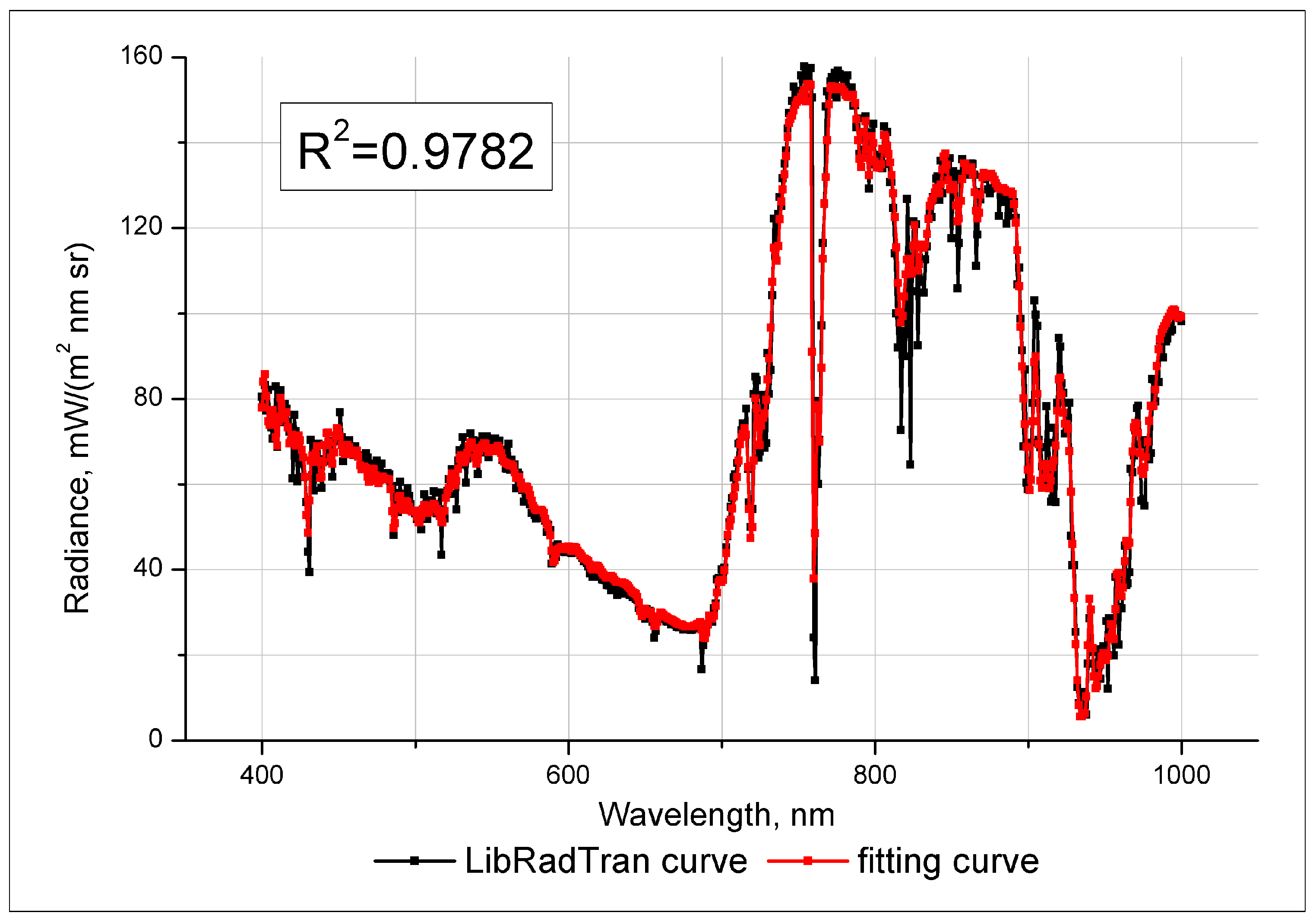
5.1. Validation Using Synthetic Spectra
5.2. Validation Using Hyperion Measurements
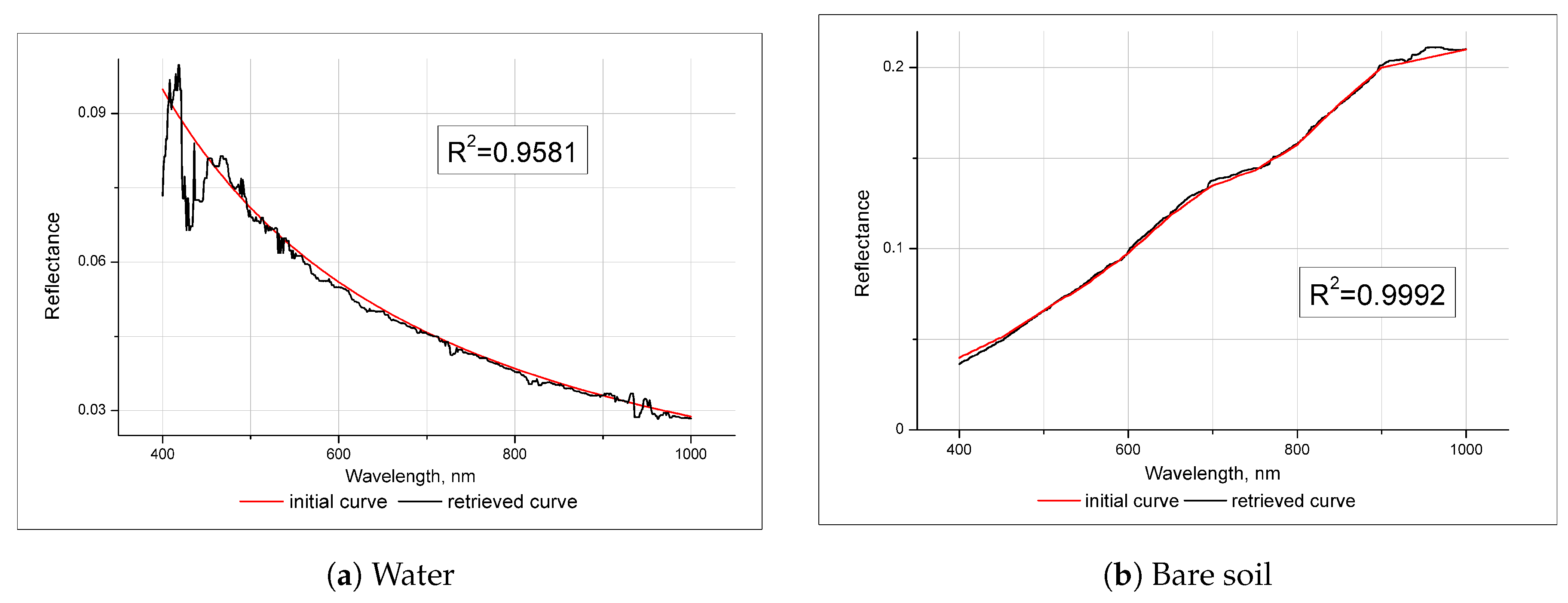
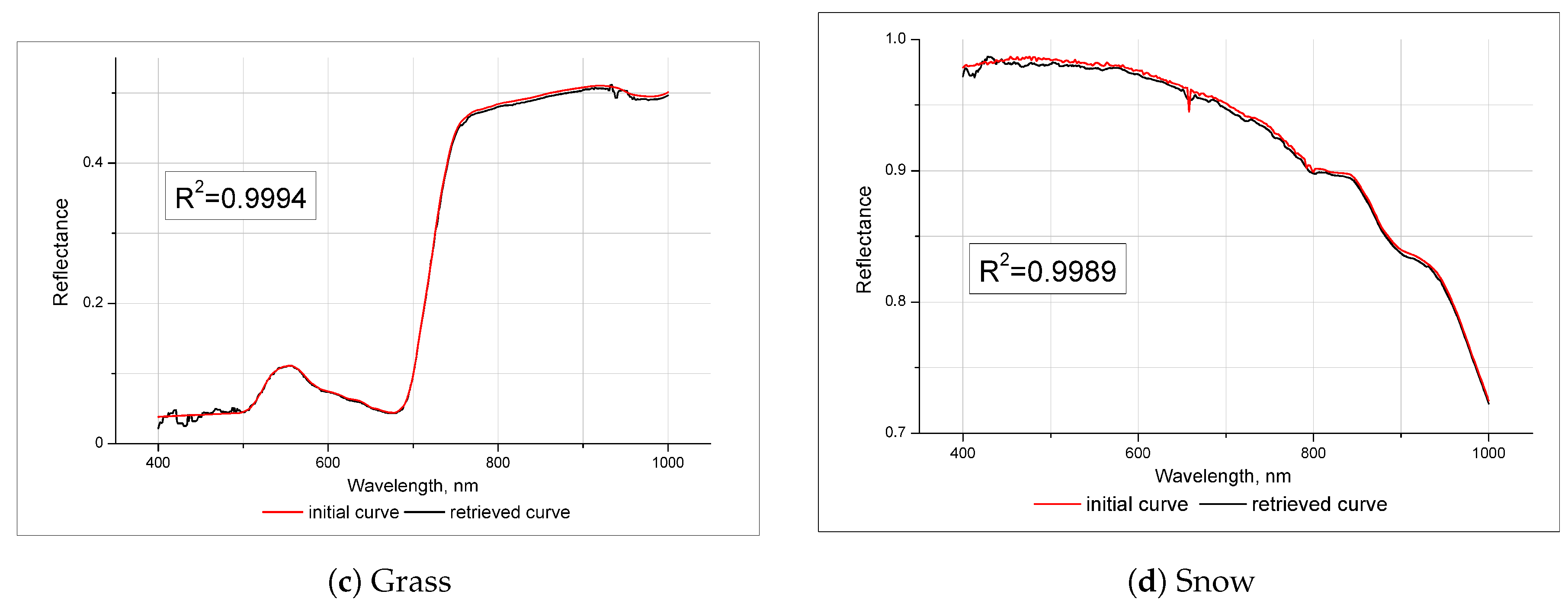
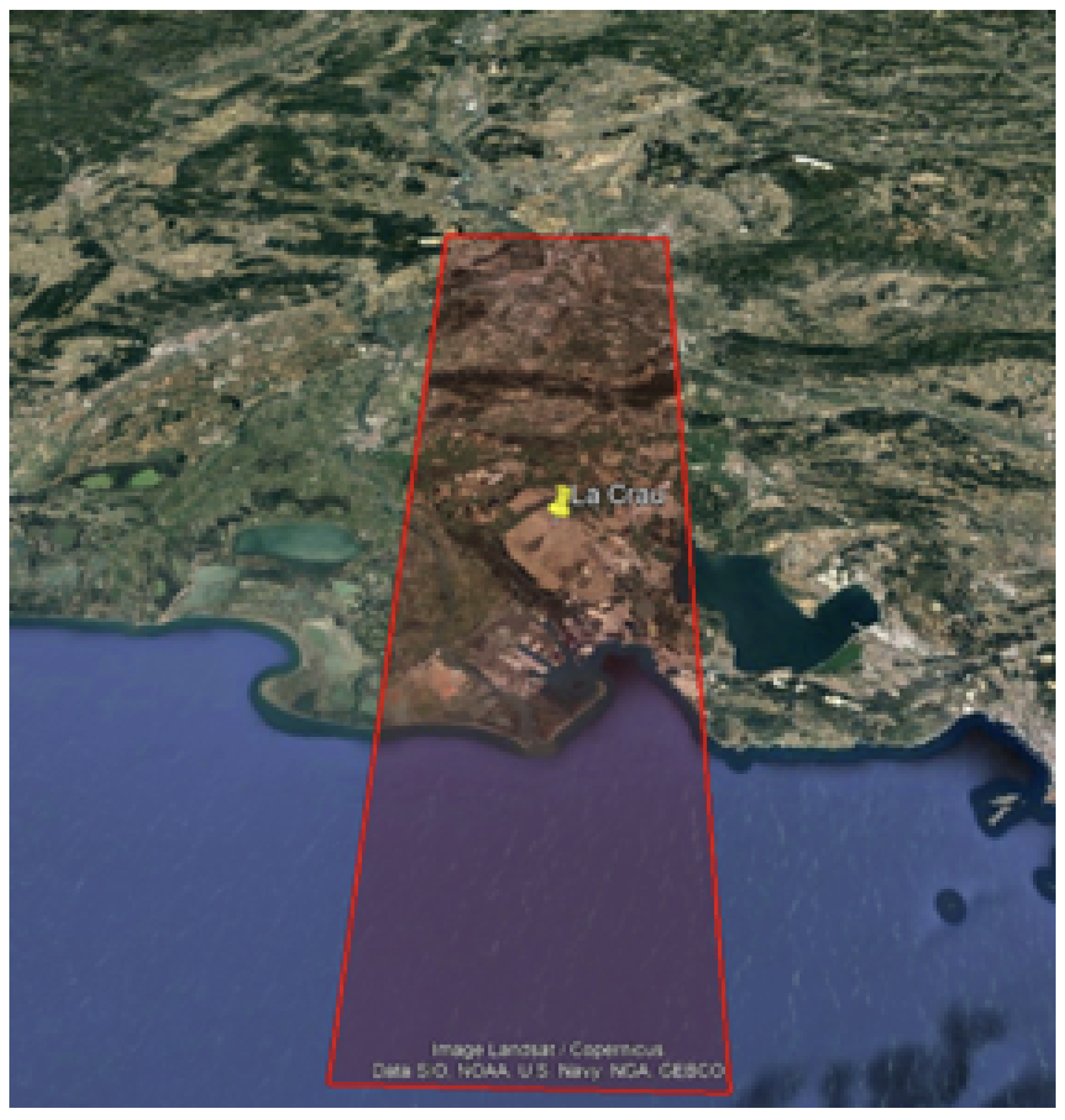
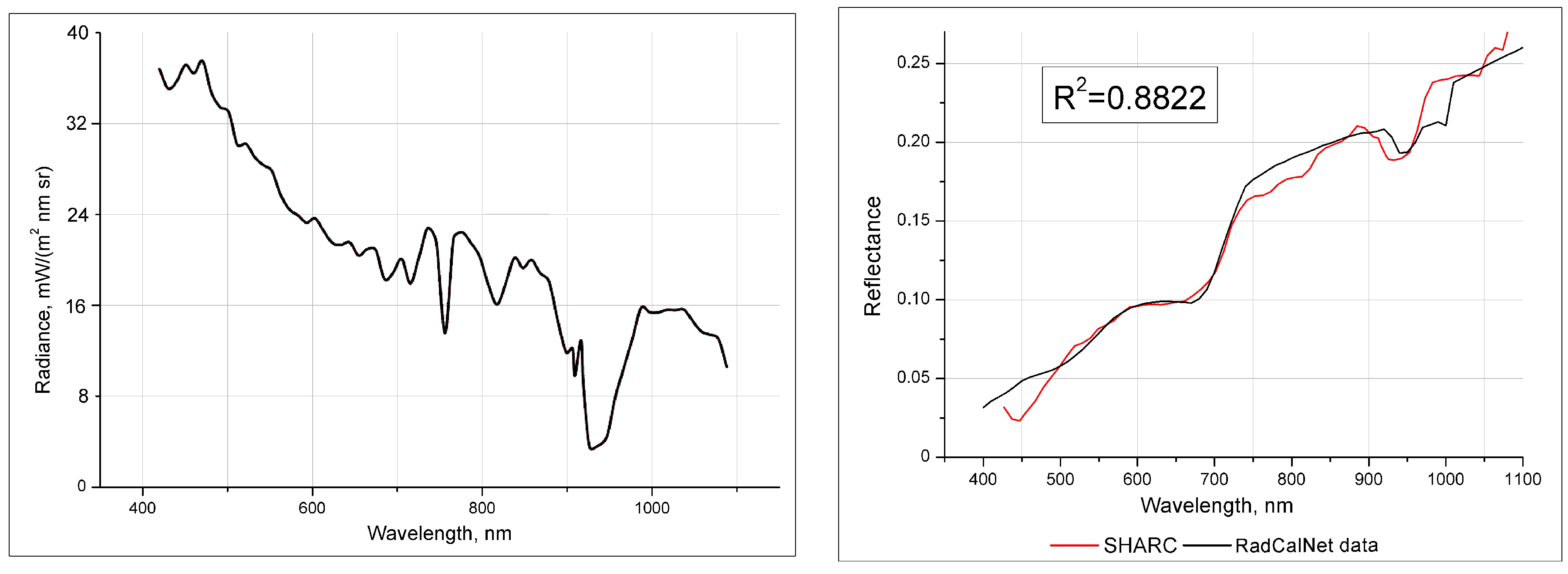
5.3. Validation Using Ground Data
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Eismann, M. Hyperspectral Remote Sensing; SPIE Press Monograph; SPIE: Washington, WA, USA, 2012; Volume PM210, p. 725. ISBN 9780819487872. [Google Scholar]
- Miller, C.J. Performance assessment of ACORN atmospheric correction algorithm. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery VIII; SPIE: Orlando, FL, USA, 2002; Volume 4725, pp. 438–449. [Google Scholar]
- Richter, R.; Schlapfer, D. Geo-atmospheric processing of airborne imaging spectrometry data. Part 2: Atmospheric/topographic correction. Int. J. Remote Sens. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Gao, B.-C.; Heidebrecht, K.B.; Goetz, A.F.H. Derivation of scaled surface reflectances from AVIRIS data. Remote Sens. Environ. 1993, 44, 165–178. [Google Scholar] [CrossRef]
- Adler-Golden, S.M.; Matthew, M.W.; Bernstein, L.S.; Levine, R.Y.; Berk, A.; Richtsmeier, S.C.; Acharya, P.K.; Anderson, G.P.; Feldeb, G.; Gardner, J.; et al. Atmospheric correction for short-wave spectral imagery based on MODTRAN4. In Imaging Spectrometry V; SPIE: Denver, CO, USA, 1999; Volume 3753, pp. 61–69. [Google Scholar]
- Goetz, A.F.H.; Kindel, B.C.; Ferri, M.; Qu, Z. HATCH: Results from simulated radiance, AVIRIS and Hyperion. JIEEE Trans. Geosci. Remote Sens. 2003, 41, 1215–1222. [Google Scholar] [CrossRef]
- Qu, Z.; Kindel, B.C.; Goetz, A.F.H. The high accuracy atmospheric correction for hyperspectral data (HATCH) model. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1223–1231. [Google Scholar]
- Montes, M.J.; Gao, B.-C.; Davis, C.O. Tafkaa atmospheric correction of hyperspectral data. In Imaging Spectrometry IX; SPIE: San Diego, CA, USA, 2003; Volume 5159, pp. 188–197. [Google Scholar]
- Leprieur, C.; Carrere, V.; Gu, X.F. Atmospheric corrections and ground reflectance recovery for Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) data: MAC Europe’91. Photogramm. Eng. Remote Sens. 1995, 61, 1233–1238. [Google Scholar]
- Katsev, I.L.; Prikhach, A.S.; Zege, E.P.; Grudo, J.O.; Kokhanovsky, A.A. Speeding up the aerosol optical thickness retrieval using analytical solutions of radiative transfer theory. Atmos. Meas. Tech. 2010, 3, 1403–1422. [Google Scholar] [CrossRef]
- Katkovsky, L.V. The parameterization of the outgoing radiation for rapid atmospheric correction of hyperspectral images. Optika Atmosfery i Okeana 2016, 29, 778–784. [Google Scholar]
- Ginzburg, A.S.; Romanov, S.V.; Fomin, B.A. The radiation-convective model use to estimate the temperature of greenhouse gas potential. Izvestiya RAN Fizika Atmosfery i Okeana 2008, 44, 324–331. [Google Scholar]
- Belyaev, B.I.; Belyaev, M.Y.; Desinov, L.V.; Katkovsky, L.V.; Sarmin, E.E. Spectral and Images Processing from Photospectral System in Space Experiment “HURRICANE” on the ISS. Izvestiya, Atmospheric and Oceanic Physics 2014, 6, 54–65. (In Russian) [Google Scholar]
- Bucholtz, A. Rayleigh-scattering calculations for the terrestrial atmosphere. Appl. Opt. 1995, 34, 2765–2773. [Google Scholar] [CrossRef] [PubMed]
- Bassani, C.; Cavalli, R.M.; Antonelli, P. Influence of aerosol and surface reflectance variability on hyperspectral observed radiance. Atmos. Meas. Tech. 2012, 5, 1193–1203. [Google Scholar] [CrossRef]
- Middleton, W.E.K. Vision Through the Atmosphere; University of Toronto Press: Toronto, ON, Canada, 1952. [Google Scholar]
- Schlapfer, D.; Borel, C.C.; Keller, J.; Itten, K.I. Atmospheric Precorrected Differential Absorption Technique to Retrieve Columnar Water Vapor. Remote Sens. Environ. 1998, 65, 353–366. [Google Scholar] [CrossRef]
- Vasil’ev, A.V.; Kuznetsov, A.D.; Mel’nikova, I.N. Remote Sensing of the Environment from Space: Practice; Baltic State Technical University: St. Petersburg, Russia, 2008; p. 33. [Google Scholar]
- Minin, I.N. Approximate equations for short-wave radiation absorption calculations in cloudless atmosphere. Izv. Akad. Nauk SSSR Fiz. Atm. Okeana 1984, 20, 999–1001. (In Russian) [Google Scholar]
- Kokhanovsky, A.A.; Mayer, B.; Rozanov, V.V. A parameterization of the diffuse transmittance and reflectance for aerosol remote sensing problems. Atmos. Res. 2005, 73, 37–43. [Google Scholar] [CrossRef]
- Vasil’ev, A.V.; Kuznetsov, A.D.; Mel’nikova, I.N. Approximation of multiply scattered solar radiation in the assumption of single scattering. In Proceedings of the International Symposium “Atmospheric Radiation and Dynamics” (ISARD 2015), Saint-Petersburg, Russia, 23–26 June 2015; p. 131. [Google Scholar]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libradtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]

| Atmospheric Model | = 0.2–0.5 m | > 0.5 m | Pressure , Mbar at the Earth’s Surface | Temperature , K at the Earth’s Surface | |
|---|---|---|---|---|---|
| B | For all models | 3.55212 | 3.99668 | ||
| C | 1.35579 | 0.00110298 | |||
| D | 0.11563 | 0.0271393 | |||
| Tropical | 0.006525841 | 0.008680089 | 1013 | 300 | |
| Midlatitude Summer | 0.006515547 | 0.008665997 | 1013 | 294 | |
| Midlatitude Winter | 0.006531896 | 0.008688402 | 1018 | 272.2 | |
| Subarctic Summer | 0.006477539 | 0.008616175 | 1010 | 287 | |
| Subarctic Winter | 0.006495823 | 0.008641742 | 1013 | 257.1 | |
| 1962 US Standard | 0.006499595 | 0.008645261 | 1013 | 288.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katkovsky, L.V.; Martinov, A.O.; Siliuk, V.A.; Ivanov, D.A.; Kokhanovsky, A.A. Fast Atmospheric Correction Method for Hyperspectral Data. Remote Sens. 2018, 10, 1698. https://doi.org/10.3390/rs10111698
Katkovsky LV, Martinov AO, Siliuk VA, Ivanov DA, Kokhanovsky AA. Fast Atmospheric Correction Method for Hyperspectral Data. Remote Sensing. 2018; 10(11):1698. https://doi.org/10.3390/rs10111698
Chicago/Turabian StyleKatkovsky, Leonid V., Anton O. Martinov, Volha A. Siliuk, Dimitry A. Ivanov, and Alexander A. Kokhanovsky. 2018. "Fast Atmospheric Correction Method for Hyperspectral Data" Remote Sensing 10, no. 11: 1698. https://doi.org/10.3390/rs10111698
APA StyleKatkovsky, L. V., Martinov, A. O., Siliuk, V. A., Ivanov, D. A., & Kokhanovsky, A. A. (2018). Fast Atmospheric Correction Method for Hyperspectral Data. Remote Sensing, 10(11), 1698. https://doi.org/10.3390/rs10111698





