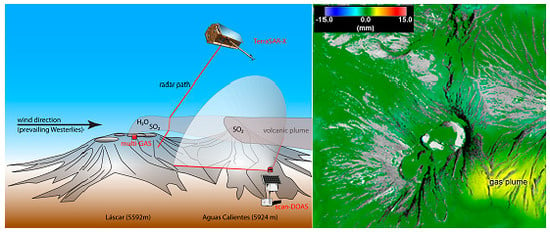
Radar Path Delay Effects in Volcanic Gas Plumes: The Case of Láscar Volcano, Northern Chile
Abstract
1. Introduction
2. Study Area
3. Data and Methods
3.1. SO2 Column Density Retrieval
3.2. Estimation of Water Vapor Contents in the Láscar Plume
3.3. SAR Data and InSAR Methods
3.4. Determination of Gas Plume Related Phase Delays
3.5. DInSAR Preparation
3.6. DInSAR Decomposition
3.7. Priors Used for DInSAR Decomposition
4. Results
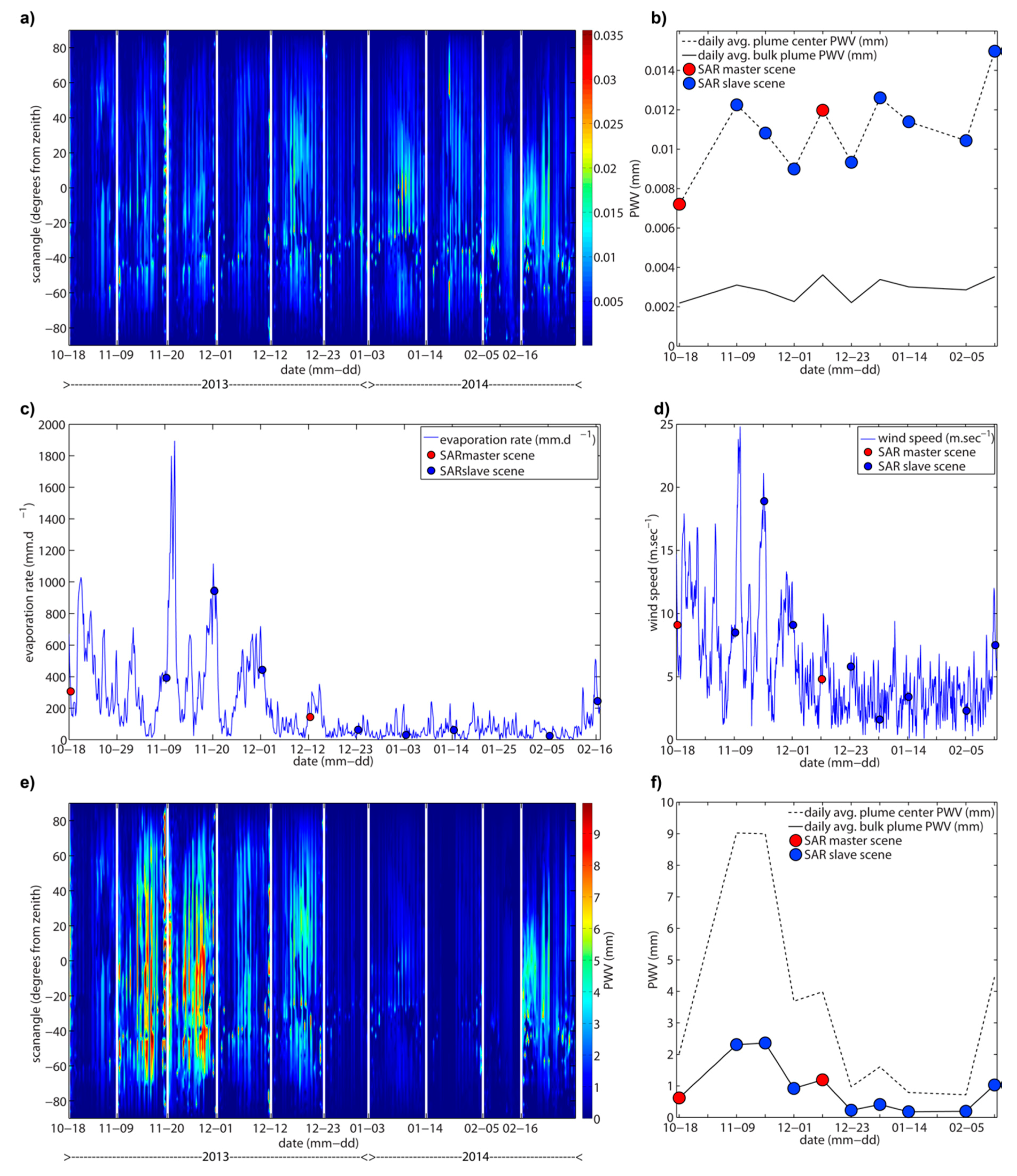
4.1. PWV Contents in the Volcanic Gas Plume of Láscar
4.2. Gas Plume Related Phase Delays
4.3. Isolation of the Gas Plume Related Signal in DInSARs
4.4. Residuals of the Refractivity Related Phase Delay and Ground Deformation
4.5. Validation of the Gas Plume Signal Estimate
5. Discussion
5.1. Why the Distinction between Periods of Volcano Deformation and Enhanced Degassing is Important
5.2. How Methodological Limitations Can be Turned into Benefit
5.3. Phase Delay Effects above the Crater and Downwind of Láscar
5.4. Gas Emission Rates from Láscar Volcano
5.5. Estimation of Background Atmospheric PWV Contents
5.6. Limitations of the Proposed Method
5.7. Advantages of the Proposed Method
6. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Estimation of PWV Contents in the Volcanic Cloud
Appendix B. Compensation of Downwind Evaporation
Appendix C. Estimation of PWV Contents in the Atmosphere
Appendix D. Wind Field during SAR Acquisitions



Appendix E. The Decomposed APS: Non-Repeating and Repeating Atmospheric Phase Delays
E.1. Single Event APS Estimates

E.2. Repeating Atmospheric Phase Delays
Appendix F. DEM Error Related Phase Delays
Appendix G. Estimation of APS Amplitude using Modeled Atmospheric PWV Contents Obtained from GDAS1 Soundings
| DInSAR # | Master Scene | Slave Scene | predicted |dSWD| (mm) | Estimated Mean APS Amplitudes = DInSAR Scale Bar Fraction (mm) | RMSD of DInSAR Amplitudes (mm) |
|---|---|---|---|---|---|
| Date | Date | ||||
| (yyyy-mm-dd) | (yyyy-mm-dd) | ||||
| subset 01 | |||||
| DInSAR 1 | 2013-12-12 | 2013-11-20 | 8.8 | 10 = 1/2*20 | 1.6 |
| DInSAR 2 | 2013-12-12 | 2013-12-01 | 11.3 | 10 = 1/2*20 | 1.4 |
| DInSAR 3 | 2013-12-12 | 2014-02-05 | 17.6 | 15 = 1/2*30 | 2.3 |
| subset 02 | |||||
| DInSAR 4 | 2013-10-18 | 2013-12-23 | 36.2 | 33.33 = 2/3*50 | 5.1 |
| DInSAR 5 | 2013-10-18 | 2014-01-03 | 18.7 | 20 = 1/2*40 | 2.5 |
| DInSAR 6 | 2013-10-18 | 2014-01-14 | 23.8 | 20 = 1/2*40 | 3.8 |
| DInSAR 7 | 2013-10-18 | 2014-02-16 | 8.5 | 10 = 1/4*40 | 3.2 |

Appendix H. Gas Plume Related Phase Delays of DInSAR Time Series Subsets 01 and 02

References
- Lengliné, O.; Marsan, D.; Got, J.L.; Pinel, V.; Ferrazzini, V.; Okubo, P.G. Seismicity and deformation induced by magma accumulation at three basaltic volcanoes. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Morita, Y.; Nakao, S.; Hayashi, Y. A quantitative approach to the dike intrusion process inferred from a joint analysis of geodetic and seismological data for the 1998 earthquake swarm off the east coast of Izu Peninsula, central Japan. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Watson, I.M.; Oppenheimer, C.; Voight, B.; Francis, P.W.; Clarke, A.; Stix, J.; Miller, A.; Pyle, D.M.; Burton, M.R.; Young, S.R.; et al. The relationship between degassing and ground deformation at Soufriere Hills Volcano, Montserrat. J. Volcanol. Geotherm. Res. 2000, 98, 117–126. [Google Scholar] [CrossRef]
- Kazahaya, R.; Aoki, Y.; Shinohara, H. Budget of shallow magma plumbing system at Asama Volcano, Japan, revealed by ground deformation and volcanic gas studies. J. Geophys. Res. Solid Earth 2015, 120, 2961–2973. [Google Scholar] [CrossRef]
- Girona, T.; Costa, F.; Newhall, C.; Taisne, B. On depressurization of volcanic magma reservoirs by passive degassing. J. Geophys. Res. Solid Earth 2014, 119, 8667–8687. [Google Scholar] [CrossRef]
- Tait, S.; Jaupart, C.; Vergniolle, S. Pressure, gas content and eruption periodicity of a shallow, crystallising magma chamber. Earth Planet. Sci. Lett. 1989, 92, 107–123. [Google Scholar] [CrossRef]
- Sparks, R.S.J. Dynamics of magma degassing. Geol. Soc. London Spec. Pub. 2003, 213, 5–22. [Google Scholar] [CrossRef]
- Green, D.N.; Neuberg, J. Waveform classification of volcanic low-frequency earthquake swarms and its implication at Soufrière Hills Volcano, Montserrat. J. Volcanol. Geotherm. Res. 2006, 153, 51–63. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
- Goldstein, R.M. Atmospheric Limitations to repeat-track radar interferometry. Geophys. Res. Lett. 1995, 22, 2517–2520. [Google Scholar] [CrossRef]
- Zebker, H.; Rosen, P.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Jung, J.; Kim, D.; Park, S.-E. Correction of Atmospheric Phase Screen in Time Series InSAR using WRF Model for Monitoring Volcanic Activities. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2678–2689. [Google Scholar] [CrossRef]
- Foster, J.; Brooks, B.; Cherubini, T.; Shacat, C.; Businger, S.; Werner, C. Mitigating atmospheric noise for InSAR using a high resolution weather model. Geophys. Res. Lett. 2006, 33, L16304. [Google Scholar] [CrossRef]
- Pichelli, E.; Ferretti, R.; Cimini, D.; Perissin, D.; Montopoli, M.; Marzano, F.S.; Pierdicca, N. Water vapour distribution at urban scale using high-resolution numerical weather model and spaceborne SAR interferometric data. Nat. Hazard Earth Sys. Sci. 2010, 10, 121–132. [Google Scholar] [CrossRef]
- Ulmer, F.-G.; Adam, N. A Synergy Method to Improve Ensemble Weather Predictions and Differential SAR Interferograms. ISPRS J. Photogramm. Remote Sens. 2015, 109, 98–107. [Google Scholar] [CrossRef]
- Ulmer, F.-G.; Adam, N. Characterisation and improvement of the structure function estimation for application in PSI. ISPRS J. Photogramm. Remote Sens. 2017, 128, 40–46. [Google Scholar] [CrossRef]
- Bonforte, A.; Ferretti, A.; Prati, C.; Puglisi, G.; Rocca, F. Calibration of atmospheric effects on SAR interferograms by GPS and local atmosphere models: First results. J. Atmos. Sol. Terr. Phys. 2001, 63, 1343–1357. [Google Scholar] [CrossRef]
- Wadge, G.; Webley, P.W.; James, I.N.; Bingley, R.; Dodson, A.; Waugh, S.; Veneboer, T.; Puglisi, G.; Mattia, M.; Baker, D.; et al. Atmospheric models, GPS and InSAR measurements of the tropospheric water vapour field over Mount Etna. Geophys. Res. Lett. 2002, 29, 1905. [Google Scholar] [CrossRef]
- Rosen, P.A.; Henley, S.; Zebker, H.A.; Webb, F.H.; Fielding, E.J. Surface deformation and coherence measurements of Kilauea volcano, Hawaii, from SIR-C radar interferometry. J. Geophys. Res. 1996, 101, 23109–23125. [Google Scholar] [CrossRef]
- Wadge, G.; Mattioli, G.S.; Herd, R.A. Ground deformation at Soufrière Hills Volcano, Montserrat during 1998–2000 measured by radar interferometry and GPS. J. Volcanol. Geotherm. Res. 2006, 152, 157–173. [Google Scholar] [CrossRef]
- González, P.J.; Bagnardi, M.; Hooper, A.J.; Larsen, Y.; Marinkovic, P.; Samsonov, S.V.; Wright, T.J. The 2014–2015 eruption of Fogo volcano: Geodetic modeling of Sentinel-1 TOPS interferometry. Geophys. Res. Lett. 2015, 42, 9239–9246. [Google Scholar] [CrossRef]
- Wadge, G.; Costa, A.; Pascal, K.; Werner, C.; Webb, T. The variability of refractivity in the atmospheric boundary layer of a tropical island volcano measured by ground-based interferometric radar. Boundary-Layer Meteorol. 2016, 161, 309–333. [Google Scholar] [CrossRef]
- Saastamoinen, J. Introduction to practical computation of astronomical refraction. B. Géod. 1972, 106, 383–397. [Google Scholar] [CrossRef]
- Hanssen, R.F.; Weckwerth, T.M.; Zebker, H.A.; Klees, R. High-resolution water vapour mapping from interferometric radar measurements. Science 1999, 283, 1295–1297. [Google Scholar] [CrossRef]
- Mateus, P.; Nico, G.; Catalão, J. Can spaceborne SAR interferometry be used to study the temporal evolution of PWV? Atmos. Res. 2013, 119, 70–80. [Google Scholar] [CrossRef]
- Burton, M.R.; Oppenheimer, C.; Horrocks, L.; Francis, P.W. Remote sensing of CO2 and H2O emission rates from Masaya volcano, Nicaragua. Geology 2000, 28, 915–918. [Google Scholar] [CrossRef]
- Fiorani, L.; Colao, F.; Palucci, A.; Poreh, D.; Aiuppa, A.; Giudice, G. First-time lidar measurement of water vapor flux in a volcanic plume. Opt. Commun. 2011, 284, 1295–1298. [Google Scholar] [CrossRef]
- Bryan, S.; Clarke, A.; Vanderkluysen, L.; Groppi, C.; Paine, S.; Bliss, D.W.; Aberle, J.; Mauskopf, P. Measuring Water Vapor and Ash in Volcanic Eruptions With a Millimeter-Wave Radar/Imager. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3177–3185. [Google Scholar] [CrossRef]
- Kern, C. The Difficulty of Measuring the Absorption of Scattered Sunlight by H2O and CO2 in Volcanic Plumes: A Comment on Pering et al. “A Novel and Inexpensive Method for Measuring Volcanic Plume Water Fluxes at High Temporal Resolution,” Remote Sensing 2017, 9, 146. Remote Sens. 2017, 9, 534. [Google Scholar] [CrossRef]
- Kern, C.; Masias, P.; Apaza, F.; Reath, K.A.; Platt, U. Remote measurement of high preeruptive water vapor emissions at Sabancaya volcano by passive differential optical absorption spectroscopy. J. Geophys. Res. Solid Earth 2017, 122, 3540–3564. [Google Scholar] [CrossRef]
- Gardeweg, M.C.; Sparks, R.S.J.; Matthews, S.J. Evolution of Lascar Volcano, northern Chile. J. Geol. Soc. 1998, 155, 89–104. [Google Scholar] [CrossRef]
- Matthews, S.J.; Sparks, R.S.J.; Gardeweg, M.C. The Piedras Grandes–Soncor eruptions, Lascar volcano, Chile; evolution of a zoned magma chamber in the central Andean upper crust. J. Petrol. 1999, 40, 1891–1919. [Google Scholar] [CrossRef]
- Tamburello, G.; Hansteen, T.H.; Bredemeyer, S.; Aiuppa, A.; Tassi, F. Gas emissions from five volcanoes in northern Chile, and implications for the volatiles budget of the Central Volcanic Zone. Geophys. Res. Lett. 2014, 41, 4961–4969. [Google Scholar] [CrossRef]
- Marín, J.C.; Pozo, D.; Mlawer, E.; Turner, D.D.; Curé, M. Dynamics of Local Circulations in Mountainous Terrain during the RHUBC-II Project. Mon. Weather Rev. 2013, 141, 3641–3656. [Google Scholar] [CrossRef]
- Giovanelli, R.; Darling, J.; Henderson, C.; Hoffman, W.; Barry, D.; Cordes, J.; Eikenberry, S.; Gull, G.; Keller, L.; Smith, J.D.; et al. The optical-infrared astronomical quality of high Atacama sites. II—Infrared characteristics. Publ. Astron. Soc. Pac. 2001, 113. [Google Scholar] [CrossRef]
- Matthews, S.J.; Jones, A.P.; Gardeweg, M.C. Lascar Volcano, northern Chile; evidence for steady-state disequilibrium. J. Petrol. 1994, 35, 401–432. [Google Scholar] [CrossRef]
- De Zeeuw-van Dalfsen, E.; Richter, N.; González, G.; Walter, T.R. Geomorphology and structural development of the nested summit crater of Láscar Volcano studied with Terrestrial Laser Scanner data and analogue modelling. J. Volcanol. Geotherm. Res. 2017, 329, 1–12. [Google Scholar] [CrossRef]
- Matthews, S.J.; Gardeweg, M.C.; Sparks, R.S.J. The 1984 to 1996 cyclic activity of Lascar Volcano, Northern Chile; cycles of dome growth, dome subsidence, degassing and explosive eruptions. Bull. Volcanol. 1997, 59, 72–82. [Google Scholar] [CrossRef]
- Pavez, A.; Remy, D.; Bonvalot, S.; Diament, M.; Gabalda, G.; Froger, J.L.; Julien, P.; Legrand, D.; Moisset, D. Insight into ground deformations at Lascar volcano (Chile) from SAR interferometry, photogrammetry and GPS data: Implications on volcano dynamics and future space monitoring. Remote Sens. Environ. 2006, 100, 307–320. [Google Scholar] [CrossRef]
- Richter, N.; Salzer, J.T.; de Zeeuw-van Dalfsen, E.; Perissin, D.; Walter, T.R. Constraints on the geomorphological evolution of the nested summit craters of Láscar Volcano from high spatio-temporal resolution TerraSAR-X interferometry. Bull. Volcanol. 2018, 80. [Google Scholar] [CrossRef]
- Tassi, F.; Aguilera, F.; Vaselli, O.; Medina, E.; Tedesco, D.; Huertas, A.D.; Poreda, R.; Kojima, S. The magmatic- and hydrothermal-dominated fumarolic system at the active crater of Lascar volcano, northern Chile. Bull. Volcanol. 2009, 71, 171–183. [Google Scholar] [CrossRef]
- Menard, G.; Moune, S.; Vlastélic, I.; Aguilera, F.; Valade, S.; Bontemps, M.; González, R. Gas and aerosol emissions from Lascar volcano (Northern Chile): Insights into the origin of gases and their links with the volcanic activity. J. Volcanol. Geotherm. Res. 2014, 287, 51–67. [Google Scholar] [CrossRef]
- González, C.; Inostroza, M.; Aguilera, F.; González, R.; Viramonte, J.; Menzies, A. Heat and mass flux measurements using Landsat images from the 2000-2004 period, Lascar volcano, northern Chile. J. Volcanol. Geotherm. Res. 2015, 301, 277–292. [Google Scholar] [CrossRef]
- Glaze, L.S.; Francis, P.W.; Rothery, D.A. Measuring thermal budgets of active volcanoes by satellite remote sensing. Nature 1989, 338, 144–146. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Francis, P.W.; Rothery, D.A.; Carlton, R.W.; Glaze, L.S. Infrared image analysis of volcanic thermal features: Lascar Volcano, Chile, 1984–1992. J. Geophys. Res. Solid Earth 1993, 98, 4269–4286. [Google Scholar] [CrossRef]
- Wooster, M.J.; Rothery, D.A. Thermal monitoring of Lascar Volcano, Chile, using infrared data from the along-track scanning radiometer: A 1992–1995 time series. Bull. Volcanol. 1997, 58, 566–579. [Google Scholar] [CrossRef]
- Wooster, M.J. Long-term infrared surveillance of Lascar Volcano: Contrasting activity cycles and cooling pyroclastics. Geophys. Res. Lett. 2001, 28, 847–850. [Google Scholar] [CrossRef]
- Murphy, S.W.; Wright, R.; Oppenheimer, C.; Souza Filho, C.R. MODIS and ASTER synergy for characterizing thermal volcanic activity. Remote Sens. Environ. 2013, 131, 195–205. [Google Scholar] [CrossRef]
- Galle, B.; Johansson, M.; Rivera, C.; Zhang, Y.; Kihlman, M.; Kern, C.; Lehmann, T.; Platt, U.; Arellano, S.; Hidalgo, S. Network for Observation of Volcanic and Atmospheric Change (NOVAC)—A global network for volcanic gas monitoring: Network layout and instrument description. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Platt, U.; Stutz, J. Differential Optical Absorption Spectroscopy—Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Vandaele, A.C.; Simon, P.C.; Guilmot, J.M.; Carleer, M.; Colin, R. SO2 absorption cross section measurement in the UV using a Fourier transform spectrometer. J. Geophys. Res. Atmos. 1994, 99, 25599–25605. [Google Scholar] [CrossRef]
- Voigt, S.; Orphal, J.; Bogumil, K.; Burrows, J.P. The temperature dependence (203–293K) of the absorption cross sections of O3 in the 230–850 nm region measured by Fourier-transform spectroscopy. J. Photoch. Photobiol. A Chem. 2001, 143, 1–9. [Google Scholar] [CrossRef]
- Solomon, S.; Schmeltekopf, A.L.; Sanders, R.W. On the interpretation of zenith sky absorption measurements. J. Geophys. Res. Atmos. 1987, 92, 8311–8319. [Google Scholar] [CrossRef]
- Kurucz, R.L.; Furenlid, I.; Brault, J.; Testerman, L. Solar Flux Atlas from 296 to 1300 nm; National Solar Observatory: Sunspot, NM, USA, 1984; 240p. [Google Scholar]
- Aiuppa, A.; Moretti, R.; Federico, C.; Giudice, G.; Gurrieri, S.; Liuzzo, M.; Papale, P.; Shinohara, H.; Valenza, M. Forecasting Etna eruptions by real-time observation of volcanic gas composition. Geology 2007, 35, 1115–1118. [Google Scholar] [CrossRef]
- Shinohara, H.; Aiuppa, A.; Guidice, G.; Gurrieri, S.; Liuzzo, M. Variation of H2O/CO2 and CO2/SO2 ratios of volcanic gases discharged by continuous degassing of Mount Etna volcano, Italy. J. Geophys. Res. Solid Earth 2008, 113, B09203. [Google Scholar] [CrossRef]
- Aiuppa, A.; Bertagnini, A.; Métrich, N.; Moretti, R.; Di Muro, A.; Liuzzo, M.; Tamburello, G. A model of degassing for Stromboli volcano. Earth Planet. Sci. Lett. 2010, 295, 195–204. [Google Scholar] [CrossRef]
- Matsushima, N.; Shinohara, H. Visible and invisible volcanic plumes. Geophys. Res. Lett. 2006, 33, L24309. [Google Scholar] [CrossRef]
- Ebmeier, S.K.; Sayer, A.M.; Grainger, R.G.; Mather, T.A.; Carboni, E. Systematic satellite observations of the impact of aerosols from passive volcanic degassing on local cloud properties. Atmos. Chem. Phys. 2014, 14, 10601–10618. [Google Scholar] [CrossRef]
- Eineder, M.; Adam, N. A flexible system for the generation of interferometric SAR products. In Proceedings of the International Geoscience and Remote Sensing Symposium IGARSS’97. Remote Sensing—A Scientific Vision for Sustainable Development, Singapore, 3–8 August 1997. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapour using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Ulmer, F.-G. On the accuracy gain of electromagnetic wave delay predictions derived by the digital filter initialization technique. J. Appl. Remote Sens. 2016, 10, 016007:1–016007:7. [Google Scholar] [CrossRef]
- Ulmer, F.-G. Cinderella: Method Generalisation of the Elimination Process to Filter Repeating Patterns. In Proceedings of the 2015 IEEE International Conference on Digital Signal Processing (DSP), Singapore, 21–24 July 2015. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Baraniuk, R.G.; Kingsbury, N.C. The dual-tree complex wavelet transform. IEEE Signal Process. Mag. 2005, 22, 123–151. [Google Scholar] [CrossRef]
- Fattahi, H.; Amelung, F. DEM error correction in InSAR time series. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4249–4259. [Google Scholar] [CrossRef]
- Smith, E.K.; Weintraub, S. The Constants in the Equation for Atmospheric Refractive Index at Radio Frequencies. Proc. IRE 1953, 41, 1035–1037. [Google Scholar] [CrossRef]
- Oppenheimer, C.; Fischer, T.P.; Scaillet, B. Volcanic degassing: Process and impact. In Treatise on Geochemistry, 2nd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2014; Volume 4, pp. 111–179. [Google Scholar] [CrossRef]
- Battaglia, M.; Troise, C.; Obrizzo, F.; Pingue, F.; De Natale, G. Evidence for fluid migration as the source of deformation at Campi Flegrei caldera (Italy). Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Tiampo, K.F.; Camacho, A.G.; Fernández, J.; González, P.J. Spatiotemporal analysis and interpretation of 1993–2013 ground deformation at Campi Flegrei, Italy, observed by advanced DInSAR. Geophys. Res. Lett. 2014, 41, 6101–6108. [Google Scholar] [CrossRef]
- Ruch, J.; Manconi, A.; Zeni, G.; Solaro, G.; Pepe, A.; Shirzaei, M.; Walter, T.R.; Lanari, R. Stress transfer in the Lazufre volcanic area, central Andes. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Werner, C.; Hurst, T.; Scott, B.; Sherburn, S.; Christenson, B.W.; Britten, K.; Cole-Barker, J.; Mullan, B. Variability of passive gas emissions, seismicity, and deformation during crater lake growth at White Island Volcano, New Zealand, 2002–2006. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Chiodini, G.; Caliro, S.; De Martino, P.; Avino, R.; Gherardi, F. Early signals of new volcanic unrest at Campi Flegrei caldera? Insights from geochemical data and physical simulations. Geology 2012, 40, 943–946. [Google Scholar] [CrossRef]
- Dinger, F.; Bobrowski, N.; Warnach, S.; Bredemeyer, S.; Hidalgo, S.; Arellano, S.; Galle, B.; Platt, U.; Wagner, T. Periodicity in the BrO/SO2 molar ratios in the volcanic gas plume of Cotopaxi and its correlation with the Earth tides during the eruption in 2015. Solid Earth Discuss. 2018, 1–28. [Google Scholar] [CrossRef]
- Fujiwara, S.; Rosen, P.A.; Tobita, M.; Murakami, M. Crustal deformation measurements using repeat-pass JERS 1 synthetic aperture radar interferometry near the Izu Peninsula, Japan. J. Geophys. Res. Solid Earth 1998, 103, 2411–2426. [Google Scholar] [CrossRef]
- Knospe, S.; Jonsson, S. Covariance estimation for dInSAR surface deformation measurements in the presence of anisotropic atmospheric noise. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2057–2065. [Google Scholar] [CrossRef]
- Aumento, F. Radon tides on an active volcanic island: Terceira, Azores. Geofís. Int. 2002, 41, 499–505. [Google Scholar]
- Bredemeyer, S.; Hansteen, T.H. Synchronous degassing patterns of the neighbouring volcanoes Llaima and Villarrica in south-central Chile: The influence of tidal forces. Int. J. Earth Sci. 2014, 103, 1999–2012. [Google Scholar] [CrossRef]
- Zimmer, M.; Walter, T.R.; Kujawa, C.; Gaete, A.; Franco-Marin, L. Thermal and gas dynamic investigations at Lastarria volcano, Northern Chile. The influence of precipitation and atmospheric pressure on the fumarole temperature and the gas velocity. J. Volcanol. Geotherm. Res. 2017, 346, 134–140. [Google Scholar] [CrossRef]
- NOAA Air Resources Laboratory: READY Archived Meteorology. Available online: https://ready.arl.noaa.gov/READYamet.php (accessed on 18 September 2018).
- Edmonds, M.; Herd, R.A.; Galle, B.; Oppenheimer, C.M. Automated, high time-resolution measurements of SO2 flux at Soufrière Hills Volcano, Montserrat. Bull. Volcanol. 2003, 65, 578–586. [Google Scholar] [CrossRef]
- Global Volcanism Program. Report on Lascar (Chile). In Bulletin of the Global Volcanism Network; Venzke, E., Ed.; Smithsonian Institution: Washington, DC, USA, 2015; Available online: https://volcano.si.edu/showreport.cfm?doi=10.5479/si.GVP.BGVN201506-355100 (accessed on 18 September 2018).
- Giovanelli, R. Optical seeing and infrared atmospheric transparency in the upper Atacama desert. Astronomical Site Evaluation in the Visible and Radio Range. In Astronomical Site Evaluation in the Visible and Radio Range. ASP Conference Proceedings, 266; Vernin, J., Benkhaldoun, Z., Muñoz-Tuñón, C., Eds.; Astronomical Society of the Pacific: San Francisco, CA, USA, 2002; p. 366. ISBN 1-58381-106-0. [Google Scholar]
- Vuille, M. Atmospheric circulation over the Bolivian Altiplano during dry and wet periods and extreme phases of the Southern Oscillation. Int. J. Climatol. 1999, 19, 1579–1600. [Google Scholar] [CrossRef]
- Messerli, B.; Grosjean, M.; Bonani, G.; Bürgi, A.; Geyh, M.A.; Graf, K.; Ramseyer, K.; Romero, H.; Schotterer, U.; Schreier, H.; Vuille, M. Climate change and natural resource dynamics of the Atacama Altiplano during the last 18,000 years: A preliminary synthesis. Mt. Res. Dev. 1993, 117–127. [Google Scholar] [CrossRef]
- Vuille, M.; Ammann, C. Regional snowfall patterns in the high, arid Andes. Clim. Chang. 1997, 36, 413–423. [Google Scholar] [CrossRef]
- Mori, T.; Mori, T.; Kazahaya, K.; Ohwada, M.; Hirabayashi, J.I.; Yoshikawa, S. Effect of UV scattering on SO2 emission rate measurements. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Symonds, R.B.; Gerlach, T.M.; Reed, M.H. Magmatic gas scrubbing: Implications for volcano monitoring. J. Volcanol. Geotherm. Res. 2001, 108, 303–341. [Google Scholar] [CrossRef]
- Rodríguez, L.A.; Watson, I.M.; Edmonds, M.; Ryan, G.; Hards, V.; Oppenheimer, C.M.; Bluth, G.J. SO2 loss rates in the plume emitted by Soufrière Hills volcano, Montserrat. J. Volcanol. Geotherm. Res. 2008, 173, 135–147. [Google Scholar] [CrossRef]
- Beirle, S.; Hörmann, C.; Penning de Vries, M.; Dörner, S.; Kern, C.; Wagner, T. Estimating the volcanic emission rate and atmospheric lifetime of SO2 from space: A case study for Kīlauea volcano, Hawaii. Atmos. Chem. Phys. 2014, 14, 8309–8322. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Trishchenko, A.P.; Tiampo, K.; González, P.J.; Zhang, Y.; Fernández, J. Removal of systematic seasonal atmospheric signal from interferometric synthetic aperture radar ground deformation time series. Geophys. Res. Lett. 2014, 41, 6123–6130. [Google Scholar] [CrossRef]
- Johansson, M.E.B. Application of passive DOAS for studies of megacity air pollution and volcanic gas emissions. Ph.D. Thesis, Chalmers University of Technology, Gothenburg, Sweden, 2009. [Google Scholar]
- Marquard, L.C.; Wagner, T.; Platt, U. Improved air mass factor concepts for scattered radiation differential optical absorption spectroscopy of atmospheric species. J. Geophys. Res. Atmos. 2000, 105, 1315–1327. [Google Scholar] [CrossRef]
- McClatchey, R.A.; Fenn, R.W.; Selby, J.A.; Volz, F.E.; Garing, J.S. Optical properties of the atmosphere (No. AFCRL-72-0497); Air Force Cambridge Research Laboratories, Hanscom AFB: Bedford, MA, USA, 1972. [Google Scholar]
- Wagner, T.; Beirle, S.; Grzegorski, M.; Platt, U. Global trends (1996–2003) of total column precipitable water observed by Global Ozone Monitoring Experiment (GOME) on ERS-2 and their relation to near-surface temperature. J. Geophys. Res. Atmos. 2006, 111, D12102. [Google Scholar] [CrossRef]
- Granger, R.J. An examination of the concept of potential evaporation. J. Hydrol. 1989, 111, 9–19. [Google Scholar] [CrossRef]
- Horrocks, L.A.; Oppenheimer, C.; Burton, M.R.; Duffell, H.J. Compositional variation in tropospheric volcanic gas plumes: Evidence from ground-based remote sensing. Geol. Soc. Lond. Spec. Pub. 2003, 213, 349–369. [Google Scholar] [CrossRef]
- Singh, V.P.; Xu, C.Y. Evaluation and generalization of 13 mass-transfer equations for determining free water evaporation. Hydrol. Process. 1997, 11, 311–323. [Google Scholar] [CrossRef]
- Dalton, J. Experimental essays on the constitution of mixed gases on the force of steam or vapor from water and other liquids in different temperatures, both in a Torricellian vacuum and in air; on evaporation and on the expansion of gases by heat. Mem. Lit. Philos. Soc. Manch. 1802, 5, 535–602. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil, and grass. P. Roy. Soc. Lond. 1948, A193, 120–146. [Google Scholar] [CrossRef]
- Van Bavel, C.H.M. Potential evaporation: The combination concept and its experimental verification. Water Resour. Res. 1996, 2, 455–467. [Google Scholar] [CrossRef]
- Tennekes, H. The logarithmic wind profile. J. Atmos. Sci. 1973, 30, 234–238. [Google Scholar] [CrossRef]
- Mason, P.J. The formation of areally-averaged roughness lengths. Q. J. Roy. Meteorol. Soc. 1988, 114, 399–420. [Google Scholar] [CrossRef]
- Magnus, G. Versuche über die Spannkräfte des Wasserdampfs. Ann. Phys. 1844, 137, 225–247. [Google Scholar] [CrossRef]
- Sonntag, D. Important new values of the physical constants of 1986, vapor pressure formulations based on the ITS-90, and psychrometer formulae. Z. Meteorol. 1990, 70, 340–344. [Google Scholar]
- Alduchov, O.A.; Eskridge, R.E. Improved Magnus form approximation of saturation vapor pressure. J. Appl. Meteorol. 1996, 35, 601–609. [Google Scholar] [CrossRef]
- Jones, F.E.; Harris, G.L. ITS-90 density of water formulation for volumetric standards calibration. J. Res. Natl. Inst. Stand. 1992, 97, 335–340. [Google Scholar] [CrossRef] [PubMed]
- Plate, E.J.; Quraishi, A.A. Modeling of Velocity Distributions Inside and Above Tall Crops. J. Appl. Meteorol. 1965, 4, 400–408. [Google Scholar] [CrossRef]
- Hansen, F.V. Surface Roughness Lengths (No. ARL-TR-61); Army Research Lab White Sands Missile Range NM: Adelphi, MD, USA, 1993; pp. 88002–85501. [Google Scholar]
- Garrison, J.D.; Adler, G.P. Estimation of precipitable water over the United States for application to the division of solar radiation into its direct and diffuse components. Sol. Energy 1990, 44, 225–241. [Google Scholar] [CrossRef]
- Nann, S.; Riordan, C. Solar spectral irradiance under clear and cloudy skies: Measurements and a semiempirical model. J. Appl. Meteorol. 1991, 30, 447–462. [Google Scholar] [CrossRef]




| Master Scene Date (yyyy-mm-dd) | Slave Scene Date (yyyy-mm-dd) | Spatial Baseline (m) | Temporal Baseline (Days) |
|---|---|---|---|
| Subset 01 | |||
| 2013-12-12 | 2013-11-20 | 11.8 | −22 |
| 2013-12-12 | 2013-12-01 | 6.2 | 11 |
| 2013-12-12 | 2014-02-05 | −0.5 | 55 |
| Subset 02 | |||
| 2013-10-18 | 2013-12-23 | 16.6 | 66 |
| 2013-10-18 | 2014-01-03 | −23.5 | 77 |
| 2013-10-18 | 2014-01-14 | 6 | 88 |
| 2013-10-18 | 2014-02-16 | −1.3 | 121 |
| Scene | Date (yyyy-mm-dd) | PWV (mm) | SWD (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Crater Rim Plume Center | Downwind Plume Center | Downwind Bulk Plume | Average Background Atmosphere | Crater rim Plume Center | Downwind Plume Center | Downwind Bulk Plume | Average Background Atmosphere | |||
| Subset 01 | ||||||||||
| Master | 2013-12-12 | 0.012 | 4.3 | 1.3 | 2.1 | 6.42 | 0.096 | 34.59 | 10.38 | 17.25 |
| Slave | 2013-11-20 | 0.011 | 9.4 | 2.4 | 1.0 | 6.58 | 0.089 | 77.01 | 20.16 | 8.46 |
| Slave | 2013-12-01 | 0.009 | 4.3 | 1.1 | 0.7 | 6.39 | 0.072 | 34.44 | 8.61 | 5.97 |
| Slave | 2014-02-05 | 0.010 | 0.8 | 0.2 | 4.3 | 6.41 | 0.084 | 6.43 | 1.76 | 34.85 |
| totals | 0.042 | 18.8 | 5.0 | 8.3 | 0.341 | 152.46 | 40.91 | 66.52 | ||
| Subset 02 | ||||||||||
| Master | 2013-10-18 | 0.007 | 2.2 | 0.7 | 0.7 | 6.51 | 0.059 | 17.98 | 5.51 | 5.31 |
| Slave | 2013-12-23 | 0.009 | 1.1 | 0.3 | 5.2 | 6.43 | 0.075 | 8.91 | 2.10 | 41.48 |
| Slave | 2014-01-03 | 0.013 | 1.8 | 0.5 | 3.0 | 6.38 | 0.101 | 14.15 | 3.64 | 23.96 |
| Slave | 2014-01-14 | 0.011 | 0.9 | 0.2 | 3.6 | 6.39 | 0.091 | 7.27 | 1.67 | 29.06 |
| Slave | 2014-02-16 | 0.015 | 4.9 | 1.1 | 1.7 | 6.44 | 0.121 | 39.30 | 9.11 | 13.78 |
| totals | 0.056 | 10.9 | 2.7 | 14.1 | 0.447 | 87.60 | 22.03 | 113.58 | ||
| Master Scene Date (yyyy-mm-dd) | Slave Scene Date (yyyy-mm-dd) | Gas plume Related Priors (dSWD) | Troposphere Related Priors | Topography Related Priors | ||||
|---|---|---|---|---|---|---|---|---|
| Crater Rim Plume Center (mm) | Downwind Bulk Plume (mm) | Relative Humidity (%) | Surface Temperature (K) | Surface Pressure (hPa) | Spatial Baseline (m) | Temporal Baseline (Days) | ||
| Subset 01 | ||||||||
| 2013-12-12 | 2013-11-20 | 0.007 | −9.78 | −0.05 | 4.60 | 0.96 | 11.8 | −22 |
| 2013-12-12 | 2013-12-01 | 0.024 | 1.77 | 18.09 | −3.32 | −1.49 | 6.2 | −11 |
| 2013-12-12 | 2014-02-05 | 0.013 | 8.62 | −37.95 | 0.05 | 0.02 | −0.5 | 55 |
| Subset 02 | ||||||||
| 2013-10-18 | 2013-12-23 | −0.016 | 3.40 | −48.55 | −4.57 | −0.19 | 16.6 | 66 |
| 2013-10-18 | 2014-01-03 | −0.042 | 1.87 | −17.55 | −3.05 | 1.85 | −23.5 | 77 |
| 2013-10-18 | 2014-01-14 | −0.032 | 3.84 | −29.09 | −4.35 | −1.09 | 6 | 88 |
| 2013-10-18 | 2014-02-16 | −0.062 | −3.60 | −9.42 | −2.73 | −0.45 | −1.3 | 121 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bredemeyer, S.; Ulmer, F.-G.; Hansteen, T.H.; Walter, T.R. Radar Path Delay Effects in Volcanic Gas Plumes: The Case of Láscar Volcano, Northern Chile. Remote Sens. 2018, 10, 1514. https://doi.org/10.3390/rs10101514
Bredemeyer S, Ulmer F-G, Hansteen TH, Walter TR. Radar Path Delay Effects in Volcanic Gas Plumes: The Case of Láscar Volcano, Northern Chile. Remote Sensing. 2018; 10(10):1514. https://doi.org/10.3390/rs10101514
Chicago/Turabian StyleBredemeyer, Stefan, Franz-Georg Ulmer, Thor H. Hansteen, and Thomas R. Walter. 2018. "Radar Path Delay Effects in Volcanic Gas Plumes: The Case of Láscar Volcano, Northern Chile" Remote Sensing 10, no. 10: 1514. https://doi.org/10.3390/rs10101514
APA StyleBredemeyer, S., Ulmer, F.-G., Hansteen, T. H., & Walter, T. R. (2018). Radar Path Delay Effects in Volcanic Gas Plumes: The Case of Láscar Volcano, Northern Chile. Remote Sensing, 10(10), 1514. https://doi.org/10.3390/rs10101514